High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth


25 Division Word Problems for Grades 3 to 5 With Tips On Supporting Students’ Progress
Steven Eastes
Division word problems are important in building proficiency in division. Division is one of the bedrocks of math alongside addition, subtraction and multiplication. Therefore, students must have a deep understanding of division, its function within arithmetic and word problems, and how to apply short division and long division successfully.
Division is the mathematical process of breaking a number up into equal parts and finding out how many equal parts you can have. It may be that you have a remainder following the division or you may have no remainder, just a whole number as your answer.
What are division word problems?
Division word problems are an extension of the arithmetic division method whereby they are word problems with division at the heart. Students are expected to use the division process to find a solution to the word problem.
Typically, word problems use a real-life or real-world scenario and students are expected to interpret what the word problem is asking and apply their division knowledge to find the answer.
Division can be introduced through grouping before advancing, in higher-grade math, to the formal long division method.
To help you with the division journey, we have put together a collection of division word problems which can be used for children between 3rd grade to 5th grade.
If you’re looking for more division word problems, explore the collection of division word problem worksheets for elementary school students.

Word Problems Grade 4 Fractions and Decimals
Download grade 4 fractions and decimals word problems to develop your students' reasoning and problem solving skills. Includes 11 questions and answers!
Division word problems in upper elementary
As children enter 3rd grade, they begin to develop their mental and written strategies for division.
Students begin to use their multiplication and times tables knowledge to assist them when solving division problems alongside their knowledge of the corresponding division and multiplication facts.
By the end of 3rd grade, students are expected to recall their multiplication and division facts for multiplication times tables up to 10 x 10. They should also use their knowledge of place value, and known and derived facts to assist with simple division such as dividing by 1 and halving.
Introducing partial quotients
Before learning the standard algorithm, also known as long division, students learn the partial quotients method. They practice their short division fluency to answer division word problems with whole number or integer answers, and those with a remainder.
Before entering 4th and 5th grade, students encounter division word problems and multi step problems . These use increasingly harder numbers, more than a single digit. Students move from simple division problems, such as:
‘If we have 30 students in our class and are divided into groups of 5, how many students will be in each group?’
‘If there are 56 books in our library and they are shared among 7 children, how many books would each child get?
Introducing standard algorithm division
4th grade students work towards dividing 4 digit numbers by a one digit number using partial quotients. They must interpret remainders in the correct context and present the remainder as a decimal or fraction.
Students should also be able to divide mentally and know how to divide by 10, 100 and 1,000 and how place value works alongside dividing a number so it is 10, 100 or 1,000 times smaller.
5th grade students are introduced to the standard algorithm, or long division method. By the end of 5th grade, students should be fluent in multiplication and division, and written strategies. They must be able to apply knowledge in fraction word problems .
In addition to the 4th grade requirements, 5th grade students are expected to consolidate these formal division methods before dividing a four digit number by a two digit number using the formal method of standard algorithm division.
Again, they should understand remainders within this and present them in the correct context.
This also flows into division word problems as children must read a multi-step problem and know how to interpret it, apply their divisional knowledge and solve the problem step-by-step.
The concept of multi-step problems builds up at each stage of your state math curriculum.
Why are word problems important for childrens’ understanding of division?
Word problems, alongside the use of concrete objects and visual representations, are important in helping children understand the complexities and possible abstract nature of division.
While children may understand that dividing results in a smaller answer, it is important to explore how division looks visually before providing them with word problem worksheets. This is the same when exploring arrays to support multiplication word problems .
Applying math to real life situations
Word problems are important because they provide a real-life context to help children understand division and where we encounter it in real life.
Allowing children to see how division is used in everyday situations, makes it more meaningful and relevant. In turn, this develops a deeper, more well—rounded understanding of the four operations.
Building problem solving skills
Word problems are vital to developing problem solving skills. First, students must read and understand the problem before identifying the relevant information within the contextual problem and apply their knowledge to find a solution.
This naturally builds critical thinking and a child’s reasoning ability, an important skill for any mathematician.
Developing mathematical language skills
Finally, the importance of moving from simple division word problems to more challenging ones enhances students’ vocabulary and language skills.
For children to develop an understanding of vocabularies such as digit divisors, quotient and remainders, they must first understand these key words and apply them to the process of division and communicate clearly what they are aiming to do.
Deepening understanding of the inverse relationship between division and multiplication
Division word problems solidify the connection between multiplication and division. Understanding these inverse operations and the ability to interchange the skills of multiplication and division will help make connections between different mathematical concepts and deepen students’ learning.
How to teach division word problem solving in elementary school.
Having taught the concept of division to students using concrete examples, for example, grouping or sharing counters and cubes, the next step is to advance to division word problems.
As with all word problems, students must carefully read the question and decipher what is asked. Do they need to add, subtract, multiply or divide? Are they solving a multi-step problem and need to do more than one step? They may decide what operation to use and then represent it visually.
Example of a division word problem
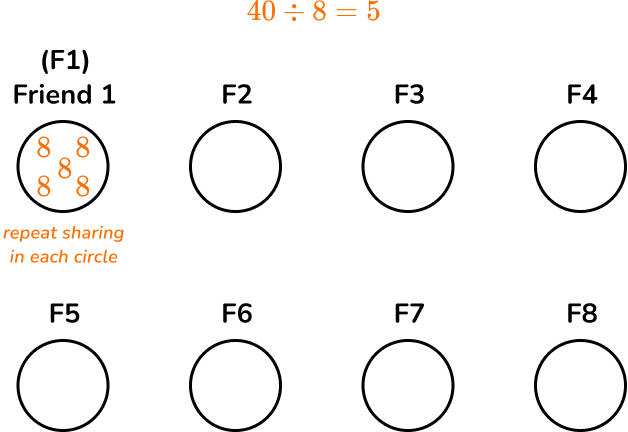
There are 40 pieces of candy ready to go in the party bags for Laura’s birthday. They are to be shared between 8 friends. How many pieces of candy will each child get?
How to solve this:
- First, we need to interpret the question. Laura has invited 8 friends to her party and she has 40 pieces of candy to share equally between her friends. So we know:
- There are 40 pieces of candy in total
- They are to be divided among 8 friends in total
- Students must divide the total number of candies by the number of friends
To solve this problem we could use the partial quotient method and divide the dividend by the the divisor which would be 40 / 8.
If we do this, we would get the quotient of 5. Each friend would get 5 pieces of candy each as 40 divided by 8 is 5.
Alternatively, we could use the inverse multiplication to solve this problem. We may not know the division fact that 40 divided by 8 = 5 but if we look to the inverse we may know what number multiplied by 8 equals 40. If we did our 8 times table we would get the answer of 5 – the correct answer.

How can we show this visually?
We could show 8 circles, each representing a child, and place a piece of candy in each circle until all 40 pieces of candy are placed equally in the circles. Each child should have 5 candies.
Students could also represent the division word problem as a bar model:
- Split the bar model into 8 sections
- Each section of the bar should have 5 pieces of candy
- Divide the 40 candies between the 8 sections
How these visual representations look:
Word problems are an important aspect of learning in Third Space Learning’s one-on-one tutoring programs.
Tutors work with students to break down word problems and identify the correct operation and strategy needed to solve the problem.
Examples of elementary division word problems
Below are examples of what can be expected in each grade with Third Space Learning’s tutoring programs from grades 3 to 5.
Students become familiar with word problems throughout their learning. They encounter word problems regularly throughout each personalized lesson.
Scaffolded and independent practice of word problems increases students’ confidence, familiarity with vocabulary and mathematical understanding.
3rd grade division word problems
Word problems for 3rd grade students, particularly division word problems, should encourage:
- Recall of their times table facts
- Division of two digit numbers by one digit numbers using mental and partial quotients
- Word problems may also involve multi-step problems
Question 1:
If a school has 90 students in 2nd grade and there are 3 classes in 2nd grade, how many students are in each class?
90 shared equally into 3 classes = 30 children per class
Question 2:
Every day a school gets a delivery of milk in a crate. There are 96 cartons of milk in the crate. If there are 8 milk cartons in a pack, how many packs will be in the crate?
96 divided by 12 = 8.
There are 8 cartons of milk in a pack.
Question 3:
A delivery of 96 footballs arrives at school for sports day. They are to be shared equally between 4 classes. How many footballs does each class get?
96 divided by 4 = 24 footballs per class
Question 4:
3rd grade is going to the beach on a school trip. If there are 100 children in 3rd grade and only 10 children can go on one mini bus, how many mini buses does Mr. Pearson need to book?
100 children divided 10 = 10 mini buses.
Question 5:
If you have 60 flowers and divide them into four flower pots, how many flowers are in each pot? Are there any left over?
Answer: 15 flowers in each pot.
If we divide 60 into 4 equal groups then we can use the partial quotient method.
When using the partial quotients method, students rely on what multiplication facts they can use.
Because we are dividing 60 by 4, we may ask ourselves, what number can I multiply 4 by, to get close to 60 without going over? Students should be familiar with their 10s time tables, and 4 x 10 = 40. We place the 10 above the quotient line, and then subtract 40 from 60, leaving 20 remaining.
We will now start the process all over again. What number can I multiply 4 by to get close to 20 without going over? We know that 4 x 5 = 20, so again, place 5 above the 10 in the quotient line and subtract 20 – 20. Because there is nothing left over, we are done dividing.
So the answer to 60 divided by 4 = 15.
This would look like:
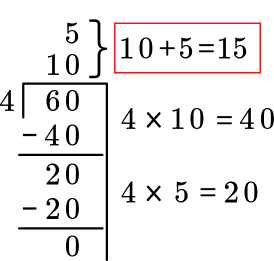
4th grade division word problems
Word problems for 4th grade center around dividing a 4 digit number by a 1 digit number using the partial products method or area model method of division. They will also be introduced to remainders and be expected to interpret remainders correctly depending on the context.
Ronan has a ball of string that is 819 cm long. He cuts it into 7 equal pieces. How long is 1 piece of string?
Answer: 117cm
819 divided by 7 = 117
In upper elementary there are 1,248 colored pencils. If there are 6 classes in upper elementary, how many pencils would each class receive?
Answer: 208
We use the division method to divide 1,248 by 6 and we get 208 as the result.
Mia buys three computer games for $84. How much is one computer game?
Answer: $28.
We divide $84.00 by 3 and we get $28.00.
The area of the school hall is 1,704m and needs to be split into four quadrants. What would be the area of each quadrant?
Answer: 426m
We take the total area of the school and divide it by 4 to represent each quadrant. In doing so, we would have 426m for each quadrant.
To check this is the correct answer, we could do the inverse and multiply 426 by 4 and we would get 1,704m.
Packets of candy are put into multi packs of 4. Today, 7,800 packets of candy were packed. How many boxes of candy were packed?
Answer: 163 boxes
We then have to take the total packets of candy– 7,800 – and divide this by 4. If we do this we will get the answer 1,950 boxes were packed.
5th grade division word problems
Word problems for 5th grade should prepare students for the end of elementary school. Students are familiar with the concept of standard algorithm division and dividing a 4 digit number by a 2 digit number using the formal method of standard algorithm division.
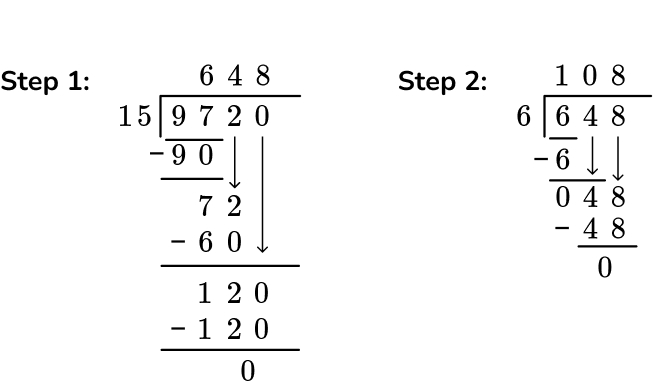
A school is selling tickets at $6 each to attend the Big Christmas Fair. Over 15 weeks it has earned an amazing $9,720! On average, how many tickets were sold each week?
Answer: 108 tickets per week
First, we need to use the formal method of standard algorithm division to divide the grand total – $9,720 by 15. If we do this correctly we will have the answer 648.
Then, we need to take this answer of 648, which is how much is earned each week, and then divide this by $6, the amount each ticket is.
This will result in the number of tickets sold each week – 108 tickets.
A square sports field has a perimeter of 2.696km. How long is each side of the field?
Answer: 674m
To answer this we need to be able to convert the 2.696km into meters. There are 1000 meters in a kilometer so that would be 2,696m. Then we divide this by 4 and get 674m for one side.
Keira is given a toy blocks kit containing 2,208 individual blocks. She wants to split the toy blocks evenly between 15 friends and herself to work on making a toy block city together. How many blocks should she give each of her friends?
Answer: 138 blocks
We need to use the formal method of standard algorithm division to solve this. We also need to ensure we include Keira and her 15 friends so we have the number 16 as the divisor.
When we divide 2,208 by 16 using long division we get the answer 138.
Wesleigh was running in the cross country race. He ran for a distance of 3,569m and it took him 11 minutes to complete the race. How many meters did he run per minute? Give your answer to the nearest whole meter.
Answer: 324 meters
We need to use standard algorithm division to divide 3,569 by 11. That will give us an answer of 324.45. As the decimal can be rounded down, the answer is 324 meters.
Sophia is preparing her candy stall for the fair. She can fit 18 tins of candy into one crate. How many crates will be needed to fit 153 tins of candy?
Answer: 9 crates
We divide 153 by 18 using standard algorithm division and we have an answer of 8, remainder 5. Therefore, having 8 crates would not be enough as we would have 85 tins left over and so we need a further tin to house the 5 tins left over. So, 9 crates are needed.
More word problems resources
Are you looking for more word problems resources? Take a look at our library of word problems practice questions including:
- Time word problems
- Ratio word problems
- Addition word problems
- Subtraction word problems
- 2nd grade word problems
Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?
The content in this article was originally written by former Deputy Headteacher Steven Eastes and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.
Related articles

25 Addition Word Problems For Grades 1-5 With Tips On Supporting Students’ Progress

What Is Box Method Multiplication? Explained For Elementary School Teachers, Parents And Pupils

20 Word Problems For 2nd Grade: Develop Their Problem Solving Skills Across Single and Mixed Topics

20 Multiplication Word Problems for 3rd to 5th Grades With Tips On Supporting Students’ Progress
Math Intervention Pack Operations and Algebraic Thinking [FREE]
Take a sneak peek behind our online tutoring with 6 intervention lessons designed by math experts while supporting your students with Operations and Algebraic Thinking.
As with our full library of lessons, each one includes questions to ask, ways to support students when they are stuck, and answers to the given questions.
Privacy Overview
Division Worksheets
Welcome to the division worksheets page at Math-Drills.com! Please give us your undivided attention while we introduce this page. Our worksheets for division help you to teach students the very important concept of division. If students have a good recall of multiplication facts, the division facts should be a breeze to teach. If you want your students to experience success in learning division, please make sure they know their multiplication facts to 81, how to multiply by 0 and how to multiply by 10. If they don't know these things, learning division will take a lot longer.
On this page you will find many Division Worksheets including division facts and long division with and without remainders. We start off with some division facts which are just the multiplication facts expressed in a different way. The main difference is that you can't divide by 0 and get a real number. If you really want your students to impress, say at their dinner table when their parents ask them what they learned today, you can teach them that division by zero is undefined.
The rest of the page is devoted to long division which for some reason is disliked among some members of the population. Long division is most difficult when students don't know their multiplication facts, so make sure they know them first! Oh, we already said that. What about a long division algorithm... maybe the one you or your parents or your grandparents learned? We adamantly say, yes! The reason that you and your ancestors used it is because it is an efficient and beautiful algorithm that will allow you to solve some of the most difficult division problems that even base ten blocks couldn't touch. It works equally well for decimals and whole numbers. Long division really isn't that hard.
Most Popular Division Worksheets this Week

Division Facts Tables

Like their counterparts on the multiplication facts page, these division facts tables can be used in a variety of ways to help students learn division facts. Students can memorize, look for patterns in the tables, compare them to multiplication tables, write answers on the versions with the answers omitted, or a variety of other learning activities. The tables come in gray, color and Montessori color depending on what fits you and your printer or school the best. For those that have already mastered the facts up to 12, they might be challenged to try the 13 to 24 versions.
- Division Facts Tables for Facts from 1 to 12 Division Facts Tables in Gray 1 to 12 Division Facts Tables in Gray 1 to 12 (Answers Omitted) Division Facts Tables in Color 1 to 12 Division Facts Tables in Color 1 to 12 (Answers Omitted) Division Facts Tables in Color 1 to 12 with Individual Facts Highlighted Division Facts Tables in Montessori Colors 1 to 12 Division Facts Tables in Montessori Colors 1 to 12 (Answers Omitted)
- Division Facts Tables for Facts from 13 to 24 Division Facts Tables in Gray 13 to 24 Division Facts Tables in Gray 13 to 24 (Answers Omitted) Division Facts Tables in Color 13 to 24 Division Facts Tables in Color 13 to 24 (Answers Omitted)
Division Facts up to the 7 Times Table

If your students aren't quite ready for all of the division facts at once, this might be a good place to start. Perhaps they are really good at the multiplying up to 5; there is a worksheet to help them practice, and when they are ready, they can include 6 then 7. This section includes vertical questions with the traditional division symbol (aka bracket) and some arranged with a division symbol like you might see addition, subtraction or multiplication arranged.
- Division Facts up to the 7 Times Table with a Long Division Symbol Vertical Division Facts Up To The 5 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 6 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 7 Times Table With Long Division Symbol/Bracket (50 per page) ✎
- Division Facts up to the 7 Times Table with a Division Sign Vertical Division Facts Dividends to 25 With Division Sign Vertical Division Facts Dividends to 36 With Division Sign Vertical Division Facts Dividends to 49 With Division Sign
More worksheets with division facts up to 7, but these ones are arranged horizontally. This is a more natural arrangement for students who are used to reading things from left to right, allows them to practice recalling the answers and it is possible to fit 100 of these questions on the page without it getting too cluttered. If clutter is a problem though, there are also 50 and 25 question options.
- Horizontally Arranged Division Facts up to the 5 Times Table Horizontally Arranged Division Facts with Dividends to 25 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 25 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 25 ( 25 Questions ; Large Print) ✎
- Horizontally Arranged Division Facts up to the 6 Times Table Horizontally Arranged Division Facts with Dividends to 36 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 36 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 36 ( 25 Questions ; Large Print) ✎
- Horizontally Arranged Division Facts up to the 7 Times Table Horizontally Arranged Division Facts with Dividends to 49 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 49 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 49 ( 25 Questions ; Large Print) ✎
Some students require chunking and more practice before they can handle the more complex pages with many different divisors. Here the worksheets only contain one divisor and there are several repetitions of the set on each page.
- Dividing by Individual Facts up to the 7 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 7 ( 50 Questions ) ✎
- Dividing by Groups of Individual Facts up to the 7 Times Table Vertically Arranged Dividing by 1, 2 and 5 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 7 ( 50 Questions ) ✎
More individual division facts worksheets but with a horizontal arrangement. This section includes 50 and 25 question options with each set repeated on the page.
- Horizontally Arranged Dividing by Individual Facts up to the 7 Times Table (50 Questions per Page) Horizontally Arranged Dividing by 1 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 7 ( 50 Questions ) ✎
- Horizontally Arranged Dividing by Individual Facts up to the 7 Times Table (25 Large Print Questions per Page) Horizontally Arranged Dividing by 1 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎
Division Facts up to the 9 Times Table

Manipulatives can help students "get" the concept of division. For example, students could regroup base ten blocks into units, then divide the units into piles. For the question 81 ÷ 9, students would start with eight ten blocks and one unit block. They would trade in the ten blocks for unit blocks and try to distribute all 81 of the unit blocks into nine piles. If they did it correctly, they would end up with 9 piles of 9 units and could say that 81 ÷ 9 = 9 as there are 9 units in each pile.
- Division Facts up to the 9 Times Table With a Long Division Symbol Vertical Division Facts Up To The 8 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 9 Times Table With Long Division Symbol/Bracket (50 per page) ✎
- Division Facts up to the 9 Times Table with a Division Sign Vertical Division Facts Dividends to 64 With Division Sign Vertical Division Facts Dividends to 81 With Division Sign Large Print Vertical Division Facts Dividends to 81 With Division Sign
If students learn up to the 9 times table and can do all the related division, they are likely to do well in later math studies. Long multiplication and long division, algebra, and many other math topics rely on students knowing these facts. Division facts worksheets up to the nine times tables can be used for students to practice, as a diagnostic test to see what gaps exist, or as a mastery test before moving on to the next topic. This section includes horizontally arranged questions which allows for a 100 per page option. Worksheets up to the 8 times table are also included to ensure a continual flow with the rest of this page, say, if you were adding one number at a time.
- Horizontally Arranged Division Facts up to the 8 Times Table Horizontally Arranged Division Facts with Dividends to 64 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 64 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 64 ( 25 Questions ; Large Print) ✎
- Horizontally Arranged Division Facts up to the 9 Times Table Horizontally Arranged Division Facts with Dividends to 81 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 81 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 81 ( 25 Questions ; Large Print) ✎
More individual facts where a single number is used as the divisor throughout the entire worksheet. The quotients end up being in the range 1 to 9. These are great for students that need more practice on one or more divisors. This might be identified using a diagnostic test of a worksheet that includes all the division facts. If students consistently get questions wrong with a certain divisor, these worksheets might help them.
- Dividing by Individual Facts up to the 9 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 8 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 9 with Quotients 1 to 9 ( 50 Questions ) ✎
- Dividing by Groups of Individual Facts up to the 9 Times Table Vertically Arranged Dividing by 1, 2 and 5 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7, 8 and 9 with Quotients 1 to 9 ( 50 Questions ) ✎
Same as the previous section except with horizontally arranged questions and more options for the number of questions per page.
- Horizontally Arranged Dividing by Individual Facts up to the 9 Times Table (100 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 9 ( 100 Questions ) ✎
- Horizontally Arranged Dividing by Individual Facts up to the 9 Times Table (50 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 9 ( 50 Questions ) ✎
- Horizontally Arranged Dividing by Individual Facts up to the 9 Times Table (25 Large Print Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎
Division Facts up to the 10 Times Table

Ten is such an important number in math. Our entire numbering system is based on tens. There are ten digits and each lower place is a tenth (divided by 10) of the place before it. Although 10 is a two-digit number, it is almost always included in multiplication and division facts learning. Multiplying and dividing by 10 is so important there is a whole page (powers of ten) on Math-Drills dedicated to it.
If you jumped right to this section, you cannot be blamed! A lot of students learn their times tables all at once and that means including the most important 10! So, when they are ready for division worksheets, they are ready for this section. For students who might be struggling a bit though, please scroll up and start them off with something a little more at their pace.
- Division Facts up to the 10 Times Table With a Long Division Symbol Vertical Division Facts Up To The 10 Times Table With Long Division Symbol/Bracket (50 per page) ✎
- Division Facts up to the 10 Times Table with a Division Sign Vertical Division Facts Dividends to 100 With Division Sign
Even with its size, 10 is often the easiest divisor to use... well, besides 1. This section includes horizontally arranged practice questions for all the division facts from the 1 times to the 10 times table.
- Horizontally Arranged Division Facts up to the 10 Times Table Horizontally Arranged Division Facts with Dividends to 100 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 100 ( 50 Questions ) ✎
The worksheets in this section are included for students that need the facts one at a time with quotients from 1 to 10.
- Dividing by Individual Facts up to the 10 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 8 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 9 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 10 with Quotients 1 to 10 ( 50 Questions ) ✎
- Dividing by Groups of Individual Facts up to the 10 Times Table Vertically Arranged Dividing by 1, 2, 5 and 10 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7, 8 and 9 with Quotients 1 to 10 ( 50 Questions ) ✎
A horizontal repeat of the previous section.
- Horizontally Arranged Dividing by Individual Facts up to the 10 Times Table (100 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 10 ( 100 Questions ) ✎
- Horizontally Arranged Dividing by Individual Facts with up to the 10 Times Table (50 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 10 ( 50 Questions ) ✎
- Horizontally Arranged Dividing by Individual Facts up to the 10 Times Table (25 Large Print Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎
Division Facts up to the 12 Times Table

Ah, twelve. Educators have a penchant for the the 12 times table likely because it is important in clocks, eggs, the Vendergood language, and definitely to the Dozenal Societies of America and Great Britain. In mathematics, it is seen mostly in the completion of both multiplication and division facts worksheets. Since Math-Drills is happy to support the base twelve system, we present worksheets with division facts up to the 12 times table in the unlikely event that the duodecimal (aka dozenal) system is ever adopted.
- Division Facts up to the 12 Times Table with a Long Division Symbol Vertical Division Facts Up To The 11 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 12 Times Table With Long Division Symbol/Bracket (50 per page) ✎
- Division Facts up to the 12 Times Table with a Division Sign Vertical Division Facts Dividends to 144 With Division Sign
Division is essentially asking the question, "How many _____'s are in _____?" For the question, 81 ÷ 9, the prompt would sound like, "How many 9's are in 81?" This prompt will benefit students in later math studies when there are more complex concepts such as dividing decimals or fractions. "How many thirds are in four?" or even better, "How many third cups are in four cups?" If necessary, get out the measuring cups.
This important section includes worksheets with division facts up to the 12 times table with a 100 question option.
- Horizontally Arranged Division Facts up to the 12 Times Table Horizontally Arranged Division Facts with Dividends to 144 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 144 ( 50 Questions ) ✎
So, if you are having your students learn division facts up to the 12 times table, it might be useful to have some worksheets with individual facts for a few students who might be overwhelmed with everything at once!
- Dividing by Individual Facts up to the 12 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 8 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 9 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 10 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 11 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 12 with Quotients 1 to 12 ( 50 Questions ) ✎
- Dividing by Groups of Individual Facts up to the 12 Times Table Vertically Arranged Dividing by 1, 2, 5 and 10 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7, 8 and 9 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 11 and 12 with Quotients 1 to 12 ( 50 Questions ) ✎
Same idea as the previous section, but with a horizontal arrangement and different numbers of questions on each page.
- Horizontally Arranged Dividing by Individual Facts up to the 12 Times Table (100 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 11 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 12 with Quotients 1 to 12 ( 100 Questions ) ✎
- Horizontally Arranged Dividing by Groups of Individual Facts up to the 12 Times Table (100 Questions) Horizontally Arranged Dividing by 1, 2, 5 and 10 (Quotient 1-12)
- Horizontally Arranged Dividing by Individual Facts up to the 12 Times Table (50 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 11 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 12 with Quotients 1 to 12 ( 50 Questions ) ✎
- Horizontally Arranged Dividing by Individual Facts up to the 12 Times Table (25 Large Print Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 11 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 12 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎
Division Facts beyond the 12 Times Table

Scenario: you have some students that have aced the division facts up to the 12 times table and need more of a challenge. This section has got you covered. Is there an argument for learning division facts for times tables beyond 9? 10? 12? Sure, why not. Students are likely to apply their knowledge in future math studies by instantly recognizing that the square root of 625 is 25, for example.
- Division Facts up to the 25 Times Table With a Long Division Symbol Vertical Division Facts Up To the 13 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 14 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 15 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 16 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 17 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 18 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 19 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 20 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 21 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 22 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 23 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 24 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 25 Times Table With Long Division Symbol/Bracket (50 per page) ✎
- Division Facts Up to the 15 Times Table With a Division Sign Vertical Division Facts Dividends to 169 With Division Sign Vertical Division Facts Dividends to 196 With Division Sign Vertical Division Facts Dividends to 225 With Division Sign
There are certainly a few questions on these worksheets that will be useful knowledge later on. If your students are interested in learning them, anything to do with 16, 20, 24, and 25 will certainly be useful, and likely someone could come up with a reason for learning the others. Sixteen is used in the base 16 (aka hexadecimal system), so converting hexadecimal numbers to decimal numbers involves dividing (and multiplying by 16). Twenty is a great number that is divisible by six different numbers and in turn is a factor of some important numbers. Twenty is also a coin unit in many countries. Twenty-four hours is the length of a day, so if you wanted to know how many days were in 288 hours, you might want to know your 24 times table division facts. Twenty-five, well that is the value of a quarter, isn't it? You could also calculate how many seconds of PAL video you have by dividing the number of frames by 25!
- Horizontally Arranged Division Facts up to the 20 Times Table Horizontally Arranged Division Facts Up to the 13 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 14 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 15 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 16 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 17 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 18 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 19 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 20 Times Table ( 100 Questions) ✎
If the previous two sections are a little tough to handle right out of the gates, perhaps start with these worksheets that only deal with one of the divisors at a time.
- Dividing by Individual Facts up to the 25 Times Table Vertically Arranged Dividing by 13 with Quotients 1 to 13 ( 50 Questions ) ✎ Vertically Arranged Dividing by 14 with Quotients 1 to 14 ( 50 Questions ) ✎ Vertically Arranged Dividing by 15 with Quotients 1 to 15 ( 50 Questions ) ✎ Vertically Arranged Dividing by 16 with Quotients 1 to 16 ( 50 Questions ) ✎ Vertically Arranged Dividing by 17 with Quotients 1 to 17 ( 50 Questions ) ✎ Vertically Arranged Dividing by 18 with Quotients 1 to 18 ( 50 Questions ) ✎ Vertically Arranged Dividing by 19 with Quotients 1 to 19 ( 50 Questions ) ✎ Vertically Arranged Dividing by 20 with Quotients 1 to 20 ( 50 Questions ) ✎ Vertically Arranged Dividing by 21 with Quotients 1 to 21 ( 50 Questions ) ✎ Vertically Arranged Dividing by 22 with Quotients 1 to 22 ( 50 Questions ) ✎ Vertically Arranged Dividing by 23 with Quotients 1 to 23 ( 50 Questions ) ✎ Vertically Arranged Dividing by 24 with Quotients 1 to 24 ( 50 Questions ) ✎ Vertically Arranged Dividing by 25 with Quotients 1 to 25 ( 50 Questions ) ✎
Even more of the previous section, but with 100 questions per page and a horizonal arrangement.
- Horizontally Arranged Dividing by Individual Facts up to the 25 Times Table Horizontally Arranged Dividing by 13 with Quotients 1 to 13 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 14 with Quotients 1 to 14 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 15 with Quotients 1 to 15 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 16 with Quotients 1 to 16 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 17 with Quotients 1 to 17 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 18 with Quotients 1 to 18 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 19 with Quotients 1 to 19 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 20 with Quotients 1 to 20 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 21 with Quotients 1 to 21 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 22 with Quotients 1 to 22 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 23 with Quotients 1 to 23 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 24 with Quotients 1 to 24 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 25 with Quotients 1 to 25 ( 100 Questions ) ✎
Long division Worksheets

Need an easier way to divide large numbers? Try this method using powers of ten. To successfully use this method, students need to be able to multiply by powers of ten and to subtract. Students subtract the dividend multiplied by decreasing powers of ten until they have zero or a remainder. Example: 1458 ÷ 54. Note 54 × 1 = 54, 54 × 10 = 540 (nothing greater is needed). 1458 - 540 - 540 = 378. Note that 540 was subtracted twice, so the number of times that 54 "goes into" 1458 so far is 20 times. Continuing, 378 - 54 - 54 - 54 - 54 - 54 - 54 - 54 = 0. Since 54 was subtracted seven times, the quotient increases by seven for a total of 27. In other words, 54 "goes into" 1458, 27 times.
We might also mention that this method can be even more sophisticated by using multiples of powers of ten. In the above example, using 54 × 5 = 270 would have helped to get to the quotient quicker.
- Long Division Worksheets with No Remainders Long Division with No Remainders with a Multiple of Ten Divisor and a 2-Digit Quotient Long Division with No Remainders with a 1-Digit Divisor and a 1-Digit Quotient Long Division with No Remainders with a 1-Digit Divisor and a 2-Digit Quotient Long Division with No Remainders with a 1-Digit Divisor and a 3-Digit Quotient Long Division with No Remainders with a 2-Digit Divisor and a 2-Digit Quotient Long Division with No Remainders with a 2-Digit Divisor and a 3-Digit Quotient Long Division with No Remainders with a 2-Digit Divisor and a 4-Digit Quotient Long Division with No Remainders with a 3-Digit Divisor and a 3-Digit Quotient Long Division with No Remainders with a 3-Digit Divisor and a 4-Digit Quotient Long Division with No Remainders with a 3-Digit Divisor and a 5-Digit Quotient
- European Format Long Division Worksheets with No Remainders European Format Long Division with No Remainders with a 1-Digit Divisor and a 1-Digit Quotient European Format Long Division with No Remainders with a 1-Digit Divisor and a 2-Digit Quotient European Format Long Division with No Remainders with a 1-Digit Divisor and a 3-Digit Quotient European Format Long Division with No Remainders with a 2-Digit Divisor and a 2-Digit Quotient European Format Long Division with No Remainders with a 2-Digit Divisor and a 3-Digit Quotient European Format Long Division with No Remainders with a 2-Digit Divisor and a 4-Digit Quotient European Format Long Division with No Remainders with a 3-Digit Divisor and a 2-Digit Quotient European Format Long Division with No Remainders with a 3-Digit Divisor and a 3-Digit Quotient European Format Long Division with No Remainders with a 3-Digit Divisor and a 4-Digit Quotient
Have you ever thought that you could help a student understand things better and get a more precise answer while still using remainders? It's quite easy really. Remainders are usually given out of context, including on the answer keys below. A remainder is really a numerator in a fractional quotient. For example 19 ÷ 3 is 6 with a remainder of 1 which is more precisely 6 1/3. Using fractional quotients means your students will always find the exact answer to all long division questions, and in many cases the answer will actually be more precise (e.g. compare 6 1/3 with 6.3333....).
- Long Division Worksheets with Remainders Long Division with Remainders with a Multiple of Ten Divisor and a 2-Digit Quotient Long Division with Remainders with a 1-Digit Divisor and a 2-Digit Dividend Long Division with Remainders with a 1-Digit Divisor and a 3-Digit Dividend Long Division with Remainders with a 1-Digit Divisor and a 4-Digit Dividend Long Division with Remainders with a 2-Digit Divisor and a 3-Digit Dividend Long Division with Remainders with a 2-Digit Divisor and a 4-Digit Dividend Long Division with Remainders with a 2-Digit Divisor and a 5-Digit Dividend Long Division with Remainders with a 3-Digit Divisor and a 4-Digit Dividend Long Division with Remainders with a 3-Digit Divisor and a 5-Digit Dividend Long Division with Remainders with a 3-Digit Divisor and a 6-Digit Dividend
- European Format Long Division Worksheets with Remainders European Format Long Division with Remainders with a 1-Digit Divisor and a 2-Digit Dividend European Format Long Division with Remainders with a 1-Digit Divisor and a 3-Digit Dividend European Format Long Division with Remainders with a 1-Digit Divisor and a 4-Digit Dividend European Format Long Division with Remainders with a 2-Digit Divisor and a 3-Digit Dividend European Format Long Division with Remainders with a 2-Digit Divisor and a 4-Digit Dividend European Format Long Division with Remainders with a 2-Digit Divisor and a 5-Digit Dividend European Format Long Division with Remainders with a 3-Digit Divisor and a 4-Digit Dividend European Format Long Division with Remainders with a 3-Digit Divisor and a 5-Digit Dividend European Format Long Division with Remainders with a 3-Digit Divisor and a 6-Digit Dividend
- Long Division Worksheets with Decimal Quotients Long Division with Decimal Quotients with a 1-Digit Divisor; 2-Digit Dividend Long Division with Decimal Quotients with a 1-Digit Divisor; 3-Digit Dividend Long Division with Decimal Quotients with a 1-Digit Divisor; 4-Digit Dividend Long Division with Decimal Quotients with a 2-Digit Divisor; 3-Digit Dividend Long Division with Decimal Quotients with a 2-Digit Divisor; 4-Digit Dividend Long Division with Decimal Quotients with a 2-Digit Divisor; 5-Digit Dividend Long Division with Decimal Quotients with a 3-Digit Divisor; 4-Digit Dividend Long Division with Decimal Quotients with a 3-Digit Divisor; 5-Digit Dividend Long Division with Decimal Quotients with a 3-Digit Divisor; 6-Digit Dividend
- European Format Long Division Worksheets with Decimal Quotients European Format Long Division with Decimal Quotients with a 1-Digit Divisor; 2-Digit Dividend European Format Long Division with Decimal Quotients with a 1-Digit Divisor; 3-Digit Dividend European Format Long Division with Decimal Quotients with a 2-Digit Divisor; 2-Digit Dividend European Format Long Division with Decimal Quotients with a 2-Digit Divisor; 3-Digit Dividend European Format Long Division with Decimal Quotients with a 2-Digit Divisor; 4-Digit Dividend European Format Long Division with Decimal Quotients with a 3-Digit Divisor; 3-Digit Dividend European Format Long Division with Decimal Quotients with a 3-Digit Divisor; 4-Digit Dividend European Format Long Division with Decimal Quotients with a 3-Digit Divisor; 5-Digit Dividend
We thought it might be helpful to include some long division worksheets with the steps shown. The answer keys for these division worksheets use the standard algorithm that you might learn if you went to an English speaking school. Learning this algorithm by itself is sometimes not enough as it may not lead to a good conceptual understanding. One tool that helps students learn the standard algorithm and develop an understanding of division is a set of base ten blocks. By teaching students division with base ten blocks first then progressing to the standard algorithm, students will gain a conceptual understanding plus have the use of an efficient algorithm for long division. Students who have both of these things will naturally experience more success in their future mathematical studies.
- Long Division with 1-Digit Divisors with the Steps Shown on the Answer Key 2-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 3-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 4-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 5-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 6-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key
- Long Division with 2-Digit Divisors with the Steps Shown on the Answer Key 3-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key 4-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key 5-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key 6-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key
- Long Division with 3-Digit Divisors with the Steps Shown on the Answer Key 4-Digit by 3-Digit Long Division with Remainders with the Steps Shown on the Answer Key 5-Digit by 3-Digit Long Division with Remainders with the Steps Shown on the Answer Key 6-Digit by 3-Digit Long Division with Remainders with the Steps Shown on the Answer Key
Some students find it difficult to get everything lined up when completing a long division algorithm, so these worksheets include a grid and wider spacing of the digits to help students get things in the right place. The answer keys include the typical steps that students would record while completing each problem; however, slight variations in implementation may occur. For example, some people don't bother with the subtraction signs,some might show steps subtracting zero, etc.
- Long Division Worksheets with Grid Assistance and Prompts (No Remainders) 2-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 3-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders
- Long Division Worksheets with Grid Assistance Only (No Remainders) 3-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders
- Long Division Worksheets with Grid Assistance and Prompts (Some Remainders) 2-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 3-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders
- Long Division Worksheets with Grid Assistance Only (Some Remainders) 3-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and some Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and some Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and some Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and some Remainders
Divisibility by 2, 5 and 10
A number is divisible by 2 if the final digit (the digit in the ones place) is even. Numbers ending in 0, 2, 4, 6, or 8 therefore are divisible by 2. A number is divisible by 5 if the final digit is a 0 or a 5. A number is divisible by 10 if the final digit is a 0.
Divisibility by 3, 6 and 9
A number is divisible by 3 if the sum of its digits is divisible by 3. For example, 285 is divisible by 3 because 2 + 8 + 5 = 15 is divisible by 3. A number is divisible by 6 if it is divisible by both 3 and 2 (see above rules). A number is divisible by 9 if the sum of its digits is divisible by 9. For examples, 285 is not divisible by 9 because 2 + 8 + 5 = 15 is not divisible by 9.
Divisibility by 4, 7 and 8
A number is divisible by 4 if the last two digits of the number are divisible by 4. For 7, there are a couple of strategies to use. Please see Divisibility Tricks for Learning Math for more information. A number is divisible by 8 if the last three digits are divisible by 8. This is the standard rule which can be a little sketchy for larger numbers, like who knows if 680 is divisible by 8? Because of this, we offer our Math-Drills.com solution which requires a little arithmetic, but can be accomplished quite easily with a little practice. As you know 8 is 2 to the third power, so we thought if you could divide the last three digits of a number by 2 three times, it would be divisible by 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. We have a winner! 680 is indeed divisible by 8.
- Divisibility Rules Worksheets with 2-Digit Numbers Divisibility of 2, 5 and 10 (2-digit) Divisibility of 3, 6 and 9 (2-digit) Divisibility of 4, 7 and 8 (2-digit) Divisibility of Numbers 2 to 10 (2-digit)
- Divisibility Rules Worksheets with 3-Digit Numbers Divisibility of 2, 5 and 10 (3-digit) Divisibility of 3, 6 and 9 (3-digit) Divisibility of 4, 7 and 8 (3-digit) Divisibility of Numbers 2 to 10 (3-digit)
- Divisibility Rules Worksheets with 4-Digit Numbers Divisibility of 2, 5 and 10 (4-digit) Divisibility of 3, 6 and 9 (4-digit) Divisibility of 4, 7 and 8 (4-digit) Divisibility of Numbers 2 to 10 (4-digit)
Dividing numbers in number systems other than decimal numbers including binary, quaternary, octal, duodecimal and hexadecimal numbers.
- Worksheets for Long Division in Other Base Number Systems Dividing Binary Numbers (Base 2) Dividing Ternary Numbers (Base 3) Dividing Quaternary Numbers (Base 4) Dividing Quinary Numbers (Base 5) Dividing Senary Numbers (Base 6) Dividing Octal Numbers (Base 8) Dividing Duodecimal Numbers (Base 12) Dividing Hexadecimal Numbers (Base 16) Dividing Vigesimal Numbers (Base 20) Dividing Hexatrigesimal Numbers (Base 36) Dividing Various Numbers (Various Bases)
Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.
Division in Math
Division is a math superpower that breaks down a whole — whether you’re cutting a pizza or divvying up some candy!

Author Christina Levandowski

Expert Reviewer Jill Padfield
Published: August 24, 2023

- Key takeaways
- Division is an opposite game – If you multiply numbers, you can “undo” them using division. It’s multiplication’s opposite function!
- There’s a few signs to look for – There are three main symbols for division.
- You won’t always get “even Stevens” – Sometimes, you’ll have a little left over. That leftover number is known as the “remainder.”
Table of contents
What is division?
Common symbols and terminology, properties of division, how to divide in 6 easy steps, what is long division, working with remainders.
- Let’s practice together!
Practice problems
Division is one of the most important math skills you’ll practice, helping you to undo multiplication problems or break off parts of a “whole.” We know it looks complicated, but it really isn’t! You just need to know what signs to look for that tell you when division is needed.
Like addition and subtraction, division uses a few special terms and symbols. Knowing these can help you to work out your problems quickly and correctly.
We know it sounds complicated right now — but with a little practice and this handy guide, you’ll be flying through your math homework in no time!
Division is a process in math that lets you break down a number into multiple, equal parts. Sometimes, you can cut everything down into whole number parts, and, sometimes, you’ll be left with a little leftover, giving you a decimal or fraction for an answer rather than a whole number.
You’ll often see division problems vertically, like this:

It can also be written horizontally: 10 ÷ 2, as 10/2 , or using a division bar: 2 ⟌ 10.
No matter how you see it, though, the use for it is always the same. You’re breaking down a number or quantity into smaller pieces.
Let’s take a look at some key terms that’ll help you build your division skills.
Division is a simple mathematical operation, but there are still a few terms to know to help you find the correct solution.
Here are the terms you need to know to solve division equations with ease:
➗ — This is known as a division sign, and it tells you that a number needs to be broken down into multiple pieces.
⟌ — This is the division bar, and it also means to divide. On the outside of the bar, you’ll see the number determining how many pieces are needed from the whole (the divisor), and the dividend on the inside, which is what you’ll be dividing. The answer goes on the top of the bar.
∕ — This is known as the division slash. Generally, the divisor comes first, and the dividend will appear second.
Important vocabulary
- Divisor – The divisor is the number that is determining how many pieces are needed from the whole. For example: in 15 ÷ 3, three would be the divisor. It’s also the number located outside of the bracket when you see a division bar.
- Dividend – The dividend is the number that’s being divided, and it’s found inside the division bar.
- Quotient – The quotient is your answer, which goes after the equals (=) sign or on the top of the division bar.
- Remainder – In some cases, you’ll have a remainder — which means that the divisor can’t be equally divided into the dividend. The remainder is written to the side of your equation next to the division bar.
Anytime you see the word “property” in math, know that it’s just a rule to remember as you work through your groups of problems. Here are some of the most important properties of division that you need to know:
- The Division By 1 Property: If a number is divided by 1, the quotient will always be the original number.
- The Division By Itself Property: If a number is divided by itself, the quotient will always be 1.
- The Division By 0 Property: If a number is divided by 0, it’s “undefined” and cannot be solved.
- The Division Of 0 By (Any) Number Property: If a 0 value is divided by any number, you’ll have 0 as your quotient.
Knowing these helpful properties can help you to do basic operations (like division) confidently. Remember — these are division facts, so these properties will always be true…no matter what problem you’re working to find the quotient to!
Now that you know the terms and properties of your division operation, it’s time to practice your skills. Let’s work the problem below together.

1. Prepare your equation
We know that the problem above can feel overwhelming — so we want to take this moment to remind you that what we’re doing is breaking down a number into smaller numbers (or smaller groups of numbers).
First things first, we have to prepare the equation. Feel free to keep it horizontal, write it vertically, or use a division bar if you’d like. Use whatever method you feel comfortable with.
Remember: The dividend (15) belongs inside the division bar if you choose to use that method.
2. Start with the first digit of the dividend from the left
As we begin to divide, we need to start from the first digit from the left (in this case, 1) and ask ourselves: Does the divisor (3) go into 1 at least once?
The answer here is “no,” so we will then evaluate the first AND second integer (making 15) as a dividend.
We ask again: Does the divisor (3) go into 15 at least once?
Now, the answer is “yes” — we just have to count how many times 3 can go into 15, starting our division process.*
*NOTE: You can do this by using basic arithmetic operations (such as multiplication) to “undo” the problem (i.e., 3 x ? = 15) or counting by threes until you reach 15.
In our case, 3 goes into 15 a total of five times.
3. Divide it by the divisor and write the answer on top as the quotient
Now that we know that 15 ÷ 3 = 5, it’s time to write it into our equation. Go ahead and write 5 behind the equals sign or standing tall at the top of your division bar.
4. Subtract the product of the divisor and the digit written in the quotient from the first digit of the dividend
Now, we have to check our work. We have to ask ourselves: What is 5 x 3? Does it equal our dividend? If it does, you’re golden — you’ve done it!
Do the multiplication, and then subtract your product to ensure that there’s no other steps remaining (like you’d see in the case of a remainder).
In our example, 15 – 15 = 0…so no remainder or further action is needed.
5. Bring down the next digit in the dividend (if possible)
In other problems, if you did have a three or four digit dividend, you might need to bring down the next digit in the dividend, and determine if your divisor divides that number cleanly.
You would then repeat the division process, putting your answer over the third or “next” place above the division bar as part of the quotient.
Next, yo would repeat step 4 to determine if more steps in the division process are needed.
In our example, we don’t have to do this, so we will leave it as is. Good work!
Congratulations! You just broke a large number down into equal, separate parts. It’s time to repeat the process for your other problems.
Long division is a form of division that’s used to break down larger numbers and will generally repeat steps 1-6 above at least three or more times.
We’ll work on that stuff later — for now, let’s just focus on mastering the basics!
What happens when you wind up with a little extra left over, you might ask? While it can look pretty scary, it’s simple to solve.
To do this, you’ll repeat steps one through five above until you get a number that cannot continue to be divided evenly. At this point, you’ll do a few additional steps:
- Determine how many times the divisor goes in to the product of your current answer and the divisor. This won’t be a clean number, and that’s OKAY — that’s what your remainder process is for.
- Complete the subtraction steps. After you get your number, complete the subtraction steps and write your answer below the subtraction bar.
- For example: In the case of 16 ➗ 3, we would write the quotient as: 5R1.
When you see that there’s zero left over, or if there is no way for the divisor to divide into the dividend, that means that your problem is solved!
Let’s practice together

- We ask: “How many times can 6 go into 2?”
- 6 is greater than 2, so we will not be able to put a number over the 2. We then consider, “How many times can 6 go into 20?”
- Well, this is a bit of a challenge! 6 does not go into 20 evenly. 6 x 3= 18, and 6 x 4= 24. So, 6 can go into 20 three times, but it won’t go evenly.
- So, we add the 3 over the 0, above the division bar.
- We put the product of 6 x 3 (our divisor x our quotient) under the dividend and subtract to determine if the a remainder in our difference.
- There is a remainder of 2. We write our quotient as: 3R2 .

- We know that our divisor is going to be 1, and our dividend (the number being divided) is 5. We identify them, and we put them properly into a division bar.
- We ask: “How many times can 1 go into 5?”
- Instead of working the problem counting or using multiplication, we remember the Division By 1 Property.
- We put 5 at the top of our division bar, since any integer that is divided by 1 will always be itself.
- There is no remainder for these types of Division By 1 Property problems. We can move on to the next problem.

- We know that our divisor is going to be 2, and our dividend (the number being divided) is 0. We identify them, and we put them properly into a division bar.
- We ask, “How many times can 2 go into 0?”
- Instead of working the problem counting or using multiplication, we remember the Division Of 0 By (Any) Number Property.
- We put 0 at the top of our division bar, since any integer that attempts to divide 0 as a dividend will always result in a quotient of zero.
- There is no remainder for these types of Division Of 0 By (Any) Number Property problems. We move on to the next problem.
Ready to give it a go?
You’ve done great so far — and you’re well on your way to mastering the art of division. Don’t be afraid to keep trying and make mistakes.
Practice makes perfect, so we’ve given you a few more problems to practice as you work to perfect your skills. Remember: You can always scroll up to walk through the tutorials and refresh yourself on the terms, placement, and properties you’ll need to solve these correctly.
By the end of this session, we’re confident that you’ll be ready to claim that A+ on your next math test. You can do it!
Click to reveal the answer.
The answer is 2 .

The answer is 1R6 .

The answer is 4 .

Parent Guide
The answer is 2.
How did we get here?
- We identify 4 as the dividend and 2 as the divisor, and place them in the division bar.
- We ask: “How many times can 2 go into 4?” We determine this using the “count by twos” method, which shows us that 2 goes into 4 a total of two times.
- We put 2 at the top of our division bar as the quotient, and multiply it by our divisor (2). We then subtract the product of our multiplication from the number to get an answer of 0, which shows us that there is no remainder. You’re done!
The answer is 1R6.
- We identify 8 as our divisor and 14 as our dividend, and place them in the division bar.
- We ask: “How many times can 8 go into 14?”, as 8 will not go into 1. We determine this using the “count by eights” method, which shows us that 8 goes into 14 just once.
- We write a 1 in the quotient place above the 4 under the division bar. We then multiply 1 x 8 to get a product of 8, which is placed below the 14 under the division bar.
- Now, we do the math and subtract 8 from 14. We’ll get 6 as our difference.
- We then write our quotient as 1R6.
The answer is 4.
How did we get here?
- We identify 5 as our divisor and 20 as our dividend, and place them in the division bar.
- We ask: “How many times can 5 go into 20,” as 5 will not go into 2 at all. We determine this using the “count by fives” method, which shows us that 5 can go into 20 cleanly four times.
- We place a “4” in our quotient place, and multiply 4 x 5 to get a product of 20. This is written under the division bar as a subtraction problem.
- We subtract 20 – 20, resulting in a difference of 0.
- This means that 4 is our final quotient with no remainder.
Sign up for the DoodleMath app today!
Turn math into an adventure when you sign up for DoodleMath.
Click here to get started for free!
FAQs about math strategies for kids
We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!
Division is the mathematical process that breaks down a big value into smaller values.
There are plenty of times you’ll use division in your everyday life. Some of the most common ways might be to break up an even quantity of something, determining how much of an ingredient to use, or grouping up items for use.
Division is the inverse of multiplication. This means that it naturally undoes any sort of operation that’s done with multiplication.
The three main parts of division are the divisor, dividend, and quotient.

Related Posts
Helpful description
Lesson credits
Christina Levandowski
Christina has written for hundreds of clients from small businesses to Indeed.com. She has extensive experience working with marketing strategy and social media marketing, and has her own business creating assets for clients in the space. She enjoys being an entrepreneur and has also started pursuing investment opportunities as time permits.

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

What we offer
Quick links
All rights reserved.

Are you a parent, teacher or student?
Get started for free!
Maths information pack
We ask for your contact info so we can send our info pack directly to your inbox for your convenience, exam prep information pack, case studies information pack.
Book a chat with our team

I’m new to Doodle

My school is already using Doodle

Information pack
We ask for your contact info so that our education consultants can get in touch with you and let you know a bit more about doodle., student login, which programme would you like to use.
DoodleMaths
DoodleTables
DoodleEnglish
DoodleSpell
If you’d like to use Doodle’s browser version, please visit this page on a desktop.
To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:

Number Sense
Understanding numbers, their relationships and numerical reasoning
Using symbols to solve equations and express patterns

Studying shapes, sizes and spatial relationships in mathematics

Measurement
Quantifying and comparing attributes like length, weight and volume
Performing mathematical operations like addition, subtraction, division

Probability and Statistics
Analyzing uncertainty and likelihood of events and outcomes
Calculator Suite
Exploring functions, solving equations, constructing geometric shapes
Graphing Calculator
Visualizing equations and functions with interactive graphs and plots
Exploring geometric concepts and constructions in a dynamic environment
3D Calculator
Graphing functions and performing calculations in 3D
Scientific Calculator
Performing calculations with fractions, statistics and exponential functions
Exploring apps bundle including free tools for geometry, spreadsheet and CAS
Learn and practice division skills and improve your understanding of dividing numbers and solving division problems with interactive resources from GeoGebra.
Upper Elementary
Division models.
Model division in a variety of ways including sharing equally, repeated subtraction, rectangular arrays, and the relationship with multiplication.
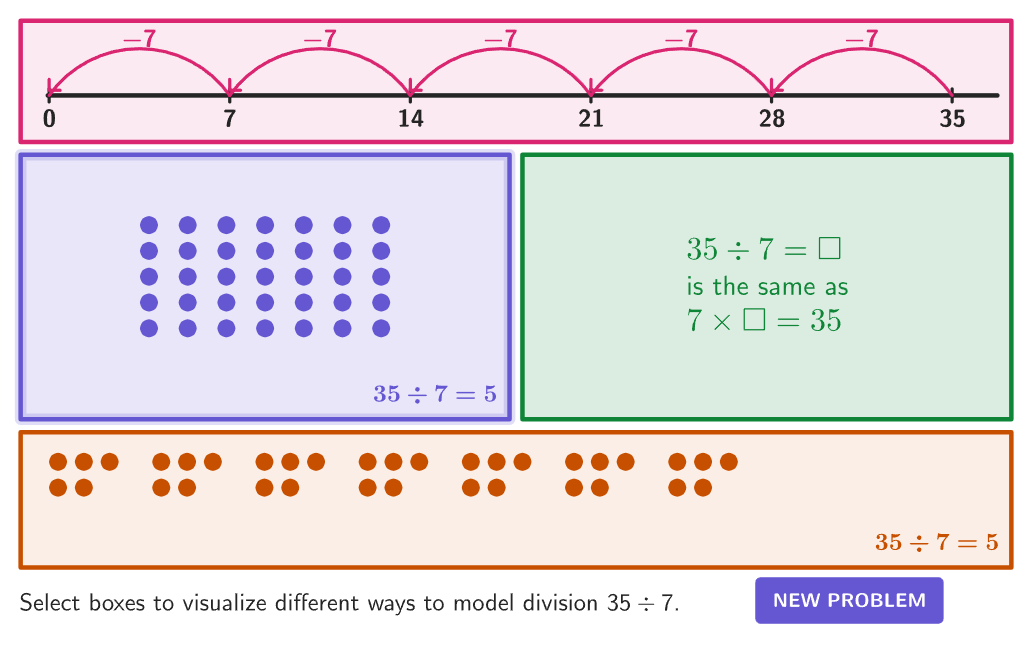
Exploration
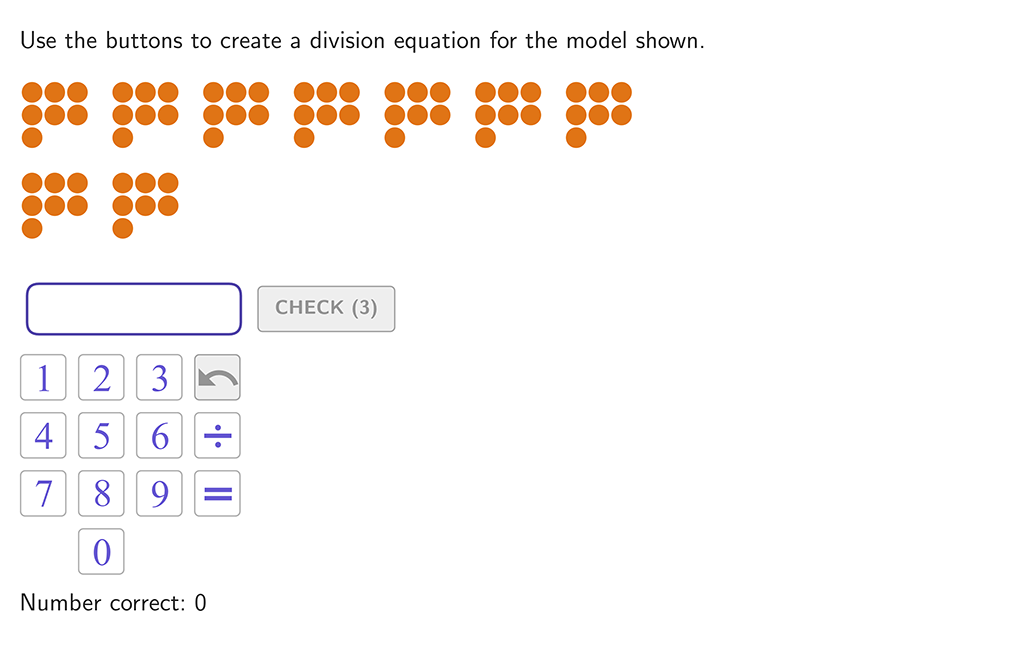
Creating Division Equations Using Visual Models
Estimating products and quotients.
Apply appropriate types of estimation for number and word problems that include estimating products and quotients.
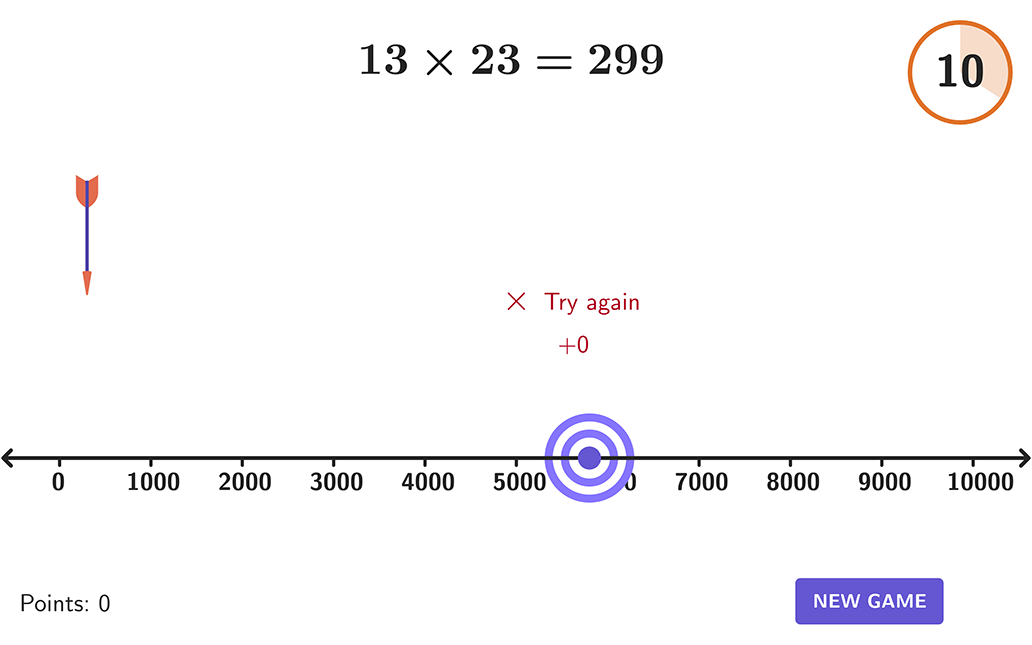
Multiplication and Division Estimation Game
Estimating quotients of whole numbers.
Estimate and solve division problems with multi-digit divisors; explain solution.
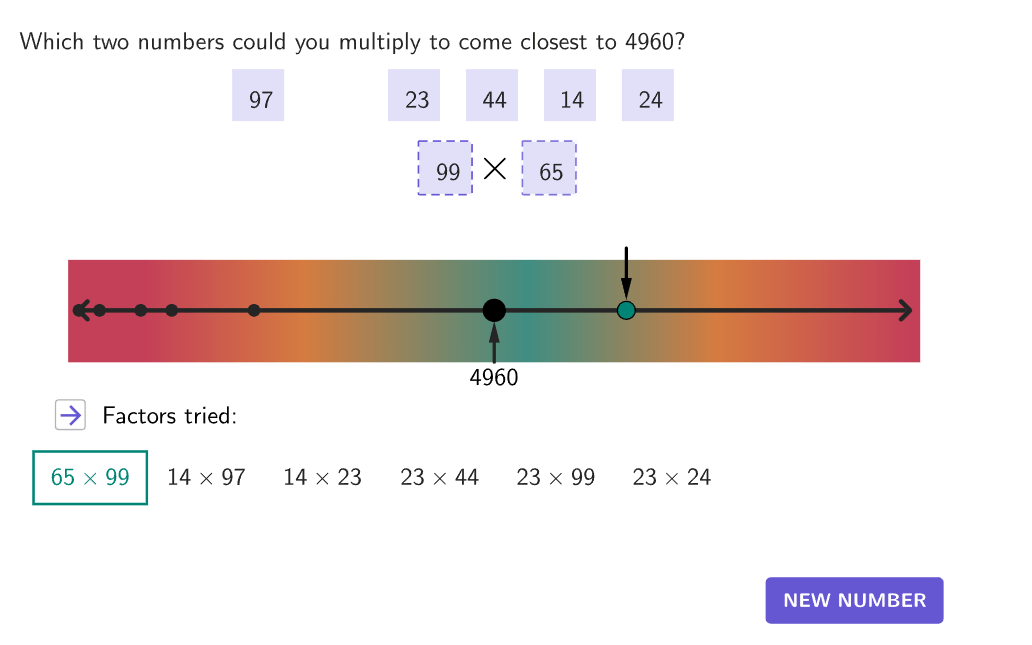
Estimating Products of 2-digit Numbers
Interpreting remainders.
Use remainders in problem-solving situations and interpret the remainder with respect to the original problem.
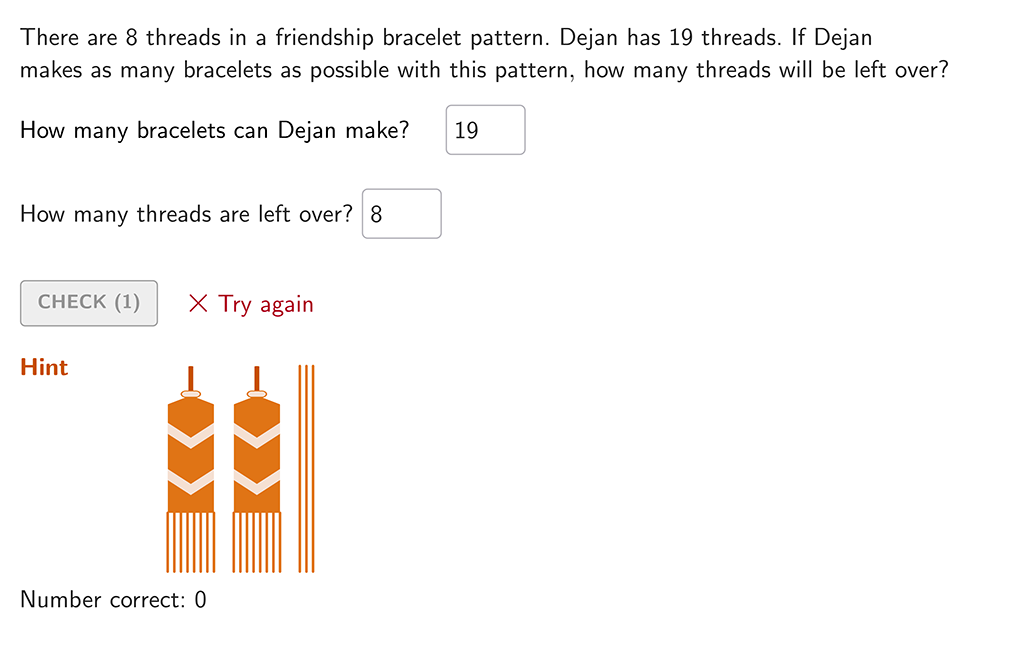
Division Problems with Remainders
Long division.
Divide using single-digit divisors with and without remainders.
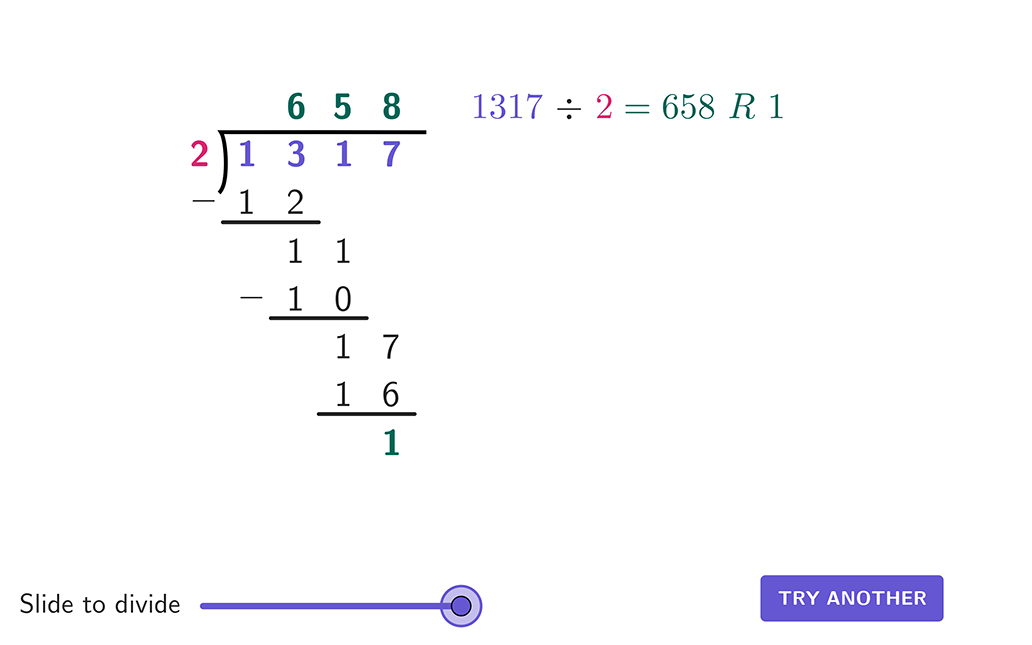
Long Division With One-Digit Divisors and Remainders

Division Using an Area Model
Multiplication and division sentences.
Write a multiplication or a division sentence to represent a number or word problem; solve.
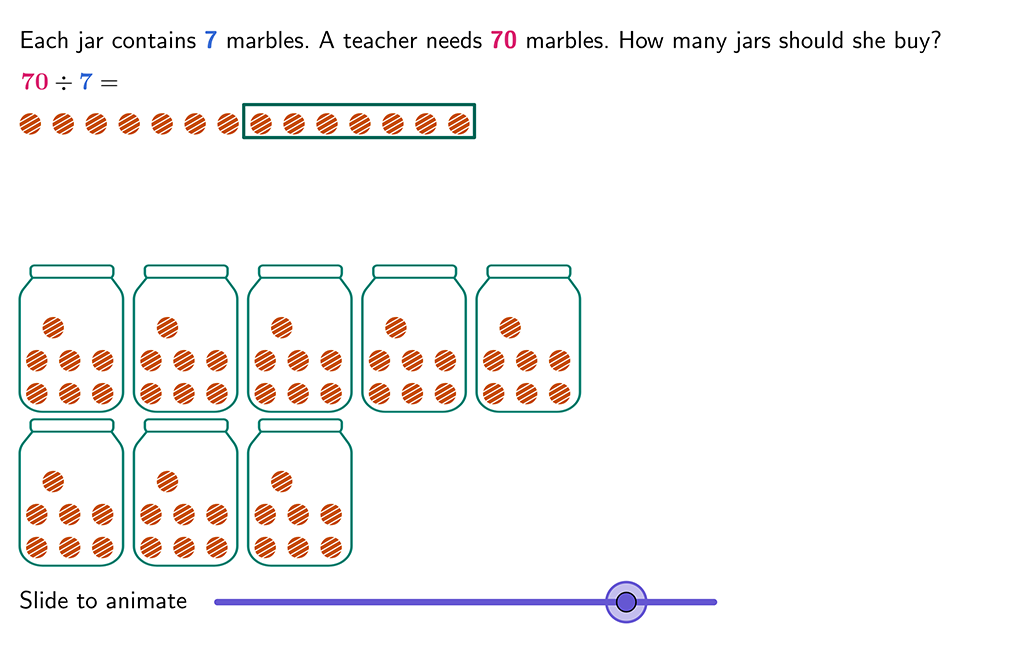
Division Word Problems
Multiplying and dividing by powers of 10.
Recognize and use patterns in powers of ten (with or without exponents) to multiply and divide whole numbers and decimals.

Multiplication and Division with Multiples of Powers of Ten
Middle school, multiplying and dividing integers.
Model or compute with integers using multiplication or division in number and word problems.
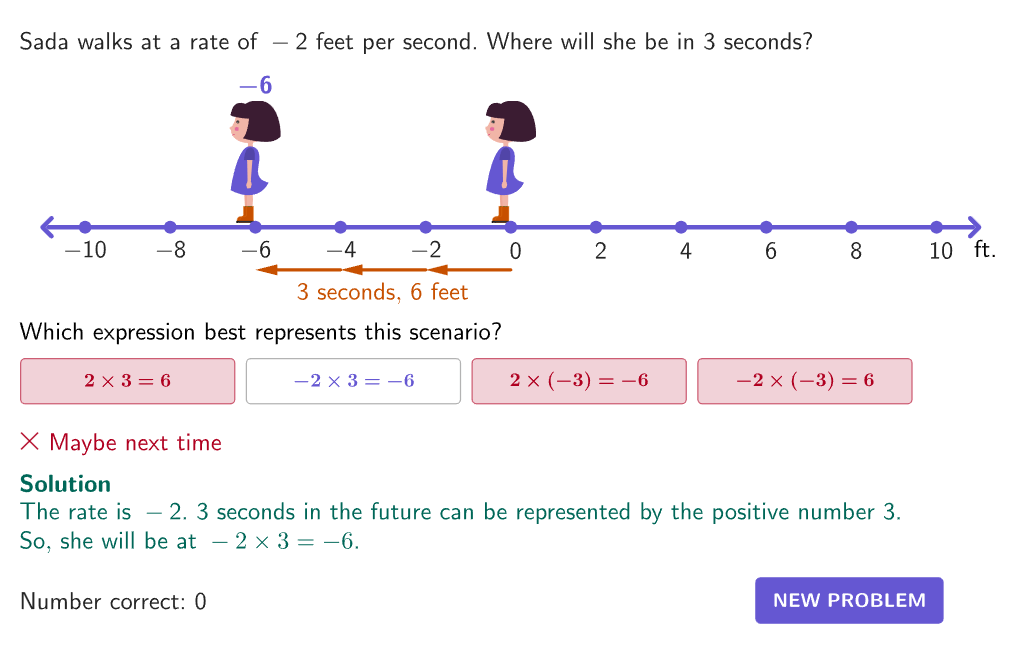
Multiplying Negative Numbers
Card Sort: Multiplying and Dividing Integers
Related topics.
Absolute Value
Decimal Numbers
Mathematical Expressions
Operations with Fractions
Inequalities
Community Resources
Explore an extensive collection of over one million math and science activities, exercises and lessons meticulously crafted by our global GeoGebra community. Immerse yourself in the boundless possibilities that await you.

Get started using GeoGebra today
Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Number Sense >
Printable Division Worksheets
Division is a basic skill we use daily! The division worksheets motivate kids of grade 3, grade 4 and grade 5 and help them see the real-life benefits division skills can bring them and help build those skills. Included here are division times tables and charts, various division models, division facts, divisibility rules, timed division drills, worksheets with grid assistance, basic and advanced division, multiplication and division fact family, estimating product and quotient, division word problems and the list goes on.
List of Division Worksheets
Division Tables and Charts
Division Models
Division Facts
- Divisibility Rule
Basic Division
- Division Drills
Division using Grids
2-digit by 1-digit Division
3-digit by 1-digit Division
3-digit by 2-digit Division
4-digit by 1-digit Division
4-digit by 2-digit Division
Dividing Large Numbers
Division Word Problems
In and Out Boxes for Division
Multiplication and Division Fact Family
- Estimating Products and Quotient
Explore Division Worksheets in Detail
Packed in this unit are division tables and charts featuring 1 to 16, 20, 25 and 50 times division tables presented as individual and as 5-in-1, 10-in-1, and 12-in-1 charts. Test skills with follow-up activities.
Learn four important strategies with this bundle of division models worksheets. Find division problems involving equal sharing and grouping, divide using arrays and on the number line model as well.
Emphasizing on each divisor ranging between 1 and 12, the division facts worksheets contain adequate exercises to develop skills. Learn to divide the numbers and complete the division facts.
Divisibility Rules
The divisibility rules worksheets comprise a divisibility rules chart stating the rules for divisors 2-12. Apply rules to test numbers with multiple divisors. Answer Yes/No questions, MCQs and more!
Bolster skills with this collection of 50+ basic division worksheets, comprehend the zero property, identity property, complete division sentences, unit price, repeated subtraction and compare quantities as well.
Timed Division Drills
Incorporate this package of timed division drills worksheets encompassing ample skills in dividing single and double digit numbers with and without a remainder. The number of problems vary per page.
Get acquainted with the concept of division using grids worksheets or graph paper worksheets involving dividends up to 4-digits. Grids provide assistance in solving division exercises with ease.
Utilize the 2-digit by 1-digit division worksheets to find the quotients and remainders, solve division word problems, comprehend the relationship between multiplication and division to mention a few.
The 3-digit by 1-digit division worksheets comprise a variety of standard division problems and division word problems involving remainders and no remainders, divide and check the answers as well.
This collection of 3-digit by 2-digit division worksheets features PDFs to find the quotient and remainder. Solve real-life word problems, multiply to check the answer, complete the process of division too.
Constructively engage students with this bundle of 4-digit by 1-digit division worksheets. Calculate the quotient and remainder, fill missing digits and understand the inverse property of multiplication as well.
Efficiently and accurately solve exclusive 4-digit by 2-digit division exercises offered as a mix of standard and word problems. Reaffirm division skills with this section of printable division worksheets.
Navigate through the dividing large numbers worksheets and find myriad pdfs with division problems involving multi-digit dividends by 1, 2 and 3 digit divisors and calculate the quotient and remainder.
Highlighting the application of the concept of division and brimming with real-life scenarios, this package of worksheets is a must-have for students to perform division with varied place values.
Walk through this assemblage of division worksheets with in and out boxes. Fill the out box using the rule, understand the pattern and write the rule, complete the in or out boxes involving divisors up to 20.
The ready-to-use multiplication and division fact family worksheets help comprehend the relationship between multiplication and division. Identify the members, write the four facts and a lot more.
Estimating Products and Quotients
Find a variety of estimating product and quotient worksheets to round numbers to the nearest tens and hundreds, round the leading digits to estimate the product, compare quotients and more.
Sample Worksheets

Become a Member
Membership Information
Printing Help
How to Use Online Worksheets
How to Use Printable Worksheets
Privacy Policy
Terms of Use
Copyright © 2024 - Math Worksheets 4 Kids

Division Practice Questions
Click here for questions, click here for answers, gcse revision cards.


5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- 🔍 Search Site
- Easter Color By Number Sheets
- Printable Easter Dot to Dot
- Easter Worksheets for kids
- Kindergarten
- All Generated Sheets
- Place Value Generated Sheets
- Addition Generated Sheets
- Subtraction Generated Sheets
- Multiplication Generated Sheets
- Division Generated Sheets
- Money Generated Sheets
- Negative Numbers Generated Sheets
- Fraction Generated Sheets
- Place Value Zones
- Number Bonds
- Addition & Subtraction
- Times Tables
- Fraction & Percent Zones
- All Calculators
- Fraction Calculators
- Percent calculators
- Area & Volume Calculators
- Age Calculator
- Height Calculator
- Roman Numeral Calculator
- Coloring Pages
- Fun Math Sheets
- Math Puzzles
- Mental Math Sheets
- Online Times Tables
- Online Addition & Subtraction
- Math Grab Packs
- All Math Quizzes
- Kindergarten Math Quizzes
- 1st Grade Quizzes
- 2nd Grade Quizzes
- 3rd Grade Quizzes
- 4th Grade Quizzes
- 5th Grade Quizzes
- 6th Grade Math Quizzes
- Place Value
- Rounding Numbers
- Comparing Numbers
- Number Lines
- Prime Numbers
- Negative Numbers
- Roman Numerals
- Subtraction
- Add & Subtract
- Multiplication
- Fraction Worksheets
- Learning Fractions
- Fraction Printables
- Percent Worksheets & Help
- All Geometry
- 2d Shapes Worksheets
- 3d Shapes Worksheets
- Shape Properties
- Geometry Cheat Sheets
- Printable Shapes
- Coordinates
- Measurement
- Math Conversion
- Statistics Worksheets
- Bar Graph Worksheets
- Venn Diagrams
- All Word Problems
- Finding all possibilities
- Logic Problems
- Ratio Word Problems
- All UK Maths Sheets
- Year 1 Maths Worksheets
- Year 2 Maths Worksheets
- Year 3 Maths Worksheets
- Year 4 Maths Worksheets
- Year 5 Maths Worksheets
- Year 6 Maths Worksheets
- All AU Maths Sheets
- Kindergarten Maths Australia
- Year 1 Maths Australia
- Year 2 Maths Australia
- Year 3 Maths Australia
- Year 4 Maths Australia
- Year 5 Maths Australia
- Meet the Sallies
- Certificates
Long Division Problems with Answers
(randomly generated).
Welcome to our Long Division Problems with Answers page.
Here you will find our free worksheet generator for generating your own long division sheets and answers.
If you are looking to create your own custom-made long or short division worksheets then look no further!
We also have several worked examples showing long division on this page so you can see how the method works.
For full functionality of this site it is necessary to enable JavaScript.
Here are the instructions how to enable JavaScript in your web browser .
Using the random sheet generator will allow you to:
- choose the number range and number of questions you wish the worksheet to have;
- print or save your worksheet and a corresponding answer sheet;
- choose your own title and instructions for completing the sheet - great for homework!
For optimal printing, please set your margins to zero on your print setup options.
To save your worksheets, select Print to PDF in the printing options.
If you have any problems with our Random Generator, please let us know using the Contact Us link at the top of each page.
Mobile View of Worksheets
Please note that our generated worksheets may have problems displaying correctly on some mobile devices.
This should not affect the printing of the sheets which should display correctly.
Long Division Problems with Answers Generator
Here is our random worksheet generator for creating your own long or short division worksheets.
You can generate a range of long division worksheets ranging from 2 digit by 1 digit up to 5 digits by 2 digits.
Using this generator will let you create your own worksheets for:
- Dividing 2, 3, 4 and 5 digit numbers by a range of different numbers up to 99;
- Dividing numbers with or without a remainder;
- Choosing exactly which divisors you want to include;
One of the best features of this generator is that you can choose individual values for the divisors for the worksheets (between 2 and 15).
This means that:
- if you were introducing long division for the first time, you could choose just to divide 2 digit numbers by, say, 2, 3 and 5.
- if you wanted to introduce dividing by two digits but you wanted to divide 3 digit numbers by 11 and 12, you could do that also.
- to access this feature, go to the 'Select divisors from a list' option.
To start creating your sheet, choose an option from the Number values box below.
Parts of a Long Division Equation
The dividend is the number being divided.
The divisor is the number you are dividing by.
The quotient is the number of times the divisor goes into the dividend.
The remainder is what is left over from the dividend when the divisor has been taken away as many times as it can be without leading to a negative answer.
The remainder can be a whole number, but it can also be expressed as a fraction or decimal.
Long Division Problems with Answers Worksheet Generator
4 Steps to Your Worksheets...
- Choose your divisor value - this is the number you are dividing by
- Choose your dividend value - this is the number you are dividing
- Choose if you want to have remainders or not
- Choose the number of questions
- View your sheet
- Print your sheet (if you want to save a hard copy of your sheet, choose 'Save to PDF'.
(Optional) Give your worksheet a title.
(Optional) Write out any instructions to go at the top of the sheet.
Divisor Value:
Remainders:
Dividend value:
Number of Questions:
Your worksheet will appear below.

Examples of Long Division Problems with Answers
Here are some examples showing some long division problems with answers, along with commentary on each step.
Example 1) Work out 84 ÷ 3
So we are working out \[ 3 \enclose {longdiv} {84} \]
FIrst step is to work out 8 ÷ 3, which means we need to find how many groups of 3 make 8.
We can get 2 groups of 3 in 8, and 2 x 3 = 6 so this gives us: \[ \begin {array}{l} \quad 2 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \end{array} \]
Next we subtract 6 from 8 to give us: \[ \begin {array}{l} \quad 2 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 2 \end{array} \]
The next step is to bring down the 4 and put it next to the 2 \[ \begin {array}{l} \quad 2 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 24 \end{array} \]
We now have to work out 24 ÷ 3, or how many groups of 3 make 24.
8 groups of 3 make 24. So this gives us: \[ \begin {array}{l} \quad 28 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 24 \\ \quad \underline{24} \end{array} \]
Finally subtract 24 from 24 to give us an answer of 0. \[ \begin {array}{l} \quad 28 \\ 3 \enclose {longdiv} {84} \\ \quad \underline{6} \\ \quad 24 \\ \quad \underline{24} \\ \quad \; \; 0 \end{array} \]
There are no more digits to bring down and we have no remainders, so we have finished.
Answer: 84 ÷ 3 = 28
Example 2) Work out 347 ÷ 4
So we are working out \[ 4 \enclose {longdiv} {347} \]
FIrst step is to work out 3 ÷ 4, which means we need to find how many groups of 4 make 3.
There are 0 groups of 4 in 3, so we keep the 3 in its place and go on to the next digit which is 4.
This gives us: \[ \begin {array}{l} \quad 0 \\ 4 \enclose {longdiv} {347} \end{array} \]
So the next step is to work out 34 ÷ 4, or find how many groups of 4 make 34.
8 groups of 4 make 32. So this gives us: \[ \begin {array}{l} \quad 08 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \end{array} \]
We subtract 32 from 34 to give us an answer of 2. This gives us: \[ \begin {array}{l} \quad 08 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 2 \end{array} \]
Next we bring the 7 down alongside the 2. \[ \begin {array}{l} \quad 08 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 27 \end{array} \]
So we need to work out 27 ÷ 4, or find how many 4s make 27.
6 groups of 4 make 24. So this gives us: \[ \begin {array}{l} \quad 086 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 27 \\ \quad \; \; \underline {24} \end{array} \]
Finally we need to subtract 24 from 27 to give us 3.
There are no more digits to bring down, so we are left with 3 as a remainder. \[ \begin {array}{l} \quad 086r3 \\ 4 \enclose {longdiv} {347} \\ \quad \underline {32} \\ \quad \; \; 27 \\ \quad \; \; \underline {24} \\ \quad \quad 3 \end{array} \]
Answer: 347 ÷ 4 = 86r3
If we wanted the remainder as a fraction, we would have 347 ÷ 4 = 86 ¾
Example 3) Work out 8165 ÷ 12
So we are working out \[ 12 \enclose {longdiv} {8165} \]
FIrst step is to work out 8 ÷ 12, which means we need to find how many groups of 12 make 8.
There are 0 groups of 12 in 8, so we keep the 8 in its place and go on to the next digit which is 1.
This gives us: \[ \begin {array}{l} \quad \; 0 \\ 12 \enclose {longdiv} {8165} \end{array} \]
So the next step is to work out 81 ÷ 12, or find how many groups of 12 make 81.
6 groups of 12 make 72. So this gives us: \[ \begin {array}{l} \quad \; 06 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \end{array} \]
6 groups of 12 make 72. So this gives us: \[ \begin {array}{l} \quad \; 06 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 9 \end{array} \]
Next we bring the 6 down alongside the 9. \[ \begin {array}{l} \quad \; 06 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \end{array} \]
So we need to work out 96 ÷ 12, or find how many 12s make 96.
8 groups of 12 make 96. So this gives us: \[ \begin {array}{l} \quad \; 068 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \end{array} \]
Now we subtract 96 from 96 to give us 0. \[ \begin {array}{l} \quad \; 068 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 0 \end{array} \]
Now we bring down the 5. \[ \begin {array}{l} \quad \; 068 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 05 \end{array} \]
Nexy we need to work out 5 ÷ 12, or how many 12s make 5.
0 groups of 12 make 5, so this gives us: \[ \begin {array}{l} \quad \; 0680 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 05 \\ \qquad \; \: \underline {00} \end{array} \]
Subtracting 0 from 5 gives us 5. There are no more digits to bring down, so 5 is the remainder. \[ \begin {array}{l} \quad \; 0680r5 \\ 12 \enclose {longdiv} {8165} \\ \quad \; \, \underline {72} \\ \qquad 96 \\ \qquad \underline{96} \\ \qquad \; \: 05 \\ \qquad \; \: \underline {00} \\ \qquad \quad 5 \end{array} \]
Answer: 8165 ÷ 12 = 680r5
If we wanted the remainder as a fraction, we would have \[ 8165 \div 12 = 680 {5 \over 12} \]
Other Recommended Worksheets & Resources
Here are some of our other related worksheets you might want to look at.
Long Division Support
We have created a calculator to help you master the long division method.
Just type in the dividend and divisor and let the calculator show you how to work out the long division, step-by-step.
The calculator also gives commentary to show you what is happending at each stage.
- Step by Step Long Division Calculator
More Randomly Generated Multiplication and Division Worksheets
As well as our long division problems with answers generator on this page, we also have a a generator for making your own division facts and several multiplication worksheet generators.
- Long Division with Money (randomly generated)
- Division Facts Worksheet Generator
- Single Digit Multiplication Worksheets Generator
- Multi Digit Multiplication Generator
- Money Multiplication Worksheets Generator
Graded (non-generated) Division Sheets
As well as our randomly generated long division worksheets, we also have a selection of carefully graded division worksheets for each grade.
These sheets are especially useful for introducing the concept and keeping the numbers to divide manageable and simple.
The sheets in the links below are not randomly generated, but have been carefully selected to progress your child through their division learning.
Learning long division starts at a 3rd grade level with learning to divide by a single digit. It then gradually gets more complex for higher grades.
Long Division Worksheets (graded)
- Long Division Worksheets 3rd Grade
- 4th Grade Long Division Worksheets
- Long Division Worksheets 5th Grade
- Long Division of Decimal Numbers
Mental Division Worksheets
As well as long division worksheets, you also need to know your division facts.
Knowing your division facts will help improve the speed and accuracy of your long division.
We have a wide variety of division fact worksheets for you to choose from.
Division Facts Worksheets
Division facts starts off with understanding the link between multiplication and division.
Once you understand this, you can start learning the division facts related to the multiplication table.
After this, at a 4th and 5th grade level, you can start learning related division facts.
This means that if you know that 12 ÷ 4 = 3 then you can work out 120 ÷ 4 = 30 or that 120 ÷ 40 = 3, etc
- Understanding Division Sheets (2nd grade)
- Division Facts to 10x10 Worksheets (3rd grade)
- Divding by Multiples of 10 and 100 Worksheets (4th grade)
- Decimal Division Facts (5th grade)
Multiply and Divide by 10 and 100
Knowing how to multiply and divide numbers by 10 and 100 is a very useful skill.
It is especially useful when converting between metric units or when using percentages.
- Multiply and Divide by 10 and 100 (decimals)
Division Math Games
Here you will find a range of Free Division Games.
The following games develop the Math skill of dividing and learning your division facts in a fun and motivating way.
Using these sheets will help your child to:
- learn their division facts;
- develop their strategic thinking skills.
- Math Division Games
Return to Division Worksheets
Return to Math Worksheets Generator
Return from Long Division Problems with Answers to Math Salamanders Home Page
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.
New! Comments
TOP OF PAGE
© 2010-2024 Math Salamanders Limited. All Rights Reserved.
- Privacy Policy
- Copyright Policy

Reading & Math for K-5
- Kindergarten
- Learning numbers
- Comparing numbers
- Place Value
- Roman numerals
- Subtraction
- Multiplication
- Order of operations
- Drills & practice
- Measurement
- Factoring & prime factors
- Proportions
- Shape & geometry
- Data & graphing
- Word problems
- Children's stories
- Leveled Stories
- Sentences & passages
- Context clues
- Cause & effect
- Compare & contrast
- Fact vs. fiction
- Fact vs. opinion
- Main idea & details
- Story elements
- Conclusions & inferences
- Sounds & phonics
- Words & vocabulary
- Reading comprehension
- Early writing
- Numbers & counting
- Simple math
- Social skills
- Other activities
- Dolch sight words
- Fry sight words
- Multiple meaning words
- Prefixes & suffixes
- Vocabulary cards
- Other parts of speech
- Punctuation
- Capitalization
- Narrative writing
- Opinion writing
- Informative writing
- Cursive alphabet
- Cursive letters
- Cursive letter joins
- Cursive words
- Cursive sentences
- Cursive passages
- Grammar & Writing
Breadcrumbs
- Word Problems

Download & Print Only $4.10
Division word problems for 3rd grade
Simple division word problems.
After reading the word problem and understanding the 'real world scenario', the student must formulate the division equation to solve the problem. Only simple division is required.

These worksheets are available to members only.
Join K5 to save time, skip ads and access more content. Learn More
More word problem worksheets
Explore all of our math word problem worksheets , from kindergarten through grade 5.
What is K5?
K5 Learning offers free worksheets , flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads.
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits
This content is available to members only.

Trending Post : Teaching Fractions with Food

5 Fun Division Word Problems | Practice Multiple Ways of Solving | Free Printable
Table of Contents
Division Word Problems
Are your children ready to conquer division? These interactive, division problem-solving worksheets will help children solve division word problems in five different ways.

Division Problems
He has done it numerous times. Sharing a group of toys with his siblings, or even sharing a bag of M&M’s. In those situations, he instinctively knows how to do division problems.
When we hit the division problem in his math book, he wasn’t quite as sure what to do.
I wanted this little man of mine to be able to relate division to what he has done over and over while creating strategies for solving division problems.
These word problems with five steps were what we came up with. These simple division worksheets are perfect for 3rd grade division word problems.
How to Solve Division Word Problems
Step 1: division word problem solving by grouping.
The first step is the way we normally teach children to solve division problems. The students grab the amounts of objects that need to be divided up and then place them in the correct amount of groups. It is very hands-on and a visual way for our children to understand what is happening when we are dividing .
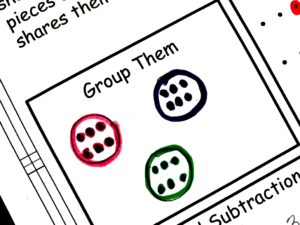
Step 2: Solving Division Word Problems by Repeated Subtraction
To solve a word problem using repeated subtraction, students start with the number being divided up or the dividend. Now they subtract the divisor or the number that tells how many groups are needed from the dividend over and over until they reach zero. The number of times they subtracted is the answer.
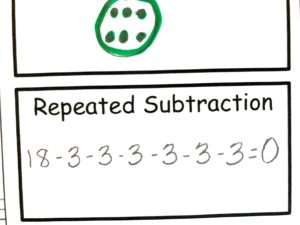
Step 3: Division Word Problem Solving with Arrays
Chances are if you taught multiplication in a hands-on way, you taught it using arrays. You can create an array when you place objects, pictures, or numbers in equal columns and equal rows.
With multiplication, you would take a problem like 4 x 5, and make 4 rows with 5 in each column. You would end up with 20 objects, which of course is the answer to the multiplication problem.
Division is a little different. If the problem is 18 ÷ 3, The student creates three rows. They then keep placing one object in each row until they have used 18 objects.
They now have an array that is a 3 by 6. The answer to the division problem is 6.
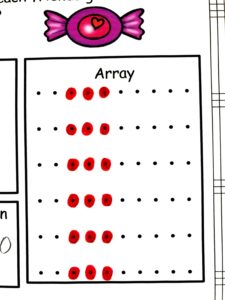
Want to know how to use arrays to divide when the numbers are larger? Check out this POST !
Step 4: Number Line to Solve Division Word Problems
Number lines have become an important tool in helping children solve problems. The beginning of this video by Ramy Melhem clearly shows how to divide using a number line, and the little frog hopping is a great visual for our little ones.
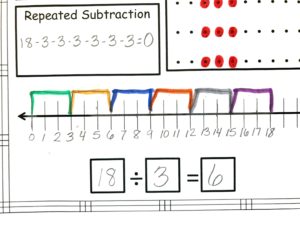
Step 5: Create an Equation
The final step is very easy after all the work above. The students simply figure out what number was divided up, and place it in the first box.
They then look at how many groups they created, and that is the number that goes into the second box. Finally, they figure out how many objects were in each group and that is the answer or quotient.
That number goes in the last box.
By throwing in markers and painting with q-tips these sheets were fun for my little man, and I could see his understanding of division grow.
We moved on to these cut-and-paste division assessments, and his thinking was challenged even more. Through all this practice he is on his way to mastering simple division problems, and your kiddos can master it too.
Get This Cut and Paste Division Assessment at my TpT Store .
You’ve Got This
Division Word Problems Printable
These free division math problems will help your students learn how to solve division problems 5 different ways. You can download this printable by clicking on the download button.
Similar Posts

A FREE No-Prep Game for Subtracting With Money

10 Real Life Examples of Acute Angles in the Home | Free Printable

Implement Art Into your Week With this Great Homeschool Art Curriculum

FREE No-Prep Adding and Subtracting Decimal Game

8 Free Number Recognition Game Worksheets

10 Square Root and Cube Root Worksheet | Free Printable
Problem Solving on Division
Problem solving on division will help us to get the idea on how to solve the basic division statement problems.
1. The teacher brought 36 books from the library. He asked Ron to put them on 3 tables. He was to put the same number of books on each table. How many books should Ron put on each table?
Number of books bought from the library = 36
Number of tables = 3
Therefore, number of books Ron put on each table = 36 ÷ 3 = 12
2. There are 48 bikes in 4 rows. How many bikes were in each row?
Number of bikes = 48
Number of rows = 4
Therefore, number of bikes in each row = 48 ÷ 4 = 12
3. Today 155 children went to see the Red Fort. They went in 5 buses. How many children were in each bus if each bus had the same number of children?
Number of children went to see the Red Fort = 155
Number of buses = 5
Therefore, number of children in each bus = 155 ÷ 5 = 31
4. On Sunday, 126 scouts are to go on a hike. There are 6 troops of the same size. How many scouts are in each troop?
Number of scouts to go on a hike = 126
Number of troops of the same size = 6
Therefore, number of scouts in each troop = 126 ÷ 6 = 21
5. How many 8 centimeter pieces of ribbon can be cut from 96 centimeters of ribbon?
Length of a ribbon = 96 cm
Length of a pieces of ribbon cut = 8 cm
Therefore, number of pieces of ribbon in 8 cm = 96 ÷ 8 = 12
6. Sharon had 56 bulbs to plant. She was going to put 4 in each flower pot. How many pots did she need?
Number of bulbs Sharon had to plant = 56
Number of bulbs in each flower pot = 4
Therefore, number of pots she need = 56 ÷ 4 = 14
More examples on statement problem solving on division:
7. The 168 chairs in the hall had to be put in rows with 8 in each. How many rows were made?
Number of chairs in the hall = 168
Number of chairs in each row = 8
Therefore, number of rows = 168 ÷ 8 = 21
8. How many packets will be made if 267 books are packed with 3 books in each?
Number of books = 267
Number of books in each packet = 3
Therefore, number of packets = 267 ÷ 3 = 89
2nd Grade Math Practice From Problem Solving on Division to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Worksheet on two digit numbers | numbers in words | two-digit numbers.
Sep 12, 24 02:09 AM

Cardinal Numbers and Ordinal Numbers | Cardinal Numbers | Ordinal Num
Sep 11, 24 09:18 AM

Worksheet on Cardinal Numbers and Ordinal Numbers | Cardinal & Ordinal
Sep 11, 24 01:47 AM
Skip Counting by 2's | Concept on Skip Counting | Skip Counting by Two
Sep 10, 24 11:58 PM
2nd Grade Math Practice | Second Grade Math |2nd Grade Math Worksheets
Sep 10, 24 02:55 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Practice Solving Division Problems
In this post, we are going to learn to analyze, think about, and solve problems that require division: division problems. At Smartick , we want to emphasize the fact that you have to know how to solve any kind of math problem accurately. As a result, we are going to give you a variety of problems that require division to solve.
Division problems nº 1
In high school, some teachers had complained that there weren’t sufficient supplies, and as a result, they had to share 18 boxes of erasers equally among 9 classes. How many eraser boxes will each class receive?
This is the easiest type of division problem that we will come across. The problem tells us that there are 18 boxes and they want to split them into equal parts among nine classes. When we talk about splitting into equal parts, we are talking about DIVISION:
Each class will receive 2 boxes of erasers.
Division problems nº 2
My town has a water supply beside the big gardens on the tallest hill, to make sure there is enough water for the irrigation, but there are only 56 gallons of water currently in the supply. If it is all shared with the recipients, 8 liters to each one, how many recipients are supplied with water?
This problem is similar to the previous one. Again, you have to share the 56 gallons of water being divided among recipients, giving 8 liters to each one. Therefore, we have to DIVIDE:
7 recipients will be supplied.
Division problems nº 3
Like every Sunday morning, Richard and Catherine have gone out for a walk through the field. As they are used to playing sports, they go quickly and without stopping on their walk. Knowing that the walk lasts three hours, and that they walk 15 miles in total and that they have walked with seven people, calculate how fast they are walking (assuming they walk at a constant speed).

They walked at a rate of 5 mi/hr (5 mph).
Division problems nº 4
Raymond and I are saving to buy a game and giving it to Carmen for her birthday, which is coming up in 5 days. He has $9 and I already have $27. How many times more money have I saved than Raymond?
The verbiage of the problem can lead to confusion, so that “more” or “fewer” times can be interpreted as an addition or subtraction. In the case of this problem, they say that Raymond has gotten $9 and that I have $27 and they ask me how many times more I have saved than he has. Raymond has less money than me; therefore, the amount that he has ($9) multiplied by some number has to give a result of the money that I have ($27). Therefore, what we have to do is DIVIDE:
I have saved 3 times more than Raymond.
And with this, we have finished how to solve one-operation problems: addition, subtraction, multiplication, and division problems. If you want to learn a lot more math register in Smartick and try it for free!
Learn More:
- Learn How to Do Division Word Problems with Decimals
- Division Problems: Different Models and Examples
- How to Solve Multiplication Word Problems
- Division Exercises Solved Using the Singapore Method
- Practice Dividing with and without Remainders
- 15 fun minutes a day
- Adapts to your child’s level
- Millions of students since 2009

- Recent Posts
- The Language of Functions and Graphs - 07/01/2024
- Educational Technology: The Christodoulou Test - 05/06/2024
- Multiplication Activities in Smartick - 04/09/2024
Add a new public comment to the blog: Cancel reply
The comments that you write here are moderated and can be seen by other users. For private inquiries please write to [email protected]
Your personal details will not be shown publicly.
I have read and accepted the Privacy and Cookies Policy
Division Word Problems (2-step word problems)
Here are some examples of division word problems that can be solved in two steps. We will illustrate how block diagrams or tape diagrams can be used to help you to visualize the division word problems in terms of the information given and the data that needs to be found. We also learn how to solve multiplication and division word problems by identifying key terms.
Related Pages 1-Step Division Word Problems Multiplication and Division Word Problems More Word Problems More Singapore Math Lessons
Block diagrams are used in Singapore Math and tape diagrams are used in the Common Core Math.
We use division or multiplication when the problem involves equal parts of a whole. Sometimes, the problem involves comparison and it becomes a 2-step problem. The following diagram shows how to use equal parts of a whole and comparison. Scroll down the page for examples and solutions.
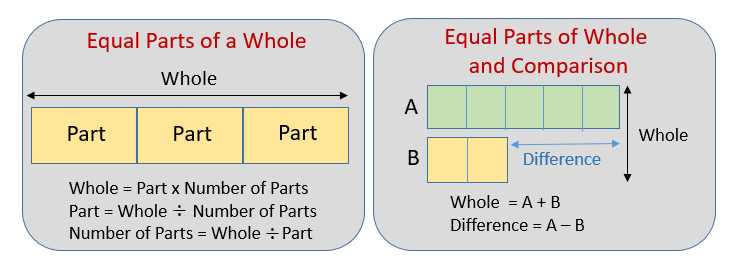
Example: Marcus had 700 marbles. He gave away 175 marbles and put the remaining marbles equally into 5 bags. How many marbles were there in each bag?
Solution: Step 1: Find how many marbles he had left.
700 – 175 = 525 He had 525 marbles left.
Step 2: Find the number of marbles in each box.
525 ÷ 5 = 105 There were 105 marbles in each box.
Example: Rosalind made 364 donuts. She put 8 donuts into each box. a) How many boxes of donuts were there? How many donuts were left over? b) If she sold each box for $3, how much money would she receive?
Solution: Step 1: Find the number of boxes of donuts.
364 ÷ 8 = 45 remainder 4 There were 45 boxes of donuts. 4 donuts were left over.
Step 2: Find how much money she would receive.
45 × 3 = 135 She would receive $135.
How to solve a 2-step division word problem using multiple tape diagrams?
Example: Ben is making math manipulatives to sell. He needs to make at least $450. Each manipulative costs $18 to make. He is selling them for $30 each. What is the minimum number he can sell to reach his goal?
How to use tape diagrams to solve fractional division problems? Basic algorithms and checks are also demonstrated.
Example: When someone donated 14 gallons of paint to Rosendale Elementary School, the fifth grade decided to use it to paint murals. They split the gallons equally among the four classes. a) How much paint did each class have to paint their mural? b) How much pain will three classes use? Show your thinking using words, numbers, or pictures. c) If 4 students share a 30 square foot wall equally, how many square feet of the wall will be painted by each student?
How to solve division word problems using the Algebra method and the Singapore Math method?
Example: Jeremy bought 8 identical pens and 5 identical notebooks. The cost of 8 pens is the same as the cost of 5 notebooks. Each notebook costs 30 cents more than each pen. How much did Jeremy spend altogether?
How to solve a multiplication and division 2-step problem? Using the comparison model, this video teaches how to approach a given 2-step problem on multiplication and division, and shows the detailed steps of how to solve it.
Example: Billy bought 5 bags of balls. Each bag contained 40 balls. He packed the balls into packets of 8 balls each. How many packets did he get?
How to solve a subtraction and division 2-step problem? Using the comparison model, this video teaches how to approach a given 2-step problem on subtraction and division, and shows the detailed steps of how to solve it.
Example: A boy collects a total of 316 stamps, stickers and coins. He collects 4 times as many stamps as stickers. There are 46 coins. How many stickers are there?
How to solve a division and fraction word problem visually?
Example: Mimi’s market sold 24 heads of lettuce one morning. That afternoon 2/7 of the remaining heads of lettuce were sold. The number of heads left was now 1/2 of the number the market had at the beginning of the day. How many heads of lettuce were there at the beginning of the day?
How to solve a part whole division word problems using bar models? Tips for Bar Modeling Division Problems
- Show units by dividing one long unit bar into its parts.
- If the question asks for the value of one of the parts of a unit bar, write your question mark right inside that section of the unit bar.
- 28 playing cards are arranged equally in 4 rows. How many playing cards are there in each row?
- If 18 cookies are arranged equally in 6 piles. How many cookies are there in each pile?
- A woman divided her lottery winnings of $92,000 into 8 equal parts. She gave 4 portions to her husband, 1 portion to her daughter, and divided the rest equally among three charities. How much more money did the husband receive than the daughter?
- Tralise has a library that she does not want to keep because she prefers digital books, so she divided to give her books away. She divided her collection of 1200 books into 10 equal parts. She gave 3 portions to her sister, 4 portions to her best friend, and the rest equally to three nieces. How many books did her best friend receive?
- Oscar had 3 times as many cookies as Zoe. After Oscar ate 50 cookies, he had half as many cookies as Zoe. How many cookies did Oscar have left?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Advertisement
How to Do Long Division: Step-by-Step Instructions
- Share Content on Facebook
- Share Content on LinkedIn
- Share Content on Flipboard
- Share Content on Reddit
- Share Content via Email
In math, few skills are as practical as knowing how to do long division . It's the art of breaking down complex problems into manageable steps, making it an essential tool for students and adults alike.
This operation has many practical uses in our daily lives. For instance, imagine you have a bag of 2,436 candies and want to share them equally among 4 friends. Long division helps you determine that each friend gets 609 candies, ensuring everyone gets their fair share.
Let's dive into the fundamentals of long division and learn about other everyday situations where we can put it to use.
What Is Long Division?
How to do long division in simple steps, long division method: an apple example, using long division in everyday life, how to divide a decimal point by a whole number, practice problems and answers.
Long division is a handy way to divide big numbers by smaller ones, helping us figure out how many times one number fits into another. It turns a tricky math problem into easier steps.
When we do long division, we work with four main parts:
- the big number we want to divide (called the " dividend ")
- the smaller number we're dividing by (the " divisor ")
- the answer to our division (the " quotient ")
- sometimes a little bit left over (the " remainder ")
Long Division vs. Short Division
Short and long division are both methods to divide numbers, but they differ in complexity. The short-division method is a quick way to find the answer when dividing simple numbers. For example, say you want to divide 36 by 6. You write it as 36 ÷ 6, using a division sign, and quickly get the answer, which is 6.
Long division is used for bigger, more complicated numbers, typically two or more digits. This method involves several steps, like writing out the numbers neatly and carefully.
Let's dive into long division with a clear example. We'll use 845 ÷ 3 to walk through this step-by-step process:
- Set up the problem. Write the dividend (845) under the division bar and the divisor (3) outside the bar.
- Divide. Look at the first digit of the dividend (8). How many times does 3 go into 8? Twice, because 3 x 2 = 6, and that's the closest we can get without going over. Write the 2 above the division bar, over the 8.
- Multiply. Multiply the quotient (2) by the divisor (3). (2 x 3 = 6). Write 6 under the 8.
- Subtract. Subtract 6 from 8 to get 2. Draw a line under the 6, subtract, and write 2 below the line.
- Bring down the next digit. Now, bring down the next digit of the dividend, which is 4, to sit next to the 2, making 24.
- Repeat the steps. 3 goes into 24 eight times (3 x 8 = 24), so write 8 above the bar next to the 2. Subtract 24 from 24 to get 0. Now, follow the same process you used in steps 1 through 5 and bring down the last digit, which is 5, to form 05. The number 3 goes into 5 once (3 x 1 = 3), leaving a remainder of 2. Write the 1 above the bar and the remainder 2 below after subtracting 3 from 5.
- The final answer with a remainder. You've divided 845 by 3 to get a final answer of 281 with a remainder of 2.
- Convert the remainder to decimal form. Depending on how far along you are in learning long division, this may be your final answer. If you've progressed to decimals, you will add .0 to 845 and put a decimal point above the division bar, right after the 1. Bring 0 down to form 20. The number 3 goes into 20 six times (3 x 6 = 18). Write 6 after the decimal point above the division bar. Normally, you would continue adding another 0 after 845. until there is no remainder, but since 20 – 18 = 2, you would be repeating this process infinitely because 3 does not divide evenly into 845. Instead, you will draw a horizontal line over the 6 in 281.6 to indicate that it is a repeating decimal. A calculator would show the answer as 281.666667 to indicate that the repeating decimal rounds up.
Now let's use a practical example to work through the long division process.
Imagine you just went apple picking and came home with a massive haul of delicious fruit. In your kitchen, you have 456 apples, and you want to share them equally among 3 baskets to give to your friends, so you're dividing 3 by 456 (456 ÷ 3).
To figure out how many apples go into each basket, you'd tackle the division problem step by step.
- 3 goes into the first digit (4) once, so you write 1 above the division bar, above the 4 in 456. Then you show the subtraction: 4 – 3 = 1.
- Bring down the next digit (5) to form 15. 3 goes into 15 five times (3 x 5 = 15), so you write 5 above the division bar, above the 5 in 456. Then you show the subtraction: 15 – 15 = 0.
- Bring down the final digit (6) to form 06. 3 goes into 6 twice (3 x 2 = 6), so you write 2 above the division bar, above the 2 in 456. Then you show the subtraction: 6 – 6 = 0.
- Since there is no remainder left to divide, you quotient is now written atop the division bar: 152. You will need to place 152 apples in each of the 3 baskets to evenly distribute the 456 apples.
Long division also pops up in real-life situations . Think about when you need to divide something, like pizza or cake, into equal parts.
Want to cut a large recipe in half or figure out how many days are left till summer vacation? Long division can help with that. It's a great way to help us figure out those splits and manage resources better.
And, of course, practicing long division sharpens our problem-solving skills . It teaches us to tackle big problems step by step, breaking them down into smaller, more manageable pieces. This approach is super helpful in math and figuring out all sorts of challenges we might face.
So, long division is more than just a bunch of steps we follow. It's a key that unlocks a lot of doors in the world of math and beyond, helping us understand and connect different concepts and apply them in all sorts of ways.
Dividing decimals by whole numbers is useful in our everyday lives. For instance, if you're splitting a sum of money equally among a certain number of people, you'll need to divide the total (a decimal) by the number of people (a whole number) to determine how much each person gets.
Dividing a decimal point (decimal number) by a whole number is similar to regular division, but you must be mindful of the placement of the decimal point. Here's how to do it:
Example : Divide 0.5 by 5.
- Set up the problem. Begin by setting up the division, with 0.5 as the dividend (the number you're dividing, which will be under the division bar) and 5 as the divisor (the number you're dividing by, which will be to the left of the division bar).
- Begin dividing. 5 goes into the first digit of the dividend 0 times, so you'll write 0 above the division bar, above the 0 in 0.5, and place a decimal point after the 0 you just wrote. It should be directly above the decimal point in the dividend.
- Bring down the next digit. Bring down the 5 to form 05 (you do not bring the decimal down). 5 goes into 5 once (5 x 1 = 5), so you'll write 1 above the division bar, above the 5 in 0.5.
- Show the final answer. When you show the subtraction (5 – 5 = 0), you'll have no remainder. This means the number above the division bar is your final answer: 0.1.
Let's put our long division skills to the test with some word problems. Tackle these problems one step at a time, and don't rush. If you get stuck, pause and review the steps. Remember, practice makes perfect, and every problem is an opportunity to improve your long-division skills.
1. Emma has 672 pieces of candy to share equally among her 4 friends. How many pieces of candy does each friend get?
Solution : To find out, divide 672 by 4. Start with the first part of 672, which is 6, and see how many times 4 can fit into it. It fits 1 time, leaving us with 2. Bringing down the 7 turns it into 27, which 4 fits into 6 times, leaving us with 3. Finally, bringing down the 2 to join the remaining 3 makes 32, which 4 divides into 8 times. So, each friend gets 168 pieces of candy.
2. A teacher has 945 stickers to distribute equally in 5 of her classes. How many stickers does each class get?
Solution : We'll divide 945 by 5. Looking at 9 first, 5 goes into it 1 time. With 4 leftover, we bring down the 4 from 945 to get 44, which 5 divides into 8 times with another 4 leftover. Lastly, bringing down the 5 to the remaining 4 makes 45, which 5 divides into 9 times. Therefore, each class receives 189 stickers.
3. A library has 2,310 books to be placed equally on 6 shelves. How many books will each shelf contain?
Solution : Divide 2,310 by 6. Starting with 23, 6 goes into it 3 times with 5 leftover. After subtracting, we bring down the 1 to get 51, which 6 divides into 8 times with 3 leftover. Bringing down the 0 to the remaining 3 gives us 30, which 6 divides into 5 times. So, each shelf will have 385 books.
This article was updated in conjunction with AI technology, then fact-checked and edited by a HowStuffWorks editor.
Please copy/paste the following text to properly cite this HowStuffWorks.com article:

Core Math Worksheets
Addition worksheets, subtraction worksheets, multiplication worksheets, division worksheets, fact family worksheets, long division worksheets, negative numbers, exponents worksheets, order of operations worksheets, fraction worksheets, fractions worksheets, graphic fractions, equivalent fractions, reducing fractions, comparing fractions, adding fractions, subtracting fractions, multiplying fractions, dividing fractions, fractions as decimals, fraction decimal percent, word problems, pre-algebra word problems, money word problems, combining like terms, properties of multiplication, exponent rules, linear equations, one step equations, two step equations, factoring polynomials, quadratic equations, other worksheets, place value, percentages, rounding numbers, ordering numbers, standard, expanded, word form, mean median mode range, ratio worksheets, probability worksheets, roman numerals, factorization, gcd, lcm, prime and composite numbers, pre-algebra, geometry worksheets, blank clocks, telling analog time, analog elapsed time, greater than and less than, arithmetic sequences, geometric sequences, venn diagram, graph worksheets, measurement & conversions, inches measurement, metric measurement, metric si unit conversions, customary unit conversions, customary and metric, patterns and puzzles, number patterns, patterns with negatives, missing operations, magic square, number grid puzzles, word search puzzles, color by number, addition color by number, subtraction color by number, multiplication color by number, division color by number, color by number, holiday & seasonal, valentine's day, st. patrick's day, thanksgiving, early learning, base ten blocks, printable flash cards, number matching, number tracing, missing numbers, picture math addition, picture math subtraction, picture math multiplication, picture math division, multiplication chart, multiplication table, prime numbers chart, hundreds chart, place value chart, roman numerals chart, handwriting paper, graph paper, coordinate plane, spaceship math check-off, square root chart, fraction chart, probability chart, measurement chart, number line, comic strip template, calculators, age calculator, factoring calculator, fraction calculator, slope calculator, degrees to radians, percentage calculator, prime factorization calculator, roman numeral converter, long division calculator, multiplication calculator, math worksheets by grade, preschool math worksheets, kindergarten math worksheets, 1st grade math worksheets, 2nd grade math worksheets, 3rd grade math worksheets, 4th grade math worksheets, 5th grade math worksheets, 6th grade math worksheets, worksheet news, word problems: division word problems.
These division story problems deal with only whole divisions (quotients without remainders.) This is a great first step to recognizing the keywords that signal you are solving a division word problem.
Easy Division Word Problems

Division Word Problems One

Division Word Problems Two

Division Word Problems Three

Division Word Problems Four

Word Problem Worksheetss for Division
Division word problems can be some of the more confusing problems for students to understand. Many division problems will use words like 'share among' or 'give to each' or similar phraseology to imply that a total amount is to be split evenly into groups. This partitioning operation is the key concept in many division story problems, and students may need to have an example explained either on paper or with manipulatives before they're ready to tackle a worksheet independently.
As with the other word problem worksheets here, these division worksheets start with very basic problems to help surmount this challenge. Once these division concepts are well understood, proceeding to worksheets that mix multiplication and division, and even addition and subtraction, can provide excellent practice to make sure students understand how each operation needs to be chosen appropriately based on the problem description.

Copyright 2008-2024 DadsWorksheets, LLC
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Problem Solving on Division | Division Word Problems Examples with Answers
Are you looking for help in solving the division problems? If yes, then you are on the correct page. This Problem Solving on Division page includes the questions prepared by math experts. Students can check the detailed process to solve all those problems in the following sections. We know that division is an arithmetic operation that is inverse of multiplication and used to split the number of items into groups of equal size.
We are providing example questions and solutions for the various division problems. Interested students can solve the practice questions related to division to become a pro in the concept. All the Questions covered clearly explain how to solve problems involving division.
- Worksheet on Division Problems by 2-Digit Divisors
- Word Problems on Division by 2 Digit Number
- Word Problems on Division
Division Problem Solving Examples
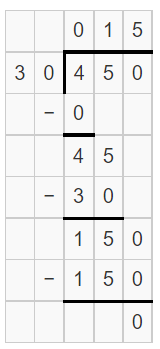
Example 2: At a parking slot, we have 52 bikes in 4 rows. Find the number of bikes in each row? Solution: The total number of bikes = 52 The number of rows = 4 The number of bikes in each row = 52 ÷ 4 = 13 Therefore, the number of bikes in each row is 13.
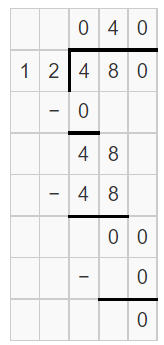
Leave a Comment Cancel Reply
You must be logged in to post a comment.
Long Division Worksheets
Without remainders.
| Worksheet | Divisor Range | |
|---|---|---|
| 2 to 9 | ||
| 6 to 12 | ||
| 10 to 20 | ||
| 20 to 50 | ||
| 50 to 199 |
With Remainders
| Worksheet | Divisor Range | |
|---|---|---|
| 2 to 9 | ||
| 6 to 12 | ||
| 10 to 20 | ||
| 20 to 50 | ||
| 50 to 199 |

COMMENTS
Solution: Total number of apples = 63. There are 9 friends of seats on the bus. To find how many apples Tom gave to each of his friends, divide the total number of apples by the number of friends. We get, divide 63 by 9. 63 ÷ 9 = 7. Therefore, Tom gives 7 apples to each of his friends. Answer: 7 Apples. 7.
Take a look at our long division problems worksheet generators. This generator will generate your own worksheets from 2-digits by 1-digit to 5-digits by 2-digits. You can also create your own long division worksheets with money amounts from up to $10 by a single digit to up to $100,000 by 2-digits.
Alternatively, we could use the inverse multiplication to solve this problem. We may not know the division fact that 40 divided by 8 = 5 but if we look to the inverse we may know what number multiplied by 8 equals 40. If we did our 8 times table we would get the answer of 5 - the correct answer.
These printable worksheets involve division word problems with three-digit dividends and single digit divisors. Apply long division method to solve each problem. Three-digit by Two-digit Word Problems. This set of word problems will require the student to perform division operations involving three-digit numbers and two-digit numbers.
We have a winner! 680 is indeed divisible by 8. Divisibility Rules Worksheets with 2-Digit Numbers. Divisibility of 2, 5 and 10 (2-digit) Divisibility of 3, 6 and 9 (2-digit) Divisibility of 4, 7 and 8 (2-digit) Divisibility of Numbers 2 to 10 (2-digit) Divisibility Rules Worksheets with 3-Digit Numbers.
Division Word Problems: Basic (Grades 3-4) Division Word Problems: Intermediate (Grades 3-5) Long Division Word Problems: Advanced (Grades 3-5) Each worksheet is available as a PDF download that is printable and also easy to share on online learning platforms like Google Classroom. To download any of the division word problems worksheets below ...
The following diagram shows how to use division to find unknown size of parts or groups or to find unknown number of parts or groups. Scroll down the page for examples and solutions. Example: There are 160 grade 3 students in a school. The students are to be equally divided into 5 classes.
Division is a process in math that lets you break down a number into multiple, equal parts. Sometimes, you can cut everything down into whole number parts, and, sometimes, you'll be left with a little leftover, giving you a decimal or fraction for an answer rather than a whole number. You'll often see division problems vertically, like this ...
Get started using GeoGebra today. Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others. Explore over 11 free and ready-to-use GeoGebra resources for grades 4-8 to improve your skills in estimating and solving division problems and using rules for divisibility.
The number of problems vary per page. Division using Grids. Get acquainted with the concept of division using grids worksheets or graph paper worksheets involving dividends up to 4-digits. Grids provide assistance in solving division exercises with ease. 2-digit by 1-digit Division
Click here for Answers. dividing. Practice Questions. Previous: Dimensional Analysis Practice Questions. Next: Multiply and Dividing by 10, 100, 1000 etc Practice Questions. The Corbettmaths Practice Questions on Division.
Division worksheets for grade 3 through grade 6. Our free division worksheets start with practicing simple division facts (e.g. 10 ÷2 = 5) and progress to long division with divisors up to 99. Exercises with and without remainders and with missing divisors or dividends are included.
0 groups of 12 make 5, so this gives us: 0680 12 8165 72 ― 96 96 ― 05 00 ―. Subtracting 0 from 5 gives us 5. There are no more digits to bring down, so 5 is the remainder. 0680 r 5 12 8165 72 ― 96 96 ― 05 00 ― 5. Answer: 8165 ÷ 12 = 680r5. If we wanted the remainder as a fraction, we would have 8165 ÷ 12 = 680 5 12.
Simple division word problems. After reading the word problem and understanding the 'real world scenario', the student must formulate the division equation to solve the problem. Only simple division is required. Worksheet #1 Worksheet #2 Worksheet #3 Worksheet #4. Worksheet #5 Worksheet #6.
Step 3: Division Word Problem Solving with Arrays. Chances are if you taught multiplication in a hands-on way, you taught it using arrays. You can create an array when you place objects, pictures, or numbers in equal columns and equal rows. With multiplication, you would take a problem like 4 x 5, and make 4 rows with 5 in each column.
Example Problem 2: Using Division to Solve Word Problems 160 people showed up for a sporting event. The people need to be divided into teams of 20 which will participate in the tournament.
Problem solving on division will help us to get the idea on how to solve the basic division statement problems. 1. The teacher brought 36 books from the library. He asked Ron to put them on 3 tables. He was to put the same number of books on each table. How many books should Ron put on each table? Number of books bought from the library = 36
This is the easiest type of division problem that we will come across. The problem tells us that there are 18 boxes and they want to split them into equal parts among nine classes. When we talk about splitting into equal parts, we are talking about DIVISION: 18 ÷ 9 = 2. Each class will receive 2 boxes of erasers.
Using the comparison model, this video teaches how to approach a given 2-step problem on subtraction and division, and shows the detailed steps of how to solve it. Example: A boy collects a total of 316 stamps, stickers and coins. He collects 4 times as many stamps as stickers.
Division. Division is splitting into equal parts or groups. It is the result of "fair sharing". Example: there are 12 chocolates, and 3 friends want to share them, how do they divide the chocolates? 12 Chocolates. 12 Chocolates Divided by 3. Answer: 12 divided by 3 is 4. They get 4 each.
Draw a line under the 6, subtract, and write 2 below the line. Bring down the next digit. Now, bring down the next digit of the dividend, which is 4, to sit next to the 2, making 24. Repeat the steps. 3 goes into 24 eight times (3 x 8 = 24), so write 8 above the bar next to the 2. Subtract 24 from 24 to get 0.
Word Problem Worksheetss for Division. Division word problems can be some of the more confusing problems for students to understand. Many division problems will use words like 'share among' or 'give to each' or similar phraseology to imply that a total amount is to be split evenly into groups. This partitioning operation is the key concept in ...
Division Problem Solving Examples. Example 1: Mr. Karthik went to a stationary shop and bought 30 notebooks costing $450. Find the cost of each book. Solution: The total amount paid at the shop = $450. The number of books bought from the shop = 30. The cost of each notebook = $450 ÷ 30. Therefore, the cost of each book is $15.
Math explained in easy language, plus puzzles, games, quizzes, videos and worksheets. For K-12 kids, teachers and parents. Long Division Worksheets Worksheets » Long Division Without Remainders. Worksheet Divisor Range; Easy : 2 to 9: Getting Tougher : 6 to 12: Intermediate : 10 to 20: Advanced : 20 to 50: Very Hard : 50 to 199: With ...