how to test hypothesis using t test

t-test Calculator

When to use a t-test, which t-test, how to do a t-test, p-value from t-test, t-test critical values, how to use our t-test calculator, one-sample t-test, two-sample t-test, paired t-test, t-test vs z-test.

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

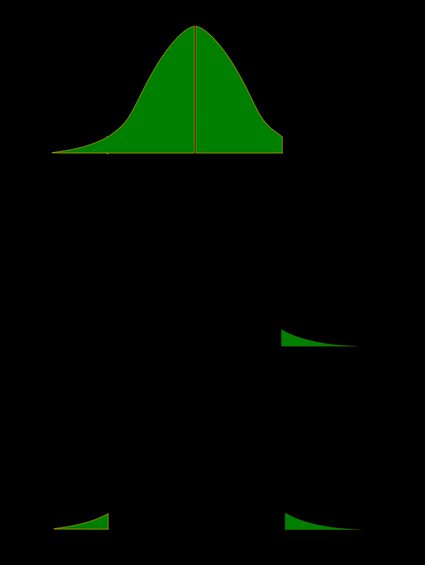
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

Bertrand's paradox

Confusion matrix, plant spacing, secretary problem (valentine's day).

• Biology (99)
• Chemistry (98)
• Construction (144)
• Conversion (292)
• Ecology (30)
• Everyday life (261)
• Finance (569)
• Health (440)
• Physics (508)
• Sports (104)
• Statistics (182)
• Other (181)
• Discover Omni (40)

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

• State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a  or H 1 ).
• Collect data in a way designed to test the hypothesis.
• Perform an appropriate statistical test .
• Decide whether to reject or fail to reject your null hypothesis.
• Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Table of contents

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

• H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

• an estimate of the difference in average height between the two groups.
• a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

Prevent plagiarism. Run a free check.

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Normal distribution
• Descriptive statistics
• Measures of central tendency
• Correlation coefficient

Methodology

• Cluster sampling
• Stratified sampling
• Types of interviews
• Cohort study
• Thematic analysis

Research bias

• Implicit bias
• Cognitive bias
• Survivorship bias
• Availability heuristic
• Nonresponse bias
• Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved March 22, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.2: Hypothesis Testing with t

• Last updated
• Save as PDF
• Page ID 7127

• Foster et al.
• University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

Hypothesis testing with the \(t\)-statistic works exactly the same way as \(z\)-tests did, following the four-step process of

• Stating the Hypothesis
• Finding the Critical Values
• Computing the Test Statistic
• Making the Decision.

We will work though an example: let’s say that you move to a new city and find a an auto shop to change your oil. Your old mechanic did the job in about 30 minutes (though you never paid close enough attention to know how much that varied), and you suspect that your new shop takes much longer. After 4 oil changes, you think you have enough evidence to demonstrate this.

Step 1: State the Hypotheses Our hypotheses for 1-sample t-tests are identical to those we used for \(z\)-tests. We still state the null and alternative hypotheses mathematically in terms of the population parameter and written out in readable English. For our example:

\(H_0\): There is no difference in the average time to change a car’s oil

\(H_0: μ = 30\)

\(H_A\): This shop takes longer to change oil than your old mechanic

\(H_A: μ > 30\)

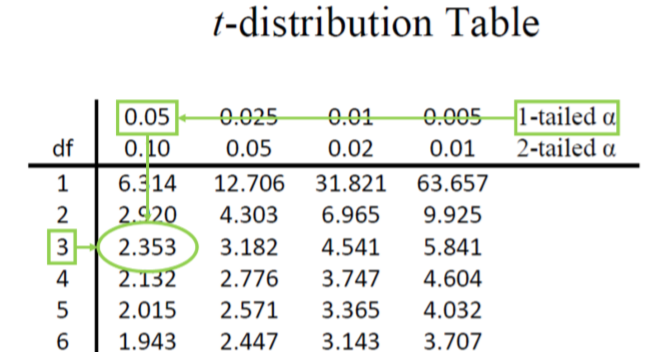
Step 2: Find the Critical Values As noted above, our critical values still delineate the area in the tails under the curve corresponding to our chosen level of significance. Because we have no reason to change significance levels, we will use \(α\) = 0.05, and because we suspect a direction of effect, we have a one-tailed test. To find our critical values for \(t\), we need to add one more piece of information: the degrees of freedom. For this example:

\[df = N – 1 = 4 – 1 = 3 \nonumber \]

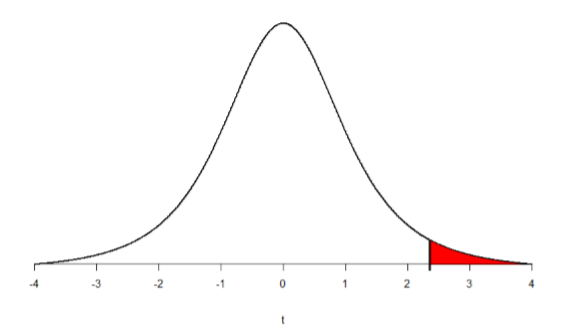
Going to our \(t\)-table, we find the column corresponding to our one-tailed significance level and find where it intersects with the row for 3 degrees of freedom. As shown in Figure \(\PageIndex{1}\): our critical value is \(t*\) = 2.353

We can then shade this region on our \(t\)-distribution to visualize our rejection region

Step 3: Compute the Test Statistic The four wait times you experienced for your oil changes are the new shop were 46 minutes, 58 minutes, 40 minutes, and 71 minutes. We will use these to calculate \(\overline{\mathrm{X}}\) and s by first filling in the sum of squares table in Table \(\PageIndex{1}\):

After filling in the first row to get \(\Sigma\)=215, we find that the mean is \(\overline{\mathrm{X}}\) = 53.75 (215 divided by sample size 4), which allows us to fill in the rest of the table to get our sum of squares \(SS\) = 564.74, which we then plug in to the formula for standard deviation from chapter 3:

\[s=\sqrt{\dfrac{\sum(X-\overline{X})^{2}}{N-1}}=\sqrt{\dfrac{S S}{d f}}=\sqrt{\dfrac{564.74}{3}}=13.72 \nonumber \]

Next, we take this value and plug it in to the formula for standard error:

\[s_{\overline{X}}=\dfrac{s}{\sqrt{n}}=\dfrac{13.72}{2}=6.86 \nonumber \]

And, finally, we put the standard error, sample mean, and null hypothesis value into the formula for our test statistic \(t\):

\[t=\dfrac{\overline{\mathrm{X}}-\mu}{s_{\overline{\mathrm{X}}}}=\dfrac{53.75-30}{6.86}=\dfrac{23.75}{6.68}=3.46 \nonumber \]

This may seem like a lot of steps, but it is really just taking our raw data to calculate one value at a time and carrying that value forward into the next equation: data  sample size/degrees of freedom  mean  sum of squares  standard deviation  standard error  test statistic. At each step, we simply match the symbols of what we just calculated to where they appear in the next formula to make sure we are plugging everything in correctly.

Step 4: Make the Decision Now that we have our critical value and test statistic, we can make our decision using the same criteria we used for a \(z\)-test. Our obtained \(t\)-statistic was \(t\) = 3.46 and our critical value was \(t* = 2.353: t > t*\), so we reject the null hypothesis and conclude:

Based on our four oil changes, the new mechanic takes longer on average (\(\overline{\mathrm{X}}\) = 53.75) to change oil than our old mechanic, \(t(3)\) = 3.46, \(p\) < .05.

Notice that we also include the degrees of freedom in parentheses next to \(t\). And because we found a significant result, we need to calculate an effect size, which is still Cohen’s \(d\), but now we use \(s\) in place of \(σ\):

\[d=\dfrac{\overline{X}-\mu}{s}=\dfrac{53.75-30.00}{13.72}=1.73 \nonumber \]

This is a large effect. It should also be noted that for some things, like the minutes in our current example, we can also interpret the magnitude of the difference we observed (23 minutes and 45 seconds) as an indicator of importance since time is a familiar metric.

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

The Ultimate Guide to T Tests

Get all of your t test questions answered here

The ultimate guide to t tests

The t test is one of the simplest statistical techniques that is used to evaluate whether there is a statistical difference between the means from up to two different samples. The t test is especially useful when you have a small number of sample observations (under 30 or so), and you want to make conclusions about the larger population.

The characteristics of the data dictate the appropriate type of t test to run. All t tests are used as standalone analyses for very simple experiments and research questions as well as to perform individual tests within more complicated statistical models such as linear regression. In this guide, we’ll lay out everything you need to know about t tests, including providing a simple workflow to determine what t test is appropriate for your particular data or if you’d be better suited using a different model.

What is a t test?

A t test is a statistical technique used to quantify the difference between the mean (average value) of a variable from up to two samples (datasets). The variable must be numeric. Some examples are height, gross income, and amount of weight lost on a particular diet.

A t test tells you if the difference you observe is “surprising” based on the expected difference. They use t-distributions to evaluate the expected variability. When you have a reasonable-sized sample (over 30 or so observations), the t test can still be used, but other tests that use the normal distribution (the z test) can be used in its place.

Sometimes t tests are called “Student’s” t tests, which is simply a reference to their unusual history.

It got its name because a brewer from the Guinness Brewery, William Gosset , published about the method under the pseudonym "Student". He wanted to get information out of very small sample sizes (often 3-5) because it took so much effort to brew each keg for his samples.

When should I use a t test?

A t test is appropriate to use when you’ve collected a small, random sample from some statistical “population” and want to compare the mean from your sample to another value. The value for comparison could be a fixed value (e.g., 10) or the mean of a second sample.

For example, if your variable of interest is the average height of sixth graders in your region, then you might measure the height of 25 or 30 randomly-selected sixth graders. A t test could be used to answer questions such as, “Is the average height greater than four feet?”

How does a t test work?

Based on your experiment, t tests make enough assumptions about your experiment to calculate an expected variability, and then they use that to determine if the observed data is statistically significant. To do this, t tests rely on an assumed “null hypothesis.” With the above example, the null hypothesis is that the average height is less than or equal to four feet.

Say that we measure the height of 5 randomly selected sixth graders and the average height is five feet. Does that mean that the “true” average height of all sixth graders is greater than four feet or did we randomly happen to measure taller than average students?

To evaluate this, we need a distribution that shows every possible average value resulting from a sample of five individuals in a population where the true mean is four. That may seem impossible to do, which is why there are particular assumptions that need to be made to perform a t test.

With those assumptions, then all that’s needed to determine the “sampling distribution of the mean” is the sample size (5 students in this case) and standard deviation of the data (let’s say it’s 1 foot).

That’s enough to create a graphic of the distribution of the mean, which is:

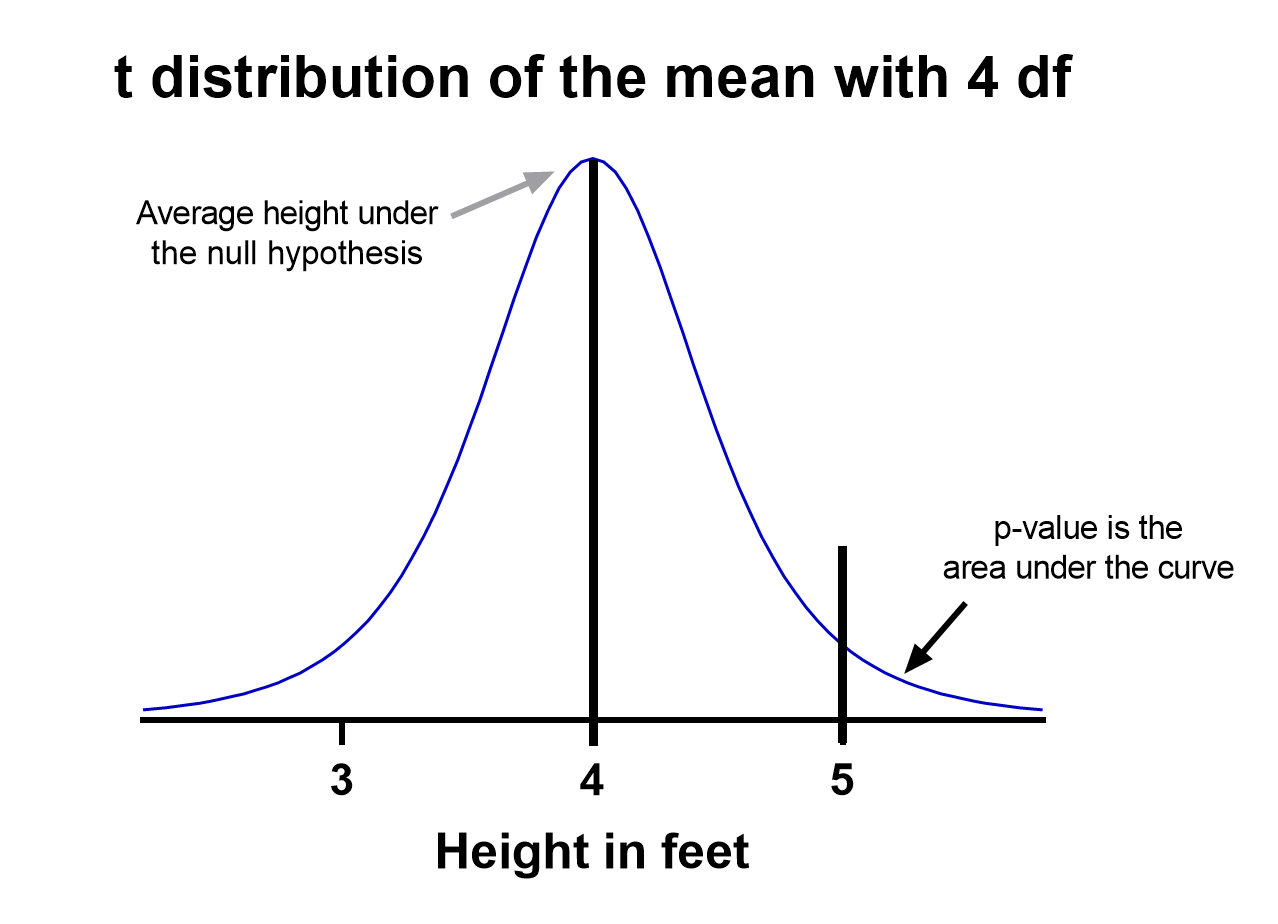
Notice the vertical line at x = 5, which was our sample mean. We (use software to) calculate the area to the right of the vertical line, which gives us the P value (0.09 in this case). Note that because our research question was asking if the average student is greater than four feet, the distribution is centered at four. Since we’re only interested in knowing if the average is greater than four feet, we use a one-tailed test in this case.

Using the standard confidence level of 0.05 with this example, we don’t have evidence that the true average height of sixth graders is taller than 4 feet.

What are the assumptions for t tests?

• One variable of interest : This is not correlation or regression, where you are interested in the relationship between multiple variables. With a t test, you can have different samples, but they are all measuring the same variable (e.g., height).
• Numeric data: You are dealing with a list of measurements that can be averaged. This means you aren’t just counting occurrences in various categories (e.g., eye color or political affiliation).
• Two groups or less: If you have more than two samples of data, a t test is the wrong technique. You most likely need to try ANOVA.
• Random sample : You need a random sample from your statistical “population of interest” in order to draw valid conclusions about the larger population. If your population is so small that you can measure everything, then you have a “census” and don’t need statistics. This is because you don’t need to estimate the truth, since you have measured the truth without variability.
• Normally Distributed : The smaller your sample size, the more important it is that your data come from a normal, Gaussian distribution bell curve. If you have reason to believe that your data are not normally distributed, consider nonparametric t test alternatives . This isn’t necessary for larger samples (usually 25 or 30 unless the data is heavily skewed). The reason is that the Central Limit Theorem applies in this case, which says that even if the distribution of your data is not normal, the distribution of the mean of your data is, so you can use a z-test rather than a t test.

How do I know which t test to use?

There are many types of t tests to choose from, but you don’t necessarily have to understand every detail behind each option.

You just need to be able to answer a few questions, which will lead you to pick the right t test. To that end, we put together this workflow for you to figure out which test is appropriate for your data.

Do you have one or two samples?

Are you comparing the means of two different samples, or comparing the mean from one sample to a fixed value? An example research question is, “Is the average height of my sample of sixth grade students greater than four feet?”

If you only have one sample of data, you can click here to skip to a one-sample t test example, otherwise your next step is to ask: 

Are observations in the two samples matched up or related in some way?

This could be as before-and-after measurements of the same exact subjects, or perhaps your study split up “pairs” of subjects (who are technically different but share certain characteristics of interest) into the two samples. The same variable is measured in both cases.

If so, you are looking at some kind of paired samples t test . The linked section will help you dial in exactly which one in that family is best for you, either difference (most common) or ratio.

If you aren’t sure paired is right, ask yourself another question:

Are you comparing different observations in each of the two samples?

If the answer is yes, then you have an unpaired or independent samples t test. The two samples should measure the same variable (e.g., height), but are samples from two distinct groups (e.g., team A and team B). 

The goal is to compare the means to see if the groups are significantly different. For example, “Is the average height of team A greater than team B?” Unlike paired, the only relationship between the groups in this case is that we measured the same variable for both. There are two versions of unpaired samples t tests (pooled and unpooled) depending on whether you assume the same variance for each sample.

Have you run the same experiment multiple times on the same subject/observational unit?

If so, then you have a nested t test (unless you have more than two sample groups). This is a trickier concept to understand. One example is if you are measuring how well Fertilizer A works against Fertilizer B. Let’s say you have 12 pots to grow plants in (6 pots for each fertilizer), and you grow 3 plants in each pot.

In this case you have 6 observational units for each fertilizer, with 3 subsamples from each pot. You would want to analyze this with a nested t test . The “nested” factor in this case is the pots. It’s important to note that we aren’t interested in estimating the variability within each pot, we just want to take it into account.

You might be tempted to run an unpaired samples t test here, but that assumes you have 6*3 = 18 replicates for each fertilizer. However, the three replicates within each pot are related, and an unpaired samples t test wouldn’t take that into account.

What if none of these sound like my experiment?

If you’re not seeing your research question above, note that t tests are very basic statistical tools. Many experiments require more sophisticated techniques to evaluate differences. If the variable of interest is a proportion (e.g., 10 of 100 manufactured products were defective), then you’d use z-tests. If you take before and after measurements and have more than one treatment (e.g., control vs a treatment diet), then you need ANOVA.

How do I perform a t test using software?

If you’re wondering how to do a t test, the easiest way is with statistical software such as Prism or an online t test calculator .

If you’re using software, then all you need to know is which t test is appropriate ( use the workflow here ) and understand how to interpret the output. To do that, you’ll also need to:

• Determine whether your test is one or two-tailed
• Choose the level of significance

Is my test one or two-tailed? 

Whether or not you have a one- or two-tailed test depends on your research hypothesis. Choosing the appropriately tailed test is very important and requires integrity from the researcher. This is because you have more “power” with one-tailed tests, meaning that you can detect a statistically significant difference more easily. Unless you have written out your research hypothesis as one directional before you run your experiment, you should use a two-tailed test.

Two-tailed tests

Two-tailed tests are the most common, and they are applicable when your research question is simply asking, “is there a difference?”

One-tailed tests

Contrast that with one-tailed tests, where the research questions are directional, meaning that either the question is, “is it greater than ” or the question is, “is it less than ”. These tests can only detect a difference in one direction.

Choosing the level of significance

All t tests estimate whether a mean of a population is different than some other value, and with all estimates come some variability, or what statisticians call “error.” Before analyzing your data, you want to choose a level of significance, usually denoted by the Greek letter alpha, 𝛼. The scientific standard is setting alpha to be 0.05.

An alpha of 0.05 results in 95% confidence intervals, and determines the cutoff for when P values are considered statistically significant.

One sample t test

If you only have one sample of a list of numbers, you are doing a one-sample t test. All you are interested in doing is comparing the mean from this group with some known value to test if there is evidence, that it is significantly different from that standard. Use our free one-sample t test calculator for this.

A one sample t test example research question is, “Is the average fifth grader taller than four feet?”

It is the simplest version of a t test, and has all sorts of applications within hypothesis testing. Sometimes the “known value” is called the “null value”. While the null value in t tests is often 0, it could be any value. The name comes from being the value which exactly represents the null hypothesis, where no significant difference exists. 

Any time you know the exact number you are trying to compare your sample of data against, this could work well. And of course: it can be either one or two-tailed.

One sample t test formula

Statistical software handles this for you, but if you want the details, the formula for a one sample t test is:

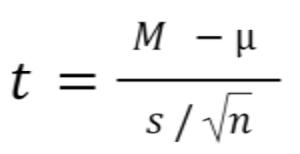
• M: Calculated mean of your sample
• μ: Hypothetical mean you are testing against
• s: The standard deviation of your sample
• n: The number of observations in your sample.

In a one-sample t test, calculating degrees of freedom is simple: one less than the number of objects in your dataset (you’ll see it written as n-1 ).

Example of a one sample t test

For our example within Prism, we have a dataset of 12 values from an experiment labeled “% of control”. Perhaps these are heights of a sample of plants that have been treated with a new fertilizer. A value of 100 represents the industry-standard control height. Likewise, 123 represents a plant with a height 123% that of the control (that is, 23% larger).

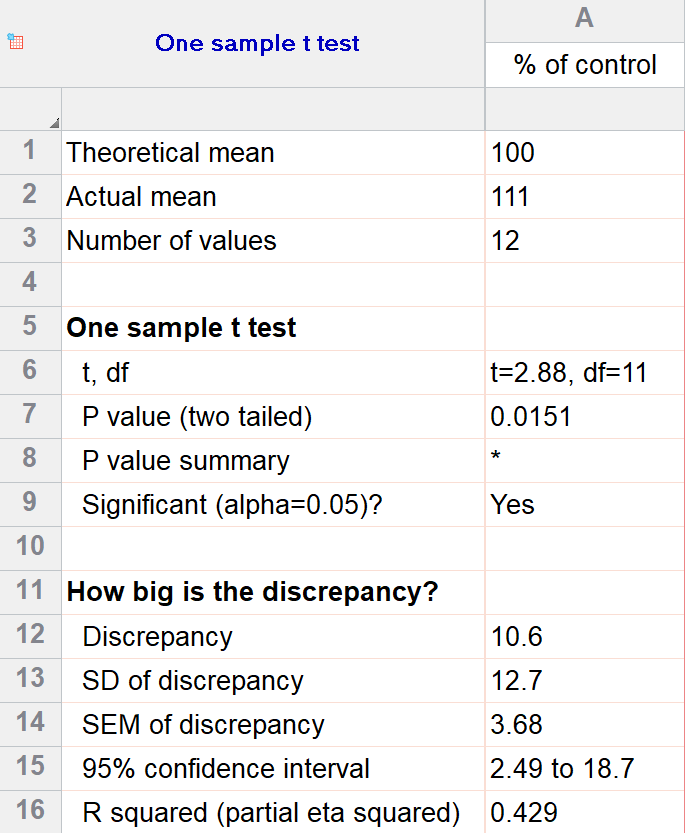
We’ll perform a two-tailed, one-sample t test to see if plants are shorter or taller on average with the fertilizer. We will use a significance threshold of 0.05. Here is the output:

You can see in the output that the actual sample mean was 111. Is that different enough from the industry standard (100) to conclude that there is a statistical difference?

The quick answer is yes, there’s strong evidence that the height of the plants with the fertilizer is greater than the industry standard (p=0.015). The nice thing about using software is that it handles some of the trickier steps for you. In this case, it calculates your test statistic (t=2.88), determines the appropriate degrees of freedom (11), and outputs a P value.

More informative than the P value is the confidence interval of the difference, which is 2.49 to 18.7. The confidence interval tells us that, based on our data, we are confident that the true difference between our sample and the baseline value of 100 is somewhere between 2.49 and 18.7. As long as the difference is statistically significant, the interval will not contain zero.

You can follow these tips for interpreting your own one-sample test.

Graphing a one-sample t test

For some techniques (like regression), graphing the data is a very helpful part of the analysis. For t tests, making a chart of your data is still useful to spot any strange patterns or outliers, but the small sample size means you may already be familiar with any strange things in your data.

Here we have a simple plot of the data points, perhaps with a mark for the average. We’ve made this as an example, but the truth is that graphing is usually more visually telling for two-sample t tests than for just one sample.

Two sample t tests

There are several kinds of two sample t tests, with the two main categories being paired and unpaired (independent) samples.

Paired samples t test

In a paired samples t test, also called dependent samples t test, there are two samples of data, and each observation in one sample is “paired” with an observation in the second sample. The most common example is when measurements are taken on each subject before and after a treatment. A paired t test example research question is, “Is there a statistical difference between the average red blood cell counts before and after a treatment?”

Having two samples that are closely related simplifies the analysis. Statistical software, such as this paired t test calculator , will simply take a difference between the two values, and then compare that difference to 0.

In some (rare) situations, taking a difference between the pairs violates the assumptions of a t test, because the average difference changes based on the size of the before value (e.g., there’s a larger difference between before and after when there were more to start with). In this case, instead of using a difference test, use a ratio of the before and after values, which is referred to as ratio t tests .

Paired t test formula

The formula for paired samples t test is:

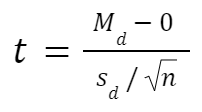
• Md: Mean difference between the samples
• sd: The standard deviation of the differences
• n: The number of differences

Degrees of freedom are the same as before. If you’re studying for an exam, you can remember that the degrees of freedom are still n-1 (not n-2) because we are converting the data into a single column of differences rather than considering the two groups independently.

Also note that the null value here is simply 0. There is no real reason to include “minus 0” in an equation other than to illustrate that we are still doing a hypothesis test. After you take the difference between the two means, you are comparing that difference to 0.

For our example data, we have five test subjects and have taken two measurements from each: before (“control”) and after a treatment (“treated”). If we set alpha = 0.05 and perform a two-tailed test, we observe a statistically significant difference between the treated and control group (p=0.0160, t=4.01, df = 4). We are 95% confident that the true mean difference between the treated and control group is between 0.449 and 2.47.

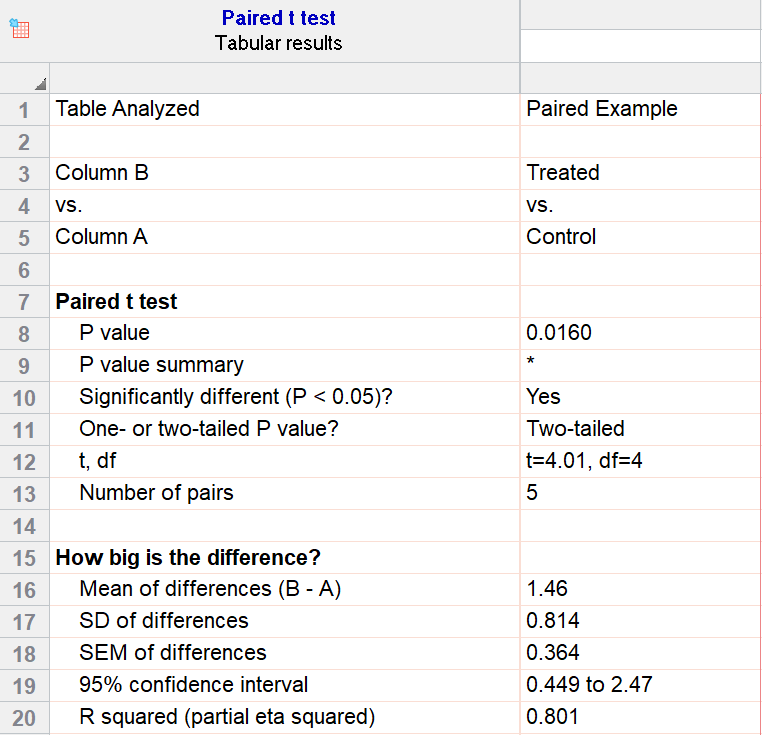
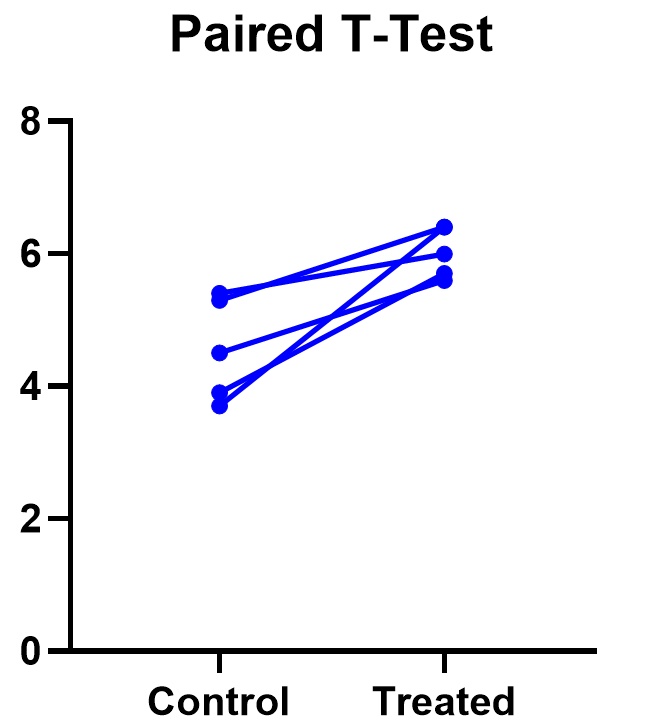
Graphing a paired t test

The significant result of the P value suggests evidence that the treatment had some effect, and we can also look at this graphically. The lines that connect the observations can help us spot a pattern, if it exists. In this case the lines show that all observations increased after treatment. While not all graphics are this straightforward, here it is very consistent with the outcome of the t test. 

Prism’s estimation plot is even more helpful because it shows both the data (like above) and the confidence interval for the difference between means. You can easily see the evidence of significance since the confidence interval on the right does not contain zero.

Here are some more graphing tips for paired t tests .

Unpaired samples t test

Unpaired samples t test, also called independent samples t test, is appropriate when you have two sample groups that aren’t correlated with one another. A pharma example is testing a treatment group against a control group of different subjects. Compare that with a paired sample, which might be recording the same subjects before and after a treatment.

With unpaired t tests, in addition to choosing your level of significance and a one or two tailed test, you need to determine whether or not to assume that the variances between the groups are the same or not. If you assume equal variances, then you can “pool” the calculation of the standard error between the two samples. Otherwise, the standard choice is Welch’s t test which corrects for unequal variances. This choice affects the calculation of the test statistic and the power of the test, which is the test’s sensitivity to detect statistical significance. 

It’s best to choose whether or not you’ll use a pooled or unpooled (Welch’s) standard error before running your experiment, because the standard statistical test is notoriously problematic. See more details about unequal variances here .

As long as you’re using statistical software, such as this two-sample t test calculator , it’s just as easy to calculate a test statistic whether or not you assume that the variances of your two samples are the same. If you’re doing it by hand, however, the calculations get more complicated with unequal variances.

Unpaired (independent) samples t test formula

The general two-sample t test formula is:

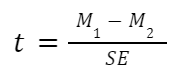
• M1 and M2: Two means you are comparing, one from each dataset
• SE : The combined standard error of the two samples (calculated using pooled or unpooled standard error)

The denominator (standard error) calculation can be complicated, as can the degrees of freedom. If the groups are not balanced (the same number of observations in each), you will need to account for both when determining n for the test as a whole.

As an example for this family, we conduct a paired samples t test assuming equal variances (pooled). Based on our research hypothesis, we’ll conduct a two-tailed test, and use alpha=0.05 for our level of significance. Our samples were unbalanced, with two samples of 6 and 5 observations respectively. 

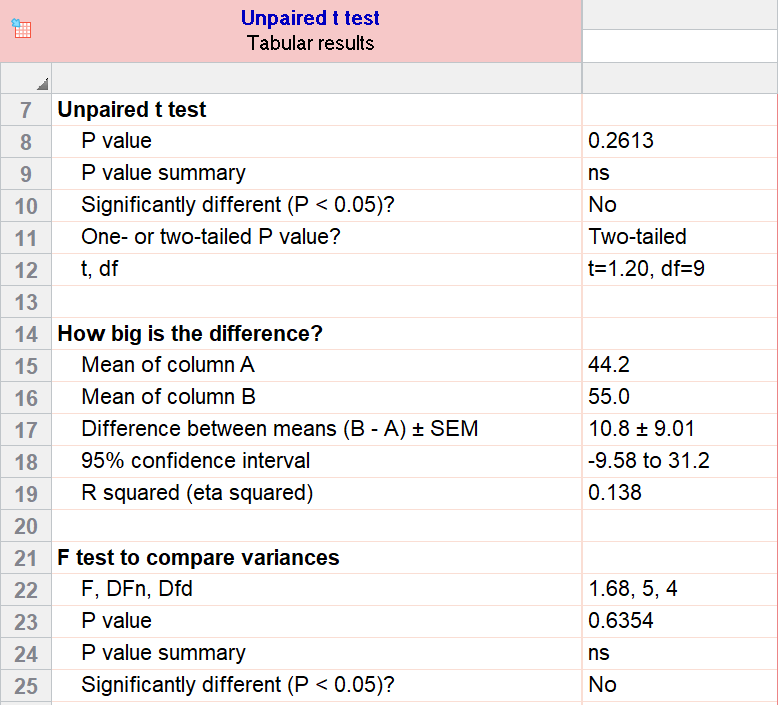
The P value (p=0.261, t = 1.20, df = 9) is higher than our threshold of 0.05. We have not found sufficient evidence to suggest a significant difference. You can see the confidence interval of the difference of the means is -9.58 to 31.2.

Note that the F-test result shows that the variances of the two groups are not significantly different from each other.

Graphing an unpaired samples t test

For an unpaired samples t test, graphing the data can quickly help you get a handle on the two groups and how similar or different they are. Like the paired example, this helps confirm the evidence (or lack thereof) that is found by doing the t test itself.

Below you can see that the observed mean for females is higher than that for males. But because of the variability in the data, we can’t tell if the means are actually different or if the difference is just by chance. 

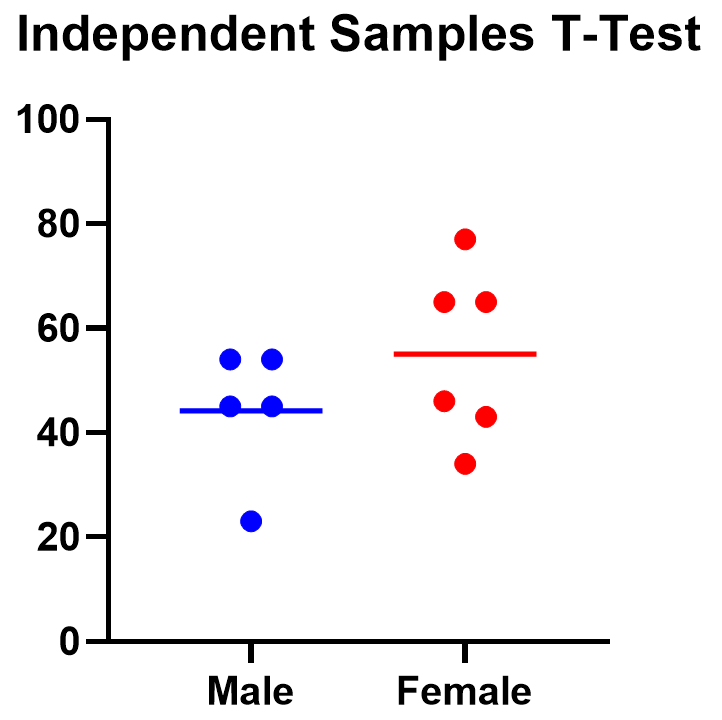
Nonparametric alternatives for t tests

If your data comes from a normal distribution (or something close enough to a normal distribution), then a t test is valid. If that assumption is violated, you can use nonparametric alternatives.

T tests evaluate whether the mean is different from another value, whereas nonparametric alternatives compare either the median or the rank. Medians are well-known to be much more robust to outliers than the mean.

The downside to nonparametric tests is that they don’t have as much statistical power, meaning a larger difference is required in order to determine that it’s statistically significant.

Wilcoxon signed-rank test

The Wilcoxon signed-rank test is the nonparametric cousin to the one-sample t test. This compares a sample median to a hypothetical median value. It is sometimes erroneously even called the Wilcoxon t test (even though it calculates a “W” statistic).

And if you have two related samples, you should use the Wilcoxon matched pairs test instead. The two versions of Wilcoxon are different, and the matched pairs version is specifically for comparing the median difference for paired samples. 

Mann-Whitney and Kolmogorov-Smirnov tests

For unpaired (independent) samples, there are multiple options for nonparametric testing. Mann-Whitney is more popular and compares the mean ranks (the ordering of values from smallest to largest) of the two samples. Mann-Whitney is often misrepresented as a comparison of medians, but that’s not always the case. Kolmogorov-Smirnov tests if the overall distributions differ between the two samples. 

More t test FAQs

What is the formula for a t test.

The exact formula depends on which type of t test you are running, although there is a basic structure that all t tests have in common. All t test statistics will have the form:

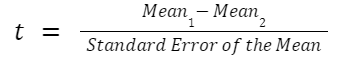
• t : The t test statistic you calculate for your test
• Mean1 and Mean2: Two means you are comparing, at least 1 from your own dataset
• Standard Error of the Mean : The standard error of the mean , also called the standard deviation of the mean, which takes into account the variance and size of your dataset

The exact formula for any t test can be slightly different, particularly the calculation of the standard error. Not only does it matter whether one or two samples are being compared, the relationship between the samples can make a difference too.

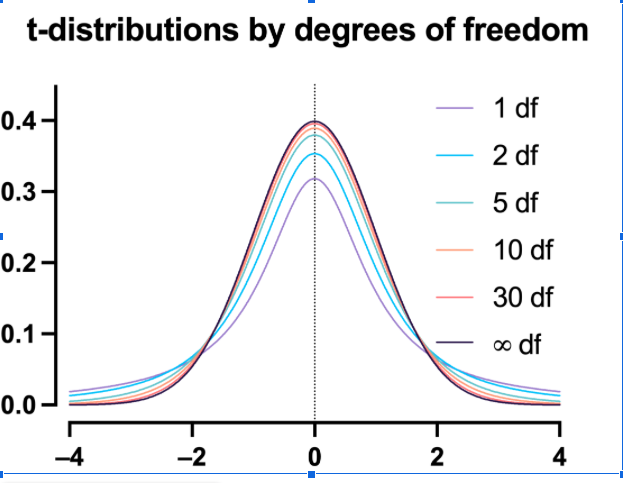
What is a t-distribution?

A t-distribution is similar to a normal distribution. It’s a bell-shaped curve, but compared to a normal it has fatter tails, which means that it’s more common to observe extremes. T-distributions are identified by the number of degrees of freedom. The higher the number, the closer the t-distribution gets to a normal distribution. After about 30 degrees of freedom, a t and a standard normal are practically the same.

What are degrees of freedom?

Degrees of freedom are a measure of how large your dataset is. They aren’t exactly the number of observations, because they also take into account the number of parameters (e.g., mean, variance) that you have estimated.

What is the difference between paired vs unpaired t tests?

Both paired and unpaired t tests involve two sample groups of data. With a paired t test, the values in each group are related (usually they are before and after values measured on the same test subject). In contrast, with unpaired t tests, the observed values aren’t related between groups. An unpaired, or independent t test, example is comparing the average height of children at school A vs school B. 

When do I use a z-test versus a t test?

Z-tests, which compare data using a normal distribution rather than a t-distribution, are primarily used for two situations. The first is when you’re evaluating proportions (number of failures on an assembly line). The second is when your sample size is large enough (usually around 30) that you can use a normal approximation to evaluate the means.

When should I use ANOVA instead of a t test?

Use ANOVA if you have more than two group means to compare.

What are the differences between t test vs chi square?

Chi square tests are used to evaluate contingency tables , which record a count of the number of subjects that fall into particular categories (e.g., truck, SUV, car). t tests compare the mean(s) of a variable of interest (e.g., height, weight).

What are P values?

P values are the probability that you would get data as or more extreme than the observed data given that the null hypothesis is true. It’s a mouthful, and there are a lot of issues to be aware of with P values.

What are t test critical values?

Critical values are a classical form (they aren’t used directly with modern computing) of determining if a statistical test is significant or not. Historically you could calculate your test statistic from your data, and then use a t-table to look up the cutoff value (critical value) that represented a “significant” result. You would then compare your observed statistic against the critical value.

How do I calculate degrees of freedom for my t test?

In most practical usage, degrees of freedom are the number of observations you have minus the number of parameters you are trying to estimate. The calculation isn’t always straightforward and is approximated for some t tests.

Statistical software calculates degrees of freedom automatically as part of the analysis, so understanding them in more detail isn’t needed beyond assuaging any curiosity.

Perform your own t test

Are you ready to calculate your own t test? Start your 30 day free trial of Prism and get access to:

• A step by step guide on how to perform a t test
• Sample data to save you time
• More tips on how Prism can help your research

With Prism, in a matter of minutes you learn how to go from entering data to performing statistical analyses and generating high-quality graphs.

Uncomplicated Reviews of Educational Research Methods

• Significance Testing (t-tests)

.pdf version of this page

In this review, we’ll look at significance testing, using mostly the t -test as a guide. As you read educational research, you’ll encounter t -test and ANOVA statistics frequently. Part I reviews the basics of significance testing as related to the null hypothesis and p values. Part II shows you how to conduct a t -test, using an online calculator. Part III deal s with interpreting t -test results. Part IV is about reporting t -test results in both text and table formats and concludes with a guide to interpreting confidence intervals.

What is Statistical Significance?

The terms “significance level” or “level of significance” refer to the likelihood that the random sample you choose (for example, test scores) is not representative of the population. The lower the significance level, the more confident you can be in replicating your results. Significance levels most commonly used in educational research are the .05 and .01 levels. If it helps, think of .05 as another way of saying 95/100 times that you sample from the population, you will get this result. Similarly, .01 suggests that 99/100 times that you sample from the population, you will get the same result. These numbers and signs (more on that later) come from Significance Testing, which begins with the Null Hypothesis.

Part I: The Null Hypothesis

We start by revisiting familiar territory, the scientific method . We’ll start with a basic research question: How does variable A affect variable B? The traditional way to test this question involves:

Step 1. Develop a research question.

Step 2. Find previous research to support, refute, or suggest ways of testing the question.

Step 3. Construct a hypothesis by revising your research question:

Step 4. Test the null hypothesis. To test the null hypothesis, A = B, we use a significance test. The italicized lowercase p you often see, followed by > or < sign and a decimal ( p ≤ .05) indicate significance. In most cases, the researcher tests the null hypothesis, A = B , because is it easier to show there is some sort of effect of A on B, than to have to determine a positive or negative effect prior to conducting the research. This way, you leave yourself room without having the burden of proof on your study from the beginning.

Step 5. Analyze data and draw a conclusion. Testing the null hypothesis leaves two possibilities:

Step 6. Communicate results. See Wording results, below.

Part II: Conducting a t -test (for Independent Means)

So how do we test a null hypothesis? One way is with a t -test. A t -test asks the question,

“Is the difference between the means of two samples different (significant) enough to say that some other characteristic (teaching method, teacher, gender, etc.) could have caused it?”

To conduct a t-test using an online calculator, complete the following steps:

Step 1. Compose the Research Question.

Step 2. Compose a Null and an Alternative Hypothesis.

Step 3. Obtain two random samples of at least 30, preferably 50, from each group.

Step 4. Conduct a t -test:

• Go to http://www.graphpad.com/quickcalcs/ttest1.cfm
• For #1, check “Enter mean, SD and N.”
• For #2, label your groups and enter data. You will need to have mean and SD. N is group size.
• For #3, check “Unpaired t test.”
• For #4, click “Calculate now.”

Step 5. Interpret the results (see below).

Step 6. Report results in text or table format (see below).

• Get p from “P value and statistical significance:” Note that this is the actual value.
• Get the confidence interval from “Confidence interval:”
• Get the t and df values from “Intermediate values used in calculations:”
• Get Mean , and SD from “Review your data.”

Part III. Interpreting a t-test (Understanding the Numbers)

Note: We acknowledge that the average scores are different. With a t -test we are deciding if that difference is significant (is it due to sampling error or something else?).

Understanding the Confidence Interval (CI)

The Confidence Interval (CI) of a mean is a region within which a score (like mean test score) may be said to fall with a certain amount of “confidence.” The CI uses sample size and standard deviation to generate a lower and upper number that you can be 95% sure will include any sample you take from a set of data.

Consider Georgia’s AYP measure, the CRCT . For a science CRCT score, we take several samples and compare the different means. After a few calculations, we could determine something like. . .the average difference (mean) between samples is -7.5, with a 95% CI of -22.08 to 6.72. In other words, among all students’ science CRCT scores, 95 out of 100 times we take group samples for comparison (for example by year, or gender, etc.), one of the groups, on average will be 7.5 points lower than the other group. We can be fairly certain that the difference in scores will be between -22.08 and 6.72 points.

Part IV. Wording Results

Wording Results in Text

In text, the basic format is to report: population ( N ), mean ( M ) and standard deviation ( SD ) for both samples, t value, degrees freedom ( df ), significance ( p ), and confidence interval (CI .95 )* .

Example 1: p ≤ .05, or Significant Results

Among 7th graders in Lowndes County Schools taking the CRCT reading exam ( N = 336), there was a statistically significant difference between the two teaching teams, team 1 ( M = 818.92, SD = 16.11) and team 2 ( M = 828.28, SD = 14.09), t (98) = 3.09, p ≤ .05, CI .95 -15.37, -3.35. Therefore, we reject the null hypothesis that there is no difference in reading scores between teaching teams 1 and 2.

Example 2: p ≥ .05, or Not Significant Results

Among 7th graders in Lowndes County Schools taking the CRCT science exam ( N = 336), there was no statistically significant difference between female students (M = 834.00, SD = 32.81) and male students (841.08, SD = 28.76), t (98) = 1.15 p ≥ .05, CI .95 -19.32, 5.16. Therefore, we fail to reject the null hypothesis that there is no difference in science scores between females and males.

Wording Results in APA Table Format

Table 1. Comparison of CRCT 7 th Grade Science Scores by Gender

Note: On the Web site, this appears blocked and should not be. See the .pdf for the correct format.

Share this:

About research rundowns.

Research Rundowns was made possible by support from the Dewar College of Education at Valdosta State University .

• Experimental Design
• What is Educational Research?
• Writing Research Questions
• Mixed Methods Research Designs
• Qualitative Coding & Analysis
• Qualitative Research Design
• Correlation
• Effect Size
• Instrument, Validity, Reliability
• Mean & Standard Deviation
• Steps 1-4: Finding Research
• Steps 5-6: Analyzing & Organizing
• Steps 7-9: Citing & Writing
• Writing a Research Report

Blog at WordPress.com.

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

What is a t- test?

A t -test (also known as Student's t -test) is a tool for evaluating the means of one or two populations using hypothesis testing. A t-test may be used to evaluate whether a single group differs from a known value ( a one-sample t-test ), whether two groups differ from each other ( an independent two-sample t-test ), or whether there is a significant difference in paired measurements ( a paired, or dependent samples t-test ).

How are t -tests used?

First, you define the hypothesis you are going to test and specify an acceptable risk of drawing a faulty conclusion. For example, when comparing two populations, you might hypothesize that their means are the same, and you decide on an acceptable probability of concluding that a difference exists when that is not true. Next, you calculate a test statistic from your data and compare it to a theoretical value from a  t- distribution. Depending on the outcome, you either reject or fail to reject your null hypothesis. 

What if I have more than two groups?

You cannot use a t -test. Use a multiple comparison method. Examples are analysis of variance ( ANOVA ) , Tukey-Kramer pairwise comparison, Dunnett's comparison to a control, and analysis of means (ANOM).  

t -Test assumptions

While t -tests are relatively robust to deviations from assumptions, t -tests do assume that:

• The data are continuous.
• The sample data have been randomly sampled from a population.
• There is homogeneity of variance (i.e., the variability of the data in each group is similar).
• The distribution is approximately normal.

For two-sample t -tests, we must have independent samples. If the samples are not independent, then a paired t -test may be appropriate.

Types of t -tests

There are three t -tests to compare means: a one-sample t -test, a two-sample t -test and a paired t -test. The table below summarizes the characteristics of each and provides guidance on how to choose the correct test. Visit the individual pages for each type of t -test for examples along with details on assumptions and calculations.

The table above shows only the t -tests for population means. Another common t -test is for correlation coefficients .  You use this t -test to decide if the correlation coefficient is significantly different from zero. 

One-tailed vs. two-tailed tests

When you define the hypothesis, you also define whether you have a one-tailed or a two-tailed test. You should make this decision before collecting your data or doing any calculations. You make this decision for all three of the t -tests for means.

To explain, let’s use the one-sample t -test. Suppose we have a random sample of protein bars, and the label for the bars advertises 20 grams of protein per bar. The null hypothesis is that the unknown population mean is 20. Suppose we simply want to know if the data shows we have a different population mean. In this situation, our hypotheses are:

$ \mathrm H_o: \mu = 20 $

$ \mathrm H_a: \mu \neq 20 $

Here, we have a two-tailed test. We will use the data to see if the sample average differs sufficiently from 20 – either higher or lower – to conclude that the unknown population mean is different from 20.

Suppose instead that we want to know whether the advertising on the label is correct. Does the data support the idea that the unknown population mean is at least 20? Or not? In this situation, our hypotheses are:

$ \mathrm H_o: \mu >= 20 $

$ \mathrm H_a: \mu < 20 $

Here, we have a one-tailed test. We will use the data to see if the sample average is sufficiently less than 20 to reject the hypothesis that the unknown population mean is 20 or higher.

See the "tails for hypotheses tests" section on the t -distribution page for images that illustrate the concepts for one-tailed and two-tailed tests.

How to perform a t -test

For all of the t -tests involving means, you perform the same steps in analysis:

• Define your null ($ \mathrm H_o $) and alternative ($ \mathrm H_a $) hypotheses before collecting your data.
• Decide on the alpha value (or α value). This involves determining the risk you are willing to take of drawing the wrong conclusion. For example, suppose you set α=0.05 when comparing two independent groups. Here, you have decided on a 5% risk of concluding the unknown population means are different when they are not.
• Check the data for errors.
• Check the assumptions for the test.
• Perform the test and draw your conclusion. All t -tests for means involve calculating a test statistic. You compare the test statistic to a theoretical value from the t- distribution . The theoretical value involves both the α value and the degrees of freedom for your data. For more detail, visit the pages for one-sample t -test , two-sample t -test and paired t -test .

• Search Search Please fill out this field.

What Is a T-Test?

Understanding the t-test, using a t-test, which t-test to use.

• T-Test FAQs
• Fundamental Analysis

T-Test: What It Is With Multiple Formulas and When To Use Them

Read how this calculation can be used for hypothesis testing in statistics

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

A t-test is an inferential statistic used to determine if there is a significant difference between the means of two groups and how they are related. T-tests are used when the data sets follow a normal distribution and have unknown variances, like the data set recorded from flipping a coin 100 times.

The t-test is a test used for hypothesis testing in statistics and uses the t-statistic, the t-distribution values, and the degrees of freedom to determine statistical significance.

Key Takeaways

• A t-test is an inferential statistic used to determine if there is a statistically significant difference between the means of two variables.
• The t-test is a test used for hypothesis testing in statistics.
• Calculating a t-test requires three fundamental data values including the difference between the mean values from each data set, the standard deviation of each group, and the number of data values.
• T-tests can be dependent or independent.

Investopedia / Sabrina Jiang

A t-test compares the average values of two data sets and determines if they came from the same population. In the above examples, a sample of students from class A and a sample of students from class B would not likely have the same mean and standard deviation. Similarly, samples taken from the placebo-fed control group and those taken from the drug prescribed group should have a slightly different mean and standard deviation.

Mathematically, the t-test takes a sample from each of the two sets and establishes the problem statement. It assumes a null hypothesis that the two means are equal.

Using the formulas, values are calculated and compared against the standard values. The assumed null hypothesis is accepted or rejected accordingly. If the null hypothesis qualifies to be rejected, it indicates that data readings are strong and are probably not due to chance.

The t-test is just one of many tests used for this purpose. Statisticians use additional tests other than the t-test to examine more variables and larger sample sizes. For a large sample size, statisticians use a  z-test . Other testing options include the chi-square test and the f-test.

Consider that a drug manufacturer tests a new medicine. Following standard procedure, the drug is given to one group of patients and a placebo to another group called the control group. The placebo is a substance with no therapeutic value and serves as a benchmark to measure how the other group, administered the actual drug, responds.

After the drug trial, the members of the placebo-fed control group reported an increase in average life expectancy of three years, while the members of the group who are prescribed the new drug reported an increase in average life expectancy of four years.

Initial observation indicates that the drug is working. However, it is also possible that the observation may be due to chance. A t-test can be used to determine if the results are correct and applicable to the entire population.

Four assumptions are made while using a t-test. The data collected must follow a continuous or ordinal scale, such as the scores for an IQ test, the data is collected from a randomly selected portion of the total population, the data will result in a normal distribution of a bell-shaped curve, and equal or homogenous variance exists when the standard variations are equal.

T-Test Formula

Calculating a t-test requires three fundamental data values. They include the difference between the mean values from each data set, or the mean difference, the standard deviation of each group, and the number of data values of each group.

This comparison helps to determine the effect of chance on the difference, and whether the difference is outside that chance range. The t-test questions whether the difference between the groups represents a true difference in the study or merely a random difference.

The t-test produces two values as its output: t-value and degrees of freedom . The t-value, or t-score, is a ratio of the difference between the mean of the two sample sets and the variation that exists within the sample sets.

The numerator value is the difference between the mean of the two sample sets. The denominator is the variation that exists within the sample sets and is a measurement of the dispersion or variability.

This calculated t-value is then compared against a value obtained from a critical value table called the T-distribution table. Higher values of the t-score indicate that a large difference exists between the two sample sets. The smaller the t-value, the more similarity exists between the two sample sets.

A large t-score, or t-value, indicates that the groups are different while a small t-score indicates that the groups are similar.

Degrees of freedom refer to the values in a study that has the freedom to vary and are essential for assessing the importance and the validity of the null hypothesis. Computation of these values usually depends upon the number of data records available in the sample set.

Paired Sample T-Test

The correlated t-test, or paired t-test, is a dependent type of test and is performed when the samples consist of matched pairs of similar units, or when there are cases of repeated measures. For example, there may be instances where the same patients are repeatedly tested before and after receiving a particular treatment. Each patient is being used as a control sample against themselves.

This method also applies to cases where the samples are related or have matching characteristics, like a comparative analysis involving children, parents, or siblings.

The formula for computing the t-value and degrees of freedom for a paired t-test is:

T = mean 1 − mean 2 s ( diff ) ( n ) where: mean 1  and  mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom \begin{aligned}&T=\frac{\textit{mean}1 - \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\&\textbf{where:}\\&\textit{mean}1\text{ and }\textit{mean}2=\text{The average values of each of the sample sets}\\&s(\text{diff})=\text{The standard deviation of the differences of the paired data values}\\&n=\text{The sample size (the number of paired differences)}\\&n-1=\text{The degrees of freedom}\end{aligned} ​ T = ( n ) ​ s ( diff ) ​ mean 1 − mean 2 ​ where: mean 1  and  mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom ​

Equal Variance or Pooled T-Test

The equal variance t-test is an independent t-test and is used when the number of samples in each group is the same, or the variance of the two data sets is similar.

The formula used for calculating t-value and degrees of freedom for equal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 n 1 + n 2 − 2 × 1 n 1 + 1 n 2 where: m e a n 1  and  m e a n 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned}&\text{T-value} = \frac{ mean1 - mean2 }{\frac {(n1 - 1) \times var1^2 + (n2 - 1) \times var2^2 }{ n1 +n2 - 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets}\\&var1 \text{ and } var2 = \text{Variance of each of the sample sets}\\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} ​ T-value = n 1 + n 2 − 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 ​ × n 1 1 ​ + n 2 1 ​ ​ m e an 1 − m e an 2 ​ where: m e an 1  and  m e an 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

Degrees of Freedom = n 1 + n 2 − 2 where: n 1  and  n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = n1 + n2 - 2 \\ &\textbf{where:}\\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} ​ Degrees of Freedom = n 1 + n 2 − 2 where: n 1  and  n 2 = Number of records in each sample set ​

Unequal Variance T-Test

The unequal variance t-test is an independent t-test and is used when the number of samples in each group is different, and the variance of the two data sets is also different. This test is also called Welch's t-test.

The formula used for calculating t-value and degrees of freedom for an unequal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( v a r 1 n 1 + v a r 2 n 2 ) where: m e a n 1  and  m e a n 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)}}}\\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets} \\&var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} ​ T-value = ( n 1 v a r 1 ​ + n 2 v a r 2 ​ ) ​ m e an 1 − m e an 2 ​ where: m e an 1  and  m e an 2 = Average values of each of the sample sets v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

Degrees of Freedom = ( v a r 1 2 n 1 + v a r 2 2 n 2 ) 2 ( v a r 1 2 n 1 ) 2 n 1 − 1 + ( v a r 2 2 n 2 ) 2 n 2 − 1 where: v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = \frac{ \left ( \frac{ var1^2 }{ n1 } + \frac{ var2^2 }{ n2 } \right )^2 }{ \frac{ \left ( \frac{ var1^2 }{ n1 } \right )^2 }{ n1 - 1 } + \frac{ \left ( \frac{ var2^2 }{ n2 } \right )^2 }{ n2 - 1}} \\ &\textbf{where:}\\ &var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} ​ Degrees of Freedom = n 1 − 1 ( n 1 v a r 1 2 ​ ) 2 ​ + n 2 − 1 ( n 2 v a r 2 2 ​ ) 2 ​ ( n 1 v a r 1 2 ​ + n 2 v a r 2 2 ​ ) 2 ​ where: v a r 1  and  v a r 2 = Variance of each of the sample sets n 1  and  n 2 = Number of records in each sample set ​

The following flowchart can be used to determine which t-test to use based on the characteristics of the sample sets. The key items to consider include the similarity of the sample records, the number of data records in each sample set, and the variance of each sample set.

Image by Julie Bang © Investopedia 2019

Example of an Unequal Variance T-Test

Assume that the diagonal measurement of paintings received in an art gallery is taken. One group of samples includes 10 paintings, while the other includes 20 paintings. The data sets, with the corresponding mean and variance values, are as follows:

Though the mean of Set 2 is higher than that of Set 1, we cannot conclude that the population corresponding to Set 2 has a higher mean than the population corresponding to Set 1.

Is the difference from 19.4 to 21.6 due to chance alone, or do differences exist in the overall populations of all the paintings received in the art gallery? We establish the problem by assuming the null hypothesis that the mean is the same between the two sample sets and conduct a t-test to test if the hypothesis is plausible.

Since the number of data records is different (n1 = 10 and n2 = 20) and the variance is also different, the t-value and degrees of freedom are computed for the above data set using the formula mentioned in the Unequal Variance T-Test section.

The t-value is -2.24787. Since the minus sign can be ignored when comparing the two t-values, the computed value is 2.24787.

The degrees of freedom value is 24.38 and is reduced to 24, owing to the formula definition requiring rounding down of the value to the least possible integer value.

One can specify a level of probability (alpha level, level of significance,  p ) as a criterion for acceptance. In most cases, a 5% value can be assumed.

Using the degree of freedom value as 24 and a 5% level of significance, a look at the t-value distribution table gives a value of 2.064. Comparing this value against the computed value of 2.247 indicates that the calculated t-value is greater than the table value at a significance level of 5%. Therefore, it is safe to reject the null hypothesis that there is no difference between means. The population set has intrinsic differences, and they are not by chance.

How Is the T-Distribution Table Used?

The T-Distribution Table is available in one-tail and two-tails formats. The former is used for assessing cases that have a fixed value or range with a clear direction, either positive or negative. For instance, what is the probability of the output value remaining below -3, or getting more than seven when rolling a pair of dice? The latter is used for range-bound analysis, such as asking if the coordinates fall between -2 and +2.

What Is an Independent T-Test?

The samples of independent t-tests are selected independent of each other where the data sets in the two groups don’t refer to the same values. They may include a group of 100 randomly unrelated patients split into two groups of 50 patients each. One of the groups becomes the control group and is administered a placebo, while the other group receives a prescribed treatment. This constitutes two independent sample groups that are unpaired and unrelated to each other.

What Does a T-Test Explain and How Are They Used?

A t-test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment has an effect on the population of interest, or whether two groups are different from one another.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

Independent t-test for two samples

Introduction.

The independent t-test, also called the two sample t-test, independent-samples t-test or student's t-test, is an inferential statistical test that determines whether there is a statistically significant difference between the means in two unrelated groups.

Null and alternative hypotheses for the independent t-test

The null hypothesis for the independent t-test is that the population means from the two unrelated groups are equal:

H 0 : u 1 = u 2

In most cases, we are looking to see if we can show that we can reject the null hypothesis and accept the alternative hypothesis, which is that the population means are not equal:

H A : u 1 ≠ u 2

To do this, we need to set a significance level (also called alpha) that allows us to either reject or accept the alternative hypothesis. Most commonly, this value is set at 0.05.

What do you need to run an independent t-test?

In order to run an independent t-test, you need the following:

• One independent, categorical variable that has two levels/groups.
• One continuous dependent variable.

Unrelated groups

Unrelated groups, also called unpaired groups or independent groups, are groups in which the cases (e.g., participants) in each group are different. Often we are investigating differences in individuals, which means that when comparing two groups, an individual in one group cannot also be a member of the other group and vice versa. An example would be gender - an individual would have to be classified as either male or female – not both.

Assumption of normality of the dependent variable

The independent t-test requires that the dependent variable is approximately normally distributed within each group.

Note: Technically, it is the residuals that need to be normally distributed, but for an independent t-test, both will give you the same result.

You can test for this using a number of different tests, but the Shapiro-Wilks test of normality or a graphical method, such as a Q-Q Plot, are very common. You can run these tests using SPSS Statistics, the procedure for which can be found in our Testing for Normality guide. However, the t-test is described as a robust test with respect to the assumption of normality. This means that some deviation away from normality does not have a large influence on Type I error rates. The exception to this is if the ratio of the smallest to largest group size is greater than 1.5 (largest compared to smallest).

What to do when you violate the normality assumption

If you find that either one or both of your group's data is not approximately normally distributed and groups sizes differ greatly, you have two options: (1) transform your data so that the data becomes normally distributed (to do this in SPSS Statistics see our guide on Transforming Data ), or (2) run the Mann-Whitney U test which is a non-parametric test that does not require the assumption of normality (to run this test in SPSS Statistics see our guide on the Mann-Whitney U Test ).

Assumption of homogeneity of variance

The independent t-test assumes the variances of the two groups you are measuring are equal in the population. If your variances are unequal, this can affect the Type I error rate. The assumption of homogeneity of variance can be tested using Levene's Test of Equality of Variances, which is produced in SPSS Statistics when running the independent t-test procedure. If you have run Levene's Test of Equality of Variances in SPSS Statistics, you will get a result similar to that below:

This test for homogeneity of variance provides an F -statistic and a significance value ( p -value). We are primarily concerned with the significance value – if it is greater than 0.05 (i.e., p > .05), our group variances can be treated as equal. However, if p < 0.05, we have unequal variances and we have violated the assumption of homogeneity of variances.

Overcoming a violation of the assumption of homogeneity of variance

If the Levene's Test for Equality of Variances is statistically significant, which indicates that the group variances are unequal in the population, you can correct for this violation by not using the pooled estimate for the error term for the t -statistic, but instead using an adjustment to the degrees of freedom using the Welch-Satterthwaite method. In all reality, you will probably never have heard of these adjustments because SPSS Statistics hides this information and simply labels the two options as "Equal variances assumed" and "Equal variances not assumed" without explicitly stating the underlying tests used. However, you can see the evidence of these tests as below:

From the result of Levene's Test for Equality of Variances, we can reject the null hypothesis that there is no difference in the variances between the groups and accept the alternative hypothesis that there is a statistically significant difference in the variances between groups. The effect of not being able to assume equal variances is evident in the final column of the above figure where we see a reduction in the value of the t -statistic and a large reduction in the degrees of freedom (df). This has the effect of increasing the p -value above the critical significance level of 0.05. In this case, we therefore do not accept the alternative hypothesis and accept that there are no statistically significant differences between means. This would not have been our conclusion had we not tested for homogeneity of variances.

Reporting the result of an independent t-test

When reporting the result of an independent t-test, you need to include the t -statistic value, the degrees of freedom (df) and the significance value of the test ( p -value). The format of the test result is: t (df) = t -statistic, p = significance value. Therefore, for the example above, you could report the result as t (7.001) = 2.233, p = 0.061.

Fully reporting your results

In order to provide enough information for readers to fully understand the results when you have run an independent t-test, you should include the result of normality tests, Levene's Equality of Variances test, the two group means and standard deviations, the actual t-test result and the direction of the difference (if any). In addition, you might also wish to include the difference between the groups along with a 95% confidence interval. For example:

Inspection of Q-Q Plots revealed that cholesterol concentration was normally distributed for both groups and that there was homogeneity of variance as assessed by Levene's Test for Equality of Variances. Therefore, an independent t-test was run on the data with a 95% confidence interval (CI) for the mean difference. It was found that after the two interventions, cholesterol concentrations in the dietary group (6.15 ± 0.52 mmol/L) were significantly higher than the exercise group (5.80 ± 0.38 mmol/L) ( t (38) = 2.470, p = 0.018) with a difference of 0.35 (95% CI, 0.06 to 0.64) mmol/L.

To know how to run an independent t-test in SPSS Statistics, see our SPSS Statistics Independent-Samples T-Test guide. Alternatively, you can carry out an independent-samples t-test using Excel, R and RStudio .

7. The t tests

• The calculation of a confidence interval for a sample mean.
• The mean and standard deviation of a sample are calculated and a value is postulated for the mean of the population. How significantly does the sample mean differ from the postulated population mean?
• The means and standard deviations of two samples are calculated. Could both samples have been taken from the same population?
• Paired observations are made on two samples (or in succession on one sample). What is the significance of the difference between the means of the two sets of observations?

Confidence interval for the mean from a small sample

One Sample T Test – Clearly Explained with Examples | ML+

• October 8, 2020
• Selva Prabhakaran

One sample T-Test tests if the given sample of observations could have been generated from a population with a specified mean.

If it is found from the test that the means are statistically different, we infer that the sample is unlikely to have come from the population.

For example: If you want to test a car manufacturer’s claim that their cars give a highway mileage of 20kmpl on an average. You sample 10 cars from the dealership, measure their mileage and use the T-test to determine if the manufacturer’s claim is true.

By end of this, you will know when and how to do the T-Test, the concept, math, how to set the null and alternate hypothesis, how to use the T-tables, how to understand the one-tailed and two-tailed T-Test and see how to implement in R and Python using a practical example.

Introduction

Purpose of one sample t test, how to set the null and alternate hypothesis, procedure to do one sample t test, one sample t test example, one sample t test implementation, how to decide which t test to perform two tailed, upper tailed or lower tailed.

• Related Posts

The ‘One sample T Test’ is one of the 3 types of T Tests . It is used when you want to test if the mean of the population from which the sample is drawn is of a hypothesized value. You will understand this statement better (and all of about One Sample T test) better by the end of this post.

T Test was first invented by William Sealy Gosset, in 1908. Since he used the pseudo name as ‘Student’ when publishing his method in the paper titled ‘Biometrika’, the test came to be know as Student’s T Test.

Since it assumes that the test statistic, typically the sample mean, follows the sampling distribution, the Student’s T Test is considered as a Parametric test.

The purpose of the One Sample T Test is to determine if a sample observations could have come from a process that follows a specific parameter (like the mean).

It is typically implemented on small samples.

For example, given a sample of 15 items, you want to test if the sample mean is the same as a hypothesized mean (population). That is, essentially you want to know if the sample came from the given population or not.

Let’s suppose, you want to test if the mean weight of a manufactured component (from a sample size 15) is of a particular value (55 grams), with a 99% confidence.

How did we determine One sample T-test is the right test for this?

Because, there is only one sample involved and you want to compare the mean of this sample against a particular (hypothesized) value..

To do this, you need to set up a null hypothesis and an alternate hypothesis .

The null hypothesis usually assumes that there is no difference in the sample means and the hypothesized mean (comparison mean). The purpose of the T Test is to test if the null hypothesis can be rejected or not.

Depending on the how the problem is stated, the alternate hypothesis can be one of the following 3 cases:

• Case 1: H1 : x̅ != µ. Used when the true sample mean is not equal to the comparison mean. Use Two Tailed T Test.
• Case 2: H1 : x̅ > µ. Used when the true sample mean is greater than the comparison mean. Use Upper Tailed T Test.
• Case 3: H1 : x̅ < µ. Used when the true sample mean is lesser than the comparison mean. Use Lower Tailed T Test.

Where x̅ is the sample mean and µ is the population mean for comparison. We will go more into the detail of these three cases after solving some practical examples.

Example 1: A customer service company wants to know if their support agents are performing on par with industry standards.

According to a report the standard mean resolution time is 20 minutes per ticket. The sample group has a mean at 21 minutes per ticket with a standard deviation of 7 minutes.

Can you tell if the company’s support performance is better than the industry standard or not?

Example 2: A farming company wants to know if a new fertilizer has improved crop yield or not.

Historic data shows the average yield of the farm is 20 tonne per acre. They decide to test a new organic fertilizer on a smaller sample of farms and observe the new yield is 20.175 tonne per acre with a standard deviation of 3.02 tonne for 12 different farms.

Did the new fertilizer work?

Step 1: Define the Null Hypothesis (H0) and Alternate Hypothesis (H1)

H0: Sample mean (x̅) = Hypothesized Population mean (µ)

H1: Sample mean (x̅) != Hypothesized Population mean (µ)

The alternate hypothesis can also state that the sample mean is greater than or less than the comparison mean.

Step 2: Compute the test statistic (T)

$$t = \frac{Z}{s} = \frac{\bar{X} – \mu}{\frac{\hat{\sigma}}{\sqrt{n}}}$$

where s is the standard error .

Step 3: Find the T-critical from the T-Table

Use the degree of freedom and the alpha level (0.05) to find the T-critical.

Step 4: Determine if the computed test statistic falls in the rejection region.

Alternately, simply compute the P-value. If it is less than the significance level (0.05 or 0.01), reject the null hypothesis.

Problem Statement:

We have the potato yield from 12 different farms. We know that the standard potato yield for the given variety is µ=20.

x = [21.5, 24.5, 18.5, 17.2, 14.5, 23.2, 22.1, 20.5, 19.4, 18.1, 24.1, 18.5]

Test if the potato yield from these farms is significantly better than the standard yield.

Step 1: Define the Null and Alternate Hypothesis

H0: x̅ = 20

H1: x̅ > 20

n = 12. Since this is one sample T test, the degree of freedom = n-1 = 12-1 = 11.

Let’s set alpha = 0.05, to meet 95% confidence level.

Step 2: Calculate the Test Statistic (T) 1. Calculate sample mean

$$\bar{X} = \frac{x_1 + x_2 + x_3 + . . + x_n}{n}$$

$$\bar{x} = 20.175$$

• Calculate sample standard deviation

$$\bar{\sigma} = \frac{(x_1 – \bar{x})^2 + (x_2 – \bar{x})^2 + (x_3 – \bar{x})^2 + . . + (x_n – \bar{x})^2}{n-1}$$

$$\sigma = 3.0211$$

• Substitute in the T Statistic formula

$$T = \frac{\bar{x} – \mu}{se} = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}$$

$$T = (20.175 – 20)/(3.0211/\sqrt{12}) = 0.2006$$

Step 3: Find the T-Critical

Confidence level = 0.95, alpha=0.05. For one tailed test, look under 0.05 column. For d.o.f = 12 – 1 = 11, T-Critical = 1.796 .

Now you might wonder why ‘One Tailed test’ was chosen. This is because of the way you define the alternate hypothesis. Had the null hypothesis simply stated that the sample means is not equal to 20, then we would have gone for a two tailed test. More details about this topic in the next section.

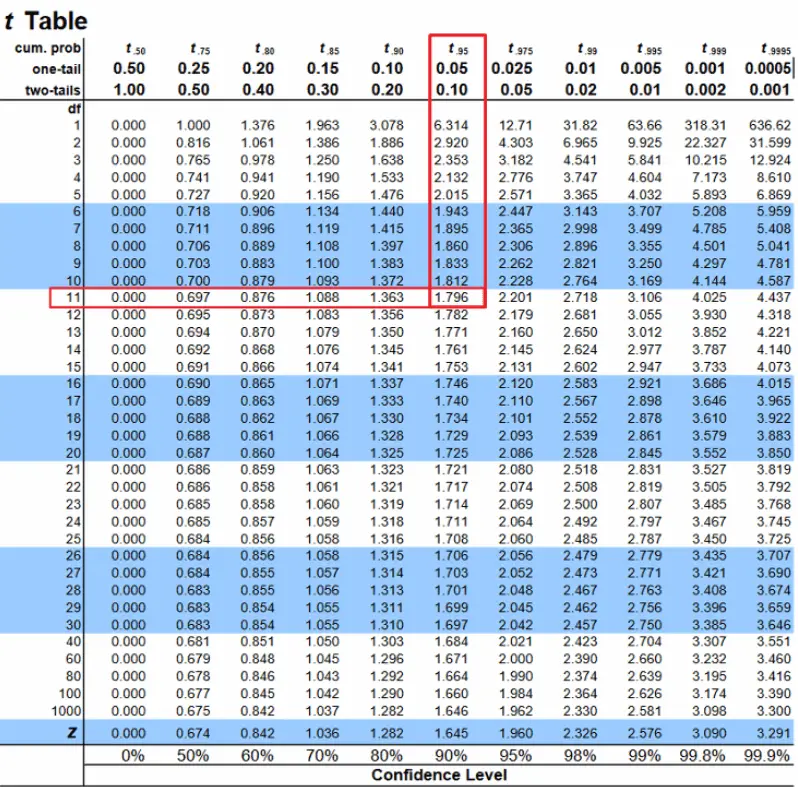
Step 4: Does it fall in rejection region?

Since the computed T Statistic is less than the T-critical, it does not fall in the rejection region.

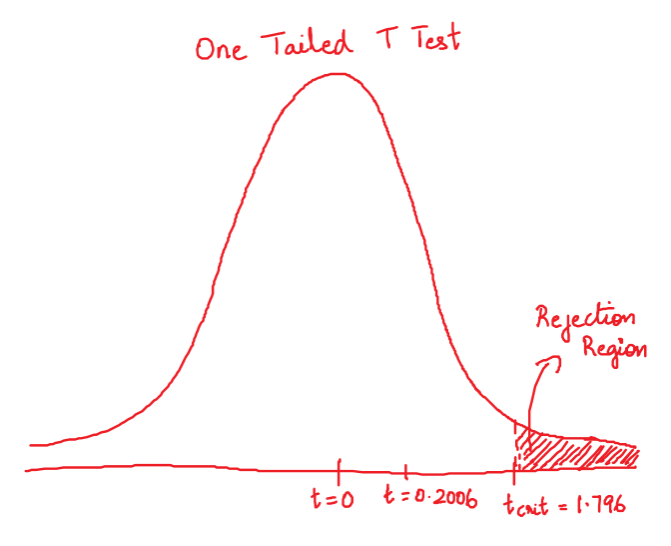
Clearly, the calculated T statistic does not fall in the rejection region. So, we do not reject the null hypothesis.

Since you want to perform a ‘One Tailed Greater than’ test (that is, the sample mean is greater than the comparison mean), you need to specify alternative='greater' in the t.test() function. Because, by default, the t.test() does a two tailed test (which is what you do when your alternate hypothesis simply states sample mean != comparison mean).

The P-value computed here is nothing but p = Pr(T > t) (upper-tailed), where t is the calculated T statistic.

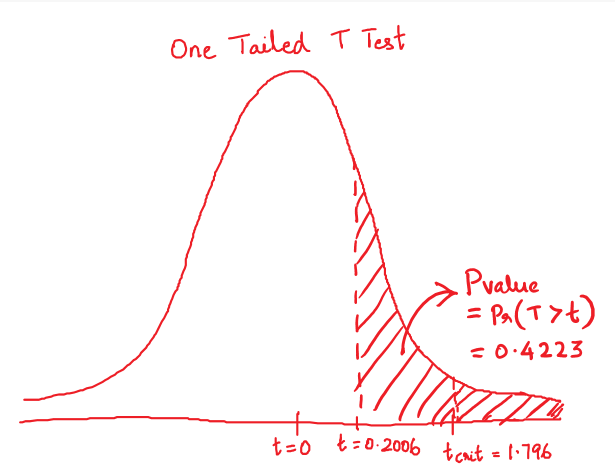
In Python, One sample T Test is implemented in ttest_1samp() function in the scipy package. However, it does a Two tailed test by default , and reports a signed T statistic. That means, the reported P-value will always be computed for a Two-tailed test. To calculate the correct P value, you need to divide the output P-value by 2.

Apply the following logic if you are performing a one tailed test:

For greater than test: Reject H0 if p/2 < alpha (0.05). In this case, t will be greater than 0. For lesser than test: Reject H0 if p/2 < alpha (0.05). In this case, t will be less than 0.

Since it is one tailed test, the real p-value is 0.8446/2 = 0.4223. We do not rejecting the Null Hypothesis anyway.

The decision of whether the computed test statistic falls in the rejection region depends on how the alternate hypothesis is defined.

We know the Null Hypothesis is H0: µD = 0. Where, µD is the difference in the means, that is sample mean minus the comparison mean.

You can also write H0 as: x̅ = µ , where x̅ is sample mean and ‘µ’ is the comparison mean.

Case 1: If H1 : x̅ != µ , then rejection region lies on both tails of the T-Distribution (two-tailed). This means the alternate hypothesis just states the difference in means is not equal. There is no comparison if one of the means is greater or lesser than the other.

In this case, use Two Tailed T Test .

Here, P value = 2 . Pr(T > | t |)

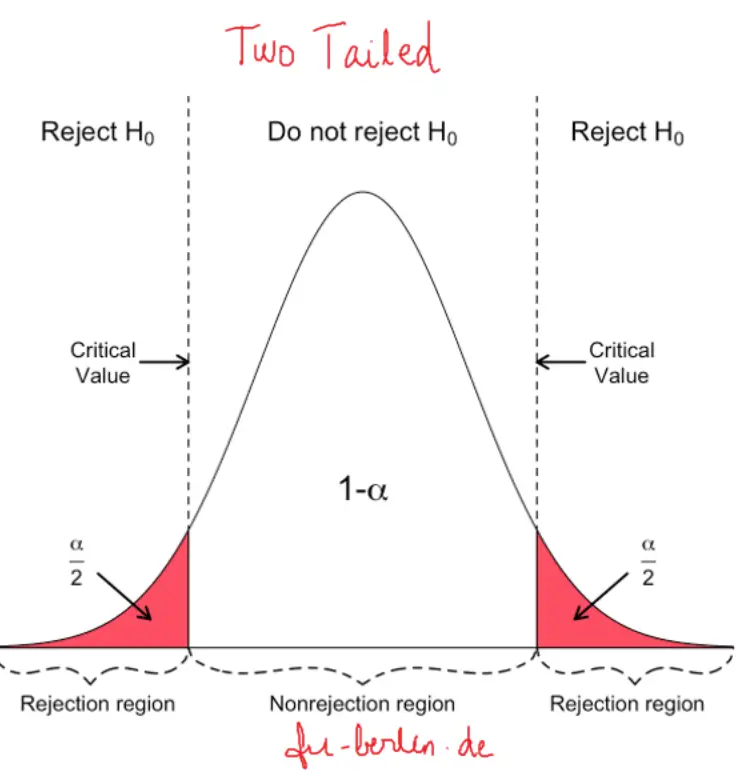
Case 2: If H1: x̅ > µ , then rejection region lies on upper tail of the T-Distribution (upper-tailed). If the mean of the sample of interest is greater than the comparison mean. Example: If Component A has a longer time-to-failure than Component B.

In such case, use Upper Tailed based test.

Here, P-value = Pr(T > t)

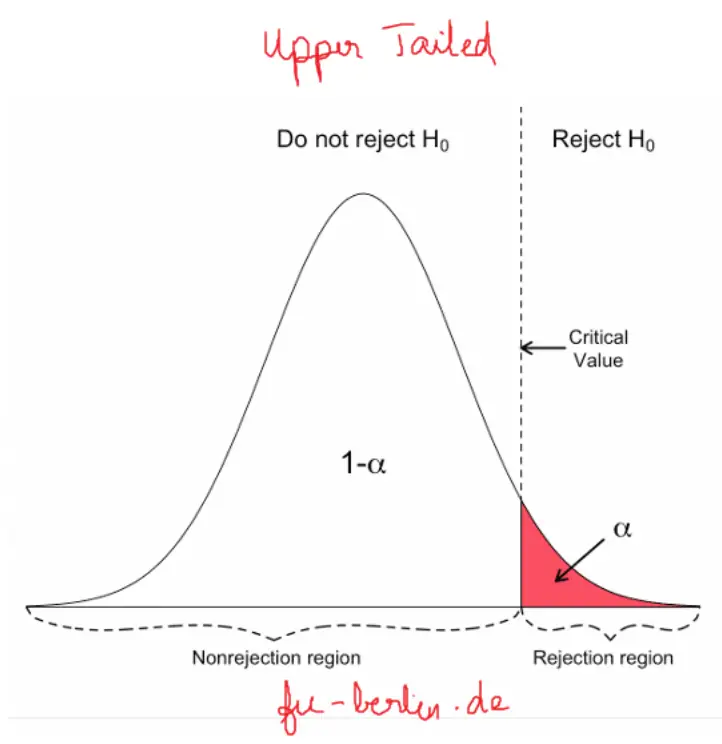
Case 3: If H1: x̅ < µ , then rejection region lies on lower tail of the T-Distribution (lower-tailed). If the mean of the sample of interest is lesser than the comparison mean.

In such case, use lower tailed test.

Here, P-value = Pr(T < t)

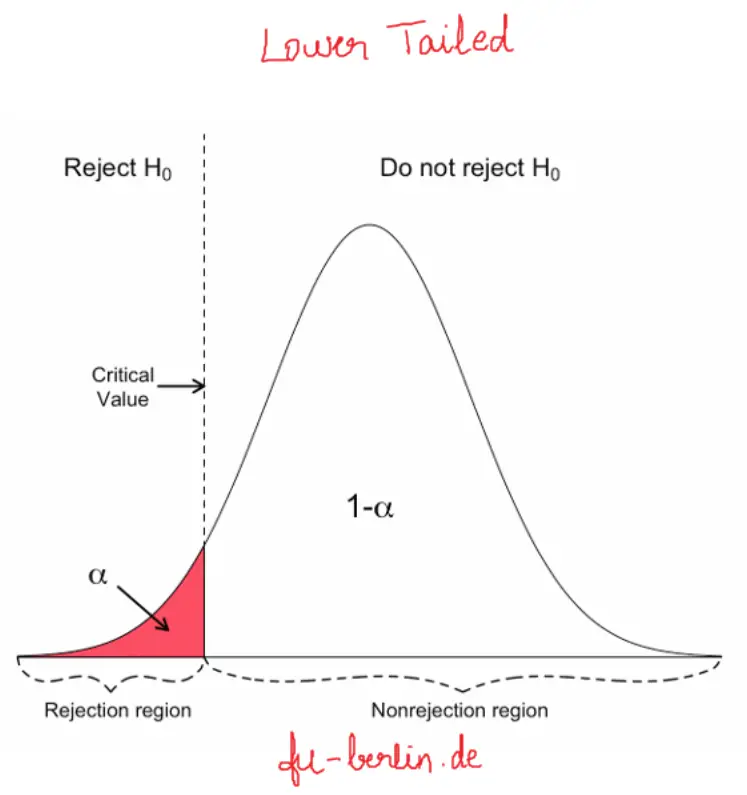
Hope you are now familiar and clear about with the One Sample T Test. If some thing is still not clear, write in comment. Next, topic is Two sample T test . Stay tuned.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, hypothesis testing – a deep dive into hypothesis testing, the backbone of statistical inference, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

• Practice Mathematical Algorithm
• Mathematical Algorithms
• Pythagorean Triplet
• Fibonacci Number
• Euclidean Algorithm
• LCM of Array
• GCD of Array
• Binomial Coefficient
• Catalan Numbers
• Sieve of Eratosthenes
• Euler Totient Function
• Modular Exponentiation
• Modular Multiplicative Inverse
• Stein's Algorithm
• Juggler Sequence
• Chinese Remainder Theorem
• Quiz on Fibonacci Numbers
• Solve Coding Problems
• Machine Learning Mathematics

Linear Algebra and Matrix

• Scalar and Vector
• Python Program to Add Two Matrices
• Python program to multiply two matrices
• Vector Operations
• Product of Vectors
• Scalar Product of Vectors
• Dot and Cross Products on Vectors
• Transpose a matrix in Single line in Python
• Transpose of a Matrix
• Adjoint and Inverse of a Matrix
• How to inverse a matrix using NumPy
• Determinant of a Matrix
• Program to find Normal and Trace of a matrix
• Data Science | Solving Linear Equations
• Data Science - Solving Linear Equations with Python
• System of Linear Equations
• System of Linear Equations in three variables using Cramer's Rule
• Eigenvalues
• Applications of Eigenvalues and Eigenvectors
• How to compute the eigenvalues and right eigenvectors of a given square array using NumPY?

Statistics for Machine Learning

• Descriptive Statistic
• Measures of Central Tendency
• Measures of Dispersion | Types, Formula and Examples
• Mean, Variance and Standard Deviation
• Calculate the average, variance and standard deviation in Python using NumPy
• Random Variables
• Difference between Parametric and Non-Parametric Methods
• Probability Distribution
• Confidence Interval
• Mathematics | Covariance and Correlation
• Program to find correlation coefficient
• Robust Correlation
• Normal Probability Plot
• Quantile Quantile plots
• True Error vs Sample Error
• Bias-Variance Trade Off - Machine Learning
• Understanding Hypothesis Testing
• Paired T-Test - A Detailed Overview
• P-value in Machine Learning
• F-Test in Statistics
• Residual Leverage Plot (Regression Diagnostic)
• Difference between Null and Alternate Hypothesis
• Mann and Whitney U test
• Wilcoxon Signed Rank Test
• Kruskal Wallis Test
• Friedman Test
• Mathematics | Probability

Probability and Probability Distributions

• Mathematics - Law of Total Probability
• Bayes's Theorem for Conditional Probability
• Mathematics | Probability Distributions Set 1 (Uniform Distribution)
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Mathematics | Probability Distributions Set 5 (Poisson Distribution)
• Uniform Distribution Formula
• Mathematics | Probability Distributions Set 2 (Exponential Distribution)
• Mathematics | Probability Distributions Set 3 (Normal Distribution)
• Mathematics | Beta Distribution Model
• Gamma Distribution Model in Mathematics
• Chi-Square Test for Feature Selection - Mathematical Explanation
• Student's t-distribution in Statistics
• Python - Central Limit Theorem
• Mathematics | Limits, Continuity and Differentiability
• Implicit Differentiation

Calculus for Machine Learning

• Engineering Mathematics - Partial Derivatives
• Advanced Differentiation
• How to find Gradient of a Function using Python?
• Optimization techniques for Gradient Descent
• Higher Order Derivatives
• Taylor Series
• Application of Derivative - Maxima and Minima | Mathematics
• Absolute Minima and Maxima
• Optimization for Data Science
• Unconstrained Multivariate Optimization
• Lagrange Multipliers
• Lagrange's Interpolation
• Linear Regression in Machine learning
• Ordinary Least Squares (OLS) using statsmodels

Regression in Machine Learning

In statistics, various tests are used to compare different samples or groups and draw conclusions about populations. These tests, known as statistical tests, focus on analyzing the likelihood or probability of obtaining the observed data under specific assumptions or hypotheses. They provide a framework for assessing evidence in support of or against a particular hypothesis.

A statistical test begins by formulating a null hypothesis (H 0 ) and an alternative hypothesis (H a ). The null hypothesis represents the default assumption, typically stating no effect or no difference, while the alternative hypothesis suggests a specific relationship or effect.

There are different statistical tests like Z-test , T-test, Chi-squared tests , ANOVA , Z-test , and F-test , etc. which are used to compute the p-value. In this article, we will learn about the T-test.

Table of Content

What is T-Test?

Assumptions in t-test, prerequisites for t-test, types of t-tests, one sample t-test, independent sample t-test, paired two-sample t-test, frequently asked questions on t-test.

The t-test is named after William Sealy Gosset’s Student’s t-distribution, created while he was writing under the pen name “Student.”

A t-test is a type of inferential statistic test used to determine if there is a significant difference between the means of two groups. It is often used when data is normally distributed and population variance is unknown.

The t-test is used in hypothesis testing to assess whether the observed difference between the means of the two groups is statistically significant or just due to random variation.

• Independence : The observations within each group must be independent of each other. This means that the value of one observation should not influence the value of another observation. Violations of independence can occur with repeated measures, paired data, or clustered data.
• Normality : The data within each group should be approximately normally distributed i.e the distribution of the data within each group being compared should resemble a normal (bell-shaped) distribution. This assumption is crucial for small sample sizes (n < 30).
• Homogeneity of Variances (for independent samples t-test) : The variances of the two groups being compared should be equal. This assumption ensures that the groups have a similar spread of values. Unequal variances can affect the standard error of the difference between means and, consequently, the t-statistic.
• Absence of Outliers: There should be no extreme outliers in the data as outliers can disproportionately influence the results, especially when sample sizes are small.

Let’s quickly review some related terms before digging deeper into the specifics of the t-test.

A t-test is a statistical method used to compare the means of two groups to determine if there is a significant difference between them. The t-test is a parametric test, meaning it makes certain assumptions about the data. Here are the key prerequisites for conducting a t-test.

Hypothesis Testing :

Hypothesis testing is a statistical method used to make inferences about a population based on a sample of data.

The p-value is the probability of observing a test statistic (or something more extreme) given that the null hypothesis is true.

• A small p-value (typically less than the chosen significance level) suggests that the observed data is unlikely to have occurred by random chance alone, leading to the rejection of the null hypothesis.
• A large p-value suggests that the observed data is likely to have occurred by random chance, and there is not enough evidence to reject the null hypothesis.

Degree of freedom (df):

Significance Level :

The significance level is the predetermined threshold that is used to decide whether to reject the null hypothesis. Commonly used significance levels are 0.05, 0.01, or 0.10. A significance level of 0.05 indicates that the researcher is willing to accept a 5% chance of making a Type I error (incorrectly rejecting a true null hypothesis).

T-statistic :

The t-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

• If the t-value is large => the two groups belong to different groups. 
• If the t-value is small => the two groups belong to the same group.

T-Distribution

The t-distribution , commonly known as the Student’s t-distribution, is a probability distribution with tails that are thicker than those of the normal distribution.

Statistical Significance

Statistical significance is determined by comparing the p-value to the chosen significance level.

• If the p-value is less than or equal to the significance level, the result is considered statistically significant, and the null hypothesis is rejected.
• If the p-value is greater than the significance level, the result is not statistically significant, and there is insufficient evidence to reject the null hypothesis.

In the context of a t-test, these concepts are applied to compare means between two groups. The t-test assesses whether the means are significantly different from each other, taking into account the variability within the groups. The p-value from the t-test is then compared to the significance level to make a decision about the null hypothesis.

A t-table, or a t-distribution table, is a reference table that provides critical values for the t-test. The table is organized by degrees of freedom and significance levels (usually 0.05 or 0.01). The t-table is used to find the critical t-value corresponding to their specific degrees of freedom and chosen significance level. If the calculated t-value is greater than the critical value from the table, it suggests that the observed difference is statistically significant.

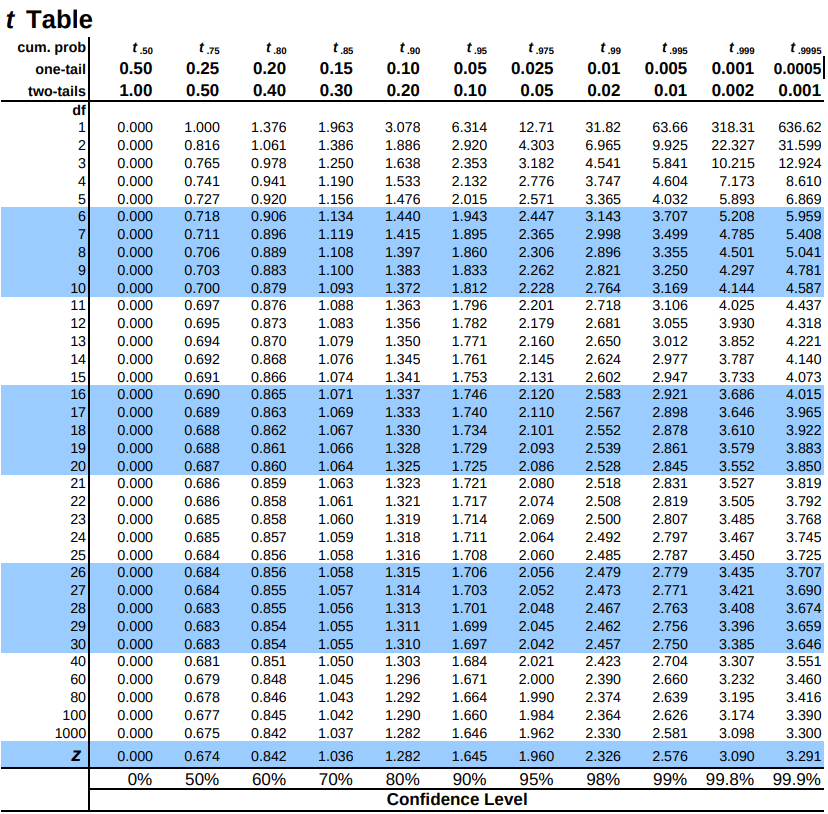
There are three types of t-tests, and they are categorized as dependent and independent t-tests.

• One sample t-test test: The mean of a single group against a known mean.
• Independent samples t-test: compares the means for two groups.
• Paired sample t-test: compares means from the same group at different times (say, one year apart).

One sample t-test is one of the widely used t-tests for comparison of the sample mean of the data to a particularly given value. Used for comparing the sample mean to the true/population mean.

We can use this when the sample size is small. (under 30) data is collected randomly and it is approximately normally distributed. It can be calculated as:

• t = t-value
• x_bar = sample mean
• μ = true/population mean
• σ = standard deviation
• n = sample size

Example Problem

Consider the following example. The weights of 25 obese people were taken before enrolling them into the nutrition camp. The population mean weight is found to be 45 kg before starting the camp. After finishing the camp, for the same 25 people, the sample mean was found to be 75 with a standard deviation of 25. Did the fitness camp work?

One-Sample T-test in Python

The T-value of 6.0 is significantly greater than the critical t-value, leading to rejection of the null hypothesis therefore, we can conclude there is a significant difference in weight before and after the fitness camp. The fitness camp had an effect on the weights of the participants.

The results strongly suggest that the fitness camp was effective in producing a statistically significant change in weight for the participants.

• The T-value and p-value both provide consistent evidence for rejecting the null hypothesis.
• The practical significance should also be considered to understand the real-world impact of this weight change.

An Independent sample t-test, commonly known as an unpaired sample t-test is used to find out if the differences found between two groups is actually significant or just a random occurrence. 

We can use this when:

• the population mean or standard deviation is unknown. (information about the population is unknown)
• the two samples are separate/independent. For eg. boys and girls (the two are independent of each other)

It can be calculated using:

Researchers are investigating whether there is a significant difference in the exam scores of two different teaching methods, A and B. Two independent samples, each representing a different teaching method, have been collected. The objective is to determine if there is enough evidence to suggest that one teaching method leads to higher exam scores compared to the other. Suppose, two independent sample data A and B are given, with the following values. We have to perform the Independent samples t-test for this data.

Two-Sample t-test in Python (Independent)

With T-Value, of 0.989 is less than the critical t-value of 2.1009. Therefore, No significant difference is found between the exam scores of Teaching Method A and Teaching Method B based on the T-value.

With P-Value, of 0.336 is greater than the significance level of 0.05. There is no evidence to reject the null hypothesis, indicating no significant difference between the two teaching methods based on the P-value.

In conclusion, The results suggest that, statistically, there is no significant difference in exam scores between Teaching Method A and Teaching Method B. Therefore, based on this analysis, there is no clear evidence to suggest that one teaching method leads to higher exam scores compared to the other.

Paired sample t-test, commonly known as dependent sample t-test is used to find out if the difference in the mean of two samples is 0. The test is done on dependent samples, usually focusing on a particular group of people or things. In this, each entity is measured twice, resulting in a pair of observations. 

We can use this when :

• Two similar (twin like) samples are given. [Eg, Scores obtained in English and Math (both subjects)]
• The dependent variable (data) is continuous.
• The observations are independent of one another.
• The dependent variable is approximately normally distributed.

It can be calculated using,

• (s_d) is the standard deviation of the differences.
• (n) is the number of paired observations.

Consider the following example. Scores (out of 25) of the subjects Math1 and Math2 are taken for a sample of 10 students. We have to perform the paired sample t-test for this data. 

Paired Two-Sample T-test in Python

The paired sample t-test suggests that there is a statistically significant difference in scores between Math1 and Math2 as T-value of -4.95 is less than the critical t-value of -2.2622 and P-value of 0.00079 is less than the significance level of 0.05. Therefore, based on this analysis, it can be concluded that there is evidence to support the claim that the two sets of scores are different, and the difference is not due to random chance.

The above-discussed types of t-tests are widely used in the fields of research in hospitals by experts to gain important information about the medical data given to them about the effects of various medicines and drugs on the population and help them draw out important inferences regarding the same. However, it is the responsibility of the person to see to it that which t-test would bring out the best results and that all the assumptions of that t-test are adhered to. For any doubt/query, comment below. 

In conclusion, t-test, play a crucial role in hypothesis testing, comparing means, and drawing conclusions about populations. The test can be one-sample, independent two-sample, or paired two-sample, each with specific use cases and assumptions. Interpretation of results involves considering T-values, P-values, and critical values.

These tests aid researchers in making informed decisions based on statistical evidence.

Q. What is the t-test for mean in Python?

The t-test for mean in Python is a statistical method used to determine if there is a significant difference between the means of two groups.

Q. What is the t-test function?

The t-test function is a statistical tool used to compare means and assess the significance of differences between groups, considering factors like sample size and variability.

Q. What is the p-value in t-test Python?

The p-value in a t-test Python indicates the probability of observing the data or more extreme results assuming the null hypothesis is true. A small p-value suggests evidence against the null hypothesis.

Q. Why is it called t-test?

The t-test is named after William Sealy Gosset, who published under the pseudonym “Student.” The name “t” refers to the t-distribution used in the test, particularly applicable for small sample sizes.

Please Login to comment...

• Machine Learning
• Mathematical
• WhatsApp To Launch New App Lock Feature
• Top Design Resources for Icons
• Node.js 21 is here: What’s new
• Zoom: World’s Most Innovative Companies of 2024
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Statistics Made Easy

Paired Samples t-test: Definition, Formula, and Example

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

This tutorial explains the following:

• The motivation for performing a paired samples t-test.
• The formula to perform a paired samples t-test.
• The assumptions that should be met to perform a paired samples t-test.
• An example of how to perform a paired samples t-test.

Paired Samples t-test: Motivation

A paired samples t-test is commonly used in two scenarios:

1. A measurement is taken on a subject before and after some treatment – e.g. the max vertical jump of college basketball players is measured before and after participating in a training program.

2. A measurement is taken under two different conditions  – e.g. the response time of a patient is measured on two different drugs.

In both cases we are interested in comparing the mean measurement between two groups in which each observation in one sample can be paired with an observation in the other sample.

Paired Samples t-test: Formula

A paired samples t-test always uses the following null hypothesis:

• H 0 : μ 1  = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

• H 1 (two-tailed): μ 1  ≠ μ 2 (the two population means are not equal)
• H 1 (left-tailed): μ 1  < μ 2  (population 1 mean is less than population 2 mean)
• H 1 (right-tailed):  μ 1 > μ 2  (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

t = x diff  / (s diff /√n)

• x diff :  sample mean of the differences
• s:  sample standard deviation of the differences
• n:  sample size (i.e. number of pairs)

If the p-value that corresponds to the test statistic t with (n-1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Paired Samples t-test: Assumptions

For the results of a paired samples t-test to be valid, the following assumptions should be met:

• The participants should be selected randomly from the population.
• The differences between the pairs should be approximately normally distributed.
• There should be no extreme outliers in the differences.

Paired Samples t-test : Example

Suppose we want to know whether or not a certain training program is able to increase the max vertical jump (in inches) of college basketball players.

To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month.

To determine whether or not the training program actually had an effect on max vertical jump, we will perform a paired samples t-test at significance level α = 0.05 using the following steps:

Step 1: Calculate the summary data for the differences.

• x diff :  sample mean of the differences =  -0.95
• s:  sample standard deviation of the differences =  1.317
• n:  sample size (i.e. number of pairs) =  20

Step 2: Define the hypotheses.

We will perform the paired samples t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic  t .

t = x diff  / (s diff /√n)  = -0.95 / (1.317/ √ 20) =  -3.226

Step 4: Calculate the p-value of the test statistic  t .

According to the T Score to P Value Calculator , the p-value associated with t = -3.226 and degrees of freedom = n-1 = 20-1 = 19 is  0.00445 .

Step 5: Draw a conclusion.

Since this p-value is less than our significance level α = 0.05, we reject the null hypothesis. We have sufficient evidence to say that the mean max vertical jump of players is different before and after participating in the training program.

Note:  You can also perform this entire paired samples t-test by simply using the Paired Samples t-test Calculator .

Additional Resources

The following tutorials explain how to perform a paired samples t-test using different statistical programs:

How to Perform a Paired Samples t-Test in Excel How to Perform a Paired Samples t-test in SPSS How to Perform a Paired Samples t-test in Stata How to Perform a Paired Samples t-test on a TI-84 Calculator How to Perform a Paired Samples t-test in R How to Perform a Paired Samples t-Test in Python How to Perform a Paired Samples t-Test by Hand

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Example of 2-Sample t

A healthcare consultant wants to compare the patient satisfaction ratings of two hospitals. The consultant collects ratings from 20 patients for each of the hospitals.

The consultant performs a 2-sample t-test to determine whether there is a difference in the patient ratings between the hospitals.

• Open the sample data, HospitalComparison.MTW .
• Choose Stat > Basic Statistics > 2-Sample t .
• From the drop-down list, select Both samples are in one column .
• In Samples , enter Rating .
• In Sample IDs , enter Hospital .

Interpret the results

The null hypothesis states that the difference between ratings for the two hospitals is 0. Because the p-value is 0.000, which is less than the significance level of 0.05, the consultant rejects the null hypothesis and concludes that the ratings for the two hospitals differ.

Descriptive Statistics: Rating

Estimation for difference.

• Minitab.com
• License Portal
• Cookie Settings

You are now leaving support.minitab.com.

Click Continue to proceed to: