- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution

Study Guides > College Algebra
Solve problems involving joint variation.
Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation . For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable c , cost, varies jointly with the number of students, n , and the distance, d .
A General Note: Joint Variation
Joint variation occurs when a variable varies directly or inversely with multiple variables.
For instance, if x varies directly with both y and z , we have x = kyz . If x varies directly with y and inversely with z , we have [latex]x=\frac{ky}{z}[/latex]. Notice that we only use one constant in a joint variation equation.
Example 4: Solving Problems Involving Joint Variation
A quantity x varies directly with the square of y and inversely with the cube root of z . If x = 6 when y = 2 and z = 8, find x when y = 1 and z = 27.
Begin by writing an equation to show the relationship between the variables.
Substitute x = 6, y = 2, and z = 8 to find the value of the constant k .
Now we can substitute the value of the constant into the equation for the relationship.
To find x when y = 1 and z = 27, we will substitute values for y and z into our equation.
x varies directly with the square of y and inversely with z . If x = 40 when y = 4 and z = 2, find x when y = 10 and z = 25.
Licenses & Attributions
Cc licensed content, shared previously.
- Precalculus. Provided by: OpenStax Authored by: Jay Abramson, et al.. Located at: https://openstax.org/books/precalculus/pages/1-introduction-to-functions. License: CC BY: Attribution . License terms: Download For Free at : http://cnx.org/contents/ [email protected] ..
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
- Texas Go Math
- Big Ideas Math
- Engageny Math
- McGraw Hill My Math
- enVision Math
- 180 Days of Math
- Math in Focus Answer Key
- Math Expressions Answer Key
- Privacy Policy
Joint Variation – Formula, Examples | How to Solve Problems Involving Joint Variation?
Joint Variation definition, rules, methods and formulae are here. Check the joint variation problems and solutions to prepare for the exam. Refer to problems of direct and inverse variations and the relationship between the variables. Know the different type of variations like inverse, direct, combined and joint variation. Go through the below sections to check definition, various properties, example problems, value tables, concepts etc.
Joint Variation – Introduction
Joint Variation refers to the scenario where the value of 1 variable depends on 2 or more and other variables that are held constant. For example, if C varies jointly as A and B, then C = ABX for which constant “X”. The joint variation will be useful to represent interactions of multiple variables at one time.
Most of the situations are complicated than the basic inverse or direct variation model. One or the other variables depends on the multiple other variables. Joint Variation is nothing but the variable depending on 2 or more variables quotient or product. To understand clearly with an example, The amount of busing candidates for each of the school trip varies with the no of candidates attending the distance from the school. The variable c (cost) varies jointly with n (number of students) and d (distance).
Joint Variation problems are very easy once you get the perfection of the lingo. These problems involve simple formulae or relationships which involves one variable which is equal to the “one” term which may be linear (with just an “x” axis), a quadratic equation (like “x²) where more than one variable (like “hr²”), and square root (like “\sqrt{4 – r^2\,}4−r2”) etc.
Functions of 2 or More Variables
It is very uncommon for the output variable to depend on 2 or more inputs. Most of the familiar formulas describe the several variables functions. For suppose, if the rectangle perimeter depends on the length and width. The cylinder volume depends on its height and radius. The travelled distance depends on the time and speed while travelling. The function notation of the formulas can be written as
P = f(l,w) = 2l + 2w where P is the perimeter and is a function of width and length
V = f(r,h) = Πr²h where V is the volume and is a function of radius and height
d = f(r,t) = rt where d is the distance and is a function of time and rate.
Tables of Values
Just for the single variable functions, we use the tables to describe two-variable functions. The heading of the table shows row and column and it shows the value if two input variables and the complete table shows the values of the output variable.
You can easily make graphs in three dimensions for two-variable functions. Instead of representing graphs, we represent functions by holding two or one variable constants.
Also, Read:
- What is Variation
- Practice Test on Ratio and Proportion
How to Solve Joint Variation Problems?
Follow the step by step procedure provided below to solve problems involving Joint Variation and arrive at the solution easily. They are along the lines
Step 1: Write the exact equation. The problems of joint variation can be solved using the equation y =kxz. While dealing with the word problems. you should also consider using variables other than x,y and z. Use the variables which are relevant to the problem being solved. Read the problem carefully and determine the changes in the equation of joint variation such as cubes, squares or square roots.
Step 2: With the help of the information in the problem, you have to find the value of k which is called the constant of proportionality and variation.
Step 3: Rewrite the equation starting with 1 substituting the value of k and found in step 2.
Step 4: Use the equation in step 3 and the information in the problem to answer the question. While solving the word problems, remember including the units in the final answer.
Joint Variation Problems with Solutions
The area of a triangle varies jointly as the base and the height. Area = 12m² when base = 6m and height = 4m. Find base when Area = 36m² and height = 8m?
The area of the triangle is represented with A
The base is represented with b
Height is represented with h
As given in the question,
A = 12m² when B = 6m and H = 4m
We know the equation,
A = kbh where k is the constant value
12 = k(6)(4)
Divide by 24 on both sides, we get
12/24 = k(24)/24
The value of k = 1/2
As the equation is
To find the base of the triangle of A = 36m² and H = 8m
36 = 1/2(b)(8)
Dividing both sides by 4, we get
36/4 = 4b/4
The value of base = 9m
Hence, the base of the triangle when A = 36m² and H = 8m is 9m
Wind resistance varies jointly as an object’s surface velocity and area. If the object travels at 80 miles per hour and has a surface area of 30 square feet which experiences 540 newtons wind resistance. How much fast will the car move with 40 square feet of the surface area in order to experience a wind resistance of 495 newtons?
Let w be the wind resistance
Let s be the object’s surface area
Let v be the object velocity
The object’s surface area = 80 newtons
The wind resistance = 540 newtons
The object velocity = 30
w = ksv where k is the constant
(540) = k (80) (30)
540 = k (2400)
540/2400 = k
The value of k is 9/40
To find the velocity of the car with s = 40, w = 495 newtons and k = 9/40
Substitute the values in the equation
495 = (9/40) (40) v
The velocity of a car is 55mph for which the object’s surface area is 40 and wind resistance is 495 newtons
Hence, the final solution is 55mph
For the given interest, SI (simple interest) varies jointly as principal and time. If 2,500 Rs left in an account for 5 years, then the interest of 625 Rs. How much interest would be earned, if you deposit 7,000 Rs for 9 years?
Let i be the interest
Let p be the principal
Let t be the time
The interest is 625 Rs
The principal is 2500
The time is 5 hours
i = kpt where k is the constant
Substituting the values in the equation,
(625) = k(2500)(5)
625 = k(12,500)
Dividing 12,500 on both the sides
625/12,500 = k (12,500)/12,500
The value of k = 1/20
To find the interest where the deposit is 7000Rs for 9 years, use the equation
i = (1/20) (7000) (9)
i = (350) (9)
Therefore, the interest is 3,150 Rs, if you deposit 7,000 Rs for 9 years
Thus, the final solution is Rs. 3,150
The volume of a pyramid varies jointly as its height and the area of the base. A pyramid with a height of 21 feet and a base with an area of 24 square feet has a volume of 168 cubic feet. Find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet?
Let v be the volume of a pyramid
Let h be the height of a pyramid
Let a be the area of a pyramid
The volume v = 168 cubic feet
The height h = 21 feet
The area a = 24 square feet
V = Kha where K is the constant,
168 = k(21)(24)
168 = k(504)
Divide 504 on both sides
168/504 = k(504)/504
The value of k = 1/3
To find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet
h = 18 feet
a = 42 square feet
V = (1/3) (18) (42)
V = (6) (42)
V = 252 ft³
The volume of the pyramid = 252 ft³ which has a height of 18 feet and a base with an area of 42 square feet
Therefore, the final solution is 252 ft³
The amount of oil used by a ship travelling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in travelling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour?
No of barrels of oil = 200
The distance at which the oil is travelling = 200 miles
The distance at which the ship is travelling = 36 miles per hour
A = kds² where k is constant
200 = k.200.(36)²
Dividing both sides by 200
200/200 = k.200.(36)²/200
1 = k.(36)²
The value of k is 1/1296
To find the no of barrels when the ship travels 360 miles at 18 miles per hour
A = 1/1296 * 360 * 18²
Therefore, 90 barrels of oil is used when the ship travels 360 miles at 18 miles per hour
Thus, the final solution is 90 barrels
Leave a Comment Cancel Reply
You must be logged in to post a comment.
- Joint Variation
If more than two variables are related directly or one variable changes with the change product of two or more variables it is called as joint variation .
If X is in joint variation with Y and Z, it can be symbolically written as X α YZ. If Y is constant also then X is in direct variation with Z. So for joint variation two or more variables are separately in direct variation. So joint variation is similar to direct variation but the variables for joint variation are more than two.
Equation for a joint variation is X = KYZ where K is constant.
One variable quantity is said to vary jointly as a number of other variable quantities, when it varies directly as their product. If the variable A varies directly as the product of the variables B, C and D, i.e., if.A ∝ BCD or A = kBCD (k = constant ), then A varies jointly as B, C and D.
For solving a problems related to joint variation first we need to build the correct equation by adding a constant and relate the variables. After that we need determine the value of the constant. Then substitute the value of the constant in the equation and by putting the values of variables for required situation we determine the answer.
We know, area of a triangle = ½ × base × altitude. Since ½ is a constant, hence area of a triangle varies jointly as its base and altitude. A is said to vary directly as B and inversely as C if A ∝ B ∙ \(\frac{1}{C}\) or A = m ∙ B ∙ \(\frac{1}{C}\) (m = constant of variation) i.e., if A varies jointly as B and \(\frac{1}{C}\) .
If x men take y days to plough z acres of land, then x varies directly as z and inversely as y.
1. The variable x is in joint variation with y and z. When the values of y and z are 4 and 6, x is 16. What is the value of x when y = 8 and z =12?
The equation for the given problem of joint variation is
x = Kyz where K is the constant.
For the given data
16 = K × 4 × 6
or, K = \(\frac{4}{6}\) .
So substituting the value of K the equation becomes
x = \(\frac{4yz}{6}\)
Now for the required condition
x = \(\frac{4 × 8 × 12}{6}\)
= 64
Hence the value of x will be 64.
2. A is in joint variation with B and square of C. When A = 144, B = 4 and C = 3. Then what is the value of A when B = 6 and C = 4?
From the given problem equation for the joint variation is
From the given data value of the constant K is
K = \(\frac{BC^{2}}{A}\)
K = \(\frac{4 × 3^{2}}{144}\)
= \(\frac{36}{144}\)
= \(\frac{1}{4}\) .
Substituting the value of K in the equation
A = \(\frac{BC^{2}}{4}\)
A = \(\frac{6 × 4^{2}}{4}\)
= 24
3. The area of a triangle is jointly related to the height and the base of the triangle. If the base is increased 10% and the height is decreased by 10%, what will be the percentage change of the area?
We know the area of triangle is half the product of base and height. So the joint variation equation for area of triangle is A = \(\frac{bh}{2}\) where A is the area, b is the base and h is the height.
Here \(\frac{1}{2}\) is the constant for the equation.
Base is increased by 10%, so it will be b x \(\frac{110}{100}\) = \(\frac{11b}{10}\) .
Height is decreased by 10%, so it will be h x \(\frac{90}{100}\) = \(\frac{9h}{10}\) .
So the new area after the changes of base and height is
\(\frac{\frac{11b}{10} \times \frac{9h}{10}}{2}\)
= (\(\frac{99}{100}\) )\(\frac{bh}{2}\) = \(\frac{99}{100}\) A.
So the area of the triangle is decreased by 1%.
4. A rectangle’s length is 6 m and width is 4 m. If length is doubled and width is halved, how much the perimeter will increase or decrease?
Formula for the perimeter of rectangle is P = 2(l + w) where P is perimeter, l is length and w is width.
This is joint variation equation where 2 is constant.
So P = 2(6 + 4) = 20 m
If length is doubled, it will become 2l.
And width is halved, so it will become \(\frac{w}{2}\) .
So the new perimeter will be P = 2(2l + \(\frac{w}{2}\) ) = 2(2 x 6 + \(\frac{4}{2}\) ) = 28 m.
So the perimeter will increase by (28 - 20) = 8 m.
● Variation
- What is Variation?
- Direct Variation
- Inverse or Indirect Variation
- Theorem of Joint Variation
- Worked out Examples on Variation
- Problems on Variation
11 and 12 Grade Math
From Joint Variation to Home Page
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Worksheet on bar graphs | bar graphs or column graphs | graphing bar.
Sep 04, 24 03:48 PM
1st Grade Numbers Worksheet | Before, After and Between | Compare Numb
Sep 03, 24 03:33 PM
Subtraction Word Problems - 2-Digit Numbers | Subtraction Problems
Sep 03, 24 02:26 AM
Days of the Week | 7 Days of the Week | What are the Seven Days?
Sep 03, 24 01:58 AM
Time Duration |How to Calculate the Time Duration (in Hours & Minutes)
Sep 03, 24 01:37 AM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Joint Variation – Formula, Examples | How to Solve Problems Involving Joint Variation?
Joint Variation definition, rules, methods and formulae are here. Check the joint variation problems and solutions to prepare for the exam. Refer to problems of direct and inverse variations and the relationship between the variables. Know the different type of variations like inverse, direct, combined and joint variation. Go through the below sections to check definition, various properties, example problems, value tables, concepts etc.
Joint Variation – Introduction
Joint Variation refers to the scenario where the value of 1 variable depends on 2 or more and other variables that are held constant. For example, if C varies jointly as A and B, then C = ABX for which constant “X”. The joint variation will be useful to represent interactions of multiple variables at one time.
Most of the situations are complicated than the basic inverse or direct variation model. One or the other variables depends on the multiple other variables. Joint Variation is nothing but the variable depending on 2 or more variables quotient or product. To understand clearly with an example, The amount of busing candidates for each of the school trip varies with the no of candidates attending the distance from the school. The variable c (cost) varies jointly with n (number of students) and d (distance).
Joint Variation problems are very easy once you get the perfection of the lingo. These problems involve simple formulae or relationships which involves one variable which is equal to the “one” term which may be linear (with just an “x” axis), a quadratic equation (like “x²) where more than one variable (like “hr²”), and square root (like “\sqrt{4 – r^2\,}4−r2”) etc.
Functions of 2 or More Variables
It is very uncommon for the output variable to depend on 2 or more inputs. Most of the familiar formulas describe the several variables functions. For suppose, if the rectangle perimeter depends on the length and width. The cylinder volume depends on its height and radius. The travelled distance depends on the time and speed while travelling. The function notation of the formulas can be written as
P = f(l,w) = 2l + 2w where P is the perimeter and is a function of width and length
V = f(r,h) = Πr²h where V is the volume and is a function of radius and height
d = f(r,t) = rt where d is the distance and is a function of time and rate.
Tables of Values
Just for the single variable functions, we use the tables to describe two-variable functions. The heading of the table shows row and column and it shows the value if two input variables and the complete table shows the values of the output variable.
You can easily make graphs in three dimensions for two-variable functions. Instead of representing graphs, we represent functions by holding two or one variable constants.
Also, Read:
- What is Variation
- Practice Test on Ratio and Proportion
How to Solve Joint Variation Problems?
Follow the step by step procedure provided below to solve problems involving Joint Variation and arrive at the solution easily. They are along the lines
Step 1: Write the exact equation. The problems of joint variation can be solved using the equation y =kxz. While dealing with the word problems. you should also consider using variables other than x,y and z. Use the variables which are relevant to the problem being solved. Read the problem carefully and determine the changes in the equation of joint variation such as cubes, squares or square roots.
Step 2: With the help of the information in the problem, you have to find the value of k which is called the constant of proportionality and variation.
Step 3: Rewrite the equation starting with 1 substituting the value of k and found in step 2.
Step 4: Use the equation in step 3 and the information in the problem to answer the question. While solving the word problems, remember including the units in the final answer.
Joint Variation Problems with Solutions
The area of a triangle varies jointly as the base and the height. Area = 12m² when base = 6m and height = 4m. Find base when Area = 36m² and height = 8m?
The area of the triangle is represented with A
The base is represented with b
Height is represented with h
As given in the question,
A = 12m² when B = 6m and H = 4m
We know the equation,
A = kbh where k is the constant value
12 = k(6)(4)
Divide by 24 on both sides, we get
12/24 = k(24)/24
The value of k = 1/2
As the equation is
To find the base of the triangle of A = 36m² and H = 8m
36 = 1/2(b)(8)
Dividing both sides by 4, we get
36/4 = 4b/4
The value of base = 9m
Hence, the base of the triangle when A = 36m² and H = 8m is 9m
Wind resistance varies jointly as an object’s surface velocity and area. If the object travels at 80 miles per hour and has a surface area of 30 square feet which experiences 540 newtons wind resistance. How much fast will the car move with 40 square feet of the surface area in order to experience a wind resistance of 495 newtons?
Let w be the wind resistance
Let s be the object’s surface area
Let v be the object velocity
The object’s surface area = 80 newtons
The wind resistance = 540 newtons
The object velocity = 30
w = ksv where k is the constant
(540) = k (80) (30)
540 = k (2400)
540/2400 = k
The value of k is 9/40
To find the velocity of the car with s = 40, w = 495 newtons and k = 9/40
Substitute the values in the equation
495 = (9/40) (40) v
The velocity of a car is 55mph for which the object’s surface area is 40 and wind resistance is 495 newtons
Hence, the final solution is 55mph
For the given interest, SI (simple interest) varies jointly as principal and time. If 2,500 Rs left in an account for 5 years, then the interest of 625 Rs. How much interest would be earned, if you deposit 7,000 Rs for 9 years?
Let i be the interest
Let p be the principal
Let t be the time
The interest is 625 Rs
The principal is 2500
The time is 5 hours
i = kpt where k is the constant
Substituting the values in the equation,
(625) = k(2500)(5)
625 = k(12,500)
Dividing 12,500 on both the sides
625/12,500 = k (12,500)/12,500
The value of k = 1/20
To find the interest where the deposit is 7000Rs for 9 years, use the equation
i = (1/20) (7000) (9)
i = (350) (9)
Therefore, the interest is 3,150 Rs, if you deposit 7,000 Rs for 9 years
Thus, the final solution is Rs. 3,150
The volume of a pyramid varies jointly as its height and the area of the base. A pyramid with a height of 21 feet and a base with an area of 24 square feet has a volume of 168 cubic feet. Find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet?
Let v be the volume of a pyramid
Let h be the height of a pyramid
Let a be the area of a pyramid
The volume v = 168 cubic feet
The height h = 21 feet
The area a = 24 square feet
V = Kha where K is the constant,
168 = k(21)(24)
168 = k(504)
Divide 504 on both sides
168/504 = k(504)/504
The value of k = 1/3
To find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet
h = 18 feet
a = 42 square feet
V = (1/3) (18) (42)
V = (6) (42)
V = 252 ft³
The volume of the pyramid = 252 ft³ which has a height of 18 feet and a base with an area of 42 square feet
Therefore, the final solution is 252 ft³
The amount of oil used by a ship travelling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in travelling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour?
No of barrels of oil = 200
The distance at which the oil is travelling = 200 miles
The distance at which the ship is travelling = 36 miles per hour
A = kds² where k is constant
200 = k.200.(36)²
Dividing both sides by 200
200/200 = k.200.(36)²/200
1 = k.(36)²
The value of k is 1/1296
To find the no of barrels when the ship travels 360 miles at 18 miles per hour
A = 1/1296 * 360 * 18²
Therefore, 90 barrels of oil is used when the ship travels 360 miles at 18 miles per hour
Thus, the final solution is 90 barrels
Leave a Comment Cancel Reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Joint or Combined Variation
These lessons help Algebra students learn about joint or combined variation.
Related Pages: Proportions Joint Variation Word Problems Direct Variation Inverse Variation More Algebra Lessons
The following figure shows Joint Variation. Scroll down the page for more examples and solutions of Joint and Combine Variations.

What is Joint Variation or Combined Variation?
Joint Variation or Combined Variation is when one quantity varies directly as the product of at least two other quantities.
For example: y = kxz y varies jointly as x and z, when there is some nonzero constant k
Joint Variation Examples
Example: Suppose y varies jointly as x and z. What is y when x = 2 and z = 3, if y = 20 when x = 4 and z = 3?
Example: z varies jointly with x and y. When x = 3, y = 8, z = 6. Find z, when x = 6 and y = 4.
Joint Variation Application
Example: The energy that an item possesses due to its motion is called kinetic energy. The kinetic energy of an object (which is measured in joules) varies jointly with the mass of the object and the square of its velocity. If the kinetic energy of a 3 kg ball traveling 12 m/s is 216 Joules, how is the mass of a ball that generates 250 Joules of energy when traveling at 10 m/s?
Distinguish between Direct, Inverse and Joint Variation
Example: Determine whether the data in the table is an example of direct, inverse or joint variation. Then, identify the equation that represents the relationship.
Combined Variation
In Algebra, sometimes we have functions that vary in more than one element. When this happens, we say that the functions have joint variation or combined variation. Joint variation is direct variation to more than one variable (for example, d = (r)(t)). With combined variation, we have both direct variation and indirect variation.
How to set up and solve combined variation problems?
Example: Suppose y varies jointly with x and z. When y = 20, x = 6 and z = 10. Find y when x = 8 and z =15.
Lesson on combining direct and inverse or joint and inverse variation
Example: y varies directly as x and inversely as the square of z, and when x = 32, y = 6 and z = 4. Find x when y = 10 and z = 3.
How to solve problems involving joint and combined variation?
If t varies jointly with u and the square of v, and t is 1152 when u is 8 and v is 4, find t when v is 5 and u is 5.
The amount of oil used by a ship traveling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in traveling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour.
Designer Dolls found that its number of Dress-Up Dolls sold, N, varies directly with their advertising budget, A, and inversely proportional with the price of each doll, P. When $54,00 was spent on advertising and the price of the doll is $90, then 9,600 units are sold. Determine the number of dolls sold if the amount of advertising budget is increased to $144,000.
Example: y varies jointly as x and z and inversely as w, and y = 3/2, when x = 2, z =3 and w = 4. Find the equation of variation.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Direct, Inverse, Joint and Combined Variation
When you start studying algebra, you will also study how two (or more) variables can relate to each other specifically. The cases you’ll study are:
- Direct Variation , where one variable is a constant multiple of another. For example, the number of dollars I make varies directly (or varies proportionally ) to the number of hours I work. Or, the perimeter of a square varies directly with the length of a side of the square.
- Inverse or Indirect Variation , where when one of the variables increases, the other one decreases (their product is constant). For example, the temperature in my house varies indirectly (same or inversely ) with the amount of time the air conditioning is running. Or, the number of people I invite to my bowling party varies inversely with the number of games they might get to play (or you can say is proportional to the inverse of ).
- Joint Variation , where at least two variables are related directly. For example, the area of a triangle is jointly related to both its height and base.
- Combined Variation , which involves a combination of direct or joint variation, and indirect variation. For example, the average number of phone calls per day between two cities has found to be jointly proportional to the populations of the cities, and inversely proportional to the square of the distance between the two cities.
- Partial (Direct) Variation , where two variables are related by a formula, such as the formula for a straight line (with a non-zero $ y$-intercept). For example, the total cost of my phone bill consists of a fixed cost per month, and also a charge per minute.
Note : Just because two variables have a direct relationship, the relationship may not necessarily be a causal relationship (causation) , meaning one variable directly affects the other. There may be another variable that affects both of the variables. For example, there may be a correlation between the number of people buying ice cream and the number of people buying shorts. People buying ice cream do not cause people to buy shorts, but most likely warm weather outside is causing both to happen.
Here is a table for the types of variation we’ll be discussing:
Direct or Proportional Variation
When two variables are related directly, the ratio of their values is always the same. If $ k$, the constant ratio is positive, the variables go up and down in the same direction. (If $ k$ is negative, as one variable goes up, the other goes down; this is still considered a direct variation, but is not seen often in these problems.) Note that $ k\ne 0$.
Think of linear direct variation as a “$ y=mx$” line, where the ratio of $ y$ to $ x$ is the slope ($ m$). With direct variation, the $ y$-intercept is always 0 (zero); this is how it’s defined. Direct variation problems are typically written: → $ \boldsymbol {y=kx}$, where $ k$ is the ratio of $ y$ to $ x$ (which is the same as the slope or rate ).
Some problems will ask for that $ k$ value (which is called the constant ratio , constant of variation or constant of proportionality – it’s like a slope!); others will just give you 3 out of the 4 values for $ x$ and $ y$ and you can simply set up a ratio to find the other value. I’m thinking the $ k$ comes from the word “constant” in another language.
Remember the example of making $10 an hour at the mall ($ y=10x$)? This is an example of direct variation, since the ratio of how much you make to how many hours you work is always constant.
We can also set up direct variation problems in a ratio , as long as we have the same variable in either the top or bottom of the ratio, or on the same side . This will look like the following. Don’t let this scare you; the subscripts just refer to either the first set of variables $ ({{x}_{1}},{{y}_{1}})$, or the second $ ({{x}_{2}},{{y}_{2}})$: $ \displaystyle \frac{{{{y}_{1}}}}{{{{x}_{1}}}}\,\,=\,\,\frac{{{{y}_{2}}}}{{{{x}_{2}}}}$.
Notes: Partial Variation (see below), or “varies partly” means that there is an extra fixed constant, so we’ll have an equation like $ y=mx+b$, which is our typical linear equation. Also, I’m assuming in these examples that direct variation is linear ; sometime I see it where it’s not, like in a Direct Square Variation where $ y=k{{x}^{2}}$. There is a word problem example of this here .
Direct Variation Word Problem: We can solve the following direct variation problem in one of two ways, as shown. We do these methods when we are given any three of the four values for $ x$ and $ y$.
It’s really that easy. Can you see why the proportion method can be the preferred method, unless you are asked to find the $ k$ constant in the formula? Again, if the problem asks for the equation that models this situation , it would be “$ y=10x$”.
Direct Variation Word Problem:
Here’s another; let’s use the proportion method :
See how similar these types of problems are to the Proportions problems we did earlier?
Direct Square Variation Word Problem:
Again, a Direct Square Variation is when $ y$ is proportional to the square of $ x$, or $ y=k{{x}^{2}}$. Let’s work a word problem with this type of variation and show both the formula and proportion methods:
Inverse or Indirect Variation
Inverse or Indirect Variation refers to relationships of two variables that go in the opposite direction (their product is a constant, $ k$). Let’s suppose you are comparing how fast you are driving (average speed) to how fast you get to your school. You might have measured the following speeds and times:
Do you see how when the $ x$ variable goes up, the $ y$ goes down, and when you multiply the $ x$ with the $ y$, we always get the same number? (Note that this is different than a negative slope, or negative $ k$ value, since with a negative slope, we can’t multiply the $ x$’s and $ y$’s to get the same number).
The formula for inverse or indirect variation is: → $ \displaystyle \boldsymbol{y=\frac{k}{x}}$ or $ \boldsymbol{xy=k}$, where $ k$ is always the same number.
(Note that you could also have an Indirect Square Variation or Inverse Square Variation , like we saw above for a Direct Variation. This would be of the form $ \displaystyle y=\frac{k}{{{{x}^{2}}}}\text{ or }{{x}^{2}}y=k$.)
We might have a problem like this; we can solve this problem in one of two ways, as shown. We do these methods when we are given any three of the four values for $ x$ and $ y$:
Here’s a more advanced problem that uses inverse proportions in a “work” word problem ; we’ll see more “work problems” here in the Systems of Linear Equations Section and here in the Rational Functions and Equations section .
In the problem below, the three different values are inversely proportional; for example, the more women you have, the less days it takes to paint the mural, and the more hours in a day the women paint, the less days they need to complete the mural:
Recognizing Direct or Indirect Variation
You might be asked to look at functions (equations or points that compare $ x$’s to unique $ y$’s – we’ll discuss later in the Algebraic Functions section) and determine if they are direct, inverse, or neither:
Joint Variation and Combined Variation
Joint variation is just like direct variation, but involves more than one other variable. All the variables are directly proportional, taken one at a time. Let’s set this up like we did with direct variation, find the $ k$, and then solve for $ y$; we need to use the Formula Method:
Another Joint Variation Word Problem:
Combined Variation
Combined variation involves a combination of direct or joint variation, and indirect variation. Since these equations are a little more complicated, you probably want to plug in all the variables, solve for $ k$, and then solve back to get what’s missing. Let’s try a problem:
Here’s another; this one looks really tough, but it’s really not that bad if you take it one step at a time:
Combined Variation Word Problem:
Partial Variation
You don’t hear about Partial Variation or something being partly varied or part varied very often, but it means that two variables are related by the sum of two or more variables (one of which may be a constant). An example of part variation is the relationship modeled by an equation of a line that doesn’t go through the origin. Here are a few examples:
We’re doing really difficult problems now – but see how, if you know the rules, they really aren’t bad at all?
Learn these rules, and practice, practice, practice!
For Practice : Use the Mathway widget below to try a Variation problem. Click on Submit (the blue arrow to the right of the problem) and click on Find the Constant of Variation to see the answer.
You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.
If you click on Tap to view steps , or Click Here , you can register at Mathway for a free trial , and then upgrade to a paid subscription at any time (to get any type of math problem solved!).
On to Introduction to the Graphing Display Calculator (GDC) . I’m proud of you for getting this far!
- > Algebra
- > Relations and Functions
Joint and Combined Variation: Formulas, Examples, and Applications Unlock the power of joint and combined variation! Learn essential formulas, explore real-world applications, and master problem-solving techniques to excel in advanced algebra and beyond.
Get the most by viewing this topic in your current grade. Pick your course now .
- Introduction to joint and combined variation
- Review: direct variation vs. inverse variation
- What is a joint variation?
- What is a combined variation and how is it different from a joint variation?
- How to solve a variation problem?
- x x x varies jointly as y y y and the square of z z z .
- The speed of a race car varies directly as the distance and inversely as the time.
- a a a varies directly with b b b and c c c . If a = 336 a=336 a = 336 when b = 4 b=4 b = 4 and c = 7 c=7 c = 7 , find a a a when b = 2 b=2 b = 2 and c = 11 c=11 c = 11 .
- p p p varies directly as q q q but inversely as r r r . If p = 14 p=14 p = 14 when q = 2 q=2 q = 2 and r = 5 r=5 r = 5 , find q q q when p = 105 p=105 p = 105 and r = 18 r=18 r = 18 .
- Find the constant of variation k k k . Round your answer to 2 decimal places.
- What is the volume of a can that has a 7 cm height and 3 cm radius?
- The time required to process a shipment at Mamazon varies directly with the number of orders being made and inversely with the number of workers. If 1344 orders can be processed by 7 workers in 12 hours, how long will it take 125 workers to process 20,000 items?
Free to Join!
Join for Free
Easily See Your Progress

Make Use of Our Learning Aids

Last Viewed
Practice accuracy, suggested tasks.
Get quick access to the topic you're currently learning.
See how well your practice sessions are going over time.
Stay on track with our daily recommendations.
Earn Achievements as You Learn

Create and Customize Your Avatar

In this lesson, we will learn:
- Identifying Types of Variations
- Translating Variation Statements Into Equations
- Solving Variation Problems
- Word Problems of Variations
- Joint variation is a direct variation, but with two or more variables. It has the equation y = k ⋅ x ⋅ z y=k \cdot x \cdot z y = k ⋅ x ⋅ z where k k k is the constant of variation and k ≠ 0 k \neq 0 k = 0 .
- A combined variation is formed when we combine any of the variations together (direct, inverse and joint). In most cases, we combine direct and inverse variations to form a combined variation. i.e. y y y varies directly with x x x and inversely with z z z ( y = k ⋅ x z ) (y = k \cdot \frac{x}{z}) ( y = k ⋅ z x )
- Steps to solving a variation problem:
- Write the general variation formula of the problem.
- Find the constant of variation k k k .
- Rewrite the formula with the value of k k k .
- Solve the problem by inputting known information.
Introduction to Joint and Combined Variation
Welcome to our exploration of joint and combined variation! These fascinating mathematical concepts are essential in understanding how multiple variables can influence each other simultaneously. Our introduction video serves as an excellent starting point, providing clear explanations and visual examples to help you grasp these ideas. Joint variation occurs when one variable is directly proportional to two or more other variables, while combined variation involves both direct and inverse relationships. As we delve deeper into these concepts, you'll discover their wide-ranging applications in fields like physics, engineering, and economics. The video will guide you through step-by-step examples, making these complex topics more accessible and relatable. By mastering joint and combined variation, you'll enhance your problem-solving skills and gain a deeper appreciation for the interconnectedness of mathematical relationships. So, let's dive in and unravel the intricacies of these important concepts together!
Solving Variation Problems Find the missing variables. a a a varies directly with b b b and c c c . If a = 336 a=336 a = 336 when b = 4 b=4 b = 4 and c = 7 c=7 c = 7 , find a a a when b = 2 b=2 b = 2 and c = 11 c=11 c = 11 .
Step 1: Identify the Type of Variation
The first step in solving this problem is to identify the type of variation we are dealing with. In this case, a a a varies directly with both b b b and c c c . This means that a a a is directly proportional to the product of b b b and c c c . This type of relationship is known as joint variation.
Step 2: Write the General Formula
Since a a a varies directly with b b b and c c c , we can write the general formula for this relationship as: a = k ⋅ b ⋅ c a = k \cdot b \cdot c a = k ⋅ b ⋅ c Here, k k k is the constant of variation. Our goal is to find the value of k k k using the given information.
Step 3: Substitute the Given Values to Find k k k
We are given that a = 336 a = 336 a = 336 when b = 4 b = 4 b = 4 and c = 7 c = 7 c = 7 . We can substitute these values into the general formula to find k k k : 336 = k ⋅ 4 ⋅ 7 336 = k \cdot 4 \cdot 7 336 = k ⋅ 4 ⋅ 7 Simplify the right-hand side: 336 = k ⋅ 28 336 = k \cdot 28 336 = k ⋅ 28 To solve for k k k , divide both sides by 28: k = 336 28 k = \frac{336}{28} k = 28 336 Simplify the division to find the value of k k k .
Step 4: Update the Formula with the Constant k k k
Once we have found the value of k k k , we can update our general formula. Suppose k k k is found to be 12 (as an example): a = 12 ⋅ b ⋅ c a = 12 \cdot b \cdot c a = 12 ⋅ b ⋅ c This updated formula will be used to find the new value of a a a when b = 2 b = 2 b = 2 and c = 11 c = 11 c = 11 .
Step 5: Substitute the New Values to Find a a a
Now, we need to find a a a when b = 2 b = 2 b = 2 and c = 11 c = 11 c = 11 . Substitute these values into the updated formula: a = 12 ⋅ 2 ⋅ 11 a = 12 \cdot 2 \cdot 11 a = 12 ⋅ 2 ⋅ 11 Simplify the multiplication: a = 12 ⋅ 22 a = 12 \cdot 22 a = 12 ⋅ 22 Continue simplifying to find the value of a a a .
Step 6: Verify the Solution
After calculating the value of a a a , it is always a good practice to verify the solution. Check if the calculated value of a a a makes sense in the context of the problem and ensure that all steps were followed correctly.
By following these steps, you can solve any joint variation problem where one variable varies directly with the product of two other variables. The key is to identify the type of variation, write the general formula, find the constant of variation, update the formula, and then substitute the new values to find the missing variable.
Here are some frequently asked questions about joint and combined variation:
1. What is the difference between joint variation and combined variation?
Joint variation occurs when one variable is directly proportional to two or more other variables, expressed as y = kxz. Combined variation involves both direct and inverse relationships, typically expressed as y = k(x/z), where y varies directly with x and inversely with z.
2. What is an example of joint variation in real life?
A real-life example of joint variation is the volume of a rectangular prism. The volume (V) varies jointly with its length (l), width (w), and height (h), expressed as V = l × w × h.

3. How do you solve a combined variation problem?
To solve a combined variation problem: 1) Identify the variables and their relationships. 2) Write the equation (e.g., y = k(x/z)). 3) Use given information to find the constant k. 4) Substitute known values to solve for the unknown variable.
4. What are the four types of variation in mathematics?
The four main types of variation in mathematics are: 1) Direct variation, 2) Inverse variation, 3) Joint variation, and 4) Combined variation. Each type describes a different relationship between variables.
5. How can you identify the type of variation in a problem?
To identify the type of variation: Look for keywords like "directly," "inversely," or "jointly." If a variable increases as another increases, it's likely direct variation. If it decreases as another increases, it's probably inverse variation. When more than two variables are involved, consider joint or combined variation.
Understanding joint and combined variation is crucial in advanced algebra and real-world applications. To fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. One of the most fundamental is direct variation , which forms the basis for understanding how variables change in proportion to each other. The direct variation formula is a key component in recognizing and solving problems involving joint variation.
Equally important is the concept of inverse variation , where one variable increases as another decreases in a specific proportion. Mastering the inverse variation formula is crucial for tackling complex problems in joint and combined variation scenarios. These two types of variation are often combined in real-world situations, making their understanding vital.
To effectively work with joint and combined variation, students must be proficient in understanding tables of values of linear relationships . This skill helps in identifying proportional relationships and interpreting data, which is essential when dealing with multiple variables in joint variation problems.
Additionally, familiarity with distance and time related questions in linear equations provides practical context for joint variation. This knowledge is particularly useful when solving inverse variation problems, as many real-world scenarios involving joint variation relate to distance, time, and rate.
While it might seem unrelated at first, understanding volume of rectangular prisms word problems can be surprisingly relevant. These problems often involve multiple variables changing in relation to each other, mirroring the principles of joint variation in a three-dimensional context.
Lastly, knowledge of Newton's Second Law of Motion provides an excellent real-world application of joint variation. This law demonstrates how force, mass, and acceleration are related in a way that perfectly exemplifies the principles of joint variation.
By mastering these prerequisite topics, students will be well-equipped to tackle the complexities of joint and combined variation. Each concept builds upon the others, creating a comprehensive understanding that is essential for success in advanced algebra and its applications in science and engineering. Remember, a strong foundation in these basics will make the journey into more complex mathematical concepts smoother and more intuitive.
Become a member to get more!
No Javascript
It looks like you have javascript disabled.
You can still navigate around the site and check out our free content, but some functionality, such as sign up, will not work.
If you do have javascript enabled there may have been a loading error; try refreshing your browser.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 2: Linear Equations
2.7 Variation Word Problems
Direct variation problems.
There are many mathematical relations that occur in life. For instance, a flat commission salaried salesperson earns a percentage of their sales, where the more they sell equates to the wage they earn. An example of this would be an employee whose wage is 5% of the sales they make. This is a direct or a linear variation, which, in an equation, would look like:
[latex]\text{Wage }(x)=5\%\text{ Commission }(k)\text{ of Sales Completed }(y)[/latex]
[latex]x=ky[/latex]
A historical example of direct variation can be found in the changing measurement of pi, which has been symbolized using the Greek letter π since the mid 18th century. Variations of historical π calculations are Babylonian [latex]\left(\dfrac{25}{8}\right),[/latex] Egyptian [latex]\left(\dfrac{16}{9}\right)^2,[/latex] and Indian [latex]\left(\dfrac{339}{108}\text{ and }10^{\frac{1}{2}}\right).[/latex] In the 5th century, Chinese mathematician Zu Chongzhi calculated the value of π to seven decimal places (3.1415926), representing the most accurate value of π for over 1000 years.
Pi is found by taking any circle and dividing the circumference of the circle by the diameter, which will always give the same value: 3.14159265358979323846264338327950288419716… (42 decimal places). Using an infinite-series exact equation has allowed computers to calculate π to 10 13 decimals.
[latex]\begin{array}{c} \text{Circumference }(c)=\pi \text{ times the diameter }(d) \\ \\ \text{or} \\ \\ c=\pi d \end{array}[/latex]
All direct variation relationships are verbalized in written problems as a direct variation or as directly proportional and take the form of straight line relationships. Examples of direct variation or directly proportional equations are:
- [latex]x[/latex] varies directly as [latex]y[/latex]
- [latex]x[/latex] varies as [latex]y[/latex]
- [latex]x[/latex] varies directly proportional to [latex]y[/latex]
- [latex]x[/latex] is proportional to [latex]y[/latex]
- [latex]x[/latex] varies directly as the square of [latex]y[/latex]
- [latex]x[/latex] varies as [latex]y[/latex] squared
- [latex]x[/latex] is proportional to the square of [latex]y[/latex]
- [latex]x[/latex] varies directly as the cube of [latex]y[/latex]
- [latex]x[/latex] varies as [latex]y[/latex] cubed
- [latex]x[/latex] is proportional to the cube of [latex]y[/latex]
- [latex]x[/latex] varies directly as the square root of [latex]y[/latex]
- [latex]x[/latex] varies as the root of [latex]y[/latex]
- [latex]x[/latex] is proportional to the square root of [latex]y[/latex]
Example 2.7.1
Find the variation equation described as follows:
The surface area of a square surface [latex](A)[/latex] is directly proportional to the square of either side [latex](x).[/latex]
[latex]\begin{array}{c} \text{Area }(A) =\text{ constant }(k)\text{ times side}^2\text{ } (x^2) \\ \\ \text{or} \\ \\ A=kx^2 \end{array}[/latex]
Example 2.7.2
When looking at two buildings at the same time, the length of the buildings’ shadows [latex](s)[/latex] varies directly as their height [latex](h).[/latex] If a 5-story building has a 20 m long shadow, how many stories high would a building that has a 32 m long shadow be?
The equation that describes this variation is:
[latex]h=kx[/latex]
Breaking the data up into the first and second parts gives:
[latex]\begin{array}{ll} \begin{array}{rrl} \\ &&\textbf{1st Data} \\ s&=&20\text{ m} \\ h&=&5\text{ stories} \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ h&=&kx \\ 5\text{ stories}&=&k\text{ (20 m)} \\ k&=&5\text{ stories/20 m}\\ k&=&0.25\text{ story/m} \end{array} & \hspace{0.5in} \begin{array}{rrl} &&\textbf{2nd Data} \\ s&=&\text{32 m} \\ h&=&\text{find 2nd} \\ k&=&0.25\text{ story/m} \\ \\ &&\text{Find }h\text{:} \\ h&=&kx \\ h&=&(0.25\text{ story/m})(32\text{ m}) \\ h&=&8\text{ stories} \end{array} \end{array}[/latex]
Inverse Variation Problems
Inverse variation problems are reciprocal relationships. In these types of problems, the product of two or more variables is equal to a constant. An example of this comes from the relationship of the pressure [latex](P)[/latex] and the volume [latex](V)[/latex] of a gas, called Boyle’s Law (1662). This law is written as:
[latex]\begin{array}{c} \text{Pressure }(P)\text{ times Volume }(V)=\text{ constant} \\ \\ \text{ or } \\ \\ PV=k \end{array}[/latex]
Written as an inverse variation problem, it can be said that the pressure of an ideal gas varies as the inverse of the volume or varies inversely as the volume. Expressed this way, the equation can be written as:
[latex]P=\dfrac{k}{V}[/latex]
Another example is the historically famous inverse square laws. Examples of this are the force of gravity [latex](F_{\text{g}}),[/latex] electrostatic force [latex](F_{\text{el}}),[/latex] and the intensity of light [latex](I).[/latex] In all of these measures of force and light intensity, as you move away from the source, the intensity or strength decreases as the square of the distance.
In equation form, these look like:
[latex]F_{\text{g}}=\dfrac{k}{d^2}\hspace{0.25in} F_{\text{el}}=\dfrac{k}{d^2}\hspace{0.25in} I=\dfrac{k}{d^2}[/latex]
These equations would be verbalized as:
- The force of gravity [latex](F_{\text{g}})[/latex] varies inversely as the square of the distance.
- Electrostatic force [latex](F_{\text{el}})[/latex] varies inversely as the square of the distance.
- The intensity of a light source [latex](I)[/latex] varies inversely as the square of the distance.
All inverse variation relationship are verbalized in written problems as inverse variations or as inversely proportional. Examples of inverse variation or inversely proportional equations are:
- [latex]x[/latex] varies inversely as [latex]y[/latex]
- [latex]x[/latex] varies as the inverse of [latex]y[/latex]
- [latex]x[/latex] varies inversely proportional to [latex]y[/latex]
- [latex]x[/latex] is inversely proportional to [latex]y[/latex]
- [latex]x[/latex] varies inversely as the square of [latex]y[/latex]
- [latex]x[/latex] varies inversely as [latex]y[/latex] squared
- [latex]x[/latex] is inversely proportional to the square of [latex]y[/latex]
- [latex]x[/latex] varies inversely as the cube of [latex]y[/latex]
- [latex]x[/latex] varies inversely as [latex]y[/latex] cubed
- [latex]x[/latex] is inversely proportional to the cube of [latex]y[/latex]
- [latex]x[/latex] varies inversely as the square root of [latex]y[/latex]
- [latex]x[/latex] varies as the inverse root of [latex]y[/latex]
- [latex]x[/latex] is inversely proportional to the square root of [latex]y[/latex]
Example 2.7.3
The force experienced by a magnetic field [latex](F_{\text{b}})[/latex] is inversely proportional to the square of the distance from the source [latex](d_{\text{s}}).[/latex]
[latex]F_{\text{b}} = \dfrac{k}{{d_{\text{s}}}^2}[/latex]
Example 2.7.4
The time [latex](t)[/latex] it takes to travel from North Vancouver to Hope varies inversely as the speed [latex](v)[/latex] at which one travels. If it takes 1.5 hours to travel this distance at an average speed of 120 km/h, find the constant [latex]k[/latex] and the amount of time it would take to drive back if you were only able to travel at 60 km/h due to an engine problem.
[latex]t=\dfrac{k}{v}[/latex]
[latex]\begin{array}{ll} \begin{array}{rrl} &&\textbf{1st Data} \\ v&=&120\text{ km/h} \\ t&=&1.5\text{ h} \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ k&=&tv \\ k&=&(1.5\text{ h})(120\text{ km/h}) \\ k&=&180\text{ km} \end{array} & \hspace{0.5in} \begin{array}{rrl} \\ \\ \\ &&\textbf{2nd Data} \\ v&=&60\text{ km/h} \\ t&=&\text{find 2nd} \\ k&=&180\text{ km} \\ \\ &&\text{Find }t\text{:} \\ t&=&\dfrac{k}{v} \\ \\ t&=&\dfrac{180\text{ km}}{60\text{ km/h}} \\ \\ t&=&3\text{ h} \end{array} \end{array}[/latex]
Joint or Combined Variation Problems
In real life, variation problems are not restricted to single variables. Instead, functions are generally a combination of multiple factors. For instance, the physics equation quantifying the gravitational force of attraction between two bodies is:
[latex]F_{\text{g}}=\dfrac{Gm_1m_2}{d^2}[/latex]
- [latex]F_{\text{g}}[/latex] stands for the gravitational force of attraction
- [latex]G[/latex] is Newton’s constant, which would be represented by [latex]k[/latex] in a standard variation problem
- [latex]m_1[/latex] and [latex]m_2[/latex] are the masses of the two bodies
- [latex]d^2[/latex] is the distance between the centres of both bodies
To write this out as a variation problem, first state that the force of gravitational attraction [latex](F_{\text{g}})[/latex] between two bodies is directly proportional to the product of the two masses [latex](m_1, m_2)[/latex] and inversely proportional to the square of the distance [latex](d)[/latex] separating the two masses. From this information, the necessary equation can be derived. All joint variation relationships are verbalized in written problems as a combination of direct and inverse variation relationships, and care must be taken to correctly identify which variables are related in what relationship.
Example 2.7.5
The force of electrical attraction [latex](F_{\text{el}})[/latex] between two statically charged bodies is directly proportional to the product of the charges on each of the two objects [latex](q_1, q_2)[/latex] and inversely proportional to the square of the distance [latex](d)[/latex] separating these two charged bodies.
[latex]F_{\text{el}}=\dfrac{kq_1q_2}{d^2}[/latex]
Solving these combined or joint variation problems is the same as solving simpler variation problems.
First, decide what equation the variation represents. Second, break up the data into the first data given—which is used to find [latex]k[/latex]—and then the second data, which is used to solve the problem given. Consider the following joint variation problem.
Example 2.7.6
[latex]y[/latex] varies jointly with [latex]m[/latex] and [latex]n[/latex] and inversely with the square of [latex]d[/latex]. If [latex]y = 12[/latex] when [latex]m = 3[/latex], [latex]n = 8[/latex], and [latex]d = 2,[/latex] find the constant [latex]k[/latex], then use [latex]k[/latex] to find [latex]y[/latex] when [latex]m=-3[/latex], [latex]n = 18[/latex], and [latex]d = 3[/latex].
[latex]y=\dfrac{kmn}{d^2}[/latex]
[latex]\begin{array}{ll} \begin{array}{rrl} \\ \\ \\ && \textbf{1st Data} \\ y&=&12 \\ m&=&3 \\ n&=&8 \\ d&=&2 \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ y&=&\dfrac{kmn}{d^2} \\ \\ 12&=&\dfrac{k(3)(8)}{(2)^2} \\ \\ k&=&\dfrac{12(2)^2}{(3)(8)} \\ \\ k&=& 2 \end{array} & \hspace{0.5in} \begin{array}{rrl} &&\textbf{2nd Data} \\ y&=&\text{find 2nd} \\ m&=&-3 \\ n&=&18 \\ d&=&3 \\ k&=&2 \\ \\ &&\text{Find }y\text{:} \\ y&=&\dfrac{kmn}{d^2} \\ \\ y&=&\dfrac{(2)(-3)(18)}{(3)^2} \\ \\ y&=&12 \end{array} \end{array}[/latex]
For questions 1 to 12, write the formula defining the variation, including the constant of variation [latex](k).[/latex]
- [latex]x[/latex] is jointly proportional to [latex]y[/latex] and [latex]z[/latex]
- [latex]x[/latex] varies jointly as [latex]z[/latex] and [latex]y[/latex]
- [latex]x[/latex] is jointly proportional with the square of [latex]y[/latex] and the square root of [latex]z[/latex]
- [latex]x[/latex] is inversely proportional to [latex]y[/latex] to the sixth power
- [latex]x[/latex] is jointly proportional with the cube of [latex]y[/latex] and inversely to the square root of [latex]z[/latex]
- [latex]x[/latex] is inversely proportional with the square of [latex]y[/latex] and the square root of [latex]z[/latex]
- [latex]x[/latex] varies jointly as [latex]z[/latex] and [latex]y[/latex] and is inversely proportional to the cube of [latex]p[/latex]
- [latex]x[/latex] is inversely proportional to the cube of [latex]y[/latex] and square of [latex]z[/latex]
For questions 13 to 22, find the formula defining the variation and the constant of variation [latex](k).[/latex]
- If [latex]A[/latex] varies directly as [latex]B,[/latex] find [latex]k[/latex] when [latex]A=15[/latex] and [latex]B=5.[/latex]
- If [latex]P[/latex] is jointly proportional to [latex]Q[/latex] and [latex]R,[/latex] find [latex]k[/latex] when [latex]P=12, Q=8[/latex] and [latex]R=3.[/latex]
- If [latex]A[/latex] varies inversely as [latex]B,[/latex] find [latex]k[/latex] when [latex]A=7[/latex] and [latex]B=4.[/latex]
- If [latex]A[/latex] varies directly as the square of [latex]B,[/latex] find [latex]k[/latex] when [latex]A=6[/latex] and [latex]B=3.[/latex]
- If [latex]C[/latex] varies jointly as [latex]A[/latex] and [latex]B,[/latex] find [latex]k[/latex] when [latex]C=24, A=3,[/latex] and [latex]B=2.[/latex]
- If [latex]Y[/latex] is inversely proportional to the cube of [latex]X,[/latex] find [latex]k[/latex] when [latex]Y=54[/latex] and [latex]X=3.[/latex]
- If [latex]X[/latex] is directly proportional to [latex]Y,[/latex] find [latex]k[/latex] when [latex]X=12[/latex] and [latex]Y=8.[/latex]
- If [latex]A[/latex] is jointly proportional with the square of [latex]B[/latex] and the square root of [latex]C,[/latex] find [latex]k[/latex] when [latex]A=25, B=5[/latex] and [latex]C=9.[/latex]
- If [latex]y[/latex] varies jointly with [latex]m[/latex] and the square of [latex]n[/latex] and inversely with [latex]d,[/latex] find [latex]k[/latex] when [latex]y=10, m=4, n=5,[/latex] and [latex]d=6.[/latex]
- If [latex]P[/latex] varies directly as [latex]T[/latex] and inversely as [latex]V,[/latex] find [latex]k[/latex] when [latex]P=10, T=250,[/latex] and [latex]V=400.[/latex]
For questions 23 to 37, solve each variation word problem.
- The electrical current [latex]I[/latex] (in amperes, A) varies directly as the voltage [latex](V)[/latex] in a simple circuit. If the current is 5 A when the source voltage is 15 V, what is the current when the source voltage is 25 V?
- The current [latex]I[/latex] in an electrical conductor varies inversely as the resistance [latex]R[/latex] (in ohms, Ω) of the conductor. If the current is 12 A when the resistance is 240 Ω, what is the current when the resistance is 540 Ω?
- Hooke’s law states that the distance [latex](d_s)[/latex] that a spring is stretched supporting a suspended object varies directly as the mass of the object [latex](m).[/latex] If the distance stretched is 18 cm when the suspended mass is 3 kg, what is the distance when the suspended mass is 5 kg?
- The volume [latex](V)[/latex] of an ideal gas at a constant temperature varies inversely as the pressure [latex](P)[/latex] exerted on it. If the volume of a gas is 200 cm 3 under a pressure of 32 kg/cm 2 , what will be its volume under a pressure of 40 kg/cm 2 ?
- The number of aluminum cans [latex](c)[/latex] used each year varies directly as the number of people [latex](p)[/latex] using the cans. If 250 people use 60,000 cans in one year, how many cans are used each year in a city that has a population of 1,000,000?
- The time [latex](t)[/latex] required to do a masonry job varies inversely as the number of bricklayers [latex](b).[/latex] If it takes 5 hours for 7 bricklayers to build a park wall, how much time should it take 10 bricklayers to complete the same job?
- The wavelength of a radio signal (λ) varies inversely as its frequency [latex](f).[/latex] A wave with a frequency of 1200 kilohertz has a length of 250 metres. What is the wavelength of a radio signal having a frequency of 60 kilohertz?
- The number of kilograms of water [latex](w)[/latex] in a human body is proportional to the mass of the body [latex](m).[/latex] If a 96 kg person contains 64 kg of water, how many kilograms of water are in a 60 kg person?
- The time [latex](t)[/latex] required to drive a fixed distance [latex](d)[/latex] varies inversely as the speed [latex](v).[/latex] If it takes 5 hours at a speed of 80 km/h to drive a fixed distance, what speed is required to do the same trip in 4.2 hours?
- The volume [latex](V)[/latex] of a cone varies jointly as its height [latex](h)[/latex] and the square of its radius [latex](r).[/latex] If a cone with a height of 8 centimetres and a radius of 2 centimetres has a volume of 33.5 cm 3 , what is the volume of a cone with a height of 6 centimetres and a radius of 4 centimetres?
- The centripetal force [latex](F_{\text{c}})[/latex] acting on an object varies as the square of the speed [latex](v)[/latex] and inversely to the radius [latex](r)[/latex] of its path. If the centripetal force is 100 N when the object is travelling at 10 m/s in a path or radius of 0.5 m, what is the centripetal force when the object’s speed increases to 25 m/s and the path is now 1.0 m?
- The maximum load [latex](L_{\text{max}})[/latex] that a cylindrical column with a circular cross section can hold varies directly as the fourth power of the diameter [latex](d)[/latex] and inversely as the square of the height [latex](h).[/latex] If an 8.0 m column that is 2.0 m in diameter will support 64 tonnes, how many tonnes can be supported by a column 12.0 m high and 3.0 m in diameter?
- The volume [latex](V)[/latex] of gas varies directly as the temperature [latex](T)[/latex] and inversely as the pressure [latex](P).[/latex] If the volume is 225 cc when the temperature is 300 K and the pressure is 100 N/cm 2 , what is the volume when the temperature drops to 270 K and the pressure is 150 N/cm 2 ?
- The electrical resistance [latex](R)[/latex] of a wire varies directly as its length [latex](l)[/latex] and inversely as the square of its diameter [latex](d).[/latex] A wire with a length of 5.0 m and a diameter of 0.25 cm has a resistance of 20 Ω. Find the electrical resistance in a 10.0 m long wire having twice the diameter.
- The volume of wood in a tree [latex](V)[/latex] varies directly as the height [latex](h)[/latex] and the diameter [latex](d).[/latex] If the volume of a tree is 377 m 3 when the height is 30 m and the diameter is 2.0 m, what is the height of a tree having a volume of 225 m 3 and a diameter of 1.75 m?
Answer Key 2.7
Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Variation Word Problems
Equations Word Problems More Prob's
It's one thing to be able to take the words for a variation equation (such as " y varies directly as the square of x and inversely as the cube root of z ") and turn this into an equation that you can solve or use. It's another thing to extract the words from a word problem. But, because the lingo for variation equations is so specific, it's not really that hard. Just look for the keywords, and you're nearly home and dry.
The only other keywords (or "key-phrases", really) you might need to know are "is proportional to" which, in the strictly-mathematical sense, means "varies directly as"; and "is inversely proportional to" which means "varies inversely with".
Content Continues Below
MathHelp.com

Suppose that y is inversely proportional to x , and that y = 0.4 when x = 2.5 . Find y when x = 4 .
Translating the above from the English into algebra, I see the key-phrase "inversely proportional to", which means "varies indirectly as". In practical terms, it means that the variable part that does the varying is going to be in the denominator. So I get the formula:
Plugging in the data point they gave me, I can solve for the value of k :
0.4 = k /(2.5)
(0.4)(2.5) = k = 1
Now that I have found the value of the variation constant, I can plug in the x -value they gave me, and find the value of y when x = 4 :
Then my answer is:
Most word problems, of course, are not nearly as simple as the above example (or the ones on the previous page). Instead, you have to figure out which values go where, what the equation is, and how to interpret it. Fortunately, the keywords and key-phrases should generally be fairly clear, telling you exactly what format to use.
According to Hooke's Law, the force needed to stretch a spring is proportional to the amount the spring is stretched. If fifty pounds of force stretches a spring five inches, how much will the spring be stretched by a force of 120 pounds?
"Is proportional to" means "varies directly with", so the formula for Hooke's Law is:
...where " F " is the force and " d " is the distance that the spring is stretched.
Note: In physics, "weight" is a force. These Hooke's Law word problems, among other types, are often stated in terms of weight, and the weight they list is the force they mean.
First I have to solve for the value of k . They've given me the data point ( d , F) = (5, 50) , so I'll plug this in to the formula:
Now I know that the formula for this particular spring is:
(Hooke's Law doesn't change, but each spring is different, so each spring will have its own " k ".)
Once I know the formula, I can answer their question: "How much will the spring be stretched by a force of 120 pounds?" I'll plug the value they've given me for the force into the equation I've found:
Note that they did not ask "What is the value of ' d '?". They asked me for a distance. I need to be sure to answer the question that they actually asked. That final answer is the distance that the spring is stretched, including the units (which are "inches", in this case):
Note: If you give the above answer as being only " 12 ", the grader will be perfectly correct to count your answer as being at least partly wrong. The answer is not a number, but is a number of units.
Kepler's third law of planetary motion states that the square of the time required for a planet to make one revolution about the sun varies directly as the cube of the average distance of the planet from the sun. If you assume that Mars is 1.5 times as far from the sun as is the earth, find the approximate length of a Martian year.
This one is a bit different from the previous exercise. Normally, I've given given a relation in terms of variation with a plain old variable, like y . In this case, though, the variation relationship is between the square of the time and the cube of the distance. This means that the left-hand side of my equation will have a squared variable!
Advertisement
My variation formula is:
t 2 = k d 3
If I take " d = 1 " to mean "the distance is one AU", an AU being an "astronomical unit" (the distance of earth from the sun), then the distance for Mars is 1.5 AU. Also, I will take " t = 1 " to stand for "one earth year". Then, in terms of the planet Earth, I get:
(1) 2 = k (1) 3
Then the formula, in terms of Earth, is:
Now I'll plug in the information for Mars (in comparison to earth):
t 2 = (1.5) 3
This is one of those times when a calculator's decimal approximation is probably going to be a little more useful in answering the question. I'll show the exact answer in my working, but I'll use a sensible approximation in my final answer. The decimal expansion starts as:
In other words, the Martian year is approximately the length of:
1.837 earth years
By the way, you can make the above answer more intuitive by finding the number of (Earth) days, approximately, represented by that " 0.837 " part of the answer above. Since the average Earth year, technically, has about 365.25 days, then the 0.837 of an Earth year is:
0.837 × 365.25 = 305.71425
Letting the "average" month have 365.25 ÷ 12 = 30.4375 days, then the above number of (Earth) days is:
305.71425 ÷ 30.4375 = 10.044
In other words, the Martian year is almost exactly one Earth year and ten Earth months long.
If you were writing for an audience (like a fellow student, as you'll be required to do in some class projects or essay questions), this "one year and ten months" form would probably be the best way to go.
The weight of a body varies inversely as the square of its distance from the center of the earth. If the radius of the earth is 4000 miles, how much would a 200 -pound man weigh 1000 miles above the surface of the earth?
Remembering that "weight" is a force, I'll let the weight be designated by " F ". The distance of a body from the center of the earth is " d ". Then my variation formula is the following:
(200)(16,000,000) = k
3,200,000,000 = k
(Hey; there's nothing that says that the value of the variation constant k has to be small!)
The distance is always measured from the center of the earth. If the guy is in orbit a thousand miles up (from the surface of the planet), then his distance (from the center of the planet) is the 4000 miles from the center to the surface plus the 1000 miles from the surface to his ship. That is, d = 5000 . I'll plug this in to my equation, and solve for the value of the force (which is here called "weight") F :
Remembering my units, my answer is that, up in his spacecraft, the guy weighs:
URL: https://www.purplemath.com/modules/variatn2.htm
Page 1 Page 2 Page 3
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
JOINT VARIATION WORD PROBLEMS
Problem 1 :
z varies directly with the sum of squares of x and y. z = 5 when x = 3 and y = 4. Find the value of z when x = 2 and y = 4.
Since z varies directly with the sum of squares of x and y,
z ∝ x 2 + x 2
z = k(x 2 + y 2 ) ----(1)
Substitute z = 5, x = 3 and y = 4 to find the value k.
5 = k(3 2 + 4 2 )
5 = k(9 + 16)
Divide both sides by 25.
Substitute k = 1/5 in (1).
z = (1/5)(x 2 + y 2 )
Substitute x = 2, y = 4 and evaluate z.
z = (1/5)( (2 2 + 4 2 )
z = (1/5)( (4 + 16)
z = (1/5)( (20)
Problem 2 :
M varies directly with the square of d and inversely with the square root of x. M = 24 when d = 4 and x = 9. Find the value of M when d = 5 and x = 4.
Since m varies directly with the square of d and inversely with the square root of x
M ∝ d 2 √ x
M = kd 2 √ x ----(1)
Substitute M = 24, d = 4 and x = 9 to find the value k.
24 = k4 2 √9
24 = k(16)(3)
Divide both sides by 48.
Substitute k = 1/2 in (1).
M = (1/2)(d 2 √ x )
Substitute d = 5, x = 4 and evaluate M.
M = (1/2) (5 2 √4 )
M = (1/2)( (25)(2)
Problem 3 :
Square of T varies directly with the cube of a and inversely with the square of d. T = 2 when a = 2 and d = 4. Find the value of s quare of T when a = 4 and d = 2
Since square of T varies directly with the cube of a and inversely with the square of d
T 2 ∝ a 3 d 2
T 2 = ka 3 d 2 ----(1)
Substitute T = 2, a = 2 and d = 4 to find the value k.
2 2 = k2 3 4 2
4 = k(4)(16)
Divide both sides by 64.
Substitute k = 1/16 in (1).
T 2 = (1/16)a 3 d 2
Substitute a = 4, d = 2 and evaluate T 2 .
T 2 = (1/16)(4 3 )(2 2 )
T 2 = (1/16)(64)(4)
T 2 = 16
Problem 4 :
The area of a rectangle varies directly with its length and square of its width. When the length is 5 cm and width is 4 cm, the area is 160 cm 2 . Find the area of the rectangle when the length is 7 cm and the width is 3 cm.
Let A represent the area of the rectangle, l represent the length and w represent width.
Since the area of the rectangle varies directly with its length and square of its width,
A ∝ lw 2
A = klw 2 ----(1)
Substitute A = 160, l = 5 and d = 4 to find the value k.
160 = k(5)(4 2 )
160 = k(5)(16 )
160 = 80k
Divide both sides by 80.
Substitute k = 2 in (1).
Substitute l = 7, w = 3 and evaluate A.
A = 2(7)(3 2 )
A = 2(7)(9)
Area of the rectangle = 126 cm 2
Problem 5 :
The volume of a cylinder varies jointly as the square of radius and two times of its height. A cylinder with radius 4 cm and height 8 cm has a volume 128 π cm 3 . Find the volume of a cylinder with radius 3 cm and height 10 cm.
Let V represent volume of the cylinder, r represent radius and h represent height.
Since t he volume of a cylinder varies jointly as the radius and the sum of the radius and the height.
V ∝ r 2 (2h)
V = kr 2 (2h) ----(1)
Substitute V = 128 π , r = 4 and h = 8 to find the value of k.
128π = k(4 2 )(2 ⋅ 8)
128π = k(16)(16)
128π = 256k
Divide both sides by 256.
π/2 = k
Substitute k = π/2 in (1).
V = ( π/2) r 2 (2h)
V = π r 2 h
Substitute r = 3, h = 10 and evaluate V.
V = π(3 2 )(10)
V = π(9) (10)
Volume of the cylinder = 90 π cm 3
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Digital sat math problems and solutions (part - 19).
Sep 04, 24 10:53 PM
Digital SAT Math Problems and Solutions (Part - 18)
Sep 04, 24 10:49 PM
Digital SAT Math Problems and Solutions (Part - 17)
Sep 04, 24 08:35 PM
{{ article.displayTitle }}
| {{ 'ml-lesson-number-slides' | message : article.intro.bblockCount }} | |
| {{ 'ml-lesson-number-exercises' | message : article.intro.exerciseCount }} | |
| {{ 'ml-lesson-time-estimation' | message }} |
- {{ item.file.title }} {{ presentation }}
Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
- Reciprocal Functions
- Graphing Reciprocal Functions
- Direct Variation and Proportional Relationships
Number of Phone Calls Per Day Between Two Cities
The average number of phone calls per day between two cities N varies directly with the populations of the cities P 1 and P 2 , and inversely with the square of distance d between the two cities.
Joint Variation
A joint variation , also known as joint proportionality , occurs when one variable varies directly with two or more variables . In other words, if a variable varies directly with the product of other variables, it is called joint variation.
Here, the variable z varies jointly with x and y , and k is the constant of variation . Here are some examples of joint variation.
| Examples of Joint Variation | ||
|---|---|---|
| Example | Rule | Comment |
| The | A=ℓw | Here, ℓ is the rectangle's length, w its width, and the constant of variation k is 1. |
| The | V=31ℓwh | Here, ℓ and w are the length and the width of the base, respectively, while h is the pyramid's height. The constant of variation k is 31. |
Television Series
Vincenzo and Emily are having a lively chat about television series they love. Emily managed to watch 1 6 4 episodes of The Flash in just 5 0 days! Each episode typically lasts 4 0 minutes.
Use the fact that if z varies jointly with x and y , the equation of variation is z = k x y , where k is the constant of variation .
Substitute values
LHS / 6 5 6 0 = RHS / 6 5 6 0
b a = b / 1 0 a / 1 0
Rearrange equation
c a ⋅ b = c a ⋅ b
Calculate quotient
Round to nearest integer
Recognzing Inverse Variation
| Width | Length |
|---|---|
| 2 | |
| 4 | |
| 8 | |
| 16 | |
| 32 |
Inverse Variation
An inverse variation , or inverse proportionality , occurs when two non-zero variables have a relationship such that their product is constant . This relationship is often written with one of the variables isolated on the left-hand side.
x y = k or y = x k
| Example | Rule | Comment |
|---|---|---|
| The gas pressure in a sealed container if the container's volume is changed, given constant temperature and constant amount of gas. | P=VnRT | The variables are the pressure P and the volume V. The amount of gas n, temperature T, and universal gas constant R are fixed values. Therefore, the constant of variation is nRT. |
| The time it takes to travel a given distance at various speeds. | t=sd | The constant of variation is the distance d and the variables are the time t and the speed s. |
Identifying the Type of Variation
Determine whether the relationship between the variables in the table shows direct or inverse variation, or neither.
Number of Songs on Emily's Phone
Emily, tired of watching shows, wants to update the playlist on her phone before starting a family road trip from Portland to San Francisco. The number of songs that can be stored on her phone varies inversely with the average size of a song.
Emily's phone can store 4 1 0 0 songs when the average size of a song is 4 megabytes (MB).
x = 4 , y = 4 1 0 0
LHS ⋅ 4 = RHS ⋅ 4
| Size, x | x16400 | Number of Songs, y |
|---|---|---|
| 3 | 216400 | 5466 |
| 4 | 416400 | 4100 |
| 5 | 516400 | 3280 |
| 6 | 616400 | ≈2733 |
In the table, as the size gets larger, the number of songs that the phone can store gets smaller. Therefore, the number of songs decreases as the average size increases.
Emily's Trip to San Francisco
Example Graph:
| r | r640 | t |
|---|---|---|
| 10 | 10640 | 64 |
| 20 | 20640 | 32 |
| 30 | 30640 | ≈ 21 |
| 40 | 40640 | 16 |
| 50 | 50640 | 12.8 |
| 60 | 60640 | ≈ 10.7 |
Ordered pairs ( r , t ) are the coordinates of the points on the graph. Plot the points and connect them with a smooth curve.
LHS ⋅ r = RHS ⋅ r
LHS / 1 2 = RHS / 1 2
Combined Variation
A combined variation , or combined proportionality , occurs when one variable depends on two or more variables, either directly , inversely , or a combination of both. This means that any joint variation is also a combined variation.
z = y k x
The variable z varies directly with x and inversely with y , and k is the constant of variation . Therefore, this is a combined variation. Here are some examples.
| Examples of Combined Variation | ||
|---|---|---|
| Example | Rule | Comment |
| Newton's Law of Gravitational Force | F=d2Gm1m2 | The gravitational force F varies directly as the masses of the objects m1 and m2, and inversely as the square of the distance d2 between the objects. The gravitational constant G is the constant of variation. |
| The Ideal Gas Law | P=VnRT | The pressure P varies directly as the number of moles n and the temperature T, and inversely as the volume V. The universal gas constant R is the constant of variation. |
Number of T-Shirts Sold
Emily is wandering around a gift shop to buy gifts for some of her friends. Emily overhears a conversation between the shopkeeper and an employee. The shopkeeper says that the number of t-shirts sold is directly proportional to their advertising budget and inversely proportional to the price of each t-shirt.
When $ 1 2 0 0 are spent on advertising and the price of each t-shirt is $ 4 . 8 0 , the number of t-shirts sold is 6 5 0 0 . How many t-shirts are sold when the advertising budget is $ 1 8 0 0 and the price of each t-shirt is $ 6 ?
Use the equation of the combined variation , z = y k x , where k is the constant of variation .
When one quantity varies with respect to two or more quantities, this variation can be regarded as a combined variation.
| Combined Variation | Equation Form |
|---|---|
| a varies with b and c. | a=kbc |
| a varies jointly with b and c, and inversely with d. | a=dkbc |
| a varies directly with b and inversely with the product dc. | a=dckb |
LHS ⋅ 4 . 8 0 = RHS ⋅ 4 . 8 0
LHS / 1 2 0 0 = RHS / 1 2 0 0
b = 1 8 0 0 , p = 6
Alternative Solution
Cross multiply
LHS / 7 2 0 0 = RHS / 7 2 0 0
Finding the Value of z
In the applet, various types of variations are shown randomly. Find the value of z by using the given values. If necessary, round the answer to the two decimal places.
In this lesson, variation types are explained with real-life examples. Considering those examples, the challenge presented at the beginning of the lesson can be solved with confidence. Recall that the average number of phone calls per day between two cities varies directly with the populations of the cities and inversely with the square of the distance between the two cities.
| San Francisco | Portland | |
|---|---|---|
| Population | 806000 | 585000 |
| Distance | 650 | |
| Number of Calls | 42000 | |
Calculate power
c a ⋅ b = a ⋅ c b
LHS / 1 1 1 6 0 0 0 = RHS / 1 1 1 6 0 0 0
Round to 3 decimal place(s)
| San Francisco | Los Angeles | |
|---|---|---|
| Population | 806000 | 3800000 |
| Distance | d | |
| Number of Calls | 806000 | |
LHS ⋅ d 2 = RHS ⋅ d 2
LHS / 8 0 6 0 0 0 = RHS / 8 0 6 0 0 0
LHS = RHS
a 2 = ± a
Calculate root
Math, Science, Test Prep, Music Theory
Easy Video Tutorials For Your Class
Home » Joint Variation and Proportion » Joint Variation and Proportion problems
- Absolute Value (2)
- Absolute Value Equations (1)
- Absolute Value Inequalities (1)
- ACT Math Practice Test (2)
- ACT Math Tips Tricks Strategies (25)
- Addition & Subtraction of Polynomials (2)
- Addition Property of Equality (2)
- Addition Tricks (1)
- Adjacent Angles (2)
- Albert Einstein's Puzzle (1)
- Algebra (3)
- Alternate Exterior Angles Theorem (1)
- Alternate Interior Angles Theorem (2)
- Alternating Series (1)
- Altitude of a Triangle (2)
- Angle Addition Postulate (1)
- Angle Angle Side Theorem (1)
- Angle Angle Similarity Postulate (1)
- Angle Bisector Theorem (2)
- Angle Side Angle Theorem (1)
- Angles (28)
- Angles Parallel Lines Transversals (1)
- Application of Differentiation (6)
- Application of Integration (8)
- Arc Addition Postulate (1)
- Arc Length of a Curve Integration (1)
- Area as a Function of Length (1)
- Area between Curves Integration (2)
- Arithmetic & Geometric Sequence (1)
- Asymptotes of Rational Functions (1)
- Atoms Molecules Ions (2)
- Avogadro Gas Law (2)
- Balancing Chemical Equations (2)
- Base Angles Theorem (1)
- Binary Ionic Compound Formulas (2)
- Binomial Distribution (4)
- Binomial Theorem (2)
- Bounded Sequence (1)
- Boyle Gas Law (2)
- Business Calculus (1)
- Calorimetry (1)
- CASTC Theorem (1)
- Central Angle (2)
- Centroid (1)
- Chain Rule of Derivatives (1)
- Charles Gas Law (2)
- Chemical Reactions in Aqueous Solutions (5)
- Chemistry Matter and Measurement (2)
- Circles (3)
- Circumcenter (1)
- Combined Gas Law (2)
- Combined Variation and Proportion (1)
- Combining Like Terms in Polynomials (1)
- Commutative Property of Multiplication (1)
- Comparison Test (1)
- Completing the Square (2)
- Complex and Imaginary Numbers (2)
- Composition of Functions (2)
- Compound Interest (1)
- Conditional Expectation (1)
- Conditional Probability (2)
- Confidence Intervals (1)
- Conic Sections (1)
- Consecutive Exterior Angles Theorem (1)
- Consecutive Interior Angles Theorem (2)
- Continuity (3)
- Continuous Random Variable (8)
- Converse of Base Angles Theorem (1)
- Corresponding Angles Theorem (1)
- Covariance (1)
- CPCTC Theorem (1)
- CSSTP Theorem (1)
- Cumulative Distribution (1)
- Curve Sketching with Differentiation (2)
- Cylindrical Coordinates (1)
- Cylindrical Shell Integration Method (2)
- Decimal and Rational Number Operations (1)
- Derivative of Exponential Functions (3)
- Derivative of Hyperbolic & Inverse Hyperbolic Functions (3)
- Derivative of Inverse Functions (3)
- Derivative of Inverse Trigonometric Functions (3)
- Derivative of Logarithmic Functions (3)
- Differential Equations (10)
- Differentials (1)
- Dilation (1)
- Direct Variation and Proportion (1)
- Discrete Mathematics and Combinatorics (4)
- Discrete Random Variable (7)
- Disk Integration Method (2)
- Distributive Property of Multiplication (1)
- Division Property of Equality (2)
- Division Tricks (1)
- Domain and Range of a Function (1)
- Double Integrals (4)
- Eigenvalues and Eigenvectors (1)
- Ellipse (1)
- Empirical and Molecular Formula (2)
- Enthalpy Change (2)
- Equilateral Triangles (1)
- Expected Value (5)
- Exponential Distribution (1)
- Exponential Equations (3)
- Exponents (3)
- Exterior Angle Theorem (1)
- Exterior Angles (1)
- Factoring Polynomials (3)
- Financial Math (6)
- First Law of Thermodynamics (2)
- Fourier Series (1)
- Fraction Multiplication Rule (1)
- Fractions (7)
- Fundamental Theorem of Calculus (2)
- Gas Pressure (2)
- Gases in Chemistry (7)
- GED Math (4)
- Geometric Distribution (1)
- Geometric Formula as a Function (1)
- Geometric Formula Proof with Integration (2)
- Geometric Series (1)
- Geometry (14)
- Graph of Trigonometric Functions (2)
- GRE Math (4)
- Greatest Common Factor (1)
- Harmonic Series (1)
- Hydrostatic Force & Work (3)
- Hyperbola (1)
- Hypergeometric Distribution (2)
- Hypotenuse Leg Theorem (1)
- Hypothesis Testing (1)
- Ideal Gas Law (2)
- Identity Property of Multiplication (1)
- Implicit Differentiation (7)
- Improper Integrals (7)
- Incenter (1)
- Increasing or Decreasing Sequence (1)
- Independent Events Probability (1)
- Infinite Sequences (8)
- Infinite Series (19)
- Infinite Series Derivative (1)
- Inscribed Angle (1)
- Integral Test (1)
- Integration by Partial Fraction Decomposition (6)
- Integration by Parts (6)
- Integration by Trigonometric Substitution (5)
- Integration of Exponential Functions by Substitution (5)
- Integration of Functions with Roots & Fractions (5)
- Integration of Hyperbolic & Inverse Hyperbolic Functions by Substitution (5)
- Integration of Inverse Trigonometric Functions by Substitution (5)
- Integration of Logarithmic Functions by Substitution (5)
- Integration of Trigonometric Functions by Substitution (5)
- Integration with Reduction Formula (1)
- Interior Angles (2)
- Inverse Functions (2)
- Inverse Trigonometric Functions (1)
- Inverse Variation and Proportion (1)
- Isosceles Triangles (1)
- Joint Distribution (1)
- Joint Moment Generating Functions (1)
- Joint Variation and Proportion (1)
- Lattice Multiplication (1)
- Law of Combining Volumes (2)
- Law of Cooling (1)
- Law of Cosines (1)
- Law of Sines (1)
- Laws of Chemical Combination (2)
- Least Common Multiple (1)
- Limit Comparison Test (1)
- Limit Definition of Derivative (3)
- Limiting Reactants (2)
- Limits (10)
- Line Segments (1)
- Linear Algebra (6)
- Linear Approximation (2)
- Linear Equations (3)
- Linear Functions (1)
- Linear Measure (1)
- Linear Pair Angles Theorem (2)
- Locus of Points (1)
- Logarithmic Differentiation (2)
- Logarithmic Equations (1)
- Logarithms (4)
- Maclaurin Series (1)
- Mass Percent Composition from Chemical Formulas (2)
- Math Puzzles (2)
- Math Tricks (7)
- Matrices (5)
- Mean Value Theorem for Integrals (1)
- Means-Extremes Property of Proportions (2)
- Median of a Triangle (1)
- Midsegment Theorem (1)
- Molar Mass (2)
- Molarity of Compounds and Ions (2)
- Mole and Avogadro's Number (2)
- Molecular and Formula Mass (2)
- Moment Generating Function (2)
- Multiple Integrals (2)
- Multiplication Property of Equality (2)
- Multiplication Tricks (1)
- Multivariable Calculus (5)
- Music Theory (3)
- Negative Binomial Distribution (1)
- Negative Exponents (1)
- NonLinear Equations (8)
- NonLinear Inequalities (2)
- Normal Approximation (1)
- Normal Distribution (3)
- Nth Term Test (1)
- Number Line (5)
- Optimization (4)
- Orthocenter (2)
- Oxidation and Reduction in Chemical Reactions (2)
- P Series (1)
- Parabola (3)
- Parametric Equations and Curves (2)
- Partial Derivatives (2)
- Partial Fraction Decomposition (1)
- Particle Motion (1)
- Pascal's Triangle (1)
- Percentage Probability (1)
- Perimeter as a Function of Area (1)
- Permutations and Combinations (1)
- Perpendicular Bisector Theorem (1)
- Physics (1)
- Piecewise Probability Distribution Functions (4)
- Poisson Distribution (2)
- Polar Coordinates (2)
- Polynomial Multiplication (1)
- Power Rule of Derivatives (5)
- Power Series (1)
- Precalculus (2)
- Precipitate Formation in Chemical Reactions (2)
- Principle of Mathematical Induction (1)
- Probability & Statistics (25)
- Probability of Outcomes (1)
- Product Rule of Derivatives (1)
- Projectile Motion (3)
- Puzzles (6)
- Quadratic Equations (3)
- Quadratic Formula (1)
- Quadratic Functions (2)
- Quadratic Inequalities (1)
- Quotient Rule of Derivatives (1)
- Radians Degrees Minutes Seconds (2)
- Radicals (1)
- Rational and Radical Expressions (3)
- Rational Equations (1)
- Rational Inequalities (1)
- Rational Numbers (2)
- Reactions of Acids and Bases (2)
- Reciprocal Rule of Division (1)
- Rectangles (1)
- Reference Angles (1)
- Reflection (2)
- Reflexive Property (1)
- Related Rates (3)
- Riemann Sum (20)
- Right Triangles (1)
- Rotation (2)
- Rotation of Axes (1)
- Rule of Product (1)
- Russian Peasant Multiplication (1)
- SAT Math Practice Test #1 (59)
- SAT Math Practice Test #2 (59)
- SAT Math Practice Test #3 (59)
- SAT Math Practice Test #4 (59)
- SAT Math Practice Test #5 (30)
- SAT Math Practice Test #6 (25)
- SAT Math Practice Test #7 (12)
- SAT Math Practice Test #8 (3)
- Scientific Notation (2)
- Segment Addition Postulate (1)
- Side Angle Side Theorem (1)
- Side Side Side Theorem (1)
- Sidelight Division (1)
- Significance Tests (1)
- Significant Figures (2)
- Similarity of Triangles (1)
- SOA Exam P (4)
- Solve for X (2)
- Specific Heat (1)
- Spherical Coordinates (1)
- Square Number (1)
- Squares (1)
- Standard Deviation (3)
- Stoichiometry Chemical Calculations (8)
- Substitution Property of Equality (2)
- Subtraction Property of Equality (2)
- Summation Formulas (2)
- Supplementary Angle Theorem (1)
- Surface Area Integration (2)
- Symmetric Property (2)
- Symmetry Tests (1)
- Synthetic and Long Division of Polynomials (1)
- System of NonLinear Equations (1)
- Systems of Linear Equations (1)
- T Distribution (1)
- Table Data (3)
- Table of Ordered Pairs (1)
- Taylor Series (1)
- Telescoping Series (1)
- Theoretical & Proofs (5)
- Thermochemistry (3)
- Titrations in Chemical Reactions (2)
- Transformation (5)
- Transitive Property (2)
- Translation (1)
- Trapezoid (1)
- Tree Diagram Probability (1)
- Triangles (22)
- Trigonometric Angle Sum Difference Multiple Half-Angle Formulas (3)
- Trigonometric Equations (4)
- Trigonometric Form of Complex Numbers (1)
- Trigonometric Functions (4)
- Trigonometric Identity Proofs (1)
- Trigonometry (19)
- Triple Integrals (1)
- Truth Tables (1)
- Two Column Proofs (2)
- Two Way Table (1)
- Uniform Distribution (1)
- Unit Circle (5)
- Unit Conversions (2)
- Variance (2)
- Variation and Proportion (4)
- Vectors (1)
- Vectors in the Plane (2)
- Venn Diagram (1)
- Vertex Form of a Parabola (1)
- Vertical Angles Theorem (2)
- Volume of the Solid of Revolution (2)
- Washer Integration Method (2)
- Whole Number Operations (3)
- World's HARDEST Easy Geometry problems (1)
- Wronskian (1)
- Yield of Chemical Reactions (2)
Joint Variation and Proportion problems
Joint variation and proportion example question.
If z varies jointly as x and y , and z = 3 when x = 4 and y = 6, find z when x = 20 and y = 9.
Solution to this Joint Variation and Proportion practice problem is provided in the video below!
Tags: joint proportion example problems , joint proportion example questions , joint proportion example solutions , joint variation example problems , joint variation example questions , joint variation example solutions , joint variation problems and solutions , joint variation video tutorial
Thank you so much, this tutorial is awesome!
Enjoyed the clarity of explanation, thank you
Very nice tutorial and good drill. My son understands now how to distinguish many different types of variation!
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Recent Posts
- Angular Speed and Linear Speed problems March 13, 2024
- Converting Repeating Decimals to Fractions problems February 29, 2024
- Geometry Puzzles and Brain Teasers December 18, 2023
- VERIFYING Whether Given Two Functions are Inverses December 15, 2023
- Trigonometric Functions WORD problems December 11, 2023
- Null Hypothesis Testing statistics problems February 9, 2021
- Variance problems February 9, 2021
- Confidence Interval statistics problems December 9, 2020
- Greatest Common Factor and Least Common Multiple problems December 3, 2020
- Translation Geometry problems December 1, 2020
- March 2024 (1)
- February 2024 (1)
- December 2023 (3)
- February 2021 (2)
- December 2020 (4)
- November 2020 (4)
- October 2020 (12)
- September 2020 (10)
- August 2020 (2)
- July 2020 (9)
- June 2020 (2)
- May 2020 (22)
- April 2020 (5)
- November 2019 (1)
- May 2019 (409)
- April 2019 (62)
- March 2019 (63)
Recent Comments
- Elliott Danielle on Pigeonhole Principle problems – Discrete Math
- Kava on Permutations & Combinations problems
- Sonya on Greatest Common Factor and Least Common Multiple problems
- Demetra on Geometric Formula Proof Double Integral problems
- Clarisa on Maclaurin & Taylor Infinite Series problems
| S | M | T | W | T | F | S |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
MathCabin.com 2019-2024 © All Rights Reserved.
- MathCabin.com
- 📕 Perfect Score SAT Math eBook
- ✅ Live Online SAT Math Practice Test
- 🎵 Relaxation Music
- ⏰ Timed SUDOKU Games
- Online Math Tutoring
Powered by WordPress / Academica WordPress Theme by WPZOOM
Module 10: Rational and Radical Functions
Inverse and joint variation, learning outcomes.
- Solve an Inverse variation problem.
- Write a formula for an inversely proportional relationship.
Water temperature in an ocean varies inversely to the water’s depth. Between the depths of 250 feet and 500 feet, the formula [latex]T=\frac{14,000}{d}[/latex] gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.
If we create a table we observe that, as the depth increases, the water temperature decreases.
| [latex]d[/latex], depth | [latex]T=\frac{\text{14,000}}{d}[/latex] | Interpretation |
|---|---|---|
| 500 ft | [latex]\frac{14,000}{500}=28[/latex] | At a depth of 500 ft, the water temperature is 28° F. |
| 350 ft | [latex]\frac{14,000}{350}=40[/latex] | At a depth of 350 ft, the water temperature is 40° F. |
| 250 ft | [latex]\frac{14,000}{250}=56[/latex] | At a depth of 250 ft, the water temperature is 56° F. |
We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations .
For our example, the graph depicts the inverse variation . We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula [latex]y=\dfrac{k}{x}[/latex] for inverse variation in this case uses [latex]k=14,000[/latex].
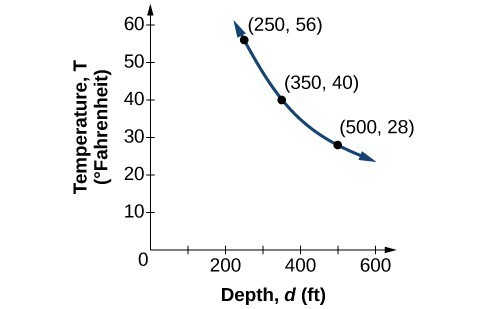
A General Note: Inverse Variation
If [latex]x[/latex] and [latex]y[/latex] are related by an equation of the form
[latex]y=\dfrac{k}{{x}^{n}}[/latex]
where [latex]k[/latex] is a nonzero constant, then we say that [latex]y[/latex] varies inversely with the [latex]n[/latex]th power of [latex]x[/latex]. In inversely proportional relationships, or inverse variations , there is a constant multiple [latex]k={x}^{n}y[/latex].
Example: Writing a Formula for an Inversely Proportional Relationship
A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.
Recall that multiplying speed by time gives distance. If we let [latex]t[/latex] represent the drive time in hours, and [latex]v[/latex] represent the velocity (speed or rate) at which the tourist drives, then [latex]vt=[/latex] distance. Because the distance is fixed at 100 miles, [latex]vt=100[/latex]. Solving this relationship for the time gives us our function.
[latex]\begin{align}t\left(v\right)&=\dfrac{100}{v} \\[1mm] &=100{v}^{-1} \end{align}[/latex]
We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction.
How To: Given a description of an indirect variation problem, solve for an unknown.
- Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
- Determine the constant of variation. You may need to multiply [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
- Use the constant of variation to write an equation for the relationship.
- Substitute known values into the equation to find the unknown.
Example: Solving an Inverse Variation Problem
A quantity [latex]y[/latex] varies inversely with the cube of [latex]x[/latex]. If [latex]y=25[/latex] when [latex]x=2[/latex], find [latex]y[/latex] when [latex]x[/latex] is 6.
The general formula for inverse variation with a cube is [latex]y=\dfrac{k}{{x}^{3}}[/latex]. The constant can be found by multiplying [latex]y[/latex] by the cube of [latex]x[/latex].
[latex]\begin{align}k&={x}^{3}y \\[1mm] &={2}^{3}\cdot 25 \\[1mm] &=200 \end{align}[/latex]
Now we use the constant to write an equation that represents this relationship.
[latex]\begin{align}y&=\dfrac{k}{{x}^{3}},\hspace{2mm}k=200 \\[1mm] y&=\dfrac{200}{{x}^{3}} \end{align}[/latex]
Substitute [latex]x=6[/latex] and solve for [latex]y[/latex].
[latex]\begin{align}y&=\dfrac{200}{{6}^{3}} \\[1mm] &=\dfrac{25}{27} \end{align}[/latex]
Analysis of the Solution
The graph of this equation is a rational function.
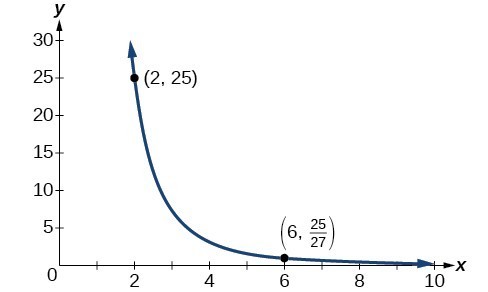
A quantity [latex]y[/latex] varies inversely with the square of [latex]x[/latex]. If [latex]y=8[/latex] when [latex]x=3[/latex], find [latex]y[/latex] when [latex]x[/latex] is 4.
[latex]\dfrac{9}{2}[/latex]
The following video presents a short lesson on inverse variation and includes more worked examples.
Joint Variation
Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation . For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable [latex]c[/latex], cost, varies jointly with the number of students, [latex]n[/latex], and the distance, [latex]d[/latex].
A General Note: Joint Variation
Joint variation occurs when a variable varies directly or inversely with multiple variables.
For instance, if [latex]x[/latex] varies directly with both [latex]y[/latex] and [latex]z[/latex], we have [latex]x=kyz[/latex]. If [latex]x[/latex] varies directly with [latex]y[/latex] and inversely with [latex]z[/latex], we have [latex]x=\dfrac{ky}{z}[/latex]. Notice that we only use one constant in a joint variation equation.
Example: Solving Problems Involving Joint Variation
A quantity [latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with the cube root of [latex]z[/latex]. If [latex]x=6[/latex] when [latex]y=2[/latex] and [latex]z=8[/latex], find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex].
Begin by writing an equation to show the relationship between the variables.
[latex]x=\dfrac{k{y}^{2}}{\sqrt[3]{z}}[/latex]
Substitute [latex]x=6[/latex], [latex]y=2[/latex], and [latex]z=8[/latex] to find the value of the constant [latex]k[/latex].
[latex]\begin{align}6&=\dfrac{k{2}^{2}}{\sqrt[3]{8}} \\[1mm] 6&=\dfrac{4k}{2} \\[1mm] 3&=k \end{align}[/latex]
Now we can substitute the value of the constant into the equation for the relationship.
[latex]x=\dfrac{3{y}^{2}}{\sqrt[3]{z}}[/latex]
To find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex], we will substitute values for [latex]y[/latex] and [latex]z[/latex] into our equation.
[latex]\begin{align}x&=\dfrac{3{\left(1\right)}^{2}}{\sqrt[3]{27}} \\[1mm] &=1 \end{align}[/latex]
[latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with [latex]z[/latex]. If [latex]x=40[/latex] when [latex]y=4[/latex] and [latex]z=2[/latex], find [latex]x[/latex] when [latex]y=10[/latex] and [latex]z=25[/latex].
[latex]x=20[/latex]
The following video provides another worked example of a joint variation problem.
Contribute!
Improve this page Learn More
- Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
- Question ID 91393,91394. Authored by : Jenck,Michael (for Lumen Learning). License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
- College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Inverse Variation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/awp2vxqd-l4 . License : CC BY: Attribution
- Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Provided by : Joint Variation: Determine the Variation Constant (Volume of a Cone). Located at : https://youtu.be/JREPATMScbM . License : CC BY: Attribution


IMAGES
VIDEO
COMMENTS
Solution. Create a joint variation formula describing the maximum safe load for the rectangular beam mentioned. Given that the width is equal to w = 0.2 meters, the depth is d = 0.45 meters, and the length is l = 6 meters long, find the value of k for the beam's maximum safe load. Note that MSL means maximum safe load.
Example 4: Solving Problems Involving Joint Variation. A quantity x varies directly with the square of y and inversely with the cube root of z.If x = 6 when y = 2 and z = 8, find x when y = 1 and z = 27.
Example 1: A quantity varies inversely as two or more other quantities. The figure below shows a rectangular solid with a fixed volume. Express its width, w, as a joint variation in terms of its length, l, and height, h. Solution: w ∝ 1/ (lh) In other words, the longer the length l or the height h, the narrower is the width w.
A General Note: Joint Variation. Joint variation occurs when a variable varies directly or inversely with multiple variables. For instance, if x varies directly with both y and z, we have x = kyz. If x varies directly with y and inversely with z, we have x=\frac {ky} {z} x = zky. Notice that we only use one constant in a joint variation equation.
Go through the below sections to check definition, various properties, example problems, value tables, concepts etc. Joint Variation - Introduction. Joint Variation refers to the scenario where the value of 1 variable depends on 2 or more and other variables that are held constant. For example, if C varies jointly as A and B, then C = ABX for ...
Solution: The equation for the given problem of joint variation is. x = Kyz where K is the constant. For the given data. 16 = K × 4 × 6. or, K = 4 6. So substituting the value of K the equation becomes. x = 4yz 6. Now for the required condition.
Step 4: Use the equation in step 3 and the information in the problem to answer the question. While solving the word problems, remember including the units in the final answer. Joint Variation Problems with Solutions. Problem 1: The area of a triangle varies jointly as the base and the height. Area = 12m² when base = 6m and height = 4m.
This video is about the definition and examples of joint variation and translating statements into the equation of variation. It also includes examples of so...
Example: Suppose y varies jointly with x and z. When y = 20, x = 6 and z = 10. Find y when x = 8 and z =15. Show Video Lesson. Lesson on combining direct and inverse or joint and inverse variation. Example: y varies directly as x and inversely as the square of z, and when x = 32, y = 6 and z = 4. Find x when y = 10 and z = 3.
This algebra video tutorial focuses on solving direct, inverse, and joint variation word problems. It shows you how to write the appropriate equation / form...
Joint and Combined Variation Practice Problems. *Make sure to use correct UNITS, when applicable. 1) If f varies jointly as g and the cube of h, and f = 200 when g = 5 and h = 4, find f when g = 3 and h = 6. 2) If y varies jointly as x and z, and y = 33 when x = 9 and z = 12, find y when x = 16 and z = 22. 3) If a varies jointly as b and the ...
The following video goes over two examples on how to apply joint variation to solve problems.
Solving Problems involving Direct, Inverse, and Joint variation. Certain relationships occur so frequently in applied situations that they are given special names. Variation equations show how one quantity changes in relation to other quantities. The relationship between the quantities can be described as direct, inverse, or joint variation.
Joint Variation, where at least two variables are related directly. For example, the area of a triangle is jointly related to both its height and base. Combined Variation, which involves a combination of direct or joint variation, and indirect variation. For example, the average number of phone calls per day between two cities has found to be ...
Steps for Solving Joint Variation Problems: Identify the variables involved in the problem. Write the joint variation equation: y = kxz. Use given information to find the constant k. Substitute known values into the equation to solve for the unknown variable. Example of Joint Variation: Problem: y varies jointly as x and z. When x = 2 and z = 3 ...
A historical example of direct variation can be found in the changing measurement of pi, which has been symbolized using the Greek letter π since the mid 18th century. ... Solving these combined or joint variation problems is the same as solving simpler variation problems. First, decide what equation the variation represents. ...
Purplemath. It's one thing to be able to take the words for a variation equation (such as " y varies directly as the square of x and inversely as the cube root of z ") and turn this into an equation that you can solve or use. It's another thing to extract the words from a word problem. But, because the lingo for variation equations is so ...
JOINT VARIATION WORD PROBLEMS. Problem 1 : z varies directly with the sum of squares of x and y. z = 5 when x = 3 and y = 4. Find the value of z when x = 2 and y = 4. Solution : ... Solving Exponential Equations Problems and Solutions (Part - 3) Aug 30, 24 01:55 AM.
Here, the variable z varies jointly with x and y, and k is the constant of variation. Here are some examples of joint variation. Here, l is the rectangle's length, w its width, and the constant of variation k is 1. Here, l and w are the length and the width of the base, respectively, while h is the pyramid's height.
This is a video about Joint Variation Examples and Word Problems. In joint variation one variable is jointly proportional or jointly varies to two or more va...
Example 1 - Abstract. Let's look at some examples of joint variation problems. If y varies jointly with x, z, and w, and the value of y is 60 when x = 2, z = 3, and w = 5, what is the value of y ...
Joint Variation and Proportion example question. If z varies jointly as x and y, and z = 3 when x = 4 and y = 6, find z when x = 20 and y = 9. Solution to this Joint Variation and Proportion practice problem is provided in the video below! Video tutorial on how to solve example questions and word problems refering to Joint Variation or Joint ...
A General Note: Joint Variation. Joint variation occurs when a variable varies directly or inversely with multiple variables. For instance, if x x varies directly with both y y and z z, we have x = kyz x = k y z. If x x varies directly with y y and inversely with z z, we have x= ky z x = k y z. Notice that we only use one constant in a joint ...