Solving Quadratics by Completing the Square
How to solve quadratic equations using the completing the square method.
If you are already familiar with the steps involved in completing the square , you may skip the introductory discussion and review the seven (7) worked examples right away.
The key step in this method is to find the constant “[latex]k[/latex]” that will allow us to express the given trinomial as the square of a binomial.
For instance,
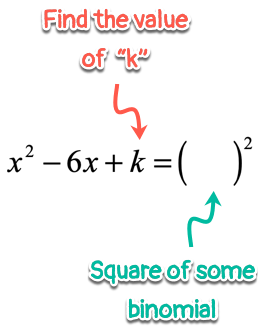
The value of “[latex]k[/latex]” is determined by squaring one-half of the coefficient of [latex]x[/latex]. In this case, the coefficient of the linear term [latex]x[/latex] is [latex] – \,6[/latex].
Therefore, half of [latex] – \,6[/latex] is [latex] – \,3[/latex], and its square [latex]{\left( { – \,3} \right)^2} = 9[/latex]. The value of [latex]k[/latex] must be [latex]9[/latex]!
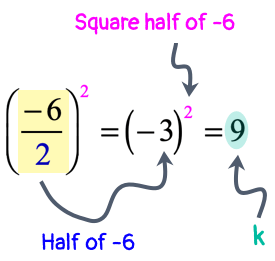
If I substitute [latex]k[/latex] by [latex]9[/latex], the trinomial is factored into two equal binomials. This is great because I can now rewrite it in a more compact form, that is, the square of a single binomial.
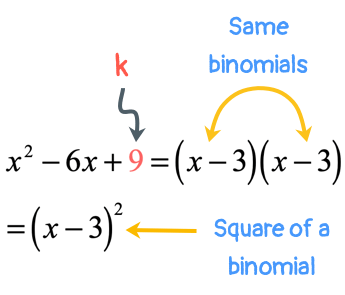
The following are the general steps involved in solving quadratic equations using completing the square method.

Key Steps in Solving Quadratic Equation by Completing the Square
1) Keep all the [latex]x[/latex]-terms (both the squared and linear) on the left side, while moving the constant to the right side.
In symbol, rewrite the general form [latex]a{x^2} + bx + c[/latex] as:
[latex]a{x^2} + bx = – \,c[/latex]
2) Now, identify what type of problem you have by looking at the coefficient of the leading term, [latex]a[/latex].
- “Easy Type” when [latex]a = 1[/latex]
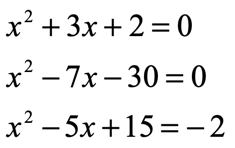
- “Difficult Type” when [latex]a \ne 1[/latex]
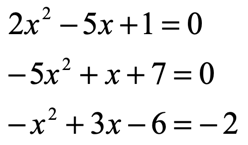
3) If you have the “Easy type”, proceed immediately to Step 4. If you have the “Difficult Type”, you must divide the entire equation first by the value of [latex]a[/latex] before moving to step 4.
4) Take the coefficient of [latex]x[/latex]-term, divide it by [latex]2[/latex] then square its result. Add this value to both sides of the equation.
5) Express the left side as a square of binomial.
6) Get the square root of both sides of the equation. Don’t forget to attach the [latex] \pm [/latex] symbol on the right side!
7) Finish it off by solving the linear equation(s) that arise from it.
Examples of How to Solve Quadratic Equations by Completing the Square
Example 1 : Solve the quadratic equation below by completing the square method.
This is an “Easy Type” since [latex]a = 1[/latex]. I will keep the “[latex]x[/latex]-terms” (both the squared and linear terms) on the left side but move the constant to the right side.
I can do that by adding [latex]15[/latex] on both sides of the equation.
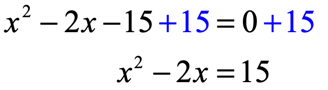
Now, take the coefficient of the linear term (which is the [latex]x[/latex]-term with power [latex]1[/latex]) and perform TWO operations on it:
- Divide by [latex]2[/latex], followed by
- Squaring (raising to the 2nd power)
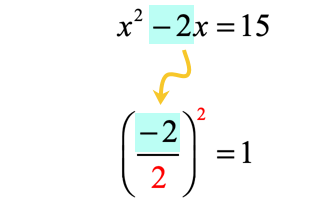
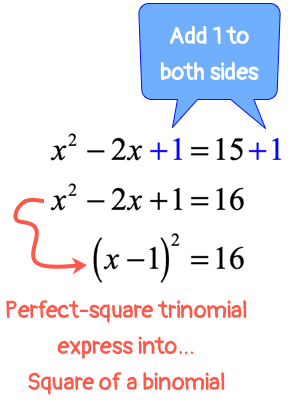
The output here, which is [latex]+1[/latex], will be added to both sides of the quadratic equation.
This step forces the left side to generate a perfect-square-trinomial which can be expressed as a square of a binomial . Great!
At this point, it is very easy to solve for [latex]x[/latex]. To get rid of the exponent [latex]2[/latex] in the binomial, I will apply square root operation on both sides of the equation.
Next, solve the pair of linear equations that arise as a result of squaring both sides.
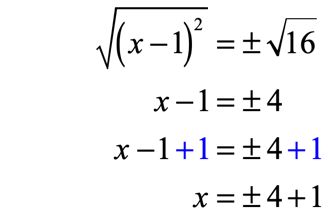
Break [latex]x = \pm \,4 + 1[/latex] into two cases, then solve.
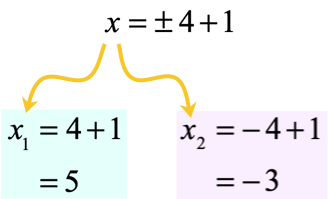
That is it! Our answers are [latex]{x_1} = 5[/latex] and [latex]{x_2} = – \,3[/latex].
Make it a habit to check your solved values of [latex]x[/latex] back into the original equation to verify if indeed they are “true” answers. I will leave it to you as an exercise.
Example 2 : Solve the quadratic equation below by completing the square method.
Obviously, I can’t proceed with the steps required in completing the square. I must isolate the [latex]x[/latex]-terms to the left, and the constant to the right.
Do that by subtracting both sides by [latex]1[/latex].
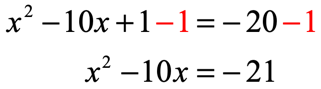
This time I am ready to perform the completing the square steps to solve this quadratic equation. Start by taking the coefficient of the linear [latex]x[/latex]-term then divide it by [latex]2[/latex] followed by squaring it. This is the MOST important step of this whole process.
Whatever number that comes out will be added to both sides of the equation. The left side becomes a perfect square trinomial which can be rewritten as the square of binomial.
Eliminate the power [latex]2[/latex] of the binomial by taking the square root of both sides. I hope that you’ll be able to follow the rest of the solution.
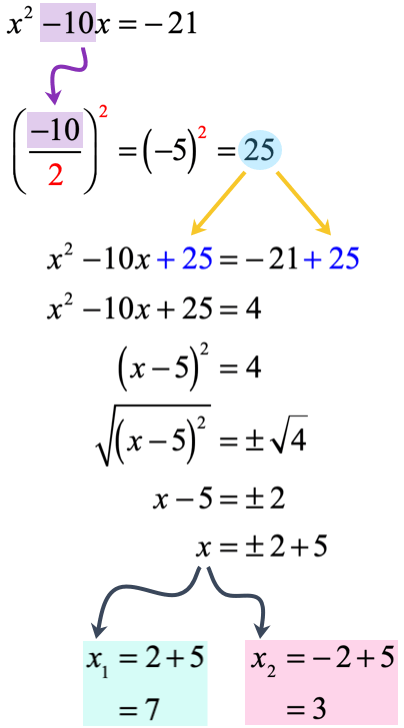
I got the following as the answers which are [latex]{x_1} = 7[/latex] and [latex]{x_2} = 3[/latex]. Go ahead and check the solutions yourself as an exercise.
Example 3 : Solve the quadratic equation below by completing the square method.
The answers are [latex]{x_1} = 2[/latex] and [latex]{x_2} = – 10[/latex]
Example 4 : Solve the quadratic equation below by completing the square method.
The first thing to do is to move the constant to the right side by subtracting each side by [latex]8[/latex].
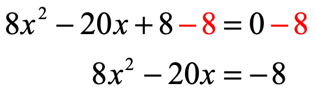
This is actually the “Difficult Type” since [latex]a \ne 1[/latex]. Thus, I need to make the coefficient of the squared [latex]x[/latex]-term equal to [latex]1[/latex]. This can be done by dividing through the entire equation by [latex]a[/latex] which equals [latex]8[/latex]!
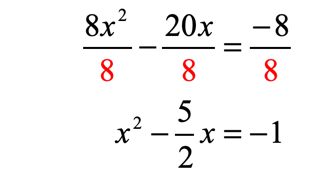
By dividing through by [latex]8[/latex], I have converted this problem into the “easy” case because the coefficient of the squared [latex]x[/latex]-term becomes [latex]+1[/latex]. Finish this off by doing the same process as seen in examples 1 and 2. The only difference is that I will deal with fractions.
Consider the coefficient of the linear [latex]x[/latex]-term, divide by [latex]2[/latex] and square it.
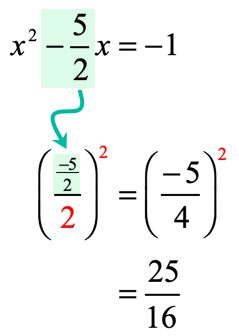
Take the output of the step above, and add to both sides of the quadratic equation. Then proceed with the rest of the steps to complete the square.
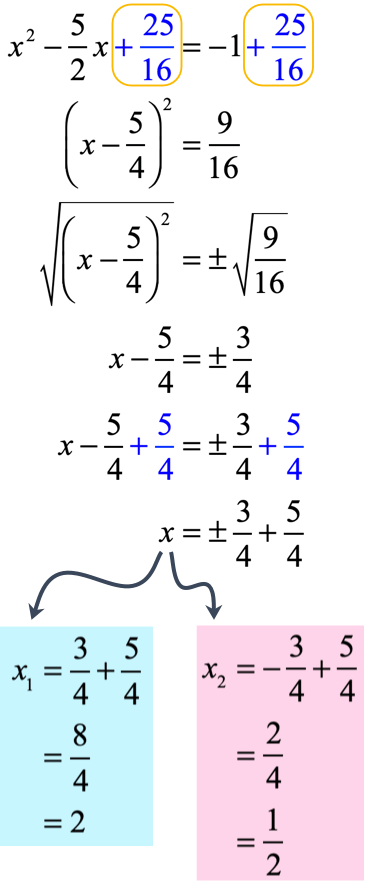
The answers should be [latex]{x_1} = 2[/latex] and [latex]{x_2} = {1 \over 2}[/latex].
Example 5 ( Practice Problem ): Solve the quadratic equation below by completing the square method.
Try solving this problem on your own first. Then click below to view the solution.
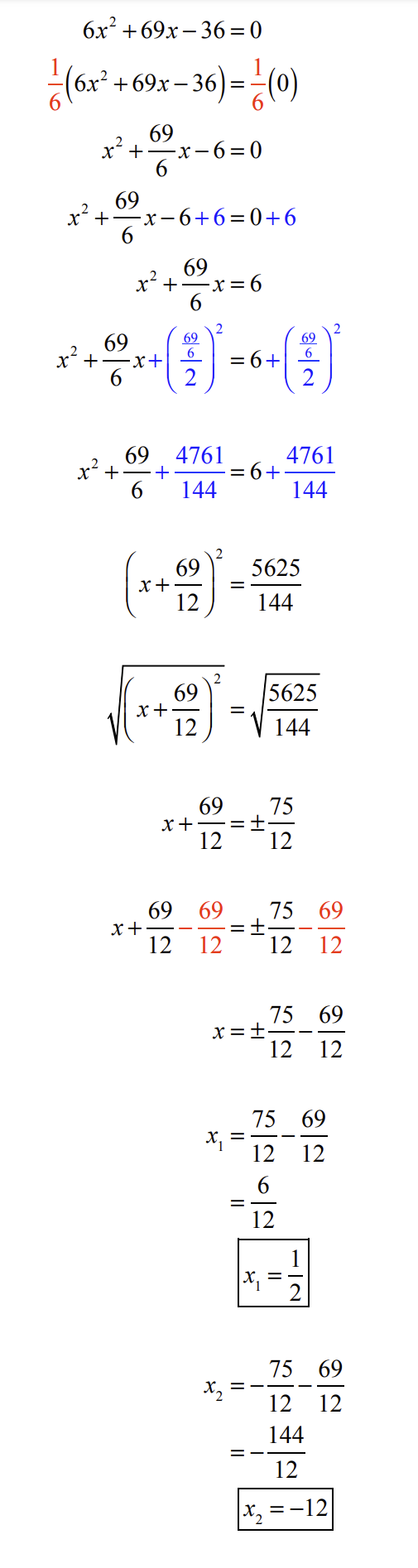
NOTE: The solution to this problem may look messy but as long as you apply the correct procedures for completing the square, you will soon realize that the answers to this problem come out nicely.
Hint : The solution set includes a rational number and a negative integer.
Example 6 : Solve the quadratic equation below by completing the square method.
I will move the constant to the right side while keeping all [latex]x[/latex]-terms on the left. Then I must divide the entire equation by [latex] – \,3[/latex] since [latex]a \ne 1[/latex].
- Subtract both sides by [latex]42[/latex]
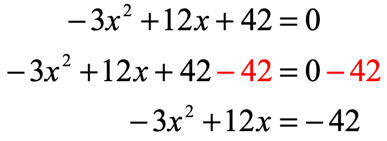
- Divide entire equation by [latex] – \,3[/latex]
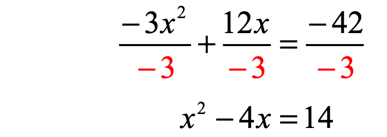
Now, I will take the coefficient of the linear term, divide it by [latex]2[/latex] and square it.
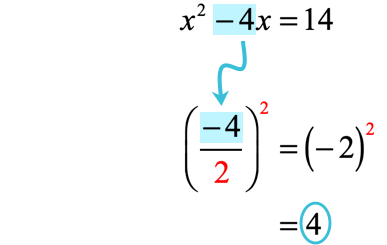
Add this output [latex]4[/latex] to both sides of the equation. This makes the left side a perfect-square-trinomial which can be rewritten as the square of a binomial.

That was easy, right? Again, the more you see how these problems are being solved correctly, the better you become!
Example 7 ( Practice Problem ): Solve the quadratic equation below using the completing the square method.
You might also like these tutorials:
- Solving Quadratic Equations by Square Root Method
- Solving Quadratic Equations by Factoring Method
- Solving Quadratic Equations by the Quadratic Formula
- AI Math Solver Graphing Calculator Popular Problems Worksheets Study Guides Cheat Sheets Calculators Verify Solution
- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| ▭\:\longdivision{▭} | \times \twostack{▭}{▭} | + \twostack{▭}{▭} | - \twostack{▭}{▭} | \left( | \right) | \times | \square\frac{\square}{\square} |
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- One-Step Addition
- One-Step Subtraction
- One-Step Multiplication
- One-Step Division
- One-Step Decimals
- Two-Step Integers
- Two-Step Add/Subtract
- Two-Step Multiply/Divide
- Two-Step Fractions
- Two-Step Decimals
- Multi-Step Integers
- Multi-Step with Parentheses
- Multi-Step Rational
- Multi-Step Fractions
- Multi-Step Decimals
- Solve by Factoring
- Completing the Square
- Quadratic Formula
- Biquadratic
- Logarithmic
- Exponential
- Rational Roots
- Floor/Ceiling
- Equation Given Roots
- Equation Given Points
- Newton Raphson
- Substitution
- Elimination
- Cramer's Rule
- Gaussian Elimination
- System of Inequalities
- Perfect Squares
- Difference of Squares
- Difference of Cubes
- Sum of Cubes
- Polynomials
- Distributive Property
- FOIL method
- Perfect Cubes
- Binomial Expansion
- Negative Rule
- Product Rule
- Quotient Rule
- Expand Power Rule
- Fraction Exponent
- Exponent Rules
- Exponential Form
- Logarithmic Form
- Absolute Value
- Rational Number
- Powers of i
- Complex Form
- Partial Fractions
- Is Polynomial
- Leading Coefficient
- Leading Term
- Standard Form
- Complete the Square
- Synthetic Division
- Linear Factors
- Rationalize Denominator
- Rationalize Numerator
- Identify Type
- Convergence
- Interval Notation
- Pi (Product) Notation
- Boolean Algebra
- Truth Table
- Mutual Exclusive
- Cardinality
- Caretesian Product
- Age Problems
- Distance Problems
- Cost Problems
- Investment Problems
- Number Problems
- Percent Problems
- Addition/Subtraction
- Multiplication/Division
- Dice Problems
- Coin Problems
- Card Problems
- Pre Calculus
- Linear Algebra
- Trigonometry
- Conversions
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| - \twostack{▭}{▭} | \lt | 7 | 8 | 9 | \div | AC |
| + \twostack{▭}{▭} | \gt | 4 | 5 | 6 | \times | \square\frac{\square}{\square} |
| \times \twostack{▭}{▭} | \left( | 1 | 2 | 3 | - | x |
| ▭\:\longdivision{▭} | \right) | . | 0 | = | + | y |
Number Line
- complete\:the\:square\:x^{2}+5x+4=0
- complete\:the\:square\:x^{2}+5x+6=0
- complete\:the\:square\:x^{2}=7x+18
- complete\:the\:square\:x^{2}=4x+21
quadratic-equation-solve-by-completing-square-calculator
- High School Math Solutions – Quadratic Equations Calculator, Part 2 Solving quadratics by factorizing (link to previous post) usually works just fine. But what if the quadratic equation...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
9.3 Solve Quadratic Equations Using the Quadratic Formula
Learning objectives.
By the end of this section, you will be able to:
- Solve quadratic equations using the Quadratic Formula
- Use the discriminant to predict the number and type of solutions of a quadratic equation
- Identify the most appropriate method to use to solve a quadratic equation
Be Prepared 9.7
Before you get started, take this readiness quiz.
Evaluate b 2 − 4 a b b 2 − 4 a b when a = 3 a = 3 and b = −2 . b = −2 . If you missed this problem, review Example 1.21 .
Be Prepared 9.8
Simplify: 108 . 108 . If you missed this problem, review Example 8.13 .
Be Prepared 9.9
Simplify: 50 . 50 . If you missed this problem, review Example 8.76 .
Solve Quadratic Equations Using the Quadratic Formula
When we solved quadratic equations in the last section by completing the square, we took the same steps every time. By the end of the exercise set, you may have been wondering ‘isn’t there an easier way to do this?’ The answer is ‘yes’. Mathematicians look for patterns when they do things over and over in order to make their work easier. In this section we will derive and use a formula to find the solution of a quadratic equation.
We have already seen how to solve a formula for a specific variable ‘in general’, so that we would do the algebraic steps only once, and then use the new formula to find the value of the specific variable. Now we will go through the steps of completing the square using the general form of a quadratic equation to solve a quadratic equation for x.
We start with the standard form of a quadratic equation and solve it for x by completing the square.
| Isolate the variable terms on one side. | |
| Make the coefficient of equal to 1, by dividing by . | |
| Simplify. | |
| To complete the square, find and add it to both sides of the equation. | |
| The left side is a perfect square, factor it. | |
| Find the common denominator of the right side and write equivalent fractions with the common denominator. | |
| Simplify. | |
| Combine to one fraction. | |
| Use the square root property. | |
| Simplify the radical. | |
| Add to both sides of the equation. | |
| Combine the terms on the right side. | |
| This equation is the Quadratic Formula. |
- Quadratic Formula
The solutions to a quadratic equation of the form ax 2 + bx + c = 0, where a ≠ 0 a ≠ 0 are given by the formula:
To use the Quadratic Formula , we substitute the values of a , b , and c from the standard form into the expression on the right side of the formula. Then we simplify the expression. The result is the pair of solutions to the quadratic equation.
Notice the formula is an equation. Make sure you use both sides of the equation.
Example 9.21
How to solve a quadratic equation using the quadratic formula.
Solve by using the Quadratic Formula: 2 x 2 + 9 x − 5 = 0 . 2 x 2 + 9 x − 5 = 0 .
Try It 9.41
Solve by using the Quadratic Formula: 3 y 2 − 5 y + 2 = 0 3 y 2 − 5 y + 2 = 0 .
Try It 9.42
Solve by using the Quadratic Formula: 4 z 2 + 2 z − 6 = 0 4 z 2 + 2 z − 6 = 0 .
Solve a quadratic equation using the quadratic formula.
- Step 1. Write the quadratic equation in standard form, ax 2 + bx + c = 0. Identify the values of a , b , and c .
- Step 2. Write the Quadratic Formula. Then substitute in the values of a , b , and c .
- Step 3. Simplify.
- Step 4. Check the solutions.
If you say the formula as you write it in each problem, you’ll have it memorized in no time! And remember, the Quadratic Formula is an EQUATION. Be sure you start with “ x =”.
Example 9.22
Solve by using the Quadratic Formula: x 2 − 6 x = −5 . x 2 − 6 x = −5 .
| Write the equation in standard form by adding 5 to each side. | |
| This equation is now in standard form. | |
| Identify the values of | |
| Write the Quadratic Formula. | |
| Then substitute in the values of | |
| Simplify. | |
| Rewrite to show two solutions. | |
| Simplify. | |
| Check: |
Try It 9.43
Solve by using the Quadratic Formula: a 2 − 2 a = 15 a 2 − 2 a = 15 .
Try It 9.44
Solve by using the Quadratic Formula: b 2 + 24 = −10 b b 2 + 24 = −10 b .
When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That can happen, too, when using the Quadratic Formula . If we get a radical as a solution, the final answer must have the radical in its simplified form.
Example 9.23
Solve by using the Quadratic Formula: 2 x 2 + 10 x + 11 = 0 . 2 x 2 + 10 x + 11 = 0 .
| This equation is in standard form. | |
| Identify the values of , , and . | |
| Write the Quadratic Formula. | |
| Then substitute in the values of , , and . | |
| Simplify. | |
| Simplify the radical. | |
| Factor out the common factor in the numerator. | |
| Remove the common factors. | |
| Rewrite to show two solutions. | |
| Check: We leave the check for you! |
Try It 9.45
Solve by using the Quadratic Formula: 3 m 2 + 12 m + 7 = 0 3 m 2 + 12 m + 7 = 0 .
Try It 9.46
Solve by using the Quadratic Formula: 5 n 2 + 4 n − 4 = 0 5 n 2 + 4 n − 4 = 0 .
When we substitute a , b , and c into the Quadratic Formula and the radicand is negative, the quadratic equation will have imaginary or complex solutions. We will see this in the next example.
Example 9.24
Solve by using the Quadratic Formula: 3 p 2 + 2 p + 9 = 0 . 3 p 2 + 2 p + 9 = 0 .
| This equation is in standard form | |
| Identify the values of | |
| Write the Quadratic Formula. | |
| Then substitute in the values of . | |
| Simplify. | |
| Simplify the radical using complex numbers. | |
| Simplify the radical. | |
| Factor the common factor in the numerator. | |
| Remove the common factors. | |
| Rewrite in standard form. | |
| Write as two solutions. |
Try It 9.47
Solve by using the Quadratic Formula: 4 a 2 − 2 a + 8 = 0 4 a 2 − 2 a + 8 = 0 .
Try It 9.48
Solve by using the Quadratic Formula: 5 b 2 + 2 b + 4 = 0 5 b 2 + 2 b + 4 = 0 .
Remember, to use the Quadratic Formula, the equation must be written in standard form, ax 2 + bx + c = 0. Sometimes, we will need to do some algebra to get the equation into standard form before we can use the Quadratic Formula.
Example 9.25
Solve by using the Quadratic Formula: x ( x + 6 ) + 4 = 0 . x ( x + 6 ) + 4 = 0 .
Our first step is to get the equation in standard form.
| Distribute to get the equation in standard form. | |
| This equation is now in standard form | |
| Identify the values of | |
| Write the Quadratic Formula. | |
| Then substitute in the values of . | |
| Simplify. | |
| Simplify the radical. | |
| Factor the common factor in the numerator. | |
| Remove the common factors. | |
| Write as two solutions. | |
| Check: We leave the check for you! |
Try It 9.49
Solve by using the Quadratic Formula: x ( x + 2 ) − 5 = 0 . x ( x + 2 ) − 5 = 0 .
Try It 9.50
Solve by using the Quadratic Formula: 3 y ( y − 2 ) − 3 = 0 . 3 y ( y − 2 ) − 3 = 0 .
When we solved linear equations, if an equation had too many fractions we cleared the fractions by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions— to solve. We can use the same strategy with quadratic equations.

Example 9.26
Solve by using the Quadratic Formula: 1 2 u 2 + 2 3 u = 1 3 . 1 2 u 2 + 2 3 u = 1 3 .
Our first step is to clear the fractions.
| Multiply both sides by the LCD, 6, to clear the fractions. | |
| Multiply. | |
| Subtract 2 to get the equation in standard form. | |
| Identify the values of , , and . | |
| Write the Quadratic Formula. | |
| Then substitute in the values of , , and . | |
| Simplify. | |
| Simplify the radical. | |
| Factor the common factor in the numerator. | |
| Remove the common factors. | |
| Rewrite to show two solutions. | |
| Check: We leave the check for you! |
Try It 9.51
Solve by using the Quadratic Formula: 1 4 c 2 − 1 3 c = 1 12 1 4 c 2 − 1 3 c = 1 12 .
Try It 9.52
Solve by using the Quadratic Formula: 1 9 d 2 − 1 2 d = − 1 3 1 9 d 2 − 1 2 d = − 1 3 .
Think about the equation ( x − 3) 2 = 0. We know from the Zero Product Property that this equation has only one solution, x = 3.
We will see in the next example how using the Quadratic Formula to solve an equation whose standard form is a perfect square trinomial equal to 0 gives just one solution. Notice that once the radicand is simplified it becomes 0 , which leads to only one solution.
Example 9.27
Solve by using the Quadratic Formula: 4 x 2 − 20 x = −25 . 4 x 2 − 20 x = −25 .
| Add 25 to get the equation in standard form. | |
| Identify the values of , , and . | |
| Write the quadratic formula. | |
| Then substitute in the values of , , and . | |
| Simplify. | |
| Simplify the radical. | |
| Simplify the fraction. | |
| Check: We leave the check for you! |
Did you recognize that 4 x 2 − 20 x + 25 is a perfect square trinomial. It is equivalent to (2 x − 5) 2 ? If you solve 4 x 2 − 20 x + 25 = 0 by factoring and then using the Square Root Property, do you get the same result?
Try It 9.53
Solve by using the Quadratic Formula: r 2 + 10 r + 25 = 0 . r 2 + 10 r + 25 = 0 .
Try It 9.54
Solve by using the Quadratic Formula: 25 t 2 − 40 t = −16 . 25 t 2 − 40 t = −16 .
Use the Discriminant to Predict the Number and Type of Solutions of a Quadratic Equation
When we solved the quadratic equations in the previous examples, sometimes we got two real solutions, one real solution, and sometimes two complex solutions. Is there a way to predict the number and type of solutions to a quadratic equation without actually solving the equation?
Yes, the expression under the radical of the Quadratic Formula makes it easy for us to determine the number and type of solutions. This expression is called the discriminant .
Discriminant
Let’s look at the discriminant of the equations in some of the examples and the number and type of solutions to those quadratic equations.
| Quadratic Equation (in standard form) | Discriminant | Value of the Discriminant | Number and Type of solutions |
|---|---|---|---|
| + | 2 real | ||
| 0 | 1 real | ||
| − | 2 complex |
Using the Discriminant, b 2 − 4 ac , to Determine the Number and Type of Solutions of a Quadratic Equation
For a quadratic equation of the form ax 2 + bx + c = 0, a ≠ 0 , a ≠ 0 ,
- If b 2 − 4 ac > 0, the equation has 2 real solutions.
- if b 2 − 4 ac = 0, the equation has 1 real solution.
- if b 2 − 4 ac < 0, the equation has 2 complex solutions.
Example 9.28
Determine the number of solutions to each quadratic equation.
ⓐ 3 x 2 + 7 x − 9 = 0 3 x 2 + 7 x − 9 = 0 ⓑ 5 n 2 + n + 4 = 0 5 n 2 + n + 4 = 0 ⓒ 9 y 2 − 6 y + 1 = 0 . 9 y 2 − 6 y + 1 = 0 .
To determine the number of solutions of each quadratic equation, we will look at its discriminant.
| The equation is in standard form, identify , , and . | |
| Write the discriminant. | |
| Substitute in the values of , , and . | |
| Simplify. | |
Since the discriminant is positive, there are 2 real solutions to the equation.
| The equation is in standard form, identify , , and . | |
| Write the discriminant. | |
| Substitute in the values of , , and . | |
| Simplify. | |
Since the discriminant is negative, there are 2 complex solutions to the equation.
| The equation is in standard form, identify , , and . | |
| Write the discriminant. | |
| Substitute in the values of , , and . | |
| Simplify. | |
Since the discriminant is 0, there is 1 real solution to the equation.
Try It 9.55
Determine the numberand type of solutions to each quadratic equation.
ⓐ 8 m 2 − 3 m + 6 = 0 8 m 2 − 3 m + 6 = 0 ⓑ 5 z 2 + 6 z − 2 = 0 5 z 2 + 6 z − 2 = 0 ⓒ 9 w 2 + 24 w + 16 = 0 . 9 w 2 + 24 w + 16 = 0 .
Try It 9.56
Determine the number and type of solutions to each quadratic equation.
ⓐ b 2 + 7 b − 13 = 0 b 2 + 7 b − 13 = 0 ⓑ 5 a 2 − 6 a + 10 = 0 5 a 2 − 6 a + 10 = 0 ⓒ 4 r 2 − 20 r + 25 = 0 . 4 r 2 − 20 r + 25 = 0 .
Identify the Most Appropriate Method to Use to Solve a Quadratic Equation
We summarize the four methods that we have used to solve quadratic equations below.
Methods for Solving Quadratic Equations
- Square Root Property
- Completing the Square
Given that we have four methods to use to solve a quadratic equation, how do you decide which one to use? Factoring is often the quickest method and so we try it first. If the equation is a x 2 = k a x 2 = k or a ( x − h ) 2 = k a ( x − h ) 2 = k we use the Square Root Property. For any other equation, it is probably best to use the Quadratic Formula. Remember, you can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method.
What about the method of Completing the Square? Most people find that method cumbersome and prefer not to use it. We needed to include it in the list of methods because we completed the square in general to derive the Quadratic Formula. You will also use the process of Completing the Square in other areas of algebra.
Identify the most appropriate method to solve a quadratic equation.
- Step 1. Try Factoring first. If the quadratic factors easily, this method is very quick.
- Step 2. Try the Square Root Property next. If the equation fits the form a x 2 = k a x 2 = k or a ( x − h ) 2 = k , a ( x − h ) 2 = k , it can easily be solved by using the Square Root Property.
- Step 3. Use the Quadratic Formula . Any other quadratic equation is best solved by using the Quadratic Formula.
The next example uses this strategy to decide how to solve each quadratic equation.
Example 9.29
Identify the most appropriate method to use to solve each quadratic equation.
ⓐ 5 z 2 = 17 5 z 2 = 17 ⓑ 4 x 2 − 12 x + 9 = 0 4 x 2 − 12 x + 9 = 0 ⓒ 8 u 2 + 6 u = 11 . 8 u 2 + 6 u = 11 .
ⓐ 5 z 2 = 17 5 z 2 = 17
Since the equation is in the a x 2 = k , a x 2 = k , the most appropriate method is to use the Square Root Property.
ⓑ 4 x 2 − 12 x + 9 = 0 4 x 2 − 12 x + 9 = 0
We recognize that the left side of the equation is a perfect square trinomial, and so factoring will be the most appropriate method.
| Put the equation in standard form. |
While our first thought may be to try factoring, thinking about all the possibilities for trial and error method leads us to choose the Quadratic Formula as the most appropriate method.
Try It 9.57
ⓐ x 2 + 6 x + 8 = 0 x 2 + 6 x + 8 = 0 ⓑ ( n − 3 ) 2 = 16 ( n − 3 ) 2 = 16 ⓒ 5 p 2 − 6 p = 9 . 5 p 2 − 6 p = 9 .
Try It 9.58
ⓐ 8 a 2 + 3 a − 9 = 0 8 a 2 + 3 a − 9 = 0 ⓑ 4 b 2 + 4 b + 1 = 0 4 b 2 + 4 b + 1 = 0 ⓒ 5 c 2 = 125 . 5 c 2 = 125 .
Access these online resources for additional instruction and practice with using the Quadratic Formula.
- Using the Quadratic Formula
- Solve a Quadratic Equation Using the Quadratic Formula with Complex Solutions
- Discriminant in Quadratic Formula
Section 9.3 Exercises
Practice makes perfect.
In the following exercises, solve by using the Quadratic Formula.
4 m 2 + m − 3 = 0 4 m 2 + m − 3 = 0
4 n 2 − 9 n + 5 = 0 4 n 2 − 9 n + 5 = 0
2 p 2 − 7 p + 3 = 0 2 p 2 − 7 p + 3 = 0
3 q 2 + 8 q − 3 = 0 3 q 2 + 8 q − 3 = 0
p 2 + 7 p + 12 = 0 p 2 + 7 p + 12 = 0
q 2 + 3 q − 18 = 0 q 2 + 3 q − 18 = 0
r 2 − 8 r = 33 r 2 − 8 r = 33
t 2 + 13 t = −40 t 2 + 13 t = −40
3 u 2 + 7 u − 2 = 0 3 u 2 + 7 u − 2 = 0
2 p 2 + 8 p + 5 = 0 2 p 2 + 8 p + 5 = 0
2 a 2 − 6 a + 3 = 0 2 a 2 − 6 a + 3 = 0
5 b 2 + 2 b − 4 = 0 5 b 2 + 2 b − 4 = 0
x 2 + 8 x − 4 = 0 x 2 + 8 x − 4 = 0
y 2 + 4 y − 4 = 0 y 2 + 4 y − 4 = 0
3 y 2 + 5 y − 2 = 0 3 y 2 + 5 y − 2 = 0
6 x 2 + 2 x − 20 = 0 6 x 2 + 2 x − 20 = 0
2 x 2 + 3 x + 3 = 0 2 x 2 + 3 x + 3 = 0
2 x 2 − x + 1 = 0 2 x 2 − x + 1 = 0
8 x 2 − 6 x + 2 = 0 8 x 2 − 6 x + 2 = 0
8 x 2 − 4 x + 1 = 0 8 x 2 − 4 x + 1 = 0
( v + 1 ) ( v − 5 ) − 4 = 0 ( v + 1 ) ( v − 5 ) − 4 = 0
( x + 1 ) ( x − 3 ) = 2 ( x + 1 ) ( x − 3 ) = 2
( y + 4 ) ( y − 7 ) = 18 ( y + 4 ) ( y − 7 ) = 18
( x + 2 ) ( x + 6 ) = 21 ( x + 2 ) ( x + 6 ) = 21
1 3 m 2 + 1 12 m = 1 4 1 3 m 2 + 1 12 m = 1 4
1 3 n 2 + n = − 1 2 1 3 n 2 + n = − 1 2
3 4 b 2 + 1 2 b = 3 8 3 4 b 2 + 1 2 b = 3 8
1 9 c 2 + 2 3 c = 3 1 9 c 2 + 2 3 c = 3
16 c 2 + 24 c + 9 = 0 16 c 2 + 24 c + 9 = 0
25 d 2 − 60 d + 36 = 0 25 d 2 − 60 d + 36 = 0
25 q 2 + 30 q + 9 = 0 25 q 2 + 30 q + 9 = 0
16 y 2 + 8 y + 1 = 0 16 y 2 + 8 y + 1 = 0
Use the Discriminant to Predict the Number of Real Solutions of a Quadratic Equation
In the following exercises, determine the number of real solutions for each quadratic equation.
ⓐ 4 x 2 − 5 x + 16 = 0 4 x 2 − 5 x + 16 = 0 ⓑ 36 y 2 + 36 y + 9 = 0 36 y 2 + 36 y + 9 = 0 ⓒ 6 m 2 + 3 m − 5 = 0 6 m 2 + 3 m − 5 = 0
ⓐ 9 v 2 − 15 v + 25 = 0 9 v 2 − 15 v + 25 = 0 ⓑ 100 w 2 + 60 w + 9 = 0 100 w 2 + 60 w + 9 = 0 ⓒ 5 c 2 + 7 c − 10 = 0 5 c 2 + 7 c − 10 = 0
ⓐ r 2 + 12 r + 36 = 0 r 2 + 12 r + 36 = 0 ⓑ 8 t 2 − 11 t + 5 = 0 8 t 2 − 11 t + 5 = 0 ⓒ 3 v 2 − 5 v − 1 = 0 3 v 2 − 5 v − 1 = 0
ⓐ 25 p 2 + 10 p + 1 = 0 25 p 2 + 10 p + 1 = 0 ⓑ 7 q 2 − 3 q − 6 = 0 7 q 2 − 3 q − 6 = 0 ⓒ 7 y 2 + 2 y + 8 = 0 7 y 2 + 2 y + 8 = 0
In the following exercises, identify the most appropriate method (Factoring, Square Root, or Quadratic Formula) to use to solve each quadratic equation. Do not solve.
ⓐ x 2 − 5 x − 24 = 0 x 2 − 5 x − 24 = 0 ⓑ ( y + 5 ) 2 = 12 ( y + 5 ) 2 = 12 ⓒ 14 m 2 + 3 m = 11 14 m 2 + 3 m = 11
ⓐ ( 8 v + 3 ) 2 = 81 ( 8 v + 3 ) 2 = 81 ⓑ w 2 − 9 w − 22 = 0 w 2 − 9 w − 22 = 0 ⓒ 4 n 2 − 10 n = 6 4 n 2 − 10 n = 6
ⓐ 6 a 2 + 14 a = 20 6 a 2 + 14 a = 20 ⓑ ( x − 1 4 ) 2 = 5 16 ( x − 1 4 ) 2 = 5 16 ⓒ y 2 − 2 y = 8 y 2 − 2 y = 8
ⓐ 8 b 2 + 15 b = 4 8 b 2 + 15 b = 4 ⓑ 5 9 v 2 − 2 3 v = 1 5 9 v 2 − 2 3 v = 1 ⓒ ( w + 4 3 ) 2 = 2 9 ( w + 4 3 ) 2 = 2 9
Writing Exercises
Solve the equation x 2 + 10 x = 120 x 2 + 10 x = 120
ⓐ by completing the square
ⓑ using the Quadratic Formula
ⓒ Which method do you prefer? Why?
Solve the equation 12 y 2 + 23 y = 24 12 y 2 + 23 y = 24
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Intermediate Algebra 2e
- Publication date: May 6, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/9-3-solve-quadratic-equations-using-the-quadratic-formula
© Jul 24, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Have an account?
Suggestions for you See more

Perfect Squares and Square Roots Quiz
Complete the square, 8th - 11th , solving quadratics by completing the squ..., 11th - 12th , square and cube roots, 7th - 8th , area of triangles and parallelograms, perfect squares and square roots, 7th - 9th , scientific notation, 8th - 9th , square roots.

Solving Quadratic Equations by Completin...
Mathematics.

Solving Quadratic Equations by Completing the Square

30 questions

Introducing new Paper mode
No student devices needed. Know more
- 1. Multiple Choice Edit 1.5 minutes 1 pt What do you do to the b value to correctly complete the square? square it divide it by 2 and square the result divide it by 2 and take the square root of the result divide it by 2 only
Complete the square for
x 2 - 12x + ____
Complete the square.
x 2 + 6x + ____
x 2 - 14x + ____
x 2 - 10x + ____
x 2 + 10x - 100
x 2 - 10x + 100
x 2 + 10x - 25
x 2 - 10x + 25
- 6. Multiple Choice Edit 45 seconds 1 pt Find the missing value "c" to create a perfect square trinomial: x 2 + 26x + ___ 13 136 169 26
- 7. Multiple Choice Edit 1.5 minutes 1 pt Find the missing value "c" to create a perfect square trinomial: x 2 – 8x + ___ -4 16 4 8
Given the perfect square trinomial, identify the equivalent expression
x 2 -18x+81
- 9. Multiple Choice Edit 5 minutes 1 pt To solve by completing the square, what needs to be moved in this equation? x 2 = 9 - 4x the -4x the 9 the x 2
- 10. Multiple Choice Edit 30 seconds 1 pt Solve by completing the square: k 2 − 12k + 23 = 0 {6 + √13, 6 - √13} {-6 + √13, -6 - √13} {6 + √59, 6 - √59} {-6 + √59, -6 - √59}
- 11. Multiple Choice Edit 2 minutes 1 pt Solve by completing the square. y 2 + 10y = -9 1 and -12 -1 and -9 1 and -9 1 and -1
Solve by Completing the Square:
2x 2 +4x-5=7
Hint: Move the 5 and you must have a lead number of 1!
-0.4 and -3.4
-2.3 and 4.3
-3.6 and 1.6
no solution
- 13. Multiple Choice Edit 5 minutes 1 pt When factoring x 2 - 4x + 4 = 20, what goes in the blank? (x - __ ) 2 = 20 4 2 8 20
- 15. Multiple Choice Edit 5 minutes 1 pt What should be added to both sides of the following equation to complete the square? x 2 - 12x = 5 -12 6 36 -5
- 16. Multiple Choice Edit 5 minutes 1 pt What is one of the solutions to this equation? (2x - 1) 2 = 49 7 -7 -4 -3
x 2 +14x+49
- 18. Multiple Choice Edit 1.5 minutes 1 pt Solve the equation by completing the square and then finding the roots. x 2 + 6x - 4 = 36 x = -7, 7 x = 4, -10 x = -4 +- √7 x = 10, -4
- 19. Multiple Choice Edit 30 seconds 1 pt Solve the following equation by completing the square: n 2 - 2n - 3 = 0 {3 and-1} {4 and -4} {5 and -3} {8 and -7}
- 20. Multiple Choice Edit 3 minutes 1 pt Solve by completing the square: k 2 − 12k + 23 = 0 {6 + √13, 6 - √13} {-6 + √13, -6 - √13} {6 + √59, 6 - √59} {-6 + √59, -6 - √59}
- 21. Multiple Choice Edit 30 seconds 1 pt Solve by completing the square. y 2 + 10y = -9 1 and -12 -1 and -9 1 and -9 1 and -1
- 22. Multiple Choice Edit 30 seconds 1 pt What is the first step to solving THIS equation by completing the square? a 2 + 10a + 21 = 0 Set the equation equal to zero Divide 10 by 2 and add the result to both sides Add a 2 and 10a together Subtract the 21
- 23. Multiple Choice Edit 1.5 minutes 1 pt When factoring x 2 - 4x + 4 = 20, what goes in the blank? (x - __ ) 2 = 20 4 2 8 20
- 24. Multiple Choice Edit 30 seconds 1 pt What is one of the solutions to this equation? (2x - 1) 2 = 49 7 -7 -4 -3
- 25. Multiple Choice Edit 3 minutes 1 pt Solve the following equation by completing the square: n 2 - 2n - 3 = 0 {3 and-1} {4 and -4} {5 and -3} {8 and -7}
- 26. Multiple Choice Edit 15 minutes 1 pt What is the first step to solving THIS equation by completing the square? a 2 + 10a + 21 = 0 Set the equation equal to zero Divide 10 by 2 and add the result to both sides Add a 2 and 10a together Subtract the 21
- 27. Multiple Choice Edit 15 minutes 1 pt What is one of the solutions to this equation? (2x - 1) 2 = 49 7 -7 -4 -3
Practice #2: a 2 - 6a + 12 = 0
x = 3 and x = 1
x = -3 and x = 4
x = 12 and x = 2
- 29. Multiple Choice Edit 30 seconds 1 pt Solve the following equation by completing the square: n 2 = 18n + 40 {11 and -11} {16 and 2} {20 and -2} {10 and -4}
x 2 −16x−33=3
x= 18, x= −2
Explore all questions with a free account

Continue with email
Continue with phone

IMAGES
COMMENTS
The two solutions are-2-1 12 . add 4, subtract 24 from 5, 2. Complete the steps for solving 7 = -2x2 + 10x. Factor -2-125 out of the variable terms. Subtract 25/2Add 25/2Subtract 25/4Add 25/4 inside the parentheses and subtract 25/2add 25/2subtract 25/4add 25/4 on the left side of the equation. Write the perfect square trinomial as a binomial ...
Yes, the equation can be solved by factoring. Using the given equation, take the square root of both sides. Both 169 and 9 are perfect squares, so the left side becomes plus or minus 13/3, which is rational. Six plus 13/3 is a rational number, and 6 minus 13/3 is also a rational number. If the solutions of a quadratic equation are rational ...
Yvonne is solving the quadratic equation 6x2 + 24x + 7 = 0 by completing the square. Her first four steps are shown in the table. In which step did Yvonne first make an error? A Step 1. Sienna is solving the quadratic equation by completing the square. 3x2 + 9x - 4 = 0. 3x2 + 9x = 4. A (x2 + 3x) = 4.
Let's start with the solution and then review it more closely. ( 1) x 2 + 6 x = − 2 ( 2) x 2 + 6 x + 9 = 7 Add 9, completing the square. ( 3) ( x + 3) 2 = 7 Factor the expression on the left. ( 4) ( x + 3) 2 = ± 7 Take the square root. ( 5) x + 3 = ± 7 ( 6) x = ± 7 − 3 Subtract 3. In conclusion, the solutions are x = 7 − 3 and x = − ...
Solve Quadratic Equations of the Form ax 2 + bx + c = 0 by Completing the Square. The process of completing the square works best when the coefficient of x 2 is 1, so the left side of the equation is of the form x 2 + bx + c.If the x 2 term has a coefficient other than 1, we take some preliminary steps to make the coefficient equal to 1.. Sometimes the coefficient can be factored from all ...
Solve a quadratic equation of the form x2 + bx + c = 0 x 2 + b x + c = 0 by completing the square. Step 1. Isolate the variable terms on one side and the constant terms on the other. Step 2. Find (12 ⋅ b)2, ( 1 2 · b) 2, ( 1 2 · b) 2, the number needed to complete the square. Add it to both sides of the equation.
Solve by completing the square: x2 + 8x = 48. Solution: Step 1: Isolate the variable terms on one side and the constant terms on the other. This equation has all the variables on the left. x2 + bx c x2 + 8x = 48. Step 2: Find (1 2 ⋅ b)2, the number to complete the square. Add it to both sides of the equation.
First, divide the polynomial by 4 (the coefficient of the x 2 term). x 2 + 5 x + 25 4 = 0. Note that the left side of the equation is already a perfect square trinomial. The coefficient of our x term is 5 , half of it is 5 2 , and squaring it gives us 25 4 , our constant term. Thus, we can rewrite the left side of the equation as a squared term.
The following are the general steps involved in solving quadratic equations using completing the square method. -terms (both the squared and linear) on the left side, while moving the constant to the right side. If you have the "Easy type", proceed immediately to Step 4. If you have the "Difficult Type", you must divide the entire ...
Quiz 3. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Solving an Equation by Completing the Square. The process of completing the square: Isolate the constant. Form a perfect square trinomial, keeping the equation balanced. Write the trinomial as a binomial squared. Use the square root property of equality. Isolate the variable. Solve x.
Solving Quadratic Equations: Completing the ... (Sample answer) To use completing the square to solve a quadratic equation when a ≠ 1, factor out the a before forming a perfect square trinomial. Isolate Factor perfect square square root. Expressions in One Variable Warm-Up 12
Solve x2 + 12x = -20 by completing the square. Add to both sides of the equation. The value of in this equation is . Write the left side of the equation as a binomial squared. The left side of the equation becomes ()2. Use the square root property of equality. Solve x2 + 8x = 33 by completing the square.
And I put this big space here for a reason. In the last video, we saw that these can be pretty straightforward to solve if the left-hand side is a perfect square. You see, completing the square is all about making the quadratic equation into a perfect square, engineering it, adding and subtracting from both sides so it becomes a perfect square.
Solve quadratic equations using completing the square step-by-step. quadratic-equation-solve-by-completing-square-calculator. High School Math Solutions - Quadratic Equations Calculator, Part 2. Solving quadratics by factorizing (link to previous post) usually works just fine. But what if the quadratic equation...
To complete the square when a is greater than 1 or less than 1 but not equal to 0, divide both sides of the equation by a. This is the same as factoring out the value of a from all other terms. As an example let's complete the square for this quadratic equation: 2x2 − 12x + 7 = 0 2 x 2 − 12 x + 7 = 0. a ≠ 1, and a = 2, so divide all terms ...
Study with Quizlet and memorize flashcards containing terms like What value of c makes x2 − 24x + c a perfect square trinomial?, What number should be added to both sides of the equation to complete the square? x2 - 6x = 5, Which are the solutions of x2 = -11x + 4? and more.
9.1 Solve Quadratic Equations Using the Square Root Property; 9.2 Solve Quadratic Equations by Completing the Square; 9.3 Solve Quadratic Equations Using the Quadratic Formula; 9.4 Solve Equations in Quadratic Form; 9.5 Solve Applications of Quadratic Equations; 9.6 Graph Quadratic Functions Using Properties; 9.7 Graph Quadratic Functions Using ...
24 = x 2 − 4 x + 3. 1) Rewrite the equation by completing the square. Your equation should look like ( x + c) 2 = d or ( x − c) 2 = d . 2) What are the solutions to the equation?
Study with Quizlet and memorize flashcards containing terms like What is the first step in writing f(x) = 3x2 + 6x - 8 in vertex form? Factor out 3 from each term. Form a perfect square trinomial by keeping the value of the function equivalent. Write the trinomial as a binomial squared. Factor out 3 from the first two terms., Write g(x) = 4x2 + 88x in vertex form. The function written in ...
Solving Quadratic Equations by Completing the Square quiz for 9th grade students. Find other quizzes for Mathematics and more on Quizizz for free! ... Solve the equation by completing the square and then finding the roots. x 2 + 6x - 4 = 36. x = -7, 7. x = 4, -10. x = -4 +- √7. x = 10, -4. 19. Multiple Choice. Edit. 30 seconds. 1 pt.
Rewrite the equation by completing the square. 2 x 2 − 9 x + 7 = 0. ( x + ) 2 =. Show Calculator. Report a problem. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for ...