assignment 2 randomized optimization

This article is part of my series of projects around Machine Learning. Click here to see the list of projects of this series.

This project is the second assignment of CS-7641 Machine Learning at the Georgia Institute of Technology. The assignment is to study the performance of four randomized optimization algorithms on three optimization problem. Then use the same algorithms to optimize the neural networks from the previous assignment

Methodology

Everything was done in Python using Visual Studio Code and the Jupyter extension. The randomized optimization library is MLrose I modified copying code from the forks by Hiive for Genetic Algorithm performance and Parkds for MIMIC performance, as well as personal code to log computation time, fitness function calls, and time limits. The machine learning library is SciKit Learn. The plotting library is MatPlotLib PyPlot.

The algorithm of MIMIC is described in Isbell et al. 1997 – MIMIC : Finding Optima by Estimating Probability Densities .

Optimization problems

To study the efficiency of the four Optimization Algorithms, I chose three Optimization Problems with differences to show which algorithm works on which kind of problem. All the problems are maximization problems.

For each problem, I first compared the average, minimum and maximum fitness obtained for different sizes of the problem over a number of run with different random seeds. If the size of the problem is too small, the optima will be reached by all algorithms and the study will be useless. The goal was to find a problem size were the advantages of one algorithm over another were clear and the computation time was reasonable.

However, some algorithms (RHC and SA) will reach a plateau very fast and the others (GA and MIMIC) take a lot longer to compute. Therefore, we have to study the fitness over computation time. For this, I modified MLrose and added several features including a time limit for problems and a way to record the fitness and computation time at each iteration. We can thus plot fitness over time for each algorithm.

I thought about studying fitness to iteration but iterations are completely different measures for each algorithm. SA and RHC iterations are simple and fast while MIMIC and GA require way more computation. This metric is meaningless for comparison.

The parameters of each algorithms would need to be tuned precisely for each new problem. For practical reasons, I fixed the parameters for all problems to the following :

However, max_attemps for SA, MIMIC and GA, and restarts for RHC are increased to arbitrary ridiculously high values when studying the fitness over time to allow the algorithm to run for longer.

For problem size and computation time plots, I ran the algorithms 10 times each as we have to take into account the randomness involved. The average is the useful metrics to compare the algorithms and the min-max envelope is given to see if the algorithms are reliable.

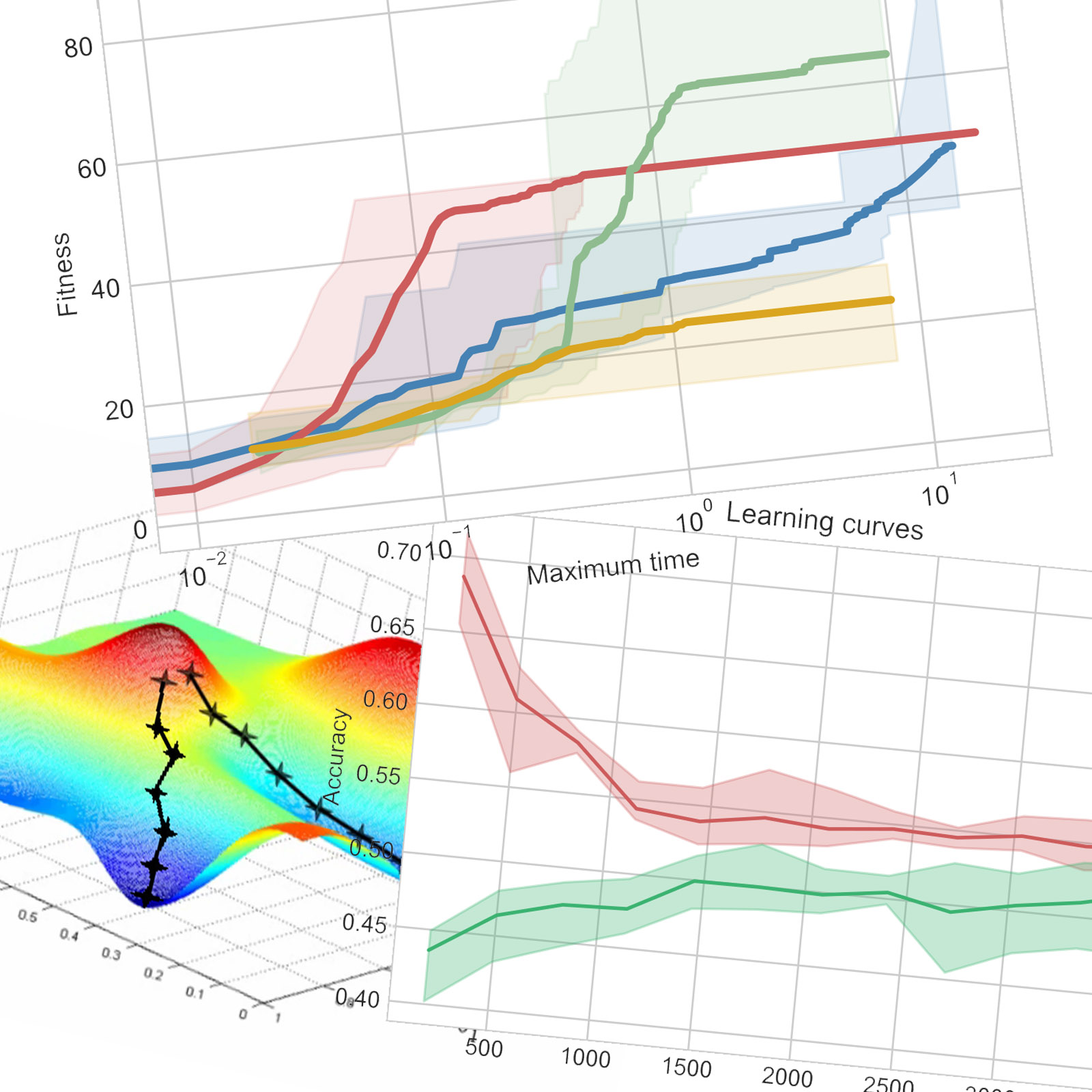
All plots of this part use the same color code : blue for Randomized Hill Climbing, red for Simulated Annealing, green for Genetic Algorithm and yellow for MIMIC. Multiple runs are computed with different random seeds. The average of all runs is the thick line and the min-max envelope is in a lighter color.

Two main experiments are run in order to plot and study the evolution of fitness over the size of the problem (length of the states), and the computation time in seconds.

The fitness of a bit-string in the four peaks problem is the maximum between the number of leading 1s and the number of trailing 0s. A bonus is given if the number of leading 1s and the number of trailing 0s are both above a threshold defined as a fraction of the size of the problem. This means there are two obvious local optima by increasing the number of leading 1s or the number of trailing 0s with the maxima being when the state is either full of 1s or full of 0s. These optima have a large basin of attraction. But the bonus creates two global optima that should be hard to reach by hill climbing. The higher the bonus threashold is, the narrower its basin of attraction is and the harder the global optima will be to reach. Here I chose the bonus threashold as 25% of the size of the state.

For small sizes of the problem (length of the bit-string), all algorithms but MIMIC reach pretty much all the time the best score (twice the size of the problem with the bonus). That is because the basin of attraction of the smaller local optima are about the same size as that of the global optima.

For larger problems, the basin of attraction is just too appealing and RHC can’t find the global optima at all, while GA and SA perform great. Up to a size of about 100, GA finds the optima almost every time and outperforms SA greatly. This is because when mixing the populations, it might combine an individual with many trailing 0s and one with many leading 1s, creating an individual benefiting from the bonus. With a larger size above 40 though, GA reaches the optimum less frequently and the difference in performance between GA and SA shrinks. Above a size of 80, even GA can’t find the global optima in any of the ten runs.

Now, for a bit-string of length 50, I compared the fitness over computation time.

SA reaches the plateau of 50 corresponding to the local optimum about ten times faster than GA reaches its higher plateau. MIMIC and GA perform about as poorly and worse than the others for short time limits (about 0.35 seconds for the chose parameters). While GA jumps in fitness after that, MIMIC stays underperforming. There is no clear structure and relation between the bits so MIMIC doesn’t have an advantage.

For this study, I increased the number of restarts of RHC to an arbitrary high number so that the algorithm only stops when stagnating for very long. This is why RHC still performs reasonably well. With so many restarts at this relatively small size, RHC has a small chance to benefit from the bonus, as we can see on the previous plot (the maximum is above 50).

The One Max optimization problem is very simple : the fitness is the number of 1s in the bit-string. This means there is only one optimum and the basin of attraction is the entire state space. RHC and SA should perform great and faster than GA and MIMIC.

Regardless of problem size, all algorithms reach the maximum fitness. This is to be expected for such a simple problem. The time comparison is where the algorithms can be ranked.

As predicted, SA and RHC perform spectacularly better, reaching the optima over ten times faster than GA or MIMIC. SA is slower than RHC as it does more calculations. MIMIC is also slightly faster than GA but not enough for a real appreciation of the algorithm better suiting the structure of the problem itself.

No this isn’t a typo. The third problem I chose is one I created because I wanted to show one situation where MIMIC performs well. This problem works on a bit-string as well. I tried different versions of the problem :

First, the 4-Pairiodic. The bit-string is divided in four equal parts. The first is the model and we want this model to be periodic on the other parts. We then evaluate the fitness as such : we iterate over the bits of the model and the corresponding bits of each parts. We count the number of times the bit of the model is equal to the bit of each parts. If the bit of the model is different from the three other bits, we give a score of 1, if it is equal to one of the other bits, we give a score of 2, if it is equal to two of the other bits, we give a score of 0 (basically a penalty) but if all bits are the same, then we give a bonus of 5. This creates an optimum harder to reach. The name Pairiodic comes from the fact that we want the pattern to be periodic but only forming pairs.

For example, for the state :

We can extract the first series :

The first bit is alone, the score for the first series is 1.

Second series :

The first bit is in a pair, the score for the second series is 2.

Third series :

The first bit is in a trio, the score for the third series is 0.

Fourth series :

The first bit is in a quartet, the score for the fourth series is 5.

The total fitness of the state is thus 8.

The 6-Pairiodic problem is similar but dividing the state in six and the score for each bits of the model is : 2 for no equal bit, 4 for 1 equal bit (1 pair), 0 for 2, 8 for 3 (2 pairs), 0 for 4 and 16 for 5 (3 pairs).

The 8-Pairiodic is similar with 8 chunks and the scores for 0 to 7 equal bits from the model are correspondingly 2, 4, 0, 8, 0, 16, 0, 32.

And so on for 10-Pairiodic following the same pattern for scores. See the source code on GitHub if necessary. The algorithm doesn't cover edge cases when the length of the states is not a multiple of the problem dimension.

Now the results. I started with the 4-Pairiodic for different problem sizes (the length of the state).

As we can see, the problem size doesn’t change the order of the algorithms and all the algorithms perform about as well. GA and MIMIC still perform slightly better than RHC and SA.

I will assume the same conclusion for the other Pairiodic problems and only study computation time. I picked a size of 100 and studied the fitness over computation time but limited to 30 seconds for practical reasons.

SA and RHC are once again very fast, but given enough time, MIMIC and then GA outperform both by a small margin. Even if MIMIC is slightly faster than GA, the latter performs slightly better.

Then for 4-Pairiodic with a size of 150.

Here MIMIC outperforms GA significantly but a longer computation time might give the first place to GA after all. The result is actually similar to 4-Pairiodic but with RHC and SA performing relatively worse.

And for 8-Pairiodic for a size of 180.

Now MIMIC isn’t as efficient and GA is slightly better at any computation time.

My interpretation is that MIMIC works well when it can detect the structure of the problem. 4-Pairiodic is simple enough that RHC and SA can achieve good fitness. 6-Pairiodic is too difficult for RHC and SA but MIMIC still detects the structure well enough. However, in 8-Pairiodic, MIMIC has more difficulties detecting the entire structure while and loses performance relative to GA that still performs well.

I then tested this hypothesis by extending the study to a 10-Pairiodic problem with a size of 160.

However, MIMIC gained again in performance and is equivalent to GA until it plateaus where GA performs better.

This means the previous explanation is incomplete. Maybe GA performs relatively better when the optima corresponds to an even number of pairs.

Overall, the clear conclusion is that for a heavily structured problem, RHC and SA are not suited and GA and MIMIC should both be considered.

General Observations

Here are some observations common to all problems and help understand the choices I made.

SA and RHC are much simpler and thus faster than MIMIC and GA so will perform way better for small time limits. However, I modified the MLrose library to log the number of calls to the fitness function. For the OneMax problem with a size of 100, RHC called the fitness function 32510 times, SA 425 times, GA 86 times and MIMIC 61 times. For toy problems like the ones use in the assignment, fitness functions are simple and fast so the overhead of each algorithms dominates : RHC is the fastest algorithm and MIMIC usually the slowest. However, more complex problems where the computation time of the fitness function dominates the overhead of each algorithm would reverse the order and the economy of function calls of smarter algorithms such as MIMIC and GA make them more appealing and reveals the huge weakness of RHC.

To illustrate this phenomenon, here is the fitness over computation time for OneMax where I modified the fitness function to add a delay to simulate a more computation expensive problem.

Original One Max

0.00001 second delay per function call

0.01 second delay per function call

As we can see, increasing the computation time of the fitness function delays the RHC and SA curves way more than the MIMIC and GA curves.

When the optimization problem has few optima and a global optimum with a large basin of attraction, SA and RHC will perform great in terms of optimization and speed. SA is slightly slower but can overcome the trap of small local optimum and it should be preferred over RHC for problems with more local optimum.

When the problem has a more complex underlying structure, SA and RHC will still reach a plateau fast and in applications with limited resources, large amount of data and time constraints, they are a valid option. However, given enough time (around 10 to 100 times longer), GA and MIMIC will usually perform better.

These toy problems have simple fitness functions but, as explained previously, real applications with computation intensive fitness calculations will slow down RHC and SA considerably. MIMIC and GA are better choices for those circumstances.

The advantages between GA and MIMIC are hard to estimate for real life applications using the toy problems described above. They should be both considered and evaluated.

Neural Network optimization

The dataset I used in the first assignment was about Wine Quality. It is made available by Paulo Cortez from the University of Minho in Portugal on the UCI Machine Learning Repository. This dataset is used in the paper P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis - Modeling wine preferences by data mining from physicochemical properties. In Decision Support Systems, Elsevier, 47(4):547-553, 2009 . While the dataset contains data for red and white wines, I restricted my analysis to the white wines because the target classes are less unbalanced.

It contains 4898 wines with 11 physiochemical proprieties and a sensory quality score which we want to predict with a classifier. All values are floating-point or integer values which I all scaled to the range from 0 to 1.

I had calculated the accuracy of the naïve distribution classifier at 32.4% and the single-minded classifier at 44.9%. The latter will be the basic comparison for the results of the algorithms.

The goal of this part is to compare the accuracy score we obtain by using randomized optimization algorithms to determine the weights and biases of a neural network used for regression on the dataset to the accuracy score of the naïve classifiers and the neural network using the default Adam solver.

For the learning curves in this part, I plot the accuracy on the training set in red and the accuracy on the testing set in green . The min-max envelope is represented with a lighter color.

Previous results

In the previous assignment, the study of neural networks didn’t lead to good results but a network structure of (12,12,12) had a slightly better accuracy. However, when testing this structure with randomized optimization algorithm, the accuracies were only about 10%. I thus tried different structures and found better results with a single hidden layer of 100 nodes. This will be the network used in every run.

Also, in the previous assignment, we determined that the ‘relu’ activation function lead to the best results. I had used a maximum of 4000 iterations. I will therefore use both of those parameters for this study as well.

Here are the results of the neural network using the Adam solver and the one-layer 100-nodes structure.

Simulated Annealing

For simulated annealing, the only parameter specific to the algorithm we can change is the schedule that determines how the temperature is adjusted during the optimization process. I decided to use the default exponential decay function as hyperparameters are not part of this study.

The first run with the default step size (learning rate) of 0.1 lead to disappointing results. I varied the step size to find a better one.

A step size around 0.75 lead to better results and I chose this value.

Looking at the learning curves, we can see the model isn’t overfitting and additional training samples wouldn’t improve accuracy by much.

The results are thus :

This is better than the single-minded classifier but not as good as the reference neural network with the Adam solver.

Random Hill Climbing

As RHC is faster, I allowed it to do 10 restarts to find the optima. This makes it about as computation expensive as SA for this problem. I chose the same step size of 0.75 after checking that there were no significant gains to be made with a different value.

With only one restart, the optimization was faster but produced networks with widely varying results.

RHC produces a better performing network than SA for this problem with enough restarts. And the results approach the original NN but without outperforming it.

Genetic Algorithm

The parameters I used for the genetic algorithm are the default values of a population size of 200 and a mutation rate of 0.1. Again, I checked if a different step size improved performance and settled for the same 0.75.

The learning curves obtained are horrible. The accuracies vary widely and are consistently worse than any of the previous algorithms.

This might be due to suboptimal hyperparameters such as a mutation rate too high (0.1) that creates too much variation and jump over optima that SA and RHC are able to approach more slowly and precisely.

With such learning curves, the accuracies obtained are not relevant, I will therefore only estimate the accuracies as :

GA took longer to compute and testing the hyper-parameters over a range of value is highly impractical. This algorithm might be too sensitive for this problem and underperform for this reason.

Let’s compare the results of the different classifiers.

The default Adam solver is both faster and performs better on this problem. All but maybe GA performed better than the single-minded classifier but the results are still rather poor.

A further study of the effects of the hyper-parameters, maybe with a subset of the dataset for practical reasons, or using a better optimized library would be required to determine conclusively if the random optimization algorithms presented in this study present any advantage over the default Gradient Descent.

The Problems Given to You

The problems you give us, what to turn in, grading criteria.

We Teach Code

• 0.00  $ 0 items

CS 7641 Assignment 2: Randomized Optimization Solved

35.00  $

If Helpful Share:

Description

This project seeks to understand the behavioral and computatitonal and predictive qualities of four random search optimzation methods:.

• Randomized Hill Climb (RHC)
• Simulated Annealing (SA)
• Genetic Algorithms (GA)
• Mutual Information Maximizing Input Clustering (MIMIC)

Prerequisites

These instructions apply for Windows 10 x64. For testing on your own machine, you need to install the following libraries.

• ABAGAIL:  https://github.com/pushkar/ABAGAIL
• Apache Ant:  https://ant.apache.org/bindownload.cgi
• Java Development Kit:  https://www.oracle.com/technetwork/java/javase/downloads/jdk10-downloads-4416644.html
• Add Java and Ant to your windows environment and path variables. A helpful guide is found at:  https://www.mkyong.com/ant/how-to-install-apache-ant-on-windows/

Once all of the prerequisites are installed, all of the methods are run from the Windows Command Prompt

Getting Started

• Download the dataset, PhishingWebsitesData_preprocessed.csv
• Original Phishing Websites Data – available at  https://www.openml.org/d/4534
• Edit the following .java files to point them towards your downloaded PhishingWebsitesData_preprocessed.csv file location. You can also use this time to edit the .java files to change the neurnal network structure
• phishing_rhc.java
• phishing_sa_val.java
• phishing_ga_val.java
• phishingwebsite_finaltest.java
• Convert all .java files to .class files with the following code from the command prompt.
• javac phishing_rhc.java
• javac phishing_sa_val.java
• javac phishing_ga_val.java
• javac phishingwebsite_finaltest.java
• Move all .class files to the location ~\ABAGAIL\opt\test
• Includes the 4 ‘phishing_’ class files and the 3 ‘_Toy’ class files

Part 1: Training a Neural Network using Random Search (RHC, SA, GA)

This section will train a neural network on the phishing websites dataset using RHC, SA, and GA. These methods are compared to each other and to the same network structure trained using backpropagation.

Running the Models (via command prompt):

• cd ~\ABAGAIL
• java -cp ABAGAIL.jar opt.test.phishing_rhc
• java -cp ABAGAIL.jar opt.test.phishing_sa_val
• java -cp ABAGAIL.jar opt.test.phishing_ga_val
• java -cp ABAGAIL.jar opt.test.phishingwebsite_finaltest

The model results (training times and neural network accuracies) are stored in .csv files located at ~\ABAGAIL\Optimization_Results

Part 2: Random Search Toy Problems

This section presents 3 toy optimization problems for which RHC, SA, GA, and MIMIC are all used to maximize the function fitness.

1. Traveling Salesman Problem – Highlights GA

• java -cp ABAGAIL.jar opt.test.TravelingSalesman_Toy

2. Continuous Peaks Problem – Highlights SA

• java -cp ABAGAIL.jar opt.test.ContinuousPeaks_Toy

3. Four Peaks Problem – Highlights MIMIC

The model results (training times and fitness function values) are stored in .csv files located at ~\ABAGAIL\Optimization_Results

Related products

CS7641-Homework 3 Image compression with SVD, PCA, Polynomial Regression and Regularization Solved

Cs7641-homework 1 linear algebra, expectation, co-variance and independence and optimization solved, cs7641-homework 2 solved.

Exhibitor Map: Data Science Day 2024

Thursday, april 4, 2024, columbia university – alfred lerner hall.

Thank you for your submission to Data Science Day 2024, DSI’s flagship annual event. We look forward to exhibiting your research. Please use this page to search for your project name and find your correlating poster or demo number using the exhibitor map. Please also look at the setup and exhibition timeline to determine when you have been scheduled to drop off your research to the venue. FAQ’s regarding registration, what to bring, and other details are included at the bottom of this page.

Exhibitor Map

Setup & Exhibition Timeline for Thursday, April 4

Check-In Location: Exhibitor Table, Broadway Lobby, Alfred Lerner Hall (2920 Broadway, New York, NY 10027). Due to public safety policy, please make sure you have your Eventbrite QR code with you when you arrive. All tickets will be checked at the door. 

8:00 AM – 8:45 AM:   SETUP: Part 1

• ALL Demos must check in at this time
• Posters P45 – P78 should plan to arrive at this time due to proximity to the stage
• If you are assigned to one of the above poster numbers and cannot drop your poster off early, we can hold and you can set up during break (~11:00 AM) or at the end of the stage program (~1:00 PM)

12:00 PM – 12:45 PM: SETUP: Part 2

• Posters  P01-P44 and  P79 – P92  can check in at this time, however, you are encouraged to come earlier!
• Posters P56 – P65 will set up in the back hallway; DSI staff will bring your easel out at the start of the session.

1:00 PM – 4:00 PM: POSTER AND DEMO SESSION

• Exhibitors must be stationed by their project during the open session time.

4:00 PM – 5:00 PM: RECEPTION

• Teams are welcome to continue presenting during the event reception, but this is optional.

5:00 PM – 5:15 PM: BREAKDOWN & EXIT

Table-Based Demos

D01 – Table 1: Demo: A Mobile Full-Duplex Jamceiver D02 – Table 1: Real-time Camera Integration for Traffic Information Extraction and Visualization D03 – Table 2: Interactively Augmenting Clinical Decisions with an Expert Knowledge-Distilled Vision Transformer D04 – Table 3: Deep Learning for Ultrasound Guided Infant Lumbar Puncture D05 – Table 3: Online Hyperparameter Optimization for Neural Ordinary Differential Equations D06 – Table 4: English-Teaching Chatbot with Adaptive, Empathetic Feedback D07 – Table 4: An NLP Framework to Crime Narrative Analysis D08 – Table 5: Superspreading shapes the early spatial spread of emerging infectious diseases D09 – Table 5: Innovating Urban Transit and Safety: VR Navigation and Intelligent Warning Systems D10 – Table 6: Attend in Lab

P01: On the Limited Representational Power of Value Functions and its Links to Statistical (In)Efficiency P02: Fourier-Based Bounds for Wasserstein Distances and Their Implications in Computational Inversion P03: Theoretical Guarantees for Data-dependent Posterior Tempering P04: Bagged Deep Image Prior for Imaging in the Presence of Speckle Noise P05: Two-Stage Stochastic Stable Matching P06: Generalizing Direct Preference Optimization with Mallows Model P07: Fair algorithms with unfair predictions P08: Generative Diffusion Models for Clinical Animal Studies Data P09: Learning-Augmented Online Packet Scheduling with Deadlines P10: Improved Algorithms for Multi-Period Multi-Class Packing Problems with Bandit Feedback P11: Model Assessment and Selection under Temporal Distribution Shift P12: CYsyphus: The Cyber Policy Decision-Support Tool and Database P13: Pioneering Palm-Vein Biometrics: Development of Advanced Evaluation Standards for Robust Biometric Authentication P14: FOX: Coverage-guided Fuzzing as Online Stochastic Control P15: Decoding Propaganda using Large Language Models P16: Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook P17: MR Research on the Cloud P18: Towards Causal Deep Learning for Vulnerability Detection P19: Energy-Efficient Scheduling with Predictions P20: Real-time Anomaly Detection AI for Particle Physics Experiments P21: In Situ Correlative Transmission Electron Microscopy for Experimental Study of Grain Growth in Thin Films P22: Inferring Causal Relations of Galaxy Formation and Evolution Processes in Galaxy Simulations P23: ML-Edex-4STEM: Teaching and Applying Machine Learning to Physical Science Students P24: Interpretable Machine Learning for multimodal analyses of materials: X-ray absorption spectra and pair distribution functions P25: An open-source benchmark for trustworthy high-dimensional symbolic regression for energetic materials P26: Mechanistic Geometric Learning for Energetic Metamaterials P27: Decision-Focused Prediction of Strategic Energy Storage Behaviors P28: Bayesian Nonparametric Ensemble (BNE) algorithm for predictions of high spatiotemporal PM2.5 concentrations P29: Experimentation with Wideband Real-Time Adaptive Full-Duplex Radios P30: mmWave Measurements For Joint Communication and Sensing in Beyond-5G Networks P31: Spectrum Sharing via Consumption Models: Prototyping and Field Testing in an Urban FCC Innovation Zone P32: Gaze-Informed Vision Transformers: Predicting Driving Decisions Under Uncertainty P33: Risk Averse Urban Drone Routing P34: Evaluating Trajectory Forecasting Models for a New York City Street Intersection P35: Designing Training Environments for Reinforcement Learning Based Building Energy System Control P36: An Internet Traffic Map of Service Delivery Patterns in a Residential Network P37: Drawing Competitive Districts in Redistricting P38: Exploring Dynamics of Popularity Among the Media: A Case Study of COVID-19, Election, and Racial Justice Discourse P39: Comparing Pre and Post-Lock Down Topics from Twitter to Gain Insights to Refine Interventions for Hispanic and African American Family Caregivers of Persons with Dementia P40: Investigating the Association Between Text-Based Indications of Foodborne Illness from Yelp Reviews and New York City Health Inspection Outcomes, 2023 P41: MLOps Pipeline – A Use Case of Malnutrition AI Screening Tool Deployment to EMR P42: Translations and Synthesis of Texts from Low Resource Indic Languages to Multiple Languages Using Neural Machine Translation and RAGs P43: Impact Evaluation of Mandated Sex Education Policies on Youth Health Outcomes P44: Imagery Data at Remote, Active Volcanoes: Autonomous Analysis for Monitoring and Forecasting P45: Contexts Matter but How? Course-Level Correlates of Performance and Fairness Shift in Predictive Model Transfer P46: LIFE – LIterature For Empowerment. A Horizon Europe Marie Curie Postdoctoral Project P47: Leveraging Brand Google Search Trends to Forecast Election Results P48: DSI Scholars Project: Words that Represent Peace P49: Patents scaling information for academia: More precise, multi-national, and up-to-date P50 : Identifying Refund Hunters with Peer Networks P51: Neighborhood Financial Access and Entrepreneurship P52: Polishing an Idea, Fostering a Community: The Effect of Barber Shops and Salons on Entrepreneurship P53: Score as actions: Diffusion Models alignment by continuous-time reinforcement learning P54: Online Auctions with Predictions P55: Index-Based Sequential Pooling P56: YouTube Stock Pundits Don’t Predict The Market P57: The Best of Many Robustness Criteria in Decision Making: Formulation and Application to Robust Pricing P58: An Algorithm for the Assignment Game Beyond Additive Valuations P59: Geometry-Aware Normalizing Wasserstein Flows for Optimal Causal Inference P60: Automated Market Making and Loss-Versus-Rebalancing (LVR) P61: Advancing volumetric breast density segmentation: A deep learning approach with digital breast tomosynthesis P62: Listen, Chat, and Edit: Text-Guided Soundscape Modification for Enhanced Auditory Experience P63: Dual-path Mamba: Efficient Short and Long-term Bidirectional Selective Structured State Space Models for Speech Separation P64: Broadening Gene Discovery for Alzheimer’s Disease P65: Mathematical Models of Genome Rearrangements and their Effects on Evolution P66: HOLiS: a high-throughput multispectral imaging pipeline for cell-type atlasing of whole human brains P67: Analysis of Cerebral Autoregulation Impairment across Different Critical Congenital Heart Diseases in Neonates P68: Shadows and Signals: Uncovering Image Traits That Compromise Brain Tumor Segmentation Accuracy P69: A Custom Bioinformatics Pipeline for investigating Circular RNAs P70: Longitudinal Multimodal Radiomic Fusion with Transformer Architecture for Outcome Prediction in Lung Diseases: A Study of COVID-19 Patients P71: MRI-based radiomic features for risk stratification of ductal carcinoma in situ P72: Radiomic Phenotypes of the Background Lung Parenchyma from [18]F-FDG PET/CT Images can Enhance Predictions of Response after Surgical Resection of Tumors in Non-Small Cell Lung Cancer Patients P73: A Custom-Designed Software for Automation of Proteomics Data Analysis: Application for Biomarker Discovery in Non-Small Cell Lung Cancer P74: Hierarchical Bayesian estimation of motor evoked potential recruitment curves yields accurate and robust estimates P75: Inference of Chromosomal Instability in Cancer from DNA-sequencing Data P76: Multimodal Learning for Structural Heart Disease Detection P77: The Dynamic Interplay of S1, M1 and M2 in the Cortex of Awake, Behaving Mice P78: Exploring RNA Editing Via A Customized Bioinformatics Pipeline P79: Brain Computer Interface for Unconscious appearing ICU patients with or without Cognitive Motor Dissociation P80: CEHR-GPT: Generating Electronic Health Records with Chronological Patient Timelines P81: Leveraging Random Forest in Mental Health Research: Insights from Two Studies in Pediatric Population P82: Long-term Visual Field Appearance Prediction Using Generative Vision Transformers for Ophthalmic Education and Patient Follow-up P83: The Role of the Cerebellar Dentate Nucleus in Learning: Insights from Visuomotor Association Tasks in Non-Human Primates P84: Functional Genomics of Human P85: EEG features predict Parkinson’s disease Given the Simon conflict task P86: Postmortem Human Hippocampal Proteome Alterations in Major Depression and Antidepressant Treatment P87: Moderation effect of persistent homology-based functional connectivity on cognitive decline in Alzheimer’s Disease P88: Leveraging machine learning explanations to assess the appropriateness of using demographic information during schizophrenia onset prediction P89: Rapid Response Teams for Proactive Sepsis Treatment P90: Using XGBoost to Predict Sleep Duration in Sexual and Gender Minority People of Color P91: Interpreting Racial Underdiagnosis Bias in AI Disease Diagnosis: A Cautionary Tale P92: Machine Learning Approach to Detect Subtle Differences between Normal and Anisometropic Eye Movements

Frequently Asked Questions

Can't find your answer, Contact Us

• Exhibitor FAQs

To register, please visit the Eventbrite page here → Select “Get Tickets” → Enter promo code RESEARCH → Register as an Exhibitor

You MUST register as an Exhibitor to confirm your presentation. Teams that do not register may lose their space on the Exhibitor floor.

Please check-in at the Exhibitor table in the Alfred Lerner Hall Broadway Lobby. There, you will receive your name badge. We will remind you where your poster or demo is located. We will have floor plans available to help you set up.

DSI will not cover the cost of printing your poster. However, DSI will provide the below items:

• An easel (for posters) or a 6-foot table and linen (for demos)
• Poster foam board
• A sign with your poster number

Please make sure you size your poster for either 30 x 40 or 20 x 30 to fit on our foam boards.

For posters, please bring your printed poster file that can be tacked. For demos, please bring any special equipment (re: laptops, computers) needed to run your demo.

See the timeline on this page (below the map) to determine when you should arrive to setup your project.

Search code, repositories, users, issues, pull requests...

Provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications