regression analysis in research example

• Privacy Policy

Buy Me a Coffee

Home » Regression Analysis – Methods, Types and Examples

Regression Analysis – Methods, Types and Examples

Table of Contents

Regression Analysis

Regression analysis is a set of statistical processes for estimating the relationships among variables . It includes many techniques for modeling and analyzing several variables when the focus is on the relationship between a dependent variable and one or more independent variables (or ‘predictors’).

Regression Analysis Methodology

Here is a general methodology for performing regression analysis:

• Define the research question: Clearly state the research question or hypothesis you want to investigate. Identify the dependent variable (also called the response variable or outcome variable) and the independent variables (also called predictor variables or explanatory variables) that you believe are related to the dependent variable.
• Collect data: Gather the data for the dependent variable and independent variables. Ensure that the data is relevant, accurate, and representative of the population or phenomenon you are studying.
• Explore the data: Perform exploratory data analysis to understand the characteristics of the data, identify any missing values or outliers, and assess the relationships between variables through scatter plots, histograms, or summary statistics.
• Choose the regression model: Select an appropriate regression model based on the nature of the variables and the research question. Common regression models include linear regression, multiple regression, logistic regression, polynomial regression, and time series regression, among others.
• Assess assumptions: Check the assumptions of the regression model. Some common assumptions include linearity (the relationship between variables is linear), independence of errors, homoscedasticity (constant variance of errors), and normality of errors. Violation of these assumptions may require additional steps or alternative models.
• Estimate the model: Use a suitable method to estimate the parameters of the regression model. The most common method is ordinary least squares (OLS), which minimizes the sum of squared differences between the observed and predicted values of the dependent variable.
• I nterpret the results: Analyze the estimated coefficients, p-values, confidence intervals, and goodness-of-fit measures (e.g., R-squared) to interpret the results. Determine the significance and direction of the relationships between the independent variables and the dependent variable.
• Evaluate model performance: Assess the overall performance of the regression model using appropriate measures, such as R-squared, adjusted R-squared, and root mean squared error (RMSE). These measures indicate how well the model fits the data and how much of the variation in the dependent variable is explained by the independent variables.
• Test assumptions and diagnose problems: Check the residuals (the differences between observed and predicted values) for any patterns or deviations from assumptions. Conduct diagnostic tests, such as examining residual plots, testing for multicollinearity among independent variables, and assessing heteroscedasticity or autocorrelation, if applicable.
• Make predictions and draw conclusions: Once you have a satisfactory model, use it to make predictions on new or unseen data. Draw conclusions based on the results of the analysis, considering the limitations and potential implications of the findings.

Types of Regression Analysis

Types of Regression Analysis are as follows:

Linear Regression

Linear regression is the most basic and widely used form of regression analysis. It models the linear relationship between a dependent variable and one or more independent variables. The goal is to find the best-fitting line that minimizes the sum of squared differences between observed and predicted values.

Multiple Regression

Multiple regression extends linear regression by incorporating two or more independent variables to predict the dependent variable. It allows for examining the simultaneous effects of multiple predictors on the outcome variable.

Polynomial Regression

Polynomial regression models non-linear relationships between variables by adding polynomial terms (e.g., squared or cubic terms) to the regression equation. It can capture curved or nonlinear patterns in the data.

Logistic Regression

Logistic regression is used when the dependent variable is binary or categorical. It models the probability of the occurrence of a certain event or outcome based on the independent variables. Logistic regression estimates the coefficients using the logistic function, which transforms the linear combination of predictors into a probability.

Ridge Regression and Lasso Regression

Ridge regression and Lasso regression are techniques used for addressing multicollinearity (high correlation between independent variables) and variable selection. Both methods introduce a penalty term to the regression equation to shrink or eliminate less important variables. Ridge regression uses L2 regularization, while Lasso regression uses L1 regularization.

Time Series Regression

Time series regression analyzes the relationship between a dependent variable and independent variables when the data is collected over time. It accounts for autocorrelation and trends in the data and is used in forecasting and studying temporal relationships.

Nonlinear Regression

Nonlinear regression models are used when the relationship between the dependent variable and independent variables is not linear. These models can take various functional forms and require estimation techniques different from those used in linear regression.

Poisson Regression

Poisson regression is employed when the dependent variable represents count data. It models the relationship between the independent variables and the expected count, assuming a Poisson distribution for the dependent variable.

Generalized Linear Models (GLM)

GLMs are a flexible class of regression models that extend the linear regression framework to handle different types of dependent variables, including binary, count, and continuous variables. GLMs incorporate various probability distributions and link functions.

Regression Analysis Formulas

Regression analysis involves estimating the parameters of a regression model to describe the relationship between the dependent variable (Y) and one or more independent variables (X). Here are the basic formulas for linear regression, multiple regression, and logistic regression:

Linear Regression:

Simple Linear Regression Model: Y = β0 + β1X + ε

Multiple Linear Regression Model: Y = β0 + β1X1 + β2X2 + … + βnXn + ε

In both formulas:

• Y represents the dependent variable (response variable).
• X represents the independent variable(s) (predictor variable(s)).
• β0, β1, β2, …, βn are the regression coefficients or parameters that need to be estimated.
• ε represents the error term or residual (the difference between the observed and predicted values).

Multiple Regression:

Multiple regression extends the concept of simple linear regression by including multiple independent variables.

Multiple Regression Model: Y = β0 + β1X1 + β2X2 + … + βnXn + ε

The formulas are similar to those in linear regression, with the addition of more independent variables.

Logistic Regression:

Logistic regression is used when the dependent variable is binary or categorical. The logistic regression model applies a logistic or sigmoid function to the linear combination of the independent variables.

Logistic Regression Model: p = 1 / (1 + e^-(β0 + β1X1 + β2X2 + … + βnXn))

In the formula:

• p represents the probability of the event occurring (e.g., the probability of success or belonging to a certain category).
• X1, X2, …, Xn represent the independent variables.
• e is the base of the natural logarithm.

The logistic function ensures that the predicted probabilities lie between 0 and 1, allowing for binary classification.

Regression Analysis Examples

Regression Analysis Examples are as follows:

• Stock Market Prediction: Regression analysis can be used to predict stock prices based on various factors such as historical prices, trading volume, news sentiment, and economic indicators. Traders and investors can use this analysis to make informed decisions about buying or selling stocks.
• Demand Forecasting: In retail and e-commerce, real-time It can help forecast demand for products. By analyzing historical sales data along with real-time data such as website traffic, promotional activities, and market trends, businesses can adjust their inventory levels and production schedules to meet customer demand more effectively.
• Energy Load Forecasting: Utility companies often use real-time regression analysis to forecast electricity demand. By analyzing historical energy consumption data, weather conditions, and other relevant factors, they can predict future energy loads. This information helps them optimize power generation and distribution, ensuring a stable and efficient energy supply.
• Online Advertising Performance: It can be used to assess the performance of online advertising campaigns. By analyzing real-time data on ad impressions, click-through rates, conversion rates, and other metrics, advertisers can adjust their targeting, messaging, and ad placement strategies to maximize their return on investment.
• Predictive Maintenance: Regression analysis can be applied to predict equipment failures or maintenance needs. By continuously monitoring sensor data from machines or vehicles, regression models can identify patterns or anomalies that indicate potential failures. This enables proactive maintenance, reducing downtime and optimizing maintenance schedules.
• Financial Risk Assessment: Real-time regression analysis can help financial institutions assess the risk associated with lending or investment decisions. By analyzing real-time data on factors such as borrower financials, market conditions, and macroeconomic indicators, regression models can estimate the likelihood of default or assess the risk-return tradeoff for investment portfolios.

Importance of Regression Analysis

Importance of Regression Analysis is as follows:

• Relationship Identification: Regression analysis helps in identifying and quantifying the relationship between a dependent variable and one or more independent variables. It allows us to determine how changes in independent variables impact the dependent variable. This information is crucial for decision-making, planning, and forecasting.
• Prediction and Forecasting: Regression analysis enables us to make predictions and forecasts based on the relationships identified. By estimating the values of the dependent variable using known values of independent variables, regression models can provide valuable insights into future outcomes. This is particularly useful in business, economics, finance, and other fields where forecasting is vital for planning and strategy development.
• Causality Assessment: While correlation does not imply causation, regression analysis provides a framework for assessing causality by considering the direction and strength of the relationship between variables. It allows researchers to control for other factors and assess the impact of a specific independent variable on the dependent variable. This helps in determining the causal effect and identifying significant factors that influence outcomes.
• Model Building and Variable Selection: Regression analysis aids in model building by determining the most appropriate functional form of the relationship between variables. It helps researchers select relevant independent variables and eliminate irrelevant ones, reducing complexity and improving model accuracy. This process is crucial for creating robust and interpretable models.
• Hypothesis Testing: Regression analysis provides a statistical framework for hypothesis testing. Researchers can test the significance of individual coefficients, assess the overall model fit, and determine if the relationship between variables is statistically significant. This allows for rigorous analysis and validation of research hypotheses.
• Policy Evaluation and Decision-Making: Regression analysis plays a vital role in policy evaluation and decision-making processes. By analyzing historical data, researchers can evaluate the effectiveness of policy interventions and identify the key factors contributing to certain outcomes. This information helps policymakers make informed decisions, allocate resources effectively, and optimize policy implementation.
• Risk Assessment and Control: Regression analysis can be used for risk assessment and control purposes. By analyzing historical data, organizations can identify risk factors and develop models that predict the likelihood of certain outcomes, such as defaults, accidents, or failures. This enables proactive risk management, allowing organizations to take preventive measures and mitigate potential risks.

When to Use Regression Analysis

• Prediction : Regression analysis is often employed to predict the value of the dependent variable based on the values of independent variables. For example, you might use regression to predict sales based on advertising expenditure, or to predict a student’s academic performance based on variables like study time, attendance, and previous grades.
• Relationship analysis: Regression can help determine the strength and direction of the relationship between variables. It can be used to examine whether there is a linear association between variables, identify which independent variables have a significant impact on the dependent variable, and quantify the magnitude of those effects.
• Causal inference: Regression analysis can be used to explore cause-and-effect relationships by controlling for other variables. For example, in a medical study, you might use regression to determine the impact of a specific treatment while accounting for other factors like age, gender, and lifestyle.
• Forecasting : Regression models can be utilized to forecast future trends or outcomes. By fitting a regression model to historical data, you can make predictions about future values of the dependent variable based on changes in the independent variables.
• Model evaluation: Regression analysis can be used to evaluate the performance of a model or test the significance of variables. You can assess how well the model fits the data, determine if additional variables improve the model’s predictive power, or test the statistical significance of coefficients.
• Data exploration : Regression analysis can help uncover patterns and insights in the data. By examining the relationships between variables, you can gain a deeper understanding of the data set and identify potential patterns, outliers, or influential observations.

Applications of Regression Analysis

Here are some common applications of regression analysis:

• Economic Forecasting: Regression analysis is frequently employed in economics to forecast variables such as GDP growth, inflation rates, or stock market performance. By analyzing historical data and identifying the underlying relationships, economists can make predictions about future economic conditions.
• Financial Analysis: Regression analysis plays a crucial role in financial analysis, such as predicting stock prices or evaluating the impact of financial factors on company performance. It helps analysts understand how variables like interest rates, company earnings, or market indices influence financial outcomes.
• Marketing Research: Regression analysis helps marketers understand consumer behavior and make data-driven decisions. It can be used to predict sales based on advertising expenditures, pricing strategies, or demographic variables. Regression models provide insights into which marketing efforts are most effective and help optimize marketing campaigns.
• Health Sciences: Regression analysis is extensively used in medical research and public health studies. It helps examine the relationship between risk factors and health outcomes, such as the impact of smoking on lung cancer or the relationship between diet and heart disease. Regression analysis also helps in predicting health outcomes based on various factors like age, genetic markers, or lifestyle choices.
• Social Sciences: Regression analysis is widely used in social sciences like sociology, psychology, and education research. Researchers can investigate the impact of variables like income, education level, or social factors on various outcomes such as crime rates, academic performance, or job satisfaction.
• Operations Research: Regression analysis is applied in operations research to optimize processes and improve efficiency. For example, it can be used to predict demand based on historical sales data, determine the factors influencing production output, or optimize supply chain logistics.
• Environmental Studies: Regression analysis helps in understanding and predicting environmental phenomena. It can be used to analyze the impact of factors like temperature, pollution levels, or land use patterns on phenomena such as species diversity, water quality, or climate change.
• Sports Analytics: Regression analysis is increasingly used in sports analytics to gain insights into player performance, team strategies, and game outcomes. It helps analyze the relationship between various factors like player statistics, coaching strategies, or environmental conditions and their impact on game outcomes.

Advantages and Disadvantages of Regression Analysis

About the author.

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

ANOVA (Analysis of variance) – Formulas, Types...

Graphical Methods – Types, Examples and Guide

Regression Analysis

Regression analysis is a quantitative research method which is used when the study involves modelling and analysing several variables, where the relationship includes a dependent variable and one or more independent variables. In simple terms, regression analysis is a quantitative method used to test the nature of relationships between a dependent variable and one or more independent variables.

The basic form of regression models includes unknown parameters (β), independent variables (X), and the dependent variable (Y).

Regression model, basically, specifies the relation of dependent variable (Y) to a function combination of independent variables (X) and unknown parameters (β)

                                    Y  ≈  f (X, β)   

Regression equation can be used to predict the values of ‘y’, if the value of ‘x’ is given, and both ‘y’ and ‘x’ are the two sets of measures of a sample size of ‘n’. The formulae for regression equation would be

Do not be intimidated by visual complexity of correlation and regression formulae above. You don’t have to apply the formula manually, and correlation and regression analyses can be run with the application of popular analytical software such as Microsoft Excel, Microsoft Access, SPSS and others.

Linear regression analysis is based on the following set of assumptions:

1. Assumption of linearity . There is a linear relationship between dependent and independent variables.

2. Assumption of homoscedasticity . Data values for dependent and independent variables have equal variances.

3. Assumption of absence of collinearity or multicollinearity . There is no correlation between two or more independent variables.

4. Assumption of normal distribution . The data for the independent variables and dependent variable are normally distributed

My e-book,  The Ultimate Guide to Writing a Dissertation in Business Studies: a step by step assistance  offers practical assistance to complete a dissertation with minimum or no stress. The e-book covers all stages of writing a dissertation starting from the selection to the research area to submitting the completed version of the work within the deadline. John Dudovskiy

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

A Refresher on Regression Analysis

Understanding one of the most important types of data analysis.

You probably know by now that whenever possible you should be making data-driven decisions at work . But do you know how to parse through all the data available to you? The good news is that you probably don’t need to do the number crunching yourself (hallelujah!) but you do need to correctly understand and interpret the analysis created by your colleagues. One of the most important types of data analysis is called regression analysis.

• Amy Gallo is a contributing editor at Harvard Business Review, cohost of the Women at Work podcast , and the author of two books: Getting Along: How to Work with Anyone (Even Difficult People) and the HBR Guide to Dealing with Conflict . She writes and speaks about workplace dynamics. Watch her TEDx talk on conflict and follow her on LinkedIn . amyegallo

Partner Center

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 31 January 2022

The clinician’s guide to interpreting a regression analysis

• Sofia Bzovsky 1 ,
• Mark R. Phillips   ORCID: orcid.org/0000-0003-0923-261X 2 ,
• Robyn H. Guymer   ORCID: orcid.org/0000-0002-9441-4356 3 , 4 ,
• Charles C. Wykoff 5 , 6 ,
• Lehana Thabane   ORCID: orcid.org/0000-0003-0355-9734 2 , 7 ,
• Mohit Bhandari   ORCID: orcid.org/0000-0001-9608-4808 1 , 2 &
• Varun Chaudhary   ORCID: orcid.org/0000-0002-9988-4146 1 , 2

on behalf of the R.E.T.I.N.A. study group

Eye volume  36 ,  pages 1715–1717 ( 2022 ) Cite this article

19k Accesses

9 Citations

1 Altmetric

Metrics details

• Outcomes research

Introduction

When researchers are conducting clinical studies to investigate factors associated with, or treatments for disease and conditions to improve patient care and clinical practice, statistical evaluation of the data is often necessary. Regression analysis is an important statistical method that is commonly used to determine the relationship between several factors and disease outcomes or to identify relevant prognostic factors for diseases [ 1 ].

This editorial will acquaint readers with the basic principles of and an approach to interpreting results from two types of regression analyses widely used in ophthalmology: linear, and logistic regression.

Linear regression analysis

Linear regression is used to quantify a linear relationship or association between a continuous response/outcome variable or dependent variable with at least one independent or explanatory variable by fitting a linear equation to observed data [ 1 ]. The variable that the equation solves for, which is the outcome or response of interest, is called the dependent variable [ 1 ]. The variable that is used to explain the value of the dependent variable is called the predictor, explanatory, or independent variable [ 1 ].

In a linear regression model, the dependent variable must be continuous (e.g. intraocular pressure or visual acuity), whereas, the independent variable may be either continuous (e.g. age), binary (e.g. sex), categorical (e.g. age-related macular degeneration stage or diabetic retinopathy severity scale score), or a combination of these [ 1 ].

When investigating the effect or association of a single independent variable on a continuous dependent variable, this type of analysis is called a simple linear regression [ 2 ]. In many circumstances though, a single independent variable may not be enough to adequately explain the dependent variable. Often it is necessary to control for confounders and in these situations, one can perform a multivariable linear regression to study the effect or association with multiple independent variables on the dependent variable [ 1 , 2 ]. When incorporating numerous independent variables, the regression model estimates the effect or contribution of each independent variable while holding the values of all other independent variables constant [ 3 ].

When interpreting the results of a linear regression, there are a few key outputs for each independent variable included in the model:

Estimated regression coefficient—The estimated regression coefficient indicates the direction and strength of the relationship or association between the independent and dependent variables [ 4 ]. Specifically, the regression coefficient describes the change in the dependent variable for each one-unit change in the independent variable, if continuous [ 4 ]. For instance, if examining the relationship between a continuous predictor variable and intra-ocular pressure (dependent variable), a regression coefficient of 2 means that for every one-unit increase in the predictor, there is a two-unit increase in intra-ocular pressure. If the independent variable is binary or categorical, then the one-unit change represents switching from one category to the reference category [ 4 ]. For instance, if examining the relationship between a binary predictor variable, such as sex, where ‘female’ is set as the reference category, and intra-ocular pressure (dependent variable), a regression coefficient of 2 means that, on average, males have an intra-ocular pressure that is 2 mm Hg higher than females.

Confidence Interval (CI)—The CI, typically set at 95%, is a measure of the precision of the coefficient estimate of the independent variable [ 4 ]. A large CI indicates a low level of precision, whereas a small CI indicates a higher precision [ 5 ].

P value—The p value for the regression coefficient indicates whether the relationship between the independent and dependent variables is statistically significant [ 6 ].

Logistic regression analysis

As with linear regression, logistic regression is used to estimate the association between one or more independent variables with a dependent variable [ 7 ]. However, the distinguishing feature in logistic regression is that the dependent variable (outcome) must be binary (or dichotomous), meaning that the variable can only take two different values or levels, such as ‘1 versus 0’ or ‘yes versus no’ [ 2 , 7 ]. The effect size of predictor variables on the dependent variable is best explained using an odds ratio (OR) [ 2 ]. ORs are used to compare the relative odds of the occurrence of the outcome of interest, given exposure to the variable of interest [ 5 ]. An OR equal to 1 means that the odds of the event in one group are the same as the odds of the event in another group; there is no difference [ 8 ]. An OR > 1 implies that one group has a higher odds of having the event compared with the reference group, whereas an OR < 1 means that one group has a lower odds of having an event compared with the reference group [ 8 ]. When interpreting the results of a logistic regression, the key outputs include the OR, CI, and p-value for each independent variable included in the model.

Clinical example

Sen et al. investigated the association between several factors (independent variables) and visual acuity outcomes (dependent variable) in patients receiving anti-vascular endothelial growth factor therapy for macular oedema (DMO) by means of both linear and logistic regression [ 9 ]. Multivariable linear regression demonstrated that age (Estimate −0.33, 95% CI − 0.48 to −0.19, p  < 0.001) was significantly associated with best-corrected visual acuity (BCVA) at 100 weeks at alpha = 0.05 significance level [ 9 ]. The regression coefficient of −0.33 means that the BCVA at 100 weeks decreases by 0.33 with each additional year of older age.

Multivariable logistic regression also demonstrated that age and ellipsoid zone status were statistically significant associated with achieving a BCVA letter score >70 letters at 100 weeks at the alpha = 0.05 significance level. Patients ≥75 years of age were at a decreased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those <50 years of age, since the OR is less than 1 (OR 0.96, 95% CI 0.94 to 0.98, p  = 0.001) [ 9 ]. Similarly, patients between the ages of 50–74 years were also at a decreased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those <50 years of age, since the OR is less than 1 (OR 0.15, 95% CI 0.04 to 0.48, p  = 0.001) [ 9 ]. As well, those with a not intact ellipsoid zone were at a decreased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those with an intact ellipsoid zone (OR 0.20, 95% CI 0.07 to 0.56; p  = 0.002). On the other hand, patients with an ungradable/questionable ellipsoid zone were at an increased odds of achieving a BCVA letter score >70 letters at 100 weeks compared to those with an intact ellipsoid zone, since the OR is greater than 1 (OR 2.26, 95% CI 1.14 to 4.48; p  = 0.02) [ 9 ].

The narrower the CI, the more precise the estimate is; and the smaller the p value (relative to alpha = 0.05), the greater the evidence against the null hypothesis of no effect or association.

Simply put, linear and logistic regression are useful tools for appreciating the relationship between predictor/explanatory and outcome variables for continuous and dichotomous outcomes, respectively, that can be applied in clinical practice, such as to gain an understanding of risk factors associated with a disease of interest.

Schneider A, Hommel G, Blettner M. Linear Regression. Anal Dtsch Ärztebl Int. 2010;107:776–82.

Google Scholar  

Bender R. Introduction to the use of regression models in epidemiology. In: Verma M, editor. Cancer epidemiology. Methods in molecular biology. Humana Press; 2009:179–95.

Schober P, Vetter TR. Confounding in observational research. Anesth Analg. 2020;130:635.

Article   Google Scholar  

Schober P, Vetter TR. Linear regression in medical research. Anesth Analg. 2021;132:108–9.

Szumilas M. Explaining odds ratios. J Can Acad Child Adolesc Psychiatry. 2010;19:227–9.

Thiese MS, Ronna B, Ott U. P value interpretations and considerations. J Thorac Dis. 2016;8:E928–31.

Schober P, Vetter TR. Logistic regression in medical research. Anesth Analg. 2021;132:365–6.

Zabor EC, Reddy CA, Tendulkar RD, Patil S. Logistic regression in clinical studies. Int J Radiat Oncol Biol Phys. 2022;112:271–7.

Sen P, Gurudas S, Ramu J, Patrao N, Chandra S, Rasheed R, et al. Predictors of visual acuity outcomes after anti-vascular endothelial growth factor treatment for macular edema secondary to central retinal vein occlusion. Ophthalmol Retin. 2021;5:1115–24.

Download references

R.E.T.I.N.A. study group

Varun Chaudhary 1,2 , Mohit Bhandari 1,2 , Charles C. Wykoff 5,6 , Sobha Sivaprasad 8 , Lehana Thabane 2,7 , Peter Kaiser 9 , David Sarraf 10 , Sophie J. Bakri 11 , Sunir J. Garg 12 , Rishi P. Singh 13,14 , Frank G. Holz 15 , Tien Y. Wong 16,17 , and Robyn H. Guymer 3,4

Author information

Authors and affiliations.

Department of Surgery, McMaster University, Hamilton, ON, Canada

Sofia Bzovsky, Mohit Bhandari & Varun Chaudhary

Department of Health Research Methods, Evidence & Impact, McMaster University, Hamilton, ON, Canada

Mark R. Phillips, Lehana Thabane, Mohit Bhandari & Varun Chaudhary

Centre for Eye Research Australia, Royal Victorian Eye and Ear Hospital, East Melbourne, VIC, Australia

Robyn H. Guymer

Department of Surgery, (Ophthalmology), The University of Melbourne, Melbourne, VIC, Australia

Retina Consultants of Texas (Retina Consultants of America), Houston, TX, USA

Charles C. Wykoff

Blanton Eye Institute, Houston Methodist Hospital, Houston, TX, USA

Biostatistics Unit, St. Joseph’s Healthcare Hamilton, Hamilton, ON, Canada

Lehana Thabane

NIHR Moorfields Biomedical Research Centre, Moorfields Eye Hospital, London, UK

Sobha Sivaprasad

Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

Peter Kaiser

Retinal Disorders and Ophthalmic Genetics, Stein Eye Institute, University of California, Los Angeles, CA, USA

David Sarraf

Department of Ophthalmology, Mayo Clinic, Rochester, MN, USA

Sophie J. Bakri

The Retina Service at Wills Eye Hospital, Philadelphia, PA, USA

Sunir J. Garg

Center for Ophthalmic Bioinformatics, Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

Rishi P. Singh

Cleveland Clinic Lerner College of Medicine, Cleveland, OH, USA

Department of Ophthalmology, University of Bonn, Bonn, Germany

Frank G. Holz

Singapore Eye Research Institute, Singapore, Singapore

Tien Y. Wong

Singapore National Eye Centre, Duke-NUD Medical School, Singapore, Singapore

You can also search for this author in PubMed   Google Scholar

• Varun Chaudhary
• , Mohit Bhandari
• , Charles C. Wykoff
• , Sobha Sivaprasad
• , Lehana Thabane
• , Peter Kaiser
• , David Sarraf
• , Sophie J. Bakri
• , Sunir J. Garg
• , Rishi P. Singh
• , Frank G. Holz
• , Tien Y. Wong
•  & Robyn H. Guymer

Contributions

SB was responsible for writing, critical review and feedback on manuscript. MRP was responsible for conception of idea, critical review and feedback on manuscript. RHG was responsible for critical review and feedback on manuscript. CCW was responsible for critical review and feedback on manuscript. LT was responsible for critical review and feedback on manuscript. MB was responsible for conception of idea, critical review and feedback on manuscript. VC was responsible for conception of idea, critical review and feedback on manuscript.

Corresponding author

Correspondence to Varun Chaudhary .

Ethics declarations

Competing interests.

SB: Nothing to disclose. MRP: Nothing to disclose. RHG: Advisory boards: Bayer, Novartis, Apellis, Roche, Genentech Inc.—unrelated to this study. CCW: Consultant: Acuela, Adverum Biotechnologies, Inc, Aerpio, Alimera Sciences, Allegro Ophthalmics, LLC, Allergan, Apellis Pharmaceuticals, Bayer AG, Chengdu Kanghong Pharmaceuticals Group Co, Ltd, Clearside Biomedical, DORC (Dutch Ophthalmic Research Center), EyePoint Pharmaceuticals, Gentech/Roche, GyroscopeTx, IVERIC bio, Kodiak Sciences Inc, Novartis AG, ONL Therapeutics, Oxurion NV, PolyPhotonix, Recens Medical, Regeron Pharmaceuticals, Inc, REGENXBIO Inc, Santen Pharmaceutical Co, Ltd, and Takeda Pharmaceutical Company Limited; Research funds: Adverum Biotechnologies, Inc, Aerie Pharmaceuticals, Inc, Aerpio, Alimera Sciences, Allergan, Apellis Pharmaceuticals, Chengdu Kanghong Pharmaceutical Group Co, Ltd, Clearside Biomedical, Gemini Therapeutics, Genentech/Roche, Graybug Vision, Inc, GyroscopeTx, Ionis Pharmaceuticals, IVERIC bio, Kodiak Sciences Inc, Neurotech LLC, Novartis AG, Opthea, Outlook Therapeutics, Inc, Recens Medical, Regeneron Pharmaceuticals, Inc, REGENXBIO Inc, Samsung Pharm Co, Ltd, Santen Pharmaceutical Co, Ltd, and Xbrane Biopharma AB—unrelated to this study. LT: Nothing to disclose. MB: Research funds: Pendopharm, Bioventus, Acumed—unrelated to this study. VC: Advisory Board Member: Alcon, Roche, Bayer, Novartis; Grants: Bayer, Novartis—unrelated to this study.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Bzovsky, S., Phillips, M.R., Guymer, R.H. et al. The clinician’s guide to interpreting a regression analysis. Eye 36 , 1715–1717 (2022). https://doi.org/10.1038/s41433-022-01949-z

Download citation

Received : 08 January 2022

Revised : 17 January 2022

Accepted : 18 January 2022

Published : 31 January 2022

Issue Date : September 2022

DOI : https://doi.org/10.1038/s41433-022-01949-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Factors affecting patient satisfaction at a plastic surgery outpatient department at a tertiary centre in south africa.

• Chrysis Sofianos

BMC Health Services Research (2023)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

The Complete Guide To Simple Regression Analysis

08.08.2023 • 8 min read

Sarah Thomas

Subject Matter Expert

Learn what simple regression analysis means and why it’s useful for analyzing data, and how to interpret the results.

In This Article

What Is Simple Linear Regression Analysis?

Linear regression equation, how to perform linear regression, linear regression assumptions, how do you find the regression line, how to interpret the results of simple regression.

What is the relationship between parental income and educational attainment or hours spent on social media and anxiety levels? Regression is a versatile statistical tool that can help you answer these types of questions. It’s a tool that lets you model the relationship between two or more variables .

The applications of regression are endless. You can use it as a machine learning algorithm to make predictions. You can use it to establish correlations, and in some cases, you can use it to uncover causal links in your data.

In this article, we’ll tell you everything you need to know about the most basic form of regression analysis: the simple linear regression model.

Simple linear regression is a statistical tool you can use to evaluate correlations between a single independent variable (X) and a single dependent variable (Y). The model fits a straight line to data collected for each variable, and using this line, you can estimate the correlation between X and Y and predict values of Y using values of X.

As a quick example, imagine you want to explore the relationship between weight (X) and height (Y). You collect data from ten randomly selected individuals, and you plot your data on a scatterplot like the one below.

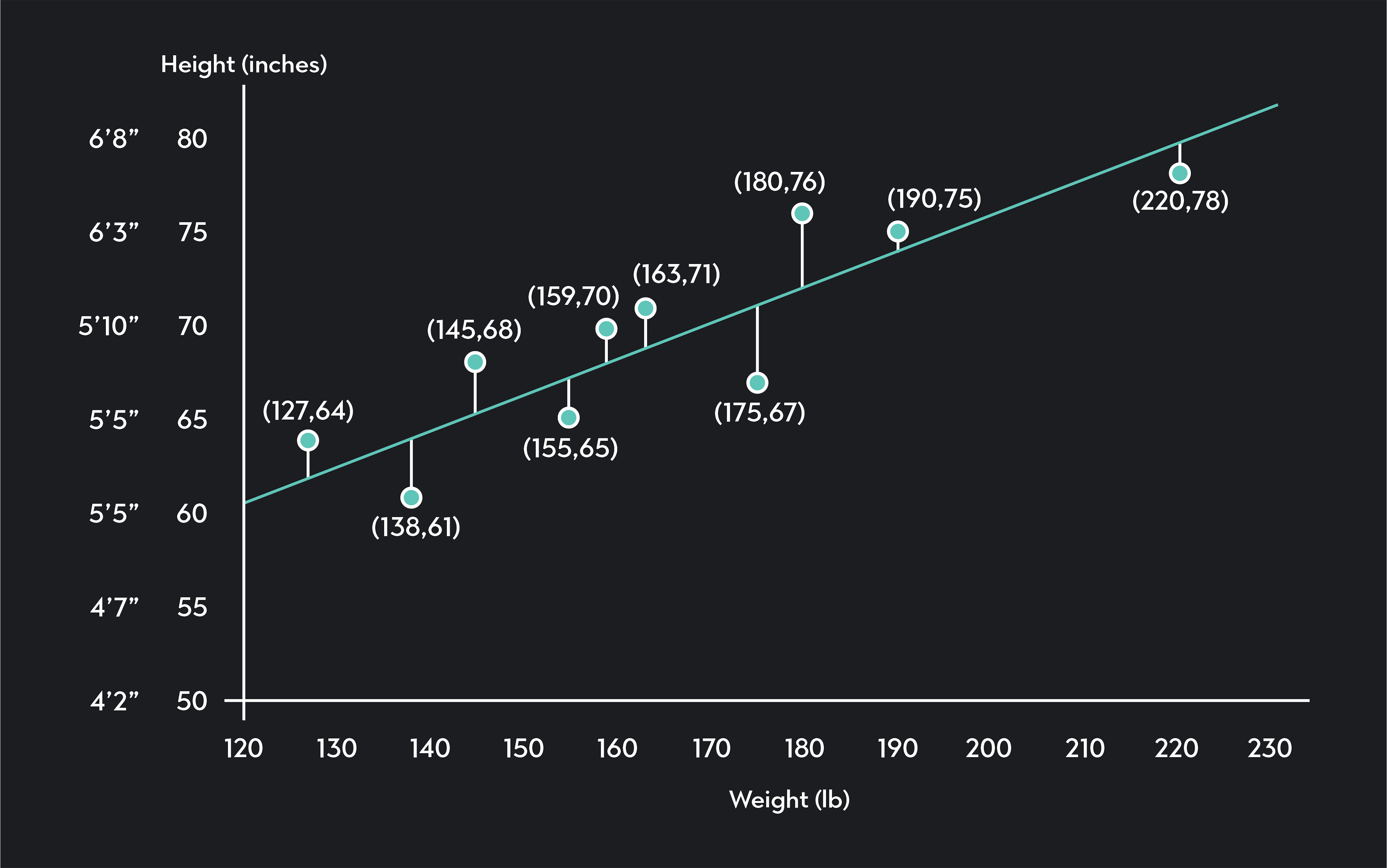
In the scatterplot, each point represents data collected for one of the individuals in your sample. The blue line is your regression line. It models the relationship between weight and height using observed data. Not surprisingly, we see ‌the regression line is upward-sloping, indicating a positive correlation between weight and height. Taller people tend to be heavier than shorter people.

Once you have this line, you can measure how strong the correlation is between height and weight. You can estimate the height of somebody ‌not in your sample by plugging their weight into the regression equation.

The equation for a simple linear regression is:

X is your independent variable

Y is an estimate of your dependent variable

β 0 \beta_0 β 0 ​ is the constant or intercept of the regression line, which is the value of Y when X is equal to zero

β 1 \beta_1 β 1 ​ is the regression coefficient, which is the slope of the regression line and your estimate for the change in Y given a 1-unit change in X

ε \varepsilon ε is the error term of the regression

You may notic‌e the formula for a regression looks very similar to the equation of a line (y=mX+b). That’s because linear regression is a line! It’s a line fitted to data that you can use to estimate the values of one variable using the value of a correlated variable.

You can build a simple linear regression model in 5 steps.

1. Collect data

Collect data for two variables (X and Y). Y is your dependent variable, which is the variable you want to estimate using the regression. X is your independent variable—the variable you use as an input in your regression.

2. Plot the data on a scatter plot

Plot the values of X and Y on a scatter plot with values of X plotted along the horizontal x-axis and values of Y plotted on the vertical y-axis.

3. Calculate a correlation coefficient

Calculate a correlation coefficient to determine the strength of the linear relationship between your two variables.

4. Fit a regression to the data

Find the regression line using the ordinary least-squares method. (You can do this by hand; but it’s much easier to use statistical software like Desmos, Excel, R, or Stata.)

5. Assess the regression line

Once you have the regression line, assess how well your model performs by checking to see how well the model predicts values of Y.

The key assumptions we make when using a simple linear regression model are:

The relationship between X and Y (if it exists) is linear.

Independence

The residuals of your model are independent.

Homoscedasticity

The variance of the residual is constant across values of the independent variable.

The residuals are normally distributed .

You should not use a simple linear regression unless it’s reasonable to make these assumptions.

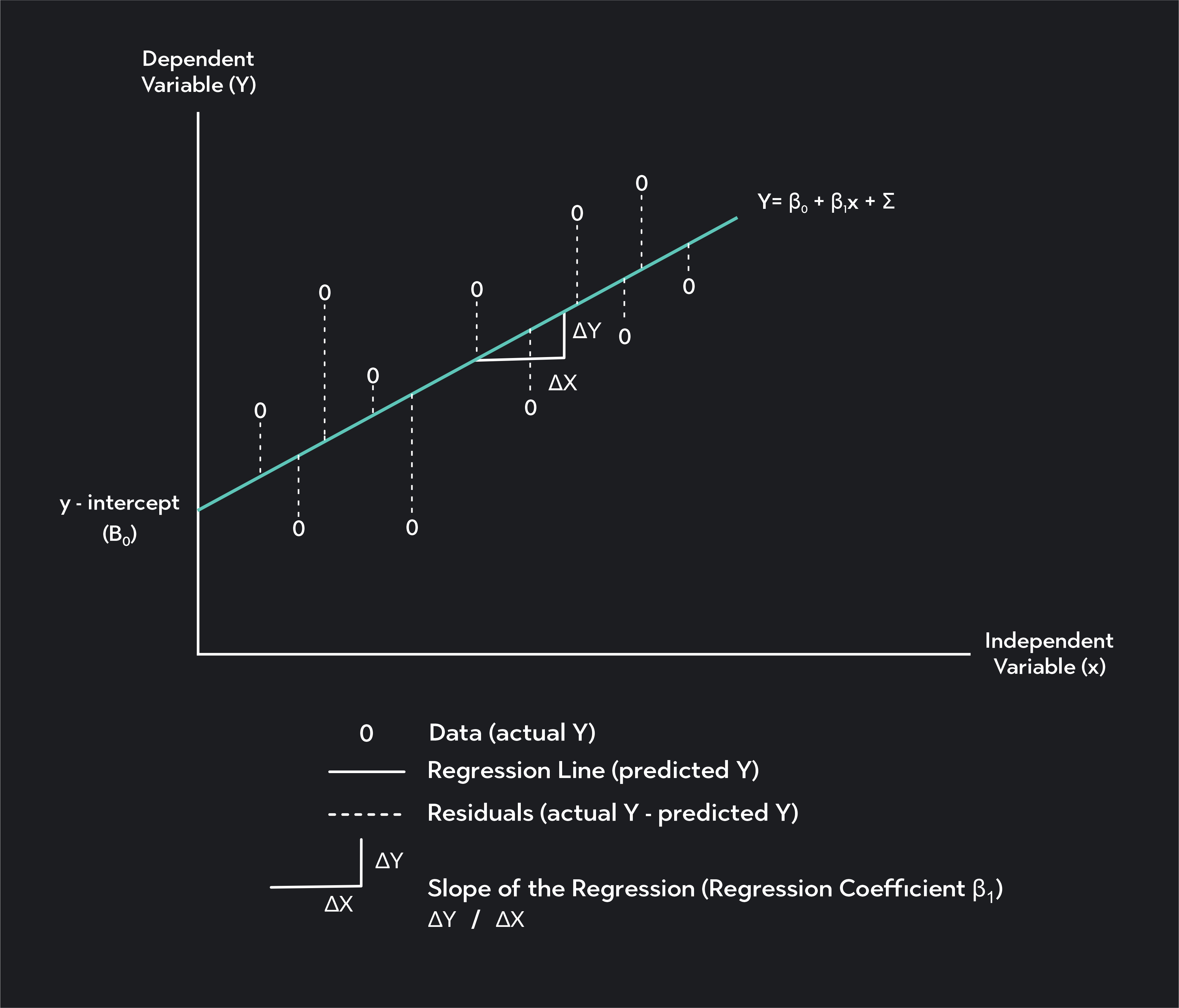
Simple linear regression involves fitting a straight line to your dataset. We call this line the line of best fit or the regression line. The most common method for finding this line is OLS (or the Ordinary Least Squares Method).

In OLS, we find the regression line by minimizing the sum of squared residuals —also called squared errors. Anytime you draw a straight line through your data, there will be a vertical distance between each ‌point on your scatter plot and the regression line. These vertical distances are called residuals (or errors).

They represent the difference between the actual values of your dependent variable Y i Y_i Y i ​ , and the predicted value of that variable, Y ^ i \widehat{Y}_i Y i ​ . The regression you find with OLS is the line that minimizes the sum of squared residuals.

You can calculate the OLS regression line by hand, but it’s much easier to do so using statistical software like Excel, Desmos, R, or Stata. In this video, Professor AnnMaria De Mars explains how to find the OLS regression equation using Desmos.

Depending on the software you use, the results of your regression analysis may look ‌different. In general, however, your software will display output tables summarizing the main characteristics of your regression.

The values you should be looking for in these output tables fall under three categories:

Coefficients

Regression statistics

This is the β 0 \beta_0 β 0 ​ value in your regression equation. It is the y-intercept of your regression line, and it is the estimate of Y when X is equal to zero.

Next to your intercept, you’ll see columns in the table showing additional information about the intercept. These include a standard error, p-value, T-stat, and confidence interval. You can use these values to test whether the estimate of your intercept is statistically significant .

Regression coefficient

This is the β 1 \beta_1 β 1 ​ of your regression equation. It’s the slope of the regression line, and it tells you how much Y should change in response to a 1-unit change in X.

Similar to the intercept, the regression coefficient will have columns to the right of it. They'll show a standard error, p-value , T-stat, and confidence interval. Use these values to test whether your parameter estimate of β 1 \beta_1 β 1 ​ is statistically significant.

Regression Statistics

Correlation coefficient (or multiple r).

This is the Pearson Correlation coefficient. It measures the strength of the correlation between X and Y.

R-squared (or the coefficient of determination)

We calculate this value by squaring the correlation coefficient. The independent variable can explain how much of the variance in your dependent variable. You can convert R 2 R^2 R 2 into a percentage by multiplying it by 100.

Standard error of the residuals

The standard error of the residuals is the average value of the errors in your model. It is the average vertical distance between each point on your scatter plot and the regression line. We measure this value in the same units as your dependent variable.

Degrees of freedom

In simple linear regression, the degrees of freedom equal the number of data points you used minus the two estimated parameters. The parameters are the intercept and regression coefficient.

Some software will also output a 5-number summary of your residuals. It'll show the minimum, first quartile , median , third quartile, and maximum values of your residuals.

P-value (or Significance F) - This is the p-value of your regression model.

It returns a hypothesis test's results where the null hypothesis is that no relationship exists between X and Y. The alternative hypothesis is that a linear relationship exists between X and Y.

If you are using a significance level (or alpha level) of 0.05, you would reject the null hypothesis if the p-value is less than or equal to 0.05. You would fail to reject the null hypothesis if your p-value is greater than 0.05.

What are correlations?

A correlation is a measure of the relationship between two variables.

Positive Correlations - If two variables, X and Y, have a positive linear correlation, Y tends to increase as X increases, and Y tends to decrease as X decreases. In other words, the two variables tend to move together in the same direction.

Negative Correlations - Two variables, X and Y, have a negative correlation if Y tends to increase as X decreases and Y tends to decrease as X increases. (i.e., The values of the two variables tend to move in opposite directions).

What’s the difference between the dependent and independent variables in a regression?

A simple linear regression involves two variables: X, the input or independent variable, and Y, the output or dependent variable. The independent variable is the variable you want to estimate using the regression. Its estimated value “depends” on the parameters and other variables of the model.

The independent variable—also called the predictor variable—is an input in the model. Its value does not depend on the other elements of the model.

Is the correlation coefficient the same as the regression coefficient?

The correlation coefficient and the regression coefficient will both have the same sign (positive or negative), but they are not the same. The only case where these two values will be equal is when the values of X and Y have been standardized to the same scale.

What is a correlation coefficient?

A correlation coefficient—or Pearson’s correlation coefficient —measures the strength of the linear relationship between X and Y. It’s a number ranging between -1 and 1. The closer a coefficient correlation is to 0, the weaker the correlation is between X and Y.

The closer the correlation coefficient is to 1 or -1, the stronger the correlation. Points on a scatter plot will be more dispersed around the regression line when the correlation between X and Y is weak, and the points will be more tightly clustered around the regression line when the correlation is strong.

What is the regression coefficient?

The regression coefficient, β 1 \beta_1 β 1 ​ , is the slope of the regression line. It provides you with an estimate of how much the dependent variable, Y, will change in response to a 1-unit increase in the dependent variable, X.

The regression coefficient can be any number from − ∞ -\infty − ∞ to ∞ \infty ∞ . A positive regression coefficient implies a positive correlation between X and Y, and a negative regression coefficient implies a negative correlation.

Can I use linear regression in Excel?

Yes. The easiest way to add a simple linear regression line in Excel is to install and use Excel’s “Analysis Toolpak” add-in. To do this, go to Tools > Excel Add-ins and select the “Analysis Toolpak.”

Next, follow these steps.

In your spreadsheet, enter your data for X and Y in two columns

Navigate to the “Data” tab and click on the “Data Analysis” icon

From the list of analysis tools, select “Regression” and click “OK”

Select the data for Y and X respectively where it says “Input Y Range” and “Input X Range”

If you’ve labeled your columns with the names of your X and Y variables, click on the “Labels” checkbox.

You can further customize where you want your regression in your workbook and what additional information you would like Excel to display.

Once you’ve finished customizing, click “OK”

Your regression results will display next to your data or in a new sheet.

Is linear regression used to establish causal relationships?

Correlations are not equivalent to causation. If two variables are correlated, you cannot immediately conclude ‌one causes the other to change. A linear regression will immediately indicate whether two variables correlate. But you’ll need to include more variables in your model and use regression with causal theories to draw conclusions about causal relationships.

What are some other types of regression analysis?

Simple linear regression is the most basic form of regression analysis. It involves ‌one independent variable and one dependent variable. Once you get a handle on this model, you can move on to more sophisticated forms of regression analysis. These include multiple linear regression and nonlinear regression.

Multiple linear regression is a model that estimates the linear relationship between variables using one dependent variable and multiple predictor variables. Nonlinear regression is a method used to estimate nonlinear relationships between variables.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Intro to Microeconomics

Why small choices have big impact.

Intro to Macroeconomics

How money moves our world.

Intro to Psychology

The science of the mind.

Related Articles

Calculating Logarithmic Regression Step-By-Step

Learn about logarithmic regression and the steps to calculate it. We’ll also break down what a logarithmic function is, why it’s useful, and a few examples.

What Is the Interquartile Range (IQR)?

Learn what the interquartile range is, why it’s used in Statistics and how to calculate it. Also read about how it can be helpful for finding outliers.

Calculate Outlier Formula: A Step-By-Step Guide

This article is an overview of the outlier formula and how to calculate it step by step. It’s also packed with examples and FAQs to help you understand it.

Further Reading

What is statistical significance & why learn it, mean absolute deviation (mad) - meaning & formula, discrete & continuous variables with examples, population vs. sample: the big difference, why is statistics important, how to make a box plot.

Root out friction in every digital experience, super-charge conversion rates, and optimize digital self-service

Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve

Increase revenue and loyalty with real-time insights and recommendations delivered to teams on the ground

Know how your people feel and empower managers to improve employee engagement, productivity, and retention

Take action in the moments that matter most along the employee journey and drive bottom line growth

Whatever they’re are saying, wherever they’re saying it, know exactly what’s going on with your people

Get faster, richer insights with qual and quant tools that make powerful market research available to everyone

Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts

Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market

Explore the platform powering Experience Management

• Free Account
• For Digital
• For Customer Care
• For Human Resources
• For Researchers
• Financial Services
• All Industries

Popular Use Cases

• Customer Experience
• Employee Experience
• Employee Exit Interviews
• Net Promoter Score
• Voice of Customer
• Customer Success Hub
• Product Documentation
• Training & Certification
• XM Institute
• Popular Resources
• Customer Stories
• Market Research
• Artificial Intelligence
• Partnerships
• Marketplace

The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results, live in Salt Lake City.

• English/AU & NZ
• Español/Europa
• Español/América Latina
• Português Brasileiro
• REQUEST DEMO
• Experience Management
• Survey Data Analysis & Reporting
• Regression Analysis

Try Qualtrics for free

The complete guide to regression analysis.

19 min read What is regression analysis and why is it useful? While most of us have heard the term, understanding regression analysis in detail may be something you need to brush up on. Here’s what you need to know about this popular method of analysis.

When you rely on data to drive and guide business decisions, as well as predict market trends, just gathering and analyzing what you find isn’t enough — you need to ensure it’s relevant and valuable.

The challenge, however, is that so many variables can influence business data: market conditions, economic disruption, even the weather! As such, it’s essential you know which variables are affecting your data and forecasts, and what data you can discard.

And one of the most effective ways to determine data value and monitor trends (and the relationships between them) is to use regression analysis, a set of statistical methods used for the estimation of relationships between independent and dependent variables.

In this guide, we’ll cover the fundamentals of regression analysis, from what it is and how it works to its benefits and practical applications.

Free eBook: 2024 global market research trends report

What is regression analysis?

Regression analysis is a statistical method. It’s used for analyzing different factors that might influence an objective – such as the success of a product launch, business growth, a new marketing campaign – and determining which factors are important and which ones can be ignored.

Regression analysis can also help leaders understand how different variables impact each other and what the outcomes are. For example, when forecasting financial performance, regression analysis can help leaders determine how changes in the business can influence revenue or expenses in the future.

Running an analysis of this kind, you might find that there’s a high correlation between the number of marketers employed by the company, the leads generated, and the opportunities closed.

This seems to suggest that a high number of marketers and a high number of leads generated influences sales success. But do you need both factors to close those sales? By analyzing the effects of these variables on your outcome,  you might learn that when leads increase but the number of marketers employed stays constant, there is no impact on the number of opportunities closed, but if the number of marketers increases, leads and closed opportunities both rise.

Regression analysis can help you tease out these complex relationships so you can determine which areas you need to focus on in order to get your desired results, and avoid wasting time with those that have little or no impact. In this example, that might mean hiring more marketers rather than trying to increase leads generated.

How does regression analysis work?

Regression analysis starts with variables that are categorized into two types: dependent and independent variables. The variables you select depend on the outcomes you’re analyzing.

Understanding variables:

1. dependent variable.

This is the main variable that you want to analyze and predict. For example, operational (O) data such as your quarterly or annual sales, or experience (X) data such as your net promoter score (NPS) or customer satisfaction score (CSAT) .

These variables are also called response variables, outcome variables, or left-hand-side variables (because they appear on the left-hand side of a regression equation).

There are three easy ways to identify them:

• Is the variable measured as an outcome of the study?
• Does the variable depend on another in the study?
• Do you measure the variable only after other variables are altered?

2. Independent variable

Independent variables are the factors that could affect your dependent variables. For example, a price rise in the second quarter could make an impact on your sales figures.

You can identify independent variables with the following list of questions:

• Is the variable manipulated, controlled, or used as a subject grouping method by the researcher?
• Does this variable come before the other variable in time?
• Are you trying to understand whether or how this variable affects another?

Independent variables are often referred to differently in regression depending on the purpose of the analysis. You might hear them called:

Explanatory variables

Explanatory variables are those which explain an event or an outcome in your study. For example, explaining why your sales dropped or increased.

Predictor variables

Predictor variables are used to predict the value of the dependent variable. For example, predicting how much sales will increase when new product features are rolled out .

Experimental variables

These are variables that can be manipulated or changed directly by researchers to assess the impact. For example, assessing how different product pricing ($10 vs $15 vs $20) will impact the likelihood to purchase.

Subject variables (also called fixed effects)

Subject variables can’t be changed directly, but vary across the sample. For example, age, gender, or income of consumers.

Unlike experimental variables, you can’t randomly assign or change subject variables, but you can design your regression analysis to determine the different outcomes of groups of participants with the same characteristics. For example, ‘how do price rises impact sales based on income?’

Carrying out regression analysis

So regression is about the relationships between dependent and independent variables. But how exactly do you do it?

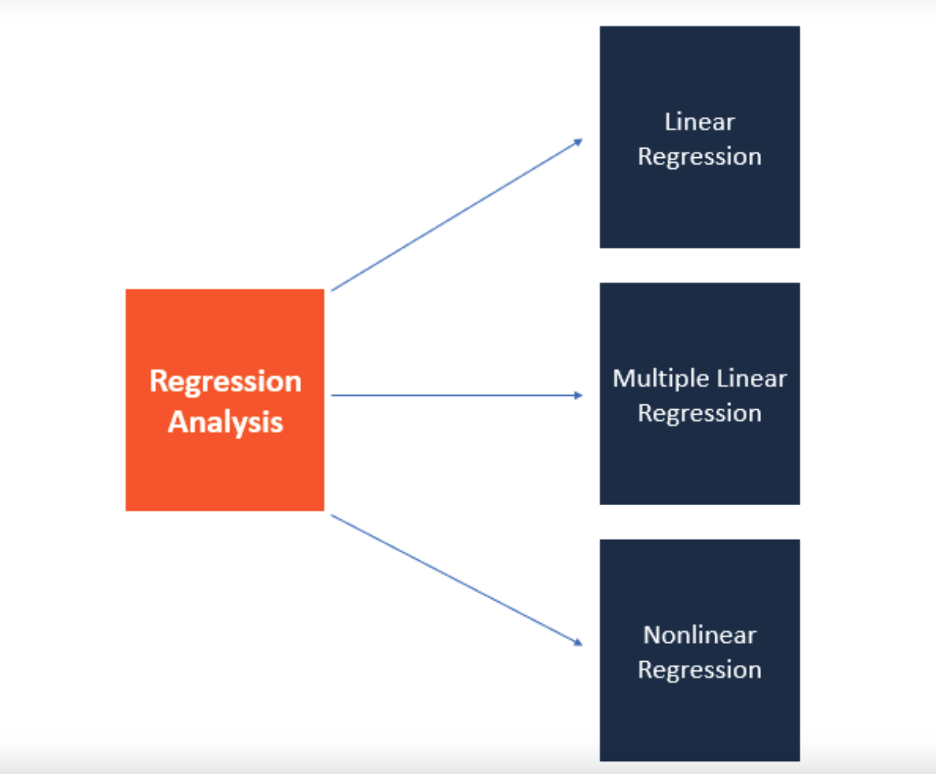
Assuming you have your data collection done already, the first and foremost thing you need to do is plot your results on a graph. Doing this makes interpreting regression analysis results much easier as you can clearly see the correlations between dependent and independent variables.

Let’s say you want to carry out a regression analysis to understand the relationship between the number of ads placed and revenue generated.

On the Y-axis, you place the revenue generated. On the X-axis, the number of digital ads. By plotting the information on the graph, and drawing a line (called the regression line) through the middle of the data, you can see the relationship between the number of digital ads placed and revenue generated.

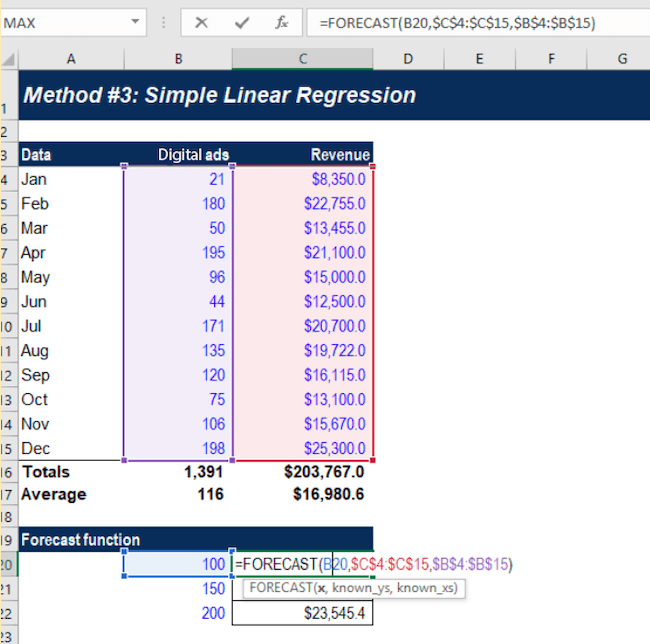
This regression line is the line that provides the best description of the relationship between your independent variables and your dependent variable. In this example, we’ve used a simple linear regression model.

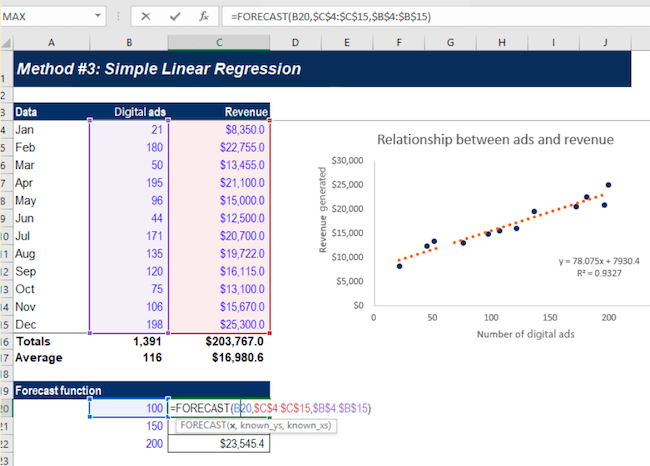
Statistical analysis software can draw this line for you and precisely calculate the regression line. The software then provides a formula for the slope of the line, adding further context to the relationship between your dependent and independent variables.

Simple linear regression analysis

A simple linear model uses a single straight line to determine the relationship between a single independent variable and a dependent variable.

This regression model is mostly used when you want to determine the relationship between two variables (like price increases and sales) or the value of the dependent variable at certain points of the independent variable (for example the sales levels at a certain price rise).

While linear regression is useful, it does require you to make some assumptions.

For example, it requires you to assume that:

• the data was collected using a statistically valid sample collection method that is representative of the target population
• The observed relationship between the variables can’t be explained by a ‘hidden’ third variable – in other words, there are no spurious correlations.
• the relationship between the independent variable and dependent variable is linear – meaning that the best fit along the data points is a straight line and not a curved one

Multiple regression analysis

As the name suggests, multiple regression analysis is a type of regression that uses multiple variables. It uses multiple independent variables to predict the outcome of a single dependent variable. Of the various kinds of multiple regression, multiple linear regression is one of the best-known.

Multiple linear regression is a close relative of the simple linear regression model in that it looks at the impact of several independent variables on one dependent variable. However, like simple linear regression, multiple regression analysis also requires you to make some basic assumptions.

For example, you will be assuming that:

• there is a linear relationship between the dependent and independent variables (it creates a straight line and not a curve through the data points)
• the independent variables aren’t highly correlated in their own right

An example of multiple linear regression would be an analysis of how marketing spend, revenue growth, and general market sentiment affect the share price of a company.

With multiple linear regression models you can estimate how these variables will influence the share price, and to what extent.

Multivariate linear regression

Multivariate linear regression involves more than one dependent variable as well as multiple independent variables, making it more complicated than linear or multiple linear regressions. However, this also makes it much more powerful and capable of making predictions about complex real-world situations.

For example, if an organization wants to establish or estimate how the COVID-19 pandemic has affected employees in its different markets, it can use multivariate linear regression, with the different geographical regions as dependent variables and the different facets of the pandemic as independent variables (such as mental health self-rating scores, proportion of employees working at home, lockdown durations and employee sick days).

Through multivariate linear regression, you can look at relationships between variables in a holistic way and quantify the relationships between them. As you can clearly visualize those relationships, you can make adjustments to dependent and independent variables to see which conditions influence them. Overall, multivariate linear regression provides a more realistic picture than looking at a single variable.

However, because multivariate techniques are complex, they involve high-level mathematics that require a statistical program to analyze the data.

Logistic regression

Logistic regression models the probability of a binary outcome based on independent variables.

So, what is a binary outcome? It’s when there are only two possible scenarios, either the event happens (1) or it doesn’t (0). e.g. yes/no outcomes, pass/fail outcomes, and so on. In other words, if the outcome can be described as being in either one of two categories.

Logistic regression makes predictions based on independent variables that are assumed or known to have an influence on the outcome. For example, the probability of a sports team winning their game might be affected by independent variables like weather, day of the week, whether they are playing at home or away and how they fared in previous matches.

What are some common mistakes with regression analysis?

Across the globe, businesses are increasingly relying on quality data and insights to drive decision-making — but to make accurate decisions, it’s important that the data collected and statistical methods used to analyze it are reliable and accurate.

Using the wrong data or the wrong assumptions can result in poor decision-making, lead to missed opportunities to improve efficiency and savings, and — ultimately — damage your business long term.

• Assumptions

When running regression analysis, be it a simple linear or multiple regression, it’s really important to check that the assumptions your chosen method requires have been met. If your data points don’t conform to a straight line of best fit, for example, you need to apply additional statistical modifications to accommodate the non-linear data. For example, if you are looking at income data, which scales on a logarithmic distribution, you should take the Natural Log of Income as your variable then adjust the outcome after the model is created.

• Correlation vs. causation

It’s a well-worn phrase that bears repeating – correlation does not equal causation. While variables that are linked by causality will always show correlation, the reverse is not always true. Moreover, there is no statistic that can determine causality (although the design of your study overall can).

If you observe a correlation in your results, such as in the first example we gave in this article where there was a correlation between leads and sales, you can’t assume that one thing has influenced the other. Instead, you should use it as a starting point for investigating the relationship between the variables in more depth.

• Choosing the wrong variables to analyze

Before you use any kind of statistical method, it’s important to understand the subject you’re researching in detail. Doing so means you’re making informed choices of variables and you’re not overlooking something important that might have a significant bearing on your dependent variable.

• Model building The variables you include in your analysis are just as important as the variables you choose to exclude. That’s because the strength of each independent variable is influenced by the other variables in the model. Other techniques, such as Key Drivers Analysis, are able to account for these variable interdependencies.

Benefits of using regression analysis

There are several benefits to using regression analysis to judge how changing variables will affect your business and to ensure you focus on the right things when forecasting.

Here are just a few of those benefits:

Make accurate predictions

Regression analysis is commonly used when forecasting and forward planning for a business. For example, when predicting sales for the year ahead, a number of different variables will come into play to determine the eventual result.

Regression analysis can help you determine which of these variables are likely to have the biggest impact based on previous events and help you make more accurate forecasts and predictions.

Identify inefficiencies

Using a regression equation a business can identify areas for improvement when it comes to efficiency, either in terms of people, processes, or equipment.

For example, regression analysis can help a car manufacturer determine order numbers based on external factors like the economy or environment.

Using the initial regression equation, they can use it to determine how many members of staff and how much equipment they need to meet orders.

Drive better decisions

Improving processes or business outcomes is always on the minds of owners and business leaders, but without actionable data, they’re simply relying on instinct, and this doesn’t always work out.

This is particularly true when it comes to issues of price. For example, to what extent will raising the price (and to what level) affect next quarter’s sales?

There’s no way to know this without data analysis. Regression analysis can help provide insights into the correlation between price rises and sales based on historical data.

How do businesses use regression? A real-life example

Marketing and advertising spending are common topics for regression analysis. Companies use regression when trying to assess the value of ad spend and marketing spend on revenue.

A typical example is using a regression equation to assess the correlation between ad costs and conversions of new customers. In this instance,

• our dependent variable (the factor we’re trying to assess the outcomes of) will be our conversions
• the independent variable (the factor we’ll change to assess how it changes the outcome) will be the daily ad spend
• the regression equation will try to determine whether an increase in ad spend has a direct correlation with the number of conversions we have

The analysis is relatively straightforward — using historical data from an ad account, we can use daily data to judge ad spend vs conversions and how changes to the spend alter the conversions.

By assessing this data over time, we can make predictions not only on whether increasing ad spend will lead to increased conversions but also what level of spending will lead to what increase in conversions. This can help to optimize campaign spend and ensure marketing delivers good ROI.

This is an example of a simple linear model. If you wanted to carry out a more complex regression equation, we could also factor in other independent variables such as seasonality, GDP, and the current reach of our chosen advertising networks.

By increasing the number of independent variables, we can get a better understanding of whether ad spend is resulting in an increase in conversions, whether it’s exerting an influence in combination with another set of variables, or if we’re dealing with a correlation with no causal impact – which might be useful for predictions anyway, but isn’t a lever we can use to increase sales.

Using this predicted value of each independent variable, we can more accurately predict how spend will change the conversion rate of advertising.

Regression analysis tools

Regression analysis is an important tool when it comes to better decision-making and improved business outcomes. To get the best out of it, you need to invest in the right kind of statistical analysis software.

The best option is likely to be one that sits at the intersection of powerful statistical analysis and intuitive ease of use, as this will empower everyone from beginners to expert analysts to uncover meaning from data, identify hidden trends and produce predictive models without statistical training being required.

To help prevent costly errors, choose a tool that automatically runs the right statistical tests and visualizations and then translates the results into simple language that anyone can put into action.

With software that’s both powerful and user-friendly, you can isolate key experience drivers, understand what influences the business, apply the most appropriate regression methods, identify data issues, and much more.

With Qualtrics’ Stats iQ™, you don’t have to worry about the regression equation because our statistical software will run the appropriate equation for you automatically based on the variable type you want to monitor. You can also use several equations, including linear regression and logistic regression, to gain deeper insights into business outcomes and make more accurate, data-driven decisions.

Related resources

Analysis & Reporting

Data Analysis 31 min read

Social media analytics 13 min read, kano analysis 21 min read, margin of error 11 min read, data saturation in qualitative research 8 min read, thematic analysis 11 min read, behavioral analytics 12 min read, request demo.

Ready to learn more about Qualtrics?

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

Lesson 1: simple linear regression, overview section  .

Simple linear regression is a statistical method that allows us to summarize and study relationships between two continuous (quantitative) variables. This lesson introduces the concept and basic procedures of simple linear regression.

• Distinguish between a deterministic relationship and a statistical relationship.
• Understand the concept of the least squares criterion.
• Interpret the intercept \(b_{0}\) and slope \(b_{1}\) of an estimated regression equation.
• Know how to obtain the estimates \(b_{0}\) and \(b_{1}\) from Minitab's fitted line plot and regression analysis output.
• Recognize the distinction between a population regression line and the estimated regression line.
• Summarize the four conditions that comprise the simple linear regression model.
• Know what the unknown population variance \(\sigma^{2}\) quantifies in the regression setting.
• Know how to obtain the estimated MSE of the unknown population variance \(\sigma^{2 }\) from Minitab's fitted line plot and regression analysis output.
• Know that the coefficient of determination (\(R^2\)) and the correlation coefficient (r) are measures of linear association. That is, they can be 0 even if there is a perfect nonlinear association.
• Know how to interpret the \(R^2\) value.
• Understand the cautions necessary in using the \(R^2\) value as a way of assessing the strength of the linear association.
• Know how to calculate the correlation coefficient r from the \(R^2\) value.
• Know what various correlation coefficient values mean. There is no meaningful interpretation for the correlation coefficient as there is for the \(R^2\) value.

Lesson 1 Code Files Section  

STAT501_Lesson01.zip

• bldgstories.txt
• carstopping.txt
• drugdea.txt
• fev_dat.txt
• heightgpa.txt
• husbandwife.txt
• oldfaithful.txt
• poverty.txt
• practical.txt
• signdist.txt
• skincancer.txt
• student_height_weight.txt

• Skip to main content
• Skip to primary sidebar
• Skip to footer
• QuestionPro

• Solutions Industries Gaming Automotive Sports and events Education Government Travel & Hospitality Financial Services Healthcare Cannabis Technology Use Case NPS+ Communities Audience Contactless surveys Mobile LivePolls Member Experience GDPR Positive People Science 360 Feedback Surveys
• Resources Blog eBooks Survey Templates Case Studies Training Help center

Home Market Research

Regression Analysis: Definition, Types, Usage & Advantages

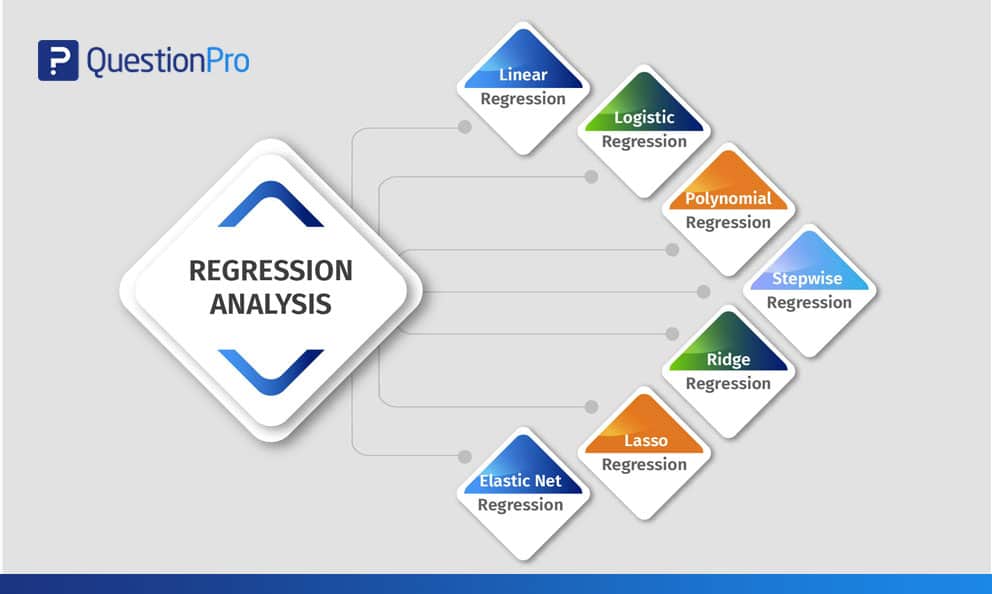
Regression analysis is perhaps one of the most widely used statistical methods for investigating or estimating the relationship between a set of independent and dependent variables. In statistical analysis , distinguishing between categorical data and numerical data is essential, as categorical data involves distinct categories or labels, while numerical data consists of measurable quantities.

It is also used as a blanket term for various data analysis techniques utilized in a qualitative research method for modeling and analyzing numerous variables. In the regression method, the dependent variable is a predictor or an explanatory element, and the dependent variable is the outcome or a response to a specific query.

LEARN ABOUT:   Statistical Analysis Methods

Content Index

Definition of Regression Analysis

Types of regression analysis, regression analysis usage in market research, how regression analysis derives insights from surveys, advantages of using regression analysis in an online survey.

Regression analysis is often used to model or analyze data. Most survey analysts use it to understand the relationship between the variables, which can be further utilized to predict the precise outcome.

For Example – Suppose a soft drink company wants to expand its manufacturing unit to a newer location. Before moving forward, the company wants to analyze its revenue generation model and the various factors that might impact it. Hence, the company conducts an online survey with a specific questionnaire.

After using regression analysis, it becomes easier for the company to analyze the survey results and understand the relationship between different variables like electricity and revenue – here, revenue is the dependent variable.

LEARN ABOUT: Level of Analysis

In addition, understanding the relationship between different independent variables like pricing, number of workers, and logistics with the revenue helps the company estimate the impact of varied factors on sales and profits.

Survey researchers often use this technique to examine and find a correlation between different variables of interest. It provides an opportunity to gauge the influence of different independent variables on a dependent variable.

Overall, regression analysis saves the survey researchers’ additional efforts in arranging several independent variables in tables and testing or calculating their effect on a dependent variable. Different types of analytical research methods are widely used to evaluate new business ideas and make informed decisions.

Create a Free Account

Researchers usually start by learning linear and logistic regression first. Due to the widespread knowledge of these two methods and ease of application, many analysts think there are only two types of models. Each model has its own specialty and ability to perform if specific conditions are met.

This blog explains the commonly used seven types of multiple regression analysis methods that can be used to interpret the enumerated data in various formats.

01. Linear Regression Analysis

It is one of the most widely known modeling techniques, as it is amongst the first elite regression analysis methods picked up by people at the time of learning predictive modeling. Here, the dependent variable is continuous, and the independent variable is more often continuous or discreet with a linear regression line.

Please note that multiple linear regression has more than one independent variable than simple linear regression. Thus, linear regression is best to be used only when there is a linear relationship between the independent and a dependent variable.

A business can use linear regression to measure the effectiveness of the marketing campaigns, pricing, and promotions on sales of a product. Suppose a company selling sports equipment wants to understand if the funds they have invested in the marketing and branding of their products have given them substantial returns or not.

Linear regression is the best statistical method to interpret the results. The best thing about linear regression is it also helps in analyzing the obscure impact of each marketing and branding activity, yet controlling the constituent’s potential to regulate the sales.

If the company is running two or more advertising campaigns simultaneously, one on television and two on radio, then linear regression can easily analyze the independent and combined influence of running these advertisements together.

LEARN ABOUT: Data Analytics Projects

02. Logistic Regression Analysis

Logistic regression is commonly used to determine the probability of event success and event failure. Logistic regression is used whenever the dependent variable is binary, like 0/1, True/False, or Yes/No. Thus, it can be said that logistic regression is used to analyze either the close-ended questions in a survey or the questions demanding numeric responses in a survey.

Please note logistic regression does not need a linear relationship between a dependent and an independent variable, just like linear regression. Logistic regression applies a non-linear log transformation for predicting the odds ratio; therefore, it easily handles various types of relationships between a dependent and an independent variable.

Logistic regression is widely used to analyze categorical data, particularly for binary response data in business data modeling. More often, logistic regression is used when the dependent variable is categorical, like to predict whether the health claim made by a person is real(1) or fraudulent, to understand if the tumor is malignant(1) or not.

Businesses use logistic regression to predict whether the consumers in a particular demographic will purchase their product or will buy from the competitors based on age, income, gender, race, state of residence, previous purchase, etc.

03. Polynomial Regression Analysis

Polynomial regression is commonly used to analyze curvilinear data when an independent variable’s power is more than 1. In this regression analysis method, the best-fit line is never a ‘straight line’ but always a ‘curve line’ fitting into the data points.

Please note that polynomial regression is better to use when two or more variables have exponents and a few do not.

Additionally, it can model non-linearly separable data offering the liberty to choose the exact exponent for each variable, and that too with full control over the modeling features available.

When combined with response surface analysis, polynomial regression is considered one of the sophisticated statistical methods commonly used in multisource feedback research. Polynomial regression is used mostly in finance and insurance-related industries where the relationship between dependent and independent variables is curvilinear.

Suppose a person wants to budget expense planning by determining how long it would take to earn a definitive sum. Polynomial regression, by taking into account his/her income and predicting expenses, can easily determine the precise time he/she needs to work to earn that specific sum amount.

04. Stepwise Regression Analysis

This is a semi-automated process with which a statistical model is built either by adding or removing the dependent variable on the t-statistics of their estimated coefficients.

If used properly, the stepwise regression will provide you with more powerful data at your fingertips than any method. It works well when you are working with a large number of independent variables. It just fine-tunes the unit of analysis model by poking variables randomly.

Stepwise regression analysis is recommended to be used when there are multiple independent variables, wherein the selection of independent variables is done automatically without human intervention.

Please note, in stepwise regression modeling, the variable is added or subtracted from the set of explanatory variables. The set of added or removed variables is chosen depending on the test statistics of the estimated coefficient.

Suppose you have a set of independent variables like age, weight, body surface area, duration of hypertension, basal pulse, and stress index based on which you want to analyze its impact on the blood pressure.

In stepwise regression, the best subset of the independent variable is automatically chosen; it either starts by choosing no variable to proceed further (as it adds one variable at a time) or starts with all variables in the model and proceeds backward (removes one variable at a time).

Thus, using regression analysis, you can calculate the impact of each or a group of variables on blood pressure.

05. Ridge Regression Analysis

Ridge regression is based on an ordinary least square method which is used to analyze multicollinearity data (data where independent variables are highly correlated). Collinearity can be explained as a near-linear relationship between variables.

Whenever there is multicollinearity, the estimates of least squares will be unbiased, but if the difference between them is larger, then it may be far away from the true value. However, ridge regression eliminates the standard errors by appending some degree of bias to the regression estimates with a motive to provide more reliable estimates.

If you want, you can also learn about Selection Bias through our blog.

Please note, Assumptions derived through the ridge regression are similar to the least squared regression, the only difference being the normality. Although the value of the coefficient is constricted in the ridge regression, it never reaches zero suggesting the inability to select variables.

Suppose you are crazy about two guitarists performing live at an event near you, and you go to watch their performance with a motive to find out who is a better guitarist. But when the performance starts, you notice that both are playing black-and-blue notes at the same time.

Is it possible to find out the best guitarist having the biggest impact on sound among them when they are both playing loud and fast? As both of them are playing different notes, it is substantially difficult to differentiate them, making it the best case of multicollinearity, which tends to increase the standard errors of the coefficients.

Ridge regression addresses multicollinearity in cases like these and includes bias or a shrinkage estimation to derive results.

06. Lasso Regression Analysis

Lasso (Least Absolute Shrinkage and Selection Operator) is similar to ridge regression; however, it uses an absolute value bias instead of the square bias used in ridge regression.

It was developed way back in 1989 as an alternative to the traditional least-squares estimate with the intention to deduce the majority of problems related to overfitting when the data has a large number of independent variables.

Lasso has the capability to perform both – selecting variables and regularizing them along with a soft threshold. Applying lasso regression makes it easier to derive a subset of predictors from minimizing prediction errors while analyzing a quantitative response.

Please note that regression coefficients reaching zero value after shrinkage are excluded from the lasso model. On the contrary, regression coefficients having more value than zero are strongly associated with the response variables, wherein the explanatory variables can be either quantitative, categorical, or both.

Suppose an automobile company wants to perform a research analysis on average fuel consumption by cars in the US. For samples, they chose 32 models of car and 10 features of automobile design – Number of cylinders, Displacement, Gross horsepower, Rear axle ratio, Weight, ¼ mile time, v/s engine, transmission, number of gears, and number of carburetors.

As you can see a correlation between the response variable mpg (miles per gallon) is extremely correlated to some variables like weight, displacement, number of cylinders, and horsepower. The problem can be analyzed by using the glmnet package in R and lasso regression for feature selection.

07. Elastic Net Regression Analysis

It is a mixture of ridge and lasso regression models trained with L1 and L2 norms. The elastic net brings about a grouping effect wherein strongly correlated predictors tend to be in/out of the model together. Using the elastic net regression model is recommended when the number of predictors is far greater than the number of observations.

Please note that the elastic net regression model came into existence as an option to the lasso regression model as lasso’s variable section was too much dependent on data, making it unstable. By using elastic net regression, statisticians became capable of over-bridging the penalties of ridge and lasso regression only to get the best out of both models.

A clinical research team having access to a microarray data set on leukemia (LEU) was interested in constructing a diagnostic rule based on the expression level of presented gene samples for predicting the type of leukemia. The data set they had, consisted of a large number of genes and a few samples.

Apart from that, they were given a specific set of samples to be used as training samples, out of which some were infected with type 1 leukemia (acute lymphoblastic leukemia) and some with type 2 leukemia (acute myeloid leukemia).

Model fitting and tuning parameter selection by tenfold CV were carried out on the training data. Then they compared the performance of those methods by computing their prediction mean-squared error on the test data to get the necessary results.

A market research survey focuses on three major matrices; Customer Satisfaction , Customer Loyalty , and Customer Advocacy . Remember, although these matrices tell us about customer health and intentions, they fail to tell us ways of improving the position. Therefore, an in-depth survey questionnaire intended to ask consumers the reason behind their dissatisfaction is definitely a way to gain practical insights.

However, it has been found that people often struggle to put forth their motivation or demotivation or describe their satisfaction or dissatisfaction. In addition to that, people always give undue importance to some rational factors, such as price, packaging, etc. Overall, it acts as a predictive analytic and forecasting tool in market research.

When used as a forecasting tool, regression analysis can determine an organization’s sales figures by taking into account external market data. A multinational company conducts a market research survey to understand the impact of various factors such as GDP (Gross Domestic Product), CPI (Consumer Price Index), and other similar factors on its revenue generation model.

Obviously, regression analysis in consideration of forecasted marketing indicators was used to predict a tentative revenue that will be generated in future quarters and even in future years. However, the more forward you go in the future, the data will become more unreliable, leaving a wide margin of error .

Case study of using regression analysis

A water purifier company wanted to understand the factors leading to brand favorability. The survey was the best medium for reaching out to existing and prospective customers. A large-scale consumer survey was planned, and a discreet questionnaire was prepared using the best survey tool .

A number of questions related to the brand, favorability, satisfaction, and probable dissatisfaction were effectively asked in the survey. After getting optimum responses to the survey, regression analysis was used to narrow down the top ten factors responsible for driving brand favorability.

All the ten attributes derived (mentioned in the image below) in one or the other way highlighted their importance in impacting the favorability of that specific water purifier brand.

It is easy to run a regression analysis using Excel or SPSS, but while doing so, the importance of four numbers in interpreting the data must be understood.

The first two numbers out of the four numbers directly relate to the regression model itself.

• F-Value: It helps in measuring the statistical significance of the survey model. Remember, an F-Value significantly less than 0.05 is considered to be more meaningful. Less than 0.05 F-Value ensures survey analysis output is not by chance.
• R-Squared: This is the value wherein the independent variables try to explain the amount of movement by dependent variables. Considering the R-Squared value is 0.7, a tested independent variable can explain 70% of the dependent variable’s movement. It means the survey analysis output we will be getting is highly predictive in nature and can be considered accurate.

The other two numbers relate to each of the independent variables while interpreting regression analysis.

• P-Value: Like F-Value, even the P-Value is statistically significant. Moreover, here it indicates how relevant and statistically significant the independent variable’s effect is. Once again, we are looking for a value of less than 0.05.
• Interpretation: The fourth number relates to the coefficient achieved after measuring the impact of variables. For instance, we test multiple independent variables to get a coefficient. It tells us, ‘by what value the dependent variable is expected to increase when independent variables (which we are considering) increase by one when all other independent variables are stagnant at the same value.

In a few cases, the simple coefficient is replaced by a standardized coefficient demonstrating the contribution from each independent variable to move or bring about a change in the dependent variable.

01. Get access to predictive analytics

Do you know utilizing regression analysis to understand the outcome of a business survey is like having the power to unveil future opportunities and risks?

For example, after seeing a particular television advertisement slot, we can predict the exact number of businesses using that data to estimate a maximum bid for that slot. The finance and insurance industry as a whole depends a lot on regression analysis of survey data to identify trends and opportunities for more accurate planning and decision-making.

02. Enhance operational efficiency

Do you know businesses use regression analysis to optimize their business processes?

For example, before launching a new product line, businesses conduct consumer surveys to better understand the impact of various factors on the product’s production, packaging, distribution, and consumption.

A data-driven foresight helps eliminate the guesswork, hypothesis, and internal politics from decision-making. A deeper understanding of the areas impacting operational efficiencies and revenues leads to better business optimization.

03. Quantitative support for decision-making

Business surveys today generate a lot of data related to finance, revenue, operation, purchases, etc., and business owners are heavily dependent on various data analysis models to make informed business decisions.

For example, regression analysis helps enterprises to make informed strategic workforce decisions. Conducting and interpreting the outcome of employee surveys like Employee Engagement Surveys, Employee Satisfaction Surveys, Employer Improvement Surveys, Employee Exit Surveys, etc., boosts the understanding of the relationship between employees and the enterprise.

It also helps get a fair idea of certain issues impacting the organization’s working culture, working environment, and productivity. Furthermore, intelligent business-oriented interpretations reduce the huge pile of raw data into actionable information to make a more informed decision.

04. Prevent mistakes from happening due to intuitions

By knowing how to use regression analysis for interpreting survey results, one can easily provide factual support to management for making informed decisions. ; but do you know that it also helps in keeping out faults in the judgment?

For example, a mall manager thinks if he extends the closing time of the mall, then it will result in more sales. Regression analysis contradicts the belief that predicting increased revenue due to increased sales won’t support the increased operating expenses arising from longer working hours.

Regression analysis is a useful statistical method for modeling and comprehending the relationships between variables. It provides numerous advantages to various data types and interactions. Researchers and analysts may gain useful insights into the factors influencing a dependent variable and use the results to make informed decisions. 

With QuestionPro Research, you can improve the efficiency and accuracy of regression analysis by streamlining the data gathering, analysis, and reporting processes. The platform’s user-friendly interface and wide range of features make it a valuable tool for researchers and analysts conducting regression analysis as part of their research projects.

Sign up for the free trial today and let your research dreams fly!

FREE TRIAL         LEARN MORE

MORE LIKE THIS

21 Best Customer Advocacy Software for Customers in 2024

Apr 19, 2024

10 Quantitative Data Analysis Software for Every Data Scientist

Apr 18, 2024

11 Best Enterprise Feedback Management Software in 2024

17 Best Online Reputation Management Software in 2024

Apr 17, 2024

Other categories

• Academic Research
• Artificial Intelligence
• Assessments
• Brand Awareness
• Case Studies
• Communities
• Consumer Insights
• Customer effort score
• Customer Engagement
• Customer Experience
• Customer Loyalty
• Customer Research
• Customer Satisfaction
• Employee Benefits
• Employee Engagement
• Employee Retention
• Friday Five
• General Data Protection Regulation
• Insights Hub
• Life@QuestionPro
• Market Research
• Mobile diaries
• Mobile Surveys
• New Features
• Online Communities
• Question Types
• Questionnaire
• QuestionPro Products
• Release Notes
• Research Tools and Apps
• Revenue at Risk
• Survey Templates
• Training Tips
• Uncategorized
• Video Learning Series
• What’s Coming Up
• Workforce Intelligence

When to Use Regression Analysis (With Examples)

Regression analysis can be used to:

• estimate the effect of an exposure on a given outcome
• predict an outcome using known factors
• balance dissimilar groups
• model and replace missing data
• detect unusual records

In the text below, we will go through these points in greater detail and provide a real-world example of each.

1. Estimate the effect of an exposure on a given outcome

Regression can model linear and non-linear associations between an exposure (or treatment) and an outcome of interest. It can also simultaneously model the relationship between more than 1 exposure and an outcome, even when these exposures interact with each other.

Example: Exploring the relationship between Body Mass Index (BMI) and all-cause mortality

De Gonzales et al. used a Cox regression model to estimate the association between BMI and mortality among 1.46 million white adults.

As expected, they found that the risk of mortality increases with progressively higher than normal levels of BMI.

The takeaway message is that regression analysis enabled them to quantify that association while adjusting for smoking, alcohol consumption, physical activity, educational level and marital status — all potential confounders of the relationship between BMI and mortality.

2. Predict an outcome using known factors

A regression model can also be used to predict things like stock prices, weather conditions, the risk of getting a disease, mortality, etc. based on a set of known predictors (also called independent variables).

Example: Predicting malaria in South Africa using seasonal climate data

Kim et al. used Poisson regression to develop a malaria prediction model using climate data such as temperature and precipitation in South Africa.

The model performed best with short-term predictions.

Anyway, the important thing to notice here is the amount of complexities that a regression model can handle. For instance in this example, the model had to be flexible enough to account for non-linear and delayed associations between malaria transmission and climate factors.

This is a recurrent theme with predictive models: We start with a simple model, then we keep adding complexities until we get a satisfying result — this is why we call it model building .

3. Balance dissimilar groups

Proving that a relationship exists between some independent variable X and an outcome Y does not mean much if this result cannot be generalized beyond your sample.

In order for your results to generalize well, the sample you’re working with has to resemble the population from which it was drawn. If it doesn’t, you can use regression to balance some important characteristics in the sample to make it representative of the population of interest.

Another case where you would want to balance dissimilar groups is in a randomized controlled trial, where the objective is to compare the outcome between the group who received the intervention and another one that serves as control/reference. But in order for the comparison to make sense, the 2 groups must have similar characteristics.

Example: Evaluating how sleep quality is affected by sleep hygiene education and behavioral therapy

Nishinoue et al. conducted a randomized controlled trial to compare sleep quality between 2 groups of participants:

• The treatment group: Participants received sleep hygiene education and behavioral therapy
• The control group: Participants received sleep hygiene education only

A generalized linear model (a generalized form of linear regression) was used to:

• Evaluate how sleep quality changed between groups
• Adjust for age, gender, job title, smoking and drinking habits, body-mass index, and mental health to make the groups more comparable

4. Model and replace missing data

Modeling missing data is an important part of data analysis, especially in cases where you have high non-response rates (so a high number of missing values) like in telephone surveys.

Before jumping into imputing missing data, first you must determine:

• How important the variables that have missing values are in your analysis
• The percentage of missing values
• If these values were missing at random or not

Based on this analysis, you can then choose to:

• Delete observations with missing values
• Replace missing data with the column’s mean or median
• Use a a regression model to replace missing data

Example: Using multiple imputation to replace missing data in a medical study

Beynon et al. studied the prognostic role of alcohol and smoking at diagnosis of head and neck cancer.

But before they built their statistical model, they noticed that 11 variables (including smoking status and alcohol intake and other covariates) had missing values, so they used a technique called MICE (Multiple Imputation by Chained Equations) which runs regression models under the hood to replace missing values.

5. Detect unusual records

Regression models alongside other statistical techniques can be used to model how “normal data” should look like, the purpose being to detect values that deviate from this norm. These are referred to as “anomalies” or “outliers” in the data.

Most applications of anomaly detection is outside the healthcare domain. It is typically used for detection of financial frauds, atypical online behavior of website visitors, detection of anomalies in machine performance in a factory, etc.

Example: Detecting critical cases of patients undergoing heart surgery

Presbitero et al. used a time-varying autoregressive model (along with other statistical measures) to flag abnormal cases of patients undergoing heart surgery using data on their blood measurements.

Their goal is to ultimately prevent patient death by allowing early intervention to take place through the use of this early warning detection algorithm.

Further reading

• Variables to Include in a Regression Model
• Understand Linear Regression Assumptions
• 7 Tricks to Get Statistically Significant p-Values
• How to Handle Missing Data in Practice: Guide for Beginners

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Dtsch Arztebl Int
• v.107(44); 2010 Nov

Linear Regression Analysis

Astrid schneider.

1 Departrment of Medical Biometrics, Epidemiology, and Computer Sciences, Johannes Gutenberg University, Mainz, Germany

Gerhard Hommel

Maria blettner.

Regression analysis is an important statistical method for the analysis of medical data. It enables the identification and characterization of relationships among multiple factors. It also enables the identification of prognostically relevant risk factors and the calculation of risk scores for individual prognostication.

This article is based on selected textbooks of statistics, a selective review of the literature, and our own experience.

After a brief introduction of the uni- and multivariable regression models, illustrative examples are given to explain what the important considerations are before a regression analysis is performed, and how the results should be interpreted. The reader should then be able to judge whether the method has been used correctly and interpret the results appropriately.

The performance and interpretation of linear regression analysis are subject to a variety of pitfalls, which are discussed here in detail. The reader is made aware of common errors of interpretation through practical examples. Both the opportunities for applying linear regression analysis and its limitations are presented.

The purpose of statistical evaluation of medical data is often to describe relationships between two variables or among several variables. For example, one would like to know not just whether patients have high blood pressure, but also whether the likelihood of having high blood pressure is influenced by factors such as age and weight. The variable to be explained (blood pressure) is called the dependent variable, or, alternatively, the response variable; the variables that explain it (age, weight) are called independent variables or predictor variables. Measures of association provide an initial impression of the extent of statistical dependence between variables. If the dependent and independent variables are continuous, as is the case for blood pressure and weight, then a correlation coefficient can be calculated as a measure of the strength of the relationship between them ( box 1 ).

Interpretation of the correlation coefficient (r)

Spearman’s coefficient:

Describes a monotone relationship

A monotone relationship is one in which the dependent variable either rises or sinks continuously as the independent variable rises.

Pearson’s correlation coefficient:

Describes a linear relationship

Interpretation/meaning:

Correlation coefficients provide information about the strength and direction of a relationship between two continuous variables. No distinction between the explaining variable and the variable to be explained is necessary:

• r = ± 1: perfect linear and monotone relationship. The closer r is to 1 or –1, the stronger the relationship.
• r = 0: no linear or monotone relationship
• r < 0: negative, inverse relationship (high values of one variable tend to occur together with low values of the other variable)
• r > 0: positive relationship (high values of one variable tend to occur together with high values of the other variable)

Graphical representation of a linear relationship:

Scatter plot with regression line

A negative relationship is represented by a falling regression line (regression coefficient b < 0), a positive one by a rising regression line (b > 0).

Regression analysis is a type of statistical evaluation that enables three things:

• Description: Relationships among the dependent variables and the independent variables can be statistically described by means of regression analysis.
• Estimation: The values of the dependent variables can be estimated from the observed values of the independent variables.
• Prognostication: Risk factors that influence the outcome can be identified, and individual prognoses can be determined.

Regression analysis employs a model that describes the relationships between the dependent variables and the independent variables in a simplified mathematical form. There may be biological reasons to expect a priori that a certain type of mathematical function will best describe such a relationship, or simple assumptions have to be made that this is the case (e.g., that blood pressure rises linearly with age). The best-known types of regression analysis are the following ( table 1 ):

• Linear regression,
• Logistic regression, and
• Cox regression.

The goal of this article is to introduce the reader to linear regression. The theory is briefly explained, and the interpretation of statistical parameters is illustrated with examples. The methods of regression analysis are comprehensively discussed in many standard textbooks ( 1 – 3 ).

Cox regression will be discussed in a later article in this journal.

Linear regression is used to study the linear relationship between a dependent variable Y (blood pressure) and one or more independent variables X (age, weight, sex).

The dependent variable Y must be continuous, while the independent variables may be either continuous (age), binary (sex), or categorical (social status). The initial judgment of a possible relationship between two continuous variables should always be made on the basis of a scatter plot (scatter graph). This type of plot will show whether the relationship is linear ( figure 1 ) or nonlinear ( figure 2 ).

A scatter plot showing a linear relationship

A scatter plot showing an exponential relationship. In this case, it would not be appropriate to compute a coefficient of determination or a regression line

Performing a linear regression makes sense only if the relationship is linear. Other methods must be used to study nonlinear relationships. The variable transformations and other, more complex techniques that can be used for this purpose will not be discussed in this article.

Univariable linear regression

Univariable linear regression studies the linear relationship between the dependent variable Y and a single independent variable X. The linear regression model describes the dependent variable with a straight line that is defined by the equation Y = a + b × X, where a is the y-intersect of the line, and b is its slope. First, the parameters a and b of the regression line are estimated from the values of the dependent variable Y and the independent variable X with the aid of statistical methods. The regression line enables one to predict the value of the dependent variable Y from that of the independent variable X. Thus, for example, after a linear regression has been performed, one would be able to estimate a person’s weight (dependent variable) from his or her height (independent variable) ( figure 3 ).

A scatter plot and the corresponding regression line and regression equation for the relationship between the dependent variable body weight (kg) and the independent variable height (m).

r = Pearsons’s correlation coefficient

R-squared linear = coefficient of determination

The slope b of the regression line is called the regression coefficient. It provides a measure of the contribution of the independent variable X toward explaining the dependent variable Y. If the independent variable is continuous (e.g., body height in centimeters), then the regression coefficient represents the change in the dependent variable (body weight in kilograms) per unit of change in the independent variable (body height in centimeters). The proper interpretation of the regression coefficient thus requires attention to the units of measurement. The following example should make this relationship clear:

In a fictitious study, data were obtained from 135 women and men aged 18 to 27. Their height ranged from 1.59 to 1.93 meters. The relationship between height and weight was studied: weight in kilograms was the dependent variable that was to be estimated from the independent variable, height in centimeters. On the basis of the data, the following regression line was determined: Y= –133.18 + 1.16 × X, where X is height in centimeters and Y is weight in kilograms. The y-intersect a = –133.18 is the value of the dependent variable when X = 0, but X cannot possibly take on the value 0 in this study (one obviously cannot expect a person of height 0 centimeters to weigh negative 133.18 kilograms). Therefore, interpretation of the constant is often not useful. In general, only values within the range of observations of the independent variables should be used in a linear regression model; prediction of the value of the dependent variable becomes increasingly inaccurate the further one goes outside this range.

The regression coefficient of 1.16 means that, in this model, a person’s weight increases by 1.16 kg with each additional centimeter of height. If height had been measured in meters, rather than in centimeters, the regression coefficient b would have been 115.91 instead. The constant a, in contrast, is independent of the unit chosen to express the independent variables. Proper interpretation thus requires that the regression coefficient should be considered together with the units of all of the involved variables. Special attention to this issue is needed when publications from different countries use different units to express the same variables (e.g., feet and inches vs. centimeters, or pounds vs. kilograms).

Figure 3 shows the regression line that represents the linear relationship between height and weight.

For a person whose height is 1.74 m, the predicted weight is 68.50 kg (y = –133.18 + 115.91 × 1.74 m). The data set contains 6 persons whose height is 1.74 m, and their weights vary from 63 to 75 kg.

Linear regression can be used to estimate the weight of any persons whose height lies within the observed range (1.59 m to 1.93 m). The data set need not include any person with this precise height. Mathematically it is possible to estimate the weight of a person whose height is outside the range of values observed in the study. However, such an extrapolation is generally not useful.

If the independent variables are categorical or binary, then the regression coefficient must be interpreted in reference to the numerical encoding of these variables. Binary variables should generally be encoded with two consecutive whole numbers (usually 0/1 or 1/2). In interpreting the regression coefficient, one should recall which category of the independent variable is represented by the higher number (e.g., 2, when the encoding is 1/2). The regression coefficient reflects the change in the dependent variable that corresponds to a change in the independent variable from 1 to 2.

For example, if one studies the relationship between sex and weight, one obtains the regression line Y = 47.64 + 14.93 × X, where X = sex (1 = female, 2 = male). The regression coefficient of 14.93 reflects the fact that men are an average of 14.93 kg heavier than women.

When categorical variables are used, the reference category should be defined first, and all other categories are to be considered in relation to this category.

The coefficient of determination, r 2 , is a measure of how well the regression model describes the observed data ( Box 2 ). In univariable regression analysis, r 2 is simply the square of Pearson’s correlation coefficient. In the particular fictitious case that is described above, the coefficient of determination for the relationship between height and weight is 0.785. This means that 78.5% of the variance in weight is due to height. The remaining 21.5% is due to individual variation and might be explained by other factors that were not taken into account in the analysis, such as eating habits, exercise, sex, or age.

Coefficient of determination (R-squared)

Definition:

• n be the number of observations (e.g., subjects in the study)
• ŷ i be the estimated value of the dependent variable for the i th observation, as computed with the regression equation
• y i be the observed value of the dependent variable for the i th observation
• y be the mean of all n observations of the dependent variable

The coefficient of determination is then defined

as follows:

In formal terms, the null hypothesis, which is the hypothesis that b = 0 (no relationship between variables, the regression coefficient is therefore 0), can be tested with a t-test. One can also compute the 95% confidence interval for the regression coefficient ( 4 ).

Multivariable linear regression

In many cases, the contribution of a single independent variable does not alone suffice to explain the dependent variable Y. If this is so, one can perform a multivariable linear regression to study the effect of multiple variables on the dependent variable.

In the multivariable regression model, the dependent variable is described as a linear function of the independent variables X i , as follows: Y = a + b1 × X1 + b2 × X 2 +…+ b n × X n . The model permits the computation of a regression coefficient b i for each independent variable X i ( box 3 ).

Regression line for a multivariable regression

Y= a + b 1 × X 1 + b 2 × X 2 + …+ b n × X n ,

Y = dependent variable

X i = independent variables

a = constant (y-intersect)

b i = regression coefficient of the variable X i

Example: regression line for a multivariable regression Y = –120.07 + 100.81 × X 1 + 0.38 × X 2 + 3.41 × X 3 ,

X 1 = height (meters)

X 2 = age (years)

X 3 = sex (1 = female, 2 = male)

Y = the weight to be estimated (kg)

Just as in univariable regression, the coefficient of determination describes the overall relationship between the independent variables X i (weight, age, body-mass index) and the dependent variable Y (blood pressure). It corresponds to the square of the multiple correlation coefficient, which is the correlation between Y and b 1 × X 1 + … + b n × X n .

It is better practice, however, to give the corrected coefficient of determination, as discussed in Box 2 . Each of the coefficients b i reflects the effect of the corresponding individual independent variable X i on Y, where the potential influences of the remaining independent variables on X i have been taken into account, i.e., eliminated by an additional computation. Thus, in a multiple regression analysis with age and sex as independent variables and weight as the dependent variable, the adjusted regression coefficient for sex represents the amount of variation in weight that is due to sex alone, after age has been taken into account. This is done by a computation that adjusts for age, so that the effect of sex is not confounded by a simultaneously operative age effect ( box 4 ).

Two important terms

• Confounder (in non-randomized studies): an independent variable that is associated, not only with the dependent variable, but also with other independent variables. The presence of confounders can distort the effect of the other independent variables. Age and sex are frequent confounders.
• Adjustment: a statistical technique to eliminate the influence of one or more confounders on the treatment effect. Example: Suppose that age is a confounding variable in a study of the effect of treatment on a certain dependent variable. Adjustment for age involves a computational procedure to mimic a situation in which the men and women in the data set were of the same age. This computation eliminates the influence of age on the treatment effect.

In this way, multivariable regression analysis permits the study of multiple independent variables at the same time, with adjustment of their regression coefficients for possible confounding effects between variables.

Multivariable analysis does more than describe a statistical relationship; it also permits individual prognostication and the evaluation of the state of health of a given patient. A linear regression model can be used, for instance, to determine the optimal values for respiratory function tests depending on a person’s age, body-mass index (BMI), and sex. Comparing a patient’s measured respiratory function with these computed optimal values yields a measure of his or her state of health.

Medical questions often involve the effect of a very large number of factors (independent variables). The goal of statistical analysis is to find out which of these factors truly have an effect on the dependent variable. The art of statistical evaluation lies in finding the variables that best explain the dependent variable.

One way to carry out a multivariable regression is to include all potentially relevant independent variables in the model (complete model). The problem with this method is that the number of observations that can practically be made is often less than the model requires. In general, the number of observations should be at least 20 times greater than the number of variables under study.

Moreover, if too many irrelevant variables are included in the model, overadjustment is likely to be the result: that is, some of the irrelevant independent variables will be found to have an apparent effect, purely by chance. The inclusion of irrelevant independent variables in the model will indeed allow a better fit with the data set under study, but, because of random effects, the findings will not generally be applicable outside of this data set ( 1 ). The inclusion of irrelevant independent variables also strongly distorts the determination coefficient, so that it no longer provides a useful index of the quality of fit between the model and the data ( Box 2 ).

In the following sections, we will discuss how these problems can be circumvented.

The selection of variables

For the regression model to be robust and to explain Y as well as possible, it should include only independent variables that explain a large portion of the variance in Y. Variable selection can be performed so that only such independent variables are included ( 1 ).

Variable selection should be carried out on the basis of medical expert knowledge and a good understanding of biometrics. This is optimally done as a collaborative effort of the physician-researcher and the statistician. There are various methods of selecting variables:

Forward selection

Forward selection is a stepwise procedure that includes variables in the model as long as they make an additional contribution toward explaining Y. This is done iteratively until there are no variables left that make any appreciable contribution to Y.

Backward selection

Backward selection, on the other hand, starts with a model that contains all potentially relevant independent variables. The variable whose removal worsens the prediction of the independent variable of the overall set of independent variables to the least extent is then removed from the model. This procedure is iterated until no dependent variables are left that can be removed without markedly worsening the prediction of the independent variable.

Stepwise selection

Stepwise selection combines certain aspects of forward and backward selection. Like forward selection, it begins with a null model, adds the single independent variable that makes the greatest contribution toward explaining the dependent variable, and then iterates the process. Additionally, a check is performed after each such step to see whether one of the variables has now become irrelevant because of its relationship to the other variables. If so, this variable is removed.

Block inclusion

There are often variables that should be included in the model in any case—for example, the effect of a certain form of treatment, or independent variables that have already been found to be relevant in prior studies. One way of taking such variables into account is their block inclusion into the model. In this way, one can combine the forced inclusion of some variables with the selective inclusion of further independent variables that turn out to be relevant to the explanation of variation in the dependent variable.

The evaluation of a regression model requires the performance of both forward and backward selection of variables. If these two procedures result in the selection of the same set of variables, then the model can be considered robust. If not, a statistician should be consulted for further advice.

The study of relationships between variables and the generation of risk scores are very important elements of medical research. The proper performance of regression analysis requires that a number of important factors should be considered and tested:

1. Causality

Before a regression analysis is performed, the causal relationships among the variables to be considered must be examined from the point of view of their content and/or temporal relationship. The fact that an independent variable turns out to be significant says nothing about causality. This is an especially relevant point with respect to observational studies ( 5 ).

2. Planning of sample size

The number of cases needed for a regression analysis depends on the number of independent variables and of their expected effects (strength of relationships). If the sample is too small, only very strong relationships will be demonstrable. The sample size can be planned in the light of the researchers’ expectations regarding the coefficient of determination (r 2 ) and the regression coefficient (b). Furthermore, at least 20 times as many observations should be made as there are independent variables to be studied; thus, if one wants to study 2 independent variables, one should make at least 40 observations.

3. Missing values

Missing values are a common problem in medical data. Whenever the value of either a dependent or an independent variable is missing, this particular observation has to be excluded from the regression analysis. If many values are missing from the dataset, the effective sample size will be appreciably diminished, and the sample may then turn out to be too small to yield significant findings, despite seemingly adequate advance planning. If this happens, real relationships can be overlooked, and the study findings may not be generally applicable. Moreover, selection effects can be expected in such cases. There are a number of ways to deal with the problem of missing values ( 6 ).

4. The data sample

A further important point to be considered is the composition of the study population. If there are subpopulations within it that behave differently with respect to the independent variables in question, then a real effect (or the lack of an effect) may be masked from the analysis and remain undetected. Suppose, for instance, that one wishes to study the effect of sex on weight, in a study population consisting half of children under age 8 and half of adults. Linear regression analysis over the entire population reveals an effect of sex on weight. If, however, a subgroup analysis is performed in which children and adults are considered separately, an effect of sex on weight is seen only in adults, and not in children. Subgroup analysis should only be performed if the subgroups have been predefined, and the questions already formulated, before the data analysis begins; furthermore, multiple testing should be taken into account ( 7 , 8 ).

5. The selection of variables

If multiple independent variables are considered in a multivariable regression, some of these may turn out to be interdependent. An independent variable that would be found to have a strong effect in a univariable regression model might not turn out to have any appreciable effect in a multivariable regression with variable selection. This will happen if this particular variable itself depends so strongly on the other independent variables that it makes no additional contribution toward explaining the dependent variable. For related reasons, when the independent variables are mutually dependent, different independent variables might end up being included in the model depending on the particular technique that is used for variable selection.

Linear regression is an important tool for statistical analysis. Its broad spectrum of uses includes relationship description, estimation, and prognostication. The technique has many applications, but it also has prerequisites and limitations that must always be considered in the interpretation of findings ( Box 5 ).

What special points require attention in the interpretation of a regression analysis?

• How big is the study sample?
• Is causality demonstrable or plausible, in view of the content or temporal relationship of the variables?
• Has there been adjustment for potential confounding effects?
• Is the inclusion of the independent variables that were used justified, in view of their content?
• What is the corrected coefficient of determination (R-squared)?
• Is the study sample homogeneous?
• In what units were the potentially relevant independent variables reported?
• Was a selection of the independent variables (potentially relevant independent variables) performed, and, if so, what kind of selection?
• If a selection of variables was performed, was its result confirmed by a second selection of variables that was performed by a different procedure?
• Are predictions of the dependent variable made on the basis of extrapolated data?

→ r 2 is the fraction of the overall variance that is explained. The closer the regression model’s estimated values ŷ i lie to the observed values y i , the nearer the coefficient of determination is to 1 and the more accurate the regression model is.

Meaning: In practice, the coefficient of determination is often taken as a measure of the validity of a regression model or a regression estimate. It reflects the fraction of variation in the Y-values that is explained by the regression line.

Problem: The coefficient of determination can easily be made artificially high by including a large number of independent variables in the model. The more independent variables one includes, the higher the coefficient of determination becomes. This, however, lowers the precision of the estimate (estimation of the regression coefficients b i ).

Solution: Instead of the raw (uncorrected) coefficient of determination, the corrected coefficient of determination should be given: the latter takes the number of explanatory variables in the model into account. Unlike the uncorrected coefficient of determination, the corrected one is high only if the independent variables have a sufficiently large effect.

Acknowledgments

Translated from the original German by Ethan Taub, MD

Conflict of interest statement

The authors declare that they have no conflict of interest as defined by the guidelines of the International Committee of Medical Journal Editors.

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

What Is Regression Analysis in Business Analytics?

• 14 Dec 2021

Countless factors impact every facet of business. How can you consider those factors and know their true impact?

Imagine you seek to understand the factors that influence people’s decision to buy your company’s product. They range from customers’ physical locations to satisfaction levels among sales representatives to your competitors' Black Friday sales.

Understanding the relationships between each factor and product sales can enable you to pinpoint areas for improvement, helping you drive more sales.

To learn how each factor influences sales, you need to use a statistical analysis method called regression analysis .

If you aren’t a business or data analyst, you may not run regressions yourself, but knowing how analysis works can provide important insight into which factors impact product sales and, thus, which are worth improving.

Access your free e-book today.

Foundational Concepts for Regression Analysis

Before diving into regression analysis, you need to build foundational knowledge of statistical concepts and relationships.

Independent and Dependent Variables

Start with the basics. What relationship are you aiming to explore? Try formatting your answer like this: “I want to understand the impact of [the independent variable] on [the dependent variable].”

The independent variable is the factor that could impact the dependent variable . For example, “I want to understand the impact of employee satisfaction on product sales.”

In this case, employee satisfaction is the independent variable, and product sales is the dependent variable. Identifying the dependent and independent variables is the first step toward regression analysis.

Correlation vs. Causation

One of the cardinal rules of statistically exploring relationships is to never assume correlation implies causation. In other words, just because two variables move in the same direction doesn’t mean one caused the other to occur.

If two or more variables are correlated , their directional movements are related. If two variables are positively correlated , it means that as one goes up or down, so does the other. Alternatively, if two variables are negatively correlated , one goes up while the other goes down.

A correlation’s strength can be quantified by calculating the correlation coefficient , sometimes represented by r . The correlation coefficient falls between negative one and positive one.

r = -1 indicates a perfect negative correlation.

r = 1 indicates a perfect positive correlation.

r = 0 indicates no correlation.

Causation means that one variable caused the other to occur. Proving a causal relationship between variables requires a true experiment with a control group (which doesn’t receive the independent variable) and an experimental group (which receives the independent variable).

While regression analysis provides insights into relationships between variables, it doesn’t prove causation. It can be tempting to assume that one variable caused the other—especially if you want it to be true—which is why you need to keep this in mind any time you run regressions or analyze relationships between variables.

With the basics under your belt, here’s a deeper explanation of regression analysis so you can leverage it to drive strategic planning and decision-making.

Related: How to Learn Business Analytics without a Business Background

What Is Regression Analysis?

Regression analysis is the statistical method used to determine the structure of a relationship between two variables (single linear regression) or three or more variables (multiple regression).

According to the Harvard Business School Online course Business Analytics , regression is used for two primary purposes:

• To study the magnitude and structure of the relationship between variables
• To forecast a variable based on its relationship with another variable

Both of these insights can inform strategic business decisions.

“Regression allows us to gain insights into the structure of that relationship and provides measures of how well the data fit that relationship,” says HBS Professor Jan Hammond, who teaches Business Analytics, one of three courses that comprise the Credential of Readiness (CORe) program . “Such insights can prove extremely valuable for analyzing historical trends and developing forecasts.”

One way to think of regression is by visualizing a scatter plot of your data with the independent variable on the X-axis and the dependent variable on the Y-axis. The regression line is the line that best fits the scatter plot data. The regression equation represents the line’s slope and the relationship between the two variables, along with an estimation of error.

Physically creating this scatter plot can be a natural starting point for parsing out the relationships between variables.

Types of Regression Analysis

There are two types of regression analysis: single variable linear regression and multiple regression.

Single variable linear regression is used to determine the relationship between two variables: the independent and dependent. The equation for a single variable linear regression looks like this:

In the equation:

• ŷ is the expected value of Y (the dependent variable) for a given value of X (the independent variable).
• x is the independent variable.
• α is the Y-intercept, the point at which the regression line intersects with the vertical axis.
• β is the slope of the regression line, or the average change in the dependent variable as the independent variable increases by one.
• ε is the error term, equal to Y – ŷ, or the difference between the actual value of the dependent variable and its expected value.

Multiple regression , on the other hand, is used to determine the relationship between three or more variables: the dependent variable and at least two independent variables. The multiple regression equation looks complex but is similar to the single variable linear regression equation:

Each component of this equation represents the same thing as in the previous equation, with the addition of the subscript k, which is the total number of independent variables being examined. For each independent variable you include in the regression, multiply the slope of the regression line by the value of the independent variable, and add it to the rest of the equation.

How to Run Regressions

You can use a host of statistical programs—such as Microsoft Excel, SPSS, and STATA—to run both single variable linear and multiple regressions. If you’re interested in hands-on practice with this skill, Business Analytics teaches learners how to create scatter plots and run regressions in Microsoft Excel, as well as make sense of the output and use it to drive business decisions.

Calculating Confidence and Accounting for Error

It’s important to note: This overview of regression analysis is introductory and doesn’t delve into calculations of confidence level, significance, variance, and error. When working in a statistical program, these calculations may be provided or require that you implement a function. When conducting regression analysis, these metrics are important for gauging how significant your results are and how much importance to place on them.

Why Use Regression Analysis?

Once you’ve generated a regression equation for a set of variables, you effectively have a roadmap for the relationship between your independent and dependent variables. If you input a specific X value into the equation, you can see the expected Y value.

This can be critical for predicting the outcome of potential changes, allowing you to ask, “What would happen if this factor changed by a specific amount?”

Returning to the earlier example, running a regression analysis could allow you to find the equation representing the relationship between employee satisfaction and product sales. You could input a higher level of employee satisfaction and see how sales might change accordingly. This information could lead to improved working conditions for employees, backed by data that shows the tie between high employee satisfaction and sales.

Whether predicting future outcomes, determining areas for improvement, or identifying relationships between seemingly unconnected variables, understanding regression analysis can enable you to craft data-driven strategies and determine the best course of action with all factors in mind.

Do you want to become a data-driven professional? Explore our eight-week Business Analytics course and our three-course Credential of Readiness (CORe) program to deepen your analytical skills and apply them to real-world business problems.

About the Author

Just one more step to your free trial.

.surveysparrow.com

Already using SurveySparrow?  Login

By clicking on "Get Started", I agree to the Privacy Policy and Terms of Service .

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Don't miss the future of CX at RefineCX USA!  Register Now

Enterprise Survey Software

Enterprise Survey Software to thrive in your business ecosystem

NPS® Software

Turn customers into promoters

Offline Survey

Real-time data collection, on the move. Go internet-independent.

360 Assessment

Conduct omnidirectional employee assessments. Increase productivity, grow together.

Reputation Management

Turn your existing customers into raving promoters by monitoring online reviews.

Ticket Management

Build loyalty and advocacy by delivering personalized support experiences that matter.

Chatbot for Website

Collect feedback smartly from your website visitors with the engaging Chatbot for website.

Swift, easy, secure. Scalable for your organization.

Executive Dashboard

Customer journey map, craft beautiful surveys, share surveys, gain rich insights, recurring surveys, white label surveys, embedded surveys, conversational forms, mobile-first surveys, audience management, smart surveys, video surveys, secure surveys, api, webhooks, integrations, survey themes, accept payments, custom workflows, all features, customer experience, employee experience, product experience, marketing experience, sales experience, hospitality & travel, market research, saas startup programs, wall of love, success stories, sparrowcast, nps® benchmarks, learning centre, apps & integrations, testimonials.

Our surveys come with superpowers ⚡

Blog Best Of

What is Regression Analysis? Definition, Types, and Examples

Kate williams.

22 January 2024

Table Of Contents

• Regression Analysis Definition
• Regression Analysis FAQs
• Regression Analysis: Importance
• Types of Regression Analysis
• Uses By Businesses
• Regression Analysis Use Cases

If you want to find data trends or predict sales based on certain variables, then regression analysis is the way to go.

In this article, we will learn about regression analysis, types of regression analysis, business applications, and its use cases. Feel free to jump to a section that’s relevant to you.

• What is the definition of regression analysis?
• Regression analysis: FAQs
• Why is regression analysis important?
• Types of regression analysis and when to use them
• How is regression analysis used by businesses
• Use cases of regression analysis

What is Regression Analysis?

Need a quick regression definition? In simple terms, regression analysis identifies the variables that have an impact on another variable .

The regression model is primarily used in finance, investing, and other areas to determine the strength and character of the relationship between one dependent variable and a series of other variables.

Regression Analysis: FAQs

Let us look at some of the most commonly asked questions about regression analysis before we head deep into understanding everything about the regression method.

1. What is multiple regression analysis meaning?

Multiple regression analysis is a statistical method that is used to predict the value of a dependent variable based on the values of two or more independent variables.

2. In regression analysis, what is the predictor variable called?

The predictor variable is the name given to an independent variable that we use in regression analysis.

The predictor variable provides information about an associated dependent variable regarding a certain outcome. At their core, predictor variables are those that are linked with particular outcomes.

3. What is a residual plot in a regression analysis?

A residual plot is a graph that shows the residuals on the vertical axis and the independent variable on the horizontal axis.

Moreover, the residual plot is a representation of how close each data point is (vertically) from the graph of the prediction equation of the regression model. If the data point is above or below the graph of the prediction equation of the model, then it is supposed to fit the data.

4. What is linear regression analysis?

Linear regression analysis is used to predict the value of a variable based on the value of another variable. The variable that you want to predict is referred to as the dependent variable. The variable that you are using to predict the other value is called the independent variable.

Please enter a valid Email ID.

14-Day Free Trial • No Credit Card Required • No Strings Attached

Why is Regression Analysis Important?

There are many business applications of regression analysis.

• For any machine learning problem which involves continuous numbers , regression analysis is essential. Some of those instances could be:
• Testing automobiles
• Weather analysis, and prediction
• Sales and promotions forecasting
• Financial forecasting
• Time series forecasting
• Regression analysis data also helps you understand whether the relationship between two different variables can give way to potential business opportunities .
• For example, if you change one variable (say delivery speed), regression analysis will tell you the kind of effect that it has on other variables (such as customer satisfaction, small value orders, etc).
• One of the best ways to solve regression issues in machine learning using a data model is through regression analysis. Plotting points on a chart, and running the best fit line , helps predict the possibility of errors.
• The insights from these patterns help businesses to see the kind of difference that it makes to their bottom line .

5 Types of Regression Analysis and When to Use Them

1. linear regression analysis.

• This type of regression analysis is one of the most basic types of regression and is used extensively in machine learning .
• Linear regression has a predictor variable and a dependent variable which is related to each linearly.
• Moreover, linear regression is used in cases where the relationship between the variables is related in a linear fashion.

Let’s say you are looking to measure the impact of email marketing on your sales. The linear analysis can be wrong as there will be aberrations. So, you should not use big data sets ( big data services ) for linear regression.

2. Logistic Regression Analysis

• If your dependent variable has discrete values , that is, if they can have only one or two values, then logistic regression SPSS is the way to go.
• The two values could be either 0 or 1, black or white, true or false, proceed or not proceed, and so on.
• To show the relationship between the target and independent variables, logistic regression uses a sigmoid curve.

This type of regression is best used when there are large data sets that have a chance of equal occurrence of values in target variables. There should not be a huge correlation between the independent variables in the dataset.

3. Lasso Regression Analysis

• Lasso regression is a regularization technique that reduces the model’s complexity.
• How does it do that? By limiting the absolute size of the regression coefficient .
• When doing so, the coefficient value becomes closer to zero. This does not happen with ridge regression.

Lass regression is advantageous as it uses feature selection – where it lets you select a set of features from the database to build your model. Since it uses only the required features, lasso regression manages to avoid overfitting.

4. Ridge Regression Analysis

• If there is a high correlation between independent variables , ridge regression is the recommended tool.
• It is also a regularization technique that reduces the complexity of the model .

Ridge regression manages to make the model less prone to overfitting by introducing a small amount of bias known as the ridge regression penalty, with the help of a bias matrix.

5. Polynomial Regression Analysis

• Polynomial regression models a non-linear dataset with the help of a linear model .
• Its working is similar to that of multiple linear regression. But it uses a non-linear curve and is mainly employed when data points are available in a non-linear fashion.
• It transforms the data points into polynomial features of a given degree and manages to model them in the form of a linear model.

Polynomial regression involves fitting the data points using a polynomial line. Since this model is susceptible to overfitting, businesses are advised to analyze the curve during the end so that they get accurate results.

While there are many more regression analysis techniques, these are the most popular ones.

How is regression analysis used by businesses?

Regression stats help businesses understand what their data points represent and how to use them with the help of business analytics techniques.

Using this regression model, you will understand how the typical value of the dependent variable changes based on how the other independent variables are held fixed.

Data professionals use this incredibly powerful statistical tool to remove unwanted variables and select the ones that are more important for the business.

Here are some uses of regression analysis:

1. Business Optimization

• The whole objective of regression analysis is to make use of the collected data and turn it into actionable insights .
• With the help of regression analysis, there won’t be any guesswork or hunches based on which decisions need to be made.
• Data-driven decision-making improves the output that the organization provides.
• Also, regression charts help organizations experiment with inputs that might not have been earlier thought of, but now that it is backed with data, the chances of success are also incredibly high.
• When there is a lot of data available, the accuracy of the insights will also be high.

2. Predictive Analytics

• For businesses that want to stay ahead of the competition, they need to be able to predict future trends. Organizations use regression analysis to understand what the future holds for them.
• To forecast trends, the data analysts predict how the dependent variables change based on the specific values given to them.
• You can use multivariate linear regression for tasks such as charting growth plans, forecasting sales volumes, predicting inventory required, and so on.
• Find out more about the area so that you can gather data from different sources
• Collect the data required for the relevant variables
• Specify and measure your regression model
• If you have a model which fits the data, then use it to come up with predictions

3. Decision-making

• For businesses to run effectively, they need to make better decisions and be aware of how each of their decisions will affect them. If they do not understand the consequences of their decisions, it can be difficult for their smooth functioning.
• Businesses need to collect information about each of their departments – sales, operations, marketing, finance, HR, expenditures, budgetary allocation, and so on. Using relevant parameters and analyzing them helps businesses improve their outcomes.
• Regression analysis helps businesses understand their data and gain insights into their operations . Business analysts use regression analysis extensively to make strategic business decisions.

4.  Understanding failures

• One of the most important things that most businesses miss doing is not reflecting on their failures.
• Without contemplating why they met with failure for a marketing campaign or why their churn rate increased in the last two years, they will never find ways to make it right.
• Regression analysis provides quantitative support to enable this kind decision-making.

5. Predicting Success

• You can use regression analysis to predict the probability of success of an organization in various aspects.
• Additionally, regression in stats analyses the data point of various sales data, including current sales data, to understand and predict the success rate in the future.

6. Risk Analysis

• When analyzing data, data analysts, sometimes, make the mistake of considering correlation and causation as the same. However, businesses should know that correlation is not causation.
• Financial organizations use regression data to assess their risk and guide them to make sound business decisions.

7. Provides New Insights

• Looking at a huge set of data will help you get new insights. But data, without analysis, is meaningless.
• With the help of regression analysis, you can find the relationship between a variety of variables to uncover patterns.
• For example, regression models might indicate that there are more returns from a particular seller. So the eCommerce company can get in touch with the seller to understand how they send their products.

Each of these issues has different solutions to them. Without regression analysis, it might have been difficult to understand exactly what was the issue in the first place.

8. Analyze marketing effectiveness

• When the company wants to know if the funds they have invested in marketing campaigns for a particular brand will give them enough ROI, then regression analysis is the way to go.
• It is possible to check the isolated impact of each of the campaigns by controlling the factors that will have an impact on the sales.
• Businesses invest in a number of marketing channels – email marketing , paid ads, Instagram influencers, etc. Regression statistics is capable of capturing the isolated ROI as well as the combined ROI of each of these companies.

7 Use Cases of Regression Analysis

1. credit card.

• Credit card companies use regression analysis to understand various user factors such as the consumer’s future behavior, prediction of credit balance, risk of customer’s credit default, etc.
• All of these data points help the company implement specific EMI options based on the results.
• This will help credit card companies take note of the risky customers.
• Simple linear regression (also called Ordinary Least Squares (OLS)) gives an overall rationale for the placing of the line of the best fit among the data points.
• One of the most common applications using the statistical model is the Capital Asset Pricing Model (CAPM) which describes the relationship between the returns and risks of investing in a security.

3. Pharmaceuticals

• Pharmaceutical companies use the process to analyze the quantitative stability data to estimate the shelf life of a product. This is because it finds the nature of the relationship between an attribute and time.
• Medical researchers use regression analysis to understand if changes in drug dosage will have an impact on the blood pressure of patients. Pharma companies leveraging best engagement platforms of HCP to increase brand awareness in the virtual space.

For example, researchers will administer different dosages of a certain drug to patients and observe changes in their blood pressure. They will fit a simple regression model where they use dosage as the predictor variable and blood pressure as the response variable.

4. Text Editing

• Logistic regression is a popular choice in a number of natural language processing (NLP) tasks s uch as text preprocessing.
• After this, you can use logistic regression to make claims about the text fragment.
• Email sorting, toxic speech detection, topic classification for questions, etc, are some of the areas where logistic regression shows great results.

5. Hospitality

• You can use regression analysis to predict the intention of users and recognize them. For example, like where do the customers want to go? What they are planning to do?
• It can even predict if the customer hasn’t typed anything in the search bar, based on how they started.
• It is not possible to build such a huge and complex system from scratch. There are already several machine learning algorithms that have accumulated data and have simple models that make such predictions possible.

6. Professional sports

• Data scientists working with professional sports teams use regression analysis to understand the effect that training regiments will have on the performance of players .
• They will find out how different types of exercises, like weightlifting sessions or Zumba sessions, affect the number of points that player scores for their team (let’s say basketball).
• Using Zumba and weightlifting as the predictor variables, and the total points scored as the response variable, they will fit the regression model.

Depending on the final values, the analysts will recommend that a player participates in more or less weightlifting or Zumba sessions to maximize their performance.

7. Agriculture

• Agricultural scientists use regression analysis t o understand the effect of different fertilizers and how it affects the yield of the crops.
• For example, the analysts might use different types of fertilizers and water on fields to understand if there is an impact on the crop’s yield.
• Based on the final results, the agriculture analysts will change the number of fertilizers and water to maximize the crop output.

Wrapping Up

Using regression analysis helps you separate the effects that involve complicated research questions. It will allow you to make informed decisions, guide you with resource allocation, and increase your bottom line by a huge margin if you use the statistical method effectively.

If you are looking for an online survey tool to gather data for your regression analysis, SurveySparrow is one of the best choices. SurveySparrow has a host of features that lets you do as much as possible with a survey tool. Get on a call with us to understand how we can help you.

Content Marketer at SurveySparrow

You Might Also Like

How hr chatbots help enhance employee onboarding, jotform vs google forms: which is best in 2024, 12 best data collection tools of 2024, cherry-picked blog posts. the best of the best..

Leave us your email, we wont spam. Promise!

Start your free trial today

No Credit Card Required. 14-Day Free Trial

Request a Demo

Want to learn more about SurveySparrow? We'll be in touch soon!

Perform Regression Analysis with a Dedicated Dashboard

Visualize and track trends in your survey data with multiple dashboards. try surveysparrow for free..

14-Day Free Trial • No Credit card required • 40% more completion rate

Hi there, we use cookies to offer you a better browsing experience and to analyze site traffic. By continuing to use our website, you consent to the use of these cookies. Learn More

Multiple Regression Analysis Example with Conceptual Framework

Data analysis using multiple regression analysis is a fairly common tool used in statistics. Many graduate students find this too complicated to understand. However, this is not that difficult to do, especially with computers as everyday household items nowadays. You can now quickly analyze more than just two sets of variables in your research using multiple regression analysis. 

How is multiple regression analysis done? This article explains this handy statistical test when dealing with many variables, then provides an example of a research using multiple regression analysis to show how it works. It explains how research using multiple regression analysis is conducted.

Multiple regression is often confused with multivariate regression. Multivariate regression, while also using several variables, deals with more than one dependent variable . Karen Grace-Martin clearly explains the difference in her post on the difference between the Multiple Regression Model and Multivariate Regression Model .

Table of Contents

Statistical software applications used in computing multiple regression analysis.

Multiple regression analysis is a powerful statistical test used to find the relationship between a given dependent variable and a set of independent variables .

Using multiple regression analysis requires a dedicated statistical software like the popular  Statistical Package for the Social Sciences (SPSS) , Statistica, Microstat, and open-source statistical software applications like SOFA statistics and Jasp, among other sophisticated statistical packages.

Two decades ago, it will be near impossible to do the calculations using the obsolete simple calculator replaced by smartphones. 

However, a standard spreadsheet application like Microsoft Excel can help you compute and model the relationship between the dependent variable and a set of predictor or independent variables. But you cannot do this without activating first the setting of statistical tools that ship with MS Excel.

Activating MS Excel

To activate the add-in for multiple regression analysis in MS Excel, you may view the two-minute Youtube tutorial below. If you already have this installed on your computer, you may proceed to the next section.

Multiple Regression Analysis Example

I will illustrate the use of multiple regression analysis by citing the actual research activity that my graduate students undertook two years ago.

The study pertains to identifying the factors predicting a current problem among high school students, the long hours they spend online for a variety of reasons. The purpose is to address many parents’ concerns about their difficulty of weaning their children away from the lures of online gaming, social networking, and other engaging virtual activities.

Review of Literature on Internet Use and Its Effect on Children

Upon reviewing the literature, the graduate students discovered that very few studies were conducted on the subject. Studies on problems associated with internet use are still in its infancy as the Internet has just begun to influence everyone’s life.

Hence, with my guidance, the group of six graduate students comprising school administrators, heads of elementary and high schools, and faculty members proceeded with the study.

Given that there is a need to use a computer to analyze multiple variable data, a principal who is nearing retirement was “forced” to buy a laptop, as she had none. Anyhow, she is very much open-minded and performed the class activities that require data analysis with much enthusiasm.

The Research on High School Students’ Use of the Internet

The brief research using multiple regression analysis is a broad study or analysis of the reasons or underlying factors that significantly relate to the number of hours devoted by high school students in using the Internet. The regression analysis is broad because it only focuses on the total number of hours devoted by high school students to activities online.

They correlated the time high school students spent online with their profile. The students’ profile comprised more than two independent variables, hence the term “multiple.” The independent variables are age, gender, relationship with the mother, and relationship with the father.

The statement of the problem in this study is:

“Is there a significant relationship between the total number of hours spent online and the students’ age, gender, relationship with their mother, and relationship with their father?”

Their parents’ relationship was gauged using a scale of 1 to 10, 1 being a poor relationship, and 10 being the best experience with parents. The figure below shows the paradigm of the study.

Notice that in research using multiple regression studies such as this, there is only one dependent variable involved. That is the total number of hours spent by high school students online.

Although many studies have identified factors that influence the use of the internet, it is standard practice to include the respondents’ profile among the set of predictor or independent variables. Hence, the standard variables age and gender are included in the multiple regression analysis.

Also, among the set of variables that may influence internet use, only the relationship between children and their parents was tested. The intention of this research using multiple regression analysis is to determine if parents spend quality time establishing strong emotional bonds between them and their children.

Findings of the Research Using Multiple Regression Analysis

What are the findings of this exploratory study? This quickly done example of a research using multiple regression analysis revealed an interesting finding.

The number of hours spent online relates significantly to the number of hours spent by a parent, specifically the mother, with her child. These two factors are inversely or negatively correlated.

The relationship means that the greater the number of hours spent by the mother with her child to establish a closer emotional bond, the fewer hours spent by her child using the internet. The number of hours spent by the children online relates significantly to the mother’s number of hours interacting with their children.

The number of hours spent by the children online relates significantly to the mother’s number of hours interacting with their children.

While this example of a research using multiple regression analysis may be a significant finding, the mother-child bond accounts for only a small percentage of the variance in total hours spent by the child online. This observation means that other factors need to be addressed to resolve long waking hours and abandonment of serious study of lessons by children.

But establishing a close bond between mother and child is a good start. Undertaking more investigations along this research concern will help strengthen the findings of this study.

The above example of a research using multiple regression analysis shows that the statistical tool is useful in predicting dependent variables’ behavior. In the above case, this is the number of hours spent by students online.

The identification of significant predictors can help determine the correct intervention to resolve the problem. Using multiple regression approaches prevents unnecessary costs for remedies that do not address an issue or a question.

Thus, this example of a research using multiple regression analysis streamlines solutions and focuses on those influential factors that must be given attention.

Once you become an expert in using multiple regression in analyzing data, you can try your hands on multivariate regression where you will deal with more than one dependent variable.

©2012 November 11 Patrick Regoniel Updated: 14 November 2020

Related Posts

Literature Review: The What, Why, Where, How, and When to Stop Writing It

What are Examples of Research Questions?

Marketing Research and Market Analysis: Definition, Goal and Objectives

About the author, patrick regoniel.

Dr. Regoniel, a faculty member of the graduate school, served as consultant to various environmental research and development projects covering issues and concerns on climate change, coral reef resources and management, economic valuation of environmental and natural resources, mining, and waste management and pollution. He has extensive experience on applied statistics, systems modelling and analysis, an avid practitioner of LaTeX, and a multidisciplinary web developer. He leverages pioneering AI-powered content creation tools to produce unique and comprehensive articles in this website.

mostly in monasteries.

Manuscript is a collective name for texts

the example is good but lacks the table of regression results. With the tables, a student could learn more on how to interpret regression results

this is so enlightening,hope it reaches most of the parents…

nice; but it is not good enough for reference

This is an action research Daniel. And I have updated it here. It can set off other studies. And please take note that blogs nowadays are already recognized sources of information. Please read my post here on why this is so: https://simplyeducate.me/wordpress_Y//2019/09/26/using-blogs-in-education/

Was this study published? It may have important implications

Dear Gabe, this study was presented by one of my students in a conference. I am just unsure if she was able to publish it in a journal.

Regression analysis for the determination of microplastics in sediments using differential scanning calorimetry

• Research Article
• Open access
• Published: 15 April 2024

Cite this article

You have full access to this open access article

• Sven Schirrmeister 1 , 3 ,
• Lucas Kurzweg 1 , 3 ,
• Xhoen Gjashta 1 ,
• Martin Socher 1 ,
• Andreas Fery 2 , 3 &
• Kathrin Harre   ORCID: orcid.org/0000-0001-8249-5606 1  

189 Accesses

Explore all metrics

This research addresses the growing need for fast and cost-efficient methods for microplastic (MP) analysis. We present a thermo-analytical method that enables the identification and quantification of different polymer types in sediment and sand composite samples based on their phase transition behavior. Differential scanning calorimetry (DSC) was performed, and the results were evaluated by using different regression models. The melting and crystallization enthalpies or the change in heat capacity at the glass transition point were measured as regression analysis data. Ten milligrams of sea sand was spiked with 0.05 to 1.5 mg of microplastic particles (size: 100 to 200 µm) of the semi-crystalline polymers LD-PE, HD-PE, PP, PA6, and PET, and the amorphous polymers PS and PVC. The results showed that a two-factorial regression enabled the unambiguous identification and robust quantification of different polymer types. The limits of quantification were 0.13 to 0.33 mg and 0.40 to 1.84 mg per measurement for semi-crystalline and amorphous polymers, respectively. Moreover, DSC is robust with regard to natural organic matrices and allows the fast and non-destructive analysis of microplastic within the analytical limits. Hence, DSC could expand the range of analytical methods for microplastics and compete with perturbation-prone chemical analyses such as thermal extraction–desorption gas chromatography–mass spectrometry or spectroscopic methods. Further work should focus on potential changes in phase transition behavior in more complex matrices and the application of DSC for MP analysis in environmental samples.

Similar content being viewed by others

Microplastic sources, formation, toxicity and remediation: a review

Ahmed I. Osman, Mohamed Hosny, … Kolajo Adedamola Akinyede

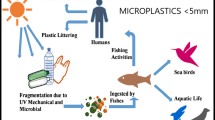
Effect of microplastics in water and aquatic systems

Merlin N Issac & Balasubramanian Kandasubramanian

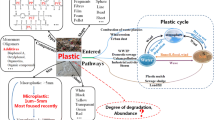
Characteristics of Plastic Pollution in the Environment: A Review

Penghui Li, Xiaodan Wang, … Hongwu Zhang

Avoid common mistakes on your manuscript.

Introduction

Microplastic (MP) is described as polymer particles with diameters of less than 5 mm, including differently shaped particles as well as fibers. Pollution due to MP is considered to be ubiquitous (Browne et al. 2011 , Akdogan and Guven 2019 ). Several studies have detected MP in various compartments of the environment such as the atmosphere (Kernchen et al. 2021 ), rivers (Klein et al. 2015 ; Skalska et al. 2020 ; Meijer et al. 2021 ), shores (Browne et al. 2011 ), the deep sea (van Cauwenberghe et al. 2013 ), Arctic ice (Peeken et al. 2018 ), and the highest mountains (Napper et al. 2020 ). Moreover, the amount of polymeric material in the oceans might double by 2050 (Lebreton et al. 2019 ). Adverse effects on plants (Souza Machado et al. 2019 ) and microorganisms, such as Daphnia magna (An et al. 2021 ), have already been demonstrated. The human health effects have not yet been adequately studied (Issac and Kandasubramanian 2021 ), but there are already indications and suggestions for future research (Wieland et al. 2022 ). Thus, legislation is already responding to the increasing environmental impact of microplastics for example, in the EU directive on the quality of water intended for human consumption, where microplastics are included on the watch list (European Parliament  2023 ). In addition, the legislation stipulates that an analysis is required by 2024 to enable a risk assessment for microplastics. Accordingly, a significant increase in the prevalence of MP analysis is expected in the coming years, with a strong focus on reliable, precise, fast, and cost-efficient methods.

At present, there is no standardized protocol for MP analysis, leading to the application of different methods for their identification and quantification, which are only comparable to a limited extent. However, comprehensive routine analysis and harmonization are urgently needed to understand the pathways, distribution, and impacts of MP (Shahul Hamid et al. 2018 ; Brander et al. 2020 ). The accurate determination of MP is rather challenging because of the diversity of polymeric materials. The molecular compositions of plastics and their modifications are very complex. However, it has been shown that the most common polymers in environmental samples are polyethylene (PE), polypropylene (PP), polyamide (PA), polyethylene terephthalate (PET), polystyrene (PS), and polyvinyl chloride (PVC), on which MP analysis may focus (Way et al. 2022 ; Yang et al. 2021 ). In total, these polymers constitute more than 70% of the globally produced plastics (Plastics Europe 2023 ).

The particle sizes of MP are comparable to the particle sizes of sediments. The challenge of MP determination in the environment lies in the similarity of natural organic material and MP from a chemical analytical point of view. In addition, an analysis can determine either the mass of MP or the number of MP particles in a particulate sample matrix. Generally, two different analytical approaches have been established so far for the analysis of MP. The first comprises spectroscopic methods (Fourier-transform infrared (FTIR) and Raman spectroscopy), which determine the number of MP particles per sample volume. However, such methods for the determination of the number of particles can only be applied after complex and time-consuming sample preparation procedures. The second approach comprises thermo-analytical methods (Peñalver et al. 2020 ). These methods provide mass-specific information (Waldman and Rillig 2020 ; Perez et al. 2022 ; Haines 2002 ), such as the mass of polymer per mass of the sample or per volume fluid medium. The information about the size and shape of the MP particles is lost in mass determination methods and cannot be detected. Currently, the establishment of thermal extraction–desorption gas chromatography-mass spectrometry (TED-GC–MS) as a thermo-analytical method is being pursued (Goedecke et al. 2020 ). This method combines thermo-gravimetry and the chemical analysis of the thermal degradation products of microplastic particles in environmental samples, and it is rather robust to matrix-related influences (Goedecke et al. 2020 ). Nevertheless, TED-GC–MS devices are expensive and require a large investment to realize comprehensive MP monitoring. Therefore, the focus of this work is the application of differential scanning calorimetry (DSC) as a fast and cost-efficient method for MP analysis. DSC is a technique used for the detection and analysis of thermal transitions in various types of polymers, including crystalline, semi-crystalline, and amorphous polymers. DSC measures the heat flow into or out of a sample as a function of the temperature, allowing the observation of events such as melting, crystallization, or glass transition. These transitions provide valuable insights into the physical properties and polymer types. DSC analysis has already been compared in inter-laboratory tests (Becker et al. 2020 ), and its suitability for the determination of microplastics has already been described (Bitter and Lackner 2021 ; Shabaka and Ghobashy 2019 ). An important advantage of DSC is the high robustness of this method against different matrices, which typically display organic contamination from environmental samples. Organic contaminants, which have chemically similar structures to the monomer units in polymers (e.g., esters, olefins, amino acids) do not show such phase transformations and therefore cannot be detected by DSC measurements. Hence, the purification of samples by using chemical or enzymatic methods is not required, and this minimizes the analytical effort by reducing the number of steps performed. Moreover, DSC can be considered a non-destructive method for the chemical structure of the polymer within certain temperature limits. Until the temperature at which the thermal degradation of a polymer begins, the chemical information about the polymer is preserved during a DSC measurement. However, at temperatures above the onset of thermal degradation, DSC is a destructive method. Therefore, the limitation of DSC as a chemically non-destructive method is the polymer-specific thermal degradation point; however, this is not reached in the procedure applied in this study. This enables the confirmation of polymer type with other methods like microscopic-spectroscopic methods.

Polymer detection by DSC is based on the degree of crystallinity or the change in the internal volume of the polymer in microplastic particles. All thermodynamic processes, such as melting or crystallization, are characterized by a melting and crystallization peak associated with each polymer. In connection with thermal degradation, a fingerprint is described in the literature (Wunderlich 2005 ) that allows the identification of different polymer types. The same applies to the glass transition point. As with all thermo-analytical methods, DSC requires calibration with external standards to determine the MP mass in a sample. Our study focuses on the evaluation of different regression models to enable DSC for MP determination. This paper describes the statistical evaluation of DSC for the identification and quantification of microplastics in particulate matrices with respect to the robustness of the limits of detection and quantification. In addition to semi-crystalline commodity polymers, namely LD-PE, HD-PE, PP, PA 6, and PET, the amorphous polymers PS and PVC are included in this study. A linear regression and a two-factorial regression based on the melting and crystallization enthalpies or the change in the specific heat capacity at the point of glass transition are compared. In addition, polycaprolactone (PCL) is discussed as a possible internal standard for environmental samples.

Materials and sample preparation

MP particles were obtained via the cryomilling (Pulverisette 0, Fritsch, Idar-Oberstein, Germany, WC r  = 50 mm, amplitude = 1.5 mm, liquid nitrogen) of eight different polymers (Table  1 ). The particles were sieved to a particle size of 100–200 µm using a vibratory sieve shaker (ANALYSETTE 3, Fritsch, Idar-Oberstein, Germany) equipped with stainless-steel sieves from Fritsch. Sea sand was used as an inorganic matrix to produce mixtures with the prepared MP particles. The sea sand was sieved to a particle size of 100–200 µm as well but without milling.

The samples were prepared by weighing 10 ± 1 mg of sea sand into a DSC crucible (Concavus 40 µl, Netzsch, Selb, Germany) and then the corresponding mass of the polymer to an accuracy level of ± 0.05 mg. The laboratory balance (XSR DU 105, Mettler Toledo, Giessen, Germany) had a certified level of tolerance of ± 0.03 mg.

The lowest polymer content was 0.05 mg per sample, following the values of 0.10, 0.15, 0.20, 0.25, 0.50, 0.75, 1.00, and 1.25 mg, and the highest polymer content was 1.50 mg per sample. For PS, the values were 1.00, 1.25, 1.50, 1.75, 2.00, 2.25, 2.50, 2.75, 3.00, and 3.25 mg. Three replicas were measured for each polymer content value. Accordingly, a total of 30 samples were prepared for each polymer, as shown in Table  1 . Each crucible was closed, and the lid was pierced with a steel needle. Each sample was prepared by weighing the sand directly in the crucible and then adding the polymer on top of the sand.

DSC measurements

The DSC measurements were conducted with the DSC Polyma 214 (Netzsch, Selb, Germany). The device was calibrated using the 6-reference kit produced by Netzsch. All applied temperature programs included an initial heating cycle, followed by a cooling cycle and a second heating cycle with a rate of 20 K/min. An isothermal phase of 3 min was set between temperature gradients. Cooling was performed to − 50 °C, and heating was performed to 300 °C in program (I), and to 130 °C in program (II).

Figure  1 shows the characteristic features of a DSC signal, which were determined from the recorded thermograms. The evaluation of the signals of the second heating cycle and of the cooling phase was conducted with the software Proteus (version 8.0.2, Netzsch, Selb, Germany). The automatic peak recognition feature of the software was used for the identification of the peak temperature ( \({T}_{p,m}\) and \({T}_{p,c}\) ).

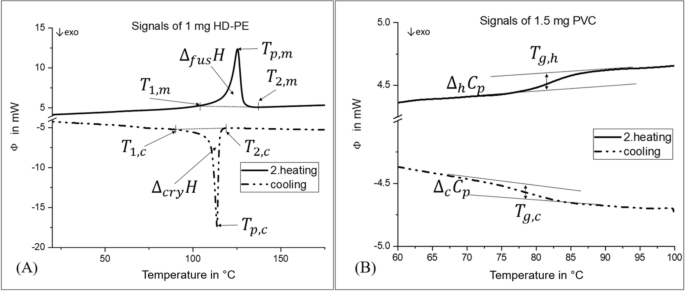
Characteristic features of thermograms for A semi-crystalline polymers and B amorphous polymers. The features can be used as regressors in linear and multiple regression models

The quantitative analysis of the melting and crystallization signals was performed using a linear baseline and integration limits fitted by using the first derivation of the curve (Fig.  2 ). In the case of the semi-crystalline polymers, the onset ( \({T}_{1,m}\) ) and offset temperature ( \({T}_{2,m}\) ) of the melting range and the crystallization range ( \({T}_{1,c}\) , \({T}_{2,c}\) ) were determined from the measured data. By setting the integration limits according to the onset and offset temperatures, the melting enthalpy ( \({\Delta }_{{\text{fus}}}H\) ) and the crystallization enthalpy \(({\Delta }_{{\text{cry}}}H)\) , the corresponding melting peak ( \({T}_{p,m}\) ) and the crystallization peak ( \({T}_{p,c}\) ) were calculated.

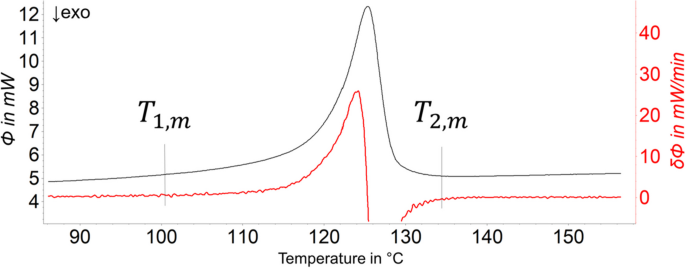
Determination of integration limits ( T 1,m and T 2,m ) for semi-crystalline polymers. Here, an example of the determination of the melting peak area of HD-PE is shown. The black line is the DSC signal, and the red line is the first derivation of the DSC signal. The temperature at which the slope of the first derivation starts to increase is set as the lower integration limit ( T 1,m ). The temperature at which the slope of the first derivation returns to zero is set as the upper integration limit ( T 2,m )

For amorphous polymers, the evaluation of glass transitions was performed by using the stepwise method with four temperatures ( \({T}_{1,m},{T}_{2,m}\) , \({T}_{3,m}\) , \({T}_{4,m}\) ). The determination of T g referred to the midpoint temperature of the DIN EN ISO ( n.d ) 11357–2 standard. The four temperatures obtained based on the first deviation of the measured curve are shown in Fig.  3 . As a result, the glass transitions on heating ( \({T}_{g,h}\) ) and cooling ( \({T}_{g,c}\) ) and the corresponding heat capacity changes on heating ( \({\Delta }_{h}{C}_{p}\) ) and cooling ( \({\Delta }_{c}{C}_{p}\) ) were calculated by the software.

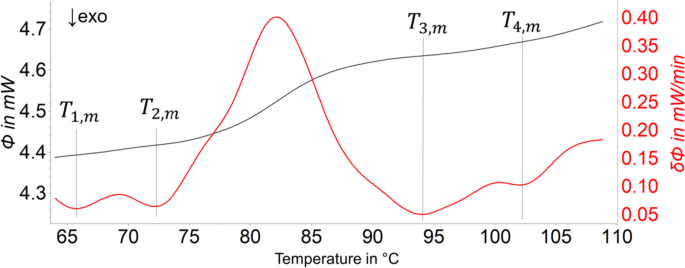
Determination of four temperatures ( \({T}_{1,m},{T}_{2,m}\) , \({T}_{3,m},\) and \({T}_{4,m}\) ) to enable the performance of the stepwise method for amorphous polymers. Here, an example of the determination of the T g,h of PVC is shown. The black line is the DSC signal, and the red line is the first derivation of the DSC signal. The temperatures \({T}_{1,m}\) and \({T}_{2,m}\) were set in front of the T g so that the baseline of the DSC signal was extended beyond the T g , which was the most suitable method. This was achieved by selecting two points on the first derivation curve with similar \(\delta \phi\) values to a linear baseline. The same was applied to determine the temperatures \({T}_{3,m}\) and \({T}_{4,m}\)

Subsequently, the correlation of the polymer mass ( m i ) to the specific phase transition enthalpy \({\Delta }_{{\text{fus}}}H\) and \({\Delta }_{{\text{cry}}}H\) ) or the change in the specific heat capacity ( \({\Delta }_{h}{C}_{p}\) and \({\Delta }_{c}{C}_{p}\) ) was investigated with linear and multiple regression.

Linear regression

The linear regression can be expressed in Eq. ( 1 ) for semi-crystalline and Eq. ( 2 ) for amorphous polymers. The common least squares regression method was used. The melting enthalpy ( \({\Delta }_{{\text{fus}}}H\) ) was used to calculate the mass of the semi-crystalline polymers m i,sc with \({b}_{sc}\) as the slope and \({n}_{sc}\) as the intercept of the regression line. The mass of the amorphous polymers ( m i,a ) was calculated using the change in specific heat capacity during heating \({\Delta }_{h}{C}_{p}\) .

The data from 20 samples were used as model data for the regression, and 10 samples were used as validation data to test the model (“ Calculation of residuals and analytical limits ” section).

Multiple regression

In addition to the linear regression, a multiple regression model was tested. All calculations were performed using R Studio 2022.02.2 Build 443. The evaluation of the parameters shown in Fig.  1 for the determination of the mass was performed using the package “leaps” (Fahrmeir et al. 2009 ). As with linear regression, the software calculates a straight line with the aim of minimizing the distances to the individual measurement points (least squares method). The multiple regression in the model was based on two regressors. For semi-crystalline polymers, the regressors for the regression were the melting enthalpy \({(\Delta }_{{\text{fus}}}H\) ) and crystallization enthalpy ( \({\Delta }_{{\text{cry}}}H\) ), resulting in Eq. ( 3 ). For amorphous polymers, they were the changes in the specific heat capacity of the cooling ( \({\Delta }_{c}{C}_{p}\) ) and second heating cycle ( \({\Delta }_{h}{C}_{p}\) ), as indicated by Eq. ( 4 ). The regression was used to determine the polymer-specific parameters \({{a}{\prime}}_{1,sc}\) and \({{a}{\prime}}_{2,sc}\) for semi-crystalline polymers or \({{a}{\prime}}_{1,a}\) and \({{a}{\prime}}_{2,a}\) for amorphous polymers. Similar to the linear regression, an intercept \({n}{\prime}{}_{sc}\) or \({n}{\prime}{}_{a}\) was considered for semi-crystalline and amorphous polymers, respectively.

The data from 20 samples were used as model data. The resulting models were tested on the validation samples ( n  = 10).

Calculation of residuals and analytical limits

As mentioned earlier, the least squares method was used for the regression models. To test the models, the residual ( \({d}_{{\text{i}},{\text{x}}}\) ) was calculated as the value of the difference in the MP mass predicted by the model and the actual MP mass in the sample for linear regression (Eq. ( 5.1 )) and for multiple regression (Eq. ( 5.2 )). In detail, the mass of the polymer in the validation samples ( \({m}_{i,x};{{m}^{\prime}}_{i,x} \quad with \quad x=\left\{sc;a\right\}\) ) was predicted through the regression of the model data. Subsequently, the calculated mass of the polymer in the validation samples ( \({m}_{i,x}\) ) was compared with the initially weighed mass ( \({m}_{i,x}^{0})\) . This mass deviation in each validation sample was described as the residue ( \({d}_{{\text{i}},{\text{x}}}\) ). The absolute value of the maximum residue ( \({d}_{i,max}\) ) was used as the uncertainty parameter in this study (Eq. ( 6 ))

The parameter \({d}_{i,max}\) was considered the largest error. Thus, the uncertainty was assumed to be \(\pm {d}_{i,max}\) for the determination of the polymer mass by DSC. The parameter \({d}_{max}\) was therefore used as the limit of detection (LOD). The limit of quantification (LOQ) was calculated according to Eq. ( 7 ) and was three times the LOD.

The uncertainty in the determination of the temperature for the melting peak ( T p,m ), the crystallization peak ( T p,c ), and the glass transition ( T g ) was calculated on the basis of the largest deviation (± Δ T x, max ) from the mean value \(\widehat{{T}_{x}}\) . Equation ( 8 ) was used for this calculation.

To evaluate the regression analysis, the sum of squared residuals (SSR) and the Akaike (AIC.c) and Bayesian (BIC) information criteria were calculated from the validation data. The parameters SSR (9), AICc (10) (Hedderich and Sachs 2018 ), and BIC (11) (Fahrmeir et al. 2009 ) were calculated using the equations shown, where z is the number of validation samples, and M is the number of regressors in the model. \(\widehat\sigma^2\) is the variance estimator from the likelihood function (Hedderich and Sachs 2018 ).

Polymer identification

The peak (Table  2 ) and glass transition (Table  3 ) temperatures were determined independently of the regression models. Our results show that DSC is suitable for identifying different polymer types in mixtures within the range of the polymer mass (see Table  1 ). Table 2 shows the mean peak temperatures and the largest deviations from the mean value for the semi-crystalline polymers ( n  = 30). The mean values of the glass transition temperature and the largest deviations from the mean value of the transition temperature are shown in Table  3 . According to Wampfler et al., the glass transition temperature is the mean value between T g,h and T g,c (Wampfler et al. 2022 ). These characteristic temperature values are used for the polymer-specific identification of MP in mixtures.

The melting and crystallization peak temperatures show a deviation from their mean value < 2.7 K for all investigated polymers except PET and PA 6. Additionally, the glass transition temperature of PS shows an increased deviation. The increased deviation in the values for PET and PA 6 could be due to the chemical and physical properties of both polymers and will be discussed later.

Figure  4 presents the results of the polymer identification. The majority of the polymers show no superposition of their thermodynamic signals, which could prevent their simultaneous identification in the same sample. However, the possible superposition of the signals from PS and LD-PE during heating and from the crystallization peaks of HD-PE and PP is identified.

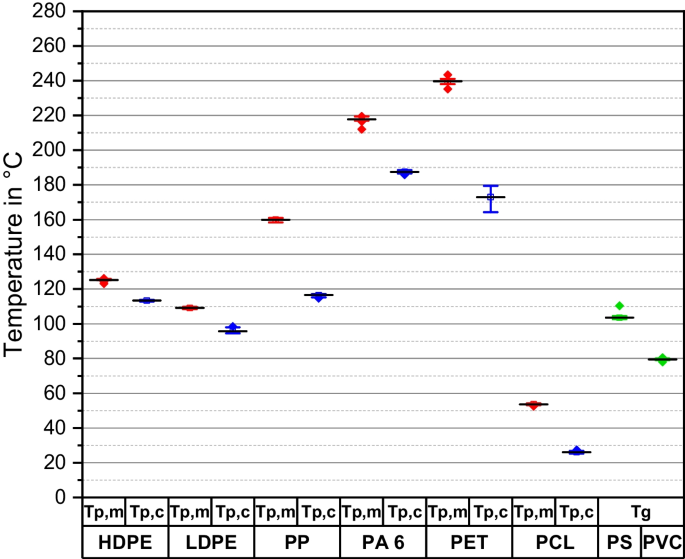
Results of polymer identification by phase transition temperature. The black bars are equal to the mean value ( n  = 30). The red data points represent the melting peak temperatures, and the blue data points represent the crystallization peak temperatures. Additionally, the green data points show the glass transition temperatures of amorphous polymers. A potential superposition was found for PS and both PE types between 100 and 110 °C and for HD-PE and PP between 112 and 118 °C

Polymer quantification using DSC

We compared one linear and one multiple regression model, which were the most suitable for the quantification of MP in mixtures. Nevertheless, the 20 model datasets were used to calculate various regression lines, but the two models presented here were the most promising. The “heating” model is a simple linear regression of the mass of the polymer to the melting enthalpy ( \({\Delta }_{fus}H\) ). The “multiple” model is a two-factorial regression that takes into account both the melting and crystallization enthalpy. The amorphous polymer data were treated equally.

Table 4 shows the results of the “heating” model according to the linear regression using the melting enthalpy or the change in heat capacity during the second heating cycle. For HD-PE, PP, PA6, and PET, the LODs were below 0.1 mg per measurement. It is striking that the LOD and thus the LOQ of semi-crystalline polymers are lower than the analytical limits of amorphous polymers.

Table 5 shows the results of the calculations according to the multiple regression for semi-crystalline and amorphous polymers. The LOD for the polymers was derived from the calculated maximum residuals ( \({d}_{i,max}\) ), in the same way as for the linear regression.

However, we found that the LODs of PET and PS had to be determined differently to obtain reasonable values. According to d i,max , the postulated LOD for PET would be 0.06 mg per measurement, but, for a sample containing 0.09 mg (0.10 ± 0.05 mg) PET, the value of the melting enthalpy in the melting range of PET was in the same order of magnitude as in the blank samples (Fig.  5 A). The crystallization signal at 0.09 mg could already be distinguished from the blank values (Fig.  5 B). Consequently, the LOD of PET was set to the polymer mass at which a signal could be evaluated unambiguously in the thermogram during heating and cooling. The empirical LOD of PET was set to 0.15 mg per measurement. Additionally, the glass transition signal of PS was too weak to be distinguished from the noise at the predicted LOD of 0.61 mg, and the empirical LOD of PS was set to 1.0 mg per measurement. Consequently, the LOQs of PET and PS were also adjusted. The LOQ can be described according to Eq. ( 12 ). The equation does not differ from that used in the previous calculation, but the variable LOD is now larger than \({d}_{i,max}\) .

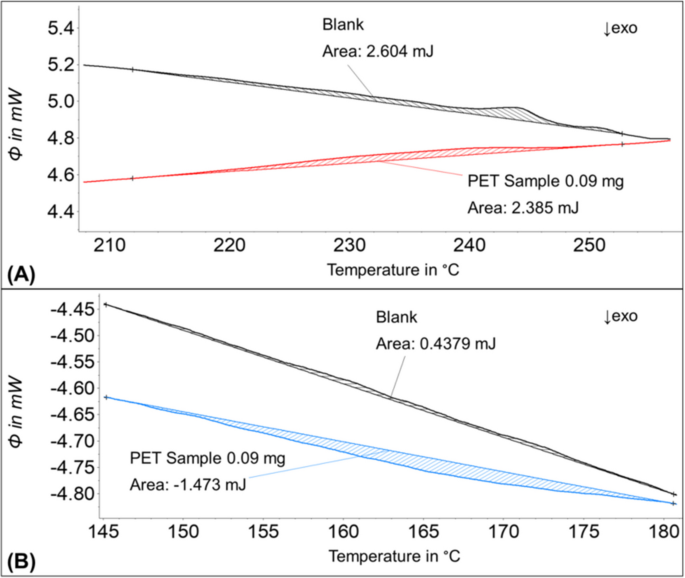
Comparison of a DSC sample containing 0.09 mg PET and sea sand (red and blue) and a blank sample containing only sea sand. A The second heating and B the cooling curves of both samples

Comparison of regression models

Figure  6 shows the residuals ( \({d}_{{\text{i}},{\text{x}}}\) and \({d}^{\prime}_{i,x}\) ) of the validation data from the expected values for the two regression models according to Eqs. 5.1 and 5.2 . Comparing the average deviations of the residuals from an optimum value ( \({d}_{{\text{i}},{\text{x}}}=0\) ) for the different polymer types, no clear trend can be derived. All regression models provide small residuals in the polymer mass range. However, in all models, the predicted masses of amorphous polymers show a larger deviation from the expected value than for semi-crystalline polymers. Nevertheless, the multiple regression model shows an increase in precision for LD-PE, PCL, and both amorphous polymers by reducing the total range of residuals. This effect is more prominent for the amorphous polymers than for the semi-crystalline polymers.

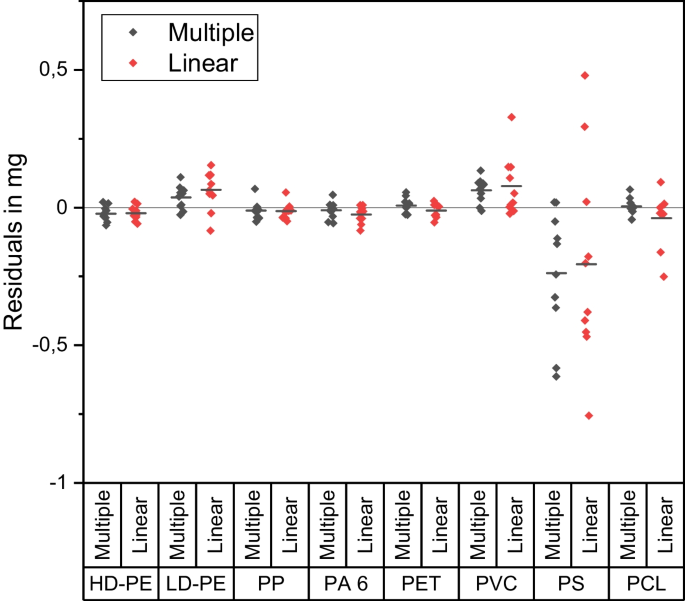
Residuals of predicted polymer mass in validation samples from expected value for different regression models. The expected value equals the actual polymer mass, which was measured during sample preparation

A more practical means to compare the regression models is the comparison of the calculated analytical limits. Figure  7 shows the LOQs of the investigated polymer types for their determination by DSC measurements. The LOQs are shown as dots for the individual polymers, and the tolerance values ( \({\pm d}_{i,max})\) are shown as error bars. This comparison is carried out for the “heating” and the “multiple” regression models. According to the LOQs, a qualitative result regarding the presence of MP in a sample can be obtained at small polymer masses per measurement. For the semi-crystalline polymers, the LOQ is below 0.25 mg (= 250 µg) or 0.11 mg (= 110 µg) for the linear or multiple regression, respectively. On the other hand, amorphous polymers show a higher LOQ in general, but the multiple regression results in lower values compared to the linear regression.

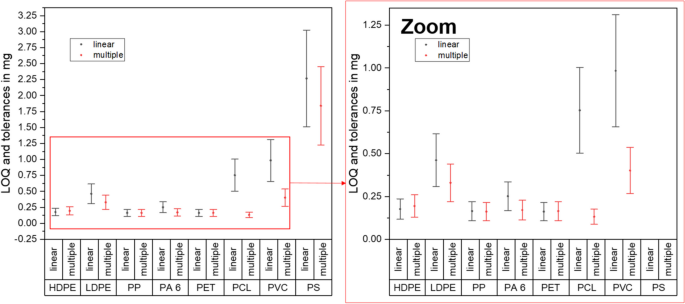
Comparison of analytical limits obtained from linear (“heating”) and multiple regression models. The dots show the LOQs; the error bars are the tolerance levels ( \(\pm {d}_{i,max}\) )

Moreover, an average LOQ below 0.50 mg per measurement is found for the polymers HD-PE, LD-PE, PP, PA 6, and PET, independently of the regression model. The highest LOQs are found for the amorphous polymers PS and PVC for both regression models. For the remaining polymers, both regression models can be treated equally. Nevertheless, the robustness of the multiple regression is higher due to the increased number of regressors. Especially for PCL and PVC, the multiple regression leads to a smaller tolerance and smaller LOQs. The tolerance of the laboratory balance used is 0.03 mg. This means that no reliable LOD below 0.03 mg can be achieved. The balance used has a considerable influence on the analysis result. At the same time, the very high precision of the DSC analysis at the level of a certified laboratory balance can be assumed.

Identification of polymeric substances

Our results show that it is possible to identify MP particles in sand mixtures according to their thermodynamic fingerprints. We were able to distinguish eight different polymers within the range of the polymer mass (Tables  2 and 3 ). The polymer-specific melting or crystallization peak temperatures showed very low uncertainty. Most investigated polymers showed a deviation < 2.7 K in the melting or crystallization peaks. The only exceptions were PET and PA 6. Hence, this parameter seems to be a suitable identification criterion for MP. The low LODs of the investigated polymers (Tables  4 and 5 ) show that MP contamination can be identified by our method. However, the LODs were polymer-specific and must be determined for each polymer individually.

PET shows broad peaks in the thermogram due to its slow crystallization behavior under the temperature gradient of 20 K/min. The broad peak results in a plateau-like signal, which prevents clear peak determination, because the peak maximum or minimum is set randomly on the plateau. Thus, an increased distribution of the determined peak temperature is obtained. The increased distribution of the peak temperature of PA 6 can be explained by the different morphological crystal structures at a heating rate of 20 K/min. These two structures show overlapping melting signals in the thermogram, leading to a double peak (Wunderlich 2005 , S. 660). The first peak belongs to the γ -phase and the second peak to the α -phase. Depending on the ratio of the two crystal structures, the intensity of the peaks varies and influences the measured peak temperature. Hence, clear peak temperature determination becomes difficult. However, the double peak in the thermogram is very distinctive for PA 6, so this feature can be used as an identification criterion too.

The simultaneous detection of different polymer types in one sample is crucial in the application of DSC for the analysis of MP in environmental samples. Therefore, it is important to identify overlapping signals of different polymer types. The visualization of the results in Fig.  4 shows the possible superposition of the signals of PS and both PE types during heating and of the crystallization peaks of HD-PE and PP. However, the identification of HD-PE in the presence of PP is still possible because of the different melting peak temperatures. Contrastingly, the identification of PS in the presence of any polyethylene would not be possible due to the width of the melting and crystallization peaks, and this requires further research. Nevertheless, one advantage of using DSC is the identification of HD-PE next to LD-PE. These polymers have similar chemical and physical properties, which prevents their simultaneous identification via spectroscopic methods, but the differences in their thermodynamic behavior make their identification by DSC possible.

Quantification

We were able to prove that DSC can be used to quantify the polymer content in particulate matrices. All investigated regression models resulted in precise regression lines. However, our results did not provide one optimal regression model for all polymers. To evaluate the quality of the regressions, we used the residue of the predicted polymer mass from the actual spiked mass. It was assumed that the optimum model would show the smallest deviation from the expected value for the polymer type. However, we found that the optimum regression model depended strongly on the polymer type. Table 6 shows an evaluation of the regression according to SSR, AICc, and BIC. The parameters for the polymers HD-PE, PP, and PET do not indicate an advantage of multiple regression over linear regression. The assertions of the parameters for model selection are consistent and do not contradict each other. However, the multiple models, evaluated based on the SSR, show no significant differences (HD-PE, PP, and PET) or higher precision (LD-PE, PCL, PA, PVC, PS) than the linear models. Consequently, it is generally possible to use multiple regression.

For the amorphous polymers (PVC and PS), a significant increase in precision and accuracy can be seen. This is shown in the form of a high average residue and a large deviation in the residues for amorphous polymers (Fig.  6 ). Such large deviations in the residue values are due to the low intensity of the exploited glass transition signal. Glass transitions are considered second-order phase transitions because the signal for a change in heat capacity is based on the change in the internal volume of a polymer. Thus, glass transitions are not classic phase transitions. The intensity of these signals is approximately one hundred times lower than that of the signal of the melting or crystallization of a semi-crystalline polymer of the same mass.

The application of multiple regression can increase the robustness of the model because it depends on two regressors. For PVC and PS, a significant reduction in the residuals in the multiple regression was found. Moreover, for the semi-crystalline polymers, a small improvement in the model output was observed. It becomes clear that multiple regression does not necessarily achieve higher precision and accuracy. However, when using multiple regression, the optimum precision can be obtained across all investigated polymers. Additionally, increasing the number of regressors also increases the capacity for the quantification of one specific polymer type. This is important with respect to potential differences in one polymer type produced by different manufacturers. In the present work, this was demonstrated by the polymer PET. Using the method of multiple regression, the postulated LOQ of 0.19 mg (Bitter and Lackner 2021 ) was achieved for a very good approximation (0.23 mg, Table  5 ). It should be noted that the polymers in the mentioned study were of different origin which highlights the robustness and representativeness of the DSC method. Bitter and Lackner ( 2021 ) also showed the high robustness of the DSC method against organic material.

The common linear regression, using the melting enthalpy to determine the crystallinity and subsequently the mass of the polymer, shows good results for semi-crystalline polymers. Additionally to the melting enthalpy, the crystallization enthalpy could be used for linear regression. However, a “cooling” model is not proposed because the cooling process, and thus the enthalpy of crystallization could not be calibrated easily due to the supercooling effect (Höhne et al. 2003 , p. 84). Due to this effect, the crystallization processes are very specific and would not allow the reliable, direct calibration of the DSC device. The calibration of the crystallization enthalpy would be possible using liquid crystals (Menczel and Prime 2009 ), but these methods were not applied in this study. Nevertheless, Höhne et al. describe a linear relationship between the crystallization enthalpy and melting enthalpy. Consequently, the calibration of DSC cooling is possible but is subject to adjustment by the calculated correction factors (Höhne et al. 2003 , p. 97). Thus, the interpretation of the thermogram of cooling depends on that of heating. For this reason, no individual cooling analysis was carried out. However, the cooling information was included in the multiple model.

Nevertheless, the use of multiple regressions must be critically assessed. A fundamental aspect of multiple regression is that there is no physical model with two independent terms. The melting enthalpy, as well as the crystallization enthalpy, depends on the degree of crystallization. However, the physical processes of melting and crystallization differ during detection using DSC. Hence, the linear factor between the melting and crystallization enthalpies is not constant. The high level of correlation based on their shared physical origin is indicated by a high level of multicollinearity.

The regressors \({\Delta }_{{\text{fus}}}H\) and \({\Delta }_{cry}H\) exhibit a high degree of multicollinearity. This means that both regressors ( \({\Delta }_{fus}H\) , \({\Delta }_{cry}H\) ) show a strong dependence on the same polymer property, which is the degree of crystallinity. Due to the high degree of multicollinearity, the uncertainty of the coefficients ( \({a^{\prime}}_{1}\) and \({a^{\prime}}_{2}\) ) increases. However, the higher uncertainty of the coefficients cannot be identified in our results compared to the linear regressions. The possible application of higher-factorial models with more than two regressors cannot be conclusively assessed at this point. The complexity of the models and the conditional dependence between individual regressors (for example, \({T}_{1,m}\) and \({T}_{2,m}\) to \({\Delta }_{{\text{fus}}}H)\) cannot necessarily be captured with multiple linear models. The coefficient of determination for the multiple regression has to be verified by using polymers from different manufacturers. In addition, a clear and reproducible definition of the integration limits or baselines in the thermograms must be established.

The use of an intercept in Eqs. 1 , 2 , 3 , and 4 must also be discussed in relation to the physically describable basis of the model. Höhne et al. do not describe an intercept in the calculation between mass and heat, but they note that it only applies to ideal parameters. Höhne et al. also show that the linearity between the peak area and mass does not apply to very small masses (Höhne et al. 2003 , p. 248). For very small sample masses, the device-specific thermal signal cannot be neglected. The linearity shown in the model used can therefore not be ideally extrapolated to the coordinate origin. For this reason, an intercept was permitted in the models.

In the context of MP analysis in environmental samples, the presented method can be used to determine the MP mass per sample mass or volume. The MP content in sediments from the Elbe River (Germany) was reported to be approximately 0.8 mg/kg PE (Laermanns et al. 2021 ) to 16 mg/l PE (Scherer et al. 2020 ). Adomat et al. reported the MP content in river sediments to be between 16 and 1000 mg/kg globally (Adomat 2021 ). Thus, the LOQs for semi-crystalline polymers are sufficient to determine MP in river sediment samples via DSC. With respect to amorphous polymers, the application of DSC analysis is limited. The high margin of error of 0.6 mg in the specification of the mass of PS in a sample only allows a limited quantitative assessment. However, the identification of PS can be achieved within the investigated range of the polymer mass. The application of more complex systems for the quantitative determination of microplastics in sediments should be considered in subsequent work. The influences of matrix-related effects by sediments should be quantified, as well as their effects on the DSC signals. Heteronucleation by fine sediment components or homonucleation during aging (Menzel et al. 2022 ), and the correspondingly different crystalline phases, might influence the phase transition behavior and thus the detected heat flow. The existing crystallization models described by Avrami (Wunderlich 2005 ) or Hoffman–Lauritzen should be discussed for a description or may need to be adapted. Hence, the crystallization process is not isothermal, and a description via the Hoffmann–Lauritzen (Vyazovkin et al. 2005 ) model would be promising.

Moreover, we provided the regression lines as the absolute mass of the polymer, which could be detected by the method. According to the experimental setup, the data could be given in content units such as mg/kg, with equal results. We suggest calculating the MP content after a measurement. Hence, the power of the presented method depends strongly on the enrichment of MP by the particulate matrix or filtration. Kurzweg et al. investigated a combination of electrostatic separation and DSC for comprehensive MP monitoring in sediments. This study postulated an LOQ of 2.3 mg/kg (Kurzweg et al. 2022 ). Additionally, the possible impact of sample preparation and matrix influences could be controlled by using an internal standard. In this context, PCL shows great potential as an internal standard due to several aspects. As a biodegradable polymer, high blank values in environmental samples are not expected. Furthermore, the signals of PCL in the thermogram ( T p,m,PCL  = 53.7 ± 1.2 °C, T p,c,PCL  = 26.0 ± 1.3 °C) do not lead to an overlap with other signals from common plastics ( T p,m and T p,c  > 90 °C), and multiple regression can achieve an LOD of 0.07 mg.

Finally, it should be noted that the polymers selected in this study were related to common plastics. No copolymers or elastomers, such as tire abrasion, were included in this study. These polymeric materials have their own characteristic thermograms, which correlate with the individual compositions of the copolymers, the degree of crosslinking (elastomers), and the composition of the additives (tire abrasion). Although these materials are detectable by DSC, they do not fulfill the criteria necessary to identify their polymer types. While a quantitative and qualitative conclusion on the mentioned polymeric materials is not possible, the artificial origin of the materials can be revealed via DSC analysis. Because of the non-destructive nature of the analysis, the samples used in DSC can be subjected to other instrumental methods for microplastic determination, which could facilitate the identification and quantification of the microplastic loads of certain samples. Polymers such as PVC indicate a limitation of the method with regard to non-destructive analysis. The thermal degradation of PVC starts at 150 °C. Consequently, polymers with thermal signals above 150 °C cannot be detected. This limitation, as well as the mutual influence of the thermal signals in the simultaneous determination of polymers in DSC, has already been discussed by Sorolla-Rosario et al. 2022 .

The proposed DSC method can considerably reduce the number of samples that need to be analyzed in a complex procedure. Thus, DSC and the thermodynamic fingerprint show high potential with regard to fast and robust MP analysis, with comparatively low investment costs.

In this study, DSC was evaluated by using regression analysis to enable MP analysis in sediments. The LODs and LOQs of eight common polymers (LD-PE, HD-PE, PP, PA, PET, PCL, PS, and PVC) were determined by using two different regression models. A linear and a multiple regression model were applied in the range of 0.05–1.50 mg per measurement. The multiple regression resulted in increased reliability and robustness in the analysis compared to the linear regression model due to its increased number of regressors. However, the precision of the linear regression models was only slightly weaker. Generally, semi-crystalline polymers can be detected to a better extent than amorphous polymers. The main reason for this is the increased intensity of the melting and crystallization signals compared to the signals of the glass transition. The determined LOQs were 0.20 mg for HDPE, 0.33 mg for LDPE, 0.16 mg for PP, 0.17 mg for PA, 0.23 mg for PET, 0.13 mg for PCL, 0.40 mg for PVC, and 2.22 mg for PS. These analytical limits would be sufficient for MP monitoring in sediments.

However, multiple regression has to be evaluated critically due to the multicollinearity of the two regressors, \({\Delta }_{{\text{fus}}}H\) and \({\Delta }_{{\text{cry}}}H\) . Both regressors depend to the same extent on the crystallinity of a polymeric material. Moreover, matrix-related effects such as heteronucleation should be investigated in future work. To improve the robustness of MP analysis against matrix-related effects, we propose the introduction of PCL as an internal standard.

We conclude that the identification and quantification of PE, PP, PA, PET, PCL, PS, and PVC by using DSC has been demonstrated successfully. The use of multiple regression in the qualitative determination of microplastics in sediments increases the robustness of the analytical method. The DSC method is therefore suitable for further studies investigating the transport and fate of microplastics in sediments. Given the possibilities of non-destructive analysis, the presented method can be complemented by further microplastic analysis methods, e.g., thermo-analytical or spectroscopic methods.

Data Availability

Data is available on request.

Adomat Y, Grischek T, (2021) Sampling and processing methods of microplastics in river sediments - a review. Sci Total Environ 758:143691. https://doi.org/10.1016/j.scitotenv.2020.143691

Article   CAS   Google Scholar  

Akdogan Z, Guven B (2019) Microplastics in the environment: a critical review of current understanding and identification of future research needs. Environ Pollut 254(Pt A):113011. https://doi.org/10.1016/j.envpol.2019.113011

An D, Na J, Song J, Jung J (2021) Size-dependent chronic toxicity of fragmented polyethylene microplastics to Daphnia magna. Chemosphere 271:129591. https://doi.org/10.1016/j.chemosphere.2021.129591

Becker R, Altmann K, Sommerfeld T, Braun U (2020) Quantification of microplastics in a freshwater suspended organic matter using different thermoanalytical methods – outcome of an interlaboratory comparison. J Anal Appl Pyrolysis 148:104829. https://doi.org/10.1016/j.jaap.2020.104829

Bitter H, Lackner S (2021) Fast and easy quantification of semi-crystalline microplastics in exemplary environmental matrices by differential scanning calorimetry (DSC). Chem Eng J 423:129941. https://doi.org/10.1016/j.cej.2021.129941

Brander SM, Renick VC, Foley MM, Steele C, Woo M, Lusher A et al (2020) Sampling and quality assurance and quality control. A Guide for Scientists Investigating the Occurrence of Microplastics Across Matrices. Appl Spectrosc 74(9):1099–1125. https://doi.org/10.1177/0003702820945713

Browne MA, Crump P, Niven SJ, Teuten E, Tonkin A, Galloway T, Thompson R (2011) Accumulation of microplastic on shorelines worldwide. Sources and sinks. Environ Sci Technol 45(21):9175–9179. https://doi.org/10.1021/es201811s

de Souza Machado AA, Lau CW, Kloas W, Bergmann J, Bachelier JB, Faltin E et al (2019) Microplastics can change soil properties and affect plant performance. Environ Sci Technol 53(10):6044–6052. https://doi.org/10.1021/acs.est.9b01339

DIN EN ISO (n.d.) 11357-2:2020-08, Plastics - Differential scanning calorimetry (DSC) - Part 2: Determination of glass transition temperature and step height (ISO_11357-2:2020); German version EN_ISO_11357-2:2020, p 10–11

European Parliament (29.01.2023) Directive (EU) 2020/2184 of the European Parliament and of the Council of 16 December 2020 on the quality of water intended for human consumption (recast) (Text with EEA relevance), 2020/2184, vom 23.12.2020. Fundstelle: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:32020L2184 . In: Official Journal of the European Union. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:32020L2184 . Accessed 29 Jan 2023

Fahrmeir L, Kneib T, Lang S (2009) Regression. Modelle, Methoden und Anwendungen. 2. Aufl. Berlin, Heidelberg: Springer-Verlag Berlin Heidelberg (Statistik und ihre Anwendungen). Available online:  https://doi.org/10.1007/978-3-642-01837-4

Goedecke C, Dittmann D, Eisentraut P, Wiesner Y, Schartel B, Klack P, Braun U (2020) Evaluation of thermoanalytical methods equipped with evolved gas analysis for the detection of microplastic in environmental samples. J Anal Appl Pyrolysis 152:104961. https://doi.org/10.1016/j.jaap.2020.104961

Haines P (2002) Principles of thermal analysis and calorimetry. Unter Mitarbeit von Peter G. Laye, S. B. Warrington, Thermal Methods Group, G. Roger Heal, Duncan M. Price and Richard Wilson. Cambridge: Royal Society of Chemistry (RSC Paperbacks, v.29). Available online:  https://doi.org/10.1039/9781847551764

Hedderich J, Sachs L (2018) Angewandte Statistik. Methodensammlung mit R. 16., überarbeitete und erweiterte Auflage. Springer Spektrum, Berlin

Google Scholar  

Höhne GWH, Hemminger W, Flammersheim H-J (2003) Differential scanning calorimetry. With 19 tables. 2., revised and enl. ed. Berlin: Springer

Issac MN, Kandasubramanian B (2021) Effect of microplastics in water and aquatic systems. Environ Sci Pollut Res 28(16):19544–19562. https://doi.org/10.1007/s11356-021-13184-2

Kernchen S, Löder MGJ, Fischer F, Fischer D, Moses SR, Georgi C et al (2021) Airborne microplastic concentrations and deposition across the Weser River catchment. Sci Total Environ 818:151812. https://doi.org/10.1016/j.scitotenv.2021.151812

Klein S, Worch E, Knepper TP (2015) Occurrence and spatial distribution of microplastics in river shore sediments of the Rhine-main area in Germany. Environ Sci Technol 49(10):6070–6076. https://doi.org/10.1021/acs.est.5b00492

Kurzweg L, Schirrmeister S, Hauffe M, Adomat Y, Socher M, Harre K (2022) Application of electrostatic separation and differential scanning calorimetry for microplastic analysis in river sediments. Front Environ Sci 10:1032005. https://doi.org/10.3389/fenvs.2022.1032005

Article   Google Scholar  

Laermanns H, Reifferscheid G, Kruse J, Földi C, Dierkes G, Schaefer D (2021)Microplastic in Water and Sediments at the Confluence of the Elbe and Mulde Rivers in Germany. Front Environ Sci 9:19. https://doi.org/10.3389/fenvs.2021.794895  

Lebreton L, Egger M, Slat B (2019) A global mass budget for positively buoyant macroplastic debris in the ocean. Sci Rep 9(1):12922. https://doi.org/10.1038/s41598-019-49413-5

Meijer LJJ, van Emmerik T, van der Ent R, Schmidt C, Lebreton L (2021) More than 1000 rivers account for 80% of global riverine plastic emissions into the ocean. Sci Adv 7(18):eaaz5803. https://doi.org/10.1126/sciadv.aaz5803

Menczel JD, Prime RB (2009) Thermal Analysis of Polymers: Fundamentals and Applications. https://doi.org/10.1002/9780470423837

Menzel T, Meides N, Mauel A, Mansfeld U, Kretschmer W, Kuhn M et al (2022) Degradation of low-density polyethylene to nanoplastic particles by accelerated weathering. Sci Total Enviro 826:154035. https://doi.org/10.1016/j.scitotenv.2022.154035

Napper IE, Davies BFR, Clifford H, Elvin S, Koldewey HJ, Mayewski PA et al (2020) Reaching new heights in plastic pollution—preliminary findings of microplastics on Mount Everest. One Earth 3(5):621–630. https://doi.org/10.1016/j.oneear.2020.10.020

Peeken I, Primpke S, Beyer B, Gütermann J, Katlein C, Krumpen T et al (2018) Arctic sea ice is an important temporal sink and means of transport for microplastic. Nat Commun 9(1):1505. https://doi.org/10.1038/s41467-018-03825-5

Peñalver R, Arroyo-Manzanares N, Ignacio López-García M (2020) An overview of microplastics characterization by thermal analysis. Chemosphere 242:125170. https://doi.org/10.1016/j.chemosphere.2019.125170

Perez CN, Carré F, Hoarau-Belkhiri A, Joris A, Leonards PEG, Lamoree MH (2022) Innovations in analytical methods to assess the occurrence of microplastics in soil. J Environ Chem Eng 10(3):107421. https://doi.org/10.1016/j.jece.2022.107421

Plastics Europe (2023) Plastics - the Facts 2022 • Plastics Europe. Available online: https://plasticseurope.org/knowledge-hub/plastics-the-facts-2022/ , latest changes: 14.03.2023. Accessed 11 Aug 2023

Scherer C, Weber A, Stock F, Vurusic S, Egerci H, Kochleus C (2020) Comparative assessment of microplastics in water and sediment of a large European river. Sci Total Environ 738:139866. https://doi.org/10.1016/j.scitotenv.2020.139866  

Shabaka SH, Ghobashy M (2019) Identification of marine microplastics in Eastern Harbor, Mediterranean Coast of Egypt, using differential scanning calorimetry. Mar Pollut Bull 142:494–503. https://doi.org/10.1016/j.marpolbul.2019.03.062

Shahul Hamid F, Bhatti MS, Anuar N, Anuar N, Mohan P, Periathamby A (2018) Worldwide distribution and abundance of microplastic: How dire is the situation? Waste Manag Res: the journal of the International Solid Wastes and Public Cleansing Association, ISWA 36(10):873–897. https://doi.org/10.1177/0734242X18785730

Skalska K, Ockelford A, Ebdon JE, Cundy AB (2020) Riverine microplastics. Behaviour, spatio-temporal variability, and recommendations for standardised sampling and monitoring. J Water Process Eng 38:101600. https://doi.org/10.1016/j.jwpe.2020.101600

Sorolla-Rosario D, Llorca-Porcel J, Pérez-Martínez M, Lozano-Castelló D, Bueno-López A (2022) Study of microplastics with semicrystalline and amorphous structure identification by TGA and DSC. J Environ Chem Eng 10(1):106886. https://doi.org/10.1016/j.jece.2021.106886

van Cauwenberghe L, Vanreusel A, Mees J, Janssen CR (2013) Microplastic pollution in deep-sea sediments. Environ Pollut 182:495–499. https://doi.org/10.1016/j.envpol.2013.08.013

Vyazovkin S, Stone J, Sbirrazzuoli N (2005) Hoffman-Lauritzen parameters for non-isothermal crystallization of poly(ethylene terephthalate) and poly(ethylene oxide) melts. J Therm Anal Calorim 80(1):177–180. https://doi.org/10.1007/s10973-005-0632-7

Waldman WR, Rillig MC (2020) Microplastic research should embrace the complexity of secondary particles. Environ Sci Technol 54(13):7751–7753. https://doi.org/10.1021/acs.est.0c02194

Wampfler B, Affolter S, Ritter A, Schmid M (2022) Measurement Uncertainty in Analysis of Plastics: Evaluation by Interlaboratory Test Results. 1st ed. Cincinnati, Ohio: Hanser Publications

Way C, Hudson MD, Williams I, Langley GJ (2022) Evidence of underestimation in microplastic research: A meta-analysis of recovery rate studies. Sci Total Environ 805:150227. https://doi.org/10.1016/j.scitotenv.2021.150227

Wieland S, Balmes A, Bender J, Kitzinger J, Meyer F, Ramsperger AF et al (2022) From properties to toxicity: comparing microplastics to other airborne microparticles. J Hazard Mater 428:128151. https://doi.org/10.1016/j.jhazmat.2021.128151

Wunderlich B (2005) Thermal analysis of polymeric materials. Berlin, Heidelberg: Springer-Verlag Berlin Heidelberg. Online verfügbar unter. https://doi.org/10.1007/b137476

Yang L, Zhang Y, Kang S, Wang Z, Wu C (2021) Microplastics in soil: a review on methods, occurrence, sources, and potential risk. Sci Total Environ 780:146546. https://doi.org/10.1016/j.scitotenv.2021.146546

Download references

Open Access funding enabled and organized by Projekt DEAL. This work was supported by the European Social Fund (ESF) and by the Federal State of Saxony (Project VEMIWA – Vorkommen und Verhalten von Mikroplastik in sächsischen Gewässern; grant no. 100382142). This article is funded by the Open Access Publication Fund of Hochschule für Technik und Wirtschaft Dresden – University of Applied Sciences and by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation grant no. 491382348).

Author information

Authors and affiliations.

Faculty of Agriculture, Environment and Chemistry, University of Applied Sciences Dresden, Friedrich-List-Platz 1, 01069, Dresden, Germany

Sven Schirrmeister, Lucas Kurzweg, Xhoen Gjashta, Martin Socher & Kathrin Harre

Leibniz Institut für Polymerforschung Dresden e.V., Institute for Physical Chemistry and Polymer Physics, Hohe Str. 6, 01069, Dresden, Germany

Andreas Fery

Faculty of Chemistry and Food Chemistry, Division of Physical Chemistry of Polymeric Materials, Technical University Dresden, Mommsenstraße 6, 01069, Dresden, Germany

Sven Schirrmeister, Lucas Kurzweg & Andreas Fery

You can also search for this author in PubMed   Google Scholar

Contributions

All authors contributed to the study conception and design. Material preparation, data collection, and analysis were performed by Sven Schirrmeister, Xhoen Gjashta, and Lucas Kurzweg. Andreas Fery, Martin Socher, as well as Kathrin Harre, did the proofreading of the scientific statements. The first draft of the manuscript was written by Sven Schirrmeister, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Kathrin Harre .

Ethics declarations

Ethical approval.

Not applicable.

Consent to participate

Consent for publication, competing interests.

The authors declare no competing interests.

Additional information

Responsible Editor: Thomas D. Bucheli

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Schirrmeister, S., Kurzweg, L., Gjashta, X. et al. Regression analysis for the determination of microplastics in sediments using differential scanning calorimetry. Environ Sci Pollut Res (2024). https://doi.org/10.1007/s11356-024-33100-8

Download citation

Received : 05 November 2023

Accepted : 22 March 2024

Published : 15 April 2024

DOI : https://doi.org/10.1007/s11356-024-33100-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Microplastic
• Thermal analysis
• Find a journal
• Publish with us
• Track your research

• Open access
• Published: 18 April 2024

The influence of Life’s Essential 8 on the link between socioeconomic status and depression in adults: a mediation analysis

• Heming Zhang 1 , 2   na1 ,
• Lin Zhang 3 , 4   na1 ,
• Jiangjing Li 1 ,
• Hongxia Xiang 2 ,
• Yongfei Liu 1 ,
• Changjun Gao 1 &
• Xude Sun 1  

BMC Psychiatry volume  24 , Article number:  296 ( 2024 ) Cite this article

25 Accesses

Metrics details

Individuals with low socioeconomic status (SES) are at a higher risk of developing depression. However, evidence on the role of cardiovascular health (CVH) in this chain is sparse and limited. The purpose of this research was to assess the mediating role of Life’s Essential 8 (LE8), a recently updated measurement of CVH, in the association between SES and depression according to a nationally representative sample of adults.

Data was drawn from the National Health and Nutrition Examination Survey (NHANES) in 2013–2018. Multivariate logistic regression analysis was applied to analyze the association of SES (measured via the ratio of family income to poverty (FIPR), occupation, educational level, and health insurance) and LE8 with clinically relevant depression (CRD) (evaluated using the Patient Health Questionnaire (PHQ-9)). Multiple linear regression analysis was performed to analyze the correlation between SES and LE8. Mediation analysis was carried out to explore the mediating effect of LE8 on the association between SES and CRD. Moreover, these associations were still analyzed by sex, age, and race.

A total of 4745 participants with complete PHQ-9 surveys and values to calculated LE8 and SES were included. In the fully adjusted model, individuals with high SES had a significantly higher risk of CRD (odds ratio = 0.21; 95% confidence interval: 0.136 to 0.325, P  < 0.01) compared with those with low SES. Moreover, LE8 was estimated to mediate 22.13% of the total association between SES and CRD, and the mediating effect of LE8 varied in different sex and age groups. However, the mediating effect of LE8 in this chain was significant in different sex, age, and racial subgroups except for Mexican American (MA) individuals.

The results of our study suggest that LE8 could mediate the association between SES and CRD. Additionally, the mediating effect of LE8 in this chain could be influenced by the race of participants.

Peer Review reports

Introduction

The World Health Organization reported that depression, one of the most common mental diseases, affected more than 264 million people worldwide, which can be a major health challenge for individuals and an enormous societal burden [ 1 ]. The etiologies of depression are multifactorial, including biological, psychological, and social factors [ 2 ]. And previous studies have indicated that socioeconomic status (SES) has a significant influence on factors related to depression [ 3 ]. Individuals with low SES may be exposed to more adversity but have fewer resources to cope with depression [ 4 ]. However, these results are inconsistent and the influencing factors are complex [ 5 ].

Cardiovascular health (CVH) is commonly considered a factor that influences both SES and depression. Evidence suggests that less ideal CVH is associated with depression, and interventions targeting diet, physical activity, and sleep may ameliorate depressive symptoms [ 6 , 7 ]. Meanwhile, individuals with low SES are often exposed to unhealthy lifestyles, which in turn significantly increase their susceptibility to cardiovascular disease [ 8 ]. However, important gaps remain. Previous studies tended to use the risk of cardiovascular disease including angina, arrhythmias, and left ventricular dysfunction to represent individual CVH, ignoring a broader, more positive construct: the CVH of individuals without disease [ 9 ]. Life’s Essential 8 (LE8) is an approach to measuring and monitoring CVH developed by the American Heart Association [ 10 ]. Building on the original metrics (Life’s Simple 7), LE8 updates the algorithm for each metric and adds the sleep-health model to reflect CVH more accurately. Furthermore, it is still unclear whether the association of CVH with SES and depression varies among subpopulations of different age, sex, and racial groups.

Therefore, the present study aimed to examine the intricate relationship between SES and depression among adult participants in the National Health and Nutrition Examination Survey (NHANES) database, and further evaluate the mediating effect of LE8 in this chain.

Data sources and the study population

Cross-sectional data was collected from three cycles (2013–2018) of the National Health and Nutrition Examination Surveys (NHANES) dataset, a nationwide health survey of the non-institutionalized, civilian, U.S. population. The NHANES sample is drawn in four stages: (a) PSUs (counties, groups of tracts within counties), (b) segments within PSUs (census blocks), (c) dwelling units (households) within segments, and (d) individuals within households. Screening is conducted at the dwelling unit level to identify sampled persons, based on oversampling criteria. All procedures were approved by the Research Ethics Review Board of the National Center for Health Statistics, and written informed consent was obtained from all participants. Out of 29,400 adults who participated in the NHANES 2013–2018, 4745 participants with complete depression-screener data, the values used to calculate Life’s Essential 8 scores, and a family-income-to-poverty ratio were included in the present study (Fig.  1 ).Missing data associated with the selected variables constituted less than 10% of the full sample (Supplementary Figure S1 ) and was compensated for by the use of multiple imputations.

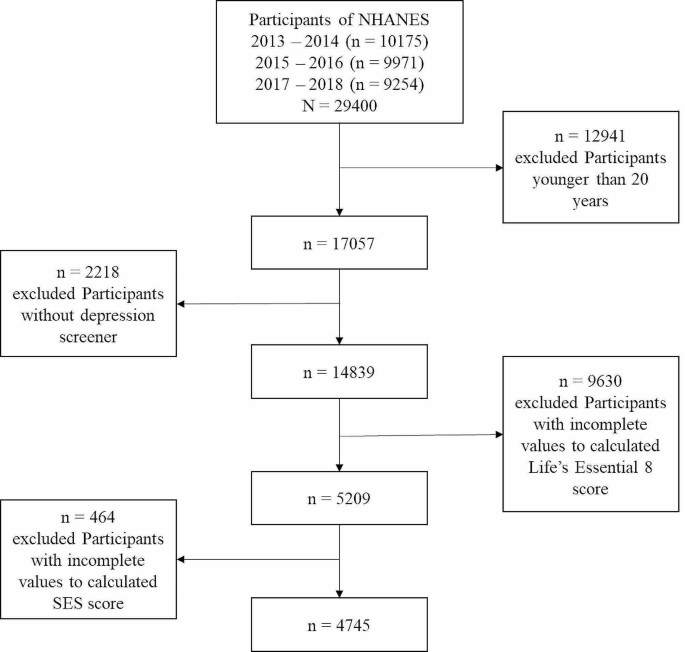
Flow chart for the selection of included sample

Depression assessment

Depression was assessed using the Patient Health Questionnaire (PHQ-9), which included nine questions about depressive symptoms over the previous two weeks. The responses ranged from 0 (“not at all”) to 1 (“several days”), 2 (“more than half the days”), and 3 (“nearly every day”), with total scores ranging from 0 to 27 [ 11 ]. According to the fourth edition of the Diagnostic and Statistical Manual of Mental Disorders, PHQ-9 scores of 10 or higher constitute clinically relevant depression (CRD), with a specificity and sensitivity of 88% [ 12 ].

Measurement of Life’s Essential 8

LE8 is an enhanced approach used to assess the construct of cardiovascular health (CVH). The components of Life’s Essential 8 include four health behaviors (diet, physical activity, nicotine exposure, and sleep health) and four health factors (body-mass index [BMI], blood lipids, blood glucose, and blood pressure). The detailed algorithms used to calculate LE8 scores can be found in Supplementary Table S1 [ 13 ]. The LE8 scores, which range between 0 and 100, represent the average of each of the 8 metrics.

Socioeconomic-status assessment

The ratios of family income to poverty (FIPR), occupation, educational level, and health insurance were used to evaluate SES [ 14 ]. FIPR was calculated in accordance with poverty guidelines published by the Department of Health and Human Services (HHS). Participants whose reported income was < $20,000 or ≥ $20,000 were excluded from the sample. The variables were divided into two or three levels, based on a practical interpretation and the sample size within levels (Supplementary Table S2 ). The SES was created using a latent class analysis to generate an unmeasured variable, based on four categorical variables above. Akaike information criterion (AIC) and Bayesian Information Criterion (BIC) decreased when the latent classes were added; these two indexes reached the bottom and rebounded when the latent class reached 3 (Supplementary Figure S2 A). The G 2 statistics continued to go down when the latent classes were added; this decrease leveled off after the three-latent-class solution (Supplementary Figure S2 B). After considering the statistics related to model selection and the meanings of latent classes, we chose the three-latent-class solution. The participants were divided into three grades (High SES, Medium SES, and Low SES) (Supplementary Table S3 ).

The study covariates, including sex, age, race, marital status, family size, alcohol consumption, and stroke are summarized in Supplementary Table S4 . These potential confounding factors are presented in the section on demographic data. Stroke was defined as self-reported physician diagnosis of stroke.

Statistical analysis

Given the complex sampling design of NHANES, all analyses in this study accounted for sample weights, clustering, and stratification. And a new sample weight was constructed in accordance with the NHANES analytical guidelines. Missing data were addressed via multiple imputation, using the R package “VIM.” A latent class analysis was conducted using the R package “poLCA.” The tolerance value for judging the point of convergence was set to 1E-10, while the maximum iterations were set to 1000. The model selection was based on the AIC, BIC, and likelihood ratio statistic G 2 .

For continuous variables, Shapiro-Wilk tests were used to confirm normality. Non-normally distributed data were presented as median (interquartile range, IQR), while Mood’s test was used to compare the CRD and non-CRD group levels. The categorical variables were presented as the number of cases and composition ratio (n [%]); chi-square tests were used to compare the percentages of these variables in different groups.

A multivariate logistic regression analysis was performed to analyze whether SES and LE8 were associated with CRD. The low FIPR group was used as the reference group for higher SES. The results are expressed as an odds ratio (OR) and corresponding 95% confidence interval (CI). Hosmer-Lemeshow test was used to assess the goodness of fit of logistic regression models. A multiple linear regression analysis was used to measure the association between SES and LE8, with the results reported as β and corresponding 95% CI. An F-test was applied to check the assumptions of the linear regression analysis. In this analysis, Model 1 was not adjusted for covariates; Model 2 was adjusted for sociodemographic variables, including sex, age, race, marital status, and family size. Model 3 was further adjusted for variables that likely influenced the results, including alcohol consumption and stroke, based on Model 2.

The mediating effect of LE8 on the association between SES and CRD was determined using the R package “mediation.” The path model in Supplementary Figure S3 indicates the mediating effect of periodontal measures. All statistical analyses were conducted by R 4.2.1 (R Foundation for Statistical Computing, Vienna, Austria). Differences with a two-sided P  < 0.05 were considered statistically significant when there were more than four latent classes.

Table  1 summarizes the demographic characteristics of the participants, categorized according to the CRD. There were 4745 participants in this study (30.348% aged 20–39 years, 34.542% aged 40–59 years and 35.111% aged ≥ 60 years; female: male ratio was 1:0.906), with 415 CRD participants. In general, participants with CRD are more likely to be female; have higher BMI; spend less time on physical activity; have a lower educational level; no domestic partner and small family size than participants without CRD. In addition, significant differences were also observed among the participants in different groups based on alcohol consumption, smoking, sleep health, occupation, health insurance, diabetes, stroke, and daily dietary intake including energy, protein, dietary-fiber, magnesium, sodium, and potassium ( P  < 0.05).

Table  2 summarizes the data on the association between SES and CRD, and no significant difference of Hosmer-Lemeshow tests were observed in all models ( P  > 0.05). In contrast to the low SES group, the high SES group were negatively correlated with CRD in all three models including Model 1 (OR = 0.199; 95% CI: 0.132 to 0.302, P  < 0.01), Model 2 (OR = 0.206; 95% CI: 0.133 to 0.319, P  < 0.01), and Model 3 (OR = 0.21; 95% CI: 0.136 to 0.325, P  < 0.01). And the correlation still significant in subgroup analysis stratified by both sex and age. However, after adjusting for all covariates, the results of the subgroup analysis stratified by race showed that SES was inversely associated with CRD in all participants apart from Mexican Americans (MA) (OR = 0.191; 95% CI: 0.027 to 1.338, P  = 0.09).

The association between LE8 and CRD is shown in Table  3 and Supplementary Table S5 . In the total sample, LE8 was negatively correlated with CRD in all three models [Model 1 (OR = 0.961, 95% CI: 0.952 to 0.971, P  < 0.01); Model 2 (OR = 0. 96, 95% CI: 0.949 to 0.971, P  < 0.01); Model 3 (OR = 0.962, 95% CI: 0.951 to 0.972, P  < 0.01)]. And the correlation still significant in all subgroup analyses ( P  < 0.05). The results of Hosmer-Lemeshow test were not statistically significant in all models ( P  > 0.05).

Table  4 presents the results of multivariate linear regression models between SES and LE8. Compared with those with low SES, participants with high SES had a higher LE8 scores in all three models [Model 1 (β = 10.407, 95% CI: 8.595 to 12.22, P  < 0.01); Model 2 (β = 10.937, 95% CI: 9.115 to 12.76, P  < 0.01); Model 3 (β = 10.852, 95% CI: 9.115 to 12.589, P  < 0.01)]. Additionally, in subgroup analyses stratified by sex and age, the trends remained the same in all three models ( P  < 0.05). However, in subgroup analyses stratified by race, the association of SES with LE8 is significant in all three models in participants except for MA. The F-test results were statistically different in all models ( P  < 0.05).

Table  5 reveals the mediation effect of LE8 on the association between SES and CRD. After all covariates adjustment, LE8 was estimated to mediate 22.13% of the association of SES with CRD. Meanwhile, the mediation effect of LE8 was statistically significant in the subgroup analyses divided by age and gender and the mediating effect ranged from 17.95 to 41.45% in Model 3. While in the subgroup analysis stratified by race, the mediating effect of LE8 could only be found in participants except for MA. In different race species, the mediating effect of LE8 ranged from 13.23 to 33.98% in fully adjusted models.

The present study investigates the association between SES and CRD and the mediating role of LE8. Community-dwelling adults in the United States with low SES exhibit more severe depressive states than those with higher SES, and the association could be influenced by race of the participants. This relationship between SES and CRD was significant in participants except for MA. In addition, LE8 significantly mediated the association between SES and CRD in participants apart from MA.

Socioeconomic inequity in depression has been widely discussed. A cross-sectional study involving 5969 Korean participants aged 60 or older found that the deleterious effect of a low material standard of living on social cohesion could indirectly influence depression in older adults [ 15 ]. Evidence based on the Iranian Prospective Epidemiological Research Studies suggests that participants with low SES are more likely to experience anxiety and depressive symptoms [ 16 ]. Furthermore, similar conclusions were also observed in a European collaborative research on ageing examined individuals aged 18 or older [ 17 ]. Inconsistent with previous studies tended to use single variables, we construct a comprehensive SES in this study and confirm the association between SES and CRD. However, this association could be influenced by race and no significant association were observed in MA participants.

The association of SES with CRD could be partially mediated by CHV. Existing research has demonstrated that cardiovascular mortality was significantly higher in the low-medium SES group than in the high SES group in the National Health Insurance Service national sample cohort of South Korea [ 18 ]. The increased cardiovascular disease burden in populations with low SES is associated with biologic, behavioral, and psychosocial risk factors, which are more prevalent among disadvantaged populations [ 19 , 20 ]. Mechanistically, individuals with low SES encounter difficulties in accessing abundant resources including knowledge, wealth, power, prestige, medical services, positive social relationships, and recreational facilities [ 21 , 22 , 23 , 24 ]. And these factors can further impact the cardiovascular disease of individuals [ 14 ]. In addition, previous study also indicated that depression is significantly correlated with poor CHV assessed by the American Heart Association 2010 [ 6 ]. At present, there is no consensus on the underlying mechanism of depression in relation to CHV. From a behavioral perspective, individuals with depression often engage in unhealthy lifestyle choices including smoking, excessive alcohol consumption, poor diet, and lack of exercise, all of which are risk factors for cardiovascular health [ 25 ]. In this study, we chose LE8, a more comprehensive approach, to measuring CVH and found that approximately 20% of the association between SES and CRD can be explained by LE8. Meanwhile, the mediating effect of LE8 was still significant in different gender or age groups.

In our study, we also found that the mediating effect of LE8 does not significantly impact the association between SES and CRD in MA participants. However, the underlying mechanisms for this race-based difference are intricate and multifactorial. One possible explanation could be dietary factors which linked to both CVD [ 26 ] and depression [ 27 ]. Evidence suggests that, among children and adults, non-Hispanic white and black Americans consume more junk food than Mexican Americans [ 28 ]. Such differences in dietary patterns may have confounded our findings. Furthermore, minority ethnic group participants exhibit higher levels of anhedonia compared to non-Hispanic white participants [ 29 ]. For instance, individuals of Latino descent exhibit higher rates of anhedonia compared to African Americans and Chinese Americans [ 30 ]. Nevertheless, it worth to known that urgent and necessary measures must be taken to actively reduce socioeconomic inequalities in order to promote mental health.

The present study has several strengths. First, the sample size is large enough to support subgroup analyses with sufficient statistical power. Second, we constructed an overall SES variable to comprehensively evaluate the complex relations of SES with CVH and CRD. In addition, LE8 offers a comprehensive and scientifically backed framework to evaluate the CVH of populations including those without cardiovascular disease.

Nevertheless, we also acknowledge several limitations. First, most indicators were measured once and thus could not provide a complete representation of the average level at different times. In addition, the longitudinal relationship between SES, LE8, and CRD could not be analyzed, due to the cross-sectional research design. Second, some measurement errors were inevitable, as the information on SES and LE8 included a self-report component. Third, we were unable to use a highly detailed group of occupations to calculate SES scores, due to the ambiguous delineation of occupation in two cycles of the NHANES dataset (2015–2016 and 2017–2018).

The results of this study indicate that SES is negatively associated with CRD and this association could be influenced by race. Meanwhile, LE8 largely mediates the relationship between SES and the risk of CRD in participants except for MA. Appropriate SES should be provided not only for a more reasonable allocation of social resources, but also for effectively protecting the CVH and mental health of the population. And it can further reduce the public health burden. Based on the reasoned findings and limitations of the present study, these results should be further confirmed via a large prospective cohort study.

Data availability

The datasets presented in this study can be found in online repositories. ( https://www.cdc.gov/nchs/index.htm )

Abbreviations

Akaike information criterion

Bayesian Information Criterion

Body mass index

Confidence interval

Clinically relevant depression

Cardiovascular health

The ratio of family income to poverty

Department of Health and Human Services

Interquartile Range

• Life’s Essential 8

Mexican American

Composition ratio

Non-Hispanic Asian

National Health and Nutrition Examination Survey

Non-Hispanic Black

Non-Hispanic White

Patient Health Questionnaire

• Socioeconomic status

Chen C, Ye Y, Zhang Y, Pan XF, Pan A. Weight change across adulthood in relation to all cause and cause specific mortality: prospective cohort study. BMJ. 2019;367:l5584.

Article   PubMed   PubMed Central   Google Scholar  

Aalbers G, McNally RJ, Heeren A, de Wit S, Fried EI. Social media and depression symptoms: a network perspective. J Exp Psychol Gen. 2019;148:8:1454–62.

Article   PubMed   Google Scholar  

Li W, Ruan W, Peng Y, Lu Z, Wang D. Associations of socioeconomic status and sleep disorder with depression among US adults. J Affect Disord. 2021;295:21–7.

Naylor-Wardle J, Rowland B, Kunadian V. Socioeconomic status and cardiovascular health in the COVID-19 pandemic. Heart. 2021;107:5:358–65.

Article   CAS   PubMed   Google Scholar  

Kessler RC, Bromet EJ. The epidemiology of depression across cultures. Annu Rev Public Health. 2013;34:119–38.

Patterson SL, Marcus M, Goetz M, Vaccarino V, Gooding HC. Depression and anxiety are associated with cardiovascular health in young adults. J Am Heart Assoc. 2022;11:24:e027610.

Xue Y, Liu G, Geng Q. Associations of cardiovascular disease and depression with memory related disease: a Chinese national prospective cohort study. J Affect Disord. 2020;266:187–93.

Shen R, Zhao N, Wang J, Guo P, Shen S, Liu D, et al. Association between socioeconomic status and arteriosclerotic cardiovascular disease risk and cause-specific and all-cause mortality: data from the 2005–2018 national health and nutrition examination survey. Front Public Health. 2022;10:1017271.

Schultz WM, Kelli HM, Lisko JC, Varghese T, Shen J, Sandesara P, et al. Socioeconomic status cardiovasc outcomes: challenges interventions. Circulation. 2018;137:20:2166–78.

Google Scholar  

Lloyd-Jones DM, Allen NB, Anderson CAM, Black T, Brewer LC, Foraker RE, et al. Life’s essential 8: updating and enhancing the American Heart Association’s construct of cardiovascular health: a presidential advisory from the American Heart Association. Circulation. 2022;146(5):e18–43.

Zhang Z, Jackson S, Merritt R, Gillespie C, Yang Q. Association between cardiovascular health metrics and depression among U.S. adults: national health and nutrition examination survey, 2007–2014. Ann Epidemiol. 2019;31:49–e5642.

Chunnan L, Shaomei S, Wannian L. The association between sleep and depressive symptoms in US adults: data from the NHANES (2007–2014). Epidemiol Psychiatr Sci. 2022;31:e63.

Lloyd-Jones DM, Ning H, Labarthe D, Brewer L, Sharma G, Rosamond W, et al. Status of cardiovascular health in us adults and children using the American Heart Association’s new Life’s Essential 8 metrics: prevalence estimates from the national health and nutrition examination survey (NHANES), 2013 through 2018. Circulation. 2022;146:11:822–35.

Zhang YB, Chen C, Pan XF, Guo J, Li Y, Franco OH, et al. Associations of healthy lifestyle and socioeconomic status with mortality and incident cardiovascular disease: two prospective cohort studies. BMJ. 2021;373:n604.

Han KM, Han C, Shin C, Jee HJ, An H, Yoon HK, et al. Social capital, socioeconomic status, and depression in community-living elderly. J Psychiatr Res. 2018;98:133–40.

Azizabadi Z, Aminisani N, Emamian MH. Socioeconomic inequality in depression and anxiety and its determinants in Iranian older adults. BMC Psychiatry. 2022;22:1:761.

Freeman A, Tyrovolas S, Koyanagi A, Chatterji S, Leonardi M, Ayuso-Mateos JL, et al. The role of socio-economic status in depression: results from the COURAGE (aging survey in Europe). BMC Public Health. 2016;16:1:1098.

Sung J, Song YM, Hong KP. Relationship between the shift of socioeconomic status and cardiovascular mortality. Eur J Prev Cardiol. 2020;27:7:749–57.

Winkleby MA, Jatulis DE, Frank E, Fortmann SP. Socioeconomic status and health: how education, income, and occupation contribute to risk factors for cardiovascular disease. Am J Public Health. 1992;82:6:816–20.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Adler NE, Glymour MM, Fielding J. Addressing social determinants of health and health inequalities. JAMA. 2016;316:16:1641–2.

Bhatnagar A. Environmental determinants of cardiovascular disease. Circ Res. 2017;121:2:162–80.

Schilbach F, Schofield H, Mullainathan S. The psychological lives of the poor. Am Econ Rev. 2016;106:5:435–40.

White JS, Hamad R, Li X, Basu S, Ohlsson H, Sundquist J, et al. Long-term effects of neighbourhood deprivation on diabetes risk: quasi-experimental evidence from a refugee dispersal policy in Sweden. Lancet Diabetes Endocrinol. 2016;4:6:517–24.

Hicken MT, Lee H, Morenoff J, House JS, Williams DR. Racial/ethnic disparities in hypertension prevalence: reconsidering the role of chronic stress. Am J Public Health. 2014;104:1:117–23.

Carney RM, Freedland KE, Miller GE, Jaffe AS. Depression as a risk factor for cardiac mortality and morbidity: a review of potential mechanisms. J Psychosom Res. 2002;53:4:897–902.

Petersen KS, Kris-Etherton PM. Diet quality assessment and the relationship between diet quality and cardiovascular disease risk. Nutrients. 2021;13:12.

Bremner JD, Moazzami K, Wittbrodt MT, Nye JA, Lima BB, Gillespie CF et al. Diet stress mental health. Nutrients. 2020;12;8.

Liu J, Lee Y, Micha R, Li Y, Mozaffarian D. Trends in junk food consumption among US children and adults, 2001–2018. Am J Clin Nutr. 2021;114:3:1039–48.

Vyas CM, Donneyong M, Mischoulon D, Chang G, Gibson H, Cook NR, et al. Association of race and ethnicity with late-life depression severity, symptom burden, and care. JAMA Netw Open. 2020;3:3:e201606.

Huang FY, Chung H, Kroenke K, Delucchi KL, Spitzer RL. Using the patient health questionnaire-9 to measure depression among racially and ethnically diverse primary care patients. J Gen Intern Med. 2006;21:6:547–52.

Download references

Acknowledgements

Not applicable.

The authors received no funding from an external source.

Author information

Heming Zhang and Lin Zhang contributed equally to this work and share first authorship.

Authors and Affiliations

Department of Anesthesiology, The Second Affiliated Hospital of Air Force Medical University, Xi’an, China

Heming Zhang, Jiangjing Li, Yongfei Liu, Changjun Gao & Xude Sun

Department of Anesthesiology, Hospital 963 of the PLA Joint Logistics Support Force, Jiamusi, China

Heming Zhang & Hongxia Xiang

Department of Geriatric Cardiology, The 2nd Medical Center, Chinese PLA General Hospital, Beijing, China

Department of Cardiology, National Center of Gerontology, Institute of Geriatric Medicine, Beijing Hospital, Chinese Academy of Medical Sciences, Beijing, China

You can also search for this author in PubMed   Google Scholar

Contributions

HZ and LZ: statistical test and data curation. HZ, LZ, and XS: methodology. HZ, YL, CG, and XS: writing– original draft. HZ, HX, JL, and XS: writing– review and editing. XS: supervision. All authors contributed to the article and approved the submitted version.

Corresponding author

Correspondence to Xude Sun .

Ethics declarations

Ethics approval and consent to participate.

The studies involving human participants were reviewed and approved by the National Center for Health Statistics Research Ethics Review Board. The patients/participants provided their written informed consent to participate in this study.

Consent for publication

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Additional file 1: Supplementary Figure S1.

Missing data of included participants. Supplementary Figure S2. (A) AIC, BIC, and (B) G2 in models with different numbers oflatent classes in NHANES. Supplementary Figure S3. Path diagram of themediation analysis models. Supplementary Table S1. Definition andscoring approach for quantifying cardiovascular health, as per the AmericanHeart Association’s Life’s Essential 8 score, and as applied in the NHANES,2013-2018. Supplementary Table S2. The classifications of variablesrelated to socioeconomic status. Supplementary Table S3 . Practicaldefinitions of high, medium, and low socioeconomic status. SupplementaryTable S4: The classifications of covariates. Supplementary Table S5: Associations of Life’s Essential 8 score with clinically relevant depression inparticipants with different socioeconomic status.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Zhang, H., Zhang, L., Li, J. et al. The influence of Life’s Essential 8 on the link between socioeconomic status and depression in adults: a mediation analysis. BMC Psychiatry 24 , 296 (2024). https://doi.org/10.1186/s12888-024-05738-8

Download citation

Received : 16 August 2023

Accepted : 04 April 2024

Published : 18 April 2024

DOI : https://doi.org/10.1186/s12888-024-05738-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• National health and nutrition examination survey
• Mediation analysis

BMC Psychiatry

ISSN: 1471-244X

• Submission enquiries: [email protected]
• General enquiries: [email protected]