What is The Null Hypothesis & When Do You Reject The Null Hypothesis
Julia Simkus
Editor at Simply Psychology
BA (Hons) Psychology, Princeton University
Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.
Learn about our Editorial Process
Saul Mcleod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.
The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).
The null hypothesis is the statement that a researcher or an investigator wants to disprove.
Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.

How to Write a Null Hypothesis
Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.
It is a default position that your research aims to challenge or confirm.
For example, if studying the impact of exercise on weight loss, your null hypothesis might be:
There is no significant difference in weight loss between individuals who exercise daily and those who do not.
Examples of Null Hypotheses
| Research Question | Null Hypothesis |
|---|---|
| Do teenagers use cell phones more than adults? | Teenagers and adults use cell phones the same amount. |
| Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil? | Tomato plants show no difference in growth rates when planted in compost rather than soil. |
| Does daily meditation decrease the incidence of depression? | Daily meditation does not decrease the incidence of depression. |
| Does daily exercise increase test performance? | There is no relationship between daily exercise time and test performance. |
| Does the new vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does flossing your teeth affect the number of cavities? | Flossing your teeth has no effect on the number of cavities. |
When Do We Reject The Null Hypothesis?
We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.
If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.
Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).
If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.
You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.
Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.
The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.
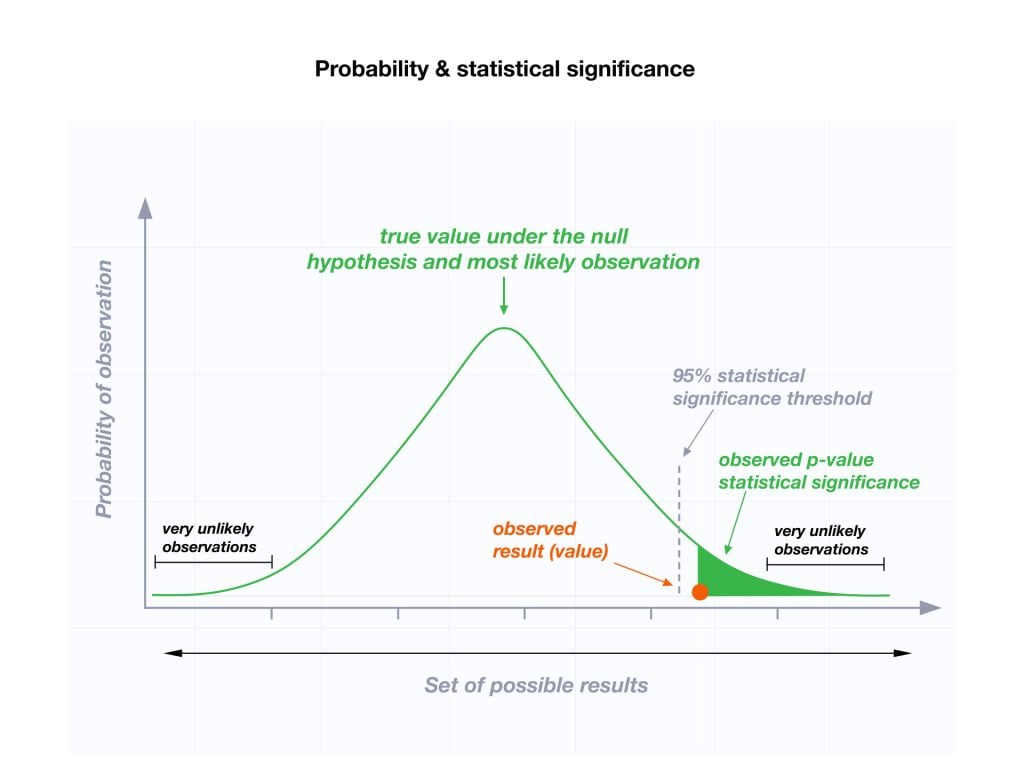
Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.
When your p-value is less than or equal to your significance level, you reject the null hypothesis.
In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.
In this case, the sample data provides insufficient data to conclude that the effect exists in the population.
Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.
When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.
Why Do We Never Accept The Null Hypothesis?
The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.
A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.
It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.
One can either reject the null hypothesis, or fail to reject it, but can never accept it.
Why Do We Use The Null Hypothesis?
We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.
The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.
Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.
Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.
It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.
Purpose of a Null Hypothesis
- The primary purpose of the null hypothesis is to disprove an assumption.
- Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
- A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.
Do you always need both a Null Hypothesis and an Alternative Hypothesis?
The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.
While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.
The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.
What is the difference between a null hypothesis and an alternative hypothesis?
The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.
It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.
What are some problems with the null hypothesis?
One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.
Why can a null hypothesis not be accepted?
We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.
We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.
Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.
If the p-value is greater than the significance level, then you fail to reject the null hypothesis.
Is a null hypothesis directional or non-directional?
A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.
A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.
A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.
The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.
Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.
Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.
Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.
Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.
Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.
Related Articles

Research Methodology
Mixed Methods Research

Conversation Analysis

Discourse Analysis

Phenomenology In Qualitative Research

Ethnography In Qualitative Research

Narrative Analysis In Qualitative Research

When Do You Reject the Null Hypothesis? (3 Examples)
A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.
We always use the following steps to perform a hypothesis test:
Step 1: State the null and alternative hypotheses.
The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.
The alternative hypothesis , denoted as H A , is the hypothesis that the sample data is influenced by some non-random cause.
2. Determine a significance level to use.
Decide on a significance level. Common choices are .01, .05, and .1.
3. Calculate the test statistic and p-value.
Use the sample data to calculate a test statistic and a corresponding p-value .
4. Reject or fail to reject the null hypothesis.
If the p-value is less than the significance level, then you reject the null hypothesis.
If the p-value is not less than the significance level, then you fail to reject the null hypothesis.
You can use the following clever line to remember this rule:
“If the p is low, the null must go.”
In other words, if the p-value is low enough then we must reject the null hypothesis.
The following examples show when to reject (or fail to reject) the null hypothesis for the most common types of hypothesis tests.
Example 1: One Sample t-test
A one sample t-test is used to test whether or not the mean of a population is equal to some value.
For example, suppose we want to know whether or not the mean weight of a certain species of turtle is equal to 310 pounds.
We go out and collect a simple random sample of 40 turtles with the following information:
- Sample size n = 40
- Sample mean weight x = 300
- Sample standard deviation s = 18.5
We can use the following steps to perform a one sample t-test:
Step 1: State the Null and Alternative Hypotheses
We will perform the one sample t-test with the following hypotheses:
- H 0 : μ = 310 (population mean is equal to 310 pounds)
- H A : μ ≠ 310 (population mean is not equal to 310 pounds)
We will choose to use a significance level of 0.05 .
We can plug in the numbers for the sample size, sample mean, and sample standard deviation into this One Sample t-test Calculator to calculate the test statistic and p-value:
- t test statistic: -3.4187
- two-tailed p-value: 0.0015
Since the p-value (0.0015) is less than the significance level (0.05) we reject the null hypothesis .
We conclude that there is sufficient evidence to say that the mean weight of turtles in this population is not equal to 310 pounds.
Example 2: Two Sample t-test
A two sample t-test is used to test whether or not two population means are equal.
For example, suppose we want to know whether or not the mean weight between two different species of turtles is equal.
We go out and collect a simple random sample from each population with the following information:
- Sample size n 1 = 40
- Sample mean weight x 1 = 300
- Sample standard deviation s 1 = 18.5
- Sample size n 2 = 38
- Sample mean weight x 2 = 305
- Sample standard deviation s 2 = 16.7
We can use the following steps to perform a two sample t-test:
We will perform the two sample t-test with the following hypotheses:
- H 0 : μ 1 = μ 2 (the two population means are equal)
- H 1 : μ 1 ≠ μ 2 (the two population means are not equal)
We will choose to use a significance level of 0.10 .
We can plug in the numbers for the sample sizes, sample means, and sample standard deviations into this Two Sample t-test Calculator to calculate the test statistic and p-value:
- t test statistic: -1.2508
- two-tailed p-value: 0.2149
Since the p-value (0.2149) is not less than the significance level (0.10) we fail to reject the null hypothesis .
We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.
Example 3: Paired Samples t-test
A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.
For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump of college basketball players.
To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month:

We can use the following steps to perform a paired samples t-test:
We will perform the paired samples t-test with the following hypotheses:
- H 0 : μ before = μ after (the two population means are equal)
- H 1 : μ before ≠ μ after (the two population means are not equal)
We will choose to use a significance level of 0.01 .
We can plug in the raw data for each sample into this Paired Samples t-test Calculator to calculate the test statistic and p-value:
- t test statistic: -3.226
- two-tailed p-value: 0.0045
Since the p-value (0.0045) is less than the significance level (0.01) we reject the null hypothesis .
We have sufficient evidence to say that the mean vertical jump before and after participating in the training program is not equal.
Bonus: Decision Rule Calculator
You can use this decision rule calculator to automatically determine whether you should reject or fail to reject a null hypothesis for a hypothesis test based on the value of the test statistic.
Featured Posts
Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Join the Statology Community
Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!
By subscribing you accept Statology's Privacy Policy.
Hypothesis Testing (cont...)
Hypothesis testing, the null and alternative hypothesis.
In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.
The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:
| Null Hypotheses (H ): | Undertaking seminar classes has no effect on students' performance. |
| Alternative Hypothesis (H ): | Undertaking seminar class has a positive effect on students' performance. |
Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:
| Null Hypotheses (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is the same in the population. |
| Alternative Hypothesis (H ): | The mean exam mark for the "seminar" and "lecture-only" teaching methods is not the same in the population. |
Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.
Significance levels
The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?
So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.
Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions
When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:
| Alternative Hypothesis (H ): | Undertaking seminar classes has a positive effect on students' performance. |
The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.
Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.
Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:
| Alternative Hypothesis (H ): | Undertaking seminar classes has an effect on students' performance. |
In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.
Rejecting or failing to reject the null hypothesis
Let's return finally to the question of whether we reject or fail to reject the null hypothesis.
If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

Accept or Fail to Reject? Understanding Hypothesis Testing
What is hypothesis testing: accept or fail to reject.
Hypothesis testing is a cornerstone of statistical analysis used to infer the properties of a population based on sample data. This method involves setting up two opposing hypotheses—the null hypothesis, which posits no effect or no difference, and the alternative hypothesis, which suggests some effect or difference.
The decision-making process in hypothesis testing hinges on whether the evidence is sufficient to reject the null hypothesis, or if we fail to reject it , implying that the data does not provide strong enough proof to support the alternative. The outcome — rejecting or failing to reject the null hypothesis — helps researchers draw conclusions about the statistical significance and implications of their findings.
Description of Hypothesis Testing
When conducting a hypothesis test, statistical methods are used to decide whether to accept the null hypothesis or fail to reject it based on the data. "Failing to reject" the null hypothesis does not necessarily mean that we accept it as true. Instead, it means that there isn't enough evidence against the null hypothesis; hence, we do not adopt the alternative hypothesis. The decision fundamentally hinges on the calculation of the probability of observing the collected data (or data more extreme) assuming that the null hypothesis is true, which is quantified by the p-value.
- 1. If the p-value is low (typically less than a predetermined threshold like 0.05), it suggests that such data is very unlikely under the null hypothesis. In this case, the null hypothesis is rejected, and the alternative hypothesis is considered more likely.
- 2. If the p-value is high , indicating that the observed data is likely under the null hypothesis, then we fail to reject the null hypothesis. This does not confirm the null hypothesis is true; rather, it suggests that the data does not provide strong evidence against it
Role of P-Values and Test Statistics
A P-value , or probability value, is a key statistic in hypothesis testing used to measure the strength of the evidence against the null hypothesis. It quantifies the probability of observing the results of a study—or more extreme results—assuming that the null hypothesis is true. It is the probability of observing a test statistic as extreme as, or more extreme than, what is observed if the null hypothesis is true. If this P-value is less than the chosen significance level (often 0.05), then the null hypothesis is rejected in favor of the alternative. If it is greater, we fail to reject the null hypothesis. Test statistics like the t-statistic, z-score, and chi-square are calculated from the data and are used to determine the P-value.Check an example by watching this video:
Critical Values and Decision Making
Critical values are essential components in the framework of hypothesis testing, acting as cutoff points that help decide whether to reject the null hypothesis. The selection of these values is directly tied to the chosen confidence level, which typically might be 90%, 95%, or 99%. This confidence level represents the probability that the confidence interval would contain the true population parameter if you were to repeat the study multiple times.
- Implications of Decision Outcomes
This part looks at the potential impacts of hypothesis testing, including the common errors associated with it and how they affect decisions in research and data analysis.
Impacts of Type I and Type II Errors
Type I errors, also known as false positives, occur when the null hypothesis is incorrectly rejected when it is actually true. This can lead researchers to believe there is an effect when there isn't one.
Type II errors, also known as false negatives, occur when the null hypothesis is not rejected even though it is false. This leads researchers to overlook a genuine effect in the data. Properly understanding and managing these errors is crucial for accurately interpreting hypothesis testing results and avoiding misleading conclusions in research and data analysis.
Learning Hypothesis Testing: Fail, Accept, or Reject with JOVE
JOVE provides an extensive range of visual and interactive materials designed specifically to teach the nuances of hypothesis testing, including how to properly handle the outcomes of failing to reject, accepting, or rejecting hypotheses. Through detailed video tutorials and comprehensive case studies, JOVE helps users grasp complex concepts
Subscribe now for your Free Trial: Hypothesis Accept or Fail to reject
The conclusion reaffirms the importance of mastering hypothesis testing techniques, highlighting their role in making informed statistical decisions in research and professional practices. This wrap-up emphasizes the necessity of a solid grasp of statistical principles for accurate data interpretation and decision-making.
Related Posts
We use cookies to enhance your experience on our website.
By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
Prevent plagiarism. Run a free check.
The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved June 24, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
13.1 Understanding Null Hypothesis Testing
Learning objectives.
- Explain the purpose of null hypothesis testing, including the role of sampling error.
- Describe the basic logic of null hypothesis testing.
- Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
The Purpose of Null Hypothesis Testing
As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)
One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any statistical relationship in a sample can be interpreted in two ways:
- There is a relationship in the population, and the relationship in the sample reflects this.
- There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.
The Logic of Null Hypothesis Testing
Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
- Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
- Determine how likely the sample relationship would be if the null hypothesis were true.
- If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”
The Misunderstood p Value
The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994). Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.
Role of Sample Size and Relationship Strength
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”
Table 13.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant
| Relationship strength | |||
|---|---|---|---|
| Sample Size | Weak | Medium | Strong |
| Small ( = 20) | No | No | = Maybe = Yes |
| Medium ( = 50) | No | Yes | Yes |
| Large ( = 100) | = Yes = No | Yes | Yes |
| Extra large ( = 500) | Yes | Yes | Yes |
Although Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.
Statistical Significance Versus Practical Significance
Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007). The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.
Key Takeaways
- Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
- The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
- The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
- Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
- Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
Practice: Use Table 13.1 “How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant” to decide whether each of the following results is statistically significant.
- The correlation between two variables is r = −.78 based on a sample size of 137.
- The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
- In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
- In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
- A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003.
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science , 16 , 259–263.
Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Failing to Reject the Null Hypothesis
By Jim Frost 69 Comments
Failing to reject the null hypothesis is an odd way to state that the results of your hypothesis test are not statistically significant. Why the peculiar phrasing? “Fail to reject” sounds like one of those double negatives that writing classes taught you to avoid. What does it mean exactly? There’s an excellent reason for the odd wording!
In this post, learn what it means when you fail to reject the null hypothesis and why that’s the correct wording. While accepting the null hypothesis sounds more straightforward, it is not statistically correct!
Before proceeding, let’s recap some necessary information. In all statistical hypothesis tests, you have the following two hypotheses:
- The null hypothesis states that there is no effect or relationship between the variables.
- The alternative hypothesis states the effect or relationship exists.
We assume that the null hypothesis is correct until we have enough evidence to suggest otherwise.
After you perform a hypothesis test, there are only two possible outcomes.

- When your p-value is greater than your significance level, you fail to reject the null hypothesis. Your results are not significant. You’ll learn more about interpreting this outcome later in this post.
Related posts : Hypothesis Testing Overview and The Null Hypothesis
Why Don’t Statisticians Accept the Null Hypothesis?
To understand why we don’t accept the null, consider the fact that you can’t prove a negative. A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. It might exist, but your study missed it. That’s a huge difference and it is the reason for the convoluted wording. Let’s look at several analogies.
Species Presumed to be Extinct

Lack of proof doesn’t represent proof that something doesn’t exist!
Criminal Trials

Perhaps the prosecutor conducted a shoddy investigation and missed clues? Or, the defendant successfully covered his tracks? Consequently, the verdict in these cases is “not guilty.” That judgment doesn’t say the defendant is proven innocent, just that there wasn’t enough evidence to move the jury from the default assumption of innocence.
Hypothesis Tests

The hypothesis test assesses the evidence in your sample. If your test fails to detect an effect, it’s not proof that the effect doesn’t exist. It just means your sample contained an insufficient amount of evidence to conclude that it exists. Like the species that were presumed extinct, or the prosecutor who missed clues, the effect might exist in the overall population but not in your particular sample. Consequently, the test results fail to reject the null hypothesis, which is analogous to a “not guilty” verdict in a trial. There just wasn’t enough evidence to move the hypothesis test from the default position that the null is true.
The critical point across these analogies is that a lack of evidence does not prove something does not exist—just that you didn’t find it in your specific investigation. Hence, you never accept the null hypothesis.
Related post : The Significance Level as an Evidentiary Standard
What Does Fail to Reject the Null Hypothesis Mean?
Accepting the null hypothesis would indicate that you’ve proven an effect doesn’t exist. As you’ve seen, that’s not the case at all. You can’t prove a negative! Instead, the strength of your evidence falls short of being able to reject the null. Consequently, we fail to reject it.
Failing to reject the null indicates that our sample did not provide sufficient evidence to conclude that the effect exists. However, at the same time, that lack of evidence doesn’t prove that the effect does not exist. Capturing all that information leads to the convoluted wording!
What are the possible implications of failing to reject the null hypothesis? Let’s work through them.
First, it is possible that the effect truly doesn’t exist in the population, which is why your hypothesis test didn’t detect it in the sample. Makes sense, right? While that is one possibility, it doesn’t end there.
Another possibility is that the effect exists in the population, but the test didn’t detect it for a variety of reasons. These reasons include the following:
- The sample size was too small to detect the effect.
- The variability in the data was too high. The effect exists, but the noise in your data swamped the signal (effect).
- By chance, you collected a fluky sample. When dealing with random samples, chance always plays a role in the results. The luck of the draw might have caused your sample not to reflect an effect that exists in the population.
Notice how studies that collect a small amount of data or low-quality data are likely to miss an effect that exists? These studies had inadequate statistical power to detect the effect. We certainly don’t want to take results from low-quality studies as proof that something doesn’t exist!
However, failing to detect an effect does not necessarily mean a study is low-quality. Random chance in the sampling process can work against even the best research projects!
If you’re learning about hypothesis testing and like the approach I use in my blog, check out my eBook!

Share this:

Reader Interactions
May 8, 2024 at 9:08 am
Thank you very much for explaining the topic. It brings clarity and makes statistics very simple and interesting. Its helping me in the field of Medical Research.
February 26, 2024 at 7:54 pm
Hi Jim, My question is that can I reverse Null hyposthesis and start with Null: µ1 ≠ µ2 ? Then, if I can reject Null, I will end up with µ1=µ2 for mean comparison and this what I am looking for. But isn’t this cheating?
February 26, 2024 at 11:41 pm
That can be done but it requires you to revamp the entire test. Keep in mind that the reason you normally start out with the null equating to no relationship is because the researchers typically want to prove that a relationship or effect exists. This format forces the researchers to collect a substantial amount of high quality data to have a chance at demonstrating that an effect exists. If they collect a small sample and/or poor quality (e.g., noisy or imprecise), then the results default back to the null stating that no effect exists. So, they have to collect good data and work hard to get findings that suggest the effect exists.
There are tests that flip it around as you suggest where the null states that a relationship does exist. For example, researchers perform an equivalency test when they want to show that there is no difference. That the groups are equal. The test is designed such that it requires a good sample size and high quality data to have a chance at proving equivalency. If they have a small sample size and/or poor quality data, the results default back to the groups being unequal, which is not what they want to show.
So, choose the null hypothesis and corresponding analysis based on what you hope to find. Choose the null hypothesis that forces you to work hard to reject it and get the results that you want. It forces you to collect better evidence to make your case and the results default back to what you don’t want if you do a poor job.
I hope that makes sense!
October 13, 2023 at 5:10 am
Really appreciate how you have been able to explain something difficult in very simple terms. Also covering why you can’t accept a null hypothesis – something which I think is frequently missed. Thank you, Jim.
February 22, 2022 at 11:18 am
Hi Jim, I really appreciate your blog, making difficult things sound simple is a great gift.
I have a doubt about the p-value. You said there are two options when it comes to hypothesis tests results . Reject or failing to reject the null, depending on the p-value and your significant level.
But… a P-value of 0,001 means a stronger evidence than a P-value of 0,01? ( both with a significant level of 5%. Or It doesn`t matter, and just every p-Value under your significant level means the same burden of evidence against the null?
I hope I made my point clear. Thanks a lot for your time.
February 23, 2022 at 9:06 pm
There are different schools of thought about this question. The traditional approach is clear cut. Your results are statistically significance when your p-value is less than or equal to your significance level. When the p-value is greater than the significance level, your results are not significant.
However, as you point out, lower p-values indicate stronger evidence against the null hypothesis. I write about this aspect of p-values in several articles, interpreting p-values (near the end) and p-values and reproducibility .
Personally, I consider both aspects. P-values near 0.05 provide weak evidence. Consequently, I’d be willing to say that p-values less than or equal to 0.05 are statistically significant, but when they’re near 0.05, I’d consider it as a preliminary result that requires more research. However, if the p-value is less 0.01, or even better 0.001, then that’s much stronger evidence and I’ll give those results more weight in my evaluation.
If you read those two articles, I think you’ll see what I mean.
January 1, 2022 at 6:00 pm
HI, I have a quick question that you may be able to help me with. I am using SPSS and carrying out a Mann W U Test it says to retain the null hypothesis. The hypothesis is that males are faster than women at completing a task. So is that saying that they are or are not
January 1, 2022 at 8:17 pm
In that case, your sample data provides insufficient evidence to conclude that males are faster. The results do not prove that males and females are the same speed. You just don’t have enough evidence to say males are faster. In this post, I cover the reasons why you can’t prove the null is true.
November 23, 2021 at 5:36 pm
What if I have to prove in my hypothesis that there shouldn’t be any affect of treatment on patients? Can I say that if my null hypothesis is accepted i have got my results (no effect)? I am confused what to do in this situation. As for null hypothesis we always have to write it with some type of equality. What if I want my result to be what i have stated in null hypothesis i.e. no effect? How to write statements in this case? I am using non parametric test, Mann whitney u test
November 27, 2021 at 4:56 pm
You need to perform an equivalence test, which is a special type of procedure when you want to prove that the results are equal. The problem with a regular hypothesis test is that when you fail to reject the null, you’re not proving that they the outcomes are equal. You can fail to reject the null thanks to a small sample size, noisy data, or a small effect size even when the outcomes are truly different at the population level. An equivalence test sets things up so you need strong evidence to really show that two outcomes are equal.
Unfortunately, I don’t have any content for equivalence testing at this point, but you can read an article about it at Wikipedia: Equivalence Test .
August 13, 2021 at 9:41 pm
Great explanation and great analogies! Thanks.
August 11, 2021 at 2:02 am
I got problems with analysis. I did wound healing experiments with drugs treatment (total 9 groups). When I do the 2-way ANOVA in excel, I got the significant results in sample (Drug Treatment) and columns (Day, Timeline) . But I did not get the significantly results in interactions. Can I still reject the null hypothesis and continue the post-hoc test?
Thank you very much.
June 13, 2021 at 4:51 am
Hi Jim, There are so many books covering maths/programming related to statistics/DS, but may be hardly any book to develop an intuitive understanding. Thanks to you for filling up that gap. After statistics, hypothesis-testing, regression, will it be possible for you to write such books on more topics in DS such as trees, deep-learning etc.
I recently started with reading your book on hypothesis testing (just finished the first chapter). I have a question w.r.t the fuel cost example (from first chapter), where a random sample of 25 families (with sample mean 330.6) is taken. To do the hypothesis testing here, we are taking a sampling distribution with a mean of 260. Then based on the p-value and significance level, we find whether to reject or accept the null hypothesis. The entire decision (to accept or reject the null hypothesis) is based on the sampling distribution about which i have the following questions : a) we are assuming that the sampling distribution is normally distributed. what if it has some other distribution, how can we find that ? b) We have assumed that the sampling distribution is normally distributed and then further assumed that its mean is 260 (as required for the hypothesis testing). But we need the standard deviation as well to define the normal distribution, can you please let me know how do we find the standard deviation for the sampling distribution ? Thanks.
April 24, 2021 at 2:25 pm
Maybe its the idea of “Innocent until proven guilty”? Your Null assume the person is not guilty, and your alternative assumes the person is guilty, only when you have enough evidence (finding statistical significance P0.05 you have failed to reject null hypothesis, null stands,implying the person is not guilty. Or, the person remain innocent.. Correct me if you think it’s wrong but this is the way I interpreted.
April 25, 2021 at 5:10 pm
I used the courtroom/trial analogy within this post. Read that for more details. I’d agree with your general take on the issue except when you have enough evidence you actually reject the null, which in the trial means the defendant is found guilty.
April 17, 2021 at 6:10 am
Can regression analysis be done using 5 companies variables for predicting working capital management and profitability positive/negative relationship?
Also, does null hypothesis rejecting means whatsoever is stated in null hypothesis that is false proved through regression analysis?
I have very less knowledge about regression analysis. Please help me, Sir. As I have my project report due on next week. Thanks in advance!
April 18, 2021 at 10:48 pm
Hi Ahmed, yes, regression analysis can be used for the scenario you describe as long as you have the required data.
For more about the null hypothesis in relation to regression analysis, read my post about regression coefficients and their p-values . I describe the null hypothesis in it.
January 26, 2021 at 7:32 pm
With regards to the legal example above. While your explanation makes sense when simplified to this statistical level, from a legal perspective it is not correct. The presumption of innocence means one does not need to be proven innocent. They are innocent. The onus of proof lies with proving they are guilty. So if you can’t prove someones guilt then in fact you must accept the null hypothesis that they are innocent. It’s not a statistical test so a little bit misleading using it an example, although I see why you would.
If it were a statistical test, then we would probably be rather paranoid that everyone is a murderer but they just haven’t been proven to be one yet.
Great article though, a nice simple and thoughtout explanation.
January 26, 2021 at 9:11 pm
It seems like you misread my post. The hypothesis testing/legal analogy is very strong both in making the case and in the result.
In hypothesis testing, the data have to show beyond a reasonable doubt that the alternative hypothesis is true. In a court case, the prosecutor has to present sufficient evidence to show beyond a reasonable doubt that the defendant is guilty.
In terms of the test/case results. When the evidence (data) is insufficient, you fail to reject the null hypothesis but you do not conclude that the data proves the null is true. In a legal case that has insufficient evidence, the jury finds the defendant to be “not guilty” but they do not say that s/he is proven innocent. To your point specifically, it is not accurate to say that “not guilty” is the same as “proven innocent.”
It’s a very strong parallel.
January 9, 2021 at 11:45 am
Just a question, in my research on hypotheses for an assignment, I am finding it difficult to find an exact definition for a hypothesis itself. I know the defintion, but I’m looking for a citable explanation, any ideas?
January 10, 2021 at 1:37 am
To be clear, do you need to come up with a statistical hypothesis? That’s one where you’ll use a particular statistical hypothesis test. If so, I’ll need to know more about what you’re studying, your variables, and the type of hypothesis test you plan to use.
There are also scientific hypotheses that you’ll state in your proposals, study papers, etc. Those are different from statistical hypotheses (although related). However, those are very study area specific and I don’t cover those types on this blog because this is a statistical blog. But, if it’s a statistical hypothesis for a hypothesis test, then let me know the information I mention above and I can help you out!
November 7, 2020 at 8:33 am
Hi, good read, I’m kind of a novice here, so I’m trying to write a research paper, and I’m trying to make a hypothesis. however looking at the literature, there are contradicting results.
researcher A found that there is relationship between X and Y
however, researcher B found that there is no relationship between X and Y
therefore, what is the null hypothesis between X and y? do we choose what we assumed to be correct for our study? or is is somehow related to the alternative hypothesis? I’m confused.
thank you very much for the help.
November 8, 2020 at 12:07 am
Hypotheses for a statistical test are different than a researcher’s hypothesis. When you’re constructing the statistical hypothesis, you don’t need to consider what other researchers have found. Instead, you construct them so that the test only produces statistically significant results (rejecting the null) when your data provides strong evidence. I talk about that process in this post.
Typically, researchers are hoping to establish that an effect or relationship exists. Consequently, the null and alternative hypotheses are typically the following:
Null: The effect or relationship doesn’t not exist. Alternative: The effect or relationship does exist.
However, if you’re hoping to prove that there is no effect or no relationship, you then need to flip those hypotheses and use a special test, such as an equivalences test.
So, there’s no need to consider what researchers have found but instead what you’re looking for. In most cases, you are looking for an effect/relationship, so you’d go with the hypotheses as I show them above.
I hope that helps!
October 22, 2020 at 6:13 pm
Great, deep detailed answer. Appreciated!
September 16, 2020 at 12:03 pm
Thank you for explaining it too clearly. I have the following situation with a Box Bohnken design of three levels and three factors for multiple responses. F-value for second order model is not significant (failing to reject null hypothesis, p-value > 0.05) but, lack of fit of the model is not significant. What can you suggest me about statistical analysis?
September 17, 2020 at 2:42 am
Are your first order effects significant?
You want the lack of fit to be nonsignificant. If it’s significant, that means the model doesn’t fit the data well. So, you’re good there! 🙂
September 14, 2020 at 5:18 pm
thank you for all the explicit explanation on the subject.
However, i still got a question about “accepting the null hypothesis”. from textbook, the p-value is the probability that a statistic would take a value that is as extreme as or more extreme than that actually observed.
so, that’s why when p<0.01 we reject the null hypothesis, because it's too rare (p0.05, i can understand that for most cases we cannot accept the null, for example, if p=0.5, it means that the probability to get a statistic from the distribution is 0.5, which is totally random.
But how about when the p is very close to 1, like p=0.95, or p=0.99999999, can’t we say that the probability that the statistic is not from this distribution is less than 0.05, | or in another way, the probability that the statistic is from the distribution is almost 1. can’t we accept the null in such circumstance?
September 11, 2020 at 12:14 pm
Wow! This is beautifully explained. “Lack of proof doesn’t represent proof that something doesn’t exist!”. This kinda, hit me with such force. Can I then, use the same analogy for many other things in life? LOL! 🙂
H0 = God does not exist; H1 = God does exist; WE fail to reject H0 as there is no evidence.
Thank you sir, this has answered many of my questions, statistically speaking! No pun intended with the above.
September 11, 2020 at 4:58 pm
Hi, LOL, I’m glad it had such meaning for you! I’ll leave the determination about the existence of god up to each person, but in general, yes, I think statistical thinking can be helpful when applied to real life. It is important to realize that lack of proof truly is not proof that something doesn’t exist. But, I also consider other statistical concepts, such as confounders and sampling methodology, to be useful keeping in mind when I’m considering everyday life stuff–even when I’m not statistically analyzing it. Those concepts are generally helpful when trying to figure out what is going on in your life! Are there other alternative explanations? Is what you’re perceiving likely to be biased by something that’s affecting the “data” you can observe? Am I drawing a conclusion based on a large or small sample? How strong is the evidence?
A lot of those concepts are great considerations even when you’re just informally assessing and draw conclusions about things happening in your daily life.
August 13, 2020 at 12:04 am
Dear Jim, thanks for clarifying. absolutely, now it makes sense. the topic is murky but it is good to have your guidance, and be clear. I have not come across an instructor as clear in explaining as you do. Appreciate your direction. Thanks a lot, Geetanjali
August 15, 2020 at 3:48 pm
Hi Geetanjali,
I’m glad my website is helpful! That makes my day hearing that. Thanks so much for writing!
August 12, 2020 at 9:37 am
Hi Jim. I am doing data analyis for my masters thesis and my hypothesis testings were insignificant. And I am ok with that. But there is something bothering me. It is the low reliabilities of the 4-Items sub-scales (.55, .68, .75), though the overall alpha is good (.85). I just wonder if it is affecting my hypothesis testings.
August 11, 2020 at 9:23 pm
Thank you sir for replying, yes sir we it’s a RCT study.. where we did within and between the groups analysis and found p>0.05 in between the groups using Mann Whitney U test. So in such cases if the results comes like this we need to Mention that we failed reject the null hypothesis? Is that correct? Whether it tells that the study is inefficient as we couldn’t accept the alternative hypothesis. Thanks is advance.
August 11, 2020 at 9:43 pm
Hi Saumya, ah, this becomes clearer. When ask statistical questions, please be sure to include all relevant information because the details are extremely important. I didn’t know it was an RCT with a treatment and control group. Yes, given that your p-value is greater than your significance level, you fail to reject the null hypothesis. The results are not significant. The experiment provides insufficient evidence to conclude that the outcome in the treatment group is different than the control group.
By the way, you never accept the alternative hypothesis (or the null). The two options are to either reject the null or fail to reject the null. In your case, you fail to reject the null hypothesis.
I hope this helps!
August 11, 2020 at 9:41 am
Sir, p value is0.05, by which we interpret that both the groups are equally effective. In this case I had to reject the alternative hypothesis/ failed to reject null hypothessis.
August 11, 2020 at 12:37 am
sir, within the group analysis the p value for both the groups is significant (p0.05, by which we interpret that though both the treatments are effective, there in no difference between the efficacy of one over the other.. in other words.. no intervention is superior and both are equally effective.
August 11, 2020 at 2:45 pm
Thanks for the additional details. If I understand correctly, there were separate analyses before that determined each treatment had a statistically significance effect. However, when you compare the two treatments, there difference between them is not statistically significant.
If that’s the case, the interpretation is fairly straightforward. You have evidence that suggests that both treatments are effective. However, you don’t have evidence to conclude that one is better than the other.
August 10, 2020 at 9:26 am
Hi thank you for a wonderful explanation. I have a doubt: My Null hypothesis says: no significant difference between the effect fo A and B treatment Alternative hypothesis: there will be significant difference between the effect of A and B treatment. and my results show that i fail to reject null hypothesis.. Both the treatments were effective, but not significant difference.. how do I interpret this?
August 10, 2020 at 1:32 pm
First, I need to ask you a question. If your p-value is not significant, and so you fail to reject the null, why do you say that the treatment is effective? I can answer you question better after knowing the reason you say that. Thanks!
August 9, 2020 at 9:40 am
Dear Jim, thanks for making stats much more understandable and answering all question so painstakingly. I understand the following on p value and null. If our sample yields a p value of .01, it means that that there is a 1% probability that our kind of sample exists in the population. that is a rare event. So why shouldn’t we accept the HO as the probability of our event was v rare. Pls can you correct me. Thanks, G
August 10, 2020 at 1:53 pm
That’s a great question! They key thing to remember is that p-values are a conditional probability. P-value calculations assume that the null hypothesis is true. So, a p-value of 0.01 indicates that there is a 1% probability of observing your sample results, or more extreme, *IF* the null hypothesis is true.
The kicker is that we don’t whether the null is true or not. But, using this process does limit the likelihood of a false positive to your significance level (alpha). But, we don’t know whether the null is true and you had an unusual sample or whether the null is false. Usually, with a p-value of 0.01, we’d reject the null and conclude it is false.
I hope that answered your question. This topic can be murky and I wasn’t quite clear which part you needed clarification.
August 4, 2020 at 11:16 pm
Thank you for the wonderful explanation. However, I was just curious to know that what if in a particular test, we get a p-value less than the level of significance, leading to evidence against null hypothesis. Is there any possibility that our interpretation of population effect might be wrong due to randomness of samples? Also, how do we conclude whether the evidence is enough for our alternate hypothesis?
August 4, 2020 at 11:55 pm
Hi Abhilash,
Yes, unfortunately, when you’re working with samples, there’s always the possibility that random chance will cause your sample to not represent the population. For information about these errors, read my post about the types of errors in hypothesis testing .
In hypothesis testing, you determine whether your evidence is strong enough to reject the null. You don’t accept the alternative hypothesis. I cover that in my post about interpreting p-values .
August 1, 2020 at 3:50 pm
Hi, I am trying to interpret this phenomenon after my research. The null hypothesis states that “The use of combined drugs A and B does not lower blood pressure when compared to if drug A or B is used singularly”
The alternate hypothesis states: The use of combined drugs A and B lower blood pressure compared to if drug A or B is used singularly.
At the end of the study, majority of the people did not actually combine drugs A and B, rather indicated they either used drug A or drug B but not a combination. I am finding it very difficult to explain this outcome more so that it is a descriptive research. Please how do I go about this? Thanks a lot
June 22, 2020 at 10:01 am
What confuses me is how we set/determine the null hypothesis? For example stating that two sets of data are either no different or have no relationship will give completely different outcomes, so which is correct? Is the null that they are different or the same?
June 22, 2020 at 2:16 pm
Typically, the null states there is no effect/no relationship. That’s true for 99% of hypothesis tests. However, there are some equivalence tests where you are trying to prove that the groups are equal. In that case, the null hypothesis states that groups are not equal.
The null hypothesis is typically what you *don’t* want to find. You have to work hard, design a good experiment, collect good data, and end up with sufficient evidence to favor the alternative hypothesis. Usually in an experiment you want to find an effect. So, usually the null states there is no effect and you have get good evidence to reject that notion.
However, there are a few tests where you actually want to prove something is equal, so you need the null to state that they’re not equal in those cases and then do all the hard work and gather good data to suggest that they are equal. Basically, set up the hypothesis so it takes a good experiment and solid evidence to be able to reject the null and favor the hypothesis that you’re hoping is true.
June 5, 2020 at 11:54 am
Thank you for the explanation. I have one question that. If Null hypothesis is failed to reject than is possible to interpret the analysis further?
June 5, 2020 at 7:36 pm
Hi Mottakin,
Typically, if your result is that you fail to reject the null hypothesis there’s not much further interpretation. You don’t want to be in a situation where you’re endlessly trying new things on a quest for obtaining significant results. That’s data mining.
May 25, 2020 at 7:55 am
I hope all is well. I am enjoying your blog. I am not a statistician, however, I use statistical formulae to provide insight on the direction in which data is going. I have used both the regression analysis and a T-Test. I know that both use a null hypothesis and an alternative hypothesis. Could you please clarity the difference between a regression analysis and a T-Test? Are there conditions where one is a better option than the other?
May 26, 2020 at 9:18 pm
t-Tests compare the means of one or two groups. Regression analysis typically describes the relationships between a set of independent variables and the dependent variables. Interestingly, you can actually use regression analysis to perform a t-test. However, that would be overkill. If you just want to compare the means of one or two groups, use a t-test. Read my post about performing t-tests in Excel to see what they can do. If you have a more complex model than just comparing one or two means, regression might be the way to go. Read my post about when to use regression analysis .
May 12, 2020 at 5:45 pm
This article is really enlightening but there is still some darkness looming around. I see that low p-values mean strong evidence against null hypothesis and finding such a sample is highly unlikely when null hypothesis is true. So , is it OK to say that when p-value is 0.01 , it was very unlikely to have found such a sample but we still found it and hence finding such a sample has not occurred just by chance which leads towards rejection of null hypothesis.
May 12, 2020 at 11:16 pm
That’s mostly correct. I wouldn’t say, “has not occurred by chance.” So, when you get a very low p-value it does mean that you are unlikely to obtain that sample if the null is true. However, once you obtain that result, you don’t know for sure which of the two occurred:
- The effect exists in the population.
- Random chance gave you an unusual sample (i.e., Type I error).
You really don’t know for sure. However, by the decision making results you set about the strength of evidence required to reject the null, you conclude that the effect exists. Just always be aware that it could be a false positive.
That’s all a long way of saying that your sample was unlikely to occur by chance if the null is true.
April 29, 2020 at 11:59 am
Why do we consult the statistical tables to find out the critical values of our test statistics?
April 30, 2020 at 5:05 pm
Statistical tables started back in the “olden days” when computers didn’t exist. You’d calculate the test statistic value for your sample. Then, you’d look in the appropriate table and using the degrees of freedom for your design and find the critical values for the test statistic. If the value of your test statistics exceeded the critical value, your results were statistically significant.
With powerful and readily available computers, researchers could analyze their data and calculate the p-values and compare them directly to the significance level.
I hope that answers your question!
April 15, 2020 at 10:12 am
If we are not able to reject the null hypothesis. What could be the solution?
April 16, 2020 at 11:13 pm
Hi Shazzad,
The first thing to recognize is that failing to reject the null hypothesis might not be an error. If the null hypothesis is false, then the correct outcome is failing to reject the null.
However, if the null hypothesis is false and you fail to reject, it is a type II error, or a false negative. Read my post about types of errors in hypothesis tests for more information.
This type of error can occur for a variety of reasons, including the following:
- Fluky sample. When working with random samples, random error can cause anomalous results purely by chance.
- Sample is too small. Perhaps the sample was too small, which means the test didn’t have enough statistical power to detect the difference.
- Problematic data or sampling methodology. There could be a problem with how you collected the data or your sampling methodology.
There are various other possibilities, but those are several common problems.
April 14, 2020 at 12:19 pm
Thank you so much for this article! I am taking my first Statistics class in college and I have one question about this.
I understand that the default position is that the null is correct, and you explained that (just like a court case), the sample evidence must EXCEED the “evidentiary standard” (which is the significance level) to conclude that an effect/relationship exists. And, if an effect/relationship exists, that means that it’s the alternative hypothesis that “wins” (not sure if that’s the correct way of wording it, but I’m trying to make this as simple as possible in my head!).
But what I don’t understand is that if the P-value is GREATER than the significance value, we fail to reject the null….because shouldn’t a higher P-value, mean that our sample evidence EXCEEDS the evidentiary standard (aka the significance level), and therefore an effect/relationship exists? In my mind it would make more sense to reject the null, because our P-value is higher and therefore we have enough evidence to reject the null.
I hope I worded this in a way that makes sense. Thank you in advance!
April 14, 2020 at 10:42 pm
That’s a great question. The key thing to remember is that higher p-values correspond to weaker evidence against the null hypothesis. A high p-value indicates that your sample is likely (high probability = high p-value) if the null hypothesis is true. Conversely, low p-values represent stronger evidence against the null. You were unlikely (low probability = low p-value) to have collect a sample with the measured characteristics if the null is true.
So, there is negative correlation between p-values and strength of evidence against the null hypothesis. Low p-values indicate stronger evidence. Higher p-value represent weaker evidence.
In a nutshell, you reject the null hypothesis with a low p-value because it indicates your sample data are unusual if the null is true. When it’s unusual enough, you reject the null.
March 5, 2020 at 11:10 am
There is something I am confused about. If our significance level is .05 and our resulting p-value is .02 (thus the strength of our evidence is strong enough to reject the null hypothesis), do we state that we reject the null hypothesis with 95% confidence or 98% confidence?
My guess is our confidence level is 95% since or alpha was .05. But if the strength of our evidence is 98%, why wouldn’t we use that as our stated confidence in our results?
March 5, 2020 at 4:19 pm
Hi Michael,
You’d state that you can reject the null at a significance level of 5% or conversely at the 95% confidence level. A key reason is to avoid cherry picking your results. In other words, you don’t want to choose the significance level based on your results.
Consequently, set the significance level/confidence level before performing your analysis. Then, use those preset levels to determine statistical significance. I always recommend including the exact p-value when you report on statistical significance. Exact p-values do provide information about the strength of evidence against the null.
March 5, 2020 at 9:58 am
Thank you for sharing this knowledge , it is very appropriate in explaining some observations in the study of forest biodiversity.
March 4, 2020 at 2:01 am
Thank you so much. This provides for my research
March 3, 2020 at 7:28 pm
If one couples this with what they call estimated monetary value of risk in risk management, one can take better decisions.
March 3, 2020 at 3:12 pm
Thank you for providing this clear insight.
March 3, 2020 at 3:29 am
Nice article Jim. The risk of such failure obviously reduces when a lower significance level is specified.One benefits most by reading this article in conjunction with your other article “Understanding Significance Levels in Statistics”.
March 3, 2020 at 2:43 am
That’s fine. My question is why doesn’t the numerical value of type 1 error coincide with the significance level in the backdrop that the type 1 error and the significance level are both the same ? I hope you got my question.
March 3, 2020 at 3:30 am
Hi, they are equal. As I indicated, the significance level equals the type I error rate.
March 3, 2020 at 1:27 am
Kindly elighten me on one confusion. We set out our significance level before setting our hypothesis. When we calculate the type 1 error, which happens to be a significance level, the numerical value doesn’t equals (either undermining value comes out or an exceeding value comescout ) our significance level that was preassigned. Why is this so ?
March 3, 2020 at 2:24 am
Hi Ratnadeep,
You’re correct. The significance level (alpha) is the same as the type I error rate. However, you compare the p-value to the significance level. It’s the p-value that can be greater than or less than the significance level.
The significance level is the evidentiary standard. How strong does the evidence in your sample need to be before you can reject the null? The p-value indicates the strength of the evidence that is present in your sample. By comparing the p-value to the significance level, you’re comparing the actual strength of the sample evidence to the evidentiary standard to determine whether your sample evidence is strong enough to conclude that the effect exists in the population.
I write about this in my post about the understanding significance levels . I think that will help answer your questions!
Comments and Questions Cancel reply
- 1.6 - Hypothesis Testing
Another way to make statistical inferences about a population parameter such as the mean is to use hypothesis testing to make decisions about the parameter’s value. Suppose that we are interested in a particular value of the mean single-family home sale price, for example, a claim from a realtor that the mean sale price in this market is \(\$\)255,000. Does the information in our sample support this claim, or does it favor an alternative claim?
The rejection region method
To decide between two competing claims, we can conduct a hypothesis test as follows.
- Express the claim about a specific value for the population parameter of interest as a null hypothesis , denoted NH. [More traditional notation uses H0.] The null hypothesis needs to be in the form "parameter = some hypothesized value," for example, NH: E(Y) = 255. A frequently used legal analogy is that the null hypothesis is equivalent to a presumption of innocence in a trial before any evidence has been presented.
- Express the alternative claim as an alternative hypothesis , denoted AH. [More traditional notation uses Ha or H1.]. The alternative hypothesis can be in a lower-tail form, for example, AH: E(Y) < 255, or an upper-tail form, for example, AH: E(Y) > 255, or a two-tail form, for example, AH: E(Y) ≠ 255. The alternative hypothesis, also sometimes called the research hypothesis, is what we would like to demonstrate to be the case, and needs to be stated before looking at the data. To continue the legal analogy, the alternative hypothesis is guilt, and we will only reject the null hypothesis (innocence) if we favor the alternative hypothesis (guilt) beyond a reasonable doubt. To illustrate, we will presume for the home prices example that we have some reason to suspect that the mean sale price is higher than claimed by the realtor (perhaps a political organization is campaigning on the issue of high housing costs and has employed us to investigate whether sale prices are "too high" in this housing market). Thus, our upper-tail alternative hypothesis is AH: E(Y) > 255.
- Calculate a test statistic based on the assumption that the null hypothesis is true. For hypothesis tests for a univariate population mean the relevant test statistic is \[\text{t-statistic}=\frac{m_Y-\text{E}(Y)}{s_Y/\sqrt{n}},\] where \(m_Y\) is the sample mean, E(Y) is the value of the population mean in the null hypothesis, \(s_Y\) is the sample standard deviation, and n is the sample size.
- For an upper-tail test, a t-statistic that is positive and far from zero would then lead us to favor the alternative hypothesis (a t-statistic that was far from zero but negative would favor neither hypothesis and the test would be inconclusive).
- For a lower-tail test, a t-statistic that is negative and far from zero would then lead us to favor the alternative hypothesis (a t-statistic that was far from zero but positive would favor neither hypothesis and the test would be inconclusive).
- For a two-tail test, any t-statistic that is far from zero (positive or negative) would lead us to favor the alternative hypothesis.
- To decide how far from zero a t-statistic would have to be before we reject the null hypothesis in favor of the alternative, recall the legal analogy. To deliver a guilty verdict (the alternative hypothesis), the jury must establish guilt beyond a reasonable doubt. In other words, a jury rejects the presumption of innocence (the null hypothesis) only if there is compelling evidence of guilt. In statistical terms, compelling evidence of guilt is found only in the tails of the t-distribution density curve. For example, in conducting an upper-tail test, if the t-statistic is way out in the upper tail, then it seems unlikely that the null hypothesis could have been true—so we reject it in favor of the alternative. Otherwise, the t-statistic could well have arisen while the null hypothesis held true—so we do not reject it in favor of the alternative. How far out in the tail does the t-statistic have to be to favor the alternative hypothesis rather than the null? Here we must make a decision about how much evidence we will require before rejecting a null hypothesis. There is always a chance that we might mistakenly reject a null hypothesis when it is actually true (the equivalent of pronouncing an innocent defendant guilty). Often, this chance—called the significance level —will be set at 5%, but more stringent tests (such as in clinical trials of new pharmaceutical drugs) might set this at 1%, while less stringent tests (such as in sociological studies) might set this at 10%. For the sake of argument, we use 5% as a default value for hypothesis tests in this course (unless stated otherwise).
- For an upper-tail test, the critical value is the 95th percentile of the t-distribution with n−1 degrees of freedom; reject the null in favor of the alternative if the t-statistic is greater than this.
- For a lower-tail test, the critical value is the 5th percentile of the t-distribution with n−1 degrees of freedom; reject the null in favor of the alternative if the t-statistic is less than this.
- For a two-tail test, the two critical values are the 2.5th and the 97.5th percentiles of the t-distribution with n−1 degrees of freedom; reject the null in favor of the alternative if the t-statistic is less than the 2.5th percentile or greater than the 97.5th percentile.
It is best to lay out hypothesis tests in a series of steps, so for the house prices example:
- State null hypothesis: NH: E(Y) = 255.
- State alternative hypothesis: AH: E(Y) > 255.
- Calculate test statistic: t-statistic = \(m_Y−\text{E}(Y)/(s_Y/\sqrt{n})=(278.6033−255)/(53.8656/\sqrt{30})=2.40\).
- Set significance level: 5%.
- Look up critical value: The 95th percentile of the t-distribution with 29 degrees of freedom is 1.699; the rejection region is therefore any t-statistic greater than 1.699.
- Make decision: Since the t-statistic of 2.40 falls in the rejection region, we reject the null hypothesis in favor of the alternative.
- Interpret in the context of the situation: The 30 sample sale prices suggest that a population mean of \(\$\)255,000 seems implausible—the sample data favor a value greater than this (at a significance level of 5%).
The p-value method
An alternative way to conduct a hypothesis test is to again assume initially that the null hypothesis is true, but then to calculate the probability of observing a t-statistic as extreme as the one observed or even more extreme (in the direction that favors the alternative hypothesis). This is known as the p-value (sometimes also called the observed significance level):
- For an upper-tail test, the p-value is the area under the curve of the t-distribution (with n−1 degrees of freedom) to the right of the observed t-statistic.
- For a lower-tail test, the p-value is the area under the curve of the t-distribution (with n−1 degrees of freedom) to the left of the observed t-statistic.
- For a two-tail test, the p-value is the sum of the areas under the curve of the t-distribution (with n−1 degrees of freedom) beyond both the observed t-statistic and the negative of the observed t-statistic.
If the p-value is too "small," then this suggests that it seems unlikely that the null hypothesis could have been true—so we reject it in favor of the alternative. Otherwise, the t-statistic could well have arisen while the null hypothesis held true—so we do not reject it in favor of the alternative. Again, the significance level chosen tells us how small is small: If the p-value is less than the significance level, then reject the null in favor of the alternative; otherwise, do not reject it. For the home prices example:
- Look up p-value: The area to the right of the t-statistic (2.40) for the t-distribution with 29 degrees of freedom is less than 0.025 but greater than 0.01 (since the 97.5th percentile of this t-distribution is 2.045 and the 99th percentile is 2.462); thus the upper-tail p-value is between 0.01 and 0.025.
- Make decision: Since the p-value is between 0.01 and 0.025, it must be less than the significance level (0.05), so we reject the null hypothesis in favor of the alternative.
The following figure shows why the rejection region method and the p-value method will always lead to the same decision (since if the t-statistic is in the rejection region, then the p-value must be smaller than the significance level, and vice versa).

Why do we need two methods if they will always lead to the same decision? Well, when learning about hypothesis tests and becoming comfortable with their logic, many people find the rejection region method a little easier to apply. However, when we start to rely on statistical software for conducting hypothesis tests in later chapters of the book, we will find the p-value method easier to use. At this stage, when doing hypothesis test calculations by hand, it is helpful to use both the rejection region method and the p-value method to reinforce learning of the general concepts. This also provides a useful way to check our calculations since if we reach a different conclusion with each method we will know that we have made a mistake.
Lower-tail tests
Lower-tail tests work in a similar way to upper-tail tests, but all the calculations are performed in the negative (left-hand) tail of the t-distribution density curve; the following figure illustrates.

A lower-tail test would result in an inconclusive result for the home prices example (since the large, positive t-statistic means that the data favor neither the null hypothesis, NH: E(Y) = 255, nor the alternative hypothesis, AH: E(Y) < 255).
Two-tail tests
Two-tail tests work similarly, but we have to be careful to work with both tails of the t-distribution; the following figure illustrates.

For the home prices example, we might want to do a two-tail hypothesis test if we had no prior expectation about how large or small sale prices are, but just wanted to see whether or not the realtor's claim of \(\$\)255,000 was plausible. The steps involved are as follows.
- State alternative hypothesis: AH: E(Y) ≠ 255.
- critical value: The 97.5th percentile of the t-distribution with 29 degrees of freedom is 2.045; the rejection region is therefore any t-statistic greater than 2.045 or less than −2.045 (we need the 97.5th percentile in this case because this is a two-tail test, so we need half the significance level in each tail).
- p-value: The area to the right of the t-statistic (2.40) for the t-distribution with 29 degrees of freedom is less than 0.025 but greater than 0.01 (since the 97.5th percentile of this t-distribution is 2.045 and the 99th percentile is 2.462); thus the upper-tail area is between 0.01 and 0.025 and the two-tail p-value is twice as big as this, that is, between 0.02 and 0.05.
- Since the t-statistic of 2.40 falls in the rejection region, we reject the null hypothesis in favor of the alternative.
- Since the p-value is between 0.02 and 0.05, it must be less than the significance level (0.05), so we reject the null hypothesis in favor of the alternative.
- Interpret in the context of the situation: The 30 sample sale prices suggest that a population mean of $255,000 seems implausible—the sample data favor a value different from this (at a significance level of 5%).
Hypothesis test errors
When we introduced the significance level above, we saw that the person conducting the hypothesis test gets to choose this value. We now explore this notion a little more fully. Whenever we conduct a hypothesis test, either we reject the null hypothesis in favor of the alternative or we do not reject the null hypothesis. "Not rejecting" a null hypothesis isn't quite the same as "accepting" it. All we can say in such a situation is that we do not have enough evidence to reject the null—recall the legal analogy where defendants are not found "innocent" but rather are found "not guilty." Anyway, regardless of the precise terminology we use, we hope to reject the null when it really is false and to "fail to reject it" when it really is true. Anything else will result in a hypothesis test error. There are two types of error that can occur, as illustrated in the following table:
| Decision | |||
| Do not reject NH in favor or AH | Reject NH in favor of AH | ||
| Reality | NH true | Correct decision | Type 1 error |
| NH false | Type 2 error | Correct decision | |
A type 1 error can occur if we reject the null hypothesis when it is really true—the probability of this happening is precisely the significance level. If we set the significance level lower, then we lessen the chance of a type 1 error occurring. Unfortunately, lowering the significance level increases the chance of a type 2 error occurring—when we fail to reject the null hypothesis but we should have rejected it because it was false. Thus, we need to make a trade-off and set the significance level low enough that type 1 errors have a low chance of happening, but not so low that we greatly increase the chance of a type 2 error happening. The default value of 5% tends to work reasonably well in many applications at balancing both goals. However, other factors also affect the chance of a type 2 error happening for a specific significance level. For example, the chance of a type 2 error tends to decrease the greater the sample size.
Start Here!
- Welcome to STAT 462!
- Search Course Materials
- 1.1 - Identifying and Summarizing Data
- 1.2 - Population Distributions
- 1.3 - Selecting Individuals at Random
- 1.4 - Random Sampling
- 1.5 - Interval Estimation
- 1.7 - Random Errors and Prediction
- Lesson 2: Simple Linear Regression (SLR) Model
- Lesson 3: SLR Evaluation
- Lesson 4: SLR Assumptions, Estimation & Prediction
- Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation
- Lesson 6: MLR Assumptions, Estimation & Prediction
- Lesson 7: Transformations & Interactions
- Lesson 8: Categorical Predictors
- Lesson 9: Influential Points
- Lesson 10: Regression Pitfalls
- Lesson 11: Model Building
- Lesson 12: Logistic, Poisson & Nonlinear Regression
- Website for Applied Regression Modeling, 2nd edition
- Notation Used in this Course
- R Software Help
- Minitab Software Help

Copyright © 2018 The Pennsylvania State University Privacy and Legal Statements Contact the Department of Statistics Online Programs
Null Hypothesis Definition and Examples, How to State
What is the null hypothesis, how to state the null hypothesis, null hypothesis overview.

Why is it Called the “Null”?
The word “null” in this context means that it’s a commonly accepted fact that researchers work to nullify . It doesn’t mean that the statement is null (i.e. amounts to nothing) itself! (Perhaps the term should be called the “nullifiable hypothesis” as that might cause less confusion).
Why Do I need to Test it? Why not just prove an alternate one?
The short answer is, as a scientist, you are required to ; It’s part of the scientific process. Science uses a battery of processes to prove or disprove theories, making sure than any new hypothesis has no flaws. Including both a null and an alternate hypothesis is one safeguard to ensure your research isn’t flawed. Not including the null hypothesis in your research is considered very bad practice by the scientific community. If you set out to prove an alternate hypothesis without considering it, you are likely setting yourself up for failure. At a minimum, your experiment will likely not be taken seriously.

- Null hypothesis : H 0 : The world is flat.
- Alternate hypothesis: The world is round.
Several scientists, including Copernicus , set out to disprove the null hypothesis. This eventually led to the rejection of the null and the acceptance of the alternate. Most people accepted it — the ones that didn’t created the Flat Earth Society !. What would have happened if Copernicus had not disproved the it and merely proved the alternate? No one would have listened to him. In order to change people’s thinking, he first had to prove that their thinking was wrong .
How to State the Null Hypothesis from a Word Problem
You’ll be asked to convert a word problem into a hypothesis statement in statistics that will include a null hypothesis and an alternate hypothesis . Breaking your problem into a few small steps makes these problems much easier to handle.
Step 2: Convert the hypothesis to math . Remember that the average is sometimes written as μ.
H 1 : μ > 8.2
Broken down into (somewhat) English, that’s H 1 (The hypothesis): μ (the average) > (is greater than) 8.2
Step 3: State what will happen if the hypothesis doesn’t come true. If the recovery time isn’t greater than 8.2 weeks, there are only two possibilities, that the recovery time is equal to 8.2 weeks or less than 8.2 weeks.
H 0 : μ ≤ 8.2
Broken down again into English, that’s H 0 (The null hypothesis): μ (the average) ≤ (is less than or equal to) 8.2
How to State the Null Hypothesis: Part Two
But what if the researcher doesn’t have any idea what will happen.
Example Problem: A researcher is studying the effects of radical exercise program on knee surgery patients. There is a good chance the therapy will improve recovery time, but there’s also the possibility it will make it worse. Average recovery times for knee surgery patients is 8.2 weeks.
Step 1: State what will happen if the experiment doesn’t make any difference. That’s the null hypothesis–that nothing will happen. In this experiment, if nothing happens, then the recovery time will stay at 8.2 weeks.
H 0 : μ = 8.2
Broken down into English, that’s H 0 (The null hypothesis): μ (the average) = (is equal to) 8.2
Step 2: Figure out the alternate hypothesis . The alternate hypothesis is the opposite of the null hypothesis. In other words, what happens if our experiment makes a difference?
H 1 : μ ≠ 8.2
In English again, that’s H 1 (The alternate hypothesis): μ (the average) ≠ (is not equal to) 8.2
That’s How to State the Null Hypothesis!
Check out our Youtube channel for more stats tips!
Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial. Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences , Wiley.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 13: Inferential Statistics
Understanding Null Hypothesis Testing
Learning Objectives
- Explain the purpose of null hypothesis testing, including the role of sampling error.
- Describe the basic logic of null hypothesis testing.
- Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.
The Purpose of Null Hypothesis Testing
As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).
Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)
One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.
In fact, any statistical relationship in a sample can be interpreted in two ways:
- There is a relationship in the population, and the relationship in the sample reflects this.
- There is no relationship in the population, and the relationship in the sample reflects only sampling error.
The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.
The Logic of Null Hypothesis Testing
Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:
- Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
- Determine how likely the sample relationship would be if the null hypothesis were true.
- If the sample relationship would be extremely unlikely, then reject the null hypothesis in favour of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .
Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”
The Misunderstood p Value
The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!
The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.
You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.
Role of Sample Size and Relationship Strength
Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.
Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”
| Sample Size | Weak relationship | Medium-strength relationship | Strong relationship |
|---|---|---|---|
| Small ( = 20) | No | No | = Maybe = Yes |
| Medium ( = 50) | No | Yes | Yes |
| Large ( = 100) | = Yes = No | Yes | Yes |
| Extra large ( = 500) | Yes | Yes | Yes |
Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.
Statistical Significance Versus Practical Significance
Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”
This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.
Key Takeaways
- Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
- The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
- The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
- Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
- Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
- The correlation between two variables is r = −.78 based on a sample size of 137.
- The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
- In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
- In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
- A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Long Descriptions
“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]
“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]
Media Attributions
- Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
- Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
- Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
- Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵
Values in a population that correspond to variables measured in a study.
The random variability in a statistic from sample to sample.
A formal approach to deciding between two interpretations of a statistical relationship in a sample.
The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.
The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.
When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.
When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.
The probability that, if the null hypothesis were true, the result found in the sample would occur.
How low the p value must be before the sample result is considered unlikely in null hypothesis testing.
When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.
Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
- Math Article
Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .
In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.
Table of contents:
- Comparison with Alternative Hypothesis
Null Hypothesis Definition
The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .
Null Hypothesis Symbol
In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .
Null Hypothesis Principle
The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.
Null Hypothesis Formula
Here, the hypothesis test formulas are given below for reference.
The formula for the null hypothesis is:
H 0 : p = p 0
The formula for the alternative hypothesis is:
H a = p >p 0 , < p 0 ≠ p 0
The formula for the test static is:
Remember that, p 0 is the null hypothesis and p – hat is the sample proportion.
Also, read:
Types of Null Hypothesis
There are different types of hypothesis. They are:
Simple Hypothesis
It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.
Composite Hypothesis
The composite hypothesis is one that does not completely specify the population distribution.
Exact Hypothesis
Exact hypothesis defines the exact value of the parameter. For example μ= 50
Inexact Hypothesis
This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60
Null Hypothesis Rejection
Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.
How do you Find the Null Hypothesis?
The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).
When is Null Hypothesis Rejected?
The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.
Null Hypothesis and Alternative Hypothesis
Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.
|
|
| |
| 1 | The null hypothesis is a statement. There exists no relation between two variables | Alternative hypothesis a statement, there exists some relationship between two measured phenomenon |
| 2 | Denoted by H | Denoted by H |
| 3 | The observations of this hypothesis are the result of chance | The observations of this hypothesis are the result of real effect |
| 4 | The mathematical formulation of the null hypothesis is an equal sign | The mathematical formulation alternative hypothesis is an inequality sign such as greater than, less than, etc. |
Null Hypothesis Examples
Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.
If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.
Few more examples are:
1). Are there is 100% chance of getting affected by dengue?
Ans: There could be chances of getting affected by dengue but not 100%.
2). Do teenagers are using mobile phones more than grown-ups to access the internet?
Ans: Age has no limit on using mobile phones to access the internet.
3). Does having apple daily will not cause fever?
Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.
4). Do the children more good in doing mathematical calculations than grown-ups?
Ans: Age has no effect on Mathematical skills.
In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives.
The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data.
Frequently Asked Questions on Null Hypothesis
What is meant by the null hypothesis.
In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.
What are the benefits of hypothesis testing?
Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.
When a null hypothesis is accepted and rejected?
The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.
Why is the null hypothesis important?
The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.
How to accept or reject the null hypothesis in the chi-square test?
If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Null hypothesis
by Marco Taboga , PhD
In a test of hypothesis , a sample of data is used to decide whether to reject or not to reject a hypothesis about the probability distribution from which the sample was extracted.
The hypothesis is called the null hypothesis, or simply "the null".

Table of contents
The null is like the defendant in a criminal trial
How is the null hypothesis tested, example 1 - proportion of defective items, measurement, test statistic, critical region, interpretation, example 2 - reliability of a production plant, rejection and failure to reject, not rejecting and accepting are not the same thing, failure to reject can be due to lack of power, rejections are easier to interpret, but be careful, takeaways - how to (and not to) formulate a null hypothesis, more examples, more details, best practices in science, keep reading the glossary.
Formulating null hypotheses and subjecting them to statistical testing is one of the workhorses of the scientific method.
Scientists in all fields make conjectures about the phenomena they study, translate them into null hypotheses and gather data to test them.
This process resembles a trial:
the defendant (the null hypothesis) is accused of being guilty (wrong);
evidence (data) is gathered in order to prove the defendant guilty (reject the null);
if there is evidence beyond any reasonable doubt, the defendant is found guilty (the null is rejected);
otherwise, the defendant is found not guilty (the null is not rejected).
Keep this analogy in mind because it helps to better understand statistical tests, their limitations, use and misuse, and frequent misinterpretation.
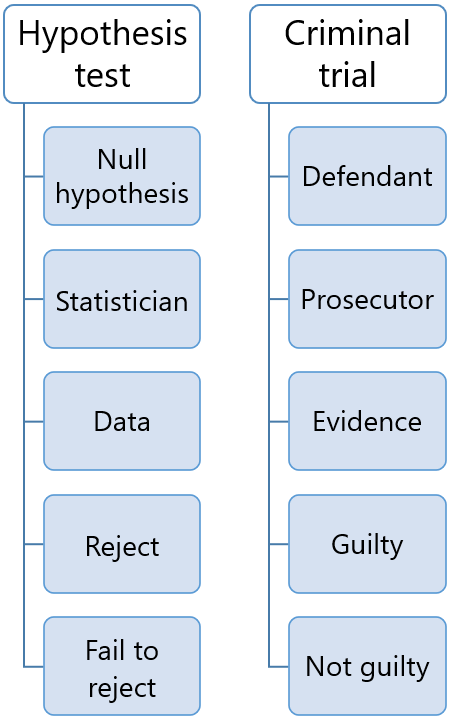
Before collecting the data:
we decide how to summarize the relevant characteristics of the sample data in a single number, the so-called test statistic ;
we derive the probability distribution of the test statistic under the hypothesis that the null is true (the data is regarded as random; therefore, the test statistic is a random variable);
we decide what probability of incorrectly rejecting the null we are willing to tolerate (the level of significance , or size of the test ); the level of significance is typically a small number, such as 5% or 1%.
we choose one or more intervals of values (collectively called rejection region) such that the probability that the test statistic falls within these intervals is equal to the desired level of significance; the rejection region is often a tail of the distribution of the test statistic (one-tailed test) or the union of the left and right tails (two-tailed test).

Then, the data is collected and used to compute the value of the test statistic.
A decision is taken as follows:
if the test statistic falls within the rejection region, then the null hypothesis is rejected;
otherwise, it is not rejected.
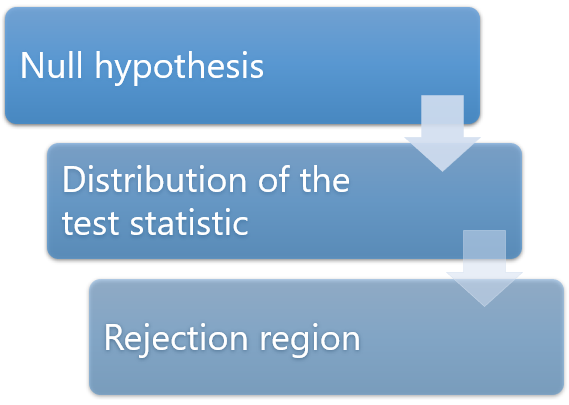
We now make two examples of practical problems that lead to formulate and test a null hypothesis.
A new method is proposed to produce light bulbs.
The proponents claim that it produces less defective bulbs than the method currently in use.
To check the claim, we can set up a statistical test as follows.
We keep the light bulbs on for 10 consecutive days, and then we record whether they are still working at the end of the test period.
The probability that a light bulb produced with the new method is still working at the end of the test period is the same as that of a light bulb produced with the old method.
100 light bulbs are tested:
50 of them are produced with the new method (group A)
the remaining 50 are produced with the old method (group B).
The final data comprises 100 observations of:
an indicator variable which is equal to 1 if the light bulb is still working at the end of the test period and 0 otherwise;
a categorical variable that records the group (A or B) to which each light bulb belongs.
We use the data to compute the proportions of working light bulbs in groups A and B.
The proportions are estimates of the probabilities of not being defective, which are equal for the two groups under the null hypothesis.
We then compute a z-statistic (see here for details) by:
taking the difference between the proportion in group A and the proportion in group B;
standardizing the difference:
we subtract the expected value (which is zero under the null hypothesis);
we divide by the standard deviation (it can be derived analytically).
The distribution of the z-statistic can be approximated by a standard normal distribution .
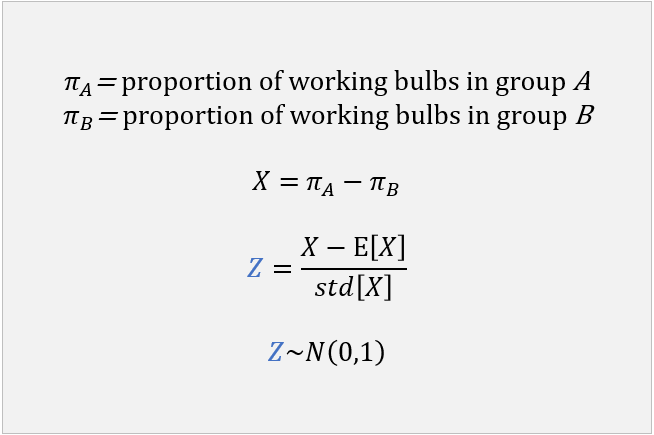
We decide that the level of confidence must be 5%. In other words, we are going to tolerate a 5% probability of incorrectly rejecting the null hypothesis.
The critical region is the right 5%-tail of the normal distribution, that is, the set of all values greater than 1.645 (see the glossary entry on critical values if you are wondering how this value was obtained).
If the test statistic is greater than 1.645, then the null hypothesis is rejected; otherwise, it is not rejected.
A rejection is interpreted as significant evidence that the new production method produces less defective items; failure to reject is interpreted as insufficient evidence that the new method is better.
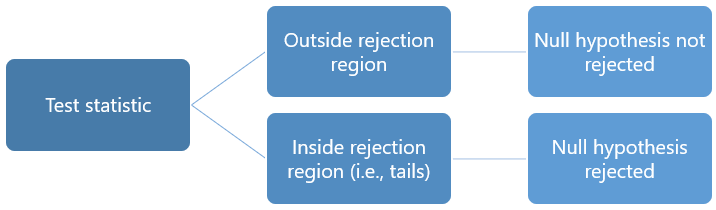
A production plant incurs high costs when production needs to be halted because some machinery fails.
The plant manager has decided that he is not willing to tolerate more than one halt per year on average.
If the expected number of halts per year is greater than 1, he will make new investments in order to improve the reliability of the plant.
A statistical test is set up as follows.
The reliability of the plant is measured by the number of halts.
The number of halts in a year is assumed to have a Poisson distribution with expected value equal to 1 (using the Poisson distribution is common in reliability testing).
The manager cannot wait more than one year before taking a decision.
There will be a single datum at his disposal: the number of halts observed during one year.
The number of halts is used as a test statistic. By assumption, it has a Poisson distribution under the null hypothesis.
The manager decides that the probability of incorrectly rejecting the null can be at most 10%.
A Poisson random variable with expected value equal to 1 takes values:
larger than 1 with probability 26.42%;
larger than 2 with probability 8.03%.
Therefore, it is decided that the critical region will be the set of all values greater than or equal to 3.
If the test statistic is strictly greater than or equal to 3, then the null is rejected; otherwise, it is not rejected.
A rejection is interpreted as significant evidence that the production plant is not reliable enough (the average number of halts per year is significantly larger than tolerated).
Failure to reject is interpreted as insufficient evidence that the plant is unreliable.
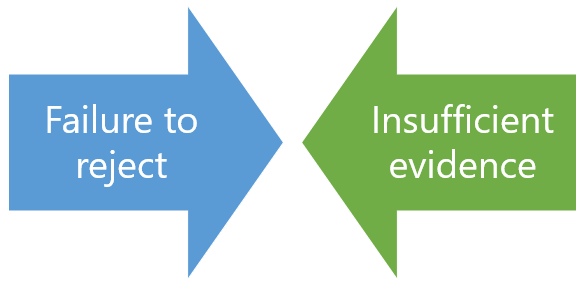
This section discusses the main problems that arise in the interpretation of the outcome of a statistical test (reject / not reject).
When the test statistic does not fall within the critical region, then we do not reject the null hypothesis.
Does this mean that we accept the null? Not really.
In general, failure to reject does not constitute, per se, strong evidence that the null hypothesis is true .
Remember the analogy between hypothesis testing and a criminal trial. In a trial, when the defendant is declared not guilty, this does not mean that the defendant is innocent. It only means that there was not enough evidence (not beyond any reasonable doubt) against the defendant.
In turn, lack of evidence can be due:
either to the fact that the defendant is innocent ;
or to the fact that the prosecution has not been able to provide enough evidence against the defendant, even if the latter is guilty .
This is the very reason why courts do not declare defendants innocent, but they use the locution "not guilty".
In a similar fashion, statisticians do not say that the null hypothesis has been accepted, but they say that it has not been rejected.

To better understand why failure to reject does not in general constitute strong evidence that the null hypothesis is true, we need to use the concept of statistical power .
The power of a test is the probability (calculated ex-ante, i.e., before observing the data) that the null will be rejected when another hypothesis (called the alternative hypothesis ) is true.
Let's consider the first of the two examples above (the production of light bulbs).
In that example, the null hypothesis is: the probability that a light bulb is defective does not decrease after introducing a new production method.
Let's make the alternative hypothesis that the probability of being defective is 1% smaller after changing the production process (assume that a 1% decrease is considered a meaningful improvement by engineers).
How much is the ex-ante probability of rejecting the null if the alternative hypothesis is true?
If this probability (the power of the test) is small, then it is very likely that we will not reject the null even if it is wrong.
If we use the analogy with criminal trials, low power means that most likely the prosecution will not be able to provide sufficient evidence, even if the defendant is guilty.
Thus, in the case of lack of power, failure to reject is almost meaningless (it was anyway highly likely).
This is why, before performing a test, it is good statistical practice to compute its power against a relevant alternative .
If the power is found to be too small, there are usually remedies. In particular, statistical power can usually be increased by increasing the sample size (see, e.g., the lecture on hypothesis tests about the mean ).
As we have explained above, interpreting a failure to reject the null hypothesis is not always straightforward. Instead, interpreting a rejection is somewhat easier.
When we reject the null, we know that the data has provided a lot of evidence against the null. In other words, it is unlikely (how unlikely depends on the size of the test) that the null is true given the data we have observed.
There is an important caveat though. The null hypothesis is often made up of several assumptions, including:
the main assumption (the one we are testing);
other assumptions (e.g., technical assumptions) that we need to make in order to set up the hypothesis test.
For instance, in Example 2 above (reliability of a production plant), the main assumption is that the expected number of production halts per year is equal to 1. But there is also a technical assumption: the number of production halts has a Poisson distribution.
It must be kept in mind that a rejection is always a joint rejection of the main assumption and all the other assumptions .
Therefore, we should always ask ourselves whether the null has been rejected because the main assumption is wrong or because the other assumptions are violated.
In the case of Example 2 above, is a rejection of the null due to the fact that the expected number of halts is greater than 1 or is it due to the fact that the distribution of the number of halts is very different from a Poisson distribution?
When we suspect that a rejection is due to the inappropriateness of some technical assumption (e.g., assuming a Poisson distribution in the example), we say that the rejection could be due to misspecification of the model .
The right thing to do when these kind of suspicions arise is to conduct so-called robustness checks , that is, to change the technical assumptions and carry out the test again.
In our example, we could re-run the test by assuming a different probability distribution for the number of halts (e.g., a negative binomial or a compound Poisson - do not worry if you have never heard about these distributions).
If we keep obtaining a rejection of the null even after changing the technical assumptions several times, the we say that our rejection is robust to several different specifications of the model .

What are the main practical implications of everything we have said thus far? How does the theory above help us to set up and test a null hypothesis?
What we said can be summarized in the following guiding principles:
A test of hypothesis is like a criminal trial and you are the prosecutor . You want to find evidence that the defendant (the null hypothesis) is guilty. Your job is not to prove that the defendant is innocent. If you find yourself hoping that the defendant is found not guilty (i.e., the null is not rejected) then something is wrong with the way you set up the test. Remember: you are the prosecutor.
Compute the power of your test against one or more relevant alternative hypotheses. Do not run a test if you know ex-ante that it is unlikely to reject the null when the alternative hypothesis is true.
Beware of technical assumptions that you add to the main assumption you want to test. Make robustness checks in order to verify that the outcome of the test is not biased by model misspecification.
More examples of null hypotheses and how to test them can be found in the following lectures.
| Where the example is found | Null hypothesis |
|---|---|
| The mean of a normal distribution is equal to a certain value | |
| The variance of a normal distribution is equal to a certain value | |
| A vector of parameters estimated by MLE satisfies a set of linear or non-linear restrictions | |
| A regression coefficient is equal to a certain value |
The lecture on Hypothesis testing provides a more detailed mathematical treatment of null hypotheses and how they are tested.
This lecture on the null hypothesis was featured in Stanford University's Best practices in science .

Previous entry: Normal equations
Next entry: Parameter
How to cite
Please cite as:
Taboga, Marco (2021). "Null hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/null-hypothesis.
Most of the learning materials found on this website are now available in a traditional textbook format.
- Permutations
- Characteristic function
- Almost sure convergence
- Likelihood ratio test
- Uniform distribution
- Bernoulli distribution
- Multivariate normal distribution
- Chi-square distribution
- Maximum likelihood
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Precision matrix
- Distribution function
- Mean squared error
- IID sequence
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Now that I've rejected the null hypothesis what's next?
I've time and again rejected or failed to reject the null hypothesis. In the failure to reject case, you conclude that there isn't sufficient evidence for rejection and you "move on" (i.e., either gather more data, end the experiment etc.,)
But when you "do" reject the null hypothesis, providing some evidence for the alternative hypothesis you can't really "prove" that your alternative hypothesis indeed holds true.
So, what are the common next steps once you reject the null hypothesis? What tools/techniques does one adopt to "analyze the problem further" to make more the findings more conclusive? What are the logical "next steps" as a statistician warranting further analysis?
For example:
$H_0: \mu_1 = \mu_0$
$H_1: \mu_1 > \mu_0$ (say we know the expected direction)
Once we reject the null hypothesis at some level of significance we have "some evidence" for the alternative to be true, but we can't draw that conclusion. If I really want to draw that conclusion conclusively (pardon the double word play) what should I do?
I've never pondered this question during my undergrad days but now that I'm doing a fair deal of hypotheses testing I can't help but wonder what's ahead :)
- hypothesis-testing
- 2 $\begingroup$ Possibly of interest: Why is "statistically significant" not enough? $\endgroup$ – gung - Reinstate Monica Commented May 28, 2014 at 4:12
- 3 $\begingroup$ Generally speaking, your actions after your decision should also be chosen before you test (how else can you weigh up the costs of the two kinds of errors and so choose a sensible $\alpha$?). At the least, you would likely move to consideration of estimated effect sizes. The null is not tenable (by criteria you chose - if that's not sufficient for you, what would be?), so what values are plausible instead? e.g. in your indicated test, what values for $\mu_1-\mu_0$ would be reasonably plausible, given the data? $\endgroup$ – Glen_b Commented May 28, 2014 at 7:12
5 Answers 5
You can generally continue to improve your estimate of whatever parameter you might be testing with more data. Stopping data collection once a test achieves some semi-arbitrary degree of significance is a good way to make bad inferences. That analysts may misunderstand a significant result as a sign that the job is done is one of many unintended consequences of the Neyman–Pearson framework, according to which people interpret p values as cause to either reject or fail to reject a null without reservation depending on which side of the critical threshold they fall on.
Without considering Bayesian alternatives to the frequentist paradigm (hopefully someone else will), confidence intervals continue to be more informative well beyond the point at which a basic null hypothesis can be rejected. Assuming collecting more data would just make your basic significance test achieve even greater significance (and not reveal that your earlier finding of significance was a false positive), you might find this useless because you'd reject the null either way. However, in this scenario, your confidence interval around the parameter in question would continue to shrink, improving the degree of confidence with which you can describe your population of interest precisely.
Here's a very simple example in r – testing the null hypothesis that $\mu=0$ for a simulated variable:
Here I just used t.test(rnorm(99)) , and I happened to get a false positive (assuming I've defaulted to $\alpha=.05$ as my choice of acceptable false positive error rate). If I ignore the confidence interval, I can claim my sample comes from a population with a mean that differs significantly from zero. Technically the confidence interval doesn't dispute this either, but it suggests that the mean could be very close to zero, or even further from it than I think based on this sample. Of course, I know the null is actually literally true here, because the mean of the rnorm population defaults to zero, but one rarely knows with real data.
Running this again as set.seed(8);t.test(rnorm(99,1)) produces a sample mean of .91, a p = 5.3E-13, and a 95% confidence interval for $\mu=[.69,1.12]$. This time I can be quite confident that the null is false, especially because I constructed it to be by setting the mean of my simulated data to 1.
Still, say it's important to know how different from zero it is; maybe a mean of .8 would be too close to zero for the difference to matter. I can see I don't have enough data to rule out the possibility that $\mu=.8$ from both my confidence interval and from a t -test with mu=.8 , which gives a p = .33. My sample mean is high enough to seem meaningfully different from zero according to this .8 threshold though; collecting more data can help improve my confidence that the difference is at least this large, and not just trivially larger than zero.
Since I'm "collecting data" by simulation, I can be a little unrealistic and increase my sample size by an order of magnitude. Running set.seed(8);t.test(rnorm(999,1),mu=.8) reveals that more data continue to be useful after rejecting the null hypothesis of $\mu=0$ in this scenario, because I can now reject a null of $\mu=.8$ with my larger sample. The confidence interval of $\mu=[.90,1.02]$ even suggests I could've rejected null hypotheses up to $\mu=.89$ if I'd set out to do so initially.
I can't revise my null hypothesis after the fact, but without collecting new data to test an even stronger hypothesis after this result, I can say with 95% confidence that replicating my "study" would allow me to reject a $H_0:\mu=.9$. Again, just because I can simulate this easily, I'll rerun the code as set.seed(9);t.test(rnorm(999,1),mu=.9) : doing so demonstrates my confidence wasn't misplaced.
Testing progressively more stringent null hypotheses, or better yet, simply focusing on shrinking your confidence intervals is just one way to proceed. Of course, most studies that reject null hypotheses lay the groundwork for other studies that build on the alternative hypothesis. E.g., if I was testing an alternative hypothesis that a correlation is greater than zero, I could test for mediators or moderators in a follow-up study next...and while I'm at it, I'd definitely want to make sure I could replicate the original result.
Another approach to consider is equivalence testing. If you want to conclude that a parameter is within a certain range of possible values, not just different from a single value, you can specify that range of values you'd want the parameter to lie within according to your conventional alternative hypothesis and test it against a different set of null hypotheses that together represent the possibility that the parameter lies outside that range. This last possibility might be most similar to what you had in mind when you wrote:
We have "some evidence" for the alternative to be true, but we can't draw that conclusion. If I really want to draw that conclusion conclusively...
Here's an example using similar data as above (using set.seed(8) , rnorm(99) is the same as rnorm(99,1)-1 , so the sample mean is -.09). Say I want to test the null hypothesis of two one-sided t -tests that jointly posit that the sample mean is not between -.2 and .2. This corresponds loosely to the previous example's premise, according to which I wanted to test if $\mu=.8$. The difference is that I've shifted my data down by 1, and I'm now going to perform two one-sided tests of the alternative hypothesis that $-.2\le\mu\le.2$. Here's how that looks:
tost sets the confidence level of the interval to 90%, so the confidence interval around the sample mean of -.09 is $\mu=[-.27,.09]$, and p = .17. However, running this again with rnorm(999) (and the same seed) shrinks the 90% confidence interval to $\mu=[-.09,.01]$, which is within the equivalence range specified in the null hypothesis with p = 4.55E-07.
I still think the confidence interval is more interesting than the equivalence test result. It represents what the data suggest the population mean is more specifically than the alternative hypothesis, and suggests I can be reasonably confident that it lies within an even smaller interval than I've specified in the alternative hypothesis. To demonstrate, I'll abuse my unrealistic powers of simulation once more and "replicate" using set.seed(7);tost(rnorm(999),epsilon=.09345092) : sure enough, p = .002.
- $\begingroup$ Enlightening! Could you please show a quick and dirty example of the last part where you talk about equivalence testing? It'd be really helpful to see at a high level how it could be applicable. $\endgroup$ – PhD Commented May 28, 2014 at 19:12
- $\begingroup$ @PhD: done. It's more "quick and dirty" than it is "at a high level" though, I think. I'm new to equivalence testing myself, and as you'll see, I'm not exactly sold on it. $\endgroup$ – Nick Stauner Commented May 28, 2014 at 20:37
Note first that @Nick Stauner makes some very important arguments regarding optional stopping . If you repeatedly test the data as samples come in, stopping once a test is significant, you're all but guaranteed a significant result. However, a guaranteed result is practically worthless.
In the following, I'll present my best attempts to elaborate on a deductivist, skeptical, falsificationist position. It's certainly not the only one, but I think a rather mainstream one, or at least one with a bit of tradition.
As far as I understand it, Fisher originally introduced significance tests as a first step in data exploration - establish which factors might be worth investigating further. Unless the null hypothesis you've put under test actually was the critical hypothesis your favoured theory depended on (unlikely), in a way, your initial test was rather exploratory in nature. Amongst the possible steps following exploration I see
- Further exploration
- Parameter Estimation
- Prediction & Confirmation
Further exploration consists of follow-up tests where you try to infer if any variables you have information on moderate or interact with your effect. For example, maybe the age of the participants plays a role? Note that such analyses must be clearly labelled as exploratory, or they basically amount to lying. If you stumble upon something, it first requires confirmation. Generally, you should always be clear- both in your thoughts, and in your writings - about when you're working exploratory, and when confirmatory.
Next, once you have established that you have no confidence in one parameter's value being precisely zero - once you have decided you'll for now consider the factor under test to have some influence - one feasible next step could be to further estimate the precise value of the parameter . For example, for now, you've only excluded one value, 0 (assuming a two-sided test). However, your data also cast doubt on many further possible values.
A (100-$\alpha$)% Confidence Interval/CI contains the range of parameter values not rejected at p<$\alpha$, corresponding to the many more possible hypotheses your data also concern beyond your initial H0. Since your test is significant, the value associated with H0 is not amongst them. But many extremely large and small values will also be excluded.
Hume famously argued we can never inductively prove correct a statement. Generally, non-trivial hypotheses are always a lot easier to falsify than to support; being easy to falsify in principle (by being non-trivial, making precise predictions), but yet not being falsified so far is in fact one of the highest virtues of a theory.
So a CI won't get you to proving a specific value. However, it narrows down the candidate set. Maybe the only candidates left alive help you decide between two theories both incompatible with H0. For example, maybe 0 is excluded, but theory 1 predicts a value around 5, and theory 2 predicts a value around 15. If your 95% CI includes 5, but excludes 15, you have now also lost confidence in theory 2, but theory 1 remains in the game. Note that this is actually independent of your initial test being significant - even if 0 is amongst the values not rejected, many values will be rejected. Maybe for some other researchers, some of these values were of interest.
After you have thus somewhat specified your understanding of the effect at hand, you could ideally make a more precise prediction for a follow-up confirmatory experiment that would aim to test a more precise hypothesis you can derive from your current analysis. Admittedly, rejecting your initial statistical null hypothesis wasn't that severe of a test of your original research hypothesis, wasn't it? Many more explanations than the one you prefer do not depend on H0. Also, since you never were in danger to actually accept H0, you were in no position to falsify your favoured theory! So you need a more severe test . Arguably, this is actually what you want; you do not want to prove your theory, you want to put it under increasingly severe tests, attempting to falsify it. Withstanding such genuine (but fair) efforts to disprove it is the best a theory can deliver. But for a severe test, you need a more precise theory than "0 it ain't".
You now have learned multiple important facts concerning a confirmatory study; for example, you have an idea of the variance and effect magnitude in question, allowing you to estimate the required sample size for a follow-up study via power analysis. You can also predict a specific value and assume a region of practical equivalence /ROPE around it. You won't ever be able to prove that this specific value is the true value; however, if the CI from a follow-up experiment falls entirely within your ROPE, you have corroborating evidence for your theory (and possibly brought in trouble the competition).
The idea that you cannot prove a positive scientific proposition, but only disprove one, is a principle of Popper's falsificationism . I do agree that you cannot prove an effect is exactly equal to any given point value (cf., my answer here: Why do statisticians say a non-significant result means "you cannot reject the null" as opposed to accept the null hypothesis? ). But so what?
People (or at least I ) complain a lot about hypothesis testing. This is because $p$-values are commonly misunderstood, and hypothesis tests are used for tasks they logically cannot accomplish. For example, hypothesis testing should not be used to generate hypotheses or to select variables. Moreover, with observational data essentially all 'nil' null hypotheses must be false, so testing such makes little sense. However, scientists often do have a-priori hypotheses suggested by current theories that they want to test, and in a true experiment a nil null could be true, so testing it is perfectly reasonable. Typically, researchers do have some reason to suspect that the null might be false, so a significant result in conjunction with a strong experiment is a valid piece of information.
You can always form confidence intervals to get a clearer picture of the precision of your estimate, and continue to collect more data to increase its precision. Nonetheless, in economic terms you will get diminishing returns . At some point, you simply do not believe the null hypothesis provides a reasonable account of the phenomenon under study. In which case, why are you bothering?
If there are others in your field who are not yet convinced, but would be with more (of the same) data, then you could continue, but this seems like an uncommon situation. It seems more likely to me that the skeptics have other, substantive concerns regarding whether that line of inquiry is sufficiently informative about the underlying question. Thus, you need to determine the nature of those concerns, and if you think they merit the work, seek out different data that more adequately address the issues at hand. For example, you might try to replicate the finding using a different measure, in a different setting, and/or with different control conditions.
On the other hand, everyone (more or less) may be satisfied with your data and conclusions (congratulations!). Under such happy circumstances, there are two directions you could pursue to further your research program:
A reductionist approach would seek to understand the mechanisms that produce the effect you have established. In statistical terms, you would often be seeking mediators and/or a refining of the pattern of causal forces that connect the variables you have shown to be related.
You could also move in the other direction by seeking to integrate your findings into a larger pattern. This is a kind of systems thinking . G.H. Hardy once defined the elegance of a theory as the range of phenomena that it could explain in conjunction with the ease and magnitude of the epistemic shift it induced. Of course, you may not be so lucky that the phenomenon you have established is quite that deep , however it can still be part of something bigger than itself. Establishing a link between $B$ and $C$ that makes it possible to see that $A$ unifies disparate phenomena can be just as important to the process, and just as much a crystallizing moment, as the discovery of $A$ itself.
tl;dr: If you have sufficient evidence for your purposes that the null is false, figure out what other theoretically motivated questions you could try to answer and move on.
One think I would like to add is that your question reminds me of my younger self: I wanted desperately to prove my hypothesis because I did not how to write "the hypothesis was wrong" in a way which helped to improve the paper I was writing. But then I realized that the "damn my absolutely lovely hypothesis cannot be proven" also holds scientific value: 1. Think about WHY your hypothesis doesn't hold water. It's some problem with the data, or probabyly something with the hypothesis itself? 2. What are the consequences for older research?
As an example: I wrote my master's thesis about ethnic conflect using a then new dataset which was larger than previous datasets. I tested several disputed hypothesis like "oil fuels ethnic conflict" or "mountaineous regrions are more likely to expierience conflict". I could not prove that oil fuels ethnic conflict - but I wrote two pages about how the quality of the available oil-dataset impacted the analysis (the dataset itself is a time-series, the oil-well dataset is not). The "mountains are causing conflict" thesis was also a failure - but a fruitful one: previous research analyzed this thesis with country-level data (e.g. mean height of the country or so), while I did it on the level of ethnic groups - so I spent a lot of paper to discuss the differences and why my analysis was better than other famous research...
Keep in mind: disproving a hypothesis is not a failure but a result as good as a proved hypothesis.
- $\begingroup$ The hypotheses you mention aren't (conventional) null hypotheses. I think you may have missed the point of the OP. $\endgroup$ – Nick Stauner Commented May 28, 2014 at 16:10
There is a method for combing probabilities across studies described here . You should not apply the formula blindly without considering the pattern of results.
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged hypothesis-testing or ask your own question .
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- We spent a sprint addressing your requests — here’s how it went
Hot Network Questions
- Logical AND (&&) does not short-circuit correctly in #if
- Examples of distribution for which first-order condition is not enough for MLE
- What does ‘a grade-hog’ mean?
- If a lambda is declared as a default argument, is it different for each call site?
- Books using the axiomatic method
- How do guitarists remember what note each string represents when fretting?
- What is the step-by-step process to solve Angle = ArcCos(R / R+h)?
- A chess engine in Java: generating white pawn moves - take II
- Ceramic capacitor has no voltage rating, recommendations?
- Duplicating Matryoshka dolls
- Imagining Graham's number in your head collapses your head to a Black hole
- Inversion naming conventions
- How to show isomorphism between an adele ring on a number field and its Pontryagin dual?
- Deleted my EFI & MSR partitions by error, how to rebuild it?
- What does Athena mean in this passage of book 3 of the Odyssey?
- How is the result of this integral obtained by the function `Integrate`?
- Correlation for Small Dataset?
- Does it matter if a fuse is on a positive or negative voltage?
- How far back in time have historians estimated the rate of economic growth and the economic power of various empires?
- Is it possible to complete a Phd on your own?
- How many steps are needed to turn one "a" into at least 100,000 "a"s using only the three functions of "select all", "copy" and "paste"?
- Where can I access records of the 1947 Superman copyright trial?
- Are there alternatives to alias I'm not aware of?
- Drinking water before Shacharis when one did not make Kidush the night before

COMMENTS
A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis. Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.
Null Hypothesis H 0: The correlation in the population is zero: ρ = 0. Alternative Hypothesis H A: The correlation in the population is not zero: ρ ≠ 0. For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.. We always use the following steps to perform a hypothesis test: Step 1: State the null and alternative hypotheses. The null hypothesis, denoted as H 0, is the hypothesis that the sample data occurs purely from chance.. The alternative hypothesis, denoted as H A, is the hypothesis that ...
Use the P-Value method to support or reject null hypothesis. Step 1: State the null hypothesis and the alternate hypothesis ("the claim"). H o :p ≤ 0.23; H 1 :p > 0.23 (claim) Step 2: Compute by dividing the number of positive respondents from the number in the random sample: 63 / 210 = 0.3. Step 3: Find 'p' by converting the stated ...
Let's return finally to the question of whether we reject or fail to reject the null hypothesis. If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above ...
The null hypothesis is the claim that there's no effect in the population. If the sample provides enough evidence against the claim that there's no effect in the population (p ≤ α), then we can reject the null hypothesis. Otherwise, we fail to reject the null hypothesis. Although "fail to reject" may sound awkward, it's the only ...
2. If the p-value is high, indicating that the observed data is likely under the null hypothesis, then we fail to reject the null hypothesis. This does not confirm the null hypothesis is true; rather, it suggests that the data does not provide strong evidence against it Role of P-Values and Test Statistics. A P-value, or probability value, is a ...
The first step in hypothesis testing is to set up two competing hypotheses. The hypotheses are the most important aspect. If the hypotheses are incorrect, your conclusion will also be incorrect. The two hypotheses are named the null hypothesis and the alternative hypothesis. The null hypothesis is typically denoted as H 0.
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with \(H_{0}\).The null is not rejected unless the hypothesis test shows otherwise.
The null hypothesis is a default hypothesis that a quantity to be measured is zero (null). Typically, the quantity to be measured is the difference between two situations. For instance, trying to determine if there is a positive proof that an effect has occurred or that samples derive from different batches. [7] [8]
In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant. If there is greater than a 5 ...
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
We can break the process of null hypothesis testing down into a number of steps: Formulate a hypothesis that embodies our prediction ( before seeing the data) Collect some data relevant to the hypothesis. Specify null and alternative hypotheses. Fit a model to the data that represents the alternative hypothesis and compute a test statistic.
The null hypothesis in a correlational study of the relationship between high school grades and college grades would typically be that the population correlation is 0. This can be written as. H0: ρ = 0 (7.3.2) (7.3.2) H 0: ρ = 0. where ρ ρ is the population correlation, which we will cover in chapter 12. Although the null hypothesis is ...
There is something I am confused about. If our significance level is .05 and our resulting p-value is .02 (thus the strength of our evidence is strong enough to reject the null hypothesis), do we state that we reject the null hypothesis with 95% confidence or 98% confidence? My guess is our confidence level is 95% since or alpha was .05.
Abstract: "null hypothesis significance testing is the statistical method of choice in biological, biomedical and social sciences to investigate if an effect is likely". No, NHST is the method to test the hypothesis of no effect. I agree - yet people use it to investigate (not test) if an effect is likely.
Since the t-statistic of 2.40 falls in the rejection region, we reject the null hypothesis in favor of the alternative. Since the p-value is between 0.02 and 0.05, it must be less than the significance level (0.05), so we reject the null hypothesis in favor of the alternative.
Null Hypothesis Overview. The null hypothesis, H 0 is the commonly accepted fact; it is the opposite of the alternate hypothesis. Researchers work to reject, nullify or disprove the null hypothesis. Researchers come up with an alternate hypothesis, one that they think explains a phenomenon, and then work to reject the null hypothesis. Read on ...
In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant. If there is greater than a 5 ...
Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis.
Null hypothesis. by Marco Taboga, PhD. In a test of hypothesis, a sample of data is used to decide whether to reject or not to reject a hypothesis about the probability distribution from which the sample was extracted.. The hypothesis is called the null hypothesis, or simply "the null".
25. I've time and again rejected or failed to reject the null hypothesis. In the failure to reject case, you conclude that there isn't sufficient evidence for rejection and you "move on" (i.e., either gather more data, end the experiment etc.,) But when you "do" reject the null hypothesis, providing some evidence for the alternative hypothesis ...