Algebra: Ratio Word Problems
Related Pages Two-Term Ratio Word Problems More Ratio Word Problems Algebra Lessons
In these lessons, we will learn how to solve ratio word problems that have two-term ratios or three-term ratios.
Ratio problems are word problems that use ratios to relate the different items in the question.
The main things to be aware about for ratio problems are:
- Change the quantities to the same unit if necessary.
- Write the items in the ratio as a fraction .
- Make sure that you have the same items in the numerator and denominator.

Ratio Problems: Two-Term Ratios
Example 1: In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?
Solution: Step 1: Assign variables: Let x = number of red sweets.
Step 2: Solve the equation. Cross Multiply 3 × 120 = 4 × x 360 = 4 x
Answer: There are 90 red sweets.
Example 2: John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?
Solution: Step 1: Sentence: Jane has 20 marbles, all of them either red or blue. Assign variables: Let x = number of blue marbles for Jane 20 – x = number red marbles for Jane
Step 2: Solve the equation
Cross Multiply 3 × x = 2 × (20 – x ) 3 x = 40 – 2 x
John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.
Answer: John has 4 more blue marbles than Jane.
How To Solve Word Problems Using Proportions?
This is another word problem that involves ratio or proportion.
Example: A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour. How much sugar should I use?
How To Solve Proportion Word Problems?
When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion.
- Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000. Estimate the total number of rabbits in Bryer Lake National Park.
- Mel fills his gas tank up with 6 gallons of premium unleaded gas for a cost of $26.58. How much would it costs to fill an 18 gallon tank? 3 If 4 US dollars can be exchanged for 1.75 Euros, how many Euros can be obtained for 144 US dollars?
Ratio problems: Three-term Ratios
Example 1: A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?
Solution: Step 1: Assign variables: Let x = amount of corn
Step 2: Solve the equation Cross Multiply 2 × x = 3 × 5 2 x = 15
Answer: The mixture contains 7.5 pounds of corn.
Example 2: Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?
Solution: Step 1: Assign variables: Let x = number of red shirts and y = number of green shirts
Step 2: Solve the equation Cross Multiply 3 × 20 = x × 4 60 = 4 x x = 15
5 × 20 = y × 4 100 = 4 y y = 25
The total number of shirts would be 15 + 25 + 20 = 60
Answer: There are 60 shirts.
Algebra And Ratios With Three Terms
Let’s study how algebra can help us think about ratios with more than two terms.
Example: There are a total of 42 computers. Each computer runs one of three operating systems: OSX, Windows, Linux. The ratio of the computers running OSX, Windows, Linux is 2:5:7. Find the number of computers that are running each of the operating systems.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Here you will learn about ratios, including how to write a ratio, simplifying ratios, unit rate math and how to solve problems involving ratios and rates.
Students will first learn about ratios as part of ratios and proportions in 6 th grade and 7 th grade.
What is a ratio?
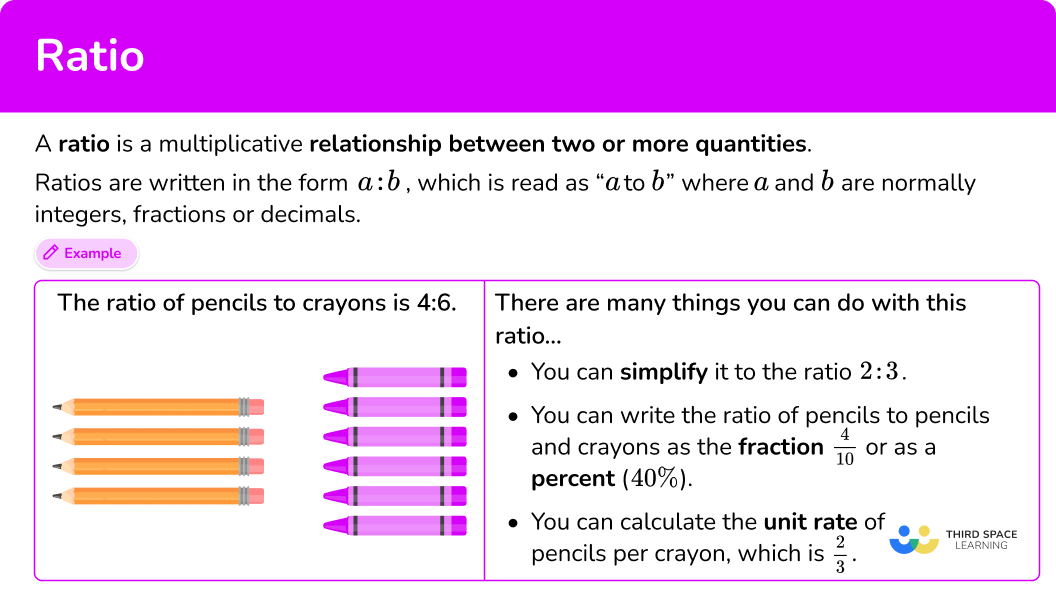
A ratio is a multiplicative relationship between two or more quantities.
Ratios are written in the form a : b, which is read as “a to b”, where a and b are normally integers, fractions, or decimals.
The order of the quantities in the ratio is important.
For example,
If there are 10 boys in a class and 15 girls, the ratio of boys to girls is 10 : 15 which is read as “10 to 15.” This is an example of a part to part ratio. You could also say the ratio of total students to girls is 15 : 25. This is an example of a part to whole ratio.
Step-by-step guide: How to write a ratio
Since a ratio represents a relationship, there is always more than one way to show it.
This includes unit rate math – which creates equivalent ratios where one part of the ratio is 1.
You can use unit rates to compare different quantities.
A grocery store sells a bag of 6 bananas for \$ 2.34 and a bag of 4 bananas for \$ 1.44.
Which bag has the better unit price?
Unit price means the price per 1 unit. In this case, the units are bananas. Divide each ratio to find the price for 1 banana.
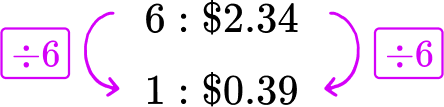
The bag of 4 bananas is \$ 0.36 per banana, which is cheaper than the bag of 6 bananas which is \$ 0.39 per banana.
Step-by-step guide: Unit rate math
Unit rates are not the only types of equivalent ratios. When simplifying fractions, use the common factors to divide all the numbers in a ratio until they cannot be divided further to write the ratio in lowest terms.
The ratio of red counters to blue counters is 16 : 12.

You can simplify the ratio to lowest terms by finding the greatest common factor \textbf{(GCF)} of each of the numbers in the ratio.
Factors of 16 \text{:} \, 1, 2, 4, 8, 16
Factor of 12 \text{:} \, 1, 2, 3, 4, 6, 12
The greatest common factor is 4. To simplify the ratio, you divide both sides by 4.
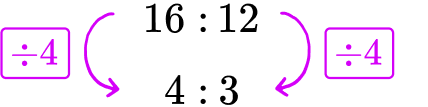
Step-by-step guide: Simplifying ratios
Another way to write ratios is by using fraction notation.
Fraction notation can be used to show a part to whole ratio relationships.
The bar model below shows the ratio of blue : red as 3 : 2 (3 to 2). There are 3 blue blocks, 2 red blocks and 5 blocks in total.
This part to whole relationship allows us to make statements like…
- \cfrac{3}{5} of the blocks are blue
- \cfrac{2}{5} of the blocks are red
- \cfrac{5}{5} of the blocks are blue or red
The ratio of blue : red as 3 : 2 can also be shown as a part to part fraction…
The fractions show the ratio relationship BETWEEN the blue and red blocks. This allows us to make statements like…
- The number of blue blocks is \cfrac{3}{2} larger than red
- The number of red blocks is \cfrac{2}{3} the amount of blue
Step-by-step guide: Ratio to fraction
Ratios can also be written with percents.

The ratio of pencils to crayons is 4 : 6.
The ratio has 10 parts, so the fractions are
\cfrac{4}{10} : \cfrac{6}{10}.
The numerator represents the numbers of the ratio, which show how many pencils or crayons there are. The denominator represents the total number of pencils and crayons.
You may be able to recognize what the fractions are as percents or you may need to use long division to help convert your fractions.
\cfrac{4}{10}=40 \%, so 40 \% are pencils.
\cfrac{6}{10}=60 \%, so 60 \% are crayons.
Step-by-step guide: Ratio to percent
Solving problems with ratios is common in the real world. One place that this shows up is in calculating exchange rates. An exchange rate is the rate at which the money of one country can be exchanged for the money of another country.
Using a currency’s exchange rate you can convert between US dollars and foreign currencies.
To convert from US dollars (USD) to Japanese yen (JPY), you must multiply by the exchange rate.
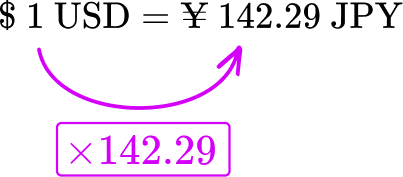
So \$ 15 \; USD would be ¥2,134.35 \; JPY because,
\$ 15 \; USD \times 142.29=¥ 2,134 .35 \; JPY.
Step-by-step guide: How to calculate exchange rates
All the skills above are examples of ratio problem solving. When solving problems with ratios, it is important to ask:
- What is the ratio involved?
- What order are the quantities in the ratio?
- What is the total amount / what is the part of the total amount known?
- What are you trying to calculate ?
In the classroom, ratio problem solving often comes in the form of real world scenarios or word problems.
\cfrac{8}{10} students are right handed. What is the ratio of left handed students to right handed students? (2 : 8)
Step-by-step guide: Ratio problem solving
[FREE] Ratio Worksheet (Grade 6 and 7)
Use this quiz to assess your 6th and 7th grade students’ understanding of ratios. Covers 10+ questions with answers on ratio topics to identify areas of strength and support!
Common Core State Standards
How does this relate to 6 th grade math and 7 th grade math?
- Grade 6 – Ratios and Proportions (6.RP.A.1) Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, “The ratio of wings to beaks in the bird house at the zoo was 2 : 1, because for every 2 wings there was 1 beak.” “For every vote candidate A received, candidate C received nearly three votes.”
- Grade 6 – Ratios and Proportions (6.RP.A.2) Understand the concept of a unit rate \cfrac{a}{b} associated with a ratio a : b with b ≠ 0, and use rate language in the context of a ratio relationship. For example, “This recipe has a ratio of 3 cups of flour to 4 cups of sugar, so there is \cfrac{3}{4} cup of flour for each cup of sugar.” “We paid \$ 75 for 15 hamburgers, which is a rate of \$ 5 per hamburger.”
- Grade 6 – Ratios and Proportions (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
- Grade 6 – Ratios and Proportions (6.RP.A.3b) Solve unit rate problems including those involving unit pricing and constant speed. For example, if it took 7 hours to mow 4 lawns, then at that rate, how many lawns could be mowed in 35 hours? At what rate were lawns being mowed?
- Grade 7 – Ratios and Proportions (7.RP.A.1) Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured in like or different units. For example, if a person walks \cfrac{1}{2} mile in each \cfrac{1}{4} hour, compute the unit rate as the complex fraction \cfrac{\cfrac{1}{2}}{\cfrac{1}{4}} miles per hour, equivalently 2 miles per hour.
How to work with a ratio
There are a lot of ways to work with a ratio. For more specific step-by-step guides, check out the ratio pages linked in the “What are ratios?” section above or read through the examples below.
Ratio examples
Example 1: how to write a ratio.

Write the ratio of apples to pears.
- Identify the different quantities being compared and their order.
There are 5 pears and 2 apples.
The order of the ratio is apples to pears.
2 Write the ratio using a colon.
Apples : Pears
\hspace{0.7cm} 5 : 2
3 Check if the ratio can be simplified.
5 and 2 only have a common factor of 1, so this ratio is already in its lowest terms (simplest form).
Example 2: unit rate calculation – decimal
A car travels 303 miles in 6 hours. If the car travels the same number of miles each hour, what is the miles per hour rate?
Write the original rate.
303 miles in 6 hours → 303 : 6.
Use multiplication or division to create a unit rate.
The miles ‘per hour’ refers to 1 hour. Divide each side of the rate by 6, to create a rate for 1 hour.
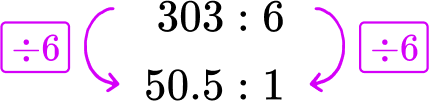
Use the unit rate to answer the question.
The car travels 50.5 miles each hour.
Example 3: simplifying ratios
Write the ratio 48 : 156 in lowest terms.
Calculate the greatest common factor of the parts of the ratio.
Factors of 48=1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Factors of 156=1, 2, 3, 4, 6, 12, 13, 26, 39, 52, 78, 156
GCF(48,156)=12
Divide each part of the ratio by the greatest common factor.
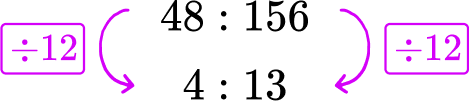
4 : 13 is in lowest terms.
Example 4: solving a problem involving ratio to percents
The ratio of adults to children in a park is 11 : 14.
One-fourth of the adults are women. What percent of the people in the park are men?
Add the parts of the ratio for the denominator of the fractions.
11+14=25. There are 25 parts in total. The denominator is 25.
Convert each part of the ratio to a fraction.
11 : 14 becomes \cfrac{11}{25} : \cfrac{14}{25}.
Convert the fractions to percents.
\begin{aligned}& \cfrac{11}{25}=\cfrac{44}{100}=44 \% \\\\ & \cfrac{14}{25}=\cfrac{56}{100}=56 \%\end{aligned}
You now know that 44 \% of the people are adults.
One-fourth of the adults are women.
\cfrac{1}{4} of 44 \%=11 \%.
11 \% of the people in the park are women and therefore 44-11=33 \% of the people are men.
Example 5: converting from KRW / USD
₩5,000 \; KRW is equal to \$ 3.85 \; USD. What is the exchange rate from \$ \; (USD) to ₩ \; (KRW)?
Use the information given to set up a rate.
When calculating the currency exchange rate from ₩ \; (KRW), you want to know how many ₩ \; (KRW) are equal to \$ 1 \; (USD). This is the ratio of ₩ to \$, so set up the rate as \cfrac{₩ 5,000}{\$ 3.85}.
Divide both parts by the base currency.
In this case, the base currency is \$ \; (USD), so divide both parts by 3.85, rounding the ₩ \; KRW is to the nearest whole:
\cfrac{₩ 5,000 \div 3.85}{\$ 3.85 \div 3.85}=\cfrac{₩ 1,299}{\$ 1}.
State the final exchange rate with the correct currency symbols.
The exchange rate from \$ \; (USD) to ₩ \; (KRW) is 1,299.
Example 6: ratio problem solving – mixed numbers
Fruit Salad Recipe:
- 2 \cfrac{1}{2} cups of blueberries
- 2 \cfrac{1}{5} cups of orange slices
- 1 \cfrac{1}{4} cups of strawberries
- 2 cups of apple slices
Write the ratio of the total cups of berries for every 1 cup of strawberries in the salad.
Identify key information within the question.
There are 1 \cfrac{1}{4} cups of strawberries and 2 \cfrac{1}{2} cups of blueberries.
Know what you are trying to calculate.
You need to create the ratio of the total cups of berries (strawberries and blueberries) for every 1 cup of strawberries.
Use prior knowledge to structure a solution.
First add 1 \cfrac{1}{4}+2 \cfrac{1}{2} to find the total cups of berries.
\begin{aligned}& 1 \cfrac{1}{4}+2 \cfrac{1}{2} \\\\ & =\cfrac{5}{4}+\cfrac{5}{2} \\\\ & =\cfrac{5}{4}+\cfrac{10}{4} \\\\ & =\cfrac{15}{4}\end{aligned}
Then write the ratio of total cups of berries to cups of strawberries.
\cfrac{15}{4} : \cfrac{5}{4}
Now multiply both sides of the ratio by \cfrac{4}{5}, to calculate the ratio of 1 cup of strawberries.
\cfrac{15}{4} \times \cfrac{4}{5} : \cfrac{5}{4} \times \cfrac{4}{5}
There are 3 total cups of berries for every 1 cup of strawberries.
*Note: To solve, you can also write the ratio \cfrac{15}{4} : \cfrac{5}{4} as the complex fraction \cfrac{\cfrac{15}{4}}{\cfrac{5}{4}} and find the quotient of the numerator and denominator.
Teaching tips for ratio
- There are many ways to engage students in ratios. One way is to introduce the golden ratio (based on Fibonacci’s sequence) and challenge students to look for it in the real world. Keep a chart or wall in the classroom for students to add any examples of this ratio that they find.
- Incorporate as many examples of ratios in the classroom as you can – even across subjects. For example, have students write ratios about the “Word of the day” – from an English or Science class. Such as “Write the ratio of nouns to adjectives” or “Write the ratio of words with the letter ‘e’ to total words.”
- As students work with ratios in different ways, keep track of successful solving strategies on a bulletin board or on chart paper. This allows students to see and utilize another students’ strategy, make connections between strategies and feel ownership in any ideas they help create.
- Be mindful of how to progress with ratio topics. Typically whole number ratios are introduced first, then ratios with rational numbers. Ratios that involve compare only fractional (or decimal values), such as \cfrac{2}{3} : \cfrac{5}{6} or 0.45 : 0.34 are the most difficult for students. As always, be mindful of your state’s curriculum when making decisions on when to introduce certain ratio topics.
Easy mistakes to make
- Writing the ratio in the wrong order A common error is to write the parts of the ratio in the wrong order. For example, The number of dogs to cats is given as the ratio 12 : 13 but the solution is incorrectly written as 13 : 12.
- Confusing ratios and fractions You can write a ratio with fraction notation. A part to whole fraction will have the same fractional language as a fraction. However, a part to part fraction will not. For example, The ratio of boys to girls is 2 : 3. Two ways to express this ratio are \cfrac{2}{3} or \cfrac{2}{5}. However, you must be careful how you read these fractions. You can say “ \cfrac{2}{5} of the kids are boys” but you cannot say “ \cfrac{2}{3} of the kids are boys.” Instead, say “The number of boys is \cfrac{2}{3} the number of girls.”
- Not fully simplified A common error is to not find the greatest common factor when simplifying a ratio. For example, Simplify the ratio 12 : 18. Dividing both numbers by only 2 leaves a ratio of 6 : 9, which is not fully simplified. This can be simplified further by dividing by 3 to get the ratio 2 : 3, which is the correct answer. By dividing both numbers by the greatest common factor, 6, would get the ratio 2 : 3 in one step.
Practice ratio questions
1. 500 people attended a concert. There were 240 boys. What is the ratio of boys to girls who went to the concert?

There are 500 people and 240 boys.
500-240=260. There are 260 girls.
The order of the ratio is boys to girls.
Boys : Girls
2. A musical requires 200 costumes. 140 costumes are for the background dancers. The rest are for the lead roles. Write the ratio of the costumes for lead roles to background dancers in the simplest form.
There are 200 costumes. 140 costumes are for background dances.
200-140=60 lead role costumes
The ratio order of the ratio is lead roles to background dancers
Lead roles : Background dancers
\hspace{1cm} 60 : 140
The greatest common factor of 60 and 140 is 20\text{:}
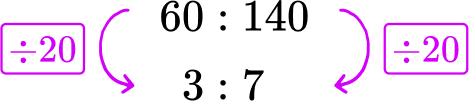
3. A shop is selling the same pencils in two different packs.
Which statement correctly compares the packs?
Pack \textbf{A}\text{:} \; 5 pens cost \$ 6.20
Pack \textbf{B}\text{:} \; 4 pens cost \$ 4.88
Pack A is \$ 1.32 cheaper per pencil than Pack B.
Pack B is \$ 1.32 cheaper per pencil than Pack A.
Pack A is \$ 0.02 cheaper per pencil than Pack B.
Pack B is \$ 0.02 cheaper per pencil than Pack A.
Offer A\text{:} \; 5 pencils cost \$ 6.20 → 5 : \$ 6.20
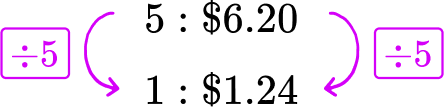
Each pencil in Pack A costs \$ 1.24.
Offer B\text{:} \; 4 pencils for \$ 4.88 → 4 : \$4.88
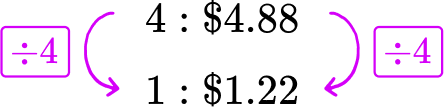
Each pencil in Pack B costs \$ 1.22.
\$ 1.24-\$ 1.22=\$ 0.02.
Offer B costs \$ 0.02 cheaper than Offer A.
4. The fraction of bananas in a bowl is \cfrac{13}{20}. Calculate the ratio of bananas to other pieces of fruit in the bowl.
The total number of pieces of fruit is 20. The number of bananas is 13.
As a bar model, this looks like
The number of other pieces of fruit is therefore 7 (this is calculated by 20-13=7 or counting the number of red bars above).
The ratio of bananas to other pieces of fruit is therefore 13 : 7.
5. Given the exchange rate between US dollars (USD) and New Zealand dollars (NZD) is \$ 1 \; USD=\$ 1.63 \; NZD, convert \$ 50 \; USD to New Zealand dollars (NZD). Round to the nearest cent.
\$ 50 \, USD=\$ \rule{0.5cm}{0.15mm} \, NZD
Since each US dollar is equal to \$ 1.63 \, NZD, multiply the USD by 1.63 to find the number of \$ \, (NZD).
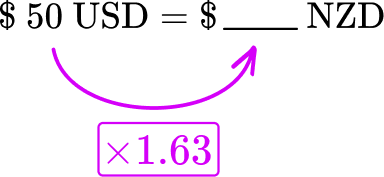
\$ 50 \, USD=\$ 81.50 \, NZD
6. A soap is made by combining lavender soap with lemon soap. Each bar of soap weighs 330 \, g. If the ratio of lavender to lemon is 4 : 7, how many grams of lemon soap are in each bar?
As there are 7+4=11 shares within the ratio
330 \div 11=30 \, g per share
The amount of Lemon in the soap is equal to 7 \times 30=210 \, g
While the term ratio is used in a variety of ways in the real world, the definition of ratio in math is the comparison of two or more values that have a constant relationship. Some examples of ratios are “ 2 dogs to 5 cats” or “ 24 miles per hour.”
A rate is a special type of ratio that compares different units. They are not synonyms, since not all ratios are rates. However, all rates are ratios, so they can be called by either name.
Ratio understanding is expanded to include more complex comparisons that involve exponents, variables and/or polynomials. This extends to include ratio relationships in proportions and linear equations. As students progress in their learning, they will become comfortable graphing, creating tables and equations that represent ratio relationships.
The next lessons are
- Converting fractions, decimals and percentages
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview

Sharing between a Ratio
Example 1: Abbie and Ben share £120 in the ratio 2:1 Work out how much each of them get.
The first step is to work out how many equal parts there are. The ratio is 2:1 so there are 3 (2 + 1) equal parts
We now need to work out how much each of the parts is worth We divide the £120 between the 3 parts £120 ÷ 3 = £40 Each part is worth £40
Now we can work out how much Abbie and Ben get Abbie has 2 parts so she gets £80 (2 × £40) Ben has one part which is worth £40
You may find it useful to draw a diagram for ratio questions
Abbie has 2 parts and Ben has 1 part, we could represent this as 2 boxes for Abbie and 1 box for Ben:
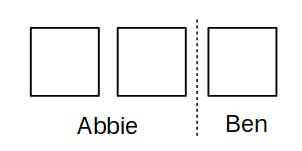
Each box must have the same amount in it and the total in all 3 boxes must be £120. We share £120 out evenly between the boxes (£120 ÷ 3 = £40)
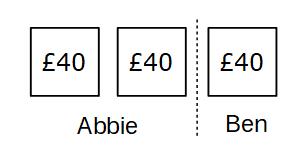
We can see that Abbie gets £80 (£40 + £40) and Ben gets £40
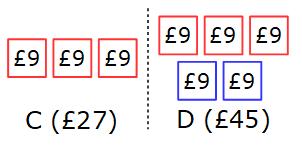
Example 2: A, B and C share £240 in the ratio 4:3:1 Work out how much each of them get.
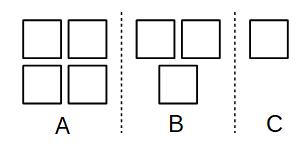
4 + 3 + 1 = 8 There are 8 equal parts
£240 ÷ 8 = £30 Each part is worth £30
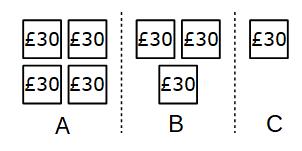
A gets 4 × £30 = £120 B gets 3 × £30 = £90 C gets 1 × £30 = £30
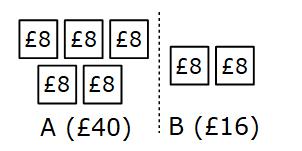
Example 3: A and B share some money in the ratio 5:2 A gets £40 Work out how much B gets.
In this example we have not been given the total amount. We have been given the amount that A gets
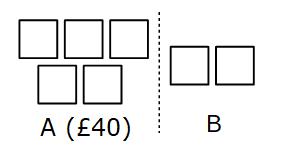
A has £40 and that is 5 parts
Each part much be equal so each part is worth £40 ÷ 5 £40 ÷ 5 = £8
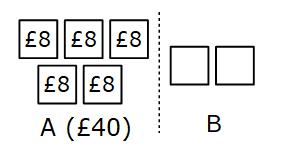
Each part is worth £8 and B has two parts £8 × 2 = £16
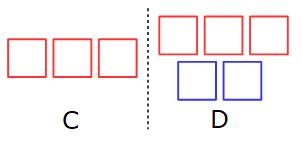
Example 4: C and D share some money in the ratio 3:5 The difference between the amount C gets and the amount D gets is £18 Work out how much each of them get.
In this example we have been given the difference between the amounts of money C and D get.
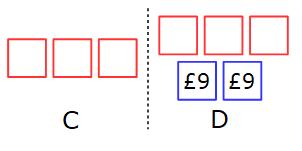
The difference between 3 parts and 5 parts is 2 parts. (5 − 3 = 2) 2 parts must be worth £18 £18 ÷ 2 = £9
Each part is worth £9
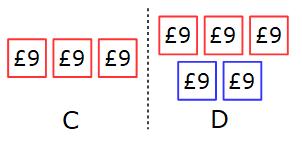
C gets 3 × £9 = £27 D gets 5 × £9 = £45
Other Links
Copyright © Maths Genie. Maths Genie Limited is a company registered in England and Wales with company number 14341280. Registered Office: 86-90 Paul Street, London, England, EC2A 4NE.
- Number Charts
- Multiplication
- Long division
- Basic operations
- Telling time
- Place value
- Roman numerals
- Fractions & related
- Add, subtract, multiply, and divide fractions
- Mixed numbers vs. fractions
- Equivalent fractions
- Prime factorization & factors
- Fraction Calculator
- Decimals & Percent
- Add, subtract, multiply, and divide decimals
- Fractions to decimals
- Percents to decimals
- Percentage of a number
- Percent word problems
- Classify triangles
- Classify quadrilaterals
- Circle worksheets
- Area & perimeter of rectangles
- Area of triangles & polygons
- Coordinate grid, including moves & reflections
- Volume & surface area
- Pre-algebra
- Square Roots
- Order of operations
- Scientific notation
- Proportions
- Ratio word problems
- Write expressions
- Evaluate expressions
- Simplify expressions
- Linear equations
- Linear inequalities
- Graphing & slope
- Equation calculator
- Equation editor
- Elementary Math Games
- Addition and subtraction
- Math facts practice
- The four operations
- Factoring and number theory
- Geometry topics
- Middle/High School
- Statistics & Graphs
- Probability
- Trigonometry
- Logic and proof
- For all levels
- Favorite math puzzles
- Favorite challenging puzzles
- Math in real world
- Problem solving & projects
- For gifted children
- Math history
- Math games and fun websites
- Interactive math tutorials
- Math help & online tutoring
- Assessment, review & test prep
- Online math curricula















































































































































IMAGES
VIDEO
COMMENTS
Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem. ...
Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.
Ratio Word Problems: relating different things using ratios and algebra, how to solve ratio word problems that have two-term ratios or three-term ratios, How to solve proportion word problems, questions and answers, with video lessons, examples and step-by-step solutions.
A ratio is a comparison of two quantities. A proportion is an equality of two ratios. To write a ratio: Determine whether the ratio is part to part or part to whole. Calculate the parts and the whole if needed. Plug values into the ratio. Simplify the ratio if needed.
Do you want to learn how to compare and measure different quantities using ratios and rates? Khan Academy's pre-algebra course offers you a comprehensive introduction to these concepts, with interactive exercises and videos. You will also learn how to use proportions to solve word problems and graph proportional relationships. Join Khan Academy and start your journey to master ratios and rates!
Discover how to solve ratio problems with a real-life example involving indoor and outdoor playtimes. Learn to use ratios to determine the number of indoor and outdoor playtimes in a class with a 2:3 ratio and 30 total playtimes. ... What you need to do in any word problem involving the ratios is exactly the same. Take the entire amount and ...
In the classroom, ratio problem solving often comes in the form of real world scenarios or word problems. For example, \cfrac{8}{10} students are right handed. What is the ratio of left handed students to right handed students? (2 : 8) Step-by-step guide: Ratio problem solving.
Practice Questions. Previous: Percentages of an Amount (Non Calculator) Practice Questions. Next: Rotations Practice Questions. The Corbettmaths Practice Questions on Ratio.
Practise solving ratio problems and explore the different forms they take with BBC Bitesize Maths. For students between the ages of 11 and 14.
The Corbettmaths Textbook Exercise on Ratio: Problem Solving. Welcome; Videos and Worksheets; Primary; 5-a-day. 5-a-day GCSE 9-1; 5-a-day Primary; 5-a-day Further Maths ... Ratio: Problem Solving Textbook Exercise. Click here for Questions. Textbook Exercise. Previous: Ratio: Difference Between Textbook Exercise. Next: Reflections Textbook ...
The first step is to work out how many equal parts there are. The ratio is 2:1 so there are 3 (2 + 1) equal parts. We now need to work out how much each of the parts is worth. We divide the £120 between the 3 parts. £120 ÷ 3 = £40. Each part is worth £40. Now we can work out how much Abbie and Ben get. Abbie has 2 parts so she gets £80 (2 ...
You are here: Home → Worksheets → Ratios Free worksheets for ratio word problems. Find here an unlimited supply of worksheets with simple word problems involving ratios, meant for 6th-8th grade math. In level 1, the problems ask for a specific ratio (such as, "Noah drew 9 hearts, 6 stars, and 12 circles. What is the ratio of circles to hearts?
Sharing an amount in a given ratio Further problems involving ratio include Ratios where you are given the difference between the two parts. E.g., Kerry is given $30 more than Kacey who is given $50; Ratios where one quantity is given and you have to find the other quantity. E.g., Kerry and Kacey are sharing money in the ratio 8 : 5, Kacey gets $50
Solving Ratio Problems. We add the parts of the ratio to find the total number of parts. There are 2 + 3 = 5 parts in the ratio in total. To find the value of one part we divide the total amount by the total number of parts. 50 ÷ 5 = 10. We multiply the ratio by the value of each part. 2:3 multiplied by 10 gives us 20:30.
Unit test. Level up on all the skills in this unit and collect up to 1,400 Mastery points! Ratios let us see how two values relate, especially when the values grow or shrink together. From baking recipes to sports, these concepts find their way into our lives on a daily basis.
Thinking Blocks Ratios - Learning Connections. Essential Skills. Problem Solving - model and solve word problems. Common Core Connection for Grades 6 and 7. Understand the concept of ratio and describe the relationship between two quantities. Use ratio and rate reasoning to solve real-world and mathematical problems.
Using Ratios. The trick with ratios is to always multiply or divide the numbers by the same value. Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk. So the ratio of flour to milk is 3 : 2. To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4: 3 ×4 : 2 ×4 = 12 : 8.
Examples. For example, ⅘ is a ratio and the proportion statement is 20/25 = ⅘. If we solve this proportional statement, we get: 20/25 = ⅘. 20 x 5 = 25 x 4. 100 = 100. Check: Ratio and Proportion PDF. Therefore, the ratio defines the relationship between two quantities such as a:b, where b is not equal to 0.
Use proportions to solve scaling problems. Ratios and proportions are used in a wide variety of situations to make comparisons. For example, using the information from Figure 5.15, we can see that the number of Facebook users compared to the number of Twitter users is 2,006 M to 328 M. Note that the "M" stands for million, so 2,006 million is ...
Learn how to solve problems involving ratio and proportion with Dr Austin Maths, a website that provides free and editable resources for maths teachers and students. You can also find topics such as equations, inequalities, graphs, calculus and statistics on the website.
The ratio 3 to 5 or 3/5 is the same thing as 12 to 20, is the same thing as 24 to 40, is the same thing as 48 to 80. Let's make sure we got the right answer. Let's do a couple more of these. The following table shows equivalent fractions to 27/75. So then they wrote all of the different equivalent fractions.
Multiplication, division, fractions, and logic games that boost sixth grade math skills. Level 6 Math Games Game Spotlight: Dirt Bike Proportions Multiplayer Math Games Four Wheel Fracas. Jumping Aliens. Martian Hoverboards. Otter Rush. ... Logic and Problem Solving Games Icy Super Slide. Arcade Golf. Rabbit Samurai 2. Duck Life 4. Icy Purple ...
Equivalent ratio word problems. A fruit basket is filled with 8 bananas, 3 oranges, 5 apples, and 6 kiwis. Complete the ratio. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education ...
When optimizing a mechanical device, the symmetry principle provides important guidance. Minimum gearbox mass and maximum gearbox efficiency are two single objectives that need to be achieved when designing a gearbox, and they are not compatible. In order to address the multi-objective optimization (MOO) problem with the above single targets involved in building a two-stage helical gearbox ...
Proportion word problems. Sam used 6 loaves of elf bread on an 8 day hiking trip. He wants to know how many loaves of elf bread ( b) he should pack for a 12 day hiking trip if he eats the same amount of bread each day. How many loaves of elf bread should Sam pack for a 12 day trip? Learn for free about math, art, computer programming, economics ...
This unit tackles the medium-difficulty problem solving and data analysis questions on the SAT Math test. Work through each skill, taking quizzes and the unit test to level up your mastery progress. ... Ratios, rates, and proportions: medium Get 3 of 4 questions to level up! Unit conversion: medium. Learn. Unit conversion | Lesson (Opens a modal)