what is problem solving method of teaching

Problem-Solving Method in Teaching

The problem-solving method is a highly effective teaching strategy that is designed to help students develop critical thinking skills and problem-solving abilities . It involves providing students with real-world problems and challenges that require them to apply their knowledge, skills, and creativity to find solutions. This method encourages active learning, promotes collaboration, and allows students to take ownership of their learning.

Table of Contents

Definition of problem-solving method.

Problem-solving is a process of identifying, analyzing, and resolving problems. The problem-solving method in teaching involves providing students with real-world problems that they must solve through collaboration and critical thinking. This method encourages students to apply their knowledge and creativity to develop solutions that are effective and practical.

Meaning of Problem-Solving Method

The meaning and Definition of problem-solving are given by different Scholars. These are-

Woodworth and Marquis(1948) : Problem-solving behavior occurs in novel or difficult situations in which a solution is not obtainable by the habitual methods of applying concepts and principles derived from past experience in very similar situations.

Skinner (1968): Problem-solving is a process of overcoming difficulties that appear to interfere with the attainment of a goal. It is the procedure of making adjustments in spite of interference

Benefits of Problem-Solving Method

The problem-solving method has several benefits for both students and teachers. These benefits include:

• Encourages active learning: The problem-solving method encourages students to actively participate in their own learning by engaging them in real-world problems that require critical thinking and collaboration
• Promotes collaboration: Problem-solving requires students to work together to find solutions. This promotes teamwork, communication, and cooperation.
• Builds critical thinking skills: The problem-solving method helps students develop critical thinking skills by providing them with opportunities to analyze and evaluate problems
• Increases motivation: When students are engaged in solving real-world problems, they are more motivated to learn and apply their knowledge.
• Enhances creativity: The problem-solving method encourages students to be creative in finding solutions to problems.

Steps in Problem-Solving Method

The problem-solving method involves several steps that teachers can use to guide their students. These steps include

• Identifying the problem: The first step in problem-solving is identifying the problem that needs to be solved. Teachers can present students with a real-world problem or challenge that requires critical thinking and collaboration.
• Analyzing the problem: Once the problem is identified, students should analyze it to determine its scope and underlying causes.
• Generating solutions: After analyzing the problem, students should generate possible solutions. This step requires creativity and critical thinking.
• Evaluating solutions: The next step is to evaluate each solution based on its effectiveness and practicality
• Selecting the best solution: The final step is to select the best solution and implement it.

Verification of the concluded solution or Hypothesis

The solution arrived at or the conclusion drawn must be further verified by utilizing it in solving various other likewise problems. In case, the derived solution helps in solving these problems, then and only then if one is free to agree with his finding regarding the solution. The verified solution may then become a useful product of his problem-solving behavior that can be utilized in solving further problems. The above steps can be utilized in solving various problems thereby fostering creative thinking ability in an individual.

The problem-solving method is an effective teaching strategy that promotes critical thinking, creativity, and collaboration. It provides students with real-world problems that require them to apply their knowledge and skills to find solutions. By using the problem-solving method, teachers can help their students develop the skills they need to succeed in school and in life.

• Jonassen, D. (2011). Learning to solve problems: A handbook for designing problem-solving learning environments. Routledge.
• Hmelo-Silver, C. E. (2004). Problem-based learning: What and how do students learn? Educational Psychology Review, 16(3), 235-266.
• Mergendoller, J. R., Maxwell, N. L., & Bellisimo, Y. (2006). The effectiveness of problem-based instruction: A comparative study of instructional methods and student characteristics. Interdisciplinary Journal of Problem-based Learning, 1(2), 49-69.
• Richey, R. C., Klein, J. D., & Tracey, M. W. (2011). The instructional design knowledge base: Theory, research, and practice. Routledge.
• Savery, J. R., & Duffy, T. M. (2001). Problem-based learning: An instructional model and its constructivist framework. CRLT Technical Report No. 16-01, University of Michigan. Wojcikowski, J. (2013). Solving real-world problems through problem-based learning. College Teaching, 61(4), 153-156

Center for Teaching

Teaching problem solving.

Print Version

Tips and Techniques

Expert vs. novice problem solvers, communicate.

• Have students  identify specific problems, difficulties, or confusions . Don’t waste time working through problems that students already understand.
• If students are unable to articulate their concerns, determine where they are having trouble by  asking them to identify the specific concepts or principles associated with the problem.
• In a one-on-one tutoring session, ask the student to  work his/her problem out loud . This slows down the thinking process, making it more accurate and allowing you to access understanding.
• When working with larger groups you can ask students to provide a written “two-column solution.” Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column. This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems. Two-Column Solution (Math) Two-Column Solution (Physics)

Encourage Independence

• Model the problem solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts and make your thinking clear
• Have students work through problems on their own. Ask directing questions or give helpful suggestions, but  provide only minimal assistance and only when needed to overcome obstacles.
• Don’t fear  group work ! Students can frequently help each other, and talking about a problem helps them think more critically about the steps needed to solve the problem. Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others

Be sensitive

• Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning. It is important to recognize this when students come to us for help, and to give each student some feeling of mastery. Do this by providing  positive reinforcement to let students know when they have mastered a new concept or skill.

Encourage Thoroughness and Patience

• Try to communicate that  the process is more important than the answer so that the student learns that it is OK to not have an instant solution. This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem solving through a step-by step process.

Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem solving skills,  a teacher should be aware of principles and strategies of good problem solving in his or her discipline .

The mathematician George Polya captured the problem solving principles and strategies he used in his discipline in the book  How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes  a summary of Polya’s problem solving heuristic as well as advice on the teaching of problem solving.

Teaching Guides

• Online Course Development Resources
• Principles & Frameworks
• Pedagogies & Strategies
• Reflecting & Assessing
• Challenges & Opportunities
• Populations & Contexts

Quick Links

• Services for Departments and Schools
• Examples of Online Instructional Modules

Center for Teaching Innovation

Resource library.

• Establishing Community Agreements and Classroom Norms
• Sample group work rubric
• Problem-Based Learning Clearinghouse of Activities, University of Delaware

Problem-Based Learning

Problem-based learning  (PBL) is a student-centered approach in which students learn about a subject by working in groups to solve an open-ended problem. This problem is what drives the motivation and the learning. 

Why Use Problem-Based Learning?

Nilson (2010) lists the following learning outcomes that are associated with PBL. A well-designed PBL project provides students with the opportunity to develop skills related to:

• Working in teams.
• Managing projects and holding leadership roles.
• Oral and written communication.
• Self-awareness and evaluation of group processes.
• Working independently.
• Critical thinking and analysis.
• Explaining concepts.
• Self-directed learning.
• Applying course content to real-world examples.
• Researching and information literacy.
• Problem solving across disciplines.

Considerations for Using Problem-Based Learning

Rather than teaching relevant material and subsequently having students apply the knowledge to solve problems, the problem is presented first. PBL assignments can be short, or they can be more involved and take a whole semester. PBL is often group-oriented, so it is beneficial to set aside classroom time to prepare students to   work in groups  and to allow them to engage in their PBL project.

Students generally must:

• Examine and define the problem.
• Explore what they already know about underlying issues related to it.
• Determine what they need to learn and where they can acquire the information and tools necessary to solve the problem.
• Evaluate possible ways to solve the problem.
• Solve the problem.
• Report on their findings.

Getting Started with Problem-Based Learning

• Articulate the learning outcomes of the project. What do you want students to know or be able to do as a result of participating in the assignment?
• Create the problem. Ideally, this will be a real-world situation that resembles something students may encounter in their future careers or lives. Cases are often the basis of PBL activities. Previously developed PBL activities can be found online through the University of Delaware’s PBL Clearinghouse of Activities .
• Establish ground rules at the beginning to prepare students to work effectively in groups.
• Introduce students to group processes and do some warm up exercises to allow them to practice assessing both their own work and that of their peers.
• Consider having students take on different roles or divide up the work up amongst themselves. Alternatively, the project might require students to assume various perspectives, such as those of government officials, local business owners, etc.
• Establish how you will evaluate and assess the assignment. Consider making the self and peer assessments a part of the assignment grade.

Nilson, L. B. (2010).  Teaching at its best: A research-based resource for college instructors  (2nd ed.).  San Francisco, CA: Jossey-Bass. 

Problem-Based Learning (PBL)

What is Problem-Based Learning (PBL)? PBL is a student-centered approach to learning that involves groups of students working to solve a real-world problem, quite different from the direct teaching method of a teacher presenting facts and concepts about a specific subject to a classroom of students. Through PBL, students not only strengthen their teamwork, communication, and research skills, but they also sharpen their critical thinking and problem-solving abilities essential for life-long learning.

See also: Just-in-Time Teaching

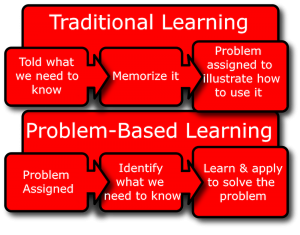
In implementing PBL, the teaching role shifts from that of the more traditional model that follows a linear, sequential pattern where the teacher presents relevant material, informs the class what needs to be done, and provides details and information for students to apply their knowledge to a given problem. With PBL, the teacher acts as a facilitator; the learning is student-driven with the aim of solving the given problem (note: the problem is established at the onset of learning opposed to being presented last in the traditional model). Also, the assignments vary in length from relatively short to an entire semester with daily instructional time structured for group work.

By working with PBL, students will:

• Become engaged with open-ended situations that assimilate the world of work
• Participate in groups to pinpoint what is known/ not known and the methods of finding information to help solve the given problem.
• Investigate a problem; through critical thinking and problem solving, brainstorm a list of unique solutions.
• Analyze the situation to see if the real problem is framed or if there are other problems that need to be solved.

How to Begin PBL

• Establish the learning outcomes (i.e., what is it that you want your students to really learn and to be able to do after completing the learning project).
• Find a real-world problem that is relevant to the students; often the problems are ones that students may encounter in their own life or future career.
• Discuss pertinent rules for working in groups to maximize learning success.
• Practice group processes: listening, involving others, assessing their work/peers.
• Explore different roles for students to accomplish the work that needs to be done and/or to see the problem from various perspectives depending on the problem (e.g., for a problem about pollution, different roles may be a mayor, business owner, parent, child, neighboring city government officials, etc.).
• Determine how the project will be evaluated and assessed. Most likely, both self-assessment and peer-assessment will factor into the assignment grade.

Designing Classroom Instruction

See also: Inclusive Teaching Strategies

• Take the curriculum and divide it into various units. Decide on the types of problems that your students will solve. These will be your objectives.
• Determine the specific problems that most likely have several answers; consider student interest.
• Arrange appropriate resources available to students; utilize other teaching personnel to support students where needed (e.g., media specialists to orientate students to electronic references).
• Decide on presentation formats to communicate learning (e.g., individual paper, group PowerPoint, an online blog, etc.) and appropriate grading mechanisms (e.g., rubric).
• Decide how to incorporate group participation (e.g., what percent, possible peer evaluation, etc.).

How to Orchestrate a PBL Activity

• Explain Problem-Based Learning to students: its rationale, daily instruction, class expectations, grading.
• Serve as a model and resource to the PBL process; work in-tandem through the first problem
• Help students secure various resources when needed.
• Supply ample class time for collaborative group work.
• Give feedback to each group after they share via the established format; critique the solution in quality and thoroughness. Reinforce to the students that the prior thinking and reasoning process in addition to the solution are important as well.

Teacher’s Role in PBL

See also: Flipped teaching

As previously mentioned, the teacher determines a problem that is interesting, relevant, and novel for the students. It also must be multi-faceted enough to engage students in doing research and finding several solutions. The problems stem from the unit curriculum and reflect possible use in future work situations.

• Determine a problem aligned with the course and your students. The problem needs to be demanding enough that the students most likely cannot solve it on their own. It also needs to teach them new skills. When sharing the problem with students, state it in a narrative complete with pertinent background information without excessive information. Allow the students to find out more details as they work on the problem.
• Place students in groups, well-mixed in diversity and skill levels, to strengthen the groups. Help students work successfully. One way is to have the students take on various roles in the group process after they self-assess their strengths and weaknesses.
• Support the students with understanding the content on a deeper level and in ways to best orchestrate the various stages of the problem-solving process.

The Role of the Students

See also: ADDIE model

The students work collaboratively on all facets of the problem to determine the best possible solution.

• Analyze the problem and the issues it presents. Break the problem down into various parts. Continue to read, discuss, and think about the problem.
• Construct a list of what is known about the problem. What do your fellow students know about the problem? Do they have any experiences related to the problem? Discuss the contributions expected from the team members. What are their strengths and weaknesses? Follow the rules of brainstorming (i.e., accept all answers without passing judgment) to generate possible solutions for the problem.
• Get agreement from the team members regarding the problem statement.
• Put the problem statement in written form.
• Solicit feedback from the teacher.
• Be open to changing the written statement based on any new learning that is found or feedback provided.
• Generate a list of possible solutions. Include relevant thoughts, ideas, and educated guesses as well as causes and possible ways to solve it. Then rank the solutions and select the solution that your group is most likely to perceive as the best in terms of meeting success.
• Include what needs to be known and done to solve the identified problems.
• Prioritize the various action steps.
• Consider how the steps impact the possible solutions.
• See if the group is in agreement with the timeline; if not, decide how to reach agreement.
• What resources are available to help (e.g., textbooks, primary/secondary sources, Internet).
• Determine research assignments per team members.
• Establish due dates.
• Determine how your group will present the problem solution and also identify the audience. Usually, in PBL, each group presents their solutions via a team presentation either to the class of other students or to those who are related to the problem.
• Both the process and the results of the learning activity need to be covered. Include the following: problem statement, questions, data gathered, data analysis, reasons for the solution(s) and/or any recommendations reflective of the data analysis.
• A well-stated problem and conclusion.
• The process undertaken by the group in solving the problem, the various options discussed, and the resources used.
• Your solution’s supporting documents, guests, interviews and their purpose to be convincing to your audience.
• In addition, be prepared for any audience comments and questions. Determine who will respond and if your team doesn’t know the answer, admit this and be open to looking into the question at a later date.
• Reflective thinking and transfer of knowledge are important components of PBL. This helps the students be more cognizant of their own learning and teaches them how to ask appropriate questions to address problems that need to be solved. It is important to look at both the individual student and the group effort/delivery throughout the entire process. From here, you can better determine what was learned and how to improve. The students should be asked how they can apply what was learned to a different situation, to their own lives, and to other course projects.

See also: Kirkpatrick Model: Four Levels of Learning Evaluation

I am a professor of Educational Technology. I have worked at several elite universities. I hold a PhD degree from the University of Illinois and a master's degree from Purdue University.

Similar Posts

Cognitive apprenticeship.

Apprenticeship is an ancient idea; skills have been taught by others for centuries. In the past, elders worked alongside their children to teach them how to grow food, wash their clothes, build homes…

Definitions of The Addie Model

What is the ADDIE Model? This article attempts to explain the ADDIE model by providing different definitions. Basically, ADDIE is a conceptual framework. ADDIE is the most commonly used instructional design framework and…

Gamification, What It Is, How It Works, Examples

For many students, the traditional classroom setting can feel like an uninspiring environment. Long lectures, repetitive tasks, and a focus on exams often leave young minds disengaged, craving a more dynamic way to…

Educational Technology: An Overview

Educational technology is a field of study that investigates the process of analyzing, designing, developing, implementing, and evaluating the instructional environment and learning materials in order to improve teaching and learning. It is…

Erikson’s Stages of Psychosocial Development

In 1950, Erik Erikson released his book, Childhood and Society, which outlined his now prominent Theory of Psychosocial Development. His theory comprises of 8 stages that a healthy individual passes through in his…

Planning for Educational Technology Integration

Why seek out educational technology? We know that technology can enhance the teaching and learning process by providing unique opportunities. However, we also know that adoption of educational technology is a highly complex…

• Illinois Online
• Illinois Remote

• TA Resources
• Teaching Consultation
• Teaching Portfolio Program
• Grad Academy for College Teaching
• Faculty Events
• The Art of Teaching
• 2022 Illinois Summer Teaching Institute
• Large Classes
• Leading Discussions
• Laboratory Classes
• Lecture-Based Classes
• Planning a Class Session
• Questioning Strategies
• Classroom Assessment Techniques (CATs)
• Problem-Based Learning (PBL)
• The Case Method
• Community-Based Learning: Service Learning
• Group Learning
• Just-in-Time Teaching
• Creating a Syllabus
• Motivating Students
• Dealing With Cheating
• Discouraging & Detecting Plagiarism
• Diversity & Creating an Inclusive Classroom
• Harassment & Discrimination
• Professional Conduct
• Foundations of Good Teaching
• Student Engagement
• Assessment Strategies
• Course Design
• Student Resources
• Teaching Tips
• Graduate Teacher Certificate
• Certificate in Foundations of Teaching
• Teacher Scholar Certificate
• Certificate in Technology-Enhanced Teaching
• Master Course in Online Teaching (MCOT)
• 2022 Celebration of College Teaching
• 2023 Celebration of College Teaching
• Hybrid Teaching and Learning Certificate
• 2024 Celebration of College Teaching
• Classroom Observation Etiquette
• Teaching Philosophy Statement
• Pedagogical Literature Review
• Scholarship of Teaching and Learning
• Instructor Stories
• Podcast: Teach Talk Listen Learn
• Universal Design for Learning

Sign-Up to receive Teaching and Learning news and events

Problem-Based Learning (PBL) is a teaching method in which complex real-world problems are used as the vehicle to promote student learning of concepts and principles as opposed to direct presentation of facts and concepts. In addition to course content, PBL can promote the development of critical thinking skills, problem-solving abilities, and communication skills. It can also provide opportunities for working in groups, finding and evaluating research materials, and life-long learning (Duch et al, 2001).

PBL can be incorporated into any learning situation. In the strictest definition of PBL, the approach is used over the entire semester as the primary method of teaching. However, broader definitions and uses range from including PBL in lab and design classes, to using it simply to start a single discussion. PBL can also be used to create assessment items. The main thread connecting these various uses is the real-world problem.

Any subject area can be adapted to PBL with a little creativity. While the core problems will vary among disciplines, there are some characteristics of good PBL problems that transcend fields (Duch, Groh, and Allen, 2001):

• The problem must motivate students to seek out a deeper understanding of concepts.
• The problem should require students to make reasoned decisions and to defend them.
• The problem should incorporate the content objectives in such a way as to connect it to previous courses/knowledge.
• If used for a group project, the problem needs a level of complexity to ensure that the students must work together to solve it.
• If used for a multistage project, the initial steps of the problem should be open-ended and engaging to draw students into the problem.

The problems can come from a variety of sources: newspapers, magazines, journals, books, textbooks, and television/ movies. Some are in such form that they can be used with little editing; however, others need to be rewritten to be of use. The following guidelines from The Power of Problem-Based Learning (Duch et al, 2001) are written for creating PBL problems for a class centered around the method; however, the general ideas can be applied in simpler uses of PBL:

• Choose a central idea, concept, or principle that is always taught in a given course, and then think of a typical end-of-chapter problem, assignment, or homework that is usually assigned to students to help them learn that concept. List the learning objectives that students should meet when they work through the problem.
• Think of a real-world context for the concept under consideration. Develop a storytelling aspect to an end-of-chapter problem, or research an actual case that can be adapted, adding some motivation for students to solve the problem. More complex problems will challenge students to go beyond simple plug-and-chug to solve it. Look at magazines, newspapers, and articles for ideas on the story line. Some PBL practitioners talk to professionals in the field, searching for ideas of realistic applications of the concept being taught.
• What will the first page (or stage) look like? What open-ended questions can be asked? What learning issues will be identified?
• How will the problem be structured?
• How long will the problem be? How many class periods will it take to complete?
• Will students be given information in subsequent pages (or stages) as they work through the problem?
• What resources will the students need?
• What end product will the students produce at the completion of the problem?
• Write a teacher's guide detailing the instructional plans on using the problem in the course. If the course is a medium- to large-size class, a combination of mini-lectures, whole-class discussions, and small group work with regular reporting may be necessary. The teacher's guide can indicate plans or options for cycling through the pages of the problem interspersing the various modes of learning.
• The final step is to identify key resources for students. Students need to learn to identify and utilize learning resources on their own, but it can be helpful if the instructor indicates a few good sources to get them started. Many students will want to limit their research to the Internet, so it will be important to guide them toward the library as well.

The method for distributing a PBL problem falls under three closely related teaching techniques: case studies, role-plays, and simulations. Case studies are presented to students in written form. Role-plays have students improvise scenes based on character descriptions given. Today, simulations often involve computer-based programs. Regardless of which technique is used, the heart of the method remains the same: the real-world problem.

Where can I learn more?

• PBL through the Institute for Transforming Undergraduate Education at the University of Delaware
• Duch, B. J., Groh, S. E, & Allen, D. E. (Eds.). (2001). The power of problem-based learning . Sterling, VA: Stylus.
• Grasha, A. F. (1996). Teaching with style: A practical guide to enhancing learning by understanding teaching and learning styles. Pittsburgh: Alliance Publishers.

Center for Innovation in Teaching & Learning

249 Armory Building 505 East Armory Avenue Champaign, IL 61820

217 333-1462

Email: [email protected]

Office of the Provost

Teaching Problem-Solving Skills

Many instructors design opportunities for students to solve “problems”. But are their students solving true problems or merely participating in practice exercises? The former stresses critical thinking and decision­ making skills whereas the latter requires only the application of previously learned procedures.

Problem solving is often broadly defined as "the ability to understand the environment, identify complex problems, review related information to develop, evaluate strategies and implement solutions to build the desired outcome" (Fissore, C. et al, 2021). True problem solving is the process of applying a method – not known in advance – to a problem that is subject to a specific set of conditions and that the problem solver has not seen before, in order to obtain a satisfactory solution.

Below you will find some basic principles for teaching problem solving and one model to implement in your classroom teaching.

Principles for teaching problem solving

• Model a useful problem-solving method . Problem solving can be difficult and sometimes tedious. Show students how to be patient and persistent, and how to follow a structured method, such as Woods’ model described below. Articulate your method as you use it so students see the connections.
• Teach within a specific context . Teach problem-solving skills in the context in which they will be used by students (e.g., mole fraction calculations in a chemistry course). Use real-life problems in explanations, examples, and exams. Do not teach problem solving as an independent, abstract skill.
• Help students understand the problem . In order to solve problems, students need to define the end goal. This step is crucial to successful learning of problem-solving skills. If you succeed at helping students answer the questions “what?” and “why?”, finding the answer to “how?” will be easier.
• Take enough time . When planning a lecture/tutorial, budget enough time for: understanding the problem and defining the goal (both individually and as a class); dealing with questions from you and your students; making, finding, and fixing mistakes; and solving entire problems in a single session.
• Ask questions and make suggestions . Ask students to predict “what would happen if …” or explain why something happened. This will help them to develop analytical and deductive thinking skills. Also, ask questions and make suggestions about strategies to encourage students to reflect on the problem-solving strategies that they use.
• Link errors to misconceptions . Use errors as evidence of misconceptions, not carelessness or random guessing. Make an effort to isolate the misconception and correct it, then teach students to do this by themselves. We can all learn from mistakes.

Woods’ problem-solving model

Define the problem.

• The system . Have students identify the system under study (e.g., a metal bridge subject to certain forces) by interpreting the information provided in the problem statement. Drawing a diagram is a great way to do this.
• Known(s) and concepts . List what is known about the problem, and identify the knowledge needed to understand (and eventually) solve it.
• Unknown(s) . Once you have a list of knowns, identifying the unknown(s) becomes simpler. One unknown is generally the answer to the problem, but there may be other unknowns. Be sure that students understand what they are expected to find.
• Units and symbols . One key aspect in problem solving is teaching students how to select, interpret, and use units and symbols. Emphasize the use of units whenever applicable. Develop a habit of using appropriate units and symbols yourself at all times.
• Constraints . All problems have some stated or implied constraints. Teach students to look for the words "only", "must", "neglect", or "assume" to help identify the constraints.
• Criteria for success . Help students consider, from the beginning, what a logical type of answer would be. What characteristics will it possess? For example, a quantitative problem will require an answer in some form of numerical units (e.g., $/kg product, square cm, etc.) while an optimization problem requires an answer in the form of either a numerical maximum or minimum.

Think about it

• “Let it simmer”.  Use this stage to ponder the problem. Ideally, students will develop a mental image of the problem at hand during this stage.
• Identify specific pieces of knowledge . Students need to determine by themselves the required background knowledge from illustrations, examples and problems covered in the course.
• Collect information . Encourage students to collect pertinent information such as conversion factors, constants, and tables needed to solve the problem.

Plan a solution

• Consider possible strategies . Often, the type of solution will be determined by the type of problem. Some common problem-solving strategies are: compute; simplify; use an equation; make a model, diagram, table, or chart; or work backwards.
• Choose the best strategy . Help students to choose the best strategy by reminding them again what they are required to find or calculate.

Carry out the plan

• Be patient . Most problems are not solved quickly or on the first attempt. In other cases, executing the solution may be the easiest step.
• Be persistent . If a plan does not work immediately, do not let students get discouraged. Encourage them to try a different strategy and keep trying.

Encourage students to reflect. Once a solution has been reached, students should ask themselves the following questions:

• Does the answer make sense?
• Does it fit with the criteria established in step 1?
• Did I answer the question(s)?
• What did I learn by doing this?
• Could I have done the problem another way?

If you would like support applying these tips to your own teaching, CTE staff members are here to help.  View the  CTE Support  page to find the most relevant staff member to contact. 

• Fissore, C., Marchisio, M., Roman, F., & Sacchet, M. (2021). Development of problem solving skills with Maple in higher education. In: Corless, R.M., Gerhard, J., Kotsireas, I.S. (eds) Maple in Mathematics Education and Research. MC 2020. Communications in Computer and Information Science, vol 1414. Springer, Cham. https://doi.org/10.1007/978-3-030-81698-8_15
• Foshay, R., & Kirkley, J. (1998). Principles for Teaching Problem Solving. TRO Learning Inc., Edina MN.  (PDF) Principles for Teaching Problem Solving (researchgate.net)
• Hayes, J.R. (1989). The Complete Problem Solver. 2nd Edition. Hillsdale, NJ: Lawrence Erlbaum Associates.
• Woods, D.R., Wright, J.D., Hoffman, T.W., Swartman, R.K., Doig, I.D. (1975). Teaching Problem solving Skills.
• Engineering Education. Vol 1, No. 1. p. 238. Washington, DC: The American Society for Engineering Education.

Catalog search

Teaching tip categories.

• Assessment and feedback
• Blended Learning and Educational Technologies
• Career Development
• Course Design
• Course Implementation
• Inclusive Teaching and Learning
• Learning activities
• Support for Student Learning
• Support for TAs
• Learning activities ,

• Faculty & Staff

Teaching problem solving

Strategies for teaching problem solving apply across disciplines and instructional contexts. First, introduce the problem and explain how people in your discipline generally make sense of the given information. Then, explain how to apply these approaches to solve the problem.

Introducing the problem

Explaining how people in your discipline understand and interpret these types of problems can help students develop the skills they need to understand the problem (and find a solution). After introducing how you would go about solving a problem, you could then ask students to:

• frame the problem in their own words
• define key terms and concepts
• determine statements that accurately represent the givens of a problem
• identify analogous problems
• determine what information is needed to solve the problem

Working on solutions

In the solution phase, one develops and then implements a coherent plan for solving the problem. As you help students with this phase, you might ask them to:

• identify the general model or procedure they have in mind for solving the problem
• set sub-goals for solving the problem
• identify necessary operations and steps
• draw conclusions
• carry out necessary operations

You can help students tackle a problem effectively by asking them to:

• systematically explain each step and its rationale
• explain how they would approach solving the problem
• help you solve the problem by posing questions at key points in the process
• work together in small groups (3 to 5 students) to solve the problem and then have the solution presented to the rest of the class (either by you or by a student in the group)

In all cases, the more you get the students to articulate their own understandings of the problem and potential solutions, the more you can help them develop their expertise in approaching problems in your discipline.

Why Every Educator Needs to Teach Problem-Solving Skills

Strong problem-solving skills will help students be more resilient and will increase their academic and career success .

Want to learn more about how to measure and teach students’ higher-order skills, including problem solving, critical thinking, and written communication?

Problem-solving skills are essential in school, careers, and life.

Problem-solving skills are important for every student to master. They help individuals navigate everyday life and find solutions to complex issues and challenges. These skills are especially valuable in the workplace, where employees are often required to solve problems and make decisions quickly and effectively.

Problem-solving skills are also needed for students’ personal growth and development because they help individuals overcome obstacles and achieve their goals. By developing strong problem-solving skills, students can improve their overall quality of life and become more successful in their personal and professional endeavors.

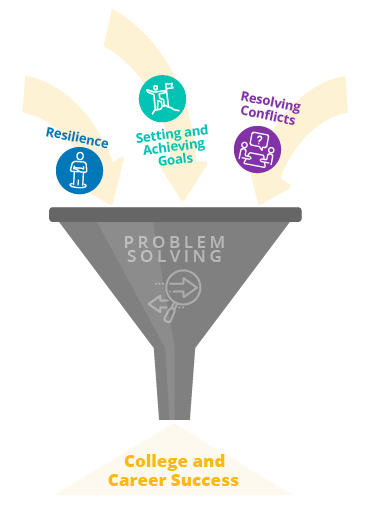
Problem-Solving Skills Help Students…

   develop resilience.

Problem-solving skills are an integral part of resilience and the ability to persevere through challenges and adversity. To effectively work through and solve a problem, students must be able to think critically and creatively. Critical and creative thinking help students approach a problem objectively, analyze its components, and determine different ways to go about finding a solution.  

This process in turn helps students build self-efficacy . When students are able to analyze and solve a problem, this increases their confidence, and they begin to realize the power they have to advocate for themselves and make meaningful change.

When students gain confidence in their ability to work through problems and attain their goals, they also begin to build a growth mindset . According to leading resilience researcher, Carol Dweck, “in a growth mindset, people believe that their most basic abilities can be developed through dedication and hard work—brains and talent are just the starting point. This view creates a love of learning and a resilience that is essential for great accomplishment.”

    Set and Achieve Goals

Students who possess strong problem-solving skills are better equipped to set and achieve their goals. By learning how to identify problems, think critically, and develop solutions, students can become more self-sufficient and confident in their ability to achieve their goals. Additionally, problem-solving skills are used in virtually all fields, disciplines, and career paths, which makes them important for everyone. Building strong problem-solving skills will help students enhance their academic and career performance and become more competitive as they begin to seek full-time employment after graduation or pursue additional education and training.

  Resolve Conflicts

In addition to increased social and emotional skills like self-efficacy and goal-setting, problem-solving skills teach students how to cooperate with others and work through disagreements and conflicts. Problem-solving promotes “thinking outside the box” and approaching a conflict by searching for different solutions. This is a very different (and more effective!) method than a more stagnant approach that focuses on placing blame or getting stuck on elements of a situation that can’t be changed.

While it’s natural to get frustrated or feel stuck when working through a conflict, students with strong problem-solving skills will be able to work through these obstacles, think more rationally, and address the situation with a more solution-oriented approach. These skills will be valuable for students in school, their careers, and throughout their lives.

    Achieve Success

We are all faced with problems every day. Problems arise in our personal lives, in school and in our jobs, and in our interactions with others. Employers especially are looking for candidates with strong problem-solving skills. In today’s job market, most jobs require the ability to analyze and effectively resolve complex issues. Students with strong problem-solving skills will stand out from other applicants and will have a more desirable skill set.

In a recent opinion piece published by The Hechinger Report , Virgel Hammonds, Chief Learning Officer at KnowledgeWorks, stated “Our world presents increasingly complex challenges. Education must adapt so that it nurtures problem solvers and critical thinkers.” Yet, the “traditional K–12 education system leaves little room for students to engage in real-world problem-solving scenarios.” This is the reason that a growing number of K–12 school districts and higher education institutions are transforming their instructional approach to personalized and competency-based learning, which encourage students to make decisions, problem solve and think critically as they take ownership of and direct their educational journey.

Problem-Solving Skills Can Be Measured and Taught

Research shows that problem-solving skills can be measured and taught. One effective method is through performance-based assessments which require students to demonstrate or apply their knowledge and higher-order skills to create a response or product or do a task.

What Are Performance-Based Assessments?

With the No Child Left Behind Act (2002), the use of standardized testing became the primary way to measure student learning in the U.S. The legislative requirements of this act shifted the emphasis to standardized testing, and this led to a  decline in nontraditional testing methods .

But   many educators, policy makers, and parents have concerns with standardized tests. Some of the top issues include that they don’t provide feedback on how students can perform better, they don’t value creativity, they are not representative of diverse populations, and they can be disadvantageous to lower-income students.

While standardized tests are still the norm, U.S. Secretary of Education Miguel Cardona is encouraging states and districts to move away from traditional multiple choice and short response tests and instead use performance-based assessment, competency-based assessments, and other more authentic methods of measuring students abilities and skills rather than rote learning. 

Performance-based assessments  measure whether students can apply the skills and knowledge learned from a unit of study. Typically, a performance task challenges students to use their higher-order skills to complete a project or process. Tasks can range from an essay to a complex proposal or design.

Preview a Performance-Based Assessment

Want a closer look at how performance-based assessments work?  Preview CAE’s K–12 and Higher Education assessments and see how CAE’s tools help students develop critical thinking, problem-solving, and written communication skills.

Performance-Based Assessments Help Students Build and Practice Problem-Solving Skills

In addition to effectively measuring students’ higher-order skills, including their problem-solving skills, performance-based assessments can help students practice and build these skills. Through the assessment process, students are given opportunities to practically apply their knowledge in real-world situations. By demonstrating their understanding of a topic, students are required to put what they’ve learned into practice through activities such as presentations, experiments, and simulations. 

This type of problem-solving assessment tool requires students to analyze information and choose how to approach the presented problems. This process enhances their critical thinking skills and creativity, as well as their problem-solving skills. Unlike traditional assessments based on memorization or reciting facts, performance-based assessments focus on the students’ decisions and solutions, and through these tasks students learn to bridge the gap between theory and practice.

Performance-based assessments like CAE’s College and Career Readiness Assessment (CRA+) and Collegiate Learning Assessment (CLA+) provide students with in-depth reports that show them which higher-order skills they are strongest in and which they should continue to develop. This feedback helps students and their teachers plan instruction and supports to deepen their learning and improve their mastery of critical skills.

Explore CAE’s Problem-Solving Assessments

CAE offers performance-based assessments that measure student proficiency in higher-order skills including problem solving, critical thinking, and written communication.

• College and Career Readiness Assessment (CCRA+) for secondary education and
• Collegiate Learning Assessment (CLA+) for higher education.

Our solution also includes instructional materials, practice models, and professional development.

We can help you create a program to build students’ problem-solving skills that includes:

• Measuring students’ problem-solving skills through a performance-based assessment    
• Using the problem-solving assessment data to inform instruction and tailor interventions
• Teaching students problem-solving skills and providing practice opportunities in real-life scenarios
• Supporting educators with quality professional development

Get started with our problem-solving assessment tools to measure and build students’ problem-solving skills today! These skills will be invaluable to students now and in the future.

Ready to Get Started?

Learn more about cae’s suite of products and let’s get started measuring and teaching students important higher-order skills like problem solving..

Teaching problem solving: Let students get ‘stuck’ and ‘unstuck’

Subscribe to the center for universal education bulletin, kate mills and km kate mills literacy interventionist - red bank primary school helyn kim helyn kim former brookings expert @helyn_kim.

October 31, 2017

This is the second in a six-part  blog series  on  teaching 21st century skills , including  problem solving ,  metacognition , critical thinking , and collaboration , in classrooms.

In the real world, students encounter problems that are complex, not well defined, and lack a clear solution and approach. They need to be able to identify and apply different strategies to solve these problems. However, problem solving skills do not necessarily develop naturally; they need to be explicitly taught in a way that can be transferred across multiple settings and contexts.

Here’s what Kate Mills, who taught 4 th grade for 10 years at Knollwood School in New Jersey and is now a Literacy Interventionist at Red Bank Primary School, has to say about creating a classroom culture of problem solvers:

Helping my students grow to be people who will be successful outside of the classroom is equally as important as teaching the curriculum. From the first day of school, I intentionally choose language and activities that help to create a classroom culture of problem solvers. I want to produce students who are able to think about achieving a particular goal and manage their mental processes . This is known as metacognition , and research shows that metacognitive skills help students become better problem solvers.

I begin by “normalizing trouble” in the classroom. Peter H. Johnston teaches the importance of normalizing struggle , of naming it, acknowledging it, and calling it what it is: a sign that we’re growing. The goal is for the students to accept challenge and failure as a chance to grow and do better.

I look for every chance to share problems and highlight how the students— not the teachers— worked through those problems. There is, of course, coaching along the way. For example, a science class that is arguing over whose turn it is to build a vehicle will most likely need a teacher to help them find a way to the balance the work in an equitable way. Afterwards, I make it a point to turn it back to the class and say, “Do you see how you …” By naming what it is they did to solve the problem , students can be more independent and productive as they apply and adapt their thinking when engaging in future complex tasks.

After a few weeks, most of the class understands that the teachers aren’t there to solve problems for the students, but to support them in solving the problems themselves. With that important part of our classroom culture established, we can move to focusing on the strategies that students might need.

Here’s one way I do this in the classroom:

I show the broken escalator video to the class. Since my students are fourth graders, they think it’s hilarious and immediately start exclaiming, “Just get off! Walk!”

When the video is over, I say, “Many of us, probably all of us, are like the man in the video yelling for help when we get stuck. When we get stuck, we stop and immediately say ‘Help!’ instead of embracing the challenge and trying new ways to work through it.” I often introduce this lesson during math class, but it can apply to any area of our lives, and I can refer to the experience and conversation we had during any part of our day.

Research shows that just because students know the strategies does not mean they will engage in the appropriate strategies. Therefore, I try to provide opportunities where students can explicitly practice learning how, when, and why to use which strategies effectively  so that they can become self-directed learners.

For example, I give students a math problem that will make many of them feel “stuck”. I will say, “Your job is to get yourselves stuck—or to allow yourselves to get stuck on this problem—and then work through it, being mindful of how you’re getting yourselves unstuck.” As students work, I check-in to help them name their process: “How did you get yourself unstuck?” or “What was your first step? What are you doing now? What might you try next?” As students talk about their process, I’ll add to a list of strategies that students are using and, if they are struggling, help students name a specific process. For instance, if a student says he wrote the information from the math problem down and points to a chart, I will say: “Oh that’s interesting. You pulled the important information from the problem out and organized it into a chart.” In this way, I am giving him the language to match what he did, so that he now has a strategy he could use in other times of struggle.

The charts grow with us over time and are something that we refer to when students are stuck or struggling. They become a resource for students and a way for them to talk about their process when they are reflecting on and monitoring what did or did not work.

For me, as a teacher, it is important that I create a classroom environment in which students are problem solvers. This helps tie struggles to strategies so that the students will not only see value in working harder but in working smarter by trying new and different strategies and revising their process. In doing so, they will more successful the next time around.

Related Content

Esther Care, Helyn Kim, Alvin Vista

October 17, 2017

David Owen, Alvin Vista

November 15, 2017

Loren Clarke, Esther Care

December 5, 2017

Global Education K-12 Education

Global Economy and Development

Center for Universal Education

Annelies Goger, Katherine Caves, Hollis Salway

May 16, 2024

Sofoklis Goulas, Isabelle Pula

Melissa Kay Diliberti, Elizabeth D. Steiner, Ashley Woo

• Python Multiline String
• Python Multiline Comment
• Python Iterate String
• Python Dictionary
• Python Lists
• Python List Contains
• Page Object Model
• TestNG Annotations
• Python Function Quiz
• Python String Quiz
• Python OOP Test
• Java Spring Test
• Java Collection Quiz
• JavaScript Skill Test
• Selenium Skill Test
• Selenium Python Quiz
• Shell Scripting Test
• Latest Python Q&A
• CSharp Coding Q&A
• SQL Query Question
• Top Selenium Q&A
• Top QA Questions
• Latest Testing Q&A
• REST API Questions
• Linux Interview Q&A
• Shell Script Questions
• Python Quizzes
• Testing Quiz
• Shell Script Quiz
• WebDev Interview
• Python Basic
• Python Examples
• Python Advanced
• Python Selenium
• General Tech

Problem-Solving Method of Teaching: All You Need to Know

Ever wondered about the problem-solving method of teaching? We’ve got you covered, from its core principles to practical tips, benefits, and real-world examples.

The problem-solving method of teaching is a student-centered approach to learning that focuses on developing students’ problem-solving skills. In this method, students are presented with real-world problems to solve, and they are encouraged to use their own knowledge and skills to come up with solutions. The teacher acts as a facilitator, providing guidance and support as needed, but ultimately the students are responsible for finding their own solutions.

Must Read: How to Tell Me About Yourself in an Interview

5 Most Important Benefits of Problem-Solving Method of Teaching

The new way of teaching primarily helps students develop critical thinking skills and real-world application abilities. It also promotes independence and self-confidence in problem-solving.

The problem-solving method of teaching has a number of benefits. It helps students to:

1. Enhances critical thinking: By presenting students with real-world problems to solve, the problem-solving method of teaching forces them to think critically about the situation and to come up with their own solutions. This process helps students to develop their critical thinking skills, which are essential for success in school and in life.

2. Fosters creativity: The problem-solving method of teaching encourages students to be creative in their approach to solving problems. There is often no one right answer to a problem, so students are free to come up with their own unique solutions. This process helps students to develop their creativity, which is an important skill in all areas of life.

3. Encourages real-world application: The problem-solving method of teaching helps students learn how to apply their knowledge to real-world situations. By solving real-world problems, students are able to see how their knowledge is relevant to their lives and to the world around them. This helps students to become more motivated and engaged learners.

4. Builds student confidence: When students are able to successfully solve problems, they gain confidence in their abilities. This confidence is essential for success in all areas of life, both academic and personal.

5. Promotes collaborative learning: The problem-solving method of teaching often involves students working together to solve problems. This collaborative learning process helps students to develop their teamwork skills and to learn from each other.

Know 6 Steps in the Problem-Solving Method of Teaching

Also Read: Do You Know the Difference Between ChatGPT and GPT-4?

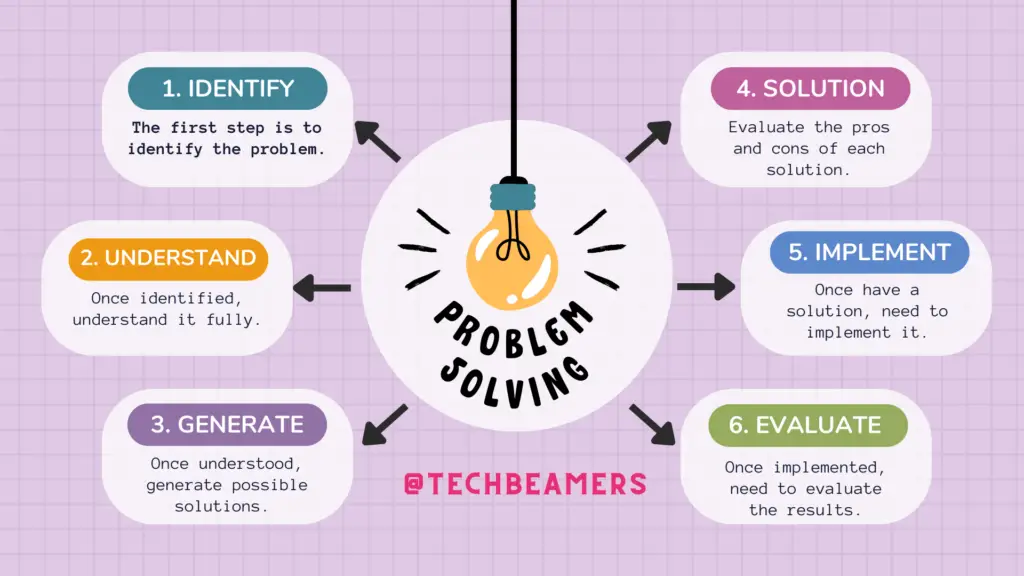
The problem-solving method of teaching typically involves the following steps:

• Identifying the problem. The first step is to identify the problem that students will be working on. This can be done by presenting students with a real-world problem, or by asking them to come up with their own problems.
• Understanding the problem. Once students have identified the problem, they need to understand it fully. This may involve breaking the problem down into smaller parts or gathering more information about the problem.
• Generating solutions. Once students understand the problem, they need to generate possible solutions. This can be done by brainstorming, or by using problem-solving techniques such as root cause analysis or the decision matrix.
• Evaluating solutions. Students need to evaluate the pros and cons of each solution before choosing one to implement.
• Implementing the solution. Once students have chosen a solution, they need to implement it. This may involve taking action or developing a plan.
• Evaluating the results. Once students have implemented the solution, they need to evaluate the results to see if it was successful. If the solution is not successful, students may need to go back to step 3 and generate new solutions.

Find Out Examples of the Problem-Solving Method of Teaching

Here are a few examples of how the problem-solving method of teaching can be used in different subjects:

• Math: Students could be presented with a real-world problem such as budgeting for a family or designing a new product. Students would then need to use their math skills to solve the problem.
• Science: Students could be presented with a science experiment, or asked to research a scientific topic and come up with a solution to a problem. Students would then need to use their science knowledge and skills to solve the problem.
• Social studies: Students could be presented with a historical event or current social issue, and asked to come up with a solution. Students would then need to use their social studies knowledge and skills to solve the problem.

5 How Tos For Using The Problem-Solving Method Of Teaching

Here are a few tips for using the problem-solving method of teaching effectively:

• Choose problems that are relevant to students’ lives and interests.
• Make sure that the problems are challenging but achievable.
• Provide students with the resources they need to solve the problems, such as books, websites, or experts.
• Encourage students to work collaboratively and to share their ideas.
• Be patient and supportive. Problem-solving can be a challenging process, but it is also a rewarding one.

Also Try: 1-10 Random Number Generator

How to Choose: Let’s Draw a Comparison

The following table compares the different problem-solving methods:

Which Method is the Most Suitable?

The most suitable method of teaching will depend on a number of factors, such as the subject matter, the student’s age and ability level, and the teacher’s own preferences. However, the problem-solving method of teaching is a valuable approach that can be used in any subject area and with students of all ages.

Here are some additional tips for using the problem-solving method of teaching effectively:

• Differentiate instruction. Not all students learn at the same pace or in the same way. Teachers can differentiate instruction to meet the needs of all learners by providing different levels of support and scaffolding.
• Use formative assessment. Formative assessment can be used to monitor students’ progress and to identify areas where they need additional support. Teachers can then use this information to provide students with targeted instruction.
• Create a positive learning environment. Students need to feel safe and supported in order to learn effectively. Teachers can create a positive learning environment by providing students with opportunities for collaboration, celebrating their successes, and creating a classroom culture where mistakes are seen as learning opportunities.

Interested in New Tech: 7 IoT Trends to Watch in 2023

Some Unique Examples to Refer to Before We Conclude

Here are a few unique examples of how the problem-solving method of teaching can be used in different subjects:

• English: Students could be presented with a challenging text, such as a poem or a short story, and asked to analyze the text and come up with their own interpretation.
• Art: Students could be asked to design a new product or to create a piece of art that addresses a social issue.
• Music: Students could be asked to write a song about a current event or to create a new piece of music that reflects their cultural heritage.

The problem-solving method of teaching is a powerful tool that can be used to help students develop the skills they need to succeed in school and in life. By creating a learning environment where students are encouraged to think critically and solve problems, teachers can help students to become lifelong learners.

You Might Also Like

How to fix load css asynchronously, how to fix accessibility issues with tables in wordpress, apache spark introduction and architecture, difference between spring and spring boot, langchain chatbot – let’s create a full-fledged app, sign up for daily newsletter, be keep up get the latest breaking news delivered straight to your inbox..

Popular Tutorials

50 SQL Practice Questions for Good Results in Interview

7 Sites to Practice Selenium for Free in 2024

SQL Exercises – Complex Queries

15 Java Coding Questions for Testers

30 Python Programming Questions On List, Tuple, and Dictionary

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Problem Solving Method Of Teaching

The problem-solving method of teaching is the learning method that allows children to learn by doing. This is because they are given examples and real-world situations so that the theory behind it can be understood better, as well as practice with each new concept or skill taught on top of what was previously learned in class before moving onto another topic at hand.

What is your preferred problem-solving technique?

Answers : - I like to brainstorm and see what works for me - I enjoy the trial and error method - I am a linear thinker

Share it with me by commenting.

For example, while solving a problem, the child may encounter terms he has not studied yet. These will further help him understand their use in context while developing his vocabulary. At the same time, being able to practice math concepts by tapping into daily activities helps an individual retain these skills better.

One way this type of teaching is applied for younger students particularly is through games played during lessons. By allowing them to become comfortable with the concepts taught through these games, they can put their knowledge into use later on. This is done by developing thinking processes that precede an action or behavior. These games can be used by teachers for different subjects including science and language.

For younger students still, the method of teaching using real-life examples helps them understand better. Through this, it becomes easier for them to relate what they learned in school with terms used outside of school settings so that the information sticks better than if all they were given were theoretical definitions. For instance, instead of just studying photosynthesis as part of biology lessons, children are asked to imagine plants growing inside a dark room because there is no sunlight present. When questioned about the plants, children will be able to recall photosynthesis more easily because they were able to see its importance in real life.

Despite being given specific examples, the act of solving problems helps students think for themselves. They learn how to approach situations and predict outcomes based on what they already know about concepts or ideas taught in class including the use of various skills they have acquired over time. These include problem-solving strategies like using drawings when describing a solution or asking advice if they are stuck to unlock solutions that would otherwise go beyond their reach.

Teachers need to point out in advance which method will be used for any particular lesson before having children engage with it. By doing this, individuals can prepare themselves mentally for what is to come. This is especially true for students who have difficulty with a particular subject. In these cases, the teacher can help them get started by providing a worked example for reference or breaking the problem down into manageable chunks that are easier to digest.

JIT (Just-in-Time): A Comprehensive Examination of its Strategic Impact

The Wisdom of Jefferson: Moving, Doing, Thinking

Root Cause Tree Analysis: Insights to Forensic Decision Making

Hazard Analysis: A Comprehensive Approach for Risk Evaluation

Ultimately, the goal of teaching using a problem-solving method is to give children the opportunity to think for themselves and to be able to do so in different contexts. Doing this helps foster independent learners who can utilize the skills they acquired in school for future endeavors.

The problem-solving method of teaching allows children to learn by doing. This is because they are given examples and real-world situations so that the theory behind it can be understood better, as practice with each new concept or skill taught on top of what was previously learned in class before moving onto another topic at hand.

One way this type of teaching is applied for younger students particularly is through games played during lessons. By allowing them to become comfortable with the concepts taught through these games, they are able to put their knowledge into use later on. This is done by developing thinking processes that precede an action or behavior. These games can be used by teachers for different subjects including science and language.

For instance, a teacher may ask students to imagine they are plants in a dark room because there is no sunlight present. When questioned about the plants, children will be able to recall photosynthesis more easily because they were able to see its importance in real life.

It is important for teachers to point out in advance which method will be used for any particular lesson before having children engage with it. By doing this, individuals can prepare themselves mentally for what is to come. This is especially true for students who have difficulty with a particular subject. In these cases, the teacher can help them get started by providing a worked example for reference or breaking the problem down into manageable chunks that are easier to digest.

lesson before having children engage with it. By doing this, individuals can prepare themselves mentally for what is to come. This is especially true for students who have difficulty with a particular subject. In these cases, the teacher can help them get started by providing a worked example for reference or breaking the problem down into manageable chunks that are easier to digest.

The teacher should have a few different ways to solve the problem.

For example, the teacher can provide a worked example for reference or break down the problem into chunks that are easier to digest.

The goal of teaching using a problem-solving method is to give children the opportunity to think for themselves and to be able to do so in different contexts. Successful problem solving allows children to become comfortable with concepts taught through games that develop thinking processes that precede an action or behavior.

Introduce the problem

The problem solving method of teaching is a popular approach to learning that allows students to understand new concepts by doing. This approach provides students with examples and real-world situations, so they can see how the theory behind a concept or skill works in practice. In addition, students are given practice with each new concept or skill taught, before moving on to the next topic. This helps them learn and retain the information better.

Explain why the problem solving method of teaching is effective.

The problem solving method of teaching is effective because it allows students to learn by doing. This means they can see how the theory behind a concept or skill works in practice, which helps them understand and remember the information better. This would not be possible if they are only told about the new concept or skill, or read a textbook to learn on their own. Since students can see how the theory works in practice through examples and real-world situations, the information is easier for them to understand.

List some advantages of using the problem solving method of teaching.

Some advantages of using the problem solving method of teaching are that it helps students retain information better since they are able to practice with each new concept or skill taught until they master it before moving on to another topic. This also allows them to learn by doing so they will have hands-on experience with facts which helps them remember important facts faster rather than just hearing about it or reading about it on their own. Furthermore, this teaching method is beneficial for students of all ages and can be adapted to different subjects making it an approach that is versatile and easily used in a classroom setting. Lastly, the problem solving method of teaching presents new information in a way that is easy to understand so students are not overwhelmed with complex material.

The problem solving method of teaching is an effective way for students to learn new concepts and skills. By providing them with examples and real-world situations, they can see how the theory behind a concept or skill works in practice. In addition, students are given practice with each new concept or skill taught, before moving on to the next topic. This them learn and retain the information better.

What has been your experience with adopting a problem-solving teaching method?

How do you feel the usefulness of your lesson plans changed since adopting this method?

What was one of your most successful attempts in using this technique to teach students, and why do you believe it was so successful?

Were there any obstacles when trying to incorporate this technique into your class? 

Did it take a while for all students to get used to the new type of teaching style before they felt comfortable enough to participate in discussions and ask questions about their newly acquired knowledge?

What are your thoughts on this method? 

“I have had the opportunity to work in several districts, including one where they used problem solving for all subjects. I never looked back after that experience--it was exciting and motivating for students and teachers alike." 

"The problem solving method of teaching is great because it makes my subject matter more interesting with hands-on activities."

What is the role of educators in facilitating problem-solving method of teaching?

Role of Educators in Facilitating Problem-Solving Understanding the Problem-Solving Method The problem-solving method of teaching encourages students to actively engage their critical thinking skills to analyze and seek solutions to real-world problems. As such, educators play a crucial part in facilitating this learning style to ensure the effective attainment of desired skills. Encouraging Collaboration and Communication One of the ways educators can facilitate problem-solving is by promoting collaboration and communication among students. Working as a team allows students to share diverse perspectives while considering multiple solutions, thereby fostering an open-minded and inclusive environment that is crucial for effective problem-solving. Creating a Safe Space for Failure Educators must recognize that failure is an integral component of the learning process in a problem-solving method. By establishing a safe environment that allows students to fail without facing judgment or embarrassment, teachers enable students to develop perseverance, resilience, and an enhanced ability to learn from mistakes. Designing Relevant and Engaging Problems The selection and design of appropriate problems contribute significantly to the success of the problem-solving method of teaching. Educators should focus on presenting issues that are relevant, engaging, and age-appropriate, thereby sparking curiosity and interest amongst students, which further improves their problem-solving abilities. Scaffolding Learning Scaffolding is essential in the problem-solving method for providing adequate support when required. Teachers need to break down complex problems into smaller, manageable steps, and gradually remove support as students develop the necessary skills, thus promoting their self-reliance and independent thinking. Providing Constructive Feedback Constructive feedback from educators is invaluable in facilitating the problem-solving method of teaching, as it enables students to reflect on their progress, recognize areas for improvement, and actively develop their critical thinking and problem-solving abilities. In conclusion, the role of educators in facilitating the problem-solving method of teaching comprises promoting collaboration, creating a safe space for failure, designing relevant problems, scaffolding learning, and providing constructive feedback. By integrating these elements, educators can help students develop essential life-long skills and effectively navigate the complex world they will experience.

Can interdisciplinary approaches be incorporated into problem-solving teaching methods, and if so, how?

Interdisciplinary Approaches in Problem-Solving Teaching Methods Integration of Interdisciplinary Approaches Incorporating interdisciplinary approaches into problem-solving teaching methods can be achieved by integrating various subject areas when presenting complex problems that require students to draw from different fields of knowledge. By doing so, learners will develop a deeper understanding of the interconnectedness of various disciplines and improve their problem-solving skills. Project-Based Learning Activities Implementing project-based learning activities in the classroom allows students to work collaboratively on real-world problems. By involving learners in tasks that necessitate the integration of diverse subjects, they develop the ability to transfer skills acquired in one context to novel situations, thereby expanding their problem-solving abilities. Role of Teachers in Interdisciplinary Teaching Teachers play a crucial role in the successful incorporation of interdisciplinary methods in problem-solving teaching. They must be prepared to facilitate student-centered learning and engage in ongoing professional development tailored towards interdisciplinary education. In doing so, educators can create inclusive learning environments that encourage individualized discovery and the application of diverse perspectives to solve complex problems. Benefits of Interdisciplinary Teaching Methods Adopting interdisciplinary teaching methods in problem-solving education not only enhances students' problem-solving abilities but also fosters the development of critical thinking, creativity, and collaboration. These essential skills enable learners to navigate and adapt to an increasingly interconnected world and have been shown to contribute to students' academic and professional success. In conclusion, incorporating interdisciplinary approaches into problem-solving teaching methods can be achieved through the integration of various subject areas, implementing project-based learning activities, and the active role of teachers in interdisciplinary education. These methods benefit students by developing problem-solving skills, critical thinking, creativity, and collaboration, preparing them for future success in an interconnected world.

In what ways can technology be integrated into the problem-solving method of instruction?

**Role of Technology in Problem-Solving Instruction** Technology can be integrated into the problem-solving method of instruction by enhancing student engagement, promoting collaboration, and supporting personalized learning. **Enhancing Student Engagement** One way technology supports the problem-solving method is by increasing students' interest through interactive and dynamic tools. For instance, digital simulations and educational games can help students develop critical thinking and problem-solving skills in a fun, engaging manner. These tools provide real-world contexts and immediate feedback, allowing students to experiment, take risks, and learn from their mistakes. **Promoting Collaboration** Technology also promotes collaboration among students, as online platforms facilitate communication and cooperation. Utilizing tools like video conferencing and shared workspaces, students can collaborate on group projects, discuss ideas, and solve problems together. This collaborative approach fosters a sense of community, mutual support, and collective problem-solving. Moreover, it helps students develop essential interpersonal skills, such as teamwork and communication, which are crucial in today's workplaces. **Supporting Personalized Learning** Finally, technology can be used to provide personalized learning experiences tailored to individual learners' needs, interests, and abilities. With access to adaptive learning platforms or online resources, students can progress at their own pace, focus on areas where they need improvement, and explore topics that interest them. This kind of personalized approach allows instructors to identify areas where students struggle and offer targeted support, enhancing the problem-solving learning experience. In conclusion, integrating technology into the problem-solving method of instruction can improve the learning process in various ways. By fostering student engagement, promoting collaboration, and facilitating personalized learning experiences, technology can be employed as a valuable resource to develop students' problem-solving skills effectively.

I graduated from the Family and Consumption Sciences Department at Hacettepe University. I hold certificates in blogging and personnel management. I have a Master's degree in English and have lived in the US for three years.

What are Problem Solving Skills?

How To Solve The Problems? Practical Problem Solving Skills

A Problem Solving Method: Brainstorming

How To Develop Problem Solving Skills?

Eberly Center

Teaching excellence & educational innovation.

This site provides practical strategies to address teaching problems across the disciplines. These strategies are firmly grounded in educational research and learning principles.

How does it work?

This site supplements our 1-on-1 teaching consultations. CONTACT US to talk with an Eberly colleague in person!

learning principles

• Students' prior knowledge can help or hinder learning. MORE
• How students organize knowledge influences how they learn and apply what they know. MORE
• Students' motivation determines, directs, and sustains what they do to learn. MORE
• To develop mastery, students must acquire component skills, practice integrating them, and know when to apply what they have learned. MORE
• Faculty Support
• Graduate Student Support
• Canvas @ Carnegie Mellon
• Quick Links

What is the most effective way to teach problem solving? A commentary on productive failure as a method of teaching

• Published: 04 May 2012
• Volume 40 , pages 731–735, ( 2012 )

Cite this article

• Allan Collins 1 , 2  

1665 Accesses

8 Citations

1 Altmetric

Explore all metrics

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Jacobson, M. J., Thompson, K., Kennedy-Clark, S. & Hu, C. (2011) Failure and success in sequencing of model - based learning activities. Paper presented at the American Educational Research Association Annual Meeting, New Orleans.

Kapur, M. (2008). Productive failure. Cognition and Instruction, 26 (3), 379–424.

Article   Google Scholar  

Kapur, M. (2009). Productive failure in mathematical problem solving. Instructional Science, 38 (6), 523–550.

Kapur, M. (2010). A further study of productive failure in mathematical problem solving: Unpacking the design components. Instructional Science, 39 (4), 561–579.

Kapur, M. (2012). Productive failure in learning the concept of variance. Instructional Science . doi: 10.1007/s11251-012-9209-6 .

Google Scholar  

Kapur, M., & Bielaczyc, K. (2012). Designing for productive failure. Journal of the Learning Sciences, 21 (1), 45–83.

Koedinger, K. R., Aleven, V., Roll, I., & Baker, R. S. J. D. (2009). In vivo experiments on whether supporting metacognition in intelligent tutoring systems yields robust learning. In D. J. Hacker, J. Dunlosky, & A. C. Graesser (Eds.), Handbook of metacognition in education (pp. 383–412). New York: Routledge.

Roll, I., Holmes, N. G., Day, J., & Bonn, D. (2012). Evaluating metacognitive scaffolding in guided invention activities. Instructional Science . doi: 10.1007/s11251-012-9208-7 .

Salden, R. J. C. M., Koedinger, K. R., Renkl, A., Aleven, V., & McLaren, B. M. (2010). Accounting for beneficial effects of worked examples in tutored problem solving. Educational Psychology Review, 22 (4), 379–392.

Schoenfeld, A. J. (1985). Mathematical problem solving . New York: Academic Press.

Schwartz, D. L., & Bransford, J. D. (1998). A time for telling. Cognition and Instruction, 16 (4), 475–522.

Schwartz, D. L., & Martin, T. (2004). Inventing to prepare for future learning: The hidden efficiency of encouraging original student production in statistics instruction. Cognition and Instruction, 22 (2), 129–184.

Stigler, J. & Hiebert, J. (2009) The teaching gap: Best ideas from the world’s teachers for improving education in the classroom (paperback edition) . New York: Free Press.

Vygotsky, L. S. (1978). Mind in society. In M. Cole, V. John-Steiner, S. Scribner & E. Souberman (Eds.), The development of higher psychological processes. Cambridge: Harvard University Press.

Westermann, K., & Rummel, N. (2012). Delaying instruction: evidence from a study in a university relearning setting. Instructional Science . doi: 10.1007/s11251-012-9207-8 .

White, B. Y., & Frederiksen, J. R. (1998). Inquiry, modeling, and metacognition: Making science accessible to all students. Cognition and Instruction, 16 (1), 3–118.

Wiedmann, M., Leach, R. C., Rummel, N., & Wiley, J. (2012). Does group composition affect learning by invention? Instructional Science . doi: 10.1007/s11251-012-9204-y .

Download references

Author information

Authors and affiliations.

School of Education and Social Policy, Northwestern University, Evanston, IL, 60208, USA

Allan Collins

135 Cedar St., Lexington, MA, 02421, USA

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Allan Collins .

Rights and permissions

Reprints and permissions

About this article

Collins, A. What is the most effective way to teach problem solving? A commentary on productive failure as a method of teaching. Instr Sci 40 , 731–735 (2012). https://doi.org/10.1007/s11251-012-9234-5

Download citation

Received : 05 April 2012

Accepted : 10 April 2012

Published : 04 May 2012

Issue Date : July 2012

DOI : https://doi.org/10.1007/s11251-012-9234-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Generation Phase
• Direct Instruction
• Productive Failure
• Invention Phase
• Canonical Solution
• Find a journal
• Publish with us
• Track your research

• Our Mission

5 Ways to Teach Students the Skill of Active Studying

Explicit instruction on studying is invaluable for students, who often choose ineffective methods of reviewing material.

As students progress through their schooling, they are exposed to concepts that vary significantly in the content and skills needed for comprehension. A student first learning fractions, another in middle school English language arts, and an AP Biology student are all undergoing quite different educational experiences. While these classes will ask different things of the students, they all require the development of study skills. Unfortunately, while all teachers recognize the importance of these skills, they are rarely, if ever, explicitly taught.

This is something that I have taken more seriously in recent years, and I have explicitly worked to teach all of my students better ways to study. In order to properly teach this, I think it’s helpful to understand why certain strategies work. If you want to learn the basics of the neuroscience of learning and memory, you might take a look at an article I wrote on that for my students . In essence, there are two general types of thinking: System 1 (which uses long-term memory and is easier) and System 2 (which uses working memory and requires more effort). Strategies that center on using System 2 thinking result in stronger neuron ensemble formation, meaning better recall and learning.

Active studying is the name of practices that involve more System 2 thinking. A lot of people think of studying as simply reading over one’s notes, which is a passive form and results in minimal learning. Active studying includes retrieval, synthesis, and analysis of the material. As these methods take longer, students are often resistant to using or attempting them. However, research has shown that these techniques result in greater recall of the studied material . As such, I believe that, along with teaching strategies for active studying, you should design lessons around their incorporation.

5 Active Studying Practices

1. Teaching others: It’s as simple as it sounds. When students work to teach others, they are coming up with information from memory (rather than just reading it), and they often need to think of new ways to explain something. This not only helps students figure out what they do or don’t know but strengthens and reinforces the memories.

2. Pure retrieval practice: This is when students retrieve the information from their memory. It can be something simple like using flash cards, but my personal favorite method is when students use a whiteboard, a piece of paper, or a tablet to write out and draw everything they can about the topic. They should then check their notes to see what they missed or got wrong before trying again later.

I like to combine the above two in class by having students work in small groups. Students take turns, with one student having a small whiteboard and teaching the others a topic, while the other students use their notes to correct their classmate or ask clarifying questions about missed aspects. We call these “whiteboard days,” and students have reported finding these days to be very helpful as a review before tests, and many use these strategies at home now.

3. Study guides: Study guides are a common form of studying and a lot of times are given to students by their teachers. Students often fall into a pit of copying definitions word-for-word from their notes, which might aid in memorization of certain terms or facts but limits understanding and the ability to apply the information.

I teach my students how to make a good study guide , where they synthesize and summarize the information into their own words. I don’t require these every unit, but once students have developed the skill, they are able to apply it to any course, and some choose to make them even if not required because they find them helpful.

4. Concept maps: These are visual representations of the connections and relationships between concepts. Although not as helpful for some subjects or topics, these cause students to think more deeply about the material and strengthen their memory of the topics, as they have to think more deeply to come up with connections they may not have otherwise thought of.

While you can assign specific words and require everyone to form maps with the same list as an in-class or homework assignment, my personal favorite way to do this is to gamify it—students draw random cards with vocabulary words on them and compete to develop the most connections.

5. Practice questions: Practice questions are a tried-and-true and very helpful way to study, especially in certain classes. The most helpful practice questions are application-based and allow students to test how well they truly understand the material, as opposed to having just memorized certain facts or definitions. I like to have students study sometimes by making their own and then trading those questions and trying to answer each other’s. By developing their own application-style questions, the students are thinking about the material in a deeper manner to put it into new contexts. They can study both by developing their own questions, attempting to answer another’s, and explaining the right answer for the other students.

There are a variety of ways to work these methods into your course, with some of my ways mentioned above. Whichever you choose, make sure you also emphasize the importance of getting enough sleep and having shorter but more frequent study sessions, as these both are necessary for maximizing retainment of concepts. By teaching these techniques, and also requiring their use, you will help to reinforce and build good study habits within students that can help them in all their future academic endeavors.

Do you teach your students strategies for active studying? Let us know what they are in the comments!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.5: Teaching Mathematics Through Problem Solving

• Last updated
• Save as PDF
• Page ID 156541

• Janet Stramel
• Fort Hays State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

Share Podcast

A Better Framework for Solving Tough Problems

Start with trust and end with speed.

• Apple Podcasts

When it comes to solving complicated problems, the default for many organizational leaders is to take their time to work through the issues at hand. Unfortunately, that often leads to patchwork solutions or problems not truly getting resolved.

But Anne Morriss offers a different framework. In this episode, she outlines a five-step process for solving any problem and explains why starting with trust and ending with speed is so important for effective change leadership. As she says, “Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.”

Morriss is an entrepreneur and leadership coach. She’s also the coauthor of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems .

Key episode topics include: strategy, decision making and problem solving, strategy execution, managing people, collaboration and teams, trustworthiness, organizational culture, change leadership, problem solving, leadership.

HBR On Strategy curates the best case studies and conversations with the world’s top business and management experts, to help you unlock new ways of doing business. New episodes every week.

• Listen to the full HBR IdeaCast episode: How to Solve Tough Problems Better and Faster (2023)
• Find more episodes of HBR IdeaCast
• Discover 100 years of Harvard Business Review articles, case studies, podcasts, and more at HBR.org .

HANNAH BATES: Welcome to HBR On Strategy , case studies and conversations with the world’s top business and management experts, hand-selected to help you unlock new ways of doing business.

When it comes to solving complicated problems, many leaders only focus on the most apparent issues. Unfortunately that often leads to patchwork or partial solutions. But Anne Morriss offers a different framework that aims to truly tackle big problems by first leaning into trust and then focusing on speed.

Morriss is an entrepreneur and leadership coach. She’s also the co-author of the book, Move Fast and Fix Things: The Trusted Leader’s Guide to Solving Hard Problems . In this episode, she outlines a five-step process for solving any problem. Some, she says, can be solved in a week, while others take much longer. She also explains why starting with trust and ending with speed is so important for effective change leadership.

This episode originally aired on HBR IdeaCast in October 2023. Here it is.

CURT NICKISCH: Welcome to the HBR IdeaCast from Harvard Business Review. I’m Curt Nickisch.

Problems can be intimidating. Sure, some problems are fun to dig into. You roll up your sleeves, you just take care of them; but others, well, they’re complicated. Sometimes it’s hard to wrap your brain around a problem, much less fix it.

And that’s especially true for leaders in organizations where problems are often layered and complex. They sometimes demand technical, financial, or interpersonal knowledge to fix. And whether it’s avoidance on the leaders’ part or just the perception that a problem is systemic or even intractable, problems find a way to endure, to keep going, to keep being a problem that everyone tries to work around or just puts up with.

But today’s guest says that just compounds it and makes the problem harder to fix. Instead, she says, speed and momentum are key to overcoming a problem.

Anne Morriss is an entrepreneur, leadership coach and founder of the Leadership Consortium and with Harvard Business School Professor Francis Frei, she wrote the new book, Move Fast and Fix Things: The Trusted Leaders Guide to Solving Hard Problems . Anne, welcome back to the show.

ANNE MORRISS: Curt, thank you so much for having me.

CURT NICKISCH: So, to generate momentum at an organization, you say that you really need speed and trust. We’ll get into those essential ingredients some more, but why are those two essential?

ANNE MORRISS: Yeah. Well, the essential pattern that we observed was that the most effective change leaders out there were building trust and speed, and it didn’t seem to be a well-known observation. We all know the phrase, “Move fast and break things,” but the people who were really getting it right were moving fast and fixing things, and that was really our jumping off point. So when we dug into the pattern, what we observed was they were building trust first and then speed. This foundation of trust was what allowed them to fix more things and break fewer.

CURT NICKISCH: Trust sounds like a slow thing, right? If you talk about building trust, that is something that takes interactions, it takes communication, it takes experiences. Does that run counter to the speed idea?

ANNE MORRISS: Yeah. Well, this issue of trust is something we’ve been looking at for over a decade. One of the headlines in our research is it’s actually something we’re building and rebuilding and breaking all the time. And so instead of being this precious, almost farbege egg, it’s this thing that is constantly in motion and this thing that we can really impact when we’re deliberate about our choices and have some self-awareness around where it’s breaking down and how it’s breaking down.

CURT NICKISCH: You said break trust in there, which is intriguing, right? That you may have to break trust to build trust. Can you explain that a little?

ANNE MORRISS:  Yeah, well, I’ll clarify. It’s not that you have to break it in order to build it. It’s just that we all do it some of the time. Most of us are trusted most of the time. Most of your listeners I imagine are trusted most of the time, but all of us have a pattern where we break trust or where we don’t build as much as could be possible.

CURT NICKISCH: I want to talk about speed, this other essential ingredient that’s so intriguing, right? Because you think about solving hard problems as something that just takes a lot of time and thinking and coordination and planning and designing. Explain what you mean by it? And also, just  how we maybe approach problems wrong by taking them on too slowly?

ANNE MORRISS: Well, Curt, no one has ever said to us, “I wish I had taken longer and done less.” We hear the opposite all the time, by the way. So what we really set out to do was to create a playbook that anyone can use to take less time to do more of the things that are going to make your teams and organizations stronger.

And the way we set up the book is okay, it’s really a five step process. Speed is the last step. It’s the payoff for the hard work you’re going to do to figure out your problem, build or rebuild trust, expand the team in thoughtful and strategic ways, and then tell a real and compelling story about the change you’re leading.

Only then do you get to go fast, but that’s an essential part of the process, and we find that either people under emphasize it or speed has gotten a bad name in this world of moving fast and breaking things. And part of our mission for sure was to rehabilitate speed’s reputation because it is an essential part of the change leader’s equation. It can be the difference between good intentions and getting anything done at all.

CURT NICKISCH: You know, the fact that nobody ever tells you, “I wish we had done less and taken more time.” I think we all feel that, right? Sometimes we do something and then realize, “Oh, that wasn’t that hard and why did it take me so long to do it? And I wish I’d done this a long time ago.” Is it ever possible to solve a problem too quickly?

ANNE MORRISS: Absolutely. And we see that all the time too. What we push people to do in those scenarios is really take a look at the underlying issue because in most cases, the solution is not to take your foot off the accelerator per se and slow down. The solution is to get into the underlying problem. So if it’s burnout or a strategic disconnect between what you’re building and the marketplace you’re serving, what we find is the anxiety that people attach to speed or the frustration people attach to speed is often misplaced.

CURT NICKISCH: What is a good timeline to think about solving a problem then? Because if we by default take too long or else jump ahead and we don’t fix it right, what’s a good target time to have in your mind for how long solving a problem should take?

ANNE MORRISS: Yeah. Well, we’re playful in the book and talking about the idea that many problems can be solved in a week. We set the book up five chapters. They’re titled Monday, Tuesday, Wednesday, Thursday, Friday, and we’re definitely having fun with that. And yet, if you count the hours in a week, there are a lot of them. Many of our problems, if you were to spend a focused 40 hours of effort on a problem, you’re going to get pretty far.

But our main message is, listen, of course it’s going to depend on the nature of the problem, and you’re going to take weeks and maybe even some cases months to get to the other side. What we don’t want you to do is take years, which tends to be our default timeline for solving hard problems.

CURT NICKISCH: So you say to start with identifying the problem that’s holding you back, seems kind of obvious. But where do companies go right and wrong with this first step of just identifying the problem that’s holding you back?

ANNE MORRISS: And our goal is that all of these are going to feel obvious in retrospect. The problem is we skip over a lot of these steps and this is why we wanted to underline them. So this one is really rooted in our observation and I think the pattern of our species that we tend to be overconfident in the quality of our thoughts, particularly when it comes to diagnosing problems.

And so we want to invite you to start in a very humble and curious place, which tends not to be our default mode when we’re showing up for work. We convince ourselves that we’re being paid for our judgment. That’s exactly what gets reinforced everywhere. And so we tend to counterintuitively, given what we just talked about, we tend to move too quickly through the diagnostic phase.

CURT NICKISCH: “I know what to do, that’s why you hired me.”

ANNE MORRISS: Exactly. “I know what to do. That’s why you hired me. I’ve seen this before. I have a plan. Follow me.” We get rewarded for the expression of confidence and clarity. And so what we’re inviting people to do here is actually pause and really lean into what are the root causes of the problem you’re seeing? What are some alternative explanations? Let’s get into dialogue with the people who are also impacted by the problem before we start running down the path of solving it.

CURT NICKISCH: So what do you recommend for this step, for getting to the root of the problem? What are questions you should ask? What’s the right thought process? What do you do on Monday of the week?

ANNE MORRISS: In our experience of doing this work, people tend to undervalue the power of conversation, particularly with other people in the organization. So we will often advocate putting together a team of problem solvers, make it a temporary team, really pull in people who have a particular perspective on the problem and create the space, make it as psychologically safe as you can for people to really, as Chris Argyris so beautifully articulated, discuss the undiscussable.

And so the conditions for that are going to look different in every organization depending on the problem, but if you can get a space where smart people who have direct experience of a problem are in a room and talking honestly with each other, you can make an extraordinary amount of progress, certainly in a day.

CURT NICKISCH: Yeah, that gets back to the trust piece.

ANNE MORRISS: Definitely.

CURT NICKISCH: How do you like to start that meeting, or how do you like to talk about it? I’m just curious what somebody on that team might hear in that meeting, just to get the sense that it’s psychologically safe, you can discuss the undiscussable and you’re also focusing on the identification part. What’s key to communicate there?

ANNE MORRISS: Yeah. Well, we sometimes encourage people to do a little bit of data gathering before those conversations. So the power of a quick anonymous survey around whatever problem you’re solving, but also be really thoughtful about the questions you’re going to ask in the moment. So a little bit of preparation can go a long way and a little bit of thoughtfulness about the power dynamic. So who’s going to walk in there with license to speak and who’s going to hold back? So being thoughtful about the agenda, about the questions you’re asking about the room, about the facilitation, and then courage is a very infectious emotion.

So if you can early on create the conditions for people to show up bravely in that conversation, then the chance that you’re going to get good information and that you’re going to walk out of that room with new insight in the problem that you didn’t have when you walked in is extraordinarily high.

CURT NICKISCH: Now, in those discussions, you may have people who have different perspectives on what the problem really is. They also bear different costs of addressing the problem or solving it. You talked about the power dynamic, but there’s also an unfairness dynamic of who’s going to actually have to do the work to take care of it, and I wonder how you create a culture in that meeting where it’s the most productive?

ANNE MORRISS: For sure, the burden of work is not going to be equitably distributed around the room. But I would say, Curt, the dynamic that we see most often is that people are deeply relieved that hard problems are being addressed. So it really can create, and more often than not in our experience, it does create this beautiful flywheel of action, creativity, optimism. Often when problems haven’t been addressed, there is a fair amount of anxiety in the organization, frustration, stagnation. And so credible movement towards action and progress is often the best antidote. So even if the plan isn’t super clear yet, if it’s credible, given who’s in the room and their decision rights and mandate, if there’s real momentum coming out of that to make progress, then that tends to be deeply energizing to people.

CURT NICKISCH: I wonder if there’s an organization that you’ve worked with that you could talk about how this rolled out and how this took shape?

ANNE MORRISS: When we started working with Uber, that was wrestling with some very public issues of culture and trust with a range of stakeholders internally, the organization, also external, that work really started with a campaign of listening and really trying to understand where trust was breaking down from the perspective of these stakeholders?

So whether it was female employees or regulators or riders who had safety concerns getting into the car with a stranger. This work, it starts with an honest internal dialogue, but often the problem has threads that go external. And so bringing that same commitment to curiosity and humility and dialogue to anyone who’s impacted by the problem is the fastest way to surface what’s really going on.

CURT NICKISCH: There’s a step in this process that you lay out and that’s communicating powerfully as a leader. So we’ve heard about listening and trust building, but now you’re talking about powerful communication. How do you do this and why is it maybe this step in the process rather than the first thing you do or the last thing you do?

ANNE MORRISS: So in our process, again, it’s the days of the week. On Monday you figured out the problem. Tuesday you really got into the sandbox in figuring out what a good enough plan is for building trust. Wednesday, step three, you made it better. You created an even better plan, bringing in new perspectives. Thursday, this fourth step is the day we’re saying you got to go get buy-in. You got to bring other people along. And again, this is a step where we see people often underinvest in the power and payoff of really executing it well.

CURT NICKISCH: How does that go wrong?

ANNE MORRISS: Yeah, people don’t know the why. Human behavior and the change in human behavior really depends on a strong why. It’s not just a selfish, “What’s in it for me?” Although that’s helpful, but where are we going? I may be invested in a status quo and I need to understand, okay, if you’re going to ask me to change, if you’re going to invite me into this uncomfortable place of doing things differently, why am I here? Help me understand it and articulate the way forward and language that not only I can understand, but also that’s going to be motivating to me.

CURT NICKISCH: And who on my team was part of this process and all that kind of stuff?

ANNE MORRISS: Oh, yeah. I may have some really important questions that may be in the way of my buy-in and commitment to this plan. So certainly creating a space where those questions can be addressed is essential. But what we found is that there is an architecture of a great change story, and it starts with honoring the past, honoring the starting place. Sometimes we’re so excited about the change and animated about the change that what has happened before or what is even happening in the present tense is low on our list of priorities.

Or we want to label it bad, because that’s the way we’ve thought about the change, but really pausing and honoring what came before you and all the reasonable decisions that led up to it, I think can be really helpful to getting people emotionally where you want them to be willing to be guided by you. Going back to Uber, when Dara Khosrowshahi came in.

CURT NICKISCH: This is the new CEO.

ANNE MORRISS: The new CEO.

CURT NICKISCH: Replaced Travis Kalanick, the founder and first CEO, yeah.

ANNE MORRISS: Yeah, and had his first all-hands meeting. One of his key messages, and this is a quote, was that he was going to retain the edge that had made Uber, “A force of nature.” And in that meeting, the crowd went wild because this is also a company that had been beaten up publicly for months and months and months, and it was a really powerful choice. And his predecessor, Travis was in the room, and he also honored Travis’ incredible work and investment in bringing the company to the place where it was.

And I would use words like grace to also describe those choices, but there’s also an incredible strategic value to naming the starting place for everybody in the room because in most cases, most people in that room played a role in getting to that starting place, and you’re acknowledging that.

CURT NICKISCH: You can call it grace. Somebody else might call it diplomatic or strategic. But yeah, I guess like it or not, it’s helpful to call out and honor the complexity of the way things have been done and also the change that’s happening.

ANNE MORRISS: Yeah, and the value. Sometimes honoring the past is also owning what didn’t work or what wasn’t working for stakeholders or segments of the employee team, and we see that around culture change. Sometimes you’ve got to acknowledge that it was not an equitable environment, but whatever the worker, everyone in that room is bringing that pass with them. So again, making it discussable and using it as the jumping off place is where we advise people to start.

Then you’ve earned the right to talk about the change mandate, which we suggest using clear and compelling language about the why. “This is what happened, this is where we are, this is the good and the bad of it, and here’s the case for change.”

And then the last part, which is to describe a rigorous and optimistic way forward. It’s a simple past, present, future arc, which will be familiar to human beings. We love stories as human beings. It’s among the most powerful currency we have to make sense of the world.

CURT NICKISCH: Yeah. Chronological is a pretty powerful order.

ANNE MORRISS: Right. But again, the change leaders we see really get it right, are investing an incredible amount of time into the storytelling part of their job. Ursula Burns, the Head of Xerox is famous for the months and years she spent on the road just telling the story of Xerox’s change, its pivot into services to everyone who would listen, and that was a huge part of her success.

CURT NICKISCH: So Friday or your fifth step, you end with empowering teams and removing roadblocks. That seems obvious, but it’s critical. Can you dig into that a little bit?

ANNE MORRISS: Yeah. Friday is the fun day. Friday’s the release of energy into the system. Again, you’ve now earned the right to go fast. You have a plan, you’re pretty confident it’s going to work. You’ve told the story of change the organization, and now you get to sprint. So this is about really executing with urgency, and it’s about a lot of the tactics of speed is where we focus in the book. So the tactics of empowerment, making tough strategic trade-offs so that your priorities are clear and clearly communicated, creating mechanisms to fast-track progress. At Etsy, CEO Josh Silverman, he labeled these projects ambulances. It’s an unfortunate metaphor, but it’s super memorable. These are the products that get to speed out in front of the other ones because the stakes are high and the clock is sticking.

CURT NICKISCH: You pull over and let it go by.

ANNE MORRISS: Yeah, exactly. And so we have to agree as an organization on how to do something like that. And so we see lots of great examples both in young organizations and big complex biotech companies with lots of regulatory guardrails have still found ways to do this gracefully.

And I think we end with this idea of conflict debt, which is a term we really love. Leanne Davey, who’s a team scholar and researcher, and anyone in a tech company will recognize the idea of tech debt, which is this weight the organization drags around until they resolve it. Conflict debt is a beautiful metaphor because it is this weight that we drag around and slows us down until we decide to clean it up and fix it. The organizations that are really getting speed right have figured out either formally or informally, how to create an environment where conflict and disagreements can be gracefully resolved.

CURT NICKISCH: Well, let’s talk about this speed more, right? Because I think this is one of those places that maybe people go wrong or take too long, and then you lose the awareness of the problem, you lose that urgency. And then that also just makes it less effective, right? It’s not just about getting the problem solved as quickly as possible. It’s also just speed in some ways helps solve the problem.

ANNE MORRISS: Oh, yeah. It really is the difference between imagining the change you want to lead and really being able to bring it to life. Speed is the thing that unlocks your ability to lead change. It needs a foundation, and that’s what Monday through Thursday is all about, steps one through four, but the finish line is executing with urgency, and it’s that urgency that releases the system’s energy, that communicates your priorities, that creates the conditions for your team to make progress.

CURT NICKISCH: Moving fast is something that entrepreneurs and tech companies certainly understand, but there’s also this awareness that with big companies, the bigger the organization, the harder it is to turn the aircraft carrier around, right? Is speed relative when you get at those levels, or do you think this is something that any company should be able to apply equally?

ANNE MORRISS: We think this applies to any company. The culture really lives at the level of team. So we believe you can make a tremendous amount of progress even within your circle of control as a team leader. I want to bring some humility to this and careful of words like universal, but we do think there’s some universal truths here around the value of speed, and then some of the byproducts like keeping fantastic people. Your best people want to solve problems, they want to execute, they want to make progress and speed, and the ability to do that is going to be a variable in their own equation of whether they stay or they go somewhere else where they can have an impact.

CURT NICKISCH: Right. They want to accomplish something before they go or before they retire or finish something out. And if you’re able to just bring more things on the horizon and have it not feel like it’s going to be another two years to do something meaningful.

ANNE MORRISS: People – I mean, they want to make stuff happen and they want to be around the energy and the vitality of making things happen, which again, is also a super infectious phenomenon. One of the most important jobs of a leader, we believe, is to set the metabolic pace of their teams and organizations. And so what we really dig into on Friday is, well, what does that look like to speed something up? What are the tactics of that?

CURT NICKISCH: I wonder if that universal truth, that a body in motion stays in motion applies to organizations, right? If an organization in motion stays in motion, there is something to that.

ANNE MORRISS: Absolutely.

CURT NICKISCH: Do you have a favorite client story to share, just where you saw speed just become a bit of a flywheel or just a positive reinforcement loop for more positive change at the organization?

ANNE MORRISS: Yeah. We work with a fair number of organizations that are on fire. We do a fair amount of firefighting, but we also less dramatically do a lot of fire prevention. So we’re brought into organizations that are working well and want to get better, looking out on the horizon. That work is super gratifying, and there is always a component of, well, how do we speed this up?

What I love about that work is there’s often already a high foundation of trust, and so it’s, well, how do we maintain that foundation but move this flywheel, as you said, even faster? And it’s really energizing because often there’s a lot of pent-up energy that… There’s a lot of loyalty to the organization, but often it’s also frustration and pent-up energy. And so when that gets released, when good people get the opportunity to sprint for the first time in a little while, it’s incredibly energizing, not just for us, but for the whole organization.

CURT NICKISCH: Anne, this is great. I think finding a way to solve problems better but also faster is going to be really helpful. So thanks for coming on the show to talk about it.

ANNE MORRISS:  Oh, Curt, it was such a pleasure. This is my favorite conversation. I’m delighted to have it anytime.

HANNAH BATES: That was entrepreneur, leadership coach, and author Anne Morriss – in conversation with Curt Nickisch on HBR IdeaCast.

We’ll be back next Wednesday with another hand-picked conversation about business strategy from Harvard Business Review. If you found this episode helpful, share it with your friends and colleagues, and follow our show on Apple Podcasts, Spotify, or wherever you get your podcasts. While you’re there, be sure to leave us a review.

When you’re ready for more podcasts, articles, case studies, books, and videos with the world’s top business and management experts, you’ll find it all at HBR.org.

This episode was produced by Mary Dooe, Anne Saini, and me, Hannah Bates. Ian Fox is our editor. Special thanks to Rob Eckhardt, Maureen Hoch, Erica Truxler, Ramsey Khabbaz, Nicole Smith, Anne Bartholomew, and you – our listener. See you next week.

• Subscribe On:

Latest in this series

This article is about strategy.

• Decision making and problem solving
• Strategy execution
• Leadership and managing people
• Collaboration and teams
• Trustworthiness
• Organizational culture

Partner Center