what is p value in statistics hypothesis testing

P-Value in Statistical Hypothesis Tests: What is it?

P value definition.

A p value is used in hypothesis testing to help you support or reject the null hypothesis . The p value is the evidence against a null hypothesis . The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

P values are expressed as decimals although it may be easier to understand what they are if you convert them to a percentage . For example, a p value of 0.0254 is 2.54%. This means there is a 2.54% chance your results could be random (i.e. happened by chance). That’s pretty tiny. On the other hand, a large p-value of .9(90%) means your results have a 90% probability of being completely random and not due to anything in your experiment. Therefore, the smaller the p-value, the more important (“ significant “) your results.

When you run a hypothesis test , you compare the p value from your test to the alpha level you selected when you ran the test. Alpha levels can also be written as percentages.

P Value vs Alpha level

Alpha levels are controlled by the researcher and are related to confidence levels . You get an alpha level by subtracting your confidence level from 100%. For example, if you want to be 98 percent confident in your research, the alpha level would be 2% (100% – 98%). When you run the hypothesis test, the test will give you a value for p. Compare that value to your chosen alpha level. For example, let’s say you chose an alpha level of 5% (0.05). If the results from the test give you:

A small p (≤ 0.05), reject the null hypothesis . This is strong evidence that the null hypothesis is invalid.
A large p (> 0.05) means the alternate hypothesis is weak, so you do not reject the null.

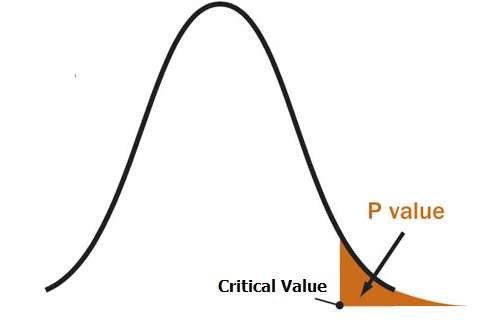
P Values and Critical Values

What if I Don’t Have an Alpha Level?

In an ideal world, you’ll have an alpha level. But if you do not, you can still use the following rough guidelines in deciding whether to support or reject the null hypothesis:

If p > .10 → “not significant”
If p ≤ .10 → “marginally significant”
If p ≤ .05 → “significant”
If p ≤ .01 → “highly significant.”

How to Calculate a P Value on the TI 83

Example question: The average wait time to see an E.R. doctor is said to be 150 minutes. You think the wait time is actually less. You take a random sample of 30 people and find their average wait is 148 minutes with a standard deviation of 5 minutes. Assume the distribution is normal. Find the p value for this test.

Press STAT then arrow over to TESTS.
Press ENTER for Z-Test .
Arrow over to Stats. Press ENTER.
Arrow down to μ0 and type 150. This is our null hypothesis mean.
Arrow down to σ. Type in your std dev: 5.
Arrow down to xbar. Type in your sample mean : 148.
Arrow down to n. Type in your sample size : 30.
Arrow to <μ0 for a left tail test . Press ENTER.
Arrow down to Calculate. Press ENTER. P is given as .014, or about 1%.

The probability that you would get a sample mean of 148 minutes is tiny, so you should reject the null hypothesis.

Note : If you don’t want to run a test, you could also use the TI 83 NormCDF function to get the area (which is the same thing as the probability value).

Dodge, Y. (2008). The Concise Encyclopedia of Statistics . Springer. Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial.

Warning: The NCBI web site requires JavaScript to function. more...

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings
Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.

Review Questions
Access free multiple choice questions on this topic.
Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

Bulk download StatPearls data from FTP

Related information

PMC PubMed Central citations
PubMed Links to PubMed

Recent Activity

Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

what is p value in statistics hypothesis testing

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.2 hypothesis testing (p-value approach).

The P -value approach involves determining "likely" or "unlikely" by determining the probability — assuming the null hypothesis was true — of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed. If the P -value is small, say less than (or equal to) $\alpha$, then it is "unlikely." And, if the P -value is large, say more than $\alpha$, then it is "likely."

If the P -value is less than (or equal to) $\alpha$, then the null hypothesis is rejected in favor of the alternative hypothesis. And, if the P -value is greater than $\alpha$, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the P -value approach to conducting any hypothesis test are:

Specify the null and alternative hypotheses.
Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. Again, to conduct the hypothesis test for the population mean μ , we use the t -statistic $t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}$ which follows a t -distribution with n - 1 degrees of freedom.
Using the known distribution of the test statistic, calculate the P -value : "If the null hypothesis is true, what is the probability that we'd observe a more extreme test statistic in the direction of the alternative hypothesis than we did?" (Note how this question is equivalent to the question answered in criminal trials: "If the defendant is innocent, what is the chance that we'd observe such extreme criminal evidence?")
Set the significance level, $\alpha$, the probability of making a Type I error to be small — 0.01, 0.05, or 0.10. Compare the P -value to $\alpha$. If the P -value is less than (or equal to) $\alpha$, reject the null hypothesis in favor of the alternative hypothesis. If the P -value is greater than $\alpha$, do not reject the null hypothesis.

Example S.3.2.1

Mean gpa section .

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * equaling 2.5. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right Tailed

The P -value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the probability that we would observe a test statistic greater than t * = 2.5 if the population mean $\mu$ really were 3. Recall that probability equals the area under the probability curve. The P -value is therefore the area under a t n - 1 = t 14 curve and to the right of the test statistic t * = 2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

t-distrbution graph showing the right tail beyond a t value of 2.5

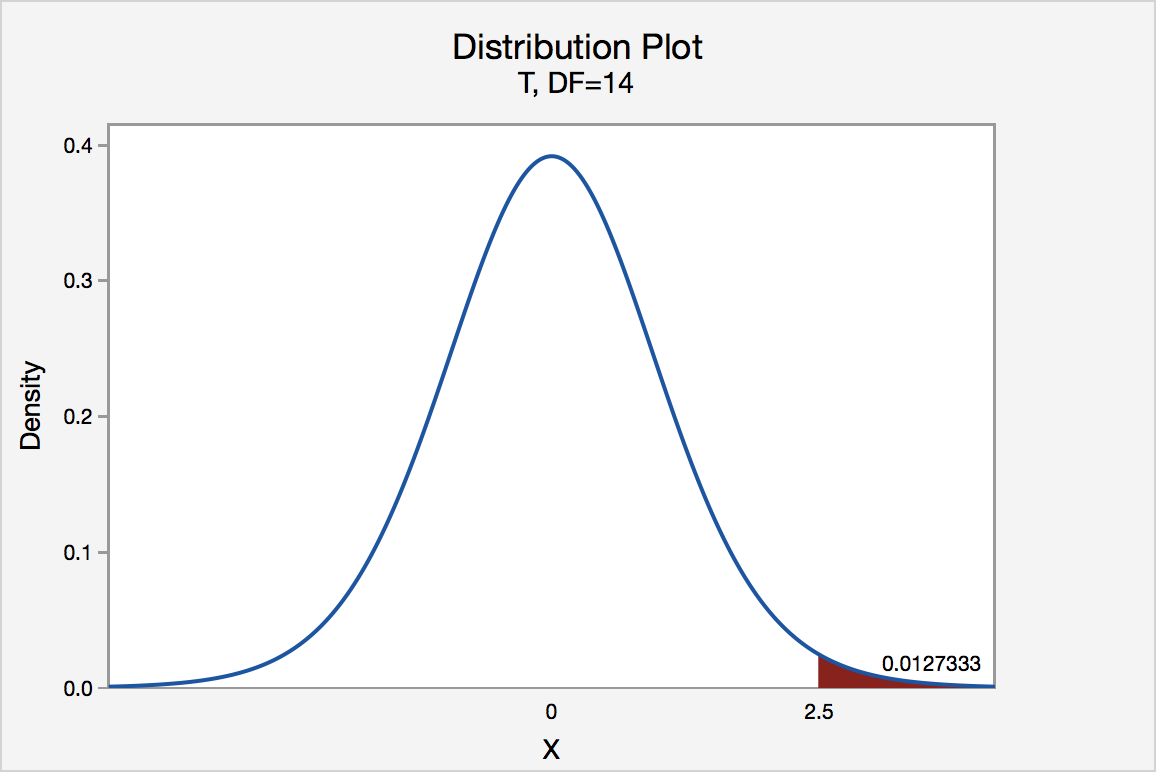
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than $\alpha$ = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ > 3 if we lowered our willingness to make a Type I error to $\alpha$ = 0.01 instead, as the P -value, 0.0127, is then greater than $\alpha$ = 0.01.

Left Tailed

In our example concerning the mean grade point average, suppose that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the probability that we would observe a test statistic less than t * = -2.5 if the population mean μ really were 3. The P -value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5. It can be shown using statistical software that the P -value is 0.0127. The graph depicts this visually.

t distribution graph showing left tail below t value of -2.5

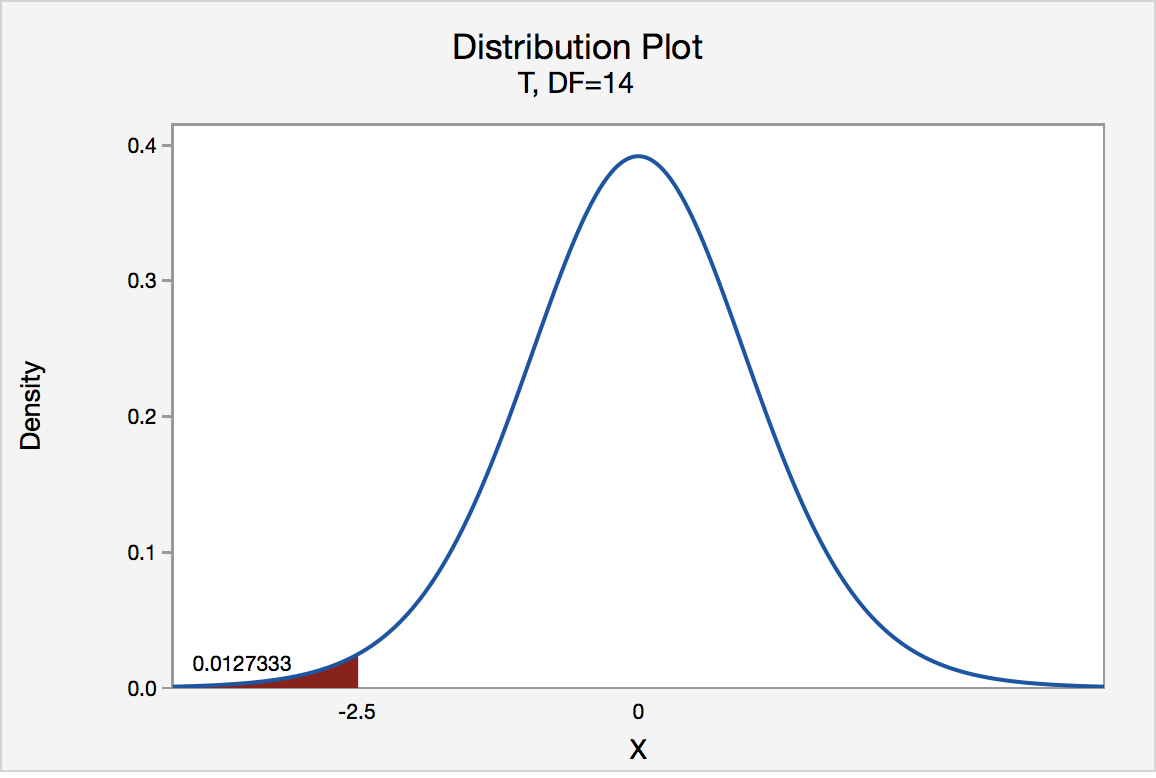
The P -value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0127, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ < 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0127, is then greater than $\alpha$ = 0.01.

In our example concerning the mean grade point average, suppose again that our random sample of n = 15 students majoring in mathematics yields a test statistic t * instead of equaling -2.5. The P -value for conducting the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 is the probability that we would observe a test statistic less than -2.5 or greater than 2.5 if the population mean μ really was 3. That is, the two-tailed test requires taking into account the possibility that the test statistic could fall into either tail (hence the name "two-tailed" test). The P -value is, therefore, the area under a t n - 1 = t 14 curve to the left of -2.5 and to the right of 2.5. It can be shown using statistical software that the P -value is 0.0127 + 0.0127, or 0.0254. The graph depicts this visually.

t-distribution graph of two tailed probability for t values of -2.5 and 2.5

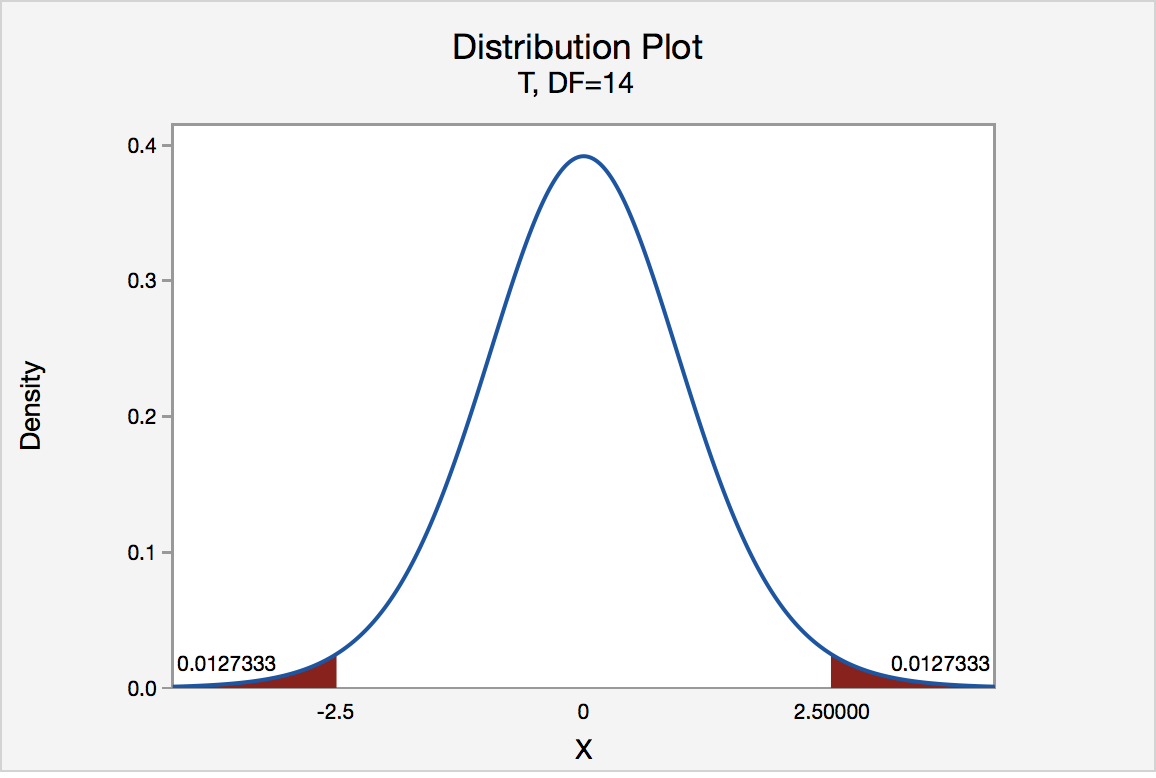
Note that the P -value for a two-tailed test is always two times the P -value for either of the one-tailed tests. The P -value, 0.0254, tells us it is "unlikely" that we would observe such an extreme test statistic t * in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect. That is, since the P -value, 0.0254, is less than α = 0.05, we reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3.

Note that we would not reject H 0 : μ = 3 in favor of H A : μ ≠ 3 if we lowered our willingness to make a Type I error to α = 0.01 instead, as the P -value, 0.0254, is then greater than $\alpha$ = 0.01.

Now that we have reviewed the critical value and P -value approach procedures for each of the three possible hypotheses, let's look at three new examples — one of a right-tailed test, one of a left-tailed test, and one of a two-tailed test.

The good news is that, whenever possible, we will take advantage of the test statistics and P -values reported in statistical software, such as Minitab, to conduct our hypothesis tests in this course.

P-Value And Statistical Significance: What It Is & Why It Matters

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

P-Value Explained in Normal Distribution

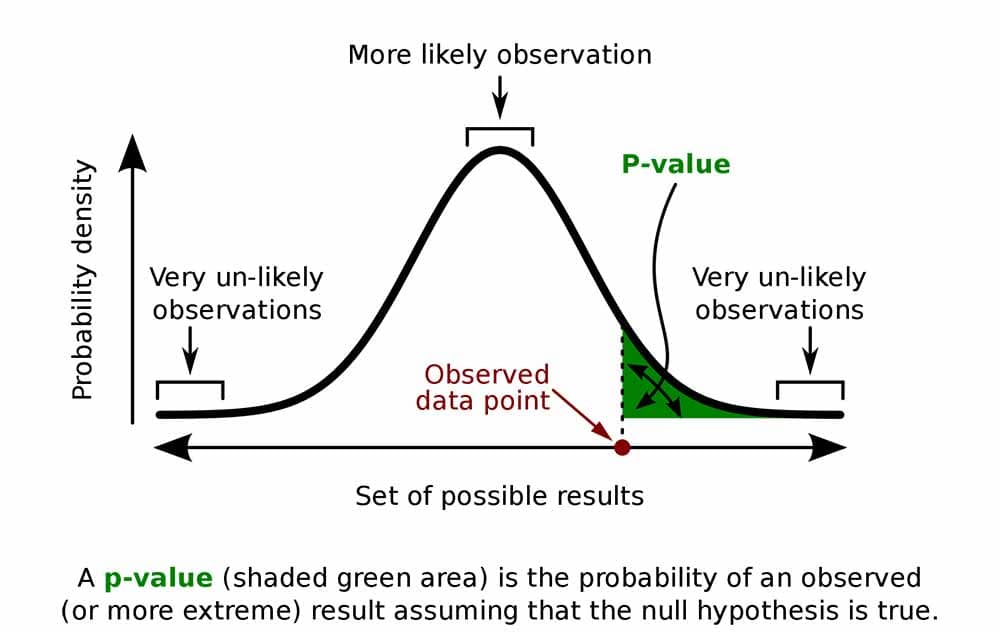
Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05.

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Probability and statistical significance in ab testing. Statistical significance in a b experiments

Two-Tailed Test

How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

P Value Calculator From T Score
P-Value Calculator For Chi-Square
P-values and significance tests (Kahn Academy)
Hypothesis testing and p-values (Kahn Academy)
Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
Criticism of using the “ p “< 0.05”.
Publication manual of the American Psychological Association
Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal , 309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health , 78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.) , 9 (1), 7-8.

p-value Calculator

What is p-value, how do i calculate p-value from test statistic, how to interpret p-value, how to use the p-value calculator to find p-value from test statistic, how do i find p-value from z-score, how do i find p-value from t, p-value from chi-square score (χ² score), p-value from f-score.

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

Symmetric case: normal distribution:

p-values for symmetric distribution — left-tailed, right-tailed, and two-tailed tests.

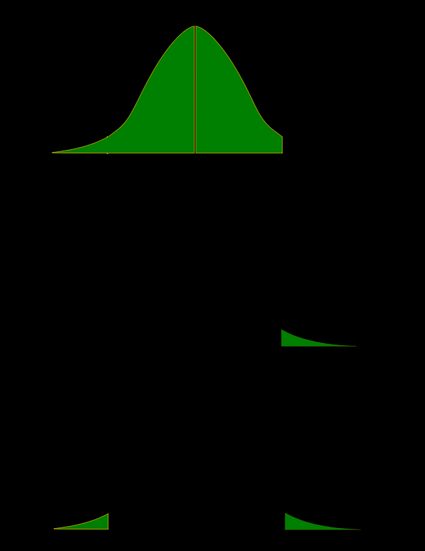
Non-symmetric case: chi-squared distribution:

p-values for non-symmetric distribution — left-tailed, right-tailed, and two-tailed tests.

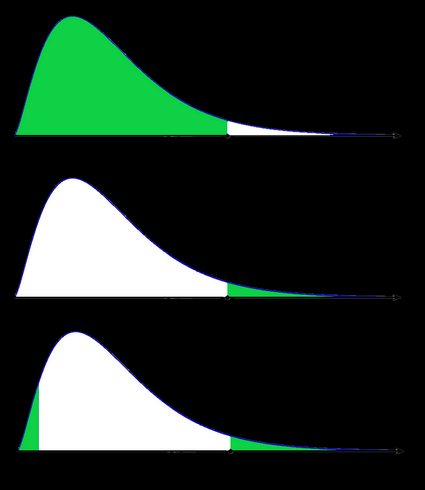
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

A high p-value means that your data is highly compatible with the null hypothesis; and
A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis. The standard significance level is 0.05 by default.

Go to the advanced mode if you need to increase the precision with which the calculations are performed or change the significance level .

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

Index of qualitative variation

Social media time alternatives.

Biology (103)
Chemistry (101)
Construction (148)
Conversion (304)
Ecology (32)
Everyday life (263)
Finance (596)
Health (443)
Physics (513)
Sports (108)
Statistics (184)
Other (186)
Discover Omni (40)

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

How Hypothesis Tests Work: Significance Levels (Alpha) and P values

By Jim Frost 45 Comments

Hypothesis testing is a vital process in inferential statistics where the goal is to use sample data to draw conclusions about an entire population . In the testing process, you use significance levels and p-values to determine whether the test results are statistically significant.

You hear about results being statistically significant all of the time. But, what do significance levels, P values, and statistical significance actually represent? Why do we even need to use hypothesis tests in statistics?

In this post, I answer all of these questions. I use graphs and concepts to explain how hypothesis tests function in order to provide a more intuitive explanation. This helps you move on to understanding your statistical results.

Hypothesis Test Example Scenario

To start, I’ll demonstrate why we need to use hypothesis tests using an example.

A researcher is studying fuel expenditures for families and wants to determine if the monthly cost has changed since last year when the average was $260 per month. The researcher draws a random sample of 25 families and enters their monthly costs for this year into statistical software. You can download the CSV data file: FuelsCosts . Below are the descriptive statistics for this year.

Table of descriptive statistics for our fuel cost example.

We’ll build on this example to answer the research question and show how hypothesis tests work.

Descriptive Statistics Alone Won’t Answer the Question

The researcher collected a random sample and found that this year’s sample mean (330.6) is greater than last year’s mean (260). Why perform a hypothesis test at all? We can see that this year’s mean is higher by $70! Isn’t that different?

Regrettably, the situation isn’t as clear as you might think because we’re analyzing a sample instead of the full population. There are huge benefits when working with samples because it is usually impossible to collect data from an entire population. However, the tradeoff for working with a manageable sample is that we need to account for sample error.

The sampling error is the gap between the sample statistic and the population parameter. For our example, the sample statistic is the sample mean, which is 330.6. The population parameter is μ, or mu, which is the average of the entire population. Unfortunately, the value of the population parameter is not only unknown but usually unknowable. Learn more about Sampling Error .

We obtained a sample mean of 330.6. However, it’s conceivable that, due to sampling error, the mean of the population might be only 260. If the researcher drew another random sample, the next sample mean might be closer to 260. It’s impossible to assess this possibility by looking at only the sample mean. Hypothesis testing is a form of inferential statistics that allows us to draw conclusions about an entire population based on a representative sample. We need to use a hypothesis test to determine the likelihood of obtaining our sample mean if the population mean is 260.

Background information : The Difference between Descriptive and Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics

A Sampling Distribution Determines Whether Our Sample Mean is Unlikely

It is very unlikely for any sample mean to equal the population mean because of sample error. In our case, the sample mean of 330.6 is almost definitely not equal to the population mean for fuel expenditures.

If we could obtain a substantial number of random samples and calculate the sample mean for each sample, we’d observe a broad spectrum of sample means. We’d even be able to graph the distribution of sample means from this process.

This type of distribution is called a sampling distribution. You obtain a sampling distribution by drawing many random samples of the same size from the same population. Why the heck would we do this?

Because sampling distributions allow you to determine the likelihood of obtaining your sample statistic and they’re crucial for performing hypothesis tests.

Luckily, we don’t need to go to the trouble of collecting numerous random samples! We can estimate the sampling distribution using the t-distribution, our sample size, and the variability in our sample.

We want to find out if the average fuel expenditure this year (330.6) is different from last year (260). To answer this question, we’ll graph the sampling distribution based on the assumption that the mean fuel cost for the entire population has not changed and is still 260. In statistics, we call this lack of effect, or no change, the null hypothesis . We use the null hypothesis value as the basis of comparison for our observed sample value.

Sampling distributions and t-distributions are types of probability distributions.

Related posts : Sampling Distributions and Understanding Probability Distributions

Graphing our Sample Mean in the Context of the Sampling Distribution

The graph below shows which sample means are more likely and less likely if the population mean is 260. We can place our sample mean in this distribution. This larger context helps us see how unlikely our sample mean is if the null hypothesis is true (μ = 260).

Sampling distribution of means for our fuel cost data.

The graph displays the estimated distribution of sample means. The most likely values are near 260 because the plot assumes that this is the true population mean. However, given random sampling error, it would not be surprising to observe sample means ranging from 167 to 352. If the population mean is still 260, our observed sample mean (330.6) isn’t the most likely value, but it’s not completely implausible either.

The Role of Hypothesis Tests

The sampling distribution shows us that we are relatively unlikely to obtain a sample of 330.6 if the population mean is 260. Is our sample mean so unlikely that we can reject the notion that the population mean is 260?

In statistics, we call this rejecting the null hypothesis. If we reject the null for our example, the difference between the sample mean (330.6) and 260 is statistically significant. In other words, the sample data favor the hypothesis that the population average does not equal 260.

However, look at the sampling distribution chart again. Notice that there is no special location on the curve where you can definitively draw this conclusion. There is only a consistent decrease in the likelihood of observing sample means that are farther from the null hypothesis value. Where do we decide a sample mean is far away enough?

To answer this question, we’ll need more tools—hypothesis tests! The hypothesis testing procedure quantifies the unusualness of our sample with a probability and then compares it to an evidentiary standard. This process allows you to make an objective decision about the strength of the evidence.

We’re going to add the tools we need to make this decision to the graph—significance levels and p-values!

These tools allow us to test these two hypotheses:

Null hypothesis: The population mean equals the null hypothesis mean (260).
Alternative hypothesis: The population mean does not equal the null hypothesis mean (260).

Related post : Hypothesis Testing Overview

What are Significance Levels (Alpha)?

A significance level, also known as alpha or α, is an evidentiary standard that a researcher sets before the study. It defines how strongly the sample evidence must contradict the null hypothesis before you can reject the null hypothesis for the entire population. The strength of the evidence is defined by the probability of rejecting a null hypothesis that is true. In other words, it is the probability that you say there is an effect when there is no effect.

For instance, a significance level of 0.05 signifies a 5% risk of deciding that an effect exists when it does not exist.

Lower significance levels require stronger sample evidence to be able to reject the null hypothesis. For example, to be statistically significant at the 0.01 significance level requires more substantial evidence than the 0.05 significance level. However, there is a tradeoff in hypothesis tests. Lower significance levels also reduce the power of a hypothesis test to detect a difference that does exist.

The technical nature of these types of questions can make your head spin. A picture can bring these ideas to life!

To learn a more conceptual approach to significance levels, see my post about Understanding Significance Levels .

Graphing Significance Levels as Critical Regions

On the probability distribution plot, the significance level defines how far the sample value must be from the null value before we can reject the null. The percentage of the area under the curve that is shaded equals the probability that the sample value will fall in those regions if the null hypothesis is correct.

To represent a significance level of 0.05, I’ll shade 5% of the distribution furthest from the null value.

Graph that displays a two-tailed critical region for a significance level of 0.05.

The two shaded regions in the graph are equidistant from the central value of the null hypothesis. Each region has a probability of 0.025, which sums to our desired total of 0.05. These shaded areas are called the critical region for a two-tailed hypothesis test.

The critical region defines sample values that are improbable enough to warrant rejecting the null hypothesis. If the null hypothesis is correct and the population mean is 260, random samples (n=25) from this population have means that fall in the critical region 5% of the time.

Our sample mean is statistically significant at the 0.05 level because it falls in the critical region.

Related posts : One-Tailed and Two-Tailed Tests Explained , What Are Critical Values? , and T-distribution Table of Critical Values

Comparing Significance Levels

Let’s redo this hypothesis test using the other common significance level of 0.01 to see how it compares.

Chart that shows a two-tailed critical region for a significance level of 0.01.

This time the sum of the two shaded regions equals our new significance level of 0.01. The mean of our sample does not fall within with the critical region. Consequently, we fail to reject the null hypothesis. We have the same exact sample data, the same difference between the sample mean and the null hypothesis value, but a different test result.

What happened? By specifying a lower significance level, we set a higher bar for the sample evidence. As the graph shows, lower significance levels move the critical regions further away from the null value. Consequently, lower significance levels require more extreme sample means to be statistically significant.

You must set the significance level before conducting a study. You don’t want the temptation of choosing a level after the study that yields significant results. The only reason I compared the two significance levels was to illustrate the effects and explain the differing results.

The graphical version of the 1-sample t-test we created allows us to determine statistical significance without assessing the P value. Typically, you need to compare the P value to the significance level to make this determination.

Related post : Step-by-Step Instructions for How to Do t-Tests in Excel

What Are P values?

P values are the probability that a sample will have an effect at least as extreme as the effect observed in your sample if the null hypothesis is correct.

This tortuous, technical definition for P values can make your head spin. Let’s graph it!

First, we need to calculate the effect that is present in our sample. The effect is the distance between the sample value and null value: 330.6 – 260 = 70.6. Next, I’ll shade the regions on both sides of the distribution that are at least as far away as 70.6 from the null (260 +/- 70.6). This process graphs the probability of observing a sample mean at least as extreme as our sample mean.

Probability distribution plot shows how our sample mean has a p-value of 0.031.

The total probability of the two shaded regions is 0.03112. If the null hypothesis value (260) is true and you drew many random samples, you’d expect sample means to fall in the shaded regions about 3.1% of the time. In other words, you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true. That’s the P value!

Learn more about How to Find the P Value .

Using P values and Significance Levels Together

If your P value is less than or equal to your alpha level, reject the null hypothesis.

The P value results are consistent with our graphical representation. The P value of 0.03112 is significant at the alpha level of 0.05 but not 0.01. Again, in practice, you pick one significance level before the experiment and stick with it!

Using the significance level of 0.05, the sample effect is statistically significant. Our data support the alternative hypothesis, which states that the population mean doesn’t equal 260. We can conclude that mean fuel expenditures have increased since last year.

P values are very frequently misinterpreted as the probability of rejecting a null hypothesis that is actually true. This interpretation is wrong! To understand why, please read my post: How to Interpret P-values Correctly .

Discussion about Statistically Significant Results

Hypothesis tests determine whether your sample data provide sufficient evidence to reject the null hypothesis for the entire population. To perform this test, the procedure compares your sample statistic to the null value and determines whether it is sufficiently rare. “Sufficiently rare” is defined in a hypothesis test by:

Assuming that the null hypothesis is true—the graphs center on the null value.
The significance (alpha) level—how far out from the null value is the critical region?
The sample statistic—is it within the critical region?

There is no special significance level that correctly determines which studies have real population effects 100% of the time. The traditional significance levels of 0.05 and 0.01 are attempts to manage the tradeoff between having a low probability of rejecting a true null hypothesis and having adequate power to detect an effect if one actually exists.

The significance level is the rate at which you incorrectly reject null hypotheses that are actually true ( type I error ). For example, for all studies that use a significance level of 0.05 and the null hypothesis is correct, you can expect 5% of them to have sample statistics that fall in the critical region. When this error occurs, you aren’t aware that the null hypothesis is correct, but you’ll reject it because the p-value is less than 0.05.

This error does not indicate that the researcher made a mistake. As the graphs show, you can observe extreme sample statistics due to sample error alone. It’s the luck of the draw!

Related posts : Statistical Significance: Definition & Meaning and Types of Errors in Hypothesis Testing

Hypothesis tests are crucial when you want to use sample data to make conclusions about a population because these tests account for sample error. Using significance levels and P values to determine when to reject the null hypothesis improves the probability that you will draw the correct conclusion.

Keep in mind that statistical significance doesn’t necessarily mean that the effect is important in a practical, real-world sense. For more information, read my post about Practical vs. Statistical Significance .

If you like this post, read the companion post: How Hypothesis Tests Work: Confidence Intervals and Confidence Levels .

You can also read my other posts that describe how other tests work:

How t-Tests Work
How the F-test works in ANOVA
How Chi-Squared Tests of Independence Work

To see an alternative approach to traditional hypothesis testing that does not use probability distributions and test statistics, learn about bootstrapping in statistics !

Reader Interactions

December 11, 2022 at 10:56 am

For very easy concept about level of significance & p-value 1.Teacher has given a one assignment to student & asked how many error you have doing this assignment? Student reply, he can has error ≤ 5% (it is level of significance). After completion of assignment, teacher checked his error which is ≤ 5% (may be 4% or 3% or 2% even less, it is p-value) it means his results are significant. Otherwise he has error > 5% (may be 6% or 7% or 8% even more, it is p-value) it means his results are non-significant. 2. Teacher has given a one assignment to student & asked how many error you have doing this assignment? Student reply, he can has error ≤ 1% (it is level of significance). After completion of assignment, teacher checked his error which is ≤ 1% (may be 0.9% or 0.8% or 0.7% even less, it is p-value) it means his results are significant. Otherwise he has error > 1% (may be 1.1% or 1.5% or 2% even more, it is p-value) it means his results are non-significant. p-value is significant or not mainly dependent upon the level of significance.

December 11, 2022 at 7:50 pm

I think that approach helps explain how to determine statistical significance–is the p-value less than or equal to the significance level. However, it doesn’t really explain what statistical significance means. I find that comparing the p-value to the significance level is the easy part. Knowing what it means and how to choose your significance level is the harder part!

December 3, 2022 at 5:54 pm

What would you say to someone who believes that a p-value higher than the level of significance (alpha) means the null hypothesis has been proven? Should you support that statement or deny it?

December 3, 2022 at 10:18 pm

Hi Emmanuel,

When the p-value is greater than the significance level, you fail to reject the null hypothesis . That is different than proving it. To learn why and what it means, click the link to read a post that I’ve written that will answer your question!

April 19, 2021 at 12:27 am

Thank you so much Sir

April 18, 2021 at 2:37 pm

Hi sir, your blogs are much more helpful for clearing the concepts of statistics, as a researcher I find them much more useful. I have some quarries:

1. In many research papers I have seen authors using the statement ” means or values are statically at par at p = 0.05″ when they do some pair wise comparison between the treatments (a kind of post hoc) using some value of CD (critical difference) or we can say LSD which is calculated using alpha not using p. So with this article I think this should be alpha =0.05 or 5%, not p = 0.05 earlier I thought p and alpha are same. p it self is compared with alpha 0.05. Correct me if I am wrong.

2. When we can draw a conclusion using critical value based on critical values (CV) which is based on alpha values in different tests (e.g. in F test CV is at F (0.05, t-1, error df) when alpha is 0.05 which is table value of F and is compared with F calculated for drawing the conclusion); then why we go for p values, and draw a conclusion based on p values, even many online software do not give p value, they just mention CD (LSD)

3. can you please help me in interpreting interaction in two factor analysis (Factor A X Factor b) in Anova.

Thank You so much!

(Commenting again as I have not seen my comment in comment list; don’t know why)

April 18, 2021 at 10:57 pm

Hi Himanshu,

I manually approve comments so there will be some time lag involved before they show up.

Regarding your first question, yes, you’re correct. Test results are significant at particular significance levels or alpha. They should not use p to define the significance level. You’re also correct in that you compare p to alpha.

Critical values are a different (but related) approach for determining significance. It was more common before computer analysis took off because it reduced the calculations. Using this approach in its simplest form, you only know whether a result is significant or not at the given alpha. You just determine whether the test statistic falls within a critical region to determine statistical significance or not significant. However, it is ok to supplement this type of result with the actual p-value. Knowing the precise p-value provides additional information that significant/not significant does not provide. The critical value and p-value approaches will always agree too. For more information about why the exact p-value is useful, read my post about Five Tips for Interpreting P-values .

Finally, I’ve written about two-way ANOVA in my post, How to do Two-Way ANOVA in Excel . Additionally, I write about it in my Hypothesis Testing ebook .

January 28, 2021 at 3:12 pm

Thank you for your answer, Jim, I really appreciate it. I’m taking a Coursera stats course and online learning without being able to ask questions of a real teacher is not my forte!

You’re right, I don’t think I’m ready for that calculation! However, I think I’m struggling with something far more basic, perhaps even the interpretation of the t-table? I’m just not sure how you came up with the p-value as .03112, with the 24 degrees of freedom. When I pull up a t-table and look at the 24-degrees of freedom row, I’m not sure how any of those numbers correspond with your answer? Either the single tail of 0.01556 or the combined of 0.03112. What am I not getting? (which, frankly, could be a lot!!) Again, thank you SO much for your time.

January 28, 2021 at 11:19 pm

Ah ok, I see! First, let me point you to several posts I’ve written about t-values and the t-distribution. I don’t cover those in this post because I wanted to present a simplified version that just uses the data in its regular units. The basic idea is that the hypothesis tests actually convert all your raw data down into one value for a test statistic, such as the t-value. And then it uses that test statistic to determine whether your results are statistically significant. To be significant, the t-value must exceed a critical value, which is what you lookup in the table. Although, nowadays you’d typically let your software just tell you.

So, read the following two posts, which covers several aspects of t-values and distributions. And then if you have more questions after that, you can post them. But, you’ll have a lot more information about them and probably some of your questions will be answered! T-values T-distributions

January 27, 2021 at 3:10 pm

Jim, just found your website and really appreciate your thoughtful, thorough way of explaining things. I feel very dumb, but I’m struggling with p-values and was hoping you could help me.

Here’s the section that’s getting me confused:

“First, we need to calculate the effect that is present in our sample. The effect is the distance between the sample value and null value: 330.6 – 260 = 70.6. Next, I’ll shade the regions on both sides of the distribution that are at least as far away as 70.6 from the null (260 +/- 70.6). This process graphs the probability of observing a sample mean at least as extreme as our sample mean.

** I’m good up to this point. Draw the picture, do the subtraction, shade the regions. BUT, I’m not sure how to figure out the area of the shaded region — even with a T-table. When I look at the T-table on 24 df, I’m not sure what to do with those numbers, as none of them seem to correspond in any way to what I’m looking at in the problem. In the end, I have no idea how you calculated each shaded area being 0.01556.

I feel like there’s a (very simple) step that everyone else knows how to do, but for some reason I’m missing it.

Again, dumb question, but I’d love your help clarifying that.

thank you, Sara

January 27, 2021 at 9:51 pm

That’s not a dumb question at all. I actually don’t show or explain the calculations for figuring out the area. The reason for that is the same reason why students never calculate the critical t-values for their test, instead you look them up in tables or use statistical software. The common reason for all that is because calculating these values is extremely complicated! It’s best to let software do that for you or, when looking critical values, use the tables!

The principal though is that percentage of the area under the curve equals the probability that values will fall within that range.

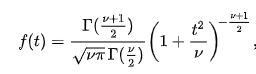
And then, for this example, you’d need to figure out the area under the curve for particular ranges!

January 15, 2021 at 10:57 am

HI Jim, I have a question related to Hypothesis test.. in Medical imaging, there are different way to measure signal intensity (from a tumor lesion for example). I tested for the same 100 patients 4 different ways to measure tumor captation to a injected dose. So for the 100 patients, i got 4 linear regression (relation between injected dose and measured quantity at tumor sites) = so an output of 4 equations Condition A output = -0,034308 + 0,0006602*input Condition B output = 0,0117631 + 0,0005425*input Condition C output = 0,0087871 + 0,0005563*input Condition D output = 0,001911 + 0,0006255*input

My question : i want to compare the 4 methods to find the best one (compared to others) : do Hypothesis test good to me… and if Yes, i do not find test to perform it. Can you suggest me a software. I uselly used JMP for my stats… but open to other softwares…

THank for your time G

November 16, 2020 at 5:42 am

Thank you very much for writing about this topic!

Your explanation made more sense to me about: Why we reject Null Hypothesis when p value < significance level

Kind greetings, Jalal

September 25, 2020 at 1:04 pm

Hi Jim, Your explanations are so helpful! Thank you. I wondered about your first graph. I see that the mean of the graph is 260 from the null hypothesis, and it looks like the standard deviation of the graph is about 31. Where did you get 31 from? Thank you

September 25, 2020 at 4:08 pm

Hi Michelle,

That is a great question. Very observant. And it gets to how these tests work. The hypothesis test that I’m illustrating here is the one-sample t-test. And this graph illustrates the sampling distribution for the t-test. T-tests use the t-distribution to determine the sampling distribution. For the t-distribution, you need to specify the degrees of freedom, which entirely defines the distribution (i.e., it’s the only parameter). For 1-sample t-tests, the degrees of freedom equal the number of observations minus 1. This dataset has 25 observations. Hence, the 24 DF you see in the graph.

Unlike the normal distribution, there is no standard deviation parameter. Instead, the degrees of freedom determines the spread of the curve. Typically, with t-tests, you’ll see results discussed in terms of t-values, both for your sample and for defining the critical regions. However, for this introductory example, I’ve converted the t-values into the raw data units (t-value * SE mean).

So, the standard deviation you’re seeing in the graph is a result of the spread of the underlying t-distribution that has 24 degrees of freedom and then applying the conversion from t-values to raw values.

September 10, 2020 at 8:19 am

Your blog is incredible.

I am having difficulty understanding why the phrase ‘as extreme as’ is required in the definition of p-value (“P values are the probability that a sample will have an effect at least as extreme as the effect observed in your sample if the null hypothesis is correct.”)

Why can’t P-Values simply be defined as “The probability of sample observation if the null hypothesis is correct?”

In your other blog titled ‘Interpreting P values’ you have explained p-values as “P-values indicate the believability of the devil’s advocate case that the null hypothesis is correct given the sample data”. I understand (or accept) this explanation. How does one move from this definition to one that contains the phrase ‘as extreme as’?

September 11, 2020 at 5:05 pm

Thanks so much for your kind words! I’m glad that my website has been helpful!

The key to understanding the “at least as extreme” wording lies in the probability plots for p-values. Using probability plots for continuous data, you can calculate probabilities, but only for ranges of values. I discuss this in my post about understanding probability distributions . In a nutshell, we need a range of values for these probabilities because the probabilities are derived from the area under a distribution curve. A single value just produces a line on these graphs rather than an area. Those ranges are the shaded regions in the probability plots. For p-values, the range corresponds to the “at least as extreme” wording. That’s where it comes from. We need a range to calculate a probability. We can’t use the single value of the observed effect because it doesn’t produce an area under the curve.

I hope that helps! I think this is a particularly confusing part of understanding p-values that most people don’t understand.

August 7, 2020 at 5:45 pm

Hi Jim, thanks for the post.

Could you please clarify the following excerpt from ‘Graphing Significance Levels as Critical Regions’:

“The percentage of the area under the curve that is shaded equals the probability that the sample value will fall in those regions if the null hypothesis is correct.”

I’m not sure if I understood this correctly. If the sample value fall in one of the shaded regions, doesn’t mean that the null hypothesis can be rejected, hence that is not correct?

August 7, 2020 at 10:23 pm

Think of it this way. There are two basic reasons for why a sample value could fall in a critical region:

The null hypothesis is correct and random chance caused the sample value to be unusual.
The null hypothesis is not correct.

You don’t know which one is true. Remember, just because you reject the null hypothesis it doesn’t mean the null is false. However, by using hypothesis tests to determine statistical significance, you control the chances of #1 occurring. The rate at which #1 occurs equals your significance level. On the hand, you don’t know the probability of the sample value falling in a critical region if the alternative hypothesis is correct (#2). It depends on the precise distribution for the alternative hypothesis and you usually don’t know that, which is why you’re testing the hypotheses in the first place!

I hope I answered the question you were asking. If not, feel free to ask follow up questions. Also, this ties into how to interpret p-values . It’s not exactly straightforward. Click the link to learn more.

June 4, 2020 at 6:17 am

Hi Jim, thank you very much for your answer. You helped me a lot!

June 3, 2020 at 5:23 pm

Hi, Thanks for this post. I’ve been learning a lot with you. My question is regarding to lack of fit. The p-value of my lack of fit is really low, making my lack of fit significant, meaning my model does not fit well. Is my case a “false negative”? given that my pure error is really low, making the computation of the lack of fit low. So it means my model is good. Below I show some information, that I hope helps to clarify my question.

SumSq DF MeanSq F pValue ________ __ ________ ______ __________

Total 1246.5 18 69.25 Model 1241.7 6 206.94 514.43 9.3841e-14 . Linear 1196.6 3 398.87 991.53 1.2318e-14 . Nonlinear 45.046 3 15.015 37.326 2.3092e-06 Residual 4.8274 12 0.40228 . Lack of fit 4.7388 7 0.67698 38.238 0.0004787 . Pure error 0.088521 5 0.017704

June 3, 2020 at 7:53 pm

As you say, a low p-value for a lack of fit test indicates that the model doesn’t fit your data adequately. This is a positive result for the test, which means it can’t be a “false negative.” At best, it could be a false positive, meaning that your data actually fit model well despite the low p-value.

I’d recommend graphing the residuals and looking for patterns . There is probably a relationship between variables that you’re not modeling correctly, such as curvature or interaction effects. There’s no way to diagnose the specific nature of the lack-of-fit problem by using the statistical output. You’ll need the graphs.

If there are no patterns in the residual plots, then your lack-of-fit results might be a false positive.

I hope this helps!

May 30, 2020 at 6:23 am

First of all, I have to say there are not many resources that explain a complicated topic in an easier manner.

My question is, how do we arrive at “if p value is less than alpha, we reject the null hypothesis.”

Is this covered in a separate article I could read?

Thanks Shekhar

May 25, 2020 at 12:21 pm

Hi Jim, terrific website, blog, and after this I’m ordering your book. One of my biggest challenges is nomenclature, definitions, context, and formulating the hypotheses. Here’s one I want to double-be-sure I understand: From above you write: ” These tools allow us to test these two hypotheses:

Null hypothesis: The population mean equals the null hypothesis mean (260). Alternative hypothesis: The population mean does not equal the null hypothesis mean (260). ” I keep thinking that 260 is the population mean mu, the underlying population (that we never really know exactly) and that the Null Hypothesis is comparing mu to x-bar (the sample mean of the 25 families randomly sampled w mean = sample mean = x-bar = 330.6).

So is the following incorrect, and if so, why? Null hypothesis: The population mean mu=260 equals the null hypothesis mean x-bar (330.6). Alternative hypothesis: The population mean mu=269 does not equal the null hypothesis mean x-bar (330.6).

And my thinking is that usually the formulation of null and alternative hypotheses is “test value” = “mu current of underlying population”, whereas I read the formulation on the webpage above to be the reverse.

Any comments appreciated. Many Thanks,

May 26, 2020 at 8:56 pm

The null hypothesis states that population value equals the null value. Now, I know that’s not particularly helpful! But, the null value varies based on test and context. So, in this example, we’re setting the null value aa $260, which was the mean from the previous year. So, our null hypothesis states:

Null: the population mean (mu) = 260. Alternative: the population mean ≠ 260.

These hypothesis statements are about the population parameter. For this type of one-sample analysis, the target or reference value you specify is the null hypothesis value. Additionally, you don’t include the sample estimate in these statements, which is the X-bar portion you tacked on at the end. It’s strictly about the value of the population parameter you’re testing. You don’t know the value of the underlying distribution. However, given the mutually exclusive nature of the null and alternative hypothesis, you know one or the other is correct. The null states that mu equals 260 while the alternative states that it doesn’t equal 260. The data help you decide, which brings us to . . .

However, the procedure does compare our sample data to the null hypothesis value, which is how it determines how strong our evidence is against the null hypothesis.

I hope I answered your question. If not, please let me know!

May 8, 2020 at 6:00 pm

Really using the interpretation “In other words, you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true”, our head seems to tie a knot. However, doing the reverse interpretation, it is much more intuitive and easier. That is, we will observe the sample effect of at least 70.6 in about 96.9% of the time, if the null is false (that is, our hypothesis is true).

May 8, 2020 at 7:25 pm

Your phrasing really isn’t any simpler. And it has the additional misfortune of being incorrect.

What you’re essentially doing is creating a one-sided confidence interval by using the p-value from a two-sided test. That’s incorrect in two ways.

Don’t mix and match one-sided and two-sided test results.
Confidence levels are determine by the significance level, not p-values.

So, what you need is a two-sided 95% CI (1-alpha). You could then state the results are statistically significant and you have 95% confidence that the population effect is between X and Y. If you want a lower bound as you propose, then you’ll need to use a one-sided hypothesis test with a 95% Lower Bound. That’ll give you a different value for the lower bound than the one you use.

I like confidence intervals. As I write elsewhere, I think they’re easier to understand and provide more information than a binary test result. But, you need to use them correctly!

One other point. When you are talking about p-values, it’s always under the assumption that the null hypothesis is correct. You *never* state anything about the p-value in relation to the null being false (i.e. alternative is true). But, if you want to use the type of phrasing you suggest, use it in the context of CIs and incorporate the points I cover above.

February 10, 2020 at 11:13 am

Muchas gracias profesor por compartir sus conocimientos. Un saliud especial desde Colombia.

August 6, 2019 at 11:46 pm

i found this really helpful . also can you help me out ?

I’m a little confused Can you tell me if level of significance and pvalue are comparable or not and if they are what does it mean if pvalue < LS . Do we reject the null hypothesis or do we accept the null hypothesis ?

August 7, 2019 at 12:49 am

Hi Divyanshu,

Yes, you compare the p-value to the significance level. When the p-value is less than the significance level (alpha), your results are statistically significant and you reject the null hypothesis.

I’d suggest re-reading the “Using P values and Significance Levels Together” section near the end of this post more closely. That describes the process. The next section describes what it all means.

July 1, 2019 at 4:19 am

sure.. I will use only in my class rooms that too offline with due credits to your orginal page. I will encourage my students to visit your blog . I have purchased your eBook on Regressions….immensely useful.

July 1, 2019 at 9:52 am

Hi Narasimha, that sounds perfect. Thanks for buying my ebook as well. I’m thrilled to hear that you’ve found it to be helpful!

June 28, 2019 at 6:22 am

I have benefited a lot by your writings….Can I share the same with my students in the classroom?

June 30, 2019 at 8:44 pm

Hi Narasimha,

Yes, you can certainly share with your students. Please attribute my original page. And please don’t copy whole sections of my posts onto another webpage as that can be bad with Google! Thanks!

February 11, 2019 at 7:46 pm

Hello, great site and my apologies if the answer to the following question exists already.

I’ve always wondered why we put the sampling distribution about the null hypothesis rather than simply leave it about the observed mean. I can see mathematically we are measuring the same distance from the null and basically can draw the same conclusions.

For example we take a sample (say 50 people) we gather an observation (mean wage) estimate the standard error in that observation and so can build a sampling distribution about the observed mean. That sampling distribution contains a confidence interval, where say, i am 95% confident the true mean lies (i.e. in repeated sampling the true mean would reside within this interval 95% of the time).

When i use this for a hyp-test, am i right in saying that we place the sampling dist over the reference level simply because it’s mathematically equivalent and it just seems easier to gauge how far the observation is from 0 via t-stats or its likelihood via p-values?

It seems more natural to me to look at it the other way around. leave the sampling distribution on the observed value, and then look where the null sits…if it’s too far left or right then it is unlikely the true population parameter is what we believed it to be, because if the null were true it would only occur ~ 5% of the time in repeated samples…so perhaps we need to change our opinion.

Can i interpret a hyp-test that way? Or do i have a misconception?

February 12, 2019 at 8:25 pm

The short answer is that, yes, you can draw the interval around the sample mean instead. And, that is, in fact, how you construct confidence intervals. The distance around the null hypothesis for hypothesis tests and the distance around the sample for confidence intervals are the same distance, which is why the results will always agree as long as you use corresponding alpha levels and confidence levels (e.g., alpha 0.05 with a 95% confidence level). I write about how this works in a post about confidence intervals .

I prefer confidence intervals for a number of reasons. They’ll indicate whether you have significant results if they exclude the null value and they indicate the precision of the effect size estimate. Corresponding with what you’re saying, it’s easier to gauge how far a confidence interval is from the null value (often zero) whereas a p-value doesn’t provide that information. See Practical versus Statistical Significance .

So, you don’t have any misconception at all! Just refer to it as a confidence interval rather than a hypothesis test, but, of course, they are very closely related.

January 9, 2019 at 10:37 pm

Hi Jim, Nice Article.. I have a question… I read the Central limit theorem article before this article…

Coming to this article, During almost every hypothesis test, we draw a normal distribution curve assuming there is a sampling distribution (and then we go for test statistic, p value etc…). Do we draw a normal distribution curve for hypo tests because of the central limit theorem…

Thanks in advance, Surya

January 10, 2019 at 1:57 am

These distributions are actually the t-distribution which are different from the normal distribution. T-distributions only have one parameter–the degrees of freedom. As the DF of increases, the t-distribution tightens up. Around 25 degrees of freedom, the t-distribution approximates the normal distribution. Depending on the type of t-test, this corresponds to a sample size of 26 or 27. Similarly, the sampling distribution of the means also approximate the normal distribution at around these sample sizes. With a large enough sample size, both the t-distribution and the sample distribution converge to a normal distribution regardless (largely) of the underlying population distribution. So, yes, the central limit theorem plays a strong role in this.

It’s more accurate to say that central limit theorem causes the sampling distribution of the means to converge on the same distribution that the t-test uses, which allows you to assume that the test produces valid results. But, technically, the t-test is based on the t-distribution.

Problems can occur if the underlying distribution is non-normal and you have a small sample size. In that case, the sampling distribution of the means won’t approximate the t-distribution that the t-test uses. However, the test results will assume that it does and produce results based on that–which is why it causes problems!

November 19, 2018 at 9:15 am

Dear Jim! Thank you very much for your explanation. I need your help to understand my data. I have two samples (about 300 observations) with biased distributions. I did the ttest and obtained the p-value, which is quite small. Can I draw the conclusion that the effect size is small even when the distribution of my data is not normal? Thank you

November 19, 2018 at 9:34 am

Hi Tetyana,

First, when you say that your p-value is small and that you want to “draw the conclusion that the effect size is small,” I assume that you mean statistically significant. When the p-value is low, the null hypothesis must go! In other words, you reject the null and conclude that there is a statistically significant effect–not a small effect.

Now, back to the question at hand! Yes, When you have a sufficiently large sample-size, t-tests are robust to departures from normality. For a 2-sample t-test, you should have at least 15 samples per group, which you exceed by quite a bit. So, yes, you can reliably conclude that your results are statistically significant!

You can thank the central limit theorem! 🙂

September 10, 2018 at 12:18 am

Hello Jim, I am very sorry; I have very elementary of knowledge of stats. So, would you please explain how you got a p- value of 0.03112 in the above calculation/t-test? By looking at a chart? Would you also explain how you got the information that “you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true”?

July 6, 2018 at 7:02 am

A quick question regarding your use of two-tailed critical regions in the article above: why? I mean, what is a real-world scenario that would warrant a two-tailed test of any kind (z, t, etc.)? And if there are none, why keep using the two-tailed scenario as an example, instead of the one-tailed which is both more intuitive and applicable to most if not all practical situations. Just curious, as one person attempting to educate people on stats to another (my take on the one vs. two-tailed tests can be seen here: http://blog.analytics-toolkit.com/2017/one-tailed-two-tailed-tests-significance-ab-testing/ )

Thanks, Georgi

July 6, 2018 at 12:05 pm

There’s the appropriate time and place for both one-tailed and two-tailed tests. I plan to write a post on this issue specifically, so I’ll keep my comments here brief.

So much of statistics is context sensitive. People often want concrete rules for how to do things in statistics but that’s often hard to provide because the answer depends on the context, goals, etc. The question of whether to use a one-tailed or two-tailed test falls firmly in this category of it depends.

I did read the article you wrote. I’ll say that I can see how in the context of A/B testing specifically there might be a propensity to use one-tailed tests. You only care about improvements. There’s probably not too much downside in only caring about one direction. In fact, in a post where I compare different tests and different options , I suggest using a one-tailed test for a similar type of casing involving defects. So, I’m onboard with the idea of using one-tailed tests when they’re appropriate. However, I do think that two-tailed tests should be considered the default choice and that you need good reasons to move to a one-tailed test. Again, your A/B testing area might supply those reasons on a regular basis, but I can’t make that a blanket statement for all research areas.

I think your article mischaracterizes some of the pros and cons of both types of tests. Just a couple of for instances. In a two-tailed test, you don’t have to take the same action regardless of which direction the results are significant (example below). And, yes, you can determine the direction of the effect in a two-tailed test. You simply look at the estimated effect. Is it positive or negative?

On the other hand, I do agree that one-tailed tests don’t increase the overall Type I error. However, there is a big caveat for that. In a two-tailed test, the Type I error rate is evenly split in both tails. For a one-tailed test, the overall Type I error rate does not change, but the Type I errors are redistributed so they all occur in the direction that you are interested in rather than being split between the positive and negative directions. In other words, you’ll have twice as many Type I errors in the specific direction that you’re interested in. That’s not good.

My big concerns with one-tailed tests are that it makes it easier to obtain the results that you want to obtain. And, all of the Type I errors (false positives) are in that direction too. It’s just not a good combination.

To answer your question about when you might want to use two-tailed tests, there are plenty of reasons. For one, you might want to avoid the situation I describe above. Additionally, in a lot of scientific research, the researchers truly are interested in detecting effects in either direction for the sake of science. Even in cases with a practical application, you might want to learn about effects in either direction.

For example, I was involved in a research study that looked at the effects of an exercise intervention on bone density. The idea was that it might be a good way to prevent osteoporosis. I used a two-tailed test. Obviously, we’re hoping that there was positive effect. However, we’d be very interested in knowing whether there was a negative effect too. And, this illustrates how you can have different actions based on both directions. If there was a positive effect, you can recommend that as a good approach and try to promote its use. If there’s a negative effect, you’d issue a warning to not do that intervention. You have the potential for learning both what is good and what is bad. The extra false-positives would’ve cause problems because we’d think that there’d be health benefits for participants when those benefits don’t actually exist. Also, if we had performed only a one-tailed test and didn’t obtain significant results, we’d learn that it wasn’t a positive effect, but we would not know whether it was actually detrimental or not.

Here’s when I’d say it’s OK to use a one-tailed test. Consider a one-tailed test when you’re in situation where you truly only need to know whether an effect exists in one direction, and the extra Type I errors in that direction are an acceptable risk (false positives don’t cause problems), and there’s no benefit in determining whether an effect exists in the other direction. Those conditions really restrict when one-tailed tests are the best choice. Again, those restrictions might not be relevant for your specific field, but as for the usage of statistics as a whole, they’re absolutely crucial to consider.

On the other hand, according to this article, two-tailed tests might be important in A/B testing !

March 30, 2018 at 5:29 am

Dear Sir, please confirm if there is an inadvertent mistake in interpretation as, “We can conclude that mean fuel expenditures have increased since last year.” Our null hypothesis is =260. If found significant, it implies two possibilities – both increase and decrease. Please let us know if we are mistaken here. Many Thanks!

March 30, 2018 at 9:59 am

Hi Khalid, the null hypothesis as it is defined for this test represents the mean monthly expenditure for the previous year (260). The mean expenditure for the current year is 330.6 whereas it was 260 for the previous year. Consequently, the mean has increased from 260 to 330.7 over the course of a year. The p-value indicates that this increase is statistically significant. This finding does not suggest both an increase and a decrease–just an increase. Keep in mind that a significant result prompts us to reject the null hypothesis. So, we reject the null that the mean equals 260.

Let’s explore the other possible findings to be sure that this makes sense. Suppose the sample mean had been closer to 260 and the p-value was greater than the significance level, those results would indicate that the results were not statistically significant. The conclusion that we’d draw is that we have insufficient evidence to conclude that mean fuel expenditures have changed since the previous year.

If the sample mean was less than the null hypothesis (260) and if the p-value is statistically significant, we’d concluded that mean fuel expenditures have decreased and that this decrease is statistically significant.

When you interpret the results, you have to be sure to understand what the null hypothesis represents. In this case, it represents the mean monthly expenditure for the previous year and we’re comparing this year’s mean to it–hence our sample suggests an increase.

Comments and Questions Cancel reply

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.

There are 5 main steps in hypothesis testing:

State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
Collect data in a way designed to test the hypothesis.
Perform an appropriate statistical test .
Decide whether to reject or fail to reject your null hypothesis.
Present the findings in your results and discussion section.

Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.

Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.

After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.

The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.

H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

Academic style
Vague sentences
Style consistency

See an example

For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.

There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).

If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.

Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.

Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .

an estimate of the difference in average height between the two groups.
a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.

Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.

In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.

In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .

In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.

In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.

However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.

If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”

These are superficial differences; you can see that they mean the same thing.

You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.

If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved September 2, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/

Is this article helpful?

Rebecca Bevans

Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

What is P-Value? – Understanding the meaning, math and methods

October 12, 2019
Selva Prabhakaran

P Value is a probability score that is used in statistical tests to establish the statistical significance of an observed effect. Though p-values are commonly used, the definition and meaning is often not very clear even to experienced Statisticians and Data Scientists. In this post I will attempt to explain the intuition behind p-value as clear as possible.

Introduction

In Data Science interviews, one of the frequently asked questions is ‘What is P-Value?”.

Believe it or not, even experienced Data Scientists often fail to answer this question. This is partly because of the way statistics is taught and the definitions available in textbooks and online sources.

According to American Statistical Association, “a p-value is the probability under a specified statistical model that a statistical summary of the data (e.g., the sample mean difference between two compared groups) would be equal to or more extreme than its observed value.”

That’s hard to grasp, yes?

Alright, lets understand what really is p value in small meaningful pieces so ultimately it all makes sense.

When and how is p-value used?

To understand p-value, you need to understand some background and context behind it. So, let’s start with the basics.

p-values are often reported whenever you perform a statistical significance test (like t-test, chi-square test etc). These tests typically return a computed test statistic and the associated p-value. This reported value is used to establish the statistical significance of the relationships being tested.

So, whenever you see a p-value, there is an associated statistical test.

That means, there is a Hypothesis testing being conducted with a defined Null Hypothesis (H0) and a corresponding Alternate hypothesis (HA).

The p-value reported is used to make a decision on whether the null hypothesis being tested can be rejected or not.

Let’s understand a little bit more about the null and alternate hypothesis.

Now, how to frame a Null hypothesis in general?

While the null hypothesis itself changes with every statistical test, there is a general principle to frame it:

The null hypothesis assumes there is ‘no effect’ or ‘relationship’ by default .

For example: if you are testing if a drug treatment is effective or not, then the null hypothesis will assume there is not difference in outcome between the treated and untreated groups. Likewise, if you are testing if one variable influences another (say, car weight influences the mileage), then null hypothesis will postulate there is no relationship between the two.

It simply implies the absence of an effect.

Examples of Statistical Tests reporting out p-value

Here are some examples of Null hypothesis (H0) for popular statistical tests:

Welch Two Sample t-Test: The true difference in means of two samples is equal to 0
Linear Regression: The beta coefficient(slope) of the X variable is zero
Chi Square test: There is no difference between expected frequencies and observed frequencies.

Get the feel?

But how would the alternate hypothesis would look like?

The alternate hypothesis (HA) is always framed to negate the null hypothesis. The corresponding HA for above tests are as follows:

Welch Two Sample t-Test: The true difference in means of two samples is NOT equal to 0
Linear Regression: The beta coefficient(slope) of the X variable is NOT zero
Chi Square test: The difference between expected frequencies and observed frequencies is NOT zero.

What p-value really is

Now, back to the discussion on p-value.

Along with every statistical test, you will get a corresponding p-value in the results output.

What is this meant for?

It is used to determine if the data is statistically incompatible with the null hypothesis.

Not clear eh?

Let me put it in another way.

The P Value basically helps to answer the question: ‘Does the data really represent the observed effect?’.

This leads us to a more mathematical definition of P-Value.

The P Value is the probability of seeing the effect(E) when the null hypothesis is true .

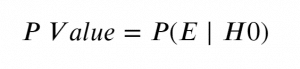
If you think about it, we want this probability to be very low.

Having said that, it is important to remember that p-value refers to not only what we observed but also observations more extreme than what was observed. That is why the formal definition of p-value contain the statement ‘would be equal to or more extreme than its observed value.’

How is p-value used to establish statistical significance

Now that you know, p value measures the probability of seeing the effect when the null hypothesis is true.

A sufficiently low value is required to reject the null hypothesis.

Notice how I have used the term ‘Reject the Null Hypothesis’ instead of stating the ‘Alternate Hypothesis is True’.

That’s because, we have tested the effect against the null hypothesis only.

So, when the p-value is low enough, we reject the null hypothesis and conclude the observed effect holds.

But how low is ‘low enough’ for rejecting the null hypothesis?

This level of ‘low enough’ cutoff is called the alpha level, and you need to decide it before conducting a statistical test.

But how low is ‘low enough’?

Practical Guidelines to set the cutoff of Statistical Significance (alpha level)

Let’s first understand what is Alpha level.

It is the cutoff probability for p-value to establish statistical significance for a given hypothesis test. For an observed effect to be considered as statistically significant, the p-value of the test should be lower than the pre-decided alpha value.

Typically for most statistical tests(but not always), alpha is set as 0.05.

In which case, it has to be less than 0.05 to be considered as statistically significant.

What happens if it is say, 0.051?

It is still considered as not significant. We do NOT call it as a weak statistical significant. It is either black or white. There is no gray with respect to statistical significance.

Now, how to set the alpha level?

Well, the usual practice is to set it to 0.05.

But when the occurrence of the event is rare, you may want to set a very low alpha. The rarer it is, the lower the alpha.

For example in the CERN’s Hadron collider experiment to detect Higgs-Boson particles(which was very rare), the alpha level was set so low to 5 Sigma levels , which means a p value of less than 3 * 10^-7 is required reject the null hypothesis.

Whereas for a more likely event, it can go up to 0.1.

Secondly, more the samples (number of observations) you have the lower should be the alpha level. Because, even a small effect can be made to produce a lower p-value just by increasing the number of observations. The opposite is also true, that is, a large effect can be made to produce high p value by reducing the sample size.

In case you don’t know how likely the event can occur, its a common practice to set it as 0.05. But, as a thumb rule, never set the alpha greater than 0.1.

Having said that the alpha=0.05 is mostly an arbitrary choice. Then why do most people still use p=0.05? That’s because thats what is taught in college courses and being traditionally used by the scientific community and publishers.

What P Value is Not

Given the uncertainty around the meaning of p-value, it is very common to misinterpret and use it incorrectly.

Some of the common misconceptions are as follows:

P-Value is the probability of making a mistake. Wrong!
P-Value measures the importance of a variable. Wrong!
P-Value measures the strength of an effect. Wrong!

A smaller p-value does not signify the variable is more important or even a stronger effect.

Because, like I mentioned earlier, any effect no matter how small can be made to produce smaller p-value only by increasing the number of observations (sample size).

Likewise, a larger value does not imply a variable is not important.

For a sound communication, it is necessary to report not just the p-value but also the sample size along with it. This is especially necessary if the experiments involve different sample sizes.

Secondly, making inferences and business decisions should not be based only on the p-value being lower than the alpha level.

Analysts should understand the business sense, understand the larger picture and bring out the reasoning before making an inference and not just rely on the p-value to make the inference for you.

Does this mean the p-value is not useful anymore?

Not really. It is a useful tool because it provides an objective standard for everyone to assess. Its just that you need to use it the right way.

Example: How to find p-value for linear regression

Linear regression is a traditional statistical modeling algorithm that is used to predict a continuous variable (a.k.a dependent variable) using one or more explanatory variables.

Let’s see an example of extracting the p-value with linear regression using the mtcars dataset. In this dataset the specifications of the vehicle and the mileage performance is recorded.

We want to use linear regression to test if one of the specs “the ‘weight’ ( wt ) of the vehicle” has a significant relationship (linear) with the ‘mileage’ ( mpg ).

This can be conveniently done using python’s statsmodels library. But first, let’s load the data.

With statsmodels library

	mpg	wt
0	4.582576	2.620
1	4.582576	2.875
2	4.774935	2.320
3	4.626013	3.215
4	4.324350	3.440

The X( wt ) and Y ( mpg ) variables are ready.

Null Hypothesis (H0): The slope of the line of best fit (a.k.a beta coefficient) is zero Alternate Hypothesis (H1): The beta coefficient is not zero.

To implement the test, use the smf.ols() function available in the formula.api of statsmodels . You can pass in the formula itself as the first argument and call fit() to train the linear model.

Once model is trained, call model.summary() to get a comprehensive view of the statistics.

The p-value is located in under the P>|t| against wt row. If you want to extract that value into a variable, use model.pvalues .

Since the p-value is much lower than the significance level (0.01), we reject the null hypothesis that the slope is zero and take that the data really represents the effect.

Well, that was just one example of computing p-value.

Whereas p-value can be associated with numerous statistical tests. If you are interested in finding out more about how it is used, see more examples of statistical tests with p-values.

In this post we covered what exactly is a p-value and how and how not to use it. We also saw a python example related to computing the p-value associated with linear regression.

Now with this understanding, let’s conclude what is the difference between Statistical Model from Machine Learning model?

Well, while both statistical as well as machine learning models are associated with making predictions, there can be many differences between these two. But most simply put, any predictive model that has p-values associated with it are considered as statistical model.

Happy learning!

To understand how exactly the P-value is computed, check out the example using the T-Test .

F statistic formula – explained, correlation – connecting the dots, the role of correlation in data analysis, hypothesis testing – a deep dive into hypothesis testing, the backbone of statistical inference, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

Search Search Please fill out this field.

What Is P-Value?

Understanding p-value.

P-Value in Hypothesis Testing

The Bottom Line

Corporate Finance
Financial Analysis

P-Value: What It Is, How to Calculate It, and Why It Matters

Yarilet Perez is an experienced multimedia journalist and fact-checker with a Master of Science in Journalism. She has worked in multiple cities covering breaking news, politics, education, and more. Her expertise is in personal finance and investing, and real estate.

In statistics, a p-value is defined as In statistics, a p-value indicates the likelihood of obtaining a value equal to or greater than the observed result if the null hypothesis is true.

The p-value serves as an alternative to rejection points to provide the smallest level of significance at which the null hypothesis would be rejected. A smaller p-value means stronger evidence in favor of the alternative hypothesis.

P-value is often used to promote credibility for studies or reports by government agencies. For example, the U.S. Census Bureau stipulates that any analysis with a p-value greater than 0.10 must be accompanied by a statement that the difference is not statistically different from zero. The Census Bureau also has standards in place stipulating which p-values are acceptable for various publications.

Key Takeaways

A p-value is a statistical measurement used to validate a hypothesis against observed data.
A p-value measures the probability of obtaining the observed results, assuming that the null hypothesis is true.
The lower the p-value, the greater the statistical significance of the observed difference.
A p-value of 0.05 or lower is generally considered statistically significant.
P-value can serve as an alternative to—or in addition to—preselected confidence levels for hypothesis testing.

Jessica Olah / Investopedia

P-values are usually calculated using statistical software or p-value tables based on the assumed or known probability distribution of the specific statistic tested. While the sample size influences the reliability of the observed data, the p-value approach to hypothesis testing specifically involves calculating the p-value based on the deviation between the observed value and a chosen reference value, given the probability distribution of the statistic. A greater difference between the two values corresponds to a lower p-value.

Mathematically, the p-value is calculated using integral calculus from the area under the probability distribution curve for all values of statistics that are at least as far from the reference value as the observed value is, relative to the total area under the probability distribution curve. Standard deviations, which quantify the dispersion of data points from the mean, are instrumental in this calculation.

The calculation for a p-value varies based on the type of test performed. The three test types describe the location on the probability distribution curve: lower-tailed test, upper-tailed test, or two-tailed test . In each case, the degrees of freedom play a crucial role in determining the shape of the distribution and thus, the calculation of the p-value.

In a nutshell, the greater the difference between two observed values, the less likely it is that the difference is due to simple random chance, and this is reflected by a lower p-value.

The P-Value Approach to Hypothesis Testing

The p-value approach to hypothesis testing uses the calculated probability to determine whether there is evidence to reject the null hypothesis. This determination relies heavily on the test statistic, which summarizes the information from the sample relevant to the hypothesis being tested. The null hypothesis, also known as the conjecture, is the initial claim about a population (or data-generating process). The alternative hypothesis states whether the population parameter differs from the value of the population parameter stated in the conjecture.

In practice, the significance level is stated in advance to determine how small the p-value must be to reject the null hypothesis. Because different researchers use different levels of significance when examining a question, a reader may sometimes have difficulty comparing results from two different tests. P-values provide a solution to this problem.

Even a low p-value is not necessarily proof of statistical significance, since there is still a possibility that the observed data are the result of chance. Only repeated experiments or studies can confirm if a relationship is statistically significant.

For example, suppose a study comparing returns from two particular assets was undertaken by different researchers who used the same data but different significance levels. The researchers might come to opposite conclusions regarding whether the assets differ.

If one researcher used a confidence level of 90% and the other required a confidence level of 95% to reject the null hypothesis, and if the p-value of the observed difference between the two returns was 0.08 (corresponding to a confidence level of 92%), then the first researcher would find that the two assets have a difference that is statistically significant , while the second would find no statistically significant difference between the returns.

To avoid this problem, the researchers could report the p-value of the hypothesis test and allow readers to interpret the statistical significance themselves. This is called a p-value approach to hypothesis testing. Independent observers could note the p-value and decide for themselves whether that represents a statistically significant difference or not.

Example of P-Value

An investor claims that their investment portfolio’s performance is equivalent to that of the Standard & Poor’s (S&P) 500 Index . To determine this, the investor conducts a two-tailed test.

The null hypothesis states that the portfolio’s returns are equivalent to the S&P 500’s returns over a specified period, while the alternative hypothesis states that the portfolio’s returns and the S&P 500’s returns are not equivalent—if the investor conducted a one-tailed test , the alternative hypothesis would state that the portfolio’s returns are either less than or greater than the S&P 500’s returns.

The p-value hypothesis test does not necessarily make use of a preselected confidence level at which the investor should reset the null hypothesis that the returns are equivalent. Instead, it provides a measure of how much evidence there is to reject the null hypothesis. The smaller the p-value, the greater the evidence against the null hypothesis.

Thus, if the investor finds that the p-value is 0.001, there is strong evidence against the null hypothesis, and the investor can confidently conclude that the portfolio’s returns and the S&P 500’s returns are not equivalent.

Although this does not provide an exact threshold as to when the investor should accept or reject the null hypothesis, it does have another very practical advantage. P-value hypothesis testing offers a direct way to compare the relative confidence that the investor can have when choosing among multiple different types of investments or portfolios relative to a benchmark such as the S&P 500.

For example, for two portfolios, A and B, whose performance differs from the S&P 500 with p-values of 0.10 and 0.01, respectively, the investor can be much more confident that portfolio B, with a lower p-value, will actually show consistently different results.

Is a 0.05 P-Value Significant?

A p-value less than 0.05 is typically considered to be statistically significant, in which case the null hypothesis should be rejected. A p-value greater than 0.05 means that deviation from the null hypothesis is not statistically significant, and the null hypothesis is not rejected.

What Does a P-Value of 0.001 Mean?

A p-value of 0.001 indicates that if the null hypothesis tested were indeed true, then there would be a one-in-1,000 chance of observing results at least as extreme. This leads the observer to reject the null hypothesis because either a highly rare data result has been observed or the null hypothesis is incorrect.

How Can You Use P-Value to Compare 2 Different Results of a Hypothesis Test?

If you have two different results, one with a p-value of 0.04 and one with a p-value of 0.06, the result with a p-value of 0.04 will be considered more statistically significant than the p-value of 0.06. Beyond this simplified example, you could compare a 0.04 p-value to a 0.001 p-value. Both are statistically significant, but the 0.001 example provides an even stronger case against the null hypothesis than the 0.04.

The p-value is used to measure the significance of observational data. When researchers identify an apparent relationship between two variables, there is always a possibility that this correlation might be a coincidence. A p-value calculation helps determine if the observed relationship could arise as a result of chance.

U.S. Census Bureau. “ Statistical Quality Standard E1: Analyzing Data .”

Terms of Service
Editorial Policy
Privacy Policy

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

6 Week 5 Introduction to Hypothesis Testing Reading

An introduction to hypothesis testing.

What are you interested in learning about? Perhaps you’d like to know if there is a difference in average final grade between two different versions of a college class? Does the Fort Lewis women’s soccer team score more goals than the national Division II women’s average? Which outdoor sport do Fort Lewis students prefer the most? Do the pine trees on campus differ in mean height from the aspen trees? For all of these questions, we can collect a sample, analyze the data, then make a statistical inference based on the analysis. This means determining whether we have enough evidence to reject our null hypothesis (what was originally assumed to be true, until we prove otherwise). The process is called hypothesis testing .

A really good Khan Academy video to introduce the hypothesis test process: Khan Academy Hypothesis Testing . As you watch, please don’t get caught up in the calculations, as we will use SPSS to do these calculations. We will also use SPSS p-values, instead of the referenced Z-table, to make statistical decisions.

The Six-Step Process

Hypothesis testing requires very specific, detailed steps. Think of it as a mathematical lab report where you have to write out your work in a particular way. There are six steps that we will follow for ALL of the hypothesis tests that we learn this semester.

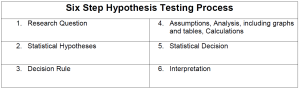
1. Research Question

All hypothesis tests start with a research question. This is literally a question that includes what you are trying to prove, like the examples earlier: Which outdoor sport do Fort Lewis students prefer the most? Is there sufficient evidence to show that the Fort Lewis women’s soccer team scores more goals than the national Division 2 women’s average?

In this step, besides literally being a question, you’ll want to include:

mention of your variable(s)
wording specific to the type of test that you’ll be conducting (mean, mean difference, relationship, pattern)
specific wording that indicates directionality (are you looking for a ‘difference’, are you looking for something to be ‘more than’ or ‘less than’ something else, or are you comparing one pattern to another?)

Consider this research question: Do the pine trees on campus differ in mean height from the aspen trees?

The wording of this research question clearly mentions the variables being studied. The independent variable is the type of tree (pine or aspen), and these trees are having their heights compared, so the dependent variable is height.
‘Mean’ is mentioned, so this indicates a test with a quantitative dependent variable.
The question also asks if the tree heights ‘differ’. This specific word indicates that the test being performed is a two-tailed (i.e. non-directional) test. More about the meaning of one/two-tailed will come later.

2. Statistical Hypotheses

A statistical hypothesis test has a null hypothesis, the status quo, what we assume to be true. Notation is H 0, read as “H naught”. The alternative hypothesis is what you are trying to prove (mentioned in your research question), H 1 or H A . All hypothesis tests must include a null and an alternative hypothesis. We also note which hypothesis test is being done in this step.

The notation for your statistical hypotheses will vary depending on the type of test that you’re doing. Writing statistical hypotheses is NOT the same as most scientific hypotheses. You are not writing sentences explaining what you think will happen in the study. Here is an example of what statistical hypotheses look like using the research question: Do the pine trees on campus differ in mean height from the aspen trees?

$LaTeX: H_0\:$

3. Decision Rule

In this step, you state which alpha value you will use, and when appropriate, the directionality, or tail, of the test. You also write a statement: “I will reject the null hypothesis if p < alpha” (insert actual alpha value here). In this introductory class, alpha is the level of significance, how willing we are to make the wrong statistical decision, and it will be set to 0.05 or 0.01.

Example of a Decision Rule:

Let alpha=0.01, two-tailed. I will reject the null hypothesis if p<0.01.

4. Assumptions, Analysis and Calculations

Quite a bit goes on in this step. Assumptions for the particular hypothesis test must be done. SPSS will be used to create appropriate graphs, and test output tables. Where appropriate, calculations of the test’s effect size will also be done in this step.

All hypothesis tests have assumptions that we hope to meet. For example, tests with a quantitative dependent variable consider a histogram(s) to check if the distribution is normal, and whether there are any obvious outliers. Each hypothesis test has different assumptions, so it is important to pay attention to the specific test’s requirements.

Required SPSS output will also depend on the test.

5. Statistical Decision

It is in Step 5 that we determine if we have enough statistical evidence to reject our null hypothesis. We will consult the SPSS p-value and compare to our chosen alpha (from Step 3: Decision Rule).

Put very simply, the p -value is the probability that, if the null hypothesis is true, the results from another randomly selected sample will be as extreme or more extreme as the results obtained from the given sample. The p -value can also be thought of as the probability that the results (from the sample) that we are seeing are solely due to chance. This concept will be discussed in much further detail in the class notes.

Based on this numerical comparison between the p-value and alpha, we’ll either reject or retain our null hypothesis. Note: You may NEVER ‘accept’ the null hypothesis. This is because it is impossible to prove a null hypothesis to be true.

Retaining the null means that you just don’t have enough evidence to prove your alternative hypothesis to be true, so you fall back to your null. (You retain the null when p is greater than or equal to alpha.)

Rejecting the null means that you did find enough evidence to prove your alternative hypothesis as true. (You reject the null when p is less than alpha.)

Example of a Statistical Decision:

Retain the null hypothesis, because p=0.12 > alpha=0.01.

The p-value will come from SPSS output, and the alpha will have already been determined back in Step 3. You must be very careful when you compare the decimal values of the p-value and alpha. If, for example, you mistakenly think that p=0.12 < alpha=0.01, then you will make the incorrect statistical decision, which will likely lead to an incorrect interpretation of the study’s findings.

6. Interpretation

The interpretation is where you write up your findings. The specifics will vary depending on the type of hypothesis test you performed, but you will always include a plain English, contextual conclusion of what your study found (i.e. what it means to reject or retain the null hypothesis in that particular study). You’ll have statistics that you quote to support your decision. Some of the statistics will need to be written in APA style citation (the American Psychological Association style of citation). For some hypothesis tests, you’ll also include an interpretation of the effect size.

Some hypothesis tests will also require an additional (non-Parametric) test after the completion of your original test, if the test’s assumptions have not been met. These tests are also call “Post-Hoc tests”.

As previously stated, hypothesis testing is a very detailed process. Do not be concerned if you have read through all of the steps above, and have many questions (and are possibly very confused). It will take time, and a lot of practice to learn and apply these steps!

This Reading is just meant as an overview of hypothesis testing. Much more information is forthcoming in the various sets of Notes about the specifics needed in each of these steps. The Hypothesis Test Checklist will be a critical resource for you to refer to during homeworks and tests.

Student Course Learning Objectives

4. Choose, administer and interpret the correct tests based on the situation, including identification of appropriate sampling and potential errors

c. Choose the appropriate hypothesis test given a situation

d. Describe the meaning and uses of alpha and p-values

e. Write the appropriate null and alternative hypotheses, including whether the alternative should be one-sided or two-sided

f. Determine and calculate the appropriate test statistic (e.g. z-test, multiple t-tests, Chi-Square, ANOVA)

g. Determine and interpret effect sizes.

h. Interpret results of a hypothesis test

Use technology in the statistical analysis of data
Communicate in writing the results of statistical analyses of data

Attributions

Adapted from “Week 5 Introduction to Hypothesis Testing Reading” by Sherri Spriggs and Sandi Dang is licensed under CC BY-NC-SA 4.0 .

Share This Book

Quality Improvement
Talk To Minitab

Understanding Hypothesis Tests: Significance Levels (Alpha) and P values in Statistics

Topics: Hypothesis Testing , Statistics

What do significance levels and P values mean in hypothesis tests? What is statistical significance anyway? In this post, I’ll continue to focus on concepts and graphs to help you gain a more intuitive understanding of how hypothesis tests work in statistics.

To bring it to life, I’ll add the significance level and P value to the graph in my previous post in order to perform a graphical version of the 1 sample t-test. It’s easier to understand when you can see what statistical significance truly means!

Here’s where we left off in my last post . We want to determine whether our sample mean (330.6) indicates that this year's average energy cost is significantly different from last year’s average energy cost of $260.

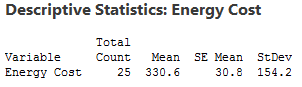
The probability distribution plot above shows the distribution of sample means we’d obtain under the assumption that the null hypothesis is true (population mean = 260) and we repeatedly drew a large number of random samples.

I left you with a question: where do we draw the line for statistical significance on the graph? Now we'll add in the significance level and the P value, which are the decision-making tools we'll need.

We'll use these tools to test the following hypotheses:

Null hypothesis: The population mean equals the hypothesized mean (260).
Alternative hypothesis: The population mean differs from the hypothesized mean (260).

What Is the Significance Level (Alpha)?

The significance level, also denoted as alpha or α, is the probability of rejecting the null hypothesis when it is true. For example, a significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference.

These types of definitions can be hard to understand because of their technical nature. A picture makes the concepts much easier to comprehend!

The significance level determines how far out from the null hypothesis value we'll draw that line on the graph. To graph a significance level of 0.05, we need to shade the 5% of the distribution that is furthest away from the null hypothesis.

Probability plot that shows the critical regions for a significance level of 0.05

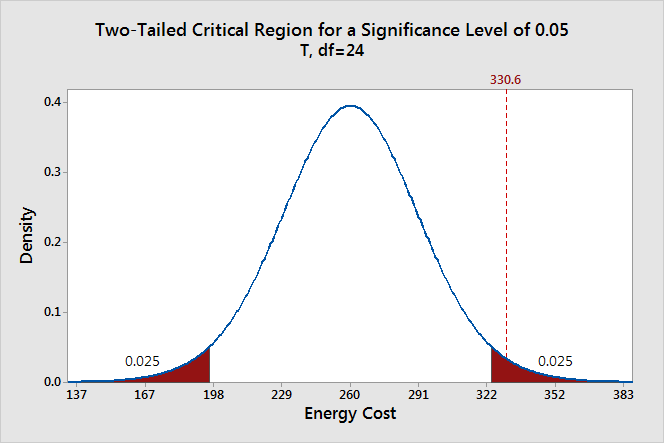
In the graph above, the two shaded areas are equidistant from the null hypothesis value and each area has a probability of 0.025, for a total of 0.05. In statistics, we call these shaded areas the critical region for a two-tailed test. If the population mean is 260, we’d expect to obtain a sample mean that falls in the critical region 5% of the time. The critical region defines how far away our sample statistic must be from the null hypothesis value before we can say it is unusual enough to reject the null hypothesis.

Our sample mean (330.6) falls within the critical region, which indicates it is statistically significant at the 0.05 level.

We can also see if it is statistically significant using the other common significance level of 0.01.

Probability plot that shows the critical regions for a significance level of 0.01

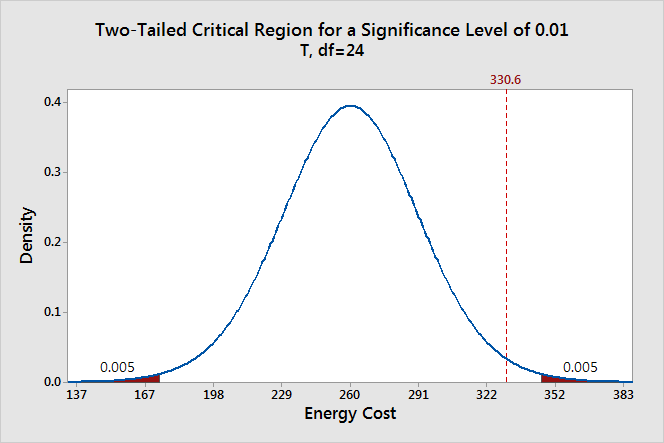
The two shaded areas each have a probability of 0.005, which adds up to a total probability of 0.01. This time our sample mean does not fall within the critical region and we fail to reject the null hypothesis. This comparison shows why you need to choose your significance level before you begin your study. It protects you from choosing a significance level because it conveniently gives you significant results!

Thanks to the graph, we were able to determine that our results are statistically significant at the 0.05 level without using a P value. However, when you use the numeric output produced by statistical software , you’ll need to compare the P value to your significance level to make this determination.

Ready for a demo of Minitab Statistical Software? Just ask!

What Are P values?

P-values are the probability of obtaining an effect at least as extreme as the one in your sample data, assuming the truth of the null hypothesis.

This definition of P values, while technically correct, is a bit convoluted. It’s easier to understand with a graph!

To graph the P value for our example data set, we need to determine the distance between the sample mean and the null hypothesis value (330.6 - 260 = 70.6). Next, we can graph the probability of obtaining a sample mean that is at least as extreme in both tails of the distribution (260 +/- 70.6).

Probability plot that shows the p-value for our sample mean

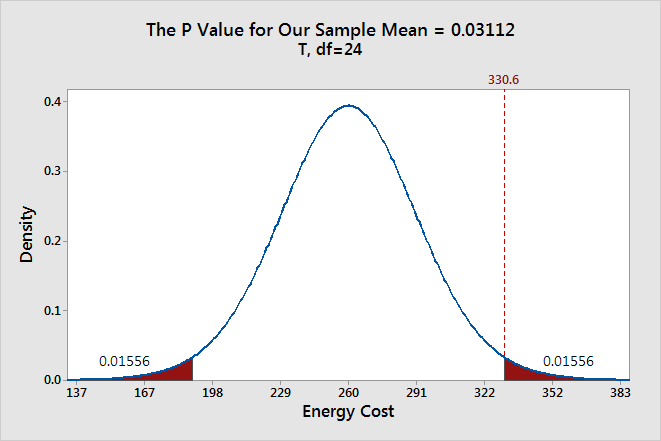
In the graph above, the two shaded areas each have a probability of 0.01556, for a total probability 0.03112. This probability represents the likelihood of obtaining a sample mean that is at least as extreme as our sample mean in both tails of the distribution if the population mean is 260. That’s our P value!

When a P value is less than or equal to the significance level, you reject the null hypothesis. If we take the P value for our example and compare it to the common significance levels, it matches the previous graphical results. The P value of 0.03112 is statistically significant at an alpha level of 0.05, but not at the 0.01 level.

If we stick to a significance level of 0.05, we can conclude that the average energy cost for the population is greater than 260.

A common mistake is to interpret the P-value as the probability that the null hypothesis is true. To understand why this interpretation is incorrect, please read my blog post How to Correctly Interpret P Values .

Discussion about Statistically Significant Results

A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data. A test result is statistically significant when the sample statistic is unusual enough relative to the null hypothesis that we can reject the null hypothesis for the entire population. “Unusual enough” in a hypothesis test is defined by:

The assumption that the null hypothesis is true—the graphs are centered on the null hypothesis value.
The significance level—how far out do we draw the line for the critical region?
Our sample statistic—does it fall in the critical region?

Keep in mind that there is no magic significance level that distinguishes between the studies that have a true effect and those that don’t with 100% accuracy. The common alpha values of 0.05 and 0.01 are simply based on tradition. For a significance level of 0.05, expect to obtain sample means in the critical region 5% of the time when the null hypothesis is true . In these cases, you won’t know that the null hypothesis is true but you’ll reject it because the sample mean falls in the critical region. That’s why the significance level is also referred to as an error rate!

This type of error doesn’t imply that the experimenter did anything wrong or require any other unusual explanation. The graphs show that when the null hypothesis is true, it is possible to obtain these unusual sample means for no reason other than random sampling error. It’s just luck of the draw.

Significance levels and P values are important tools that help you quantify and control this type of error in a hypothesis test. Using these tools to decide when to reject the null hypothesis increases your chance of making the correct decision.

If you like this post, you might want to read the other posts in this series that use the same graphical framework:

Previous: Why We Need to Use Hypothesis Tests
Next: Confidence Intervals and Confidence Levels

If you'd like to see how I made these graphs, please read: How to Create a Graphical Version of the 1-sample t-Test .

Trust Center

Terms of Use
Privacy Policy
Cookies Settings

Data Science
Data Analysis
Data Visualization
Machine Learning
Deep Learning
Computer Vision
Artificial Intelligence
AI ML DS Interview Series
AI ML DS Projects series
Data Engineering
Web Scrapping

Understanding Hypothesis Testing

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.

To test the validity of the claim or assumption about the population parameter:

A sample is drawn from the population and analyzed.
The results of the analysis are used to decide whether the claim is true or not.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis. Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.

Key Terms of Hypothesis Testing

Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 : [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]

To delve deeper into differences into both types of test: Refer to link

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).

	Null Hypothesis is True	Null Hypothesis is False
Null Hypothesis is True (Accept)	Correct Decision	Type II Error (False Negative)
Alternative Hypothesis is True (Reject)	Type I Error (False Positive)	Correct Decision

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ), suggesting an effect or difference.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

If Test Statistic>Critical Value: Reject the null hypothesis.
If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]

[Tex]\bar{x} [/Tex] is the sample mean,
μ represents the population mean,
σ is the standard deviation
and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]

t = t-score,
x̄ = sample mean
μ = population mean,
s = standard deviation of the sample,
n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]

[Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
i,j are the rows and columns index respectively.
[Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]

Real life Examples of Hypothesis Testing

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

m = mean of the difference i.e X after, X before
s = standard deviation of the difference (d) i.e d i = X after, i − X before,
n = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Case A

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

import numpy as np from scipy import stats # Data before_treatment = np . array ([ 120 , 122 , 118 , 130 , 125 , 128 , 115 , 121 , 123 , 119 ]) after_treatment = np . array ([ 115 , 120 , 112 , 128 , 122 , 125 , 110 , 117 , 119 , 114 ]) # Step 1: Null and Alternate Hypotheses # Null Hypothesis: The new drug has no effect on blood pressure. # Alternate Hypothesis: The new drug has an effect on blood pressure. null_hypothesis = "The new drug has no effect on blood pressure." alternate_hypothesis = "The new drug has an effect on blood pressure." # Step 2: Significance Level alpha = 0.05 # Step 3: Paired T-test t_statistic , p_value = stats . ttest_rel ( after_treatment , before_treatment ) # Step 4: Calculate T-statistic manually m = np . mean ( after_treatment - before_treatment ) s = np . std ( after_treatment - before_treatment , ddof = 1 ) # using ddof=1 for sample standard deviation n = len ( before_treatment ) t_statistic_manual = m / ( s / np . sqrt ( n )) # Step 5: Decision if p_value <= alpha : decision = "Reject" else : decision = "Fail to reject" # Conclusion if decision == "Reject" : conclusion = "There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different." else : conclusion = "There is insufficient evidence to claim a significant difference in average blood pressure before and after treatment with the new drug." # Display results print ( "T-statistic (from scipy):" , t_statistic ) print ( "P-value (from scipy):" , p_value ) print ( "T-statistic (calculated manually):" , t_statistic_manual ) print ( f "Decision: { decision } the null hypothesis at alpha= { alpha } ." ) print ( "Conclusion:" , conclusion )

T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05.

The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] and we get accordingly , Z =2.039999999999992.

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Python Implementation of Case B

import scipy.stats as stats import math import numpy as np # Given data sample_data = np . array ( [ 205 , 198 , 210 , 190 , 215 , 205 , 200 , 192 , 198 , 205 , 198 , 202 , 208 , 200 , 205 , 198 , 205 , 210 , 192 , 205 , 198 , 205 , 210 , 192 , 205 ]) population_std_dev = 5 population_mean = 200 sample_size = len ( sample_data ) # Step 1: Define the Hypotheses # Null Hypothesis (H0): The average cholesterol level in a population is 200 mg/dL. # Alternate Hypothesis (H1): The average cholesterol level in a population is different from 200 mg/dL. # Step 2: Define the Significance Level alpha = 0.05 # Two-tailed test # Critical values for a significance level of 0.05 (two-tailed) critical_value_left = stats . norm . ppf ( alpha / 2 ) critical_value_right = - critical_value_left # Step 3: Compute the test statistic sample_mean = sample_data . mean () z_score = ( sample_mean - population_mean ) / \ ( population_std_dev / math . sqrt ( sample_size )) # Step 4: Result # Check if the absolute value of the test statistic is greater than the critical values if abs ( z_score ) > max ( abs ( critical_value_left ), abs ( critical_value_right )): print ( "Reject the null hypothesis." ) print ( "There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL." ) else : print ( "Fail to reject the null hypothesis." ) print ( "There is not enough evidence to conclude that the average cholesterol level in the population is different from 200 mg/dL." )

Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.

Limitations of Hypothesis Testing

Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( [Tex]H_o [/Tex] ): No effect or difference exists. Alternative Hypothesis ( [Tex]H_1 [/Tex] ): An effect or difference exists. Significance Level ( [Tex]\alpha [/Tex] ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
A P-value calculator is used to determine the statistical significance of an observed result in hypothesis testing. It takes as input the observed test statistic, the null hypothesis, and the relevant parameters of the statistical test (such as degrees of freedom), and computes the p-value. The p-value represents the probability of obtaining results as extreme as, or more extreme than, the observed data, assuming the null hypothesis is true. A lower p-value suggests stronger evidence against the null hypothesis, indicating that the observed result is unlikely to have occurred by random chance alone. The calculated p-value is used in comparison with a predefined significance level (alpha) to make decisions about the null hypothesis. If the p-value is less than or equal to alpha, typically 0.05, the results are considered statistically significant, leading to the rejection of the null hypothesis in favor of the alternative hypothesis. If the p-value is greater than alpha, there is insufficient evidence to reject the null hypothesis.
How do I calculate p-value?
The p-value is calculated by determining the probability of observing a test statistic as extreme as, or more extreme than, the observed one under the assumption of the null hypothesis.
What is p-value in Z test?
In a Z-test, the p-value is the probability of observing a Z-statistic as extreme as, or more extreme than, the calculated one, assuming a normal distribution and under the null hypothesis.
What is the p-value?
The p-value, or probability value, is a measure in statistics that quantifies the strength of evidence against a null hypothesis. It indicates the likelihood of observing a test statistic as extreme as, or more extreme than, the one obtained from the data, assuming the null hypothesis is true.
What is the alpha for p-value?
The alpha (α) for a p-value is the chosen level of significance that determines the threshold for rejecting the null hypothesis. It represents the maximum probability of making a Type I error (incorrectly rejecting a true null hypothesis) and is typically set at common values such as 0.05 or 0.01.
What does p-value under 0.05 mean?
A p-value under 0.05 typically suggests that there is statistically significant evidence to reject the null hypothesis in favor of an alternative hypothesis.

We want your feedback

Please add a message.

Message received. Thanks for the feedback.

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, chi-square test, what is hypothesis testing in statistics types and examples, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, mean squared error: overview, examples, concepts and more, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, hypothesis testing in statistics - types | examples.

Lesson 10 of 24 By Avijeet Biswal

What Is Hypothesis Testing in Statistics? Types and Examples

In today’s data-driven world, decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

The Ultimate Ticket to Top Data Science Job Roles

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life -

A teacher assumes that 60% of his college's students come from lower-middle-class families.
A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

Here, x̅ is the sample mean,
μ0 is the population mean,
σ is the standard deviation,
n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternative Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average.

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps in Hypothesis Testing

Hypothesis testing is a statistical method to determine if there is enough evidence in a sample of data to infer that a certain condition is true for the entire population. Here’s a breakdown of the typical steps involved in hypothesis testing:

Formulate Hypotheses

Null Hypothesis (H0): This hypothesis states that there is no effect or difference, and it is the hypothesis you attempt to reject with your test.
Alternative Hypothesis (H1 or Ha): This hypothesis is what you might believe to be true or hope to prove true. It is usually considered the opposite of the null hypothesis.

Choose the Significance Level (α)

The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. Common choices for α are 0.05 (5%), 0.01 (1%), and 0.10 (10%).

Select the Appropriate Test

Choose a statistical test based on the type of data and the hypothesis. Common tests include t-tests, chi-square tests, ANOVA, and regression analysis. The selection depends on data type, distribution, sample size, and whether the hypothesis is one-tailed or two-tailed.

Collect Data

Gather the data that will be analyzed in the test. This data should be representative of the population to infer conclusions accurately.

Calculate the Test Statistic

Based on the collected data and the chosen test, calculate a test statistic that reflects how much the observed data deviates from the null hypothesis.

Determine the p-value

The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.

Make a Decision

Compare the p-value to the chosen significance level:

If the p-value ≤ α: Reject the null hypothesis, suggesting sufficient evidence in the data supports the alternative hypothesis.
If the p-value > α: Do not reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.

Report the Results

Present the findings from the hypothesis test, including the test statistic, p-value, and the conclusion about the hypotheses.

Perform Post-hoc Analysis (if necessary)

Depending on the results and the study design, further analysis may be needed to explore the data more deeply or to address multiple comparisons if several hypotheses were tested simultaneously.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Become a Data Scientist through hands-on learning with hackathons, masterclasses, webinars, and Ask-Me-Anything! Start learning now!

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

The null hypothesis is (H0 <= 90) or less change.
A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true].

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Our Data Scientist Master's Program covers core topics such as R, Python, Machine Learning, Tableau, Hadoop, and Spark. Get started on your journey today!

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

Learn All The Tricks Of The BI Trade

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore the Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is H0 and H1 in statistics?

In statistics, H0 and H1 represent the null and alternative hypotheses. The null hypothesis, H0, is the default assumption that no effect or difference exists between groups or conditions. The alternative hypothesis, H1, is the competing claim suggesting an effect or a difference. Statistical tests determine whether to reject the null hypothesis in favor of the alternative hypothesis based on the data.

3. What is a simple hypothesis with an example?

A simple hypothesis is a specific statement predicting a single relationship between two variables. It posits a direct and uncomplicated outcome. For example, a simple hypothesis might state, "Increased sunlight exposure increases the growth rate of sunflowers." Here, the hypothesis suggests a direct relationship between the amount of sunlight (independent variable) and the growth rate of sunflowers (dependent variable), with no additional variables considered.

4. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:

Name	Date	Place
	21 Sep -6 Oct 2024, Weekend batch	Your City
	12 Oct -27 Oct 2024, Weekend batch	Your City
	26 Oct -10 Nov 2024, Weekend batch	Your City

About the Author

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

Pardon Our Interruption

As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:

You've disabled JavaScript in your web browser.
You're a power user moving through this website with super-human speed.
You've disabled cookies in your web browser.
A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .

To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

Data Science

Caltech Bootcamp / Blog / /

What is Bayesian Statistics, and How Does it Differ from Classical Methods?

Written by John Terra
Updated on August 14, 2024

We humans are creatures of belief. Our beliefs guide us, shape our perceptions, and dictate many actions. However, people who value personal growth and learning will modify their beliefs by acquiring new information. Fields like artificial intelligence and machine learning embrace this kind of growth, and that’s what we’re here for today.

This article explores Bayesian statistics, including its definition, fundamentals, usage, pros and cons, and how a data science bootcamp can help you learn how to use statistical tools (and others) to bolster your career skill set.

So, what are Bayesian statistics?

What is Bayesian Statistics?

Put simply, Bayesian statistics is a data analysis approach based on Bayes’ theorem. According to this theorem, available knowledge regarding parameters in statistical models is updated using the information gathered from observed data. So, Bayesian statistics gives us the mathematical tools to update our beliefs regarding random events by incorporating new evidence or data about said events.

The Bayes theorem is a mathematical formula that determines the conditional probability of any given event. Conditional probability is defined as the chance a given event will happen based on previous knowledge of the occurrences of prior outcomes.

Bayesian statistics is used today in statistical analysis to make data-based decisions, deal with uncertainty and probability, and draw inferences from analyses.

Also Read: Technology at Work: Data Science in Finance

Digging into Bayesian Statistical Fundamentals

Let’s break down Bayesian statistics into its fundamental components.

Conditional probability is the probability of an event (A), given (B), which is essential for updating beliefs. For instance, a medical researcher may want to explore the conditional probability of someone developing cancer, given a specific risk factor, like smoking. We can carry this into Bayesian statistics and update our beliefs using Bayes’ rule, working alongside the three essential elements in any given Bayesian analysis: prior distribution, likelihood, and posterior distribution.
Prior distribution is a reasonable belief about the plausibility of an unknown parameter’s values of interest without any evidence from the new data we are analyzing.
Likelihood covers the different possible values of the parameter based on new data analysis.
Posterior distribution combines prior distribution and the likelihood using Bayes’ rule:

P(A|B) = [P(B|A). P(A)]/P(B)

In this rule, P(A) and P(B) represent the probabilities of the events A and B.

P(A|B) represents the probability of event A happening, given B.

P(B|A) represents the probability of event B happening, given A.

This process of updating prior beliefs using Bayes’ rule is known as Bayesian updating. The information we are trying to update can be called the prior. Note that the prior can take other data forms. For example, a prior could be a statistical estimate from a previous analysis or an estimate based on domain knowledge or belief. A prior belief doesn’t have to be quantifiable as a probability and, in some cases, could be subjective or qualitative. For instance, the prior belief could be our researcher mentioned above’s opinion on whether a patient had a specific form of cancer before any diagnostic tests could be conducted. The resulting information is the posterior after using the Bayes’ rule to update the prior. Thus, posterior distributions form the basis of statistical inferences made with a Bayesian analysis.

So, how does Bayesian statistics differ from frequentist statistics? And what is a frequentist statistic, anyway?

Bayesian vs. Frequentist Statistics

Frequentist statistics, also called classical statistics, assumes that probabilities are the frequency of particular random events happening in a long series of repeated trials. The primary difference between these two methodologies hinges on how they deal with uncertainty. For example, a Frequentist relies on long-term frequencies and assumes that probabilities are fixed and objective. On the other hand, Bayesians embrace subjectivity and the belief that probabilities change depending on additional new information.

Let’s look at the example of rolling a fair, balanced, six-sided die. If you roll that die 500 times, you may encounter a situation where you roll four sixes in a row. However, throughout those 500 rolls, you will get a six result once out of every six times. Thus, a Frequentist would conclude that a die roller has a one in six probability of obtaining a six result on their next roll.

Bayesians see it differently. For example, consider the probability of rolling greater than a four on that six-sided die. Two numbers (five and six) are greater than four and six possibilities. So, you divide two by six and get 0.33333, and that’s your probability of rolling greater than a four on the die.

Also Read: Five Outstanding Data Visualization Examples for Marketing

Should You Use Bayesian or Frequentist Statistics in A/B Testing?

A/B testing, alternately referred to as split testing, compares two or more different versions of something to determine which works better. A/B testing in a digital format, like for a website or a marketing e-mail campaign, tries to identify which version performs better in creating a desired outcome, such as clicks, signups, or engagement.

In the frequentist approach to A/B testing, tests begin by assuming that there is no difference between the two variations. The goal is to determine whether the results are meaningful enough to disprove that initial assumption.

However, with the Bayesian statistical methodology, prior knowledge forms the initial hypothesis, and the beliefs are adjusted and updated as new data surfaces. Unlike the frequentist approach, which establishes strict boundaries on whether something’s 100% true or false, the Bayesian approach gives probabilities of whether the hypothesis is true or false. For example, there could be a 75 percent chance the hypothesis is true and a 25 percent chance it’s false.

So, the best methodology for conducting your next A/B test should depend on the sample size, context, and whether or not you’re incorporating beliefs or prior knowledge into your process.

How to Use Bayesian Methodology When Conducting an A/B Test

You don’t have to be a data scientist to effectively use Bayesian methodology in running an A/B test. Follow these simple steps:

Form your hypothesis

Suppose you hypothesize that a more accessible sign-up form will encourage more people to sign up for free product trials. You believe reducing the form’s required fields will make things easier, minimize friction, and streamline the process, resulting in greater participation.

Determine the probability that the hypothesis is true

You’ve had good results using shorter lead capture forms for similar campaigns, such as product demo requests. Based on that experience and information, you guess there’s a 70 percent chance of success if you condensed the new user sign-up form.

Collect the data and calculate posterior probabilities

Collect the data on sign-up rates as users interact with your new form. Update the hypothesis and assumptions as the new data rolls in. This updated value becomes your posterior probability.

Iterate, collect more data, repeat

Now, that new posterior probability becomes the prior probability for the next round of testing. For this example, sign-up rates increased by 25 percent with the new form, so this information becomes the new prior probability. Repeat the cycle, refining and optimizing as needed.

Also Read: Data Science Bootcamps vs. Traditional Degrees: Which Learning Path to Choose?

The Advantages vs. Disadvantages of Bayesian Statistics

Let’s briefly explore the pros and cons of Bayesian statistics.

Advantages of Bayesian Statistics

It handles multiple tests well. Since testing isn’t forced into a true/false proposition, Bayesian statistics is well-suited for multiple testing situations.
It offers incorporation of previous information and continuous updating. Bayesian statistics shines in situations where there’s a lot of prior data. This information boosts the statistical power to find relevant associations and make studies more efficient. The current posterior can be used as the prior knowledge element in future studies.
It’s an intuitive interpretation. The Bayesian process is remarkably similar to how humans process information in their minds, making it more intuitive to use.
It generalizes classical analysis. Classical statistical inference assumes no prior knowledge. Bayesian statistics helps narrow down what could be an infinite number (due to no prior information) based on prior knowledge.

Disadvantages of Bayesian Statistics

Defining prior distributions can be challenging. Implementing prior information isn’t straightforward, and experts may find it difficult to translate the knowledge into statistical terms.
It poses greater technical complexity. Many calculations that power Bayesian analysis require integral computations and operations with distributions. Skills in Bayesian programming are also helpful.
It can be computationally intense. Computing complex integrals and using iterative methods for estimation can slow down the process and unduly absorb a significant amount of computer processing.
There’s a strong potential for subjectivity. Although Bayesian statistics is typically more intuitive and results are easier to interpret, probabilistic outputs are arguably more subjective, leading to different interpretations and decision-making choices. Everyone assesses risks and probabilities differently so that other actions might be taken based on the same result.

Also Read: Data Scientist vs. Machine Learning Engineer

How to Increase Your Data Science Proficiency

Bayesian statistics is part of data science, an exciting field that figures prominently in many of today’s hot technologies, such as artificial intelligence and machine learning. If you want to learn more about data science and how to turn it into a career asset, consider an online data science program . This 44-week bootcamp covers descriptive and inferential statistics, exploratory data analysis, model building and fine-tuning, large language models (LLM), generative AI, and more.

Glassdoor.com reports that data scientists earn an average salary of $112,874. Check out this course if you want to immerse yourself in the world of data science and make it a career path.

You might also like to read:

What is Natural Language Generation in Data Science, and Why Does It Matter?

What is Data Wrangling? Importance, Tools, and More

What is Spatial Data Science? Definition, Applications, Careers & More

Data Science and Marketing: Transforming Strategies and Enhancing Engagement

An Introduction to Natural Language Processing in Data Science

Data Science Bootcamp

Learning Format:

Online Bootcamp

What is Data Imputation, and How Can You Use it to Handle Missing Data?

This article defines data imputation and demonstrates its importance, techniques, and challenges.

What is Data Governance, How Does it Work, Who Performs it, and Why is it Essential?

What is data governance? This article explores its goals and components, how to implement it, best practices, and more.

What is Data Visualization, and What is its Role in Data Science?

Visualizing data can transform complex information into meaningful insights. This guide answers the question: “What is data visualization?” and discusses everything you need to know about it.

Technology at Work: Data Science in Finance

In today’s data-driven world, industries leverage advanced data analytics and AI-powered tools to improve services and their bottom line. The financial services industry is at the forefront of this innovation. This blog discusses data science in finance, including how companies use it, the skills required to leverage it, and more.

The Top Data Science Interview Questions for 2024

This article covers popular basic and advanced data science interview questions and the difference between data analytics and data science.

Big Data and Analytics: Unlocking the Future

Unlock the potential and benefits of big data and analytics in your career. Explore essential roles and discover the advantages of data-driven decision-making.

Learning Format

Program Benefits

12+ tools covered, 25+ hands-on projects
Masterclasses by distinguished Caltech CTME instructors
Caltech CTME Circle Membership
Industry-specific training from global experts
Call us on : 1800-212-7688

Information

Author Services

Initiatives

You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.

All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .

Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.

Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.

Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.

Original Submission Date Received: .

Active Journals
Find a Journal
Proceedings Series
For Authors
For Reviewers
For Editors
For Librarians
For Publishers
For Societies
For Conference Organizers
Open Access Policy
Institutional Open Access Program
Special Issues Guidelines
Editorial Process
Research and Publication Ethics
Article Processing Charges
Testimonials
Preprints.org
SciProfiles
Encyclopedia

Article Menu

Subscribe SciFeed
Recommended Articles
Google Scholar
on Google Scholar
Table of Contents

Find support for a specific problem in the support section of our website.

Please let us know what you think of our products and services.

Visit our dedicated information section to learn more about MDPI.

JSmol Viewer

Cardiovascular disease risk stratification using hybrid deep learning paradigm: first of its kind on canadian trial data.

1. Introduction

2. the background literature, 3. methodology, 3.1. patient demographics and baseline characteristics, 3.2. acquisition of ultrasound scans and intraplaque neovascularization, 3.3. cardiovascular disease endpoint: angiographic score, 3.4. overall architecture, 3.4.1. data preparation and pre-processing, 3.4.2. model building, 3.4.3. the rationale behind using rnn, gru, and lstm, 3.5. experimental protocols, 3.5.1. experimental protocol 1: three unidirectional models, 3.5.2. experimental protocol 2: three bidirectional models, 3.5.3. experimental protocol 3: six hybrid models, 3.6. loss function and training parameters, 3.7. performance metrics, 4.1. accuracy and loss curves, 4.2. results of experimental protocol 1, 4.3. results of experimental protocol 2, 4.4. results of experimental protocol 3, 4.5. comparison of three feature selection methods for three machine learning models, 5. performance evaluation, 5.1. receiver operating characteristics of all four kinds of ai models, 5.2. effect of sample sizes on the training system, 5.3. hybrid deep learning performance against other ai models, 6. scientific validation, 7. reliability and stability of hybrid deep learning system, 8. discussion, 8.1. benchmarking table, 8.2. a special note on hybrid deep learning, 8.3. strengths, weaknesses, and extensions, 9. conclusions, author contributions, institutional review board statement, informed consent statement, data availability statement, acknowledgments, conflicts of interest, appendix a. unidirectional architecture.

SN	Risk Factors or Target Variable	Samples (N) or Mean	Pr (%)
1	Age	64.49 years	-
2	Gender	349	69.8
3	Obesity	215	43.0
4	Ethnicity	486	97.2
5	BMI	31.12 kg/m	-
6	Hypertension	338	67.6
7	Angina	124	24.8
8	Diastolic blood pressure	76.7 mmHg	-
9	Systolic blood pressure	135.35 mmHg	-
10	Smoking history	330	66.0
11	Casual smoker	15	3.0
12	Current smoker	100	20.0
13	Previous smoker	218	43.6
14	Drinks	4.94 ± 10.4 per week	-
15	Family history of diabetics	195	39.0
16	Premature CVD in the family	146	29.2
17	CVD in the family	321	64.2
18	Pre-diabetic	20	40.0
19	Hyperlipidemia	288	57.6
20	Type II diabetes	114	22.8
21	Type I diabetes	5	1.0
22	Creatinine	83.99 ± 22.6 μmol/L	-
23	Estimated glomerular filtration rate	78.96 mL/min/1.73 m	-
24	Diabetes of any type	118	23.6
25	Total plaque area (TPA)	47.68 mm	-
26	Maximum plaque height (MPH)	2.64 mm	-
27	Intra-plaque neovascularization (IPN)	1.16	-
28	Angiotensin-converting enzyme (ACE) inhibitors	191	38.2
29	HMG-Co reductase inhibitors	272	54.4
30	Angiotensin receptor blockers (ARBs)	45	9.0
31	Other antilipemic agents	9	1.80
32	Alpha-blockers	30	6.0
33	Calcium channel-blockers	93	18.6
34	Beta-blockers	236	47.2
35	Diuretics	99	19.8
36	Anti-platelet	368	73.6
37	Insulin	38	7.6
38	Anti-anginals and NSAIDS	81	16.20
39	Non-insulin diabetes medications	72	14.4

Appendix B. Unidirectional Architecture

Click here to enlarge figure

Appendix C. Bidirectional Architecture

Appendix d. hybrid deep learning architecture, appendix e. scientific validation with the unseen data.

Unseen Data (Train A-Test B)				Unseen Data (Train B-Test A)
SN	Models	Mean AUC	p-Value	Mean AUC	p-Value
1	ML	0.683	<0.005	0.683	<0.005
2	UniDL	0.884	<0.001	0.880	<0.001
3	BiDL	0.905	<0.001	0.900	<0.001
4	HDL	0.947	<0.001	0.940	<0.001

Appendix F. Confusion Matrix for Unidirectional HDL and Bidirectional HDL Model

Kaptoge, S.; Pennells, L.; De Bacquer, D.; Cooney, M.T.; Kavousi, M.; Stevens, G.; Riley, L.M.; Savin, S.; Khan, T.; Altay, S.; et al. World Health Organization cardiovascular disease risk charts: Revised models to estimate risk in 21 global regions. Lancet Glob. Health 2019 , 7 , e1332–e1345. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Suri, J.S.; Agarwal, S.; Gupta, S.K.; Puvvula, A.; Biswas, M.; Saba, L.; Bit, A.; Tandel, G.S.; Agarwal, M.; Patrick, A.; et al. A narrative review on characterization of acute respiratory distress syndrome in COVID-19-infected lungs using artificial intelligence. Comput. Biol. Med. 2021 , 130 , 104210. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Jamthikar, A.D.; Puvvula, A.; Gupta, D.; Johri, A.M.; Nambi, V.; Khanna, N.N.; Saba, L.; Mavrogeni, S.; Laird, J.R.; Pareek, G. Cardiovascular disease and stroke risk assessment in patients with chronic kidney disease using integration of estimated glomerular filtration rate, ultrasonic image phenotypes, and artificial intelligence: A narrative review. Int. Angiol. A J. Int. Union Angiol. 2020 , 40 , 150–164. [ Google Scholar ] [ CrossRef ]
Saba, L.; Anzidei, M.; Sanfilippo, R.; Montisci, R.; Lucatelli, P.; Catalano, C.; Passariello, R.; Mallarini, G. Imaging of the carotid artery. Atherosclerosis 2012 , 220 , 294–309. [ Google Scholar ] [ CrossRef ]
Griffin, M.; Nicolaides, A.N.; Belcaro, G.; Shah, E. Cardiovascular risk assessment using ultrasound: The value of arterial wall changes including the presence, severity and character of plaques. Pathophysiol. Haemost. Thromb. 2002 , 32 , 367–370. [ Google Scholar ] [ CrossRef ]
Suri, J.S.; Kathuria, C.; Molinari, F. Atherosclerosis Disease Management ; Springer: Berlin/Heidelberg, Germany, 2010. [ Google Scholar ]
Saba, L.; Jamthikar, A.; Gupta, D.; Khanna, N.N.; Viskovic, K.; Suri, H.S.; Gupta, A.; Mavrogeni, S.; Turk, M.; Laird, J.R. Global perspective on carotid intima-media thickness and plaque: Should the current measurement guidelines be revisited? Int. Angiol. 2019 , 38 , 451–465. [ Google Scholar ] [ CrossRef ]
Giannopoulos, A.A.; Kyriacou, E.; Griffin, M.; Pattichis, C.S.; Michael, J.; Richards, T.; Geroulakos, G.; Nicolaides, A.N. Dynamic carotid plaque imaging using ultrasonography. J. Vasc. Surg. 2021 , 73 , 1630–1638. [ Google Scholar ] [ CrossRef ]
Amato, M.; Montorsi, P.; Ravani, A.; Oldani, E.; Galli, S.; Ravagnani, P.M.; Tremoli, E.; Baldassarre, D. Carotid intima-media thickness by B-mode ultrasound as surrogate of coronary atherosclerosis: Correlation with quantitative coronary angiography and coronary intravascular ultrasound findings. Eur. Heart J. 2007 , 28 , 2094–2101. [ Google Scholar ] [ CrossRef ]
Bots, M.L. Carotid intima-media thickness as a surrogate marker for cardiovascular disease in intervention studies. Curr. Med. Res. Opin. 2006 , 22 , 2181–2190. [ Google Scholar ] [ CrossRef ]
Spence, J.D. Ultrasound measurement of carotid plaque as a surrogate outcome for coronary artery disease. Am. J. Cardiol. 2002 , 89 , 10–15. [ Google Scholar ] [ CrossRef ]
Puvvula, A.; Jamthikar, A.D.; Gupta, D.; Khanna, N.N.; Porcu, M.; Saba, L.; Viskovic, K.; Ajuluchukwu, J.N.; Gupta, A.; Mavrogeni, S. Morphological carotid plaque area is associated with glomerular filtration rate: A study of south asian indian patients with diabetes and chronic kidney disease. Angiology 2020 , 71 , 520–535. [ Google Scholar ] [ CrossRef ]
Biswas, M.; Saba, L.; Chakrabartty, S.; Khanna, N.N.; Song, H.; Suri, H.S.; Sfikakis, P.P.; Mavrogeni, S.; Viskovic, K.; Laird, J.R. Two-stage artificial intelligence model for jointly measurement of atherosclerotic wall thickness and plaque burden in carotid ultrasound: A screening tool for cardiovascular/stroke risk assessment. Comput. Biol. Med. 2020 , 123 , 103847. [ Google Scholar ] [ CrossRef ]
Landry, A.; Spence, J.D.; Fenster, A. Measurement of carotid plaque volume by 3-dimensional ultrasound. Stroke 2004 , 35 , 864–869. [ Google Scholar ] [ CrossRef ]
Johri, A.M.; Lajkosz, K.A.; Grubic, N.; Islam, S.; Li, T.Y.; Simpson, C.S.; Ewart, P.; Suri, J.S.; Hétu, M.-F. Maximum plaque height in carotid ultrasound predicts cardiovascular disease outcomes: A population-based validation study of the American society of echocardiography’s grade II–III plaque characterization and protocol. Int. J. Cardiovasc. Imaging 2021 , 37 , 1601–1610. [ Google Scholar ] [ CrossRef ]
Mantella, L.E.; Colledanchise, K.N.; Hetu, M.-F.; Feinstein, S.B.; Abunassar, J.; Johri, A.M. Carotid intraplaque neovascularization predicts coronary artery disease and cardiovascular events. Eur. Heart J. Cardiovasc. Imaging 2019 , 20 , 1239–1247. [ Google Scholar ] [ CrossRef ]
Goldstein, B.A.; Navar, A.M.; Carter, R.E. Moving beyond regression techniques in cardiovascular risk prediction: Applying machine learning to address analytic challenges. Eur. Heart J. 2017 , 38 , 1805–1814. [ Google Scholar ] [ CrossRef ]
Jamthikar, A.D.; Gupta, D.; Saba, L.; Khanna, N.N.; Viskovic, K.; Mavrogeni, S.; Laird, J.R.; Sattar, N.; Johri, A.M.; Pareek, G. Artificial intelligence framework for predictive cardiovascular and stroke risk assessment models: A narrative review of integrated approaches using carotid ultrasound. Comput. Biol. Med. 2020 , 126 , 104043. [ Google Scholar ] [ CrossRef ]
Alaa, A.M.; Bolton, T.; Di Angelantonio, E.; Rudd, J.H.; Van der Schaar, M. Cardiovascular disease risk prediction using automated machine learning: A prospective study of 423,604 UK Biobank participants. PLoS ONE 2019 , 14 , e0213653. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Weng, S.F.; Reps, J.; Kai, J.; Garibaldi, J.M.; Qureshi, N. Can machine-learning improve cardiovascular risk prediction using routine clinical data? PLoS ONE 2017 , 12 , e0174944. [ Google Scholar ] [ CrossRef ]
Biswas, M.; Kuppili, V.; Saba, L.; Edla, D.R.; Suri, H.S.; Cuadrado-Godia, E.; Laird, J.R.; Marinhoe, R.T.; Sanches, J.M.; Nicolaides, A. State-of-the-art review on deep learning in medical imaging. Front. Biosci. Landmark 2019 , 24 , 380–406. [ Google Scholar ]
Saba, L.; Biswas, M.; Kuppili, V.; Godia, E.C.; Suri, H.S.; Edla, D.R.; Omerzu, T.; Laird, J.R.; Khanna, N.N.; Mavrogeni, S. The present and future of deep learning in radiology. Eur. J. Radiol. 2019 , 114 , 14–24. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Hosny, A.; Parmar, C.; Quackenbush, J.; Schwartz, L.H.; Aerts, H.J. Artificial intelligence in radiology. Nat. Rev. Cancer 2018 , 18 , 500–510. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Pianykh, O.S.; Langs, G.; Dewey, M.; Enzmann, D.R.; Herold, C.J.; Schoenberg, S.O.; Brink, J.A. Continuous learning AI in radiology: Implementation principles and early applications. Radiology 2020 , 297 , 6–14. [ Google Scholar ] [ CrossRef ]
Thrall, J.H.; Li, X.; Li, Q.; Cruz, C.; Do, S.; Dreyer, K.; Brink, J. Artificial intelligence and machine learning in radiology: Opportunities, challenges, pitfalls, and criteria for success. J. Am. Coll. Radiol. 2018 , 15 , 504–508. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Shrivastava, V.K.; Londhe, N.D.; Sonawane, R.S.; Suri, J.S. Reliable and accurate psoriasis disease classification in dermatology images using comprehensive feature space in machine learning paradigm. Expert Syst. Appl. 2015 , 42 , 6184–6195. [ Google Scholar ] [ CrossRef ]
Shrivastava, V.K.; Londhe, N.D.; Sonawane, R.S.; Suri, J.S. A novel and robust Bayesian approach for segmentation of psoriasis lesions and its risk stratification. Comput. Methods Programs Biomed. 2017 , 150 , 9–22. [ Google Scholar ] [ CrossRef ]
Du-Harpur, X.; Watt, F.; Luscombe, N.; Lynch, M. What is AI? Applications of artificial intelligence to dermatology. Br. J. Dermatol. 2020 , 183 , 423–430. [ Google Scholar ] [ CrossRef ]
Li, C.-X.; Shen, C.-B.; Xue, K.; Shen, X.; Jing, Y.; Wang, Z.-Y.; Xu, F.; Meng, R.-S.; Yu, J.-B.; Cui, Y. Artificial intelligence in dermatology: Past, present, and future. Chin. Med. J. 2019 , 132 , 2017–2020. [ Google Scholar ] [ CrossRef ]
Fritzsche, K.; Can, A.; Shen, H.; Tsai, C.; Turner, J.; Tanenbuam, H.; Stewart, C.; Roysam, B.; Suri, J.; Laxminarayan, S. Automated model based segmentation, tracing and analysis of retinal vasculature from digital fundus images. In State-of-The-Art Angiography, Applications and Plaque Imaging Using MR, CT, Ultrasound and X-rays ; CRC Press: Boca Raton, FL, USA, 2003; Volume 29, pp. 225–298. [ Google Scholar ]
Hogarty, D.T.; Mackey, D.A.; Hewitt, A.W. Current state and future prospects of artificial intelligence in ophthalmology: A review. Clin. Exp. Ophthalmol. 2019 , 47 , 128–139. [ Google Scholar ] [ CrossRef ]
Tong, Y.; Yu, Y.; Xing, Y.; Chen, C.; Shen, Y. Applications of artificial intelligence in ophthalmology: General overview. J. Ophthalmol. 2018 , 2018 , 5278196. [ Google Scholar ]
Ting, D.S.W.; Pasquale, L.R.; Peng, L.; Campbell, J.P.; Lee, A.Y.; Raman, R.; Tan, G.S.W.; Schmetterer, L.; Keane, P.A.; Wong, T.Y. Artificial intelligence and deep learning in ophthalmology. Br. J. Ophthalmol. 2019 , 103 , 167–175. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Schmidt-Erfurth, U.; Reiter, G.S.; Riedl, S.; Seeböck, P.; Vogl, W.-D.; Blodi, B.A.; Domalpally, A.; Fawzi, A.; Jia, Y.; Sarraf, D. AI-based monitoring of retinal fluid in disease activity and under therapy. Prog. Retin. Eye Res. 2022 , 86 , 100972. [ Google Scholar ] [ CrossRef ]
Sorrentino, F.S.; Jurman, G.; De Nadai, K.; Campa, C.; Furlanello, C.; Parmeggiani, F. Application of artificial intelligence in targeting retinal diseases. Curr. Drug Targets 2020 , 21 , 1208–1215. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Saba, L.; Sanfilippo, R.; Sannia, S.; Anzidei, M.; Montisci, R.; Mallarini, G.; Suri, J.S. Association between carotid artery plaque volume, composition, and ulceration: A retrospective assessment with MDCT. Am. J. Roentgenol. 2012 , 199 , 151–156. [ Google Scholar ] [ CrossRef ]
Acharya, U.R.; Sree, S.V.; Krishnan, M.M.R.; Krishnananda, N.; Ranjan, S.; Umesh, P.; Suri, J.S. Automated classification of patients with coronary artery disease using grayscale features from left ventricle echocardiographic images. Comput. Methods Programs Biomed. 2013 , 112 , 624–632. [ Google Scholar ] [ CrossRef ]
Johnson, K.W.; Soto, J.T.; Glicksberg, B.S.; Shameer, K.; Miotto, R.; Ali, M.; Ashley, E.; Dudley, J.T. Artificial intelligence in cardiology. J. Am. Coll. Cardiol. 2018 , 71 , 2668–2679. [ Google Scholar ] [ CrossRef ]
Lopez-Jimenez, F.; Attia, Z.; Arruda-Olson, A.M.; Carter, R.; Chareonthaitawee, P.; Jouni, H.; Kapa, S.; Lerman, A.; Luong, C.; Medina-Inojosa, J.R. Artificial intelligence in cardiology: Present and future. In Mayo Clinic Proceedings ; Elsevier: Amsterdam, The Netherlands, 2020. [ Google Scholar ]
Molinari, F.; Mantovani, A.; Deandrea, M.; Limone, P.; Garberoglio, R.; Suri, J.S. Characterization of single thyroid nodules by contrast-enhanced 3-D ultrasound. Ultrasound Med. Biol. 2010 , 36 , 1616–1625. [ Google Scholar ] [ CrossRef ]
Gubbi, S.; Hamet, P.; Tremblay, J.; Koch, C.A.; Hannah-Shmouni, F. Artificial intelligence and machine learning in endocrinology and metabolism: The dawn of a new era. Front. Endocrinol. 2019 , 10 , 185. [ Google Scholar ] [ CrossRef ]
Giorgini, F.; Di Dalmazi, G.; Diciotti, S. Artificial intelligence in endocrinology: A comprehensive review. J. Endocrinol. Investig. 2024 , 47 , 1067–1082. [ Google Scholar ] [ CrossRef ]
Thomasian, N.M.; Kamel, I.R.; Bai, H.X. Machine intelligence in non-invasive endocrine cancer diagnostics. Nat. Rev. Endocrinol. 2022 , 18 , 81–95. [ Google Scholar ] [ CrossRef ]
Jamthikar, A.; Gupta, D.; Khanna, N.N.; Saba, L.; Araki, T.; Viskovic, K.; Suri, H.S.; Gupta, A.; Mavrogeni, S.; Turk, M. A low-cost machine learning-based cardiovascular/stroke risk assessment system: Integration of conventional factors with image phenotypes. Cardiovasc. Diagn. Ther. 2019 , 9 , 420. [ Google Scholar ] [ CrossRef ]
Kakadiaris, I.A.; Vrigkas, M.; Yen, A.A.; Kuznetsova, T.; Budoff, M.; Naghavi, M. Machine learning outperforms ACC/AHA CVD risk calculator in MESA. J. Am. Heart Assoc. 2018 , 7 , e009476. [ Google Scholar ] [ CrossRef ]
Arsenescu, T.; Chifor, R.; Marita, T.; Santoma, A.; Lebovici, A.; Duma, D.; Vacaras, V.; Badea, A.F. 3D ultrasound reconstructions of the carotid artery and thyroid gland using artificial-intelligence-based automatic segmentation—Qualitative and quantitative evaluation of the segmentation results via comparison with CT angiography. Sensors 2023 , 23 , 2806. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Acharya, U.R.; Mookiah, M.R.K.; Sree, S.V.; Yanti, R.; Martis, R.; Saba, L.; Molinari, F.; Guerriero, S.; Suri, J.S. Evolutionary algorithm-based classifier parameter tuning for automatic ovarian cancer tissue characterization and classification. Ultraschall Med. Eur. J. Ultrasound 2014 , 35 , 237–245. [ Google Scholar ]
Araki, T.; Ikeda, N.; Shukla, D.; Jain, P.K.; Londhe, N.D.; Shrivastava, V.K.; Banchhor, S.K.; Saba, L.; Nicolaides, A.; Shafique, S. PCA-based polling strategy in machine learning framework for coronary artery disease risk assessment in intravascular ultrasound: A link between carotid and coronary grayscale plaque morphology. Comput. Methods Programs Biomed. 2016 , 128 , 137–158. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Anaya-Isaza, A.; Mera-Jiménez, L.; Zequera-Diaz, M. An overview of deep learning in medical imaging. Inform. Med. Unlocked 2021 , 26 , 100723. [ Google Scholar ] [ CrossRef ]
Lee, J.-G.; Jun, S.; Cho, Y.-W.; Lee, H.; Kim, G.B.; Seo, J.B.; Kim, N. Deep learning in medical imaging: General overview. Korean J. Radiol. 2017 , 18 , 570–584. [ Google Scholar ] [ CrossRef ]
Aggarwal, R.; Sounderajah, V.; Martin, G.; Ting, D.S.; Karthikesalingam, A.; King, D.; Ashrafian, H.; Darzi, A. Diagnostic accuracy of deep learning in medical imaging: A systematic review and meta-analysis. NPJ Digit. Med. 2021 , 4 , 65. [ Google Scholar ] [ CrossRef ]
Khanna, N.N.; Maindarkar, M.A.; Viswanathan, V.; Puvvula, A.; Paul, S.; Bhagawati, M.; Ahluwalia, P.; Ruzsa, Z.; Sharma, A.; Kolluri, R. Cardiovascular/Stroke Risk Stratification in Diabetic Foot Infection Patients Using Deep Learning-Based Artificial Intelligence: An Investigative Study. J. Clin. Med. 2022 , 11 , 6844. [ Google Scholar ] [ CrossRef ]
Suri, J.S.; Bhagawati, M.; Paul, S.; Protogerou, A.D.; Sfikakis, P.P.; Kitas, G.D.; Khanna, N.N.; Ruzsa, Z.; Sharma, A.M.; Saxena, S. A powerful paradigm for cardiovascular risk stratification using multiclass, multi-label, and ensemble-based machine learning paradigms: A narrative review. Diagnostics 2022 , 12 , 722. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Johri, A.M.; Singh, K.V.; Mantella, L.E.; Saba, L.; Sharma, A.; Laird, J.R.; Utkarsh, K.; Singh, I.M.; Gupta, S.; Kalra, M.S. Deep learning artificial intelligence framework for multiclass coronary artery disease prediction using combination of conventional risk factors, carotid ultrasound, and intraplaque neovascularization. Comput. Biol. Med. 2022 , 150 , 106018. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Konstantonis, G.; Singh, K.V.; Sfikakis, P.P.; Jamthikar, A.D.; Kitas, G.D.; Gupta, S.K.; Saba, L.; Verrou, K.; Khanna, N.N.; Ruzsa, Z. Cardiovascular disease detection using machine learning and carotid/femoral arterial imaging frameworks in rheumatoid arthritis patients. Rheumatol. Int. 2022 , 42 , 215–239. [ Google Scholar ] [ CrossRef ]
Jamthikar, A.D.; Gupta, D.; Mantella, L.E.; Saba, L.; Laird, J.R.; Johri, A.M.; Suri, J.S. Multiclass machine learning vs. conventional calculators for stroke/CVD risk assessment using carotid plaque predictors with coronary angiography scores as gold standard: A 500 participants study. Int. J. Cardiovasc. Imaging 2021 , 37 , 1171–1187. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Johri, A.M.; Mantella, L.E.; Jamthikar, A.D.; Saba, L.; Laird, J.R.; Suri, J.S. Role of artificial intelligence in cardiovascular risk prediction and outcomes: Comparison of machine-learning and conventional statistical approaches for the analysis of carotid ultrasound features and intra-plaque neovascularization. Int. J. Cardiovasc. Imaging 2021 , 37 , 3145–3156. [ Google Scholar ] [ CrossRef ]
Wilson, P.W.; D’Agostino, R.B.; Levy, D.; Belanger, A.M.; Silbershatz, H.; Kannel, W.B. Prediction of coronary heart disease using risk factor categories. Circulation 1998 , 97 , 1837–1847. [ Google Scholar ] [ CrossRef ]
Conroy, R.M.; Pyörälä, K.; Fitzgerald, A.E.; Sans, S.; Menotti, A.; De Backer, G.; De Bacquer, D.; Ducimetiere, P.; Jousilahti, P.; Keil, U. Estimation of ten-year risk of fatal cardiovascular disease in Europe: The SCORE project. Eur. Heart J. 2003 , 24 , 987–1003. [ Google Scholar ] [ CrossRef ]
Golf, D.C., Jr.; Lloyd-Jones, D.M.; Bennett, G.; Coady, S.; D’agostino, R.B.; Gibbons, R.; Greenland, P.; Lackland, D.T.; Levy, D.; O’donnell, C.J. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation 2014 , 129 (Suppl. S2), S49–S73. [ Google Scholar ]
Kumar, K.; Araki, T.; Rajan, J.; Saba, L.; Lavra, F.; Ikeda, N.; Sharma, A.M.; Shafique, S.; Nicolaides, A.; Laird, J.R. Accurate lumen diameter measurement in curved vessels in carotid ultrasound: An iterative scale-space and spatial transformation approach. Med. Biol. Eng. Comput. 2017 , 55 , 1415–1434. [ Google Scholar ] [ CrossRef ]
Detrano, R.; Guerci, A.D.; Carr, J.J.; Bild, D.E.; Burke, G.; Folsom, A.R.; Liu, K.; Shea, S.; Szklo, M.; Bluemke, D.A. Coronary calcium as a predictor of coronary events in four racial or ethnic groups. N. Engl. J. Med. 2008 , 358 , 1336–1345. [ Google Scholar ] [ CrossRef ]
Poplin, R.; Varadarajan, A.V.; Blumer, K.; Liu, Y.; McConnell, M.V.; Corrado, G.S.; Peng, L.; Webster, D.R. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nat. Biomed. Eng. 2018 , 2 , 158–164. [ Google Scholar ] [ CrossRef ]
Escaned, J.; Baptista, J.; Di Mario, C.; Haase, J.R.; Ozaki, Y.; Linker, D.T.; De Feyter, P.J.; Roelandt, J.R.; Serruys, P.W. Significance of automated stenosis detection during quantitative angiography: Insights gained from intracoronary ultrasound imaging. Circulation 1996 , 94 , 966–972. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Bourantas, C.V.; Kalatzis, F.G.; Papafaklis, M.I.; Fotiadis, D.I.; Tweddel, A.C.; Kourtis, I.C.; Katsouras, C.S.; Michalis, L.K. ANGIOCARE: An automated system for fast three-dimensional coronary reconstruction by integrating angiographic and intracoronary ultrasound data. Catheter. Cardiovasc. Interv. 2008 , 72 , 166–175. [ Google Scholar ] [ CrossRef ]
Joseph, J.; Kiran, R.; Nabeel, P.; Shah, M.I.; Bhaskar, A.; Ganesh, C.; Seshadri, S.; Sivaprakasam, M. ARTSENS® Pen—Portable easy-to-use device for carotid stiffness measurement: Technology validation and clinical-utility assessment. Biomed. Phys. Eng. Express 2020 , 6 , 025013. [ Google Scholar ] [ CrossRef ]
Daigle, R.J. Techniques in Noninvasive Vascular Diagnosis: An Encyclopedia of Vascular Testing ; Summer Publishing LLC: Littleton, CO, USA, 2008. [ Google Scholar ]
Nicolaides, A.N.; Kakkos, S.K.; Griffin, M.; Sabetai, M.; Dhanjil, S.; Thomas, D.J.; Geroulakos, G.; Georgiou, N.; Francis, S.; Ioannidou, E. Effect of image normalization on carotid plaque classification and the risk of ipsilateral hemispheric ischemic events: Results from the asymptomatic carotid stenosis and risk of stroke study. Vascular 2005 , 13 , 211–221. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002 , 16 , 321–357. [ Google Scholar ] [ CrossRef ]
Elreedy, D.; Atiya, A.F. A comprehensive analysis of synthetic minority oversampling technique (SMOTE) for handling class imbalance. Inf. Sci. 2019 , 505 , 32–64. [ Google Scholar ] [ CrossRef ]
Santoso, B.; Wijayanto, H.; Notodiputro, K.A.; Sartono, B. Synthetic over sampling methods for handling class imbalanced problems: A review. In IOP Conference Series: Earth and Environmental Science ; IOP Publishing: Bristol, UK, 2017. [ Google Scholar ]
Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018 , 61 , 863–905. [ Google Scholar ] [ CrossRef ]
Blagus, R.; Lusa, L. SMOTE for high-dimensional class-imbalanced data. BMC Bioinform. 2013 , 14 , 1–16. [ Google Scholar ] [ CrossRef ]
Deepa, B.; Ramesh, K. Epileptic seizure detection using deep learning through min max scaler normalization. Int. J. Health Sci. 2022 , 6 , 10981–10996. [ Google Scholar ] [ CrossRef ]
Sembiring, I.; Wahyuni, S.N.; Sediyono, E. LSTM algorithm optimization for COVID-19 prediction model. Heliyon 2024 , 10 , e26158. [ Google Scholar ] [ CrossRef ]
O’Donncha, F.; Hu, Y.; Palmes, P.; Burke, M.; Filgueira, R.; Grant, J. A spatio-temporal LSTM model to forecast across multiple temporal and spatial scales. Ecol. Inform. 2022 , 69 , 101687. [ Google Scholar ] [ CrossRef ]
Olhosseiny, H.H.; Mirzaloo, M.; Bolic, M.; Dajani, H.R.; Groza, V.; Yoshida, M. Identifying high risk of atherosclerosis using deep learning and ensemble learning. In Proceedings of the 2021 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Lausanne, Switzerland, 23–25 June 2021. [ Google Scholar ]
An, Y.; Huang, N.; Chen, X.; Wu, F.; Wang, J. High-risk prediction of cardiovascular diseases via attention-based deep neural networks. IEEE ACM Trans. Comput. Biol. Bioinform. 2019 , 18 , 1093–1105. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Baccouche, A.; Garcia-Zapirain, B.; Olea, C.C.; Elmaghraby, A. Ensemble deep learning models for heart disease classification: A case study from Mexico. Information 2020 , 11 , 207. [ Google Scholar ] [ CrossRef ]
Bai, S.; Yan, M.; Wan, Q.; He, L.; Wang, X.; Li, J. DL-RNN: An accurate indoor localization method via double RNNs. IEEE Sens. J. 2019 , 20 , 286–295. [ Google Scholar ] [ CrossRef ]
Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017. [ Google Scholar ]
Wang, J.J.; Yan, J.; Li, C.; Gao, R.X.; Zhao, R. Deep heterogeneous GRU model for predictive analytics in smart manufacturing: Application to tool wear prediction. Comput. Ind. 2019 , 111 , 1–14. [ Google Scholar ] [ CrossRef ]
Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018 , 35 , 53–65. [ Google Scholar ] [ CrossRef ]
Dhyani, M.; Kumar, R. An intelligent Chatbot using deep learning with Bidirectional RNN and attention model. Mater. Today Proc. 2021 , 34 , 817–824. [ Google Scholar ] [ CrossRef ]
Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Part C Emerg. Technol. 2020 , 118 , 102674. [ Google Scholar ] [ CrossRef ]
Chen, D.; Yongchareon, S.; Lai, E.M.-K.; Yu, J.; Sheng, Q.Z.; Li, Y. Transformer with bidirectional GRU for nonintrusive, sensor-based activity recognition in a multiresident environment. IEEE Internet Things J. 2022 , 9 , 23716–23727. [ Google Scholar ] [ CrossRef ]
Mostafa, A.L.; Abdel-Galil, H.; Belal, M. Ensemble Model-based Weighted Categorical Cross-entropy Loss for Facial Expression Recognition. In Proceedings of the 2021 Tenth International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–6 December 2021. [ Google Scholar ]
Feng, L.; Shu, S.; Lin, Z.; Lv, F.; Li, L.; An, B. Can cross entropy loss be robust to label noise? In Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, Online, 7–15 January 2021.
Ruby, U.; Yendapalli, V. Binary cross entropy with deep learning technique for image classification. Int. J. Adv. Trends Comput. Sci. Eng. 2020 , 9 , 5393–5397. [ Google Scholar ]
Hernández-Vázquez, M.A.; Hernández-Rodríguez, Y.M.; Cortes-Rojas, F.D.; Bayareh-Mancilla, R.; Cigarroa-Mayorga, O.E. Hybrid Feature Mammogram Analysis: Detecting and Localizing Microcalcifications Combining Gabor, Prewitt, GLCM Features, and Top Hat Filtering Enhanced with CNN Architecture. Diagnostics 2024 , 14 , 1691. [ Google Scholar ] [ CrossRef ]
Suri, J.S.; Agarwal, S.; Carriero, A.; Paschè, A.; Danna, P.S.; Columbu, M.; Saba, L.; Viskovic, K.; Mehmedović, A.; Agarwal, S. COVLIAS 1.0 vs. MedSeg: Artificial intelligence-based comparative study for automated COVID-19 computed tomography lung segmentation in Italian and Croatian Cohorts. Diagnostics 2021 , 11 , 2367. [ Google Scholar ] [ CrossRef ]
Daneshjou, R.; Smith, M.P.; Sun, M.D.; Rotemberg, V.; Zou, J. Lack of transparency and potential bias in artificial intelligence data sets and algorithms: A scoping review. JAMA Dermatol. 2021 , 157 , 1362–1369. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Dubey, A.K.; Chabert, G.L.; Carriero, A.; Pasche, A.; Danna, P.S.; Agarwal, S.; Mohanty, L.; Nillmani; Sharma, N.; Yadav, S. Ensemble Deep Learning Derived from Transfer Learning for Classification of COVID-19 Patients on Hybrid Deep-Learning-Based Lung Segmentation: A Data Augmentation and Balancing Framework. Diagnostics 2023 , 13 , 1954. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Saba, L.; Than, J.C.; Noor, N.M.; Rijal, O.M.; Kassim, R.M.; Yunus, A.; Ng, C.R.; Suri, J.S. Inter-observer variability analysis of automatic lung delineation in normal and disease patients. J. Med. Syst. 2016 , 40 , 1–18. [ Google Scholar ] [ CrossRef ]
Suri, J.S.; Agarwal, S.; Saba, L.; Chabert, G.L.; Carriero, A.; Paschè, A.; Danna, P.; Mehmedović, A.; Faa, G.; Jujaray, T. Multicenter study on COVID-19 lung computed tomography segmentation with varying glass ground opacities using unseen deep learning artificial intelligence paradigms: COVLIAS 1.0 validation. J. Med. Syst. 2022 , 46 , 62. [ Google Scholar ] [ CrossRef ]
Unnikrishnan, P.; Kumar, D.K.; Arjunan, S.P.; Kumar, H.; Mitchell, P.; Kawasaki, R. Development of health parameter model for risk prediction of CVD using SVM. Comput. Math. Methods Med. 2016 , 2016 , 3016245. [ Google Scholar ] [ CrossRef ]
Zhou, R.; Guo, F.; Azarpazhooh, M.R.; Hashemi, S.; Cheng, X.; Spence, J.D.; Ding, M.; Fenster, A. Deep learning-based measurement of total plaque area in B-mode ultrasound images. IEEE J. Biomed. Health Inform. 2021 , 25 , 2967–2977. [ Google Scholar ] [ CrossRef ]
Jain, P.K.; Sharma, N.; Giannopoulos, A.A.; Saba, L.; Nicolaides, A.; Suri, J.S. Hybrid deep learning segmentation models for atherosclerotic plaque in internal carotid artery B-mode ultrasound. Comput. Biol. Med. 2021 , 136 , 104721. [ Google Scholar ] [ CrossRef ]
Jain, P.K.; Sharma, N.; Saba, L.; Paraskevas, K.I.; Kalra, M.K.; Johri, A.; Laird, J.R.; Nicolaides, A.N.; Suri, J.S. Unseen artificial intelligence—Deep learning paradigm for segmentation of low atherosclerotic plaque in carotid ultrasound: A multicenter cardiovascular study. Diagnostics 2021 , 11 , 2257. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Jain, P.K.; Sharma, N.; Saba, L.; Paraskevas, K.I.; Kalra, M.K.; Johri, A.; Nicolaides, A.N.; Suri, J.S. Automated deep learning-based paradigm for high-risk plaque detection in B-mode common carotid ultrasound scans: An asymptomatic Japanese cohort study. Int. Angiol. 2021 , 41 , 9–23. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Agarwal, M.; Agarwal, S.; Saba, L.; Chabert, G.L.; Gupta, S.; Carriero, A.; Pasche, A.; Danna, P.; Mehmedovic, A.; Faa, G. Eight pruning deep learning models for low storage and high-speed COVID-19 computed tomography lung segmentation and heatmap-based lesion localization: A multicenter study using COVLIAS 2.0. Comput. Biol. Med. 2022 , 146 , 105571. [ Google Scholar ] [ CrossRef ]
Suri, J.S.; Bhagawati, M.; Paul, S.; Protogeron, A.; Sfikakis, P.P.; Kitas, G.D.; Khanna, N.N.; Ruzsa, Z.; Sharma, A.M.; Saxena, S. Understanding the bias in machine learning systems for cardiovascular disease risk assessment: The first of its kind review. Comput. Biol. Med. 2022 , 142 , 105204. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Narayanan, R.; Werahera, P.; Barqawi, A.; Crawford, E.; Shinohara, K.; Simoneau, A.; Suri, J. Adaptation of a 3D prostate cancer atlas for transrectal ultrasound guided target-specific biopsy. Phys. Med. Biol. 2008 , 53 , N397. [ Google Scholar ] [ CrossRef ]
Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [ Google Scholar ]
Bartlett, P.L.; Wegkamp, M.H. Classification with a Reject Option using a Hinge Loss. J. Mach. Learn. Res. 2008 , 9 , 1823–1840. [ Google Scholar ]
Bénédict, G.; Koops, V.; Odijk, D.; de Rijke, M. SigmoidF1: A smooth F1 score surrogate loss for multilabel classification. arXiv 2021 , arXiv:2108.10566. [ Google Scholar ]
Kyriacou, E.C.; Petroudi, S.; Pattichis, C.S.; Pattichis, M.S.; Griffin, M.; Kakkos, S.; Nicolaides, A. Prediction of high-risk asymptomatic carotid plaques based on ultrasonic image features. IEEE Trans. Inf. Technol. Biomed. 2012 , 16 , 966–973. [ Google Scholar ] [ CrossRef ]
El-Barghouty, N.; Nicolaides, A.; Bahal, V.; Geroulakos, G.; Androulakis, A. The identification of the high risk carotid plaque. Eur. J. Vasc. Endovasc. Surg. 1996 , 11 , 470–478. [ Google Scholar ] [ CrossRef ]
Stoitsis, J.; Golemati, S.; Nikita, K.; Nicolaides, A. Characterization of carotid atherosclerosis based on motion and texture features and clustering using fuzzy c-means. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004. [ Google Scholar ]
Loizou, C.P.; Petroudi, S.; Pantziaris, M.; Nicolaides, A.N.; Pattichis, C.S. An integrated system for the segmentation of atherosclerotic carotid plaque ultrasound video. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2014 , 61 , 86–101. [ Google Scholar ] [ CrossRef ]
Stoitsis, J.; Golemati, S.; Kendros, S.; Nikita, K. Automated detection of the carotid artery wall in B-mode ultrasound images using active contours initialized by the Hough transform. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–25 August 2008. [ Google Scholar ]
Matsakou, A.I.; Golemati, S.; Stoitsis, J.S.; Nikita, K.S. Automated detection of the carotid artery wall in longitudinal B-mode images using active contours initialized by the Hough transform. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–2 September 2011. [ Google Scholar ]
Suri, J.S. Two-dimensional fast magnetic resonance brain segmentation. IEEE Eng. Med. Biol. Mag. 2001 , 20 , 84–95. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Kiernan, M.J.; Al Mukaddim, R.; Mitchell, C.C.; Maybock, J.; Wilbrand, S.M.; Dempsey, R.J.; Varghese, T. Lumen segmentation using a Mask R-CNN in carotid arteries with stenotic atherosclerotic plaque. Ultrasonics 2024 , 137 , 107193. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Zhou, R.; Guo, F.; Azarpazhooh, M.R.; Spence, J.D.; Gan, H.; Ding, M.; Fenster, A. Carotid vessel-wall-volume ultrasound measurement via a UNet++ ensemble algorithm trained on small data sets. Ultrasound Med. Biol. 2023 , 49 , 1031–1036. [ Google Scholar ] [ CrossRef ] [ PubMed ]
El-Baz, A.; Suri, J.S. Big Data in Multimodal Medical Imaging ; CRC Press: Boca Raton, FL, USA, 2019. [ Google Scholar ]
Rumsfeld, J.S.; Joynt, K.E.; Maddox, T.M. Big data analytics to improve cardiovascular care: Promise and challenges. Nat. Rev. Cardiol. 2016 , 13 , 350–359. [ Google Scholar ] [ CrossRef ]
Krittanawong, C.; Johnson, K.W.; Hershman, S.G.; Tang, W.W. Big data, artificial intelligence, and cardiovascular precision medicine. Expert Rev. Precis. Med. Drug Dev. 2018 , 3 , 305–317. [ Google Scholar ] [ CrossRef ]
Hulsen, T.; Friedecký, D.; Renz, H.; Melis, E.; Vermeersch, P.; Fernandez-Calle, P. From big data to better patient outcomes. Clin. Chem. Lab. Med. CCLM 2023 , 61 , 580–586. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Dabla, P.K. Unlocking new potential of clinical diagnosis with artificial intelligence: Finding new patterns of clinical and lab data. World J. Diabetes 2024 , 15 , 308. [ Google Scholar ] [ CrossRef ]
Wang, S.; Xie, T.; Liu, H.; Zhang, X.; Cheng, J. PSE-Net: Channel pruning for Convolutional Neural Networks with parallel-subnets estimator. Neural Netw. 2024 , 174 , 106263. [ Google Scholar ] [ CrossRef ]
Louati, H.; Louati, A.; Bechikh, S.; Kariri, E. Embedding channel pruning within the CNN architecture design using a bi-level evolutionary approach. J. Supercomput. 2023 , 79 , 16118–16151. [ Google Scholar ] [ CrossRef ]
Hong, W.; Li, G.; Liu, S.; Yang, P.; Tang, K. Multi-objective evolutionary optimization for hardware-aware neural network pruning. Fundam. Res. 2022 , 4 , 941–950. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Hollmann, N.; Müller, S.; Eggensperger, K.; Hutter, F. Tabpfn: A transformer that solves small tabular classification problems in a second. arXiv 2022 , arXiv:2207.01848. [ Google Scholar ]
Huang, X.; Khetan, A.; Cvitkovic, M.; Karnin, Z. Tabtransformer: Tabular data modeling using contextual embeddings. arXiv 2020 , arXiv:2012.06678. [ Google Scholar ]
Somepalli, G.; Goldblum, M.; Schwarzschild, A.; Bruss, C.B.; Goldstein, T. Saint: Improved neural networks for tabular data via row attention and contrastive pre-training. arXiv 2021 , arXiv:2106.01342. [ Google Scholar ]
Makris, G.C.; Lavida, A.; Griffin, M.; Geroulakos, G.; Nicolaides, A.N. Three-dimensional ultrasound imaging for the evaluation of carotid atherosclerosis. Atherosclerosis 2011 , 219 , 377–383. [ Google Scholar ] [ CrossRef ]
Kyriacou, E.C.; Pattichis, C.; Pattichis, M.; Loizou, C.; Christodoulou, C.; Kakkos, S.K.; Nicolaides, A. A review of noninvasive ultrasound image processing methods in the analysis of carotid plaque morphology for the assessment of stroke risk. IEEE Trans. Inf. Technol. Biomed. 2010 , 14 , 1027–1038. [ Google Scholar ] [ CrossRef ]
Chen, Z.; Jiang, M.; Chiu, B. Unsupervised shape-and-texture-based generative adversarial tuning of pre-trained networks for carotid segmentation from 3D ultrasound images. Med. Phys. 2024 . early view . [ Google Scholar ] [ CrossRef ]

CVP	Models	ACC (%)	SPEC (%)	SEN (%)	p-Value	AUC (0–1)
K2	RNN	80.11	82.96	81.87	<0.001	0.883
	GRU	81.12	83.32	82.16	<0.001	0.892
	LSTM	81.81	85.67	83.36	<0.001	0.907
K4	RNN	82.52	81.97	83.88	<0.001	0.850
	GRU	83.13	82.33	84.17	<0.001	0.897
	LSTM	84.82	84.68	85.37	<0.001	0.908
K5	RNN	83.50	82.95	84.86	<0.001	0.895
	GRU	84.11	83.31	85.15	<0.001	0.900
	LSTM	85.80	85.66	86.35	<0.001	0.916
K10	RNN	84.20	83.15	83.86	<0.001	0.896
	GRU	85.12	84.11	86.15	<0.001	0.902
	LSTM	86.80	86.67	87.35	<0.001	0.918

CVP.	Models	ACC (%)	SPEC (%)	SEN (%)	p-Value	AUC (0–1)
K2	BiRNN	82.22	80.16	82.34	<0.001	0.891
	BiGRU	83.42	81.17	83.18	<0.001	0.905
	BiLSTM	84.32	83.29	84.12	<0.001	0.913
K4	BiRNN	83.28	82.66	83.94	<0.001	0.910
	BiGRU	84.24	83.12	84.28	<0.001	0.915
	BiLSTM	85.13	85.68	86.52	<0.001	0.923
K5	BiRNN	84.28	83.66	84.94	<0.001	0.920
	BiGRU	85.24	84.12	85.28	<0.001	0.925
	BiLSTM	86.13	86.68	87.52	<0.001	0.933
K10	BiRNN	85.27	84.65	85.93	<0.001	0.920
	BiGRU	86.23	85.11	86.27	<0.001	0.925
	BiLSTM	87.00	86.67	88.51	<0.001	0.935

CVP	Models	ACC (%)	SPEC (%)	SEN (%)	p-Value	AUC (0–1)
K2	RNN + GRU	85.00	82.76	82.62	<0.001	0.930
	RNN + LSTM	85.91	85.37	83.56	<0.001	0.939
	LSTM + GRU	88.02	88.16	84.62	<0.001	0.943
	BiRNN + BiGRU	90.53	89.75	88.32	<0.001	0.954
	BiRNN + BiLSTM	91.84	90.18	88.32	<0.001	0.968
	BiLSTM + BiGRU	94.14	92.22	89.12	<0.001	0.974
K4	RNN + GRU	86.66	83.76	83.62	<0.001	0.931
	RNN + LSTM	86.02	86.37	84.56	<0.001	0.940
	LSTM + GRU	89.02	89.16	85.62	<0.001	0.944
	BiRNN + BiGRU	91.53	90.75	87.32	<0.001	0.955
	BiRNN + BiLSTM	92.84	91.18	89.32	<0.001	0.969
	BiLSTM + BiGRU	95.14	93.22	90.12	<0.001	0.975
K5	RNN + GRU	86.45	82.76	84.62	<0.001	0.947
	RNN + LSTM	86.50	85.37	86.56	<0.001	0.957
	LSTM + GRU	91.02	88.16	87.62	<0.001	0.959
	BiRNN + BiGRU	93.53	84.75	87.32	<0.001	0.972
	BiRNN + BiLSTM	94.84	86.18	87.32	<0.001	0.976
	BiLSTM + BiGRU	96.14	92.22	93.12	<0.001	0.982
K10	RNN + GRU	88.14	82.75	84.61	<0.001	0.948
	RNN + LSTM	88.24	84.36	85.55	<0.001	0.958
	LSTM + GRU	92.01	87.15	86.61	<0.001	0.960
	BiRNN + BiGRU	94.52	88.74	87.31	<0.001	0.975
	BiRNN + BiLSTM	95.83	89.17	87.31	<0.001	0.979
	BiLSTM + BiGRU	97.25	92.21	93.11	<0.001	0.985

SN	PCA	CST	RFR
1	Age	Age	Age
2	Diabetes T1D	Diabetes T1D	Diabetes T1 D
3	Avg Sys before angio	Avg Sys before angio	Avg Sys before angio
4	IPN	IPN	IPN
5	Creatinine	Creatinine	Creatinine
6	Hyperlipidemia	Hyperlipidemia	Hyperlipidemia
7	Alpha-Blockers	Alpha-Blockers	Alpha-Blockers
8	Insulin	Family Hx of CVD	Current Smoker
9	Angina	Current Smoker	BMI
10	Anti-Platelet/Anti-Coagulants	Anti-Platelet/Anti-Coagulants	TPA

SN	M1 (a)	M2 (b)	% Increase (a − b/a) × 100
1	ML	HDL	30.20%
2	UniDL	HDL	8.72%
3	BiDL	HDL	7.26%

Seen Data				Unseen Data
SN	Models	Mean AUC (0–1)	p-Value	Mean AUC (0–1)	p-Value	Difference (%)
1	ML	0.702	<0.005	0.683	<0.005	2.78%
2	UniDL	0.910	<0.001	0.884	<0.001	2.94%
3	BiDL	0.931	<0.001	0.905	<0.001	2.87%
4	HDL	0.956	<0.001	0.939	<0.001	1.79%

SN	Model1	Model2	Mann-Whitney
1	BiRNN	RNN	p < 0.05
2	BiGRU + BiRNN	RNN	p < 0.05
3	BiRNN + BiLSTM	BiRNN	p < 0.05
4	BiRNN + BiLSTM	RNN	p < 0.05
5	BiRNN + BiGRU	BiRNN	p < 0.05
6	BiRNN + BiGRU	RNN	p < 0.05
7	BiLSTM + BiGRU	RNN	p < 0.05
8	BiLSTM + BiGRU	BiRNN	p < 0.05

C0	C1	C2	C3	C4	C5	C6	C7
SN	Authors	NOF	ML/DL Models Used	#Patients/#Images	CV	SV	Results Obtained
R1	Unnikrishnan et al. [ ]	09	SVM	2.4 K	K5	🗴	AUC for ML = 0.71; for CCVRC = 0.57
R2	Jamthikar et al. [ ]	39	RF, SVM, XGBoost	500	K10	✓	AUC for ML = 0.95; for CCVRC = 0.50
R3	Alaa et al. [ ]	473	SVM, GBM, RF, AdaBoost	423.6 K	K10	🗴	AUC for ML = 0.724; for CCVRC = 0.774
R4	Zhou et al. [ ]	🗴	UNet++	144/510 497/638	K5	🗴	TPA error = 5.55 ± 4.34 mm ; DSC = 83.3–85.7%
R5	Jain et al. [ ]	🗴	UNet+, UNet, SegNetUNet, SegNet, Unet + SegNet	97/970	K5	🗴	AUC for UNet = 0.91, for UNet + = 0.91, for SegNet-UNet = 0.908, for SegNet = 0.905, and for SegNetUNet+ = 0.898 (using CE-loss models) and 0.883, 0.889, 0.905, 0.889, and 0.907 (using DSC-loss models); PA error = 3.49 mm for SDL and 4.21 mm for HDL
R6	Jain et al. [ ]	24	UNet	379, 300	K10	🗴	Unseen FoM: 70.96 and 91.14 Seen FoM: 97.57, 88.89, and 99.14
R7	Jain et al. [ ]	24	🗴 AtheroEdge 2.0, UNet, UNetSegNet	379	K10	🗴	AUC for UNet = 0.93, for SegNet-UNet = 0.94; for AtheroEdge™ 2.0 = 0.95, respectively; SDL PA error = 9.9 mm ; HDL PA error = 8 mm ; AtheroEdge™ = 2.0 mm ; PA error = 9.6 mm
R8	Johri et al. [ ]	39	RF, SVM, RNN, LSTM	500	K10	✓	AUC for DL AUC = 0.99, for ML = 0.89, for CCVRC = 0.50
R9	Akari et al. [ ]	56	SVM	4004	K10	✓	ACC = 98.43; reliability index = 97.32%
R10	Proposed method	39	SVM, RF, XGBoost, UniDL, BiDL, HDL	500	K2, K4, K5, K10	✓	AUC for ML = 0.702, for UniDL = 0.910, for BiDL = 0.931, and for HDL = 0.956

The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

Bhagawati, M.; Paul, S.; Mantella, L.; Johri, A.M.; Gupta, S.; Laird, J.R.; Singh, I.M.; Khanna, N.N.; Al-Maini, M.; Isenovic, E.R.; et al. Cardiovascular Disease Risk Stratification Using Hybrid Deep Learning Paradigm: First of Its Kind on Canadian Trial Data. Diagnostics 2024 , 14 , 1894. https://doi.org/10.3390/diagnostics14171894

Bhagawati M, Paul S, Mantella L, Johri AM, Gupta S, Laird JR, Singh IM, Khanna NN, Al-Maini M, Isenovic ER, et al. Cardiovascular Disease Risk Stratification Using Hybrid Deep Learning Paradigm: First of Its Kind on Canadian Trial Data. Diagnostics . 2024; 14(17):1894. https://doi.org/10.3390/diagnostics14171894

Bhagawati, Mrinalini, Sudip Paul, Laura Mantella, Amer M. Johri, Siddharth Gupta, John R. Laird, Inder M. Singh, Narendra N. Khanna, Mustafa Al-Maini, Esma R. Isenovic, and et al. 2024. "Cardiovascular Disease Risk Stratification Using Hybrid Deep Learning Paradigm: First of Its Kind on Canadian Trial Data" Diagnostics 14, no. 17: 1894. https://doi.org/10.3390/diagnostics14171894

Article Metrics

Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals

IMAGES

P-Value
What is P-value in hypothesis testing
P-Value Method For Hypothesis Testing
Understanding P-Values and Statistical Significance
Hypothesis testing tutorial using p value method
Understanding P-Values and Statistical Significance

VIDEO

A P-Value Explanation That You Won't Forget
24. p-Value in Hypothesis Testing
Statistics: Hypothesis Testing
Elementary Statistics Hypothesis testing for the Difference Between Two Means using t-test
What is Hypothesis Testing?
Chapter 9

COMMENTS

P-Value in Statistical Hypothesis Tests: What is it?
P Value Definition. A p value is used in hypothesis testing to help you support or reject the null hypothesis. The p value is the evidence against a null hypothesis. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis. P values are expressed as decimals although it may be easier to understand what they ...
Hypothesis Testing, P Values, Confidence Intervals, and Significance
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting ...
How to Find the P value: Process and Calculations
To find the p value for your sample, do the following: Identify the correct test statistic. Calculate the test statistic using the relevant properties of your sample. Specify the characteristics of the test statistic's sampling distribution. Place your test statistic in the sampling distribution to find the p value.
S.3.2 Hypothesis Testing (P-Value Approach)
It can be shown using statistical software that the P-value is 0.0127. The graph depicts this visually. The P-value, 0.0127, tells us it is "unlikely" that we would observe such an extreme test statistic t* in the direction of H A if the null hypothesis were true. Therefore, our initial assumption that the null hypothesis is true must be incorrect.
Understanding P-Values and Statistical Significance
A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true). The level of statistical significance is often expressed as a p-value between 0 and 1. The smaller the p -value, the less likely the results occurred by random chance, and the ...
Interpreting P values
Here is the technical definition of P values: P values are the probability of observing a sample statistic that is at least as extreme as your sample statistic when you assume that the null hypothesis is true. Let's go back to our hypothetical medication study. Suppose the hypothesis test generates a P value of 0.03.
p-value
The p -value is used in the context of null hypothesis testing in order to quantify the statistical significance of a result, the result being the observed value of the chosen statistic . [note 2] The lower the p -value is, the lower the probability of getting that result if the null hypothesis were true. A result is said to be statistically ...
p-value Calculator
To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true.Then, with the help of the cumulative distribution function (cdf) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:Left-tailed test:
How Hypothesis Tests Work: Significance Levels (Alpha) and P values
Hypothesis testing is a vital process in inferential statistics where the goal is to use sample data to draw conclusions about an entire population. In the testing process, you use significance levels and p-values to determine whether the test results are statistically significant.
Hypothesis Testing
The results of hypothesis testing will be presented in the results and discussion sections of your research paper, dissertation or thesis. In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p-value).
P-Value: Comprehensive Guide to Understand, Apply, and Interpret
The p-value, or probability value, is a statistical measure used in hypothesis testing to assess the strength of evidence against a null hypothesis. It represents the probability of obtaining results as extreme as, or more extreme than, the observed results under the assumption that the null hypothesis is true.
What is P-Value?
It is the cutoff probability for p-value to establish statistical significance for a given hypothesis test. For an observed effect to be considered as statistically significant, the p-value of the test should be lower than the pre-decided alpha value. Typically for most statistical tests (but not always), alpha is set as 0.05.
P-Value: What It Is, How to Calculate It, and Why It Matters
P-value is the level of marginal significance within a statistical hypothesis test, representing the probability of the occurrence of a given event.
6 Week 5 Introduction to Hypothesis Testing Reading
A statistical hypothesis test has a null hypothesis, the status quo, what we assume to be true. Notation is H 0, read as "H naught". ... The p-value can also be thought of as the probability that the results (from the sample) that we are seeing are solely due to chance. This concept will be discussed in much further detail in the class notes.
Khan Academy
Khanmigo is now free for all US educators! Plan lessons, develop exit tickets, and so much more with our AI teaching assistant.
Understanding Hypothesis Tests: Significance Levels (Alpha) and P
When a P value is less than or equal to the significance level, you reject the null hypothesis. If we take the P value for our example and compare it to the common significance levels, it matches the previous graphical results. The P value of 0.03112 is statistically significant at an alpha level of 0.05, but not at the 0.01 level.
Understanding Hypothesis Testing
Note: The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
What Is P-Value in Statistical Hypothesis?
The p-value or probability value is a number, calculated from a statistical test, that tells how likely it is that your results would have occurred under the null hypothesis of the test. P-values are usually automatically calculated using statistical software. They can also be calculated using p-value tables for the relevant statistical test.
P-Value (Definition, Formula, Table & Example)
The P-value is known as the level of marginal significance within the hypothesis testing that represents the probability of occurrence of the given event. The P-value is used as an alternative to the rejection point to provide the least significance at which the null hypothesis would be rejected. If the P-value is small, then there is stronger ...
P-value Calculator
A P-value calculator is used to determine the statistical significance of an observed result in hypothesis testing. It takes as input the observed test statistic, the null hypothesis, and the relevant parameters of the statistical test (such as degrees of freedom), and computes the p-value. The p-value represents the probability of obtaining ...
Hypothesis Testing in Statistics
The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.
PDF Quantitative Understanding in Biology 1.4 p-Values and Formal
1.4 p-Values and Formal Statistical Tests Jason Banfelder September 21st, 2023 1 Introduction to p-values We have already seen one example of formal statistical testing when we tested for the normality of a sample from a univariate distribution. To reiterate, formal statistical testing begins with a statement of the null hypothesis, H 0. The ...
Inferential Statistics: Hypothesis Testing and Confidence
Statistics document from University of Mississippi, 2 pages, Question 1 A. Hypotheses: H0:μ=60 Ha:μ≠60 Test statistic = (58.5-60)/(6/7) = -1.75 P-Value P(Z≤−1.75)≈0.0401 Two-tailed P-value=2×0.0401=0.0802 Since P=0.0802>0.05, we fail to reject H 0. There is not enough evidence to conclude the true mean is different
What is Bayesian Statistics, and How Does it Differ from Classical
Advantages of Bayesian Statistics. It handles multiple tests well. Since testing isn't forced into a true/false proposition, Bayesian statistics is well-suited for multiple testing situations. It offers incorporation of previous information and continuous updating. Bayesian statistics shines in situations where there's a lot of prior data.
Diagnostics
The AtheroEdge™ 3.0 HDL was scientifically validated using seen and unseen datasets while the reliability and statistical tests were conducted using CST along with p-value significance. The performance of AtheroEdge™ 3.0 HDL was evaluated by measuring the p-value and area-under-the-curve for both seen and unseen data.

P-Value in Statistical Hypothesis Tests: What is it?

P Value vs Alpha level

P Values and Critical Values

What if I Don’t Have an Alpha Level?

How to Calculate a P Value on the TI 83

StatPearls [Internet].

Affiliations

In this Page

Related information

Similar articles in PubMed

Recent Activity

User Preferences

Keyboard Shortcuts

Example S.3.2.1

Right Tailed

Left Tailed

P-Value And Statistical Significance: What It Is & Why It Matters

Hypothesis testing

What a p-value tells you

Example: Test Statistic and p-Value

P-value interpretation

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

Example: Statistical Significance

What does a p-value of 0.001 mean?

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

One-Tailed Test

Two-Tailed Test

How do you calculate the p-value ?

Example: Choosing a Statistical Test

How to report

Example: Reporting the results

Why is the p -value not enough?

When do you reject the null hypothesis?

What does p-value of 0.05 mean?

Are all p-values below 0.05 considered statistically significant?

How does sample size affect the interpretation of p-values?

Can a non-significant p-value indicate that there is no effect or difference in the data?

Can P values be exactly zero?

Further Information

p-value Calculator

Can p-value be negative?

What does a high p-value mean?

What does a low p-value mean?

Index of qualitative variation

How Hypothesis Tests Work: Significance Levels (Alpha) and P values

Hypothesis Test Example Scenario

Descriptive Statistics Alone Won’t Answer the Question

A Sampling Distribution Determines Whether Our Sample Mean is Unlikely

Graphing our Sample Mean in the Context of the Sampling Distribution

The Role of Hypothesis Tests

What are Significance Levels (Alpha)?

Graphing Significance Levels as Critical Regions

Comparing Significance Levels

What Are P values?

Using P values and Significance Levels Together

Discussion about Statistically Significant Results

Share this:

Reader Interactions

Comments and Questions Cancel reply

Have a language expert improve your writing

Hypothesis Testing | A Step-by-Step Guide with Easy Examples

Table of contents

Receive feedback on language, structure, and formatting

Here's why students love Scribbr's proofreading services

Cite this Scribbr article

Is this article helpful?

Rebecca Bevans

What is P-Value? – Understanding the meaning, math and methods

Introduction

Examples of Statistical Tests reporting out p-value

What p-value really is

How is p-value used to establish statistical significance

Practical Guidelines to set the cutoff of Statistical Significance (alpha level)

What P Value is Not

Example: How to find p-value for linear regression

More Articles

Machine Learning A-Z™: Hands-On Python & R In Data Science

What Is P-Value?

The Bottom Line

P-Value: What It Is, How to Calculate It, and Why It Matters