student solves unsolvable math problem homework

The Legend of the 'Unsolvable Math Problem'

A student mistook examples of unsolved math problems for a homework assignment and solved them., david mikkelson, published dec. 3, 1996.

About this rating

A legend about the "unsolvable math problem" combines one of the ultimate academic wish-fulfillment fantasies — a student not only proves himself the smartest one in his class, but also bests his professor and every other scholar in his field of study — with a "positive thinking" motif that turns up in other urban legends: when people are free to pursue goals unfettered by presumed limitations on what they can accomplish, they just may manage some extraordinary feats through the combined application of native talent and hard work:

A young college student was working hard in an upper-level math course, for fear that he would be unable to pass. On the night before the final, he studied so long that he overslept the morning of the test. When he ran into the classroom several minutes late, he found three equations written on the blackboard. The first two went rather easily, but the third one seemed impossible. He worked frantically on it until — just ten minutes short of the deadline — he found a method that worked, and he finished the problems just as time was called. The student turned in his test paper and left. That evening he received a phone call from his professor. "Do you realize what you did on the test today?" he shouted at the student. "Oh, no," thought the student. I must not have gotten the problems right after all. "You were only supposed to do the first two problems," the professor explained. "That last one was an example of an equation that mathematicians since Einstein have been trying to solve without success. I discussed it with the class before starting the test. And you just solved it!"

And this particular version is all the more interesting for being based on a real-life incident!

One day in 1939, George Bernard Dantzig, a doctoral candidate at the University of California, Berkeley, arrived late for a graduate-level statistics class and found two problems written on the board. Not knowing they were examples of "unsolved" statistics problems, he mistook them for part of a homework assignment, jotted them down, and solved them. (The equations Dantzig tackled are more accurately described not as unsolvable problems, but rather as unproven statistical theorems for which he worked out proofs.)

Six weeks later, Dantzig's statistics professor notified him that he had prepared one of his two "homework" proofs for publication, and Dantzig was given co-author credit on a second paper several years later when another mathematician independently worked out the same solution to the second problem.

George Dantzig recounted his feat in a 1986 interview for the College Mathematics Journal :

It happened because during my first year at Berkeley I arrived late one day at one of [Jerzy] Neyman's classes. On the blackboard there were two problems that I assumed had been assigned for homework. I copied them down. A few days later I apologized to Neyman for taking so long to do the homework — the problems seemed to be a little harder than usual. I asked him if he still wanted it. He told me to throw it on his desk. I did so reluctantly because his desk was covered with such a heap of papers that I feared my homework would be lost there forever. About six weeks later, one Sunday morning about eight o'clock, [my wife] Anne and I were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: "I've just written an introduction to one of your papers. Read it so I can send it out right away for publication." For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard that I had solved thinking they were homework were in fact two famous unsolved problems in statistics. That was the first inkling I had that there was anything special about them. A year later, when I began to worry about a thesis topic, Neyman just shrugged and told me to wrap the two problems in a binder and he would accept them as my thesis. The second of the two problems, however, was not published until after World War II. It happened this way. Around 1950 I received a letter from Abraham Wald enclosing the final galley proofs of a paper of his about to go to press in the Annals of Mathematical Statistics. Someone had just pointed out to him that the main result in his paper was the same as the second "homework" problem solved in my thesis. I wrote back suggesting we publish jointly. He simply inserted my name as coauthor into the galley proof.

Dr. Dantzig also explained how his story passed into the realm of urban legendry:

The other day, as I was taking an early morning walk, I was hailed by Don Knuth as he rode by on his bicycle. He is a colleague at Stanford. He stopped and said, "Hey, George — I was visiting in Indiana recently and heard a sermon about you in church. Do you know that you are an influence on Christians of middle America?" I looked at him, amazed. "After the sermon," he went on, "the minister came over and asked me if I knew a George Dantzig at Stanford, because that was the name of the person his sermon was about." The origin of that minister's sermon can be traced to another Lutheran minister, the Reverend Schuler [sic] of the Crystal Cathedral in Los Angeles. He told me his ideas about thinking positively, and I told him my story about the homework problems and my thesis. A few months later I received a letter from him asking permission to include my story in a book he was writing on the power of positive thinking. Schuler's published version was a bit garbled and exaggerated but essentially correct. The moral of his sermon was this: If I had known that the problem were not homework but were in fact two famous unsolved problems in statistics, I probably would not have thought positively, would have become discouraged, and would never have solved them.

The version of Dantzig's story published by Christian televangelist Robert Schuller contained a good deal of embellishment and misinformation which has since been propagated in urban legend-like forms of the tale such as the one quoted at the head of this page: Schuller converted the mistaken homework assignment into a "final exam" with ten problems (eight of which were real and two of which were "unsolvable"), claimed that "even Einstein was unable to unlock the secrets" of the two extra problems, and erroneously stated that Dantzig's professor was so impressed that he "gave Dantzig a job as his assistant, and Dantzig has been at Stanford ever since."

George Dantzig (himself the son of a mathematician) received a Bachelor's degree from University of Maryland in 1936 and a Master's from the University of Michigan in 1937 before completing his Doctorate (interrupted by World War II) at UC Berkeley in 1946. He later worked for the Air Force, took a position with the RAND Corporation as a research mathematician in 1952, became professor of operations research at Berkeley in 1960, and joined the faculty of Stanford University in 1966, where he taught and published as a professor of operations research until the 1990s. In 1975, Dr. Dantzig was awarded the National Medal of Science by President Gerald Ford.

George Dantzig passed away at his Stanford home at age 90 on 13 May 2005.

Sightings:   This legend is used as the setup of the plot in the 1997 movie Good Will Hunting . As well, one of the early scenes in the 1999 film Rushmore shows the main character daydreaming about solving the impossible question and winning approbation from all.

Albers, Donald J. and Constance Reid.   "An Interview of George B. Dantzig: The Father of Linear Programming."     College Mathematics Journal.   Volume 17, Number 4; 1986   (pp. 293-314).

Brunvand, Jan Harold.   Curses! Broiled Again!     New York: W. W. Norton, 1989.   ISBN 0-393-30711-5   (pp. 278-283).

Dantzig, George B.     "On the Non-Existence of Tests of 'Student's' Hypothesis Having Power Functions Independent of Sigma."     Annals of Mathematical Statistics .   No. 11; 1940   (pp. 186-192).

Dantzig, George B. and Abraham Wald.   "On the Fundamental Lemma of Neyman and Pearson."     Annals of Mathematical Statistics .   No. 22; 1951   (pp. 87-93).

Pearce, Jeremy.   "George B. Dantzig Dies at 90."     The New York Times .   23 May 2005.

By David Mikkelson

David Mikkelson founded the site now known as snopes.com back in 1994.

Article Tags

A College Student Just Solved a Notoriously Impossible Math Problem

And the answer came from an incredibly unlikely place.

Gear-obsessed editors choose every product we review. We may earn commission if you buy from a link. Why Trust Us?

• A mathematician may have just proved the impossible possible.
• For 30 years, mathematicians wondered if you could have an infinite set of numbers where each pair of numbers adds up to a unique value, and have those values each be fairly large.
• In March, a graduate student from Oxford University finally solved the problem by turning to an unlikely solution: geometry.

Let us explain.

Named after another Hungarian mathematician, Simon Sidon, these sets are basically a collection of numbers where no two numbers in the set add up to the same integer. For example, in the simple Sidon set (1, 3, 5, 11), when any of the two numbers in the set are added together, they equal a unique number. Constructing a Sidon set with only four numbers is extremely easy, but as the set increases in size, it just gets harder and harder. As soon as two sums are the same, the collection of numbers is no longer considered a Sidon set.

The second element of Erdős’ problem—that scary-sounding “asymptotic basis of order three” part—means that:

• a set must be infinitely large
• any large enough integer can be written as the result of adding together at most 3 numbers in the set.

So, this 30-year-old conundrum centered on whether or not these two elements could exist in the same set of numbers. For decades, the answer seemed to be no.

But in March of this year, Oxford graduate student Cédric Pilatte published a proof confirming the existence of such a Sidon set. Reaching that milestone wasn’t easy. In 2010, mathematicians proved that a Sidon set can be be an asymptotic basis of order 5 , and three years later, they proved that is was also possible for a Sidon set to “ be an asymptotic basis of order 4 .” But “order 3” remained elusive—some considered it theoretically possible but incredibly difficult (and potentially impossible) to prove.

“They’re pulling in opposite directions,” Pilatte told Quanta Magazine . “Sidon sets are constrained to be small, and an asymptotic basis is constrained to be large. It was not obvious that it could work.”

So how did Pilatte get a mathematically square peg to fit a seemingly round hole? He took an unconventional approach and turned to geometry rather than the probabilistic method championed by Erdős and what’s called additive number theory. Pilatte replaced numbers with polynomials and made use of the recent work of Columbia University mathematicians . Combining these ideas, Pilatte successfully created a Sidon set dense enough and random enough to finally solve Erdős’s original problem.

Pilatte’s work relied on the discoveries of many mathematicians across different disciplines, and even combined seemingly unrelated fields of mathematics to answer the question. “It’s cool that these very deep techniques from algebraic geometry can also be used for this simple and concrete question about sets of numbers,” Pilatte told Quanta Magazine.

And with that, yet another “impossible” math question is found to be very much possible.

Darren lives in Portland, has a cat, and writes/edits about sci-fi and how our world works. You can find his previous stuff at Gizmodo and Paste if you look hard enough. 

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Math .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

Can AI Help Solve Math’s Thorniest Mysteries?

The History of Pi

Experts Discovered the Secret Geometry of Life

Scientists Solved a 141-Year-Old Problem

The Perfect Table Size for Your Jigsaw Puzzle

Breaking the 1880s Silk Dress Cryptogram

10 of the Hardest Math Problems Ever Solved

Solution to Riddle of the Week #12: Licking Frogs

Solution to Riddle of the Week #8

Can You Solve These 20 Tough Riddles for Adults?

Solution to Riddle of the Week #7

Trending →

Was beethoven’s musicality in his genes, do monkeys also get cranky with age , fall of the western roman empire in 476: history, causes and consequences, vase of soissons: legendary relic of french history, jean jaurès: socialist icon of france, george dantzig: the story of the overlooked genius.

The unappreciated talent. George Dantzig “accidentally” solved two unresolved statistics questions. But he was passed up for the Nobel Prize.

In 1939, George Bernard Dantzig, a doctorate candidate at the University of California, Berkeley, arrived a few minutes late to Jerzy Neyman’s statistics lecture while there were two homework problems posted on the board. He wrote them down and spent many days figuring out the answers. He was unaware that these were really two well-known statistics theorems that had never been proved before, not just regular exercise problems.

Dantzig subsequently said in an interview that:

A few days later I apologized to Neyman for taking so long to do the homework—the problems seemed to be a little harder than usual. I asked him if he still wanted it. He told me to throw it on his desk. I did so reluctantly because his desk was covered with such a heap of papers that I feared my homework would be lost there forever. About six weeks later, one Sunday morning about eight o’clock, we were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: “I’ve just written an introduction to one of your papers. Read it so I can send it out right away for publication.” For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard that I had solved thinking they were homework were in fact two famous unsolved problems in statistics.

The most renowned statistician in the world at the time, Neyman, was then asked by Dantzig the next year what subject he should choose for his doctoral thesis. Neyman shrugged and said, “Just put your treatments of the two issues in a folder.” He would accept it as a doctoral thesis.

Dantzig’s Early Life

The eldest child of Tobias Dantzig and Anja Ourisson, George Bernard Dantzig was born in Portland, Oregon. The parents had met while attending Henri Poincaré lectures at the Sorbonne in Paris, where they were both students.

They moved to the United States after getting married, where Tobias Dantzig, a native of Lithuania, had to start out by working odd jobs like a road builder and a lumberjack due to language barriers before obtaining a Ph.D. in mathematics from Indiana University; his wife took the master’s degree in French.

The parents thought that their children would have better chances in life if they were given the first names of famous people. Thus, the younger boy was given the first name Henri (after Henri Poincaré) in the hopes that he would one day become a mathematician, while the elder son was given the name George Bernard in the hopes that he would one day become a writer (like George Bernard Shaw).

The father taught mathematics at different institutions, including Johns Hopkins (Baltimore, Maryland), Columbia University (New York), and the University of Maryland, while the mother worked at the Library of Congress in Washington, DC. A book he released in 1930 on the history of the evolution of mathematics, Number – The Language of Science , has been reissued several times (most recently in 2005).

Dantzig continued to struggle with arithmetic in the early grades, but owing to his father’s daily assignment training regimen, particularly in geometry, Dantzig finally received top marks.

George Dantzig started his mathematical studies at the University of Maryland because, despite the fact that both of his parents were employed, the family did not have enough money to finance his studies in physics and mathematics at a prestigious university.

George Dantzig moved to the University of Michigan after receiving a bachelor’s degree, where he went on to complete his graduate studies in 1937. He subsequently accepted a position at the U.S. Bureau of Labor Statistics and participated in research on urban consumers’ purchasing habits after becoming weary of abstract mathematics.

Dantzig Was a Heartfelt Statistician

Dantzig first became interested in statistical concerns and techniques while working in this position. He requested Jerzy Neyman’s permission in 1939 to attend his PhD studies at the University of California, Berkeley (with a “teaching assistantship”). And thus, one day, the event that was described above occurred.

The PhD program was still in progress when the United States joined World War II . Dantzig relocated to Washington, D.C., and accepted a post as the director of the Statistical Control Division at the headquarters of the U.S. Air Force. He discovered that the military’s knowledge of the real inventory of aircraft and equipment was insufficient.

He devised a method to collect the necessary data in detail, particularly to make a thorough contract award, including the need for nuts and bolts.

Dantzig briefly returned to Berkeley after the war, where he eventually received his degree. Not simply for financial reasons but also because he preferred the chances and challenges of working for the Air Force, he declined an offer from the university to continue working there.

Dantzig saw the need to dynamize this rather static model and was motivated by the input-output analysis approach of the Russian-American mathematician Wassily Leontief, who had a position at Harvard University in Cambridge starting in 1931. Additionally, he aimed to improve it to the point where hundreds or even thousands of actions and locations could be recorded and optimized; at the time, this was a fascinating computing hurdle.

Dantzig’s Advancements in Military Planning

While employed by the Pentagon, Dantzig came to the conclusion that many planning choices were based solely on experience rather than objective criteria, yielding less than ideal outcomes. Linear inequalities are often used to characterize the requirements (restrictions), and specifying an objective function establishes the purpose of optimization, such as maximizing profit or decreasing resource consumption.

In English, the planning technique created by Dantzig is known as “linear programming,” where “ programming ” refers not to programming in the modern meaning of the word but rather to the phrase used in the military for the planning of procedures. The selected linear function modeling is referred to as being “linear.”

A half-plane in two dimensions and a half-space in three dimensions are both defined by a linear inequality. Convex polygons or convex polyhedrons are produced when many inequalities are taken into account; in the n-dimensional case, the corresponding convex structure is known as a “simplex”.

The so-called Simplex Algorithm , which Dantzig created in 1947, is a systematic approach for computing the best answer. Dantzig himself said of it: “The tremendous power of the simplex method is a constant surprise to me.”

The creation of the simplex algorithm, a technique for resolving linear programming problems, is widely regarded as one of Dantzig’s most important accomplishments. The goal of linear programming is to maximize a linear objective function within a set of linear constraints using a mathematical approach. The simplex algorithm has had a significant influence on many fields, including business, economics, and engineering, as a tool for tackling problems in linear programming.

His work on duality in linear programming is a cornerstone of modern optimization theory. To describe the association between a dependent variable and one or more independent variables, he also made significant contributions to the statistical procedure known as linear regression. George Dantzig is called “the father of linear programming” for that.

He Wasn’t Seen Worthy of the Nobel Prize

When Dantzig visited Princeton University to speak with John von Neumann towards the end of the year, the algorithm saw its first refinement. This bright mathematician and computer scientist quickly saw similarities between the methods he and Oskar Morgenstern outlined in their newly released book, “The Theory of Games,” (1944) and the linear optimization approach.

The search techniques have significantly improved over time, notably with the advent of computer use. Although other strategies, such as nonlinear modeling, were also studied, Dantzig’s “linear programming” technique was finally proven to be adequate.

Tjalling C. Koopmans, professor of research in economics at the University of Chicago, realized the value of linear planning from an economic perspective after speaking with Dantzig. His famous theory on the optimal use of exhaustible resources was born out of this. To the surprise of everyone in the field, Dantzig was left unaccomplished when Koopmans received the Nobel Prize in Economics in 1975, together with the Russian mathematician Leonid Vitaliyevich Kantorovich, who had earlier proposed comparable methods in 1939. But it took the West two decades to learn about them. Dantzig, who was always kind to his fellow men, handled this with remarkable perseverance, demonstrating his high degree of expertise.

Dantzig went to the RAND Corporation in Santa Monica in 1952 to continue developing computerized execution of processes after his work with the Air Force. He established the Operations Research Center after accepting a post at Berkeley’s Department of Industrial Engineering in 1960.

When it was first published in 1963 by Princeton University Press, his book Linear Programming and Extensions established the field of linear optimization. Dantzig began working at Stanford in 1966, when he also established the Systems Optimization Lab (SOL). He oversaw a total of 41 PhD students over the course of more than 30 years; all of them had bright futures in academia and the workplace after receiving their degrees from Dantzig.

Dantzig has received multiple honorary degrees and memberships in academies in recognition of his significant scientific accomplishments, including the National Medal of Science and the John von Neumann Theory Prize. The George B. Dantzig Prize is given every three years by the Mathematical Optimization Society (MOS) and the Society for Industrial and Applied Mathematics (SIAM) in recognition of the scientist and his achievements.

His health quickly deteriorated shortly after a celebration of his 90th birthday in 2004; a diabetes condition mixed with cardiovascular issues ultimately caused his death.

The Two Unsolved Homework Problems That George Dantzig Solved

The doctoral student George Bernard Dantzig came late to Jerzy Neyman’s statistics lecture in 1939, when two homework assignments were already written on the board. He put them in writing and spent many days trying to solve them. To him, these seemed like ordinary math exercises, but upon further investigation, he discovered that they were, in fact, proofs of two well-known theorems in statistics that had never been proven previously.

1. “On the Non-Existence of Tests of “Student’s” Hypothesis Having Power Functions Independent of σ”, 1940

In the paper, Dantzig investigates whether or not the power function (i.e., the likelihood of rejecting the null hypothesis) of the statistical test for the “Student’s” hypothesis (commonly known as the t-test) can be designed to be independent of the standard deviation of the population (σ).

The “Student’s” hypothesis is a statistical hypothesis test used to evaluate whether the means of two populations are substantially different from each other; it was named after the statistician William Sealy Gosset, who wrote under the pseudonym “Student.” A common statistical procedure for comparing the means of two samples, the t-test is based on the “Student’s” hypothesis and has extensive use.

Dantzig demonstrated that a power function independent of σ cannot be designed for a statistical test of the “Student’s” hypothesis. He then explained his results and gave evidence for them. The study has received several citations because of its significance for the development of statistical theory.

2. “On the Fundamental Lemma of Neyman and Pearson”, 1951

In 1951, George Dantzig published an article in the Annals of Mathematical Statistics titled “On the Fundamental Lemma of Neyman and Pearson.” As a result of statistical theory, Neyman and Pearson’s fundamental lemma has to do with the power of statistical tests, which Dantzig proves in his article.

Neyman and Pearson’s “fundamental lemma” is a universal conclusion that establishes a connection between the null and alternative hypotheses in a statistical test. If the null hypothesis holds, then the likelihood of detecting a test statistic that is more extreme than a specified value (the critical value) is proportional to the sample size of the test. If the null hypothesis is correct, then the test’s power (the probability of rejecting the null) will be proportional to the test size.

Dantzig provides a demonstration of Neyman and Pearson’s fundamental lemma and examines how this finding has practical consequences for statistical testing in his work. The study has again received a lot of attention for its groundbreaking addition to statistical theory.

George Dantzig, the Real Good Will Hunting

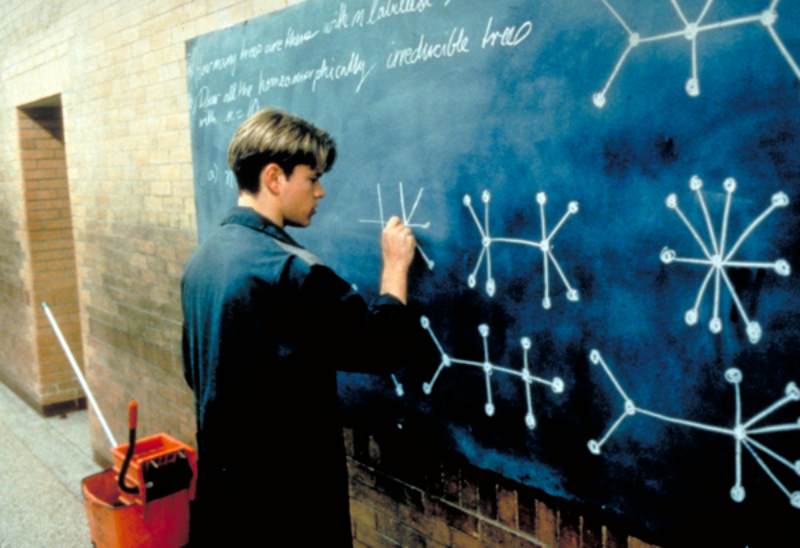
The American drama film “Good Will Hunting,” starring Matt Damon and Robin Williams, was directed by Gus Van Sant and released in 1997. Will Hunting, a young guy from South Boston who is a math prodigy yet works as a janitor at MIT, is the protagonist of this film. An MIT professor sees potential in Will, encourages him to pursue mathematics, and ultimately helps him conquer his own personal issues.

A memorable scene from Good Will Hunting has Matt Damon’s character, a janitor at a university, tackling an almost impossible graph problem on a chalkboard. Certain details were changed for dramatic effect, but the basic tale is based on real events related to George Dantzig. One day, future renowned mathematician George Dantzig was running late to his statistics class when he saw two statistical questions written on the whiteboard and assumed they were homework assignments. Dantzig later casually solved the long-unsolved problems of statistics.

George Dantzig’s Discoveries and Contributions

George Dantzig made important contributions to operations research and mathematical modeling. These are the important discoveries and contributions he made that bear mentioning:

• The simplex algorithm : In particular, Dantzig is lauded for creating the simplex algorithm, a standard technique for resolving linear programming issues. If you have a linear objective function and linear constraints, the simplex method may help you find the best solution.
• The theory of duality in linear programming : Dantzig established a cornerstone notion in optimization theory known as the principle of duality in linear programming. The best solution to a linear programming problem can be found with the help of duality theory, which establishes a link between the original problem and its dual problem.
• Contributions to linear regression : Dantzig’s contributions to the field of linear regression are substantial. Linear regression is a statistical technique for modeling the association between a dependent variable and one or more independent variables, and Dantzig made significant contributions to this area.
• Work on the transportation problem : Dantzig also did important work in the area of transportation problems, a kind of linear programming issue that includes determining the best possible route for resources to take between different points on a map.

When taken as a whole, Dantzig’s contributions to the fields of mathematics and computer science were influential and shaped the manner in which modern corporations and organizations use mathematical modeling to address difficult issues.

• Joe Holley (2005).  “Obituaries of George Dantzig” .
• Donald J.  Albers. (1990). “ More Mathematical People: Contemporary Conversations “
• On the Fundamental Lemma of Neyman and Pearson – Projecteuclid.org
• On the Non-Existence of Tests of “Student’s” Hypothesis Having Power Functions Independent of σ – Projecteuclid.org
• Dantzig, George (1940). “ On the non-existence of tests of “Student’s” hypothesis having power functions independent of σ “

The Northern Star Magazine Online

Student solves unsolvable problems, student solves ‘unsolvable’ statistical problems.

Mr. George Bernard Dantzig, a doctoral candidate at the University of California (USC), Berkeley in 1939, arrived late for his graduate-level statistics class and found two problems written upon the blackboard. Not knowing that they were examples of ‘unsolvable’ statistical problems, he mistook them for a homework assignment, jotted them down and solved them. The equations that he solved are actually more accurately described best as unproved statistical theorems, rather than unsolvable problems.

Assumed They’d Been Assigned For Homework

In 1986, George recalled the event in a College Mathematics Journal interview: “It happened because during my first year at Berkeley, I had arrived late one day for a Jerzy Neyman class. On the blackboard there were two problems. I assumed they’d been assigned for homework, so I copied them down. A few days later I apologized to Neyman for taking so long, but the problems seemed to be harder than usual. I asked him if he still wanted them. He said yes, and told me to put them on his desk.

All Excited

About six weeks later, around eight o’clock on a Sunday morning, we were woke by someone banging on our front door. It was Neyman. He rushed in with the papers in hand, all excited. “I’ve just written an introduction to one of your papers. Please read it so I can send it off right away for publication.” For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard that I had solved, thinking that they were homework, were in fact two famous unsolvable math problems in statistics. That was the first inkling I had that there was anything special about them.”

Related Articles

Shadow Theatre Group | You Will Not Believe Your Eyes

The Story Of The Song White Rabbit

About the author.

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Credit card rates
• Balance transfer credit cards
• Business credit cards
• Cash back credit cards
• Rewards credit cards
• Travel credit cards
• Checking accounts
• Online checking accounts
• High-yield savings accounts
• Money market accounts
• Personal loans
• Student loans
• Car insurance
• Home buying
• Options pit
• Investment ideas
• Research reports
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

A College Student Just Solved a Notoriously Impossible Math Problem

"Hearst Magazines and Yahoo may earn commission or revenue on some items through these links."

In 1993, Hungarian mathematician Paul Erdős—one of the most prolific mathematicians of the 20th century—posed a question with two components seemingly at odds with one another: Could a Sidon set be an “asymptotic basis of order three?”

Let us explain.

Named after another Hungarian mathematician, Simon Sidon, these sets are basically a collection of numbers where no two numbers in the set add up to the same integer. For example, in the simple Sidon set (1, 3, 5, 11), when any of the two numbers in the set are added together, they equal a unique number. Constructing a Sidon set with only four numbers is extremely easy, but as the set increases in size, it just gets harder and harder. As soon as two sums are the same, the collection of numbers is no longer considered a Sidon set.

The second element of Erdős’ problem—that scary-sounding “asymptotic basis of order three” part—means that:

a set must be infinitely large

any large enough integer can be written as the result of adding together at most 3 numbers in the set.

So, this 30-year-old conundrum centered on whether or not these two elements could exist in the same set of numbers. For decades, the answer seemed to be no.

But in March of this year, Oxford graduate student Cédric Pilatte published a proof confirming the existence of such a Sidon set. Reaching that milestone wasn’t easy. In 2010, mathematicians proved that a Sidon set can be be an asymptotic basis of order 5 , and three years later, they proved that is was also possible for a Sidon set to “ be an asymptotic basis of order 4 .” But “order 3” remained elusive—some considered it theoretically possible but incredibly difficult (and potentially impossible) to prove.

“They’re pulling in opposite directions,” Pilatte told Quanta Magazine . “Sidon sets are constrained to be small, and an asymptotic basis is constrained to be large. It was not obvious that it could work.”

So how did Pilatte get a mathematically square peg to fit a seemingly round hole? He took an unconventional approach and turned to geometry rather than the probabilistic method championed by Erdős and what’s called additive number theory. Pilatte replaced numbers with polynomials and made use of the recent work of Columbia University mathematicians . Combining these ideas, Pilatte successfully created a Sidon set dense enough and random enough to finally solve Erdős’s original problem.

Pilatte’s work relied on the discoveries of many mathematicians across different disciplines, and even combined seemingly unrelated fields of mathematics to answer the question. “It’s cool that these very deep techniques from algebraic geometry can also be used for this simple and concrete question about sets of numbers,” Pilatte told Quanta Magazine.

And with that, yet another “impossible” math question is found to be very much possible.

You Might Also Like

The Best Hair Growth Shampoos for Men to Buy Now

25 Vegetables That Are Surprising Sources of Protein

Recommended Stories

Trump media stock tanks as new filing reveals heavy losses, 'greater risks' on trump's involvement.

After a strong debut last week, shares of Donald Trump's media company were under pressure Monday after meager sales and deep losses were revealed in a new filing with the SEC.

Mock Draft Monday with Field Yates: You will be shocked how early Bo Nix goes

'Mock Draft Monday' rolls on ESPN's Field Yates joining Matt Harmon to break down his latest mock draft. Harmon has Yates break down his mock draft methodology and what goes into his decision making when placing certain prospects on certain teams.

NFL mock draft: Trades galore as one of the best QB prospects slides outside the top 10

Charles McDonald and Nate Tice's latest mock draft has five quarterbacks off the board in the top 13, a big-time weapon for Aaron Rodgers and some steals in the second half of the first round.

Longtime ESPN anchor John Anderson says he's retiring from 'SportsCenter:' 'The operation has changed'

Anderson has been hosting "SportsCenter" since 1999.

The 'extreme' Social Security move that actually makes sense

The election year battle over cherished retirement programs is a microcosm explaining why Washington doesn't solve solvable problems.

One fateful decision summed up North Carolina's Sweet 16 demise

Jae’Lyn Withers shot UNC's most important 3-pointer of the game when he had no business firing away. And now the No. 1 Tar Heels are going home.

Mets pitcher ejected for throwing behind Brewers' Rhys Hoskins a day after heated exchange

Rhys Hoskins had a big day for the Milwaukee Brewers on Saturday, continuing his grudge match against the New York Mets.

Mavericks star Luka Dončić drops 47 points, sinks wild trick shot to snap Rockets’ 11-game win streak

The Rockets, who are in the midst of an incredible postseason push, just lost their first game since March 6.

Massive changes coming to Google Chrome threaten to reshape the modern internet

Google is ending third-party cookies in Chrome. Here’s what that means for publishers trying to stay afloat in a brutal market.

2024 New York International Auto Show Editors' Top 5 Picks

Though not the biggest New York International Auto Show, there were still some exciting reveals and even a surprise or two. We pick the best of show.

Kenny Brooks leaves Virginia Tech for Kentucky job in stunning end of era

Within a couple of weeks, Virginia Tech's Final Four hopes dropped because of Elizabeth Kitley's injury and Brooks exited for the SEC.

Final Four: UConn's odds of winning back-to-back national championships are staggeringly low

You're not going to get much of a return if you bet UConn to win two more games.

USWNT's Korbin Albert apologizes after Megan Rapinoe calls out anti-LGBTQ social media content

Albert took over Rapinoe's No. 15 jersey number this year.

Ex-Jaguars employee who once hacked team's Jumbotron sentenced to 220 years in prison for child molestation

The FBI searched Samuel Arthur Thompson's home after figuring out he hacked the Jaguars' jumbotron. What they found next was awful.

Kentucky's 5-star recruits recognize pressure on program next year: 'We're not losing in the first round'

John Calipari and Kentucky's incoming star freshmen have something to prove next season after the Wildcats had another early exit in the NCAA tournament.

2025 Ram 1500's 'Hurricane' I6 tops V8 in fuel economy

2025 Ram 1500 full-size pickup truck now has fuel economy numbers, and the Hurricane inline-six delivers better numbers than the V8 it replaces.

76ers' Kelly Oubre Jr. confronts officials after missed call on final play in loss to Clippers

"You're a b*tch. You’re a b*tch. You’re a b*tch," Oubre told each official after the defeat.

New Angels manager Ron Washington calls team meeting after just 2 games: ‘We can’t get off track’

Though the meeting came with 160 games still left on the schedule, the Angels were outscored 24-7 in their first two blowout losses of the season.

J.J. McCarthy second overall? + QB class red flags, Dak Prescott on the open market | Inside Coverage

Jason Fitz is joined by Senior NFL Reporters Charles Robinson and Jori Epstein to go behind the scenes on the latest rumors and news around the NFL. The trio start with takeaways from the NFL owner's meetings as Jori was on the ground in Orlando. The hosts discuss the fallout of the new kickoff rule (are rosters going to change because of it?), the two Christmas Day games and what the heck Jerry Jones was doodling in his notebook. Next, it's time to pull out the crystal ball as the hosts attempt to look into the future for some key quarterbacks, starting with Michigan QB J.J. McCarthy. McCarthy's draft stock has been skyrocketing lately as some rumors emerged that he could go as high as second overall. Charles gives his thoughts and what he's hearing from GMs around the league before moving onto Brock Purdy and whether San Francisco will be willing to pay him when the time comes. Charles dives deeper into the 2024 quarterback class and why every prospect has a massive red flag, and Jori gives us the latest on the Dak Prescott contract negotiations, which seem to be heading in the wrong direction. All signs are pointing towards Dak hitting free agency next offseason. Finally, Fitz wraps things up by asking about Deion Sanders' comments about choosing where his sons get drafted and whether or not player empowerment could be ascending to a new level with the emergence of NIL.

In new surroundings and a very different role, LSU's Hailey Van Lith has gone through a mental evolution

Van Lith is a different player in a different place than a year ago, and now she's in position to win a championship after watching LSU cut down the nets last season.

Did the Math Problem-Solving Scene in Good Will Hunting Actually Happen in Real Life?

In the latest Movie Legends Revealed, discover the shocking real life inspiration for the iconic Good Will Hunting math problem-solving scene.

MOVIE URBAN LEGEND : The iconic math problem-solving scene in Good Will Hunting was based on a real life incident of a student shockingly solving a seemingly unsolvable problem.

In the world of film and television, "based on a true story" gets used quite frequently with movies and TV shows, as plenty of films and series are nominally docudramas, from Erin Brockovich to Inventing Anna to The Conjuring films (where the films take the stories of Edward and Lorraine Warren's real life "paranormal investigations" and treats them as fact). However, for every movie that is explicitly based on a true story, there are plenty other films that simply feature segments that are taken from real life, whether they are incidents that occurred to the filmmakers themselves or just repeated stories from the public consciousness.

A problem that filmmakers sometimes face, though, is when they use a seemingly unbelievable real life story, and then they get accused of the story coming off as, well, unbelievable. As the saying goes, from Mark Twain's Pudd'nhead Wilson , “truth is stranger than fiction, because fiction is obliged to stick to probability, and truth ain't.” William Goldman wrote the brilliant 1977 World War II film, A Bridge Too Far , and among the many memorable sequences (the way that the filmmakers were able to afford an All-Star cast of actors was to have many short sequences, so they would get Robert Redford...for a day of shooting) is one in which James Caan plays a staff sergeant who drives through enemy lines with his plainly dead Captain next to him to get his superior to a doctor. He succeeds in finding a medical tent where Sir Laurence Olivier plays an Army Surgeon who takes one look at the captain and turns away, informing the Sergeant that his Captain is dead. The Sergeant then pulls a gun on the doctor and insists that he examine the Captain or that he will kill him. The doctor does so and, of course, is shocked to find out that the seemingly dead Captain really IS alive!

Goldman wrote about how hard it was to keep the scene in the film, as it seemed too absurd, but it actually happened ! Such is the case when life is stranger than fiction.

In any event, that was also the case with one of the more memorable scenes in the award-winning 1997 hit film, Good Will Hunting .

RELATED: Did Orson Welles Die Before Finishing All of His Lines for Transformers: The Movie?

WHAT IS THE FAMOUS MATH PROBLEM-SOLVING SCENE IN GOOD WILL HUNTING?

As I've written about in an old Movie Legends Revealed , Good Will Hunting was originally written by Matt Damon and Ben Affleck as an action thriller. Affleck described the film as:

We came up with this idea of the brilliant kid and his townie friends, where he was special and the government wanted to get their mitts on him. And it had a very “Beverly Hills Cop”, “Midnight Run” sensibility, where the kids from Boston were giving the NSA the slip all the time. We would improvise and drink like six or twelve beers or whatever and record it with a tape recorder. At the time we imagined the professor and the shrink would be Morgan Freeman and De Niro, so we’d do our imitations of Freeman and De Niro. It was kind of hopelessly naive and probably really embarrassing in that respect.

In any event, the film executives at Castle Rock (the production company that initially bought the script) told them that there were two stories here worth being told, the action thriller stuff and the story of a townie math genius and insisted that Affleck and Damon concentrate on just one. They fatefully picked the math genius plot and that, of course, is what Good Will Hunting ended up becoming, a townie math genius with a dark past deals with the effects of his genius being discovered by a famous Massachusetts Institute of Technology (MIT) professor of advanced mathematics (amusingly, Affleck and Damon originally planned for Will Hunting to be a physics genius, but discovered that most physics work was done in group settings, so the tortured solo genius angle didn't really work).

The iconic sequence is that Will is working as a janitor at MIT when he sees a math problem that is meant to perhaps be solved by one student in the professor's class by the end of the semester and Will solves it overnight. Then, when the professor puts up an even more difficult problem, Will solves it once again, only this time he is caught doing so...

Great scene, but shockingly, also taken from real life!

RELATED: The Alan Smithee Pseudonym Wasn't Created for Bad Movies - It Was Quite the Opposite

WHAT WAS THE REAL LIFE MATH INCIDENT THAT INSPIRED THE GOOD WILL HUNTING FILMMAKERS?

While of course not literally being the case of a janitor solving an "impossible" problem, the gist of the story is based on the tale of George Dantzig, a doctoral student at the University of California, Berkley, taking Statistics from the famed mathematician, Jerzy Neyman.

Dantzig related his story to The College Mathematics Journal in 1986:

It happened because during my first year at Berkeley I arrived late one day at one of [Jerzy] Neyman’s classes. On the blackboard there were two problems that I assumed had been assigned for homework. I copied them down. A few days later I apologized to Neyman for taking so long to do the homework — the problems seemed to be a little harder than usual. I asked him if he still wanted it. He told me to throw it on his desk. I did so reluctantly because his desk was covered with such a heap of papers that I feared my homework would be lost there forever. About six weeks later, one Sunday morning about eight o’clock, [my wife] Anne and I were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: “I’ve just written an introduction to one of your papers. Read it so I can send it out right away for publication.” For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard that I had solved thinking they were homework were in fact two famous unsolved problems in statistics. That was the first inkling I had that there was anything special about them.

A year later, when I began to worry about a thesis topic, Neyman just shrugged and told me to wrap the two problems in a binder and he would accept them as my thesis.

The second of the two problems, however, was not published until after World War II. It happened this way. Around 1950 I received a letter from Abraham Wald enclosing the final galley proofs of a paper of his about to go to press in the Annals of Mathematical Statistics. Someone had just pointed out to him that the main result in his paper was the same as the second “homework” problem solved in my thesis. I wrote back suggesting we publish jointly. He simply inserted my name as coauthor into the galley proof.

Truth, it's stranger than fiction!

And legends sometimes are...

STATUS : True

Be sure to check out my archive of Movie Legends Revealed for more urban legends about the world of film.

Feel free (heck, I implore you!) to write in with your suggestions for future installments! My e-mail address is [email protected].

• Statistics and Probability
• College Statistics

Significance tests

Dantzig's unsolved homework problems An event in George Dantzig's life became the origin of a famou

Jaydan Aguirre

Answered question

Answer & explanation.

Jordan Mcpherson

Beginner 2022-07-06 Added 16 answers

Do you have a similar question?

Recalculate according to your conditions!

New Questions in College Statistics

The product of the ages, in years, of three (3) teenagers os 4590. None of the have the sane age. What are the ages of the teenagers???

Use the row of numbers shown below to generate 12 random numbers between 01 and 99 78038 18022 84755 23146 12720 70910 49732 79606 Starting at the beginning of the row, what are the first 12 numbers between 01 and 99 in the sample?

How many different 10 letter words (real or imaginary) can be formed from the following letters H,T,G,B,X,X,T,L,N,J.

Is every straight line the graph of a function?

For the 1s orbital of the Hydrogen atom, the radial wave function is given as: R ( r ) = 1 π ( 1 a O ) 3 2 e − r a O (Where a O = 0.529 ∘A) The ratio of radial probability density of finding an electron at r = a O to the radial probability density of finding an electron at the nucleus is given as ( x . e − y ). Calculate the value of (x+y).

Find the sets A and B if A B = 1 , 5 , 7 , 8 , B A = 2 , 10 and A ∩ B = 3 , 6 , 9 . Are they unique?

What are the characteristics of a good hypothesis?

If x is 60% of y, find x y − x . A) 1 2 B) 3 2 C) 7 2 D) 5 2

The numbers of significant figures in 9.1 × 10 − 31 k g are: A)Two B)Three C)Ten D)Thirty one

What is positive acceleration?

Is power scalar or vector?

What is the five-step process for hypothesis testing?

How to calculate Type 1 error and Type 2 error probabilities?

How long will it take to drive 450 km if you are driving at a speed of 50 km per hour? 1) 9 Hours 2) 3.5 Hours 3) 6 Hours 4) 12.5 Hours

What is the square root of 106?

Ask your question. Get an expert answer.

Let our experts help you. Answer in as fast as 15 minutes.

• Answer & Explanation
• New Questions

Didn't find what you were looking for?

• High School Questions
• College Questions
• Math Solver
• Top Questions
• Top Questions 2
• Term of Service
• Payment Policy

Connect with us

Get Plainmath App

• Google Play

E-mail us: [email protected]

Our Service is useful for:

Plainmath is a platform aimed to help users to understand how to solve math problems by providing accumulated knowledge on different topics and accessible examples.

2023 Plainmath. All rights reserved

USC Digital Folklore Archives

A database of folklore performances, student inadvertently solves never-before-solved math problems.

My informant told me about a story she heard about a student waking up late and rushing to their final, then frantically trying to finish the three equations on the board. The first two weren’t so bad, but the third was difficult. He finally finished and turned it into the professor only to find out later the third was actually not part of the test. Instead, it was a problem that had as of yet been unsolved. He had figured it out, though. My informant likes it because she thinks it would be cool to accidentally become famous like that and because it relates to one of her favorite movies, Good Will Hunting, since the main character in it easily solves equations no else could.

I like how the story reflects how we believe what we hear; when we are told something is impossible, it will seem much harder in our mind. But when we think something is supposed to be solvable, it may be easier to figure out, even if it’s never been done before. Limitations we place on ourselves are often illusory.

I looked into the story and found that it is actually based in truth. In 1939, George Dantzig arrived late to his graduate statistics class and saw two problems on the board, not knowing they were examples of problems that had never been solved. He thought they were a homework assignment and was able to solve them. He found out the reality six weeks later when his teacher let him know and helped him publish a paper about one of the problems.

Annotation: Cottle, Richard, Ellis Johnson, and Roger Wets. “George B. Dantzig.” Notices of the AMS 54.3 (2007). Web. April 23 2012.

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

PhD dissertations that solve an established open problem

I search for a big list of open problems which have been solved in a PhD thesis by the Author of the thesis (or with collaboration of her/his supervisor).

In my question I search for every possible open problem but I prefer (but not limited) to receive answers about those open problems which had been unsolved for at least (about) 25 years and before the appearance of the ultimate solution, there had been significant attentions and efforts for solving it. I mean that the problem was not a forgotten problem.

If the Gauss proof of the fundamental theorem of algebra did not had a gap, then his proof could be an important example of such dissertations.

I ask the moderators to consider this question as a wiki question.

• soft-question
• open-problems
• mathematics-education
• 17 $\begingroup$ Godel's thesis comes to mind. $\endgroup$ –  user2277550 Apr 24, 2018 at 7:39
• 81 $\begingroup$ Don't all PhD theses solve open problems...? $\endgroup$ –  Najib Idrissi Apr 24, 2018 at 7:42
• 20 $\begingroup$ @NajibIdrissi: I understood this question to be about open problems in the narrow sense of a precise mathematical question that at least some researcher(s) have previously articulated and tried to answer , e.g. “what is the dimension of such-and-such space?”. Most theses I know only solve open problems only in a much broader sense: open-ended questions that researchers may have wondered about, like “what can we say about the homology of such-and-such space?”, or “can we develop a useful theory of homotopy-coherent diagrams in such-and-such setting?”. $\endgroup$ –  Peter LeFanu Lumsdaine Apr 24, 2018 at 9:04
• 9 $\begingroup$ @NajibIdrissi: Not always: sometimes a thesis provides a new insight into an already solved problem, or a better way to solve it. Tate's thesis is the first to come to mind. $\endgroup$ –  Alex M. Apr 24, 2018 at 11:27
• 6 $\begingroup$ Eric Larson proved the Maximal Rank Conjecture (a significant problem in the algebraic geometry of curves) in his MIT PhD thesis this year: math.mit.edu/research/graduate/thesis-defenses-2018.php $\endgroup$ –  Sam Hopkins Apr 24, 2018 at 13:32

24 Answers 24

I find George Dantzig's story particularly impressive and inspiring.

While he was a graduate student at UC Berkeley, near the beginning of a class for which Dantzig was late, professor Jerzy Neyman wrote two examples of famously unsolved statistics problems on the blackboard. When Dantzig arrived, he assumed that the two problems were a homework assignment and wrote them down. According to Dantzig, the problems "seemed to be a little harder than usual", but a few days later he handed in completed solutions for the two problems, still believing that they were an assignment that was overdue. Six weeks later, Dantzig received a visit from an excited professor Neyman, who was eager to tell him that the homework problems he had solved were two of the most famous unsolved problems in statistics. Neyman told Dantzig to wrap the two problems in a binder and he would accept them as a Ph.D. thesis.

The two problems that Dantzig solved were eventually published in: On the Non-Existence of Tests of "Student's" Hypothesis Having Power Functions Independent of σ (1940) and in On the Fundamental Lemma of Neyman and Pearson (1951).

• 2 $\begingroup$ Thank you for this very interesting answer on George Dantzig's story. $\endgroup$ –  Ali Taghavi Apr 24, 2018 at 7:54
• 9 $\begingroup$ For those who like the story, a Snopes article contains some interesting excerpts from an interview with George Dantzig: snopes.com/fact-check/the-unsolvable-math-problem $\endgroup$ –  JohnEye Apr 24, 2018 at 10:20
• 10 $\begingroup$ That's freaking crazy. $\endgroup$ –  iammax Apr 24, 2018 at 18:45
• 5 $\begingroup$ If the problems were solved concurrently, why were they published 11 years apart? $\endgroup$ –  Michael Sep 25, 2018 at 20:39
• 3 $\begingroup$ @Michael --- Wikipedia explains that "Years later another researcher, Abraham Wald, was preparing to publish an article that arrived at a conclusion for the second problem, and included Dantzig as its co-author when he learned of the earlier solution." $\endgroup$ –  Carlo Beenakker Sep 26, 2018 at 0:31

I am quite surprised that nobody has mentioned Grothendieck's thesis. Apparently Laurent Schwartz gave Grothendieck a recent paper listing a number of open problems in functional analysis at one of their initial meetings. (Schwartz had just won the Fields at the time.) Grothendieck went away for a few weeks/ months and then returned with solutions to many (or all?) of the questions. In the course of the next few years Grothendieck became one of the world's leading functional analysts, before turning his attention to algebraic geometry.

This is the story I heard as part of mathematical gossip many, many years ago. Maybe someone who is more knowledgeable can chime in.

Another utterly spectacular thesis was Noam Elkies'. Among other things he settled a 200 year old problem posed by Euler!

• 7 $\begingroup$ I’d upvote this a dozen times if I could. As I understand it, we owe the modern theory of tensor products of topological vector spaces—and hence, in particular, the theory of nuclear topological vector spaces—entirely to Grothendieck’s PhD thesis. A quick sketch can be found, for instance, in this survey chapter by Fernando Bombal. $\endgroup$ –  Branimir Ćaćić Sep 30, 2020 at 0:00
• $\begingroup$ I just skimmed the Ph.D. thesis of Noam Elkies. I don't think that the result you mentioned is in there. He did solve that problem of Euler's around the same time that he wrote his Ph.D. thesis, but the solution doesn't appear in his Ph.D. thesis as far as I can tell. $\endgroup$ –  Timothy Chow Nov 26, 2022 at 18:27

Godel's Completeness Theorem, was part of his PHD thesis.

It was definitely an active field of research, but I don't know to what degree the problem was an open one, in the way we understand it today.

.. when Kurt Gödel joined the University of Vienna in 1924, he took up theoretical physics as his major. Sometime before this, he had read Goethe’s theory of colors and became interest in the subject. At the same time, he attended classes on mathematics and philosophy as well. Soon he came in contact with great mathematicians and in 1926, influenced by number theorist Philipp Furtwängler, he decided to change his subject and take up mathematics. Besides that, he was highly influenced by Karl Menger’s course in dimension theory and attended Heinrich Gomperz’s course in the history of philosophy. Also in 1926, he entered the Vienna Circle, a group of positivist philosophers formed around Moritz Schlick, and until 1928, attended their meetings regularly. After graduation, he started working for his doctoral degree under Hans Hahn. His dissertation was on the problem of completeness. In the summer of 1929, Gödel submitted his dissertation, titled ‘Über die Vollständigkeit des Logikkalküls’ (On the Completeness of the Calculus of Logic). Subsequently in February 1930, he received his doctorate in mathematics from the University of Vienna. Sometime now, he also became an Austrian citizen.

• $\begingroup$ I don't know whether this specific question was open, but it is certainly in the family of open problems highlighted by Hilbert's 2nd Problem and the Entscheidungsproblem. $\endgroup$ –  Joshua Grochow Sep 26, 2018 at 2:37
• 2 $\begingroup$ It was an open problem (posed by Hilbert and Ackermann) but only a few years earlier. It also falls out of earlier results by Skolem. $\endgroup$ –  none Sep 26, 2018 at 7:11

The thesis of Martin Hertweck answered the at that time 60-years-old isomorphism problem for integral group rings in the negative, by constructing a counterexample. That is, a pair of non-isomorphic finite groups $G$ and $H$ such that the group rings $\mathbb{Z}G$ and $\mathbb{Z}H$ are isomorphic. This result has been published afterwards in the Annals of Mathematics .

• 1 $\begingroup$ I never heard about this very great thesis. Thank you for this answer. $\endgroup$ –  Ali Taghavi May 20, 2018 at 19:12
• $\begingroup$ @AliTaghavi: You are welcome. -- And thank YOU! $\endgroup$ –  Stefan Kohl ♦ Sep 11, 2022 at 18:52

Scott Aaronson's thesis , Limits on Efficient Computation in the Physical World , refuted some popular wisdom .

In the first part of the thesis, I attack the common belief that quantum computing resembles classical exponential parallelism, by showing that quantum computers would face serious limitations on a wider range of problems than was previously known. In particular, any quantum algorithm that solves the collision problem -- that of deciding whether a sequence of $n$ integers is one-to-one or two-to-one -- must query the sequence $\Omega(n^{1/5})$ times. This resolves a question that was open for years; previously no lower bound better than constant was known. A corollary is that there is no "black-box" quantum algorithm to break cryptographic hash functions or solve the Graph Isomorphism problem in polynomial time.

There was even a second part to that thesis...

...Next I ask what happens to the quantum computing model if we take into account that the speed of light is finite -- and in particular, whether Grover's algorithm still yields a quadratic speedup for searching a database. Refuting a claim by Benioff, I show that the surprising answer is yes.

Lisa Piccirillo, who recently obtained her PhD from the University of Texas, Austin, showed that the Conway knot is not slice, answering a relatively famous open problem in topology. You can read a popular account of her work in Quanta here: https://www.quantamagazine.org/graduate-student-solves-decades-old-conway-knot-problem-20200519/ . Her paper proving this result was published in the Annals of Math; but I'm pretty sure it also constituted her dissertation (see https://gradschool.utexas.edu/news/studying-knots-and-four-dimensional-spaces ).

John von Neumann's dissertation seems to be an example with just the right timing.

But at the beginning of the 20th century [ in 1901, to be precise ], efforts to base mathematics on naive set theory suffered a setback due to Russell's paradox (on the set of all sets that do not belong to themselves). The problem of an adequate axiomatization of set theory was resolved implicitly about twenty years later by Ernst Zermelo and Abraham Fraenkel [i.e. there was active research on the question]. Zermelo–Fraenkel set theory provided a series of principles that allowed for the construction of the sets used in the everyday practice of mathematics, but they did not explicitly exclude the possibility of the existence of a set that belongs to itself. In his doctoral thesis of 1925, von Neumann demonstrated two techniques to exclude such sets—the axiom of foundation and the notion of class. The axiom of foundation proposed that every set can be constructed from the bottom up in an ordered succession of steps by way of the principles of Zermelo and Fraenkel. If one set belongs to another then the first must necessarily come before the second in the succession. This excludes the possibility of a set belonging to itself. To demonstrate that the addition of this new axiom to the others did not produce contradictions, von Neumann introduced a method of demonstration, called the method of inner models, which later became an essential instrument in set theory. The second approach to the problem of sets belonging to themselves took as its base the notion of class, and defines a set as a class which belongs to other classes, while a proper class is defined as a class which does not belong to other classes. Under the Zermelo–Fraenkel approach, the axioms impede the construction of a set of all sets which do not belong to themselves. In contrast, under the von Neumann approach, the class of all sets which do not belong to themselves can be constructed, but it is a proper class and not a set. Van Heijenoort, Jean (1967). From Frege to Gödel: a Source Book in Mathematical Logic, 1879–1931. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-32450-3. OCLC 523838.

A question, a book, and a couple of dissertations; the most relevant, I think, is the thesis by Petkovšek. Hopefully this is an acceptable MO answer. First, the question comes from Knuth in The Art of Computer Programming :

[50] Develop computer programs for simplifying sums that involve binomial coefficients. Exercise 1.2.6.63 in The Art of Computer Programming, Volume 1: Fundamental Algorithms by Donald E. Knuth, Addison Wesley, Reading, Massachusetts, 1968.

(For those unfamiliar, there is a pseudo log scale to rate each problem such that [50], as above, is the most difficult exercise, expected to take some years to answer).

A solution to this exercise is given by the book A = B by Marko Petkovsek, Herbert Wilf, and Doron Zeilberger (fully availble from the linked page).

On page 29 of the book, the authors mention a Ph.D. dissertation, and one of the author's Ph.D. thesis (among a few other works) that provide the main content of the book:

[Fase45] is the Ph.D. dissertation of Sister Mary Celine Fasenmyer, in 1945. It showed how recurrences for certain polynomial sequences could be found algorithmically. (See Chapter 4.) ... [Petk91] is the Ph.D. thesis of Marko Petkovšek, in 1991. In it he discovered the algorithm for deciding if a given recurrence with polynomial coefficients has a "simple" solution, which, together with the algorithms above, enables the automated discovery of the simple evaluation of a given definite sum, if one exists, or a proof of nonexistence, if none exists (see Chapter 8). A definite hypergeometric sum is one of the form $f(n) = \sum^{\infty}_{k=-\infty} F(n, k)$, where $F$ is hypergeometric.

Sources are

[Fase45] Fasenmyer, Sister Mary Celine, Some generalized hypergeometric polynomials , Ph.D. dissertation, University of Michigan, November, 1945.

[Petk91] Petkovšek, M., Finding closed-form solutions of difference equations by symbolic methods , Ph.D. thesis, Carnegie-Mellon University, CMU-CS-91-103, 1991.

• $\begingroup$ Thank you very much for your very interesting answer and your attention to my question. $\endgroup$ –  Ali Taghavi Sep 10, 2022 at 19:16

June Huh's recent proof of Rota's conjecture (stated by Read in 1968 for graphical matroids and Rota in 1971 for all matroids) formed his 2014 Ph. D. thesis . For matroids over $\mathbb{C}$ , this appeared first in Huh's 2010 preprint ; for matroids over any field, this appeared in his work with Eric Katz (2011) ; for arbitrary matroids, see Adiprasito, Huh and Katz (2015) . As the dates would suggest, the thesis covers matroids over any field, but not the result on general matroids.

• 7 $\begingroup$ Just to clarify: this is not the Rota's conjecture , but a conjecture by Rota; which apparently also is known as Rota-Heron-Welsh conjecture. $\endgroup$ –  Max Horn Sep 29, 2020 at 22:08
• 1 $\begingroup$ Is this the work for which Huh was awarded a Fields medal? $\endgroup$ –  Gerry Myerson Aug 28, 2022 at 1:41
• 1 $\begingroup$ @GerryMyerson It was indeed one of the things for which he was awarded a Fields medal, according to the short citation . $\endgroup$ –  Timothy Chow Nov 26, 2022 at 18:31

Vladimir Arnold's thesis was about his solution to Hilbert's 13th problem, which he had done a few years earlier. This info is missing from Wikipedia but some details are in Mactutor: https://mathshistory.st-andrews.ac.uk/Biographies/Arnold/

Does Serre's (Jean-Pierre) thesis qualifies ? He computed there a lot of homotopy groups of spheres. But I don't know how old was this problem in 1951.

• 2 $\begingroup$ +1 (!!!). The problem of computing the homotopy groups of spheres must be as old as Witold Hurewicz's definition of homotopy groups. Every single computation was a huge success, there were very few of them. Then Serre's revolution came. $\endgroup$ –  Wlod AA Nov 5, 2020 at 20:04

Stephen Bigelow showed that braid groups are linear in his thesis at Berkeley in 2000 (the paper had already appeared in 1999 in JAMS, but he included it in his thesis).

John Thompson's thesis solved the famous and long-standing conjecture that a Frobenius kernel is nilpotent in the late 1950s. Not only was this noteworthy enough to be reported in the New York Times, but many of the techniques developed in the thesis played a major role in shaping finite group theory for decades to come.

Richard Laver's dissertation proved a long-standing conjecture of Fraïssé, that the scattered order types are well-quasi-ordered. But maybe that was not quite 25 years old at the time.

A very recent example is Eric Larson's 2018 dissertation The maximal rank conjecture [Lar1], which proves the following old conjecture:

Conjecture. (Maximal rank conjecture) Let $C \subseteq \mathbb P^r$ be a general Brill-Noether¹ curve. Then the restriction map $$H^0(\mathbb P^r, \mathcal O_{\mathbb P^r}(k)) \to H^0(C, \mathcal O_C(k))$$ has maximal rank, i.e. is injective if $h^0(\mathbb P^r, \mathcal O(k)) \leq h^0(C, \mathcal O(k))$ and surjective otherwise.

Historical remarks. Although I have been unable to find a definite place where this conjecture was stated, it is attributed to M. Noether by Arbarello and Ciliberto [AC83, p. 4]. Cases of the problem have been studied by M. Noether [Noe82, §8], Castelnuovo [Cas93, §7], and Severi [Sev15, §10].

In modern days, the conjecture had regained attention by 1982 [Har82, p. 79]. Partial results from around that time are mentioned in the introduction to [Lar2].

Larson's work culminates a lot of activity, including many papers by himself with other authors. An overview of the proof and how the different papers fit together is given in [Lar3].

References.

[AC83] E. Arbarello and C. Ciliberto, Adjoint hypersurfaces to curves in $\mathbb P^n$ following Petri . In: Commutative algebra (Trento, 1981) . Lect. Notes Pure Appl. Math. 84 (1983), p. 1-21. ZBL0516.14024 .

[Cas93] G. Castelnuovo, Sui multipli di una serie lineare di gruppi di punti appartenente ad una curva algebrica . Palermo Rend. VII (1893), p. 89-110. ZBL25.1035.02 .

[Har82] J. D. Harris, Curves in projective space . Séminaire de mathématiques supérieures, 85 (1982). Les Presses de l’Université de Montréal. ZBL0511.14014 .

[Lar1] E. K. Larson, The maximal rank conjecture . PhD dissertation, 2018.

[Lar2] E. K. Larson, The maximal rank conjecture . Preprint, arXiv:1711.04906 .

[Lar3] E. K. Larson, Degenerations of Curves in Projective Space and the Maximal Rank Conjecture . Preprint, arXiv:1809.05980 .

[Noe82] M. Nöther, Zur Grundlegung der Theorie der algebraischen Raumcurven . Abh. d. K. Akad. d. Wissensch. Berlin (1882). ZBL15.0684.01 .

[Sev15] F. Severi, Sulla classificazione delle curve algebriche e sul teorema d’esistenza di Riemann . Rom. Acc. L. Rend. 24 .5 (1915), p. 877-888, 1011-1020. ZBL45.1375.02 .

¹ Brill-Noether curves form a suitable component of the Kontsevich moduli space $\overline M_g(\mathbb P^r, d)$ of stable maps $\phi \colon C \to \mathbb P^r$ from a genus $g$ curve whose image has degree $d$ .

• 2 $\begingroup$ Unfortunately, the references given in [Larson2] (which I blindly copied) are not accurate. I have been unable to find the conjecture in either [Harris] or the Severi reference given therein. I spent a few hours trying to sort this out, which got me a bit closer, but I still didn't really find the original sources. I would be grateful if someone could clear this up. $\endgroup$ –  R. van Dobben de Bruyn Sep 26, 2018 at 1:21
• 2 $\begingroup$ In arxiv.org/abs/1505.05460 Jensen and Payne cite "F. Severi. Sulla classificazione delle curve algebriche e sul teorema di esistenza di Riemann. Rend. R. Acc. Naz. Lincei, 24(5):887–888, 1915." and " J. Harris. Curves in projective space, volume 85 of Séminaire de Mathématiques Supérieures. Presses de l’Université de Montréal, Montreal, Que., 1982. With the collaboration of David Eisenbud" as sources for the Maximal Rank Conjecture. (By the way, I posted this example as a comment earlier- glad to see it upgraded into an answer.) $\endgroup$ –  Sam Hopkins Sep 26, 2018 at 15:13
• $\begingroup$ @SamHopkins: Thanks, I had found those as well. But they do not settle the question of the origin of the conjecture. If I understand the paper correctly, Severi does not state the general case as a conjecture. $\endgroup$ –  R. van Dobben de Bruyn Sep 26, 2018 at 23:02

Does Scholze's PhD thesis count, as if I remember rightly he applied perfectoid spaces to prove some important special case of Deligne's weight-monodromy conjecture? (Not an expert, correct me if I'm wrong).

Also I believe Mirzakhani gave a proof of the Witten conjecture when she was still a student, so I don't know if that proof is incorporated into her PhD thesis. Coincidentally, Kontsevich's proof of the Witten conjecture was also given in his PhD dissertation and then published as a journal article Intersection Theory on the Moduli Space of Curves and the Matrix Airy Function .

Edit: I have not read Mirzakhani's thesis, but it does indeed seem to be the case that she gave a new proof of Witten's conjecture in that thesis. Taken from the following article :

In 2002 I received a rather apologetic letter from Maryam, then a student at Harvard, together with a rough draft thesis and a request for comments. After reading only a few pages, I was transfixed. Starting with a formula discovered by Greg McShane in his 1991 Warwick PhD, she had developed some amazingly original and beautiful machinery which culminated in a completely new proof of Witten’s conjecture, a relation between integrable systems of Hamiltonian PDEs and the geometry of certain families of 2D topological field theories.

A recent and rather spectacular quasi-example is the Ph.D. thesis of María Pe (advisor Javier Fernández de Bobadilla), entitled “On the Nash Problem for Quotient Surface Singularities” (2011).

While it was not was the full solution of the Nash problem (dated back to 1968) it included great steps towards the full solution, eventually presented by María and Javier themselves in Annals of Math. in 2012.

Peter Weinberger's Ph.D. thesis is a superb example:

    Proof of a Conjecture of Gauss on Class Number Two

See: https://en.wikipedia.org/wiki/Peter_J._Weinberger

• $\begingroup$ I couln't find this PhD thesis online. How is his strategy of proof? $\endgroup$ –  user19475 Sep 27, 2018 at 3:06
• $\begingroup$ @TKe, sorry, you need to ask a specialist, I am not (too bad). $\endgroup$ –  Wlod AA Sep 27, 2018 at 7:29

Since the OP mentions Gauss, this entry could be an appropriate addition to the list:

Manjul Bhargava's PhD thesis, Higher composition laws (2001), concerns a problem going back to Gauss. In the nineteenth century, Gauss had discovered a fundamental composition law for binary quadratic forms which are homogeneous polynomial functions of degree two in two variables. No formula or law of the Gauss type was known for cubic or higher degree forms. Bhargava broke the impasse of 200 years by producing a composition law for cubic and higher degree forms.

What makes Bhargava’s work especially remarkable is that he was able to explain all his revolutionary ideas using only elementary mathematics. In commenting on Bhargava’s results Andrew Wiles, his Ph.D. advisor said “He did it in a way that Gauss himself could have understood and appreciated.”

[ source1 and source2 ]

I found this interview from 2014, after Bhargava won the Fields medal, an inspiring read: "Somehow, he extracts ideas that are completely new or are retwisted in a way that changes everything. But it all feels very natural and unforced — it’s as if he found the right way to think.”

• $\begingroup$ I just now noticed that M. Khan suggested in a 2018 comment to the OP that Bhargava should be on this list. So here he is. $\endgroup$ –  Carlo Beenakker Aug 30, 2022 at 21:28

A bit surprised that Leslie F. Greengard has not been mentioned. His PhD thesis from Yale was supervised by Vladimir Rokhlin, and is often cited for the development of the fast multipole method (FMM) which reduces the computation of the electrostatic or gravitational potential field/force for an N-particle system from $O(N^2)$ to $O(N)$ . Together with FFT, the Monte Carlo method, the simplex method for linear programming, Quicksort, QR algorithm, etc., FMM is regarded as one of the top 10 algorithms of the 20th century . To quote from the link,

This algorithm overcomes one of the biggest headaches of $N$ -body simulations: the fact that accurate calculations of the motions of $N$ particles interacting via gravitational or electrostatic forces (think stars in a galaxy, or atoms in a protein) would seem to require $O(N^2)$ computations—one for each pair of particles. The fast multipole algorithm gets by with $O(N)$ computations. It does so by using multipole expansions (net charge or mass, dipole moment, quadrupole, and so forth) to approximate the effects of a distant group of particles on a local group. A hierarchical decomposition of space is used to define ever-larger groups as distances increase. One of the distinct advantages of the fast multipole algorithm is that it comes equipped with rigorous error estimates, a feature that many methods lack.

Maria Chudnovsky's PhD thesis gives a proof of the Strong Perfect Graph Conjecture . This is a conjecture of Claude Berge from 1961 (hence meets the 25 year criterion), and was considered one of the hardest and most important open problems in graph theory at the time. It is joint work with Neil Robertson, Paul Seymour, and Robin Thomas and was published in the Annals in 2006. See The strong perfect graph theorem .

I suppose my own thesis fulfils this. Let $M$ be a monoid generated by a finite set $A$ and defined by a single defining relation $w=1$ . The language of all words $v \in A^\ast$ representing the identity element in $M$ is called the congruential language for $M$ . If the congruential language for $M$ is a context-free language, then Louxin Zhang [1] proved that the group of all units (two-sided invertible elements) $U(M)$ of $M$ is a virtually free group.

Zhang then asked in 1992 (conference held in 1990) the following questions:

• If $U(M)$ is virtually free, is the congruential language of $M$ a context-free language?
• Is it decidable, taking $w$ as input, whether the congruential language of $M$ is context-free?

In Chapter 3 of my thesis, I give an affirmative answer to both questions. In fact, I generalise the answer to Question 1 to to all monoids defined by arbitrarily many relations of the form $w_i = 1$ .

My thesis can be found on my website .

[1] Zhang, Louxin , Congruential languages specified by special string-rewriting systems, Ito, Masami (ed.), Words, languages and combinatorics, Kyoto, Japan, August 28–31, 1990. Singapore: World Scientific. 551-563 (1992). ZBL0875.68589 .

Robin Moser in his PhD thesis found a constructive proof for the Lovasz Local Lemma , a problem that was essentially open for decades. This earned him a Godel Prize.

Bart Plumstead's 1979 thesis at Chicago included (among other things) proofs of all three of the Eisenbud-Evans conjectures, which were widely considered to be among the most significant open questions in commutative algebra at the time.

• $\begingroup$ That is very interesting thank you but it does not satisfy the condition of at least 25 years of openness. I give the bounty to your answer and I will give another bounty to other recent answer which satisfy (i think) this c9nditiin $\endgroup$ –  Ali Taghavi Sep 3, 2022 at 20:13

Your Answer

Sign up or log in, post as a guest.

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged soft-question big-list open-problems mathematics-education or ask your own question .

• Featured on Meta
• New Focus Styles & Updated Styling for Button Groups
• Upcoming initiatives on Stack Overflow and across the Stack Exchange network

• About the Editors

Unsolved Problems in Math Class

Credit: Randall Munroe. CC BY-NC 2.5

A few years ago, I directed a high school summer math program. Half the day was devoted to exploring the delights of modular arithmetic —we ended the summer with a cake decorated with Fermat’s Little theorem!—and half to learning to program in Python, with number theory questions as motivation. One Friday afternoon, we included these questions in the programming part of the day.

Goldbach conjecture : Any even number larger than 2 is the sum of two prime numbers. Is there a counterexample to this conjecture for an even number less than 10,000 Prove this conjecture. Collatz conjecture : Choose some number a 0 . Define a n by a n =3a n-1 +1 if a n-1 is odd or a n-1 /2 if a n-1 is even. Then a n will be 1 for some n. Is there a counterexample to this conjecture for a 0 <10,000? Prove this conjecture.

Perhaps it was a tiny bit evil to give these longstanding open problems to high school students without warning them, but it was a lot of fun to watch them come up with programs to search for counterexamples and brainstorm about ways of approaching the proofs. (And yes, we did eventually tell them the questions were still open. We didn’t want to ruin their weekends completely!)

Math teachers Annie Perkins and Sam Shah have written about the benefits of exposing kids to advanced math concepts early rather than waiting until they’ve mastered all the easy stuff. If you too would like to torture your students kindle your students’ curiosity and challenge their intuition, with unsolved math problems, there are lots of places to go for inspiration.

The MathPickle site (tagline: “Put your students in a pickle!”) has puzzles organized by grade level, board game suggestions , and a blog . I’ve seen this site mentioned in a few places, including a discussion on Dan Meyer’s blog .

Lior Patcher has a list of suggestions for how to use unsolved problems in K-12 classrooms at his computational biology blog Bits of DNA . I was especially excited to see a question involving Namibia’s mysterious “fairy circles,” circular patches of bare ground surrounded by vegetation. It’s nice to see some modeling and applied math get some love there. Why should number theory have all the fun?

Mike Lawler often discusses advanced and unsolved problems with his kids, and the Collatz conjecture has made several appearances on his blog. In his most recent post on the topic, his kids make music with John Conway’s “amusical” variation of the problem. (As a violist, I’m delighted that one of them does so in alto clef!)

Ben Braun writes about using unsolved problems in his college math classes at the AMS math education blog On Teaching and Learning Mathematics. He highlights some of the benefits for his students, including mindset shifts away from answer-getting and toward seeing failure as part of mathematical productivity.

It goes without saying that your students probably won’t solve the Goldbach conjecture or get a definitive answer about fairy circles in one or two class periods, but you never know. Some open problems might end up being easy to solve, or at least easier than we might think. The Gödel’s Lost Letter and P=NP blog has a fun post about open problems with short solutions .

4 Responses to Unsolved Problems in Math Class

Several years ago Tim Gowers did a very long post relating to math pedagogy, with LOTS of ideas, that may interest your readers: https://gowers.wordpress.com/2012/06/08/how-should-mathematics-be-taught-to-non-mathematicians/

I wrote an article about 10 years ago describing my undergrad research seminar at Illinois, which helps teach math majors how to come up with their own questions and attempt to solve them:

“One Introduction to Mathematical Research”, Math Horizons Vol. 14, No. 2 (November 2006), pp. 16-17, 38.

A copy can be found at http://www.jstor.org/stable/25678652 or https://faculty.math.illinois.edu/~reznick/mhoriz.pdf

Particularly valuable resource at MathPickle is the list by grade of unsolved problems from a conference Gordon organized. http://mathpickle.com/wp-content/uploads/2016/01/Unsolved-K-12-winners.pdf

He mentions another collection by Lior Prachter: https://liorpachter.wordpress.com/2015/09/20/unsolved-problems-with-the-common-core/#comment-4987

Whoops! Don’t know why I missed your mention of Lior on first read.

Comments are closed.

Opinions expressed on these pages were the views of the writers and did not necessarily reflect the views and opinions of the American Mathematical Society.

• Search for:
• 3D printing
• Applied Math
• Artificial Intelligence
• Black History Month
• BlackLivesMatter
• Category Theory
• Combinatorics
• Current Events
• Data Science
• Game Theory
• Hispanic Heritage Month
• History of Mathematics
• Interactive
• Issues in Higher Education
• K-12 Mathematics
• Linear Algebra
• Math Communication
• Math Education
• mathematical physics
• Mathematics and Computing
• Mathematics and the Arts
• Mental Health
• Number Theory
• people in math
• planet math
• Popular Culture
• Publishing in Math
• Recreational Mathematics
• Sustainability
• Theoretical Mathematics
• Traffic Modeling
• Uncategorized
• Visualizations
• women in math
• February 2021
• January 2021
• December 2020
• November 2020
• October 2020
• September 2020
• August 2020
• February 2020
• January 2020
• December 2019
• November 2019
• October 2019
• September 2019
• August 2019
• February 2019
• January 2019
• December 2018
• November 2018
• October 2018
• September 2018
• August 2018
• February 2018
• January 2018
• December 2017
• November 2017
• October 2017
• September 2017
• August 2017
• February 2017
• January 2017
• December 2016
• November 2016
• October 2016
• September 2016
• August 2016
• February 2016
• January 2016
• December 2015
• November 2015
• October 2015
• September 2015
• August 2015
• February 2015
• January 2015
• December 2014
• November 2014
• October 2014
• September 2014
• August 2014
• February 2014
• January 2014
• December 2013
• November 2013
• October 2013
• September 2013
• August 2013

Retired Blogs

• A Mathematical Word
• inclusion/exclusion
• Living Proof
• On Teaching and Learning Mathematics
• PhD + epsilon

Unsolved Problems

There are many unsolved problems in mathematics. Some prominent outstanding unsolved problems (as well as some which are not necessarily so well known) include

1. The Goldbach conjecture .

2. The Riemann hypothesis .

3. The conjecture that there exists a Hadamard matrix for every positive multiple of 4.

4. The twin prime conjecture (i.e., the conjecture that there are an infinite number of twin primes ).

5. Determination of whether NP-problems are actually P-problems .

6. The Collatz problem .

7. Proof that the 196-algorithm does not terminate when applied to the number 196.

8. Proof that 10 is a solitary number .

11. Finding an Euler brick whose space diagonal is also an integer.

12. Proving which numbers can be represented as a sum of three or four (positive or negative) cubic numbers .

14. Determining if the Euler-Mascheroni constant is irrational .

15. Deriving an analytic form for the square site percolation threshold .

16. Determining if any odd perfect numbers exist.

The Clay Mathematics Institute ( http://www.claymath.org/millennium/ ) of Cambridge, Massachusetts (CMI) has named seven "Millennium Prize Problems," selected by focusing on important classic questions in mathematics that have resisted solution over the years. A $7 million prize fund has been established for the solution to these problems, with $1 million allocated to each. The problems consist of the Riemann hypothesis , Poincaré conjecture , Hodge conjecture , Swinnerton-Dyer Conjecture , solution of the Navier-Stokes equations, formulation of Yang-Mills theory, and determination of whether NP-problems are actually P-problems .

In 1900, David Hilbert proposed a list of 23 outstanding problems in mathematics ( Hilbert's problems ), a number of which have now been solved, but some of which remain open. In 1912, Landau proposed four simply stated problems, now known as Landau's problems , which continue to defy attack even today. One hundred years after Hilbert, Smale (2000) proposed a list of 18 outstanding problems.

K. S. Brown, D. Eppstein, S. Finch, and C. Kimberling maintain webpages of unsolved problems in mathematics. Classic texts on unsolved problems in various areas of mathematics are Croft et al. (1991), in geometry , and Guy (2004), in number theory .

Explore with Wolfram|Alpha

More things to try:

• abc conjecture
• 30-sided polyhedron

Referenced on Wolfram|Alpha

Cite this as:.

Weisstein, Eric W. "Unsolved Problems." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/UnsolvedProblems.html

Subject classifications

March 12, 2024

The Simplest Math Problem Could Be Unsolvable

The Collatz conjecture has plagued mathematicians for decades—so much so that professors warn their students away from it

By Manon Bischoff

Mathematicians have been hoping for a flash of insight to solve the Collatz conjecture.

James Brey/Getty Images

At first glance, the problem seems ridiculously simple. And yet experts have been searching for a solution in vain for decades. According to mathematician Jeffrey Lagarias, number theorist Shizuo Kakutani told him that during the cold war, “for about a month everybody at Yale [University] worked on it, with no result. A similar phenomenon happened when I mentioned it at the University of Chicago. A joke was made that this problem was part of a conspiracy to slow down mathematical research in the U.S.”

The Collatz conjecture—the vexing puzzle Kakutani described—is one of those supposedly simple problems that people tend to get lost in. For this reason, experienced professors often warn their ambitious students not to get bogged down in it and lose sight of their actual research.

The conjecture itself can be formulated so simply that even primary school students understand it. Take a natural number. If it is odd, multiply it by 3 and add 1; if it is even, divide it by 2. Proceed in the same way with the result x : if x is odd, you calculate 3 x + 1; otherwise calculate x / 2. Repeat these instructions as many times as possible, and, according to the conjecture, you will always end up with the number 1.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example: If you start with 5, you have to calculate 5 x 3 + 1, which results in 16. Because 16 is an even number, you have to halve it, which gives you 8. Then 8 / 2 = 4, which, when divided by 2, is 2—and 2 / 2 = 1. The process of iterative calculation brings you to the end after five steps.

Of course, you can also continue calculating with 1, which gives you 4, then 2 and then 1 again. The calculation rule leads you into an inescapable loop. Therefore 1 is seen as the end point of the procedure.

Following iterative calculations, you can begin with any of the numbers above and will ultimately reach 1.

Credit: Keenan Pepper/Public domain via Wikimedia Commons

It’s really fun to go through the iterative calculation rule for different numbers and look at the resulting sequences. If you start with 6: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1. Or 42: 42 → 21 → 64 → 32 → 16 → 8 → 4 → 2 → 1. No matter which number you start with, you always seem to end up with 1. There are some numbers, such as 27, where it takes quite a long time (27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → ...), but so far the result has always been 1. (Admittedly, you have to be patient with the starting number 27, which requires 111 steps.)

But strangely there is still no mathematical proof that the Collatz conjecture is true. And that absence has mystified mathematicians for years.

The origin of the Collatz conjecture is uncertain, which is why this hypothesis is known by many different names. Experts speak of the Syracuse problem, the Ulam problem, the 3 n + 1 conjecture, the Hasse algorithm or the Kakutani problem.

German mathematician Lothar Collatz became interested in iterative functions during his mathematics studies and investigated them. In the early 1930s he also published specialist articles on the subject , but the explicit calculation rule for the problem named after him was not among them. In the 1950s and 1960s the Collatz conjecture finally gained notoriety when mathematicians Helmut Hasse and Shizuo Kakutani, among others, disseminated it to various universities, including Syracuse University.

Like a siren song, this seemingly simple conjecture captivated the experts. For decades they have been looking for proof that after repeating the Collatz procedure a finite number of times, you end up with 1. The reason for this persistence is not just the simplicity of the problem: the Collatz conjecture is related to other important questions in mathematics. For example, such iterative functions appear in dynamic systems, such as models that describe the orbits of planets. The conjecture is also related to the Riemann conjecture, one of the oldest problems in number theory.

Empirical Evidence for the Collatz Conjecture

In 2019 and 2020 researchers checked all numbers below 2 68 , or about 3 x 10 20 numbers in the sequence, in a collaborative computer science project . All numbers in that set fulfill the Collatz conjecture as initial values. But that doesn’t mean that there isn’t an outlier somewhere. There could be a starting value that, after repeated Collatz procedures, yields ever larger values that eventually rise to infinity. This scenario seems unlikely, however, if the problem is examined statistically.

An odd number n is increased to 3 n + 1 after the first step of the iteration, but the result is inevitably even and is therefore halved in the following step. In half of all cases, the halving produces an odd number, which must therefore be increased to 3 n + 1 again, whereupon an even result is obtained again. If the result of the second step is even again, however, you have to divide the new number by 2 twice in every fourth case. In every eighth case, you must divide it by 2 three times, and so on.

In order to evaluate the long-term behavior of this sequence of numbers , Lagarias calculated the geometric mean from these considerations in 1985 and obtained the following result: ( 3 / 2 ) 1/2 x ( 3 ⁄ 4 ) 1/4 x ( 3 ⁄ 8 ) 1/8 · ... = 3 ⁄ 4 . This shows that the sequence elements shrink by an average factor of 3 ⁄ 4 at each step of the iterative calculation rule. It is therefore extremely unlikely that there is a starting value that grows to infinity as a result of the procedure.

There could be a starting value, however, that ends in a loop that is not 4 → 2 → 1. That loop could include significantly more numbers, such that 1 would never be reached.

Such “nontrivial” loops can be found, for example, if you also allow negative integers for the Collatz conjecture: in this case, the iterative calculation rule can end not only at –2 → –1 → –2 → ... but also at –5 → –14 → –7 → –20 → –10 → –5 → ... or –17 → –50 → ... → –17 →.... If we restrict ourselves to natural numbers, no nontrivial loops are known to date—which does not mean that they do not exist. Experts have now been able to show that such a loop in the Collatz problem, however, would have to consist of at least 186 billion numbers .

The length of the Collatz sequences for all numbers from 1 to 9,999 varies greatly.

Credit: Cirne/Public domain via Wikimedia Commons

Even if that sounds unlikely, it doesn’t have to be. In mathematics there are many examples where certain laws only break down after many iterations are considered. For instance,the prime number theorem overestimates the number of primes for only about 10 316 numbers. After that point, the prime number set underestimates the actual number of primes.

Something similar could occur with the Collatz conjecture: perhaps there is a huge number hidden deep in the number line that breaks the pattern observed so far.

A Proof for Almost All Numbers

Mathematicians have been searching for a conclusive proof for decades. The greatest progress was made in 2019 by Fields Medalist Terence Tao of the University of California, Los Angeles, when he proved that almost all starting values of natural numbers eventually end up at a value close to 1.

“Almost all” has a precise mathematical meaning: if you randomly select a natural number as a starting value, it has a 100 percent probability of ending up at 1. ( A zero-probability event, however, is not necessarily an impossible one .) That’s “about as close as one can get to the Collatz conjecture without actually solving it,” Tao said in a talk he gave in 2020 . Unfortunately, Tao’s method cannot generalize to all figures because it is based on statistical considerations.

All other approaches have led to a dead end as well. Perhaps that means the Collatz conjecture is wrong. “Maybe we should be spending more energy looking for counterexamples than we’re currently spending,” said mathematician Alex Kontorovich of Rutgers University in a video on the Veritasium YouTube channel .

Perhaps the Collatz conjecture will be determined true or false in the coming years. But there is another possibility: perhaps it truly is a problem that cannot be proven with available mathematical tools. In fact, in 1987 the late mathematician John Horton Conway investigated a generalization of the Collatz conjecture and found that iterative functions have properties that are unprovable. Perhaps this also applies to the Collatz conjecture. As simple as it may seem, it could be doomed to remain unsolved forever.

This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.

• Our Mission

3 Simple Strategies to Improve Students’ Problem-Solving Skills

These strategies are designed to make sure students have a good understanding of problems before attempting to solve them.

Research provides a striking revelation about problem solvers. The best problem solvers approach problems much differently than novices. For instance, one meta-study showed that when experts evaluate graphs , they tend to spend less time on tasks and answer choices and more time on evaluating the axes’ labels and the relationships of variables within the graphs. In other words, they spend more time up front making sense of the data before moving to addressing the task.

While slower in solving problems, experts use this additional up-front time to more efficiently and effectively solve the problem. In one study, researchers found that experts were much better at “information extraction” or pulling the information they needed to solve the problem later in the problem than novices. This was due to the fact that they started a problem-solving process by evaluating specific assumptions within problems, asking predictive questions, and then comparing and contrasting their predictions with results. For example, expert problem solvers look at the problem context and ask a number of questions:

• What do we know about the context of the problem?
• What assumptions are underlying the problem? What’s the story here?
• What qualitative and quantitative information is pertinent?
• What might the problem context be telling us? What questions arise from the information we are reading or reviewing?
• What are important trends and patterns?

As such, expert problem solvers don’t jump to the presented problem or rush to solutions. They invest the time necessary to make sense of the problem.

Now, think about your own students: Do they immediately jump to the question, or do they take time to understand the problem context? Do they identify the relevant variables, look for patterns, and then focus on the specific tasks?

If your students are struggling to develop the habit of sense-making in a problem- solving context, this is a perfect time to incorporate a few short and sharp strategies to support them.

3 Ways to Improve Student Problem-Solving

1. Slow reveal graphs: The brilliant strategy crafted by K–8 math specialist Jenna Laib and her colleagues provides teachers with an opportunity to gradually display complex graphical information and build students’ questioning, sense-making, and evaluating predictions.

For instance, in one third-grade class, students are given a bar graph without any labels or identifying information except for bars emerging from a horizontal line on the bottom of the slide. Over time, students learn about the categories on the x -axis (types of animals) and the quantities specified on the y -axis (number of baby teeth).

The graphs and the topics range in complexity from studying the standard deviation of temperatures in Antarctica to the use of scatterplots to compare working hours across OECD (Organization for Economic Cooperation and Development) countries. The website offers a number of graphs on Google Slides and suggests questions that teachers may ask students. Furthermore, this site allows teachers to search by type of graph (e.g., scatterplot) or topic (e.g., social justice).

2. Three reads: The three-reads strategy tasks students with evaluating a word problem in three different ways . First, students encounter a problem without having access to the question—for instance, “There are 20 kangaroos on the grassland. Three hop away.” Students are expected to discuss the context of the problem without emphasizing the quantities. For instance, a student may say, “We know that there are a total amount of kangaroos, and the total shrinks because some kangaroos hop away.”

Next, students discuss the important quantities and what questions may be generated. Finally, students receive and address the actual problem. Here they can both evaluate how close their predicted questions were from the actual questions and solve the actual problem.

To get started, consider using the numberless word problems on educator Brian Bushart’s site . For those teaching high school, consider using your own textbook word problems for this activity. Simply create three slides to present to students that include context (e.g., on the first slide state, “A salesman sold twice as much pears in the afternoon as in the morning”). The second slide would include quantities (e.g., “He sold 360 kilograms of pears”), and the third slide would include the actual question (e.g., “How many kilograms did he sell in the morning and how many in the afternoon?”). One additional suggestion for teams to consider is to have students solve the questions they generated before revealing the actual question.

3. Three-Act Tasks: Originally created by Dan Meyer, three-act tasks follow the three acts of a story . The first act is typically called the “setup,” followed by the “confrontation” and then the “resolution.”

This storyline process can be used in mathematics in which students encounter a contextual problem (e.g., a pool is being filled with soda). Here students work to identify the important aspects of the problem. During the second act, students build knowledge and skill to solve the problem (e.g., they learn how to calculate the volume of particular spaces). Finally, students solve the problem and evaluate their answers (e.g., how close were their calculations to the actual specifications of the pool and the amount of liquid that filled it).

Often, teachers add a fourth act (i.e., “the sequel”), in which students encounter a similar problem but in a different context (e.g., they have to estimate the volume of a lava lamp). There are also a number of elementary examples that have been developed by math teachers including GFletchy , which offers pre-kindergarten to middle school activities including counting squares , peas in a pod , and shark bait .

Students need to learn how to slow down and think through a problem context. The aforementioned strategies are quick ways teachers can begin to support students in developing the habits needed to effectively and efficiently tackle complex problem-solving.