WORD PROBLEMS INVOLVING OPERATIONS OF WHOLE NUMBERS
Problem 1 :
What number must be increased by 293 to get 648?
Let x be the required number.
What must be increased by 293 to get 648
x + 293 = 648
x = 648 - 293
Problem 2 :
A woman has $255 in her purse. She gives $35 to each of her five children. How much money does she have left?
Amount she has in her purse = $255
Each child gets = $35
Amount distributed :
Amount she has left :
= $255 - $175
Problem 3 :
The Year 8 students at a school are split into 4 equal classes of 27 students each. The school decides to increase the number of classes to 6. How many students will there be in each of the new classes, if the students are divided equally between them?
Number of existing classes = 4
Number of students in total :
Number of classes increased = 6
Number of students in each class :
= ¹⁰⁸⁄₆
Problem 4 :
My bank account contains $3621 and I make monthly withdrawals of $78 for 12 months. What is my new bank balance.
My old balance = $3621
I make withfrawals $78 each month for 12 months.
Amount of withdrawal :
My new balance :
= old balance - withdrawal
= $3621 - $936
Problem 5 :
A contractor bought 34 loads of soil, each weighing 12 tonnes. If the soil cost $23 per tonne, what was the total cost ?
Number of loads = 34
Weight of 1 load = 12 tonnes
Cost of soil = $23 per tonne
Number of tonnes :
= 408 tonnes
Required cost :
= $9384
Problem 6 :
4 less than three times of a whole number is equal to 8. Find the whole number.
Let x be the required whole number.
From the given information,
Add 4 to both sides.
Divide both sides by 3.
The whole number is 4.
Problem 7 :
The sum of two whole numbers is 8 and that of the difference is 2. Find the two whole numbers.
Let x and y be the two required whole numbers such that x > y .
x + y = 8 ----(1)
x - y = 2 ----(2)
Add (1) and (2) :
Divide both sides by 2.
Substitute x = 5 into (1).
Subtract 5 from both sides.
The two whole numbers are 5 and 3.
Problem 8 :
In a two-digit whole number, the digit at the tens place is twice the digit at the ones place. If 18 is subtracted from it, the digits are reversed. Find the two-digit whole number.
Let x be the digit in ones place.
Then the two-digit number is (2x)(x).
(2x)(x) - 18 = (x)(2x)
(10 ⋅ 2x) + (1 ⋅ x) - 18 = (10 ⋅ x) + (1 ⋅ 2x)
20x + x - 18 = 10x + 2x
21x - 18 = 12x
Subtract 12x from both sides.
9x - 18 = 0
Add 18 to both sides.
The digit at the ones place is 2 and the digit at the tens place is 4.
So, the required two-digit number is 42.
Problem 9 :
A whole number consisting of two digits is four times the sum of its digits and if 27 be added to it, the digits are reversed. Find the whole number.
Let xy be the required two-digit whole number.
Given : The two-digit whole is equal four times the sum of its digits
xy = 4(x + y)
(10 ⋅ x) + (1 ⋅ y) = 4x + 4y
10x + y = 4x + 4y
6x - 3y = 0
y = 2x ----(1)
Given : If 27 be added to it, the digits are reversed.
xy + 27 = yx
(10 ⋅ x) + (1 ⋅ y) + 27 = (10 ⋅ y) + (1 ⋅ x)
10 x + y + 27 = 10y + x
9x - 9y + 27 = 0
x - y + 3 = 0
Substitute y = 2x.
x - 2x + 3 = 0
Substitute x = 1 into (1).
Therefore, the required two-digit whole number is 36.
Problem 10 :
What are the smallest and largest three-digit whole numbers which are evenly divisible by 7?
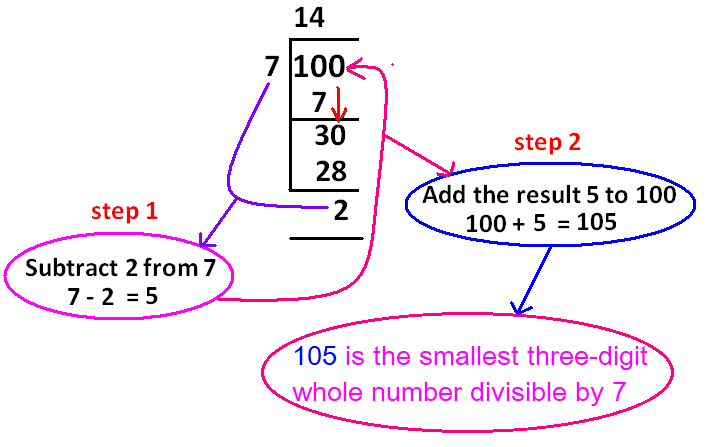
Steps to find the smallest three-digit whole number divisible by 7 :
The smallest three-digit whole number is 100. Divide 100 by 7 and get the quotient and remainder.
When 100 is divided by 7, the quotient is 14 and the remainder is 2.
Subtract the remainder 2 from the divisor 7.
Add 5 to the dividend 100.
105 is the smallest three-digit number divisible by 7.
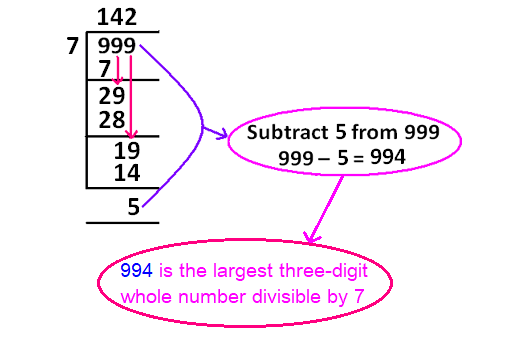
Steps to find the largest three-digit whole number divisible by 7 :
The largest three-digit whole number is 999. Divide 999 by 7 and get the quotient and remainder.
When 999 is divided by 7, the quotient is 142 and the remainder is 5.
Subtract the remainder 5 from the dividend 999.
994 is the largest three-digit number divisible by 7.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents

Recent Articles
Sat math practice videos (part - 4).
Jun 22, 24 05:38 AM
SAT Math Videos (Part - 17)
Jun 22, 24 05:05 AM
Factorial Problems and Solutions
Jun 22, 24 03:13 AM
Operations On Whole Numbers
Operations on whole numbers are discussed here:
The four basic operations on whole numbers are addition; subtraction; multiplication and division. We will learn about the basic operations in more detailed explanations along with the examples.
Worked-out problems related to Operations on whole numbers
1. Solve using rearrangement: (a) 784 + 127 + 216 Solution: 784 + 127 + 216
= (784 + 216) + 127
= 1000 + 127
= 1127
(b) 25 × 8 × 125 × 4
Solution: 25 × 8 × 125 × 4
= (125 × 8) × (25 × 4)
= 1000 × 100
2. Find the value using distributive property. (a) 2651 × 62 + 2651 × 38 Solution: 2651 × 62 + 2651 × 38
Property: a × b + a × c = a × (b + c)
= 2651 × (62 + 38)
= 2651 × 100
= 265100
(b) 347 × 163 - 347 × 63 Solution: 347 × 163 - 347 × 63
Property: a × b - a × c = a × (b - c)
= 347 × (163 - 63)
= 347 × 100
= 34700
(c) 128 × 99 + 128 Solution: 128 × 99 + 128
Property: a × b - a × c = a × (b + c)
= 128 × 99 + 128
= 128 × (99 + 1)
= 12800
3. Find the product using distributive property: (a) 237 × 103 Solution: 237 × 103
237 × (100 + 3)
Property: a × (b + c) = a × b + a × c
Therefore, 237 × (100 + 3)
= 237 × 100 + 237 × 3
= 23700 + 711
= 24411
(b) 510 × 99
Solution: 510 × 99
510 × (100 - 1)
Property: a × (b - c) = a × b - a × c
Therefore, 510 × (100 - 1)
= 510 × 100 - 510 × 1
= 51000 - 510
4. Verify the following: (a) 537 + 265 = 265 + 537 Solution: 537 + 265 =265 + 537
L.H.S. = 537 + 265 = 802
R.H.S. = 265 + 537 = 802
Property: a + b =b + a
Therefore, L.H.S. = R.H.S.
Hence, verified.
(b) 25 × (36 × 50) = (25 × 36) × 50 Solution: 25 × (36 × 50) = (25 × 36) × 50
L.H.S.= 25 × (36 × 50) = 25 × 1800 = 45000
R.H.S. = (25 × 36) × 50 = 900 × 50 = 45000
Property: a × (a × c) = (a × b) × c
5. Find the least number that must be subtracted from 1000 so that 45 divides the difference exactly. Solution: Divide 1000 by 45.
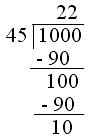
Now 1000 - 10 = 990
Therefore, 10 should be subtracted from 1000 so that difference 990 is divisible by 45.
6. Find the least number that should be added to 1000 so that 65 divides the sum exactly. Solution: Divide 1000 by 65.
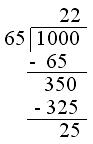
Now finding the difference between the divisor and remainder, we get
65 - 25 = 40
Therefore, 40 must be added to 1000 so that the sum 1040 is exactly divisible by 65.
7. Find the number which when divided by 15 gives 7 as the quotient and 3 as the remainder. Solution: Dividend = divisor × quotient + remainder
= 15 × 7 + 3
= 105 + 3 = 108
Therefore, the required number is 108
● Operations On Whole Numbers
● Addition Of Whole Numbers.
● Subtraction Of Whole Numbers.
● Multiplication Of Whole Numbers.
● Properties Of Multiplication.
● Division Of Whole Numbers.
● Properties Of Division.
5th Grade Math Problems From Operations On Whole Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
|
What’s this? | Facebook X Pinterest WhatsApp Messenger |
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Circle math | parts of a circle | terms related to the circle | symbol.
Jun 22, 24 11:46 AM
Worksheet on Triangle | Homework on Triangle | Different types|Answers
Jun 21, 24 02:19 AM

Worksheet on Circle |Homework on Circle |Questions on Circle |Problems
Jun 21, 24 01:59 AM
Circle | Interior and Exterior of a Circle | Radius|Problems on Circle
Jun 21, 24 01:00 AM
Quadrilateral Worksheet |Different Types of Questions in Quadrilateral
Jun 19, 24 09:49 AM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Understanding multiplication
Whole numbers
Here you will learn about whole numbers, including how to identify whole numbers, whole numbers on a number line, and the properties of whole numbers.
Students will first learn about whole numbers as part of counting and cardinality in Kindergarten and will expand their knowledge of whole numbers throughout elementary and middle school when learning about the properties of whole numbers and performing the four operations with whole numbers.
What are whole numbers?
Whole numbers are a set of numbers starting at zero and increasing by one each time.
Whole numbers do not include fractions, decimals, or negative numbers. They are positive integers.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10….
All whole numbers are integers, but not all integers are whole numbers since integers also include negative numbers. Both whole numbers and integers are rational numbers.
For example,
0 \quad \quad \quad \quad 100 \quad \quad \quad \quad 857 \quad 1,524 \quad \quad 125,031 \quad \quad 1,000,000 | -5 \quad \quad \quad \quad \cfrac{1}{2} \quad \quad \quad \quad 0.75 \quad 0.\overline{88} \quad \quad \quad \;\, 2\cfrac{1}{4} \,\;\; \quad \quad \quad \quad \pi \quad \quad |
Properties of whole numbers
Commutative property of whole numbers
- The commutative property of whole numbers states that the order of two numbers being added or multiplied together does not matter and that changing the order of the numbers will still give the same result.
a+b=b+a 4+5=5+4 | a \times b=b \times a 6 \times 3=3 \times 6 |
See also : Commutative property
Associative property of whole numbers
- The associative property of whole numbers states that, when adding or multiplying three numbers, the grouping of two numbers within the expression can change and still give the same result.
(a+b)+c=a+(b+c) (8+4)+6=8+(4+6) | (a \times b) \times c=a \times(b \times c) (2 \times 5) \times 7=2 \times(5 \times 7) |
See also : Associative property
Distributive property
- The distributive property of whole numbers says that multiplication is distributive over addition or subtraction. This means that when multiplying a number by a sum or difference of 2 numbers, you can multiply by each number separately and then add or subtract the products.
| | |
|---|---|
a(b+c)=(a \times b)+(a \times c) \begin{aligned} 5(3+9) & =(5 \times 3)+(5 \times 9) \\ & =15+45 \\ & =60 \end{aligned} | a(b-c)=(a \times b)-(a \times c) \begin{aligned} 8(10-1) & =(8 \times 10)-(8 \times 1) \\ & =80-8 \\ & =72 \end{aligned} |
See also : Distributive property
Closure property
- The closure property of whole numbers says that the sum or product of two whole numbers will always be a whole number.
a+b=c If a and b are whole numbers, c will be a whole number. 9+6=15 | a \times b=c If a and b are whole numbers, c will be a whole number. 8 \times 4=32 |
Common Core State Standards
How does this relate to Kindergarten math through 6th grade math?
- Kindergarten – Counting and Cardinality (K.CC.1, K.CC.2, K.CC.3) Count to 100 by ones and by tens; Count forward beginning from a given number within the known sequence (instead of having to begin at 1 ); Write numbers from 0 to 20. Represent a number of objects with a written numeral 0-20 (with 0 representing a count of no objects).
- Grade 1 – Operations and Algebraic Thinking (1.0A.B.3 ) Apply properties of operations as strategies to add and subtract. Examples: If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of addition). To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition).
- Grade 2 – Operations and Algebraic Thinking (2.OA.C.3) Determine whether a group of objects (up to 20 ) has an odd or even number of members, for example, by pairing objects or counting them by 2 s; write an equation to express an even number as a sum of two equal addends.
- Grade 3 – Operations and Algebraic Thinking (3.OA.B.5) Apply properties of operations as strategies to multiply and divide. Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication). 3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication). Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Distributive property).
- Grade 4 – Number and Operations Base Ten (4.NBT.B.5) Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
- Grade 6 – Number Systems (6.NS.B.4) Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1–100 with a common factor as a multiple of a sum of two whole numbers with no common factor. For example, express 36 + 8 as 4 \, (9 + 2).
How to use whole numbers
In order to identify whole numbers:
Recall the definition of the type of number needed.
Show whether the number fits or does not fit the definition.
In order to apply a property of whole numbers:
Recall the property.
Use the property to get an answer.
![problem solving using whole numbers [FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/06/Types-of-number-check-for-understanding-listing-image.jpg)
[FREE] Types of Number Check for Understanding Quiz (Grade 2, 4 and 6)
Use this quiz to check your grade 6 students’ understanding of types of numbers. 10+ questions with answers covering a range of 2nd, 4th and 6th grade types of numbers topics to identify areas of strength and support!
Identifying whole numbers examples
Example 1: identifying whole numbers.
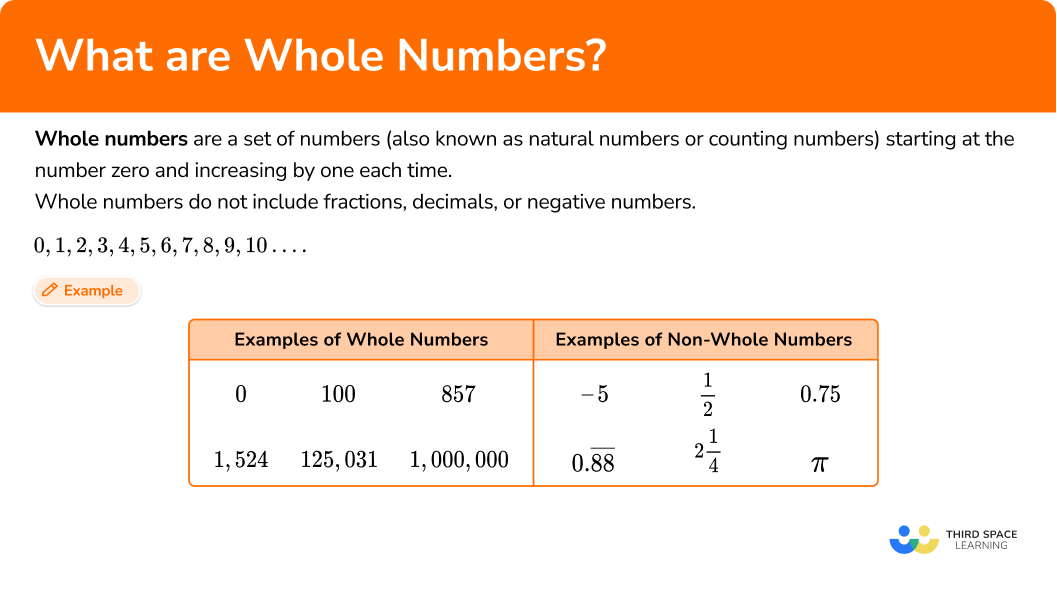
Which of the following are whole numbers?
0, \, 8.5, \, -1, \, 32, \, 6 \cfrac{1}{4} \, , \, 3.05, \, 927
Since the set of whole numbers does not include decimals, fractions, and negative numbers, you can eliminate 8.5, -1, 6 \cfrac{1}{4} \, , and 3.05 from the list.
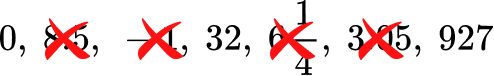
2 Show whether the number fits or does not fit the definition.
The remaining numbers are 0, 32, and 927. All three fit the definition and are whole numbers.
Answer: 0, 32, and 927
Example 2: identifying whole numbers
Maya says -4 is a whole number since it doesn’t have a decimal or fractional part. Is she correct?
The set of whole numbers includes all positive integers starting at zero. Whole numbers do not include negative numbers, fractions, or decimals.
-4 is not a whole number since it is not a positive number. Negative numbers are not whole numbers. Therefore, Maya is incorrect.
Example 3: identifying whole numbers
Which point on the number line represents a whole number?

The only point on the number line that shows a whole number is B, which represents 5.
Point A represents 3 \cfrac{1}{2} \, , point C represents 6 \cfrac{1}{2} \, and point D represents a fraction or decimal between 7 \cfrac{1}{2} and 8.
Since whole numbers do not include fractions or decimals, point B is the only whole number.
Example 4: identifying whole numbers
Which whole number fills in the blank in the sequence?
26, \, 27, \, 28, \, \rule{0.5cm}{0.15mm} \, , \, 30, \, 31
26, \, 27, \, 28, \, {\bf{29}}, \, 30, \, 31
Although there are many fractions and decimals in between 28 and 30, there is only one whole number, which is 29.
Example 5: apply a property of whole numbers
Fill in the blank using your knowledge of the commutative property of multiplication to make the equation true.
\rule{0.5cm}{0.15mm} \, \times 15=15 \times 3
The commutative property of multiplication states that the order of two numbers being multiplied together does not matter and that changing the order of the numbers will still give the same result.
a \times b = b \times a
\underline{3} \times 15=15 \times 3
The number 3 makes the equation true.
Example 6: apply a property of whole numbers
Fill in the blank using your knowledge of the distributive property to make the equation true.
3 \times(7 + 9)= \, \rule{0.5cm}{0.15mm} \, +27
The distributive property states that multiplication is distributive over addition. This means that when multiplying a number by a sum of 2 numbers, you can multiply by each number separately and then add the products.
a(b + c) =(a \times b) + (a \times c)
Since this equation can also be solved as (3 \times 7) + (3 \times 9), I know that the missing number is 21.
3 \times(7 + 9)=\underline{21}+27
Teaching tips for whole numbers
- Allow students to use concrete manipulatives to explore whole numbers when first building number sense.
- Use a number line to give students a visual representation of whole numbers. As they progress to higher grades, the number line can be partitioned into fractional and decimal parts as well, so students can see the difference between whole numbers and fractions/decimals. Later, a number line can also be extended past the number zero to show negative numbers. Students will gain better number sense when they are able to see non-examples of whole numbers.
- Display a chart or poster in the classroom showing the different types of numbers – whole numbers, natural numbers, integers, real numbers, etc. New types of numbers can be added to these displays in higher grade levels. This will help students differentiate between the sets of numbers.
Easy mistakes to make
- Thinking that zero is not a whole number Zero is the first and smallest whole number. The set of whole numbers begins at zero and increases by one with each number.
- Thinking that whole numbers are the same as integers Whole numbers are a subset of integers. Integers include all negative numbers, positive numbers, and zero, while whole numbers include only non-negative integers.
Related types of numbers lessons
This whole numbers topic guide is part of our series on types of numbers. You may find it helpful to start with the main types of numbers topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other topic guides in this series include:
- Types of numbers
- Irrational numbers
- Rational numbers
- Prime numbers
- Natural numbers
- Prime and composite numbers
- Number sets
- Even numbers
- Odd numbers
- Absolute value
Practice identifying whole numbers questions
1. What is the smallest whole number?

The set of whole numbers starts at zero. Whole numbers do not include negative numbers, fractions, or decimals. Therefore, the smallest whole number listed is zero.
2. Look at the number line. What is the missing whole number?
When counting whole numbers by ones, the number after 19 will be 20.
3. Colin wrote a set of whole numbers on the whiteboard using the numbers 0, 1, 3, and 9. What number should he not have included?
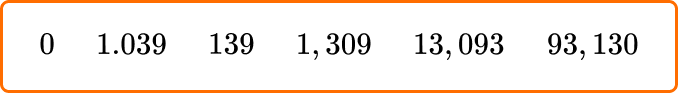
1.039 should not have been included because it is a decimal, not a whole number.
4. Select the group of numbers made up of only whole numbers.
101, \, 556, \, 18,000, \, 1 is the only group of numbers comprised of only whole numbers. The other groups include at least one fraction or decimal.
5. Which property is demonstrated by the following equation?
5(9+8)=(5 \times 9)+(5 \times 8)
Associative property
Commutative property
This shows the distributive property because multiplication is being distributed over addition. The distributive property allows you to perform the multiplication separately, then add the products.
6. Fill in the blank to make the equation true.
8 \times\left(6 \times \, \rule{0.5cm}{0.15mm} \, \right)=(8 \times 6) \times 4
This equation shows the associative property of multiplication, which states that when multiplying three numbers, the grouping of two numbers within the expression can change and still give the same result.
Therefore, since the right side shows 8, 6, and 4 being multiplied, I know the same 3 numbers are being multiplied on the left side of the equation.
Whole numbers FAQs
Whole numbers are a set of numbers (also known as natural numbers or counting numbers) starting at the number zero and increasing by one each time. Whole numbers do not include fractions, decimals, or negative numbers.
Whole numbers and natural numbers are very similar but not the same. The set of natural numbers starts at one instead of zero.
Whole numbers are a subset of integers. Integers include positive whole numbers, negative whole numbers, and zero, while whole numbers only include non-negative integers.
If the fraction has the same numerator and denominator, or if its numerator is a multiple of its denominator, it can be written as a whole number. For example, the fraction \cfrac{4}{2} can be written as the whole number 2.
The next lessons are
- Rounding numbers
- Factors and multiples
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview

Whole Number Word Problems
Free video lessons on how to solve whole number word problems using the math models (tape diagrams/block models) taught in Singapore Math .
Related Topics: Whole Number Operations , Previous set of video math lessons in this series. , Next set of video math lessons in this series.
Singapore Math: Primary 5 - Whole Numbers, Word Problem Q5
Singapore Math: Primary 5 - Whole Numbers, Word Problem Q6
Singapore Math: Primary 5 - Whole Numbers, Word Problem Q7
Singapore Math: Primary 5 - Whole Numbers, Word Problem Q8
Previous | Next set of videos in this series

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
4th Grade Resources - Use the four operations with whole numbers to solve problems.
Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
Newest 4th Grade Resources - Use the four operations with whole numbers to solve problems.
(Click on a resource to see our full catalog)
Operator Arithmetic
Use the four operators to solve multi-step equations
Mixed matching
Match pairs of equivalent equations to score points

Balloon Pop Mixed Operators
Pop ballons with mixed operators from smallest to largest
Calculator Chaos
Use knowledge of operations to solve several math problems using a single set of numbers.

Rate and keep track of your favorite activities! Sign Up to Rate Activities!
Create an Account!
Please pick a grade, elementary school math games, middle school math games, elementary school videos, middle school videos, elementary school worksheets, middle school worksheets, elementary school activities, middle school activities.

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
We think you are located in Russian Federation . Is this correct?
- Yes, I reside in Russian Federation
- Change country/curriculum
We use this information to present the correct curriculum and to personalise content to better meet the needs of our users.
1.1 Revision
Chapter 1: Working with whole numbers
In this chapter you will learn more about whole numbers. You will learn about different ways to express whole numbers as sums and products. You will learn about different ways of doing calculations, and different ways of recording your work when doing calculations. You will strengthen your skills to do calculations and to solve problems.
Do not use a calculator at all in section 1.1.
Build numbers up and break numbers down
Write each of the following sums as a single number:
The word sum is used to indicate two or more numbers that have to be added.
\( 4 000 + 800 + 60 + 5\)
\( 8 000 + 300 + 7\)
\( 40 000 + 9 000 + 200 + 3\)
\( 800 000 + 70 000 + 3 000 + 900 + 2\)
The answer obtained when the numbers are added, is also called the sum . We say: 20 is the sum of 15 and 5.
- \( 8 \text{ thousands} + 7 \text{ hundreds} + 8 \text{ units}\)
\(4 \text{ hundred thousands} + 8 \text{ ten thousands} + 4 \text{ hundreds} + 9 \text{ tens}\)
What is the sum of \(8 000\) and \(24\)?
Write each of the numbers below as a sum of units, tens, hundreds, thousands, ten thousands and hundred thousands, like the numbers were given in question 1(e) and (f).
When a number is written as a sum of units, tens, hundreds, thousands etc., it is called the expanded notation .
\(8 706 =\)
\(449 203 =\)
\(83 490 = \)
\(873 092 =\)
Arrange the numbers in question 3 from smallest to biggest.
Write the numbers in expanded notation (for example, \(791 = 700 + 90 + 1\)).
\(493 020\)
\(409 302\)
\(490 032 \)
\(400 932\)
Arrange the numbers in question 5 from biggest to smallest.
Write each sum as a single number.
\(600 000 + 40 000 + 27 000 + 100 + 20 + 34\)
\(320 000 + 40 000 + 8 000 + 670 + 10 + 5 \)
\( 500 000 + 280 000 + 7 000 + 300 + 170 + 38\)
\( 4 \text{ hundred thousands} + 18 \text{ ten thousands} + 4 \text{ hundreds} + 29 \text{ tens} + 5 \text{ units}\)
\(300 000 + 70 000 + 6 000 + 400 + 80 + 6\)
\(400 000 + 20 000 + 2 000 + 500 + 10 + 3 \)
\( 500 000 + 40 000 + 7 000 + 300 + 60 + 6\)
\(800 000 + 90 000 + 7 000 + 800 + 90 + 8\)
\(300 000 + 110 000 + 12 000 + 400 + 110 + 3\)
In each case, add the two numbers. Write the answer in expanded form and also as a single number.
(a) The number in 8(a) and the number in 8(b)
The number in 8(c) and the number in 8(b)
The number in 8(c) and the number in 8(a)
The number in 8(d) and the number in 8(a)
Subtract the number in 8(b) from the number in 8(d).
Are the numbers in 8(b) and 8(e) the same?
Subtract the number in 8(a) from the number in 8(b).
Write each of the following products as a single number:
The word product is used to indicate two or more numbers that have to be multiplied.
\(2 \times 3\)
\(2 \times 3 \times 5\)
\(2 \times 3 \times 5 \times 7\)
\(2 \times 3 \times 5 \times 7 \times 2\)
The answer obtained when numbers are multiplied, is also called the product . We say: 20 is the product of 2 and 10.
\(2 \times 3 \times 5 \times 7 \times 2 \times 2\)
What is the product of 20 and 500?
Write 1 000 as a product of 5 and another number.
Write 1 000 as a product of 50 and another number.
Write 1 000 as a product of 25 and another number.
What is the product of 2 500 and 4?
What is the product of 250 and 40?
In the table on the right, the number in each yellow cell is formed by adding the number in the red row above it to the number in the blue column to its left. Write the correct numbers in all the empty yellow cells.
| \(+\) | 2 | 3 | 4 | 5 |
| 10 | ||||
| 20 | ||||
| 30 | 34 | |||
| 40 | ||||
| 50 | ||||
| 60 | 63 | 65 | ||
| 70 |
The table below is formed in the same way as the table on the right. Fill in all the cells for which you know the answers immediately. Leave the other cells open for now.
| \(+\) | 8 | 5 | 4 | 9 | 7 | 3 | 6 | 18 | 36 | 57 |
| 7 | 64 | |||||||||
| 3 | 6 | |||||||||
| 9 | ||||||||||
| 5 | ||||||||||
| 8 | ||||||||||
| 6 | ||||||||||
| 4 |

How would you go about finding the number of blue dots below, if you do not want to count them one by one?
Implement your plan, to find out how many blue dots there are.

Suppose you want to know how many black dots there are in the arrangement on page 6. One way is to count in groups of three. When you do this, you may have to point with your finger or pencil to keep track.
The counting will go like this: three , six , nine , twelve , fifteen , eighteen . . .
Another way to find out how many black dots there are is to analyse the arrangement and do some calculations . In the arrangement, there are ten rows of threes from the top to the bottom, and three columns of threes from left to right, just as in the table alongside.
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
| 3 | 3 | 3 |
One way to calculate the total number of black dots is to do \(3 \times 10 = 30\) for the dots in each column, and then \(30 + 30 + 30 = 90\). Another way is to add up in each row \((3 + 3 + 3 = 9)\) and then multiply by 10: \(10 \times 9 = 90\). A third way is to notice that there are \(3 \times 10 = 30\) groups of three, so the total is \(3 \times 30 = 90\).
When you determined the number of blue dots in question 1(b), did you count in fives, or did you analyse and calculate, or did you use some other method? Now use a different method to determine the number of blue dots and check whether you get the same answer as before. Describe the method that you now use.
The numbers that you get when you count in fives are called multiples of five. Draw circles around all the multiples of 5 in the table below.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
How many red dots are there in the arrangement on page 6? Describe the method that you use to find this out.
Underline all the multiples of 7 in the table in question 3.
A number that is a multiple of 5, and also a multiple of 7, is called a common multiple of 5 and 7.
Which multiples of 5 in the table are also multiples of 7?
How many yellow dots are there in the arrangement on page 6? Describe the method that you use to find this out.
- Cross out all the multiples of 9 in the table in question 3.
Which numbers in the table in question 3 are common multiples of 7 and 9?
- Look at the numbers in the yellow cells of the table below. How are these numbers formed from the numbers in the red row and the numbers in the blue column?
Fill in all the cells for which you know the answers immediately. Leave the other cells open for now.
| \(\times\) | 8 | 5 | 4 | 9 | 7 | 3 | 6 | 2 | 10 | 20 |
| 7 | ||||||||||
| 3 | ||||||||||
| 9 | 90 | |||||||||
| 5 | 20 | |||||||||
| 8 | ||||||||||
| 6 | ||||||||||
| 4 | ||||||||||
| 2 | ||||||||||
| 10 | 50 | |||||||||
| 20 | 60 |
Write down the first thirteen multiples of each of the numbers in the column on the left. The multiples of 4 are already written in, as an example.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 2 | ||||||||||||
| 3 | ||||||||||||
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 |
| 5 | ||||||||||||
| 6 | ||||||||||||
| 7 | ||||||||||||
| 8 | ||||||||||||
| 9 | ||||||||||||
| 10 | ||||||||||||
| 11 | ||||||||||||
| 12 | ||||||||||||
| 13 |
Complete this table. For some cells, you may find your table of multiples above helpful.
| \(\times\) | 6 | 5 | 7 | 9 | 4 | 5 | 3 | 8 | 10 | 50 |
| 8 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 9 | ||||||||||
| 5 | ||||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 2 |
Go back to the table in question 8(b). If you can easily fill in the numbers in some of the open spaces now, do it.
Suppose there are 10 small black spots on each of the yellow dots in the arrangement on page 6. How many small black spots would there be on all the yellow dots together, in the arrangement on page 6?

Multiples of and
How many spotted yellow dots are there on page 11? Explain what you did to find out.
How many learners are there in your class?
Suppose each learner in the class has a book like this. How many spotted yellow dots are there on the same page (that is, on page 11) of all these books together?
Each yellow dot has 10 small black spots, as you can see on this enlarged picture.

How many small black spots are there on page 11?
How many small black spots are there on page 11 in all the books in your class?
Here is a very big enlargement of one of the black spots on the yellow dots. There are 10 very small white spots on each small black spot. How many very small white spots are there on all the black spots on page 11 together?

How many very small white spots are there on 10 pages like page 11?
How many very small white spots are there on 100 pages like page 11?
10 tens are a hundred : \(10 \times 10 = 100\)
10 hundreds are a thousand :\( 10 \times 100 = 1 000\)
10 thousands are a ten thousand : \(10 \times 1 000 = 10 000\)
10 ten thousands are a hundred thousand : \(10 \times 10 000 = 100 000\)
10 hundred thousands are a million : \(10 \times 100 000 = 1 000 000\)

Write \(7 000 + 600 + 80 + 4\) as a single number.
Write 10 times the number in (a) in expanded notation and as a single number.
Write 100 times the number in (a) in expanded notation and as a single number.
Write each of the following numbers in expanded notation:
Write 10 000 as a product of 10 and one other number.
Write 10 000 as a product of 100 and one other number.
Write 100 000 as a product of 10 and one other number.
Write 100 000 as a product of 1 000 and one other number.
Write 1 000 000 as a product of 1 000 and one other number.
In the table below, fill in all the cells for which you know the answers immediately. Leave the other cells open for now.
| \(\times\) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 2 | ||||||||||
| 3 | ||||||||||
| 4 | ||||||||||
| 5 | ||||||||||
| 6 | ||||||||||
| 7 | ||||||||||
| 8 | ||||||||||
| 9 | ||||||||||
| 10 | ||||||||||
| 11 | ||||||||||
| 12 |
Fill in all the cells in the table for which you know the answers immediately. Leave the other cells open for now.
| \(\times\) | 100 | 200 | 300 | 400 | 500 | 600 |
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | ||||||
| 9 | ||||||
| 10 | ||||||
| 11 | ||||||
| 12 |
How many multiples of 10 are smaller than 250? You may make an estimate, and then write the multiples down to check.
In each case first estimate, then check by writing all the multiples down and counting them.
How many multiples of 100 are smaller than 2 500?
How many multiples of 250 are smaller than 2 500?
How many numbers smaller than 2 500 are multiples of both 100 and 250?
How many numbers smaller than 2 500 are multiples of both 250 and 400?
In each of the tins below, there are three R10 notes, three R20 notes, three R100 notes and three R200 notes.

Zain wants to know what the total value of all the R10 notes in all the tins is. He decides to find this out by counting in 30s, so he says: thirty , sixty , ninety . . . and so on while he points at one tin after another.
Complete what Zain started to do.
Count in 300s to find out what the total value of all the R100 notes in all the tins is.
How much money is there in total in the eight yellow tins in question 13?
Join with two classmates and tell them how you worked to find the total amount of money.
- Investigate what is easiest for you, to count in twenties or in thirties or in fifties, up to 500.
- Many people find it easier to count in fifties than in thirties. Why do you think this is so?
What do you expect to be the most difficult, to count in forties or in seventies or in nineties? Investigate this and write a short report.
Here is some advice that can make it easier to count in certain counting units, for example in seventies.
It feels easier to count in fifties than in seventies because you get to multiples of 100 at every second step:
fifty, hundred , one hundred and fifty, two hundred , two hundred and fifty, 300 ,
350, 400 , 450, 500 ... and so on.
When you count in seventies, this does not happen:
seventy, one hundred and forty, two hundred and ten, two hundred and eighty ...
It may help you to cross over the multiples of 100 in two steps each time, like this:

In this way, you make the multiples of 100 act as "stepping stones" for your counting.
Count in forties up to 1 000. Try to use multiples of 100 as stepping stones. You can write the numbers below while you count.
Write down the first twenty multiples of 80.
Write down the first twenty multiples of 90.
Write down the first ten multiples of 700.
Complete this table.
| \(\times\) | 60 | 50 | 70 | 90 | 40 | 20 | 30 | 80 |
| 8 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 9 | ||||||||
| 5 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 2 | ||||||||
| 70 | ||||||||
| 30 | ||||||||
| 60 | ||||||||
| 80 | ||||||||
| 40 | ||||||||
| 90 | ||||||||
| 50 | ||||||||
| 20 |
Doubling and halving
Write the next eight numbers in each pattern:
1, 2, 4, 8, 16, 32
3 ,6, 12, 24
5, 10, 20, 40
5, 10, 15, 20
6, 12, 24, 48
Which pattern or patterns in question 1 are not formed by repeated doubling ?
The pattern 3, 6, 12, 24, 48 ... may be called the repeated doubling pattern that starts with 3.
Write the first nine terms of the repeated doubling patterns that start with the numbers in the left column of the table. The pattern for 13 has been completed as an example.
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
| 6 | ||||||||
| 7 | ||||||||
| 8 | ||||||||
| 9 | ||||||||
| 10 | ||||||||
| 11 | ||||||||
| 12 | ||||||||
| 13 | 26 | 52 | 104 | 208 | 416 | 832 | 1 664 | 3 328 |
| 14 | ||||||||
| 15 | ||||||||
| 16 | ||||||||
| 17 | ||||||||
| 18 | ||||||||
| 19 |
Doubling can be used to do multiplication.
For example, \(29 \times 8\) can be calculated as follows:
8 doubled is 16, so \(16 = 2 \times 8\) (step 1)
16 doubled is 32, so \(32 = 4 \times 8\) (step 2)
32 doubled is 64, so \(64 = 8 \times 8\) (step 3)
64 doubled is 128, so \(128 = 16 \times 8\) (step 4). Doubling again will go past \(29 \times 8\).
\(16 \times 8 + 8 \times 8 + 4 \times 8 = (16 + 8 + 4) \times 8 = 28 \times 8\).
So \(28 \times 8 = 128 + 64 + 32\) which is 224. So \(29 \times 8 = 224 + 8 = 232\).
Work as in the above example to calculate each of the following. Write only what you need to write.
\(37 \times 21\)
\( 17 \times 41\)
Continue each repeated halving pattern as far as you can:
1 024 ,512, 256 ,128
64 000, 32 000, 16 000, 8 000
Halving can also be used to do multiplication.
For example, \( 37 \times 28\) can be calculated as follows:
\(100 \times 28 = 2 800\). Half of that is \(50 \times 28\) which is half of 2 800, that is 1 400.
Half of \(50 \times 28\) is half of 1 400, so \(25 \times 28\) is 700.
\(10 \times 28 = 280\), so \(25 \times 28 + 10 \times 28 = 980\), so \(35 \times 28 = 980\).
\(2 \times 28 = 2 \times 25 + 2 \times 3 = 56\), so \(37 \times 28\) is \(980 + 56 = 1 036\).
\(80 \times 78 = 6 240\). Use this information to work out each of the following:
\(20 \times 78\)
\(37 \times 78\)
If chickens cost R27 each, how many chickens can you buy with R2 400? A way to use halving to work this out is shown on the next page.
100 chickens cost (100 \(\times\) 27 = R2 700. That is more than R2 400. 50 chickens cost half as much, that is R1 350.
So I can buy 50 chickens and even more.
Half of 50 is 25 and half of R1 350 is R675.
So 75 chickens cost R1 350 + R675, which is R2 025. So there is R375 left.
10 chickens cost R270, so 85 chickens cost R2 025 + R270 = R2 295. There is R105 left.
3 chickens cost 3 \( \times\) R25 + 3 \(\times\) R2 = R81.
I can buy 88 chickens and that will cost R2 376.
|
|
| |
| 100 | R2 700 | |
| 50 | R1 350 | half of R2 700 |
| 25 | R675 | half of R1 350 |
| 75 | R2 025 | 50 + 25 chickens |
| 10 | R270 | \(10 \times \text{R }27\) |
| 85 | R2 295 | 75 + 10 chickens |
| 3 | R81 | \(3 \times \text{R }27\) |
| 88 | R2 376 | 85 + 3 chickens |
Use halving as in the above example to work out how many books at R67 each a school can buy with R5 000.
|
|
| |
Using multiplication to do division
R7 500 must be shared between 27 netball players. The money is in R10 notes, and no small change is available.
How much money will be used to give each player R100?
Do you think there is enough money to give each player R200?
Do you think there is enough money to give each player R300?
How much of the R7 500 will be left over, if each player is given R200?
Is there enough money left to give each player R50 more, in other words a total of R250 each?
What is the highest amount that can be given to each player, so that less than R270 is left over? Remember that you cannot split up the R10 notes.
Work like you did in question 1 to solve this problem:
There is 4 580 m of string on a big roll. How many pieces of 17 m each can be cut from this roll?
Hint : You may start by asking yourself how much string will be used if you cut off 100 pieces of 17 m each.
Work like you did in questions 1 and 2 to solve this problem:
A shop owner has R1 800 available with which he can buy chickens from a farmer. The farmer wants R26 for each chicken. How many chickens can the shop owner buy?
What you actually did in questions 1, 2 and 3 was to calculate \(7 500 \div 27\), \(4 580 \div 17\) and \(1 800 \div 26\). You solved division problems. Yet most of the work was to do multiplication, and a little bit of subtraction.
When you had to calculate \(1 800 \div 26\) in question 3, you may have asked yourself:
With what must I multiply 26, to get as close to 1 800 as possible?
Division is called the inverse of multiplication.
Multiplication is called the inverse of division.
Multiplication and division are inverse operations .

Ordering and comparing whole numbers
How far can you count, and how far is far.
How long will it take to count to a million? Let us say it takes one second to count each number. Find out how long is one million seconds. Work in your exercise book. Give your final answer in days, hours and seconds.
Write 234 500 320 in words.
In each case insert one of the symbols > or < to indicate which number is the smaller of the two.
876 243 ☐ 876 234
534 616 ☐ 543 016
701 02 1 ☐ 698 769
103 232 ☐ 99 878
In each case place the numbers on the number line as carefully as you can.
185 000; 178 000; 170 900; 180 500

1 110 000; 1 102 900; 1 100 500; 1 105 050

The first row in the table shows the average distances of the planets from the Sun. These distances are given in millions of kilometres .
The distances from the Sun are called average distances, because the planets are not always the same distance from the Sun. Their orbits are not circles.
One million kilometres is 1 000 000 km .
| Planet | Mercury | Venus | Earth | Mars | Jupiter | Saturn | Uranus | Neptune |
| Distance from the Sun | 58 million km | 108 million km | 150 million km | 228 million km | 778 million km | 1 427 million km | 2 870 million km | 4 497 million km |
| Equatorial diameter | 4 880 km | 12 102 km | 12 756 km | 6 794 km | 142 800 km | 120 000 km | 52 400 km | 49 500 km |
The information in the table is also given in the drawings on page 2. Study the top drawing to find out what equatorial diameter means.
Which planet is the second farthest planet from the Sun?
How does Mars' distance from the Sun compare to that of Venus? Give two possible answers.
Arrange the planets from the smallest to the biggest.
Sometimes we do not need to know the exact number or exact amount. We say a loaf of bread costs about R10, or a bag of mealie meal costs about R20. The loaf of bread may cost R8 or R12 but it is close to R10. The mealie meal may cost R18 or R21 but it is close to R20.
When you read in a newspaper that there were 15 000 spectators at a soccer game, you know that that is not the actual number. In the language of mathematics we call this process rounding off or rounding .
Rounding to s , s , s and s
To round off to the nearest 5 , we round numbers that end in 1 or 2, or 6 or 7 down to the closest multiple of 5. We round numbers that end in 3 or 4, or 8 or 9 up to the closest multiple of 5.
For example, 233 is rounded down to 230, 234 is rounded up to 235, 237 is rounded down to 235 and 238 is rounded up to 240.
Round the following numbers to the nearest 5 by checking the unit value :
To round off to the nearest 10 , we round numbers that end in 1, 2, 3 or 4 down to the closest multiple of 10 (or decade). We round numbers that end in 5, 6, 7, 8 or 9 up to the closest multiple of 10.
For example, if you want to round off 534 to the nearest 10, you have to look at the units digit. The units digit is 4 and it is closer to 0 than to 10. The rounded off number will be 530.
Round the following numbers to the nearest 10 by checking the unit value :
When rounding to the nearest 100 , we look at the last two digits of the number. If the number is less than 50 we round down to the lower 100. If the number is 50 or more we round up to the higher 100.
Complete the table.
|
|
|
| |
| 681 |
|
|
|
| 5 639 |
|
|
|
| 5 361 |
|
|
|
| 12 458 |
|
|
|
When rounding to the nearest 1 000 , we look at the hundreds. Is the hundreds value less than, equal to or greater than 500? If less than 500, round down (the thousands value stays the same), if equal to 500 round up, and if greater than 500 round up too.
When rounding to the nearest 10 000 , we look at the thousands. Is the thousands value less than, equal to or greater than 5 000 ?If less than 5 00,round down (the ten thousands value stays the same ),if equal to 5 00 or greater than 5 000 round up
|
|
| |
| 142 389 | ||
| 343 621 | ||
| 356 552 | ||
| 100 489 |
Factors, prime numbers and common multiples
Different ways to produce the same number.
The number 80 can be produced by multiplying 4 and 20: \(4 \times 20 = 80\).
The number 80 can also be produced by multiplying 5 and 16.
In what other ways can 80 be produced by multiplying two numbers?
The number 80 can also be produced by multiplying 2, 10 and 4:
\(2 \times 10 = 20\) and \(20 \times 4 = 80\) or \(10 \times 4 = 40\) and \(40 \times 2 = 80\).
We can use brackets to describe what calculation is done first. So instead of writing "\(2 \times 10 = 20\) and \(20 \times 4 = 80\)" we may write \((2 \times 10) \times 4\). Instead of writing "\(10 \times 4 = 40 \)and \(40 \times 2\)" we may write \(2 \times (10 \times 4)\).
Show how the number 80 can be produced by multiplying four numbers. Describe how you do it in two ways: without using brackets and by using brackets.
Show three different ways in which the number 30 can be produced by multiplying two numbers.
Which three whole numbers?
Can the number 30 be produced by multiplying four whole numbers that do not include the number 1?
If you answered "yes", which four numbers?
The number 105 can be produced by multiplying 3, 5 and 7, hence we can write \(105 = 3 \times 5 \times 7\). Mathematicians often describe this by saying "105 is the product of 3, 5 and 7" or "105 can be expressed as the product \(3 \times 5 \times 7\)".
Express each of the following numbers as a product of three numbers.
The whole numbers that are multiplied to form a number are called factors of the number. For example, 6 and 8 are factors of 48 because \(6 \times 8 = 48\).
But 6 and 8 are not the only numbers that are factors of 48. 2 is also a factor of 48 because \(48 = 2 \times 24\). And 24 is a factor of 48. The numbers 3 and 16 are also factors of 48 because \(48 = 3 \times 16\).
Describe all the different ways in which 48 can be expressed as a product of two factors.
The number 36 can be formed by \(2 \times 2 \times 3 \times 3\). Because 2 is used twice, it is called a repeated factor of 36. The number 3 is also a repeated factor of 36.
Express 48 as a product of three factors.
Express 75 as a product of three factors.
Can 36 be expressed as a product of three factors? How?
Can 36 be expressed as a product of five factors? How?
Express each of the following numbers as a product of as many factors as possible, including repeated factors. Do not use 1 as a factor.
Prime numbers
Which of the numbers in question 1 cannot be expressed as a product of two whole numbers, except as the product \(1 \times \textit{the number itself}\) ?
A number that cannot be expressed as a product of two whole numbers, except as the product \( 1 \times \textit{the number itself}\), is called a prime number .
Which of the numbers in question 1 are prime?
Which numbers between 20 and 30 are prime?
Are 11 and 17 prime numbers?
Eratosthenes, a Greek mathematician who lived a long time ago, designed a method to find the prime numbers. The process is called "the sieve of Eratosthenes".
Work on the table below.
Follow the steps to find all the prime numbers up to 100.
Step 1: Cross out 1.
Step 2: Circle 2, and then cross out all the multiples of 2.
Step 3: Circle 3, then cross out all the multiples of 3.
Step 4: Find the next number that has not been crossed out and cross out all its multiples.
Continue like this.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
What is the smallest number that can be formed as a product of three prime numbers, if the same factor may be repeated?
What is the smallest number that can be formed as a product of three prime numbers, if no repeated factors are allowed?
Manare did a lot of work, and found out that 840 can be formed as the product of 2, 2, 2, 3, 5 and 7. Check whether Manare is correct.
We can say that Manare found the prime factors of 840, or Manare factorised 840 completely .
\(2\times 2 \rightarrow 4\times 2\rightarrow 24\times 5 \rightarrow 120 \times 7 = 840. \)
The prime factors of some numbers are given below. What are the numbers?
3, 5, 5 and 11
3, 3, 5 and 7
2, 7, 11 and 13
Investigate which of the following statements you agree with. Give reasons for your agreement or disagreement in each case.
If a number is even, 2 is one of its prime factors.
If half an even number is also even, 2 is a repeated prime factor.
If a number is odd, 3 is one of its prime factors.
If a number ends in 0 or 5, then 5 is one of its prime factors.
Here is a method to find the prime factors of a number:
If the number is even, divide it by 2. If the answer is even, divide by 2 again. Continue like this as long as it is possible. If the answer is odd, divide by 3, if it is possible. Continue to divide by 3 as long as it is possible. Then switch to 5. Continue like this by each time trying to divide by the next prime number.
Find all the prime factors of each of the following numbers. Work in your exercise book or on loose paper, and write only your answers below.
Find at least three prime numbers between 800 and 850.
Highest common factor and lowest common multiple
Factorise 195 and 385 completely.
Is 7 a factor of both 195 and 385?
Is 5 a factor of both 195 and 385?
When a number is a factor of two or more other numbers, it is called a common factor of the other numbers. For example, the number 5 is a common factor of 195 and 385.
The factors of a certain number are 2; 2; 5; 7; 7; 11 and 17. The factors of another number are 2; 3; 3; 7; 7; 11; 13 and 23. The common prime factors of these two numbers are 2; 7; 7 and 11.
The biggest number that is a factor of two or more numbers is called the highest common factor (HCF) of the numbers.
Find the HCF of the two numbers in each of the following cases.
\(2 \times 2 \times 5 \times 7 \times 7 \times 11 \times 17\) and \(2 \times 3 \times 3 \times 7 \times 7 \times 11 \times 13 \times 23\)
Write five different numbers, all different from 35, that have 35 as a highest common factor.
Write the next seven numbers in each pattern:
A: 12 24 36 48
B: 15 30 45 60
The numbers in pattern A are called the multiples of 12. The numbers in pattern B are called the multiples of 15. The numbers, for example 60 and 120, that occur in both patterns, are called the common multiples of 12 and 15. The smallest of these numbers, namely 60, is called the lowest common multiple (LCM) of 12 and 15.
Continue writing multiples of 18 and 24 below, until you find the LCM:
Find the HCF and LCM of the given numbers in each case below:
Properties of operations
Order of operations and the associative property.
Suppose you want to tell another person to do some calculations. You may do this by writing instructions. For example, you may write the instruction 200 - 130 - 30. This may be called a numerical expression .
Suppose you have given the instruction \(200 - 130 - 30\) to two people, whom we will call Ben and Sara.
This is what Ben does: \(200 - 130 = 70\) and \(70 - 30 = 40\).
This is what Sara does: \(130 - 30 = 100\) and \(200 - 100 = 100\).
To prevent such different interpretations or understandings of the same numerical expression, mathematicians have made the following agreement, and this is followed all over the world:
An agreement like this is called a mathematical convention .
In a numerical expression that involves addition and subtraction only , the operations should be performed from left to right , unless otherwise indicated in some way.
Who followed this convention in the above story, Ben or Sara?
Follow the above convention and calculate each of the following:
\( 8 000 + 6 000 - 3 000\)
\(8 000 - 3 000 + 6 000\)
\( 8 000 + 3 000 - 6 000\)
\( \text{R }25 000 + \text{R }30 000 + \text{R }13 000 + \text{R }6 000\)
\( \text{R }13 000 + \text{R }6 000 + \text{R }30 000 +\text{R }25 000\)
\( \text{R }30 000 + \text{R }25 000 + \text{R }6 000 + \text{R }13 000 \)
In question 3, all your answers should be the same. When three or more numbers are added, the order in which you perform the calculations makes no difference. This is called the associative property of addition . We also say: addition is associative .
Investigate whether multiplication is associative. Use the numbers 2, 3, 5 and 10.
What must be added to each of the following numbers to get 100?
73, 56, 66, 41, 34,23, 88
Calculate each of the following. Note that you can make the work simple by being smart in deciding which additions to do first.
\(73 + 54 + 27 + 46 + 138\)
\(34 + 88 + 41 + 66 + 59 + 12 + 127\)
The commutative property of addition and multiplication
What is the total cost of 20 chairs at R250 each?
What is the total cost of 250 exercise books at R20 each?
R5 000 was paid for 100 towels. What is the price for 1 towel?
R100 was paid for 5 000 beads. What is the price for 1 bead?
Which of the following calculations will produce the same answer? Mark those that will produce the same answers with a ✔ and those that won't with a ✘.
\(20 \times 250 \text{ and } 250 \times 20\)
\(5 000 \div 100 \text{ and } 100 \div 5 000\)
\( 730 + 270 \text{ and } 270 + 730 \)
\(730 - 270 \text{ and } 270 - 730\)
\(25 + 75 \text{ and } 75 + 25 \)have the same answer. The same is true for any other two numbers. We say: addition is commutative ; the numbers can be swopped around.
Demonstrate each of your answers with two different examples.
Is subtraction commutative?
Is multiplication commutative?
Is division commutative?
More conventions and the distributive property
Do the following:
Multiply 5 by 3, then add the answer to 20.
Add 5 to 20, then multiply the answer by 5.
Mathematicians have agreed that unless otherwise indicated, multiplication and division should be done before addition and subtraction . According to this convention, the expression \(20 + 5 \times 3\) should be taken to mean "multiply 5 by 3, then add the answer to 20" and not "add 5 to 20, then multiply the answer by 3".
\(500 + 20 \times 10\)
\( 500 - 20 \times 10 \)
\( 500 + 20 - 10 \)
\( 500 - 20 + 10 \)
\( 500 + 200 \div 5 \)
\( 500 - 200 \div 5 \)
If some of your answers are the same, you have made mistakes.
The above convention creates a problem. How can one describe the calculations in question 1(b) with a numerical expression, without using words?
To solve this problem, mathematicians have agreed to use brackets in numerical expressions. Brackets are used to specify that the operations within the brackets should be done first. Hence the numerical expression for 1(b) above is \((20 + 5) \times 5\), and the answer is 125.
The expression \(12 + 3 \times 5 \) means "multiply 3 by 5, then add 12". It does not mean "add 12 and 3, then multiply by 5".
If you wish to say "add 5 and 12, then multiply by 3", the numerical expression should be \( 3 \times (5 + 12)\) or \( (5 + 12) \times 3\). They mean the same.
If there are no brackets in a numerical expression, it means that multiplication and division should be done first, and addition and subtraction only later.
If you wish to specify that addition or subtraction should be done first,that part of the expression should be enclosed in brackets.
Keep the various mathematical conventions about numerical expressions in mind when you calculate each of the following:
- \(500 + 30 \times 10 \)
- \( (500 + 30) \times 10\)
- \(100 \times 500 + 30 \)
- \(100 \times (500 + 30)\)
- \( 500 - 30 \times 10\)
- \( (500 - 30) \times 10\)
- \( 100 \times 500 - 30 \)
- \(100 \times (500 - 30)\)
- \( (200 + 300) \div 20\)
- \( 200 \div 20 + 300 \div 20\)
- \( 600 \div (20 + 30)\)
- \( 600 \div 20 + 600 \div 30\)
Calculate the following:
- \( 50 \times (70 + 30) \)
- \( 50 \times 70 + 50 \times 30\)
- \( 50 \times (70 - 30) \)
- \( 50 \times 70 - 50 \times 30\)
Your answers for 4(a) and 4(b) should be the same.
Your answers for 4(c) and 4(d) should also be the same.
Do not do calculations A to I below. Just answer these questions about them. You will check your answers later.
Will A and B have the same answers?
Will G and H have the same answers?
Will A and D have the same answers?
Will A and G have the same answers?
Will A and F have the same answers?
Will D and E have the same answers?
A: \(5 \times (200 + 3)\)
B: \( 5 \times 200 + 3 \)
C: \(5 \times 200 + 5 \times 3\)
D: \(5 + 200 \times 3 \)
E: \((5 + 200) \times 3 \)
F: \((200 + 3) \times 5\)
G: \( 5 \times 203 \)
H: \(5 \times 100 + 5 \times 103\)
I: \(5 \times 300 - 5 \times 70\)
Now do calculations A to I. Then check the answers you gave in question 5.
Choose three different numbers between 3 and 11, and write them down below.
Your first number:
Your second number:
Your third number:
Add your first number to your third number. Multiply the answer by your second number.
Multiply your first number by your second number. Also multiply your third number by your second number. Add the two answers.
If you worked correctly, you should get the same answers in b and c. Do you think you will get the same result with numbers between 10 and 100, or any other numbers?
The fact that your answers for calculations like those in 7 b and 7 c are equal, for any numbers that you may choose, is called the distributive property of multiplication over addition .
It may be described as follows:
\(\text{first number} \times \text{second number} + \text{first number} \times \text{third number}\)
\(= \text{first number } \times (\text{second number } + \text{third number })\).
This can be described by saying that multiplication distributes over addition .
Check whether the distributive property is true for the following sets of numbers:
100, 50 and 10
any three numbers of your own choice (you may use a calculator to do this)
Use the numbers in question 8 a to investigate whether multiplication also distributes over subtraction.
It is quite fortunate that multiplication distributes over addition, because it makes it easier to multiply.
For example, \( 8 \times 238\) can be calculated by calculating \(8 \times 200\),\( 8 \times 30 \)and \(8 \times 8\), and adding the answers:\( 8 \times 238 = 8 \times 200 + 8 \times 30 + 8 \times 8 = 1 600 + 240 + 64 = 1 904\).
Check whether \( 8 \times 238 \) is actually 1 904 by calculating \(238 + 238 + 238 + 238 + 238 + 238 + 238 + 238\), or by using a calculator.
Basic operations
A method of addition.
To add two numbers, the one may be written below the other.
For example, to calculate \(378 539 + 46 285 \) the one number may be written below the other so that the units are below the units, the tens below the tens, and so on.
Writing the numbers like this has the advantage that
- the units parts (9 and 5) of the two numbers are now in the same column,
- the tens parts (30 and 80) are in the same column,
- the hundreds parts (500 and 200) are in the same column, and so on.
This makes it possible to work with each kind of part separately.
| We only write this: | In your mind you can see this: | |||||
| 378 539 | 300 000 | 70 000 | 8 000 | 500 | 30 | 9 |
| 46 285 | 40 000 | 6 000 | 200 | 80 | 5 | |
The numbers in each column can be added to get a new set of numbers:
| 378 539 | 300 000 | 70 000 | 8 000 | 500 | 30 | 9 |
|
| 40 000 | 6 000 | 200 | 80 | 5 | |
| 14 | 14 | |||||
| 110 | 110 | |||||
| 700 | 700 | |||||
| 14 000 | 14 000 | |||||
| 110 000 | 110 000 | |||||
|
| 300 000 | |||||
| 424 824 | It is easy to add the new set of numbers to get the answer. | |||||
Note that you can do the above steps in any order. Instead of starting with the units parts as shown above, you can start with the hundred thousands, or any other parts.
Starting with the units parts has an advantage though: it makes it possible to do more of the work mentally and to write less, as shown below:
| 378 539 |
|
|
| 424 824 |
To achieve this, only the units digit 4 of the 14 is written in the first step. The 10 of the 14 is remembered and added to the 30 and 80 of the tens column, to get 120.
We say the 10 is carried from the units column to the tens column. The same is done when the tens parts are added to get 120: only the digit "2" is written (in the tens column, so it means 20), and the 100 is carried to the next step.
Calculate each of the following:
- \(237 847 + 87 776\)
- \(567 298 + 392 076\)
- \( 28 387 + 365 667\)
A municipal manager is working on the municipal budget for a year. He has to try to keep the total expenditure on new office equipment below R800 000. He still has to budget for new computers that are badly needed, but this is what he has written so far:
| 74 new office chairs | R 54 020 |
| 42 new computer screens | R 100 800 |
| 12 new printers | R 141 600 |
| 18 new tea trolleys | R 25 740 |
| 8 new carpets for senior staff offices | R 144 000 |
| 108 small plastic filing cabinets | R 52 380 |
| new table for the boardroom | R 48 000 |
| 18 new chairs for the boardroom | |
| R ______ |
How much has the municipal manager budgeted for printers and computer screens together?
How much, in total, has the municipal manager budgeted for chairs and tables?
Work out the total cost of all the items the municipal manager has budgeted for.
23 809 + 2 009 + 23
- 320 293 + 16 923 + 349 + 200 323
Methods of subtraction
There are many ways to subtract one number from another. For example, R835 234 - R687 885 can be calculated by "filling up" from R687 885 to R835 234:
\(687 885 + 15 → 687 900 + 100→688 000 + 12 000 →700 000 + 135 234→ 835 234\)
| 15 |
| 100 |
| 12 000 |
|
|
| 147 349 |
The difference between R687 885 and R835 234 can now be calculated by adding up the numbers that had to be added to 687 885 to get 835 234.
So \(\text{R}835 234 - \text{R}687 885 = \text{R}147 349\).
Another easy way to subtract is to round off and compensate . For example, to calculate \(\text{R }3 224 - \text{R }1 885\), the R1 885 may be rounded up to R2 000. The calculation can proceed as follows:
- Rounding R1 885 up to R2 000 can be done in two steps: \(1 885 + 15 = 1 900\), and \(1 900 + 100 = 2 000\). In total, 115 was added.
- 115 can now be added to 3 224 too: \(3 224 + 115 = 3 339\).
Instead of calculating \( \text{R }3 224 - \text{R }1 885 \), which is a bit difficult, \( \text{R }3 339 - \text{R } 2 000 \) may be calculated. This is easy: \( \text{R }3 339 - \text{R }2 000 = \text{R }1 339 \).
This means that \(\text{R }3 224 - \text{R }1 885 = \text{R }1 339\), because \(\text{R }3 224 - \text{R }1 885 = (\text{R }3 224 + \text{R }115) - (\text{R }1 885 + \text{R }115)\).
To do question 1, you may use any one of the above two methods, or any other method you may know and prefer. Do not use a calculator, because the purpose of this work is for you to come to understand how subtraction may be done. What you will learn here, will later help you to understand algebra .
\(6 234 - 2 992\)
\(76 214 - 34 867\)
\( 134 372 - 45 828 \)
\(623 341 - 236 768\)
Check each of your answers in question 1 by doing addition, or by doing subtraction with a different method than the method you have already used.
Another method of subtraction is to think of the numbers in expanded notation . For example, to calculate \(\text{R}835 234 - \text{R}687 885\), which was already done in a different way on the previous page, we could work like this:
| We may write this: | In your mind you can see this: | |||||
| 835 234 | 800 000 | 30 000 | 5 000 | 200 | 30 | 4 |
| 687 885 | 600 000 | 80 000 | 7 000 | 800 | 80 | 5 |
Unfortunately, it is not possible to subtract in the columns now. However, the parts of the bigger number can be rearranged to make the subtraction in each column possible:
| 835 234 | 700 000 | 120 000 | 14 000 | 1100 | 120 | 14 |
| 687 885 | 600 000 | 80 000 | 7 000 | 800 | 80 | 5 |
| 100 000 | 40 000 | 7 000 | 300 | 40 | 9 | |
| The answer is now clearly visible; it is 147 349. | ||||||
The rearrangement, also called "borrowing", was done like this: 10 was taken from the 30 in the tens column, and added to the 4 in the units column. 100 was taken from the 200 in the hundreds column, and added to the 20 that remained in the tens column. 1 000 was taken from the 5 000 in the thousands column, and added to the 100 that remained in the hundreds column.
Describe the other rearrangements that were made in the above work.
It is not practical to write the expanded notation and the rearrangements each time you do a subtraction. However, with some practice you can learn to do it all in your mind without writing it down. Some people make small marks above the digits of the bigger number, or even change the digits, to keep track of the rearrangements they make in their minds.
| 835 234 |
|
|
| 147 349 |
Calculate the difference between the two car prices in each case.
- R73 463 and R88 798
- R63 378 and R96 889
In each case, first estimate the answer to the nearest 100 000, then calculate.
\(238 769 - 141 453\)
- \(856 333 - 439 878\)
In each case, first estimate the answer to the nearest 10 000, then calculate.
\(88 023 - 45 664\)
- \(342 029 - 176 553\)
Look again at the municipal budget on page 35. How much money does the municipal manager have left to buy new computers?
\(670 034 - 299 999\)
- \(670 034 - 300 000\)
\(376 539 - 175 998\)
- \(376 541 - 176 000\)
A method of multiplication
\(6 \times \text{R}3 258 \) can be calculated in parts, as shown below.
\(6 \times \text{R}3 000 = \text{R}18 000\)
\(6 \times \text{R}200 = \text{R}1 200\)
\(6 \times \text{R}50 = \text{R}300\)
\(6 \times \text{R}8 = \text{R}48\)
| 3 | 2 | 5 | 8 | |
| \(\times\) | 6 | |||
| 4 | 8 | |||
| 3 | 0 | 0 | ||
| 1 | 2 | 0 | 0 | |
| 1 | 8 | 0 | 0 | 0 |
| 1 | 9 | 5 | 4 | 8 |
The four partial products can now be added to get the answer, which is R19 548. It is convenient to write the work in vertical columns for units, tens, hundreds and so on, as shown on the right above.
In fact, if you are willing to do some hard thinking you can produce the answer with even less writing. You can achieve this by working from right to left to calculate the partial products, and by "carrying" parts of the partial answers to the next column, as you can do when working from right to left in columns. It works like this:
| 3 | 2 | 5 | 8 | |
| \(\times\) | 6 | |||
| 1 | 9 | 5 | 4 | 8 |
When \( 6 \times 8 = 48\) is calculated, only the "8" is written down, in the units column. The "4" that represents 40 is not written. It is kept "on hold" in your mind.
When \(6 \times 50 = 300 \) is calculated, the 40 from the previous step is added to 300 to get 340. Again, only the "4" that represents 40 is written. The 300 is kept on hold or "carried" to add to the answer of the next step. The work continues like this.
Calculate each of the following. Do not use a calculator.
\(8 \times 786\)
- \(9 \times 3 453\)
\(60 \times 786 \)
\(60 \times 7 860\)
You may use a calculator to check your answers for question 1. Repeat the work if your answers are not correct, so that you can learn where you make mistakes. Then put your calculator away again.
Use your answers for questions 1(a) and (c) to find out how much \(68 \times 786 \) is.
To calculate \(36 \times 378\), the work can be broken up in two parts, namely \(30 \times 378 \)and \(6 \times 378\).
Calculate \(36 \times 378\).
A complete write-up of calculating \(76 \times 2 348 \)in columns is shown below.
| 2 | 3 | 4 | 8 | |||
| \( \times \) | 7 | 6 | ||||
| A | 4 | 8 | ||||
| B | 2 | 4 | 0 | |||
| C | 1 | 8 | 0 | 0 | ||
| D | 1 | 2 | 0 | 0 | 0 | |
| E | 5 | 6 | 0 | |||
| F | 2 | 8 | 0 | 0 | ||
| G | 2 | 1 | 0 | 0 | 0 | |
| H | 1 | 4 | 0 | 0 | 0 | 0 |
| 1 | 7 | 8 | 4 | 4 | 8 |
Explain how the 240 in row B was obtained.
Explain how the 560 in row E was obtained.
Explain how the 21 000 in row G was obtained.
A short write-up of calculating \(76 \times 2 348\) in columns is shown on the right.
| 2 | 3 | 4 | 8 | ||
| \(\times\) | 7 | 6 | |||
| 1 | 4 | 0 | 8 | 8 | |
| 1 | 6 | 4 | 3 | 6 | 0 |
| 1 | 7 | 8 | 4 | 4 | 8 |
You may try to do the calculations in question 6 in this way. If you find it difficult, you may first write some of them up completely, and then try again to write less when you multiply.
Calculate each of the following.
\(53 \times 738 \)
\(73 \times 3 457\)
\(64 \times 3 478 \)
- \( 78 \times 1 298\)
\(37 \times 3 428\)
- \(78 \times 7 285\)
Use a calculator to check your answers for question 7. Redo the questions that you had wrong, so that you can learn to work correctly.
Use your correct answers for question 7 to give the answers to the following, without doing any calculations:
\( 101 244 \div 1 298\)
\( 568 230 \div 7 285\)
Calculate, without using a calculator.
\( 3 659 \times 38 \)
\(27 \times 23 487 \)
\( 486 \times 278\)
- \(2 135 \times 232\)
A process called long division
You may use a calculator to do questions 1 to 6.
You want to buy some live chickens at R37 each and you have R920 available. How many live chickens can you buy in total?
R880 is to be shared equally among 34 learners? How many full rands can each learner get?
You want to buy live chickens at R47 each. You have R1 280 available.How many live chickens can you buy?
42 equal bags of rice weigh a total of 7 560 g. How much does one bag weigh?
The number 26 was multiplied by a secret number and the answer was 2 184. What was the secret number?
This is an accurate sketch of the back of a house. The red line on the sketch is 70 mm long and it shows the width of the house. The blue line on the sketch indicates the height of the chimney. Do not measure the blue line now.
The width of the actual house is 5 600 mm, and the height of the chimney is 3 360 mm.

- How many times is the house bigger than the sketch? Describe what you can do to find this out.
Calculate how long the blue line on the sketch should be.
Now measure the blue line to check your answer for (b).
Division is used for different purposes:
In question 1 you knew that the amount is split into equal parts. You had to find out how many parts there are (how many chickens). This is called grouping .
In question 2 you knew that the amount was split into 34 equal parts. You needed to find out how big each part is (how much money each learner will get). This is called sharing .
What does question 3 require, sharing or grouping?
What does question 4 require, sharing or grouping?
In question 6 division was done for a different purpose than sharing or grouping.
Put your calculator away now. It is very important to be able to solve division problems by using your own mind. The activities that follow will help you to do this better than before. While you work on these activities, you will often have to estimate the product of two numbers. If you can estimate products well, division becomes easier to do. Hence, to start, do question 8, which will provide you with opportunities to practise your product estimation skills.
\(10 \times 74 \) or \( 30 \times 74\) or \(50 \times 74\) or \(70 \times 74\) or \( 90 \times 74 \)?
Calculate some of the products to check your answer.
What do you think is closest to \(9 238: 30 \times 38 \) or \( 50 \times 38\) or \( 100 \times 38 \) or \(150 \times 38\) or \(200 \times 38\) or \(250 \times 38\) or \(300 \times 38\)
What do you think is closest to \(9 746: 10 \times 287\) or \(20 \times 287\) or \(30 \times 287 \) or \(40 \times 287\) or \( 50 \times 287\) or \(60 \times 287 \) or \(70 \times 287\)?
By what multiple of 10 should you multiply 27 to get as close to 6 487 as possible?
A principal wants to buy T-shirts for the 115 Grade 7 learners in the school. The T-shirts cost R67 each, and an amount of R8 500 is available. Do you think there is enough money to buy T-shirts for all the learners? Explain your answer.
How much will 100 of the T-shirts cost?
How much money will be left if 100 T-shirts are bought?
How much money will be left if 20 more T-shirts are bought?
The principal wants to work out exactly how many T-shirts, at R67 each, she can buy with R8 500. Her thinking and writing are described below.
| What she writes: | What she thinks: | ||||
| 67 | 8 500 |
| |||
| What she writes: | What she thinks: | ||||
| 100 |
| ||||
| 67 | 8 500 | ||||
|
|
| ||||
| 1 800 |
| ||||
Step 3 (She has to rub out the one "0" of the 100 on top, to make space.)
| What she writes: | What she thinks: | ||||
| 120 |
| ||||
| 67 | 8 500 | ||||
|
| |||||
| 1 800 | |||||
|
|
| ||||
| 460 |
| ||||
Step 4 (She rubs out another "0".)
| What she writes: | What she thinks: | ||||
| 125 |
| ||||
| 67 | 8 500 | ||||
|
| |||||
| 1 800 | |||||
|
| |||||
| 460 | |||||
|
|
| ||||
| 125 |
| ||||
Step 5 (She rubs out the "5".)
| What she writes: | What she thinks: | ||||
| 126 |
| ||||
| 67 | 8 500 | ||||
|
| |||||
| 1 800 | |||||
|
| |||||
| 460 | |||||
|
| |||||
| 125 | |||||
|
|
| ||||
| 58 |
| ||||
Do not use a calculator in the questions that follow. The purpose of this work is for you to develop a good understanding of how division can be done. Check all your answers by doing multiplication.
Selina bought 85 chickens, all at the same price.She paid R3 995 in total. What did each of the chickens cost? Your first step can be to work out how much Selina would have paid if she paid R10 per chicken, but you can start with a bigger step if you wish
Anton has R4 850. He wants to buy some young goats. The goats cost R78 each. How many goats can he buy?
Calculate the following without using a calculator:
\( 7 234 \div 48 \)
\( 3 267 \div 24\)
\( 9 500 \div 364\)
\( 8 347 \div 24\)
A chocolate factory made 9 325 chocolates of a very special kind one day. The chocolates were packed in small decorated boxes,with 24 chocolates per box.How many cartons many boxes were filled?
A farmer sells eggs packed in cartons to the local supermarkets. There are 36 eggs in one carton. One month, the farmer sold 72 468 eggs to the supermarkets.How many cartoons is this?
Problem solving
Rate and ratio.
You may use a calculator for doing the work in this section.
The people in a village get their water from a nearby dam. On a certain day the dam contains 688 000 litres of water. The village people use about 85 000 litres of water each day. For how many days will the water in the dam last, if no rains fall?
Instead of saying "85 000 litres each day" or "8 cm each hour", people often say " at a rate of 85 000 litres per day " or " at a rate of 8 cm per hour ".
During a period of very heavy rain, the water level in a certain river increases at a rate of 8 cm each hour. If it continues like this, by how much will the water level increase in 24 hours?
A woman is driving from Johannesburg to Durban. Her distance from Durban decreases at a rate of about 95 km per hour. How far does she travel, approximately, in 4 hours?
The number of unemployed people in a certain province increases at a rate of approximately 35 000 people per year. If there were 860 000 unemployed people in the year 2000, how many unemployed people will there be, approximately, in the year 2020?
In pattern A below, there are 5 red beads for every 4 yellow beads.
Describe patterns B and C in the same way.

In a certain food factory, two machines are used to produce tins of baked beans. Machine A produces at a rate of 800 tins per hour, and machine B produces at a rate of 2 400 tins per hour.
Complete the following table, to show how many tins of beans will be produced at the two machines, in different periods of time.
| Number of hours | 1 | 2 | 3 | 5 | 8 |
| Number of tins at machine A | 800 | 1 600 | 2 400 | 4 000 | |
| Number of tins at machine B | 2 400 | 4 800 |
- How much faster is machine B than machine A?
How many tins will be produced at machine B in the time that it takes machine A to produce 30 tins?
How many tins will be produced at machine B in the time that it takes machine A to produce 200 tins?
How many tins will be produced at machine B in the time that it takes machine A to produce 1 tin?
The patterns in question 5 can be described like this:
In pattern A, the ratio of yellow beads to red beads is 4 to 5. This is written as 4 : 5.
In pattern B, the ratio between yellow beads and red beads is 3 : 6, and in pattern C the ratio is 2 : 7. In question 6, machine A produces 1 tin for every 3 tins that machine B produces. This can be described by saying that the ratio between the production speeds of machines A and B is 1 : 3.
Two huge trucks are travelling very slowly on a highway. Truck A covers 20 km per hour, and truck B covers 30 km per hour. Both trucks keep these speeds all the time.
What distance will truck B cover in the same time that truck A covers 10 km?
In the table below, the distances that truck A covers in certain periods of time are given. Complete the table, to show the distances covered by truck B, in the same periods of time.
| Distance covered by truck A | 10 km | 18 km | 50 km | 100 km | 30 km |
| Distance covered by truck B |
What distance will truck B cover in the same time that truck A covers 1 km?
What is the ratio between the speed at which truck A travels and the speed at which truck B travels?
R240 will be divided between David and Sally in the ratio 3 : 5. This means Sally gets R5 for every R3 David gets. How much will David and Sally each get in total?
How much will each person get, if R14 400 is shared between two people in each of the following ways?
In the ratio 1 : 3
In the ratio 5 : 7
Financial mathematics
A man borrows R12 000 from a bank for one year. He has to pay 15% interest to the bank. This means that, apart from paying the R12 000 back to the bank after a year, he has to pay 15 hundredths of R12 000 for the privilege of using the money that actually belongs to the bank.
15% is read as 15 per cent , and it is just a different way to say 15 hundredths .
One hundredth of R12 000 can be calculated by dividing R12 000 by 100. This amount can then be multiplied by 15 to get 15 hundredths of R12 000.
The money paid for using another person's house is called rent . The money paid for using another person's money is called interest .
Do not use a calculator when you do the following questions.
Calculate \(12 000 \div 100\), then multiply the answer by 15.
12% of R8 000
18% of R24 000
In each case below, calculate how much interest must be paid.
An amount of R6 000 is borrowed for 1 year at 9% interest.
An amount of R21 000 is borrowed for 3 years at 11% interest per year.
An amount of R45 000 is borrowed for 10 years at 12% interest per year.
A car dealer buys a car for R60 000 and sells it for R75 000. The difference of R15 000 is called the profit . In this case, the profit is a quarter of R60 000, which is the same as 25 hundredths or 25%. This can be described by saying "the car dealer made a profit of 25%".
Calculate the amount of profit in each of the following cases. The information is about a car dealer who buys and sells used vehicles.
A car is bought for R40 000 and sold for R52 000.
A small truck is bought for R100 000 and sold at a profit of 28%.
A bakkie is bought for R120 000 and sold at a profit of 30%.
A shop owner bought a stove for R2 000 and sold it for R1 600. The shop owner did not make a profit, he sold the stove at a loss of R400.
How much is 1 hundredth of R2 000?
How many hundredths of R2 000 is R400?
How much is 20% of R2 000?
Notice that by doing question 5(b) you have worked out at what percentage loss the shop owner sold the stove.
The shop owner also sold a fridge that normally sells for R4 000 at a discount of 20%. This means the customer paid 20% less than the normal price. Calculate the discount in rands and the amount that the customer paid for the fridge.
- Math Article
- Properties Of Whole Numbers
Properties of Whole Numbers

Properties of whole numbers are defined to operate basic arithmetic operations such as addition and multiplication, in an easy way. Applying these properties helps us to solve such Maths problems quickly, without even using calculators. These properties are almost similar to the properties of integers , although the definition for whole numbers and integers are different.
In this article, we are going to discuss the properties of whole numbers along with examples. Students of Class 6 can learn the properties here at BYJU’S and also solve the mathematical questions based on them. Before we begin with the properties, let us discuss whole numbers.
What are Whole Numbers?
Whole numbers are the set of positive integers or natural numbers along with the zero. But they cannot be a negative integer. Usually, the set of whole numbers is represented by ‘W’.
W = {0,1,2,3,4,5,6,7,8,9,10,….}
| Learn more: |
What are the Properties of Whole Numbers?
Properties of whole numbers are:
Closure Property
- Commutative Property of Addition and Multiplication
- Associative Property of Addition and Multiplication
- Distributive Property of multiplication over addition
- Identity Property
According to the Closure Property “Whole numbers are closed under addition and multiplication”. It means, when we add or multiply two whole numbers, then the resulting value is also a whole number.
If A and B are two whole numbers, then,
Where W represents whole numbers.
See some examples of closure property below:
| Closure property of Addition | Closure property of multiplication |
| 2 + 3 = 5 | 2 x 3 = 6 |
| 10 + 9 = 19 | 10 x 9 = 90 |
In the above examples, we can see, the resulting values such as 5, 6, 19 and 90 are also whole numbers. Therefore, the closure property is closed under addition and multiplication.
Commutativity of Addition and Multiplication
According to the commutative property of whole numbers, if two whole numbers are added or multiplied together, then the change in order of the numbers does not change the result. We can add or multiply two whole numbers in any order.
If A and B are two whole numbers, then;
- A + B = B + A
- A x B = B x A
Examples are given below:
| Commutativity of Addition | Commutativity of Multiplication |
| 3 + 5 = 5 + 3 ⇒ 8 | 3 x 5 = 5 x 3 ⇒ 15 |
| 4 + 6 = 6 + 4 ⇒ 10 | 4 x 6 = 6 x 4 ⇒ 24 |
As we can see from the above examples, if we change the order of the numbers, the result remains the same.
| Note: |
Associativity of Addition and Multiplication
The associative property of addition and multiplication states that the regrouping of three whole numbers does not change the result of their sum and product.
Let A, B and C are three whole numbers, then as per associativity,
We can understand the above two expressions, with the help of examples given below.
| (2 + 3) + 4 = 2 + (3 + 4) ⇒ 9 | (2 x 3) x 4 = 2 x (3 x 4) ⇒ 24 |
| (4 + 4) + 5 = 4 + (4 + 5) ⇒ 13 | (4 x 4) x 5 = 4 x (4 x 5) ⇒ 80 |
From the above examples, we can see, the regrouping of the numbers does not change the actual result.
| Associativity of subtraction and division of whole numbers does not exist. |
Distributivity of Multiplication over Addition
In this property, the multiplication is distributive over addition. It means, if A, B and C are three whole numbers, then;
Let us see the examples.
1. 6 × (5 + 3) = (6 × 5) + (6 × 3)
LHS = 6 × (5 + 3) = 6 × 8 = 48
RHS = (6 × 5) + (6 × 3) = 30 + 18 = 48
Hence, proved.
2. 7 × (11 + 9) = 7 × 11 + 7 × 9
LHS = 7 × (11 + 9) = 7 × 20 = 140
RHS = 7 × 11 + 7 × 9 = 77 + 63 = 140
Identity Property (for addition and multiplication)
The identity property of whole numbers for addition and multiplication states that:
Where W is any whole number.
Thus, by the above given expression, we can conclude that, if zero is added to any whole number, then the value of the original number does not change. Similarly, when we multiply any whole number by 1, then the value of the actual number remains unchanged. Hence, identity property holds both for addition and multiplication.
See some examples here:
| 2 + 0 = 2 | 2 x 1 = 2 |
| 5 + 0 = 5 | 5 x 1 = 5 |
| 7 + 0 = 7 | 7 x 1 = 7 |
| 10 + 0 = 10 | 10 x 1 = 10 |
| 50 + 0 = 50 | 50 x 1 = 50 |
| 100 + 0 = 100 | 100 x 1 = 100 |
Therefore, 0 is the additive identity and 1 is the multiplicative identity of any whole number.
Video Lesson on Numbers

- Difference Between Natural and Whole numbers
- Number Patterns In Whole Numbers
Solved Examples
Q.1: Add the numbers 134, 97 and 203, using suitable identity.
Solution: 134 + 97 + 203
= 134 + 300
Q.2: Simplify using suitable identity: 126 × 55 + 126 × 45
Solution: 126 × 55 + 126 × 45
= 126 × 100
| 1. Find the product by suitable rearrangement: 2. Find the product using identities: |
Frequently Asked Questions on Properties of Whole Numbers
What are the five properties of whole numbers.
The five properties of whole numbers are: Closure for addition and multiplication Commutative property for addition and multiplication Associative property for addition and multiplication Distributive property of multiplication over addition Identity for addition and multiplication
What is the commutative property of whole numbers?
As per the commutative property of whole numbers, changing the order of the two numbers, when added or multiplied, does not change the result.
Under which property are the whole numbers closed?
Whole numbers are closed under addition and multiplication. It means the addition and multiplication of two or more whole numbers results in a whole number only. 20 + 30 = 50, a whole number. 20 x 30 = 600, a whole number.
What is the formula of distributive property?
The formula for distributive property is given by: A x (B + C) = A x B + A x C Thus, distributive property is finding the product over the sum.
What is the identity for the addition of whole numbers?
Zero is the identity for the addition of whole numbers.
What is the identity for multiplication of whole numbers?
One (1) is the identity for multiplication of whole numbers
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Computer Vision
- Federated Learning
- Reinforcement Learning
- Natural Language Processing
- New Releases
- Advisory Board Members
- 🐝 Partnership and Promotion

Tanya Malhotra
Tanya Malhotra is a final year undergrad from the University of Petroleum & Energy Studies, Dehradun, pursuing BTech in Computer Science Engineering with a specialization in Artificial Intelligence and Machine Learning. She is a Data Science enthusiast with good analytical and critical thinking, along with an ardent interest in acquiring new skills, leading groups, and managing work in an organized manner.
- Firecrawl: A Powerful Web Scraping Tool for Turning Websites into Large Language Model (LLM) Ready Markdown or Structured Data
- Key Metrics for Evaluating Large Language Models (LLMs)
- This AI Paper Presents a Direct Experimental Comparison between 8B-Parameter Mamba, Mamba-2, Mamba-2-Hybrid, and Transformer Models Trained on Upto 3.5T Tokens
- BiGGen Bench: A Benchmark Designed to Evaluate Nine Core Capabilities of Language Models
RELATED ARTICLES MORE FROM AUTHOR
Mapo: the memory-friendly maestro – a new standard for aligning generative models with diverse preferences, enhancing llm reliability: detecting confabulations with semantic entropy, the rise of diffusion-based language models: comparing sedd and gpt-2, supervision by roboflow enhances computer vision projects: installation, features, and community support guide, planrag: a plan-then-retrieval augmented generation for generative large language models as decision makers, microsoft researchers introduce a theoretical framework using variational bayesian theory incorporating a bayesian intention variable, mapo: the memory-friendly maestro – a new standard for aligning generative models with diverse..., microsoft researchers introduce a theoretical framework using variational bayesian theory incorporating a bayesian intention....
- AI Magazine
- Privacy & TC
- Cookie Policy
🐝 🐝 Join the Fastest Growing AI Research Newsletter...
Thank You 🙌
Privacy Overview

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1.2.1: Adding Whole Numbers and Applications
- Last updated
- Save as PDF
- Page ID 60623

- The NROC Project
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Add whole numbers without regrouping.
- Add whole numbers with regrouping.
- Find the perimeter of a polygon.
- Solve application problems using addition.
Introduction
Adding is used to find the total number of two or more quantities. The total is called the sum , or the number that results from the addition. You use addition to find the total distance that you travel if the first distance is 1,240 miles and the second distance is 530 miles. The two numbers to be added, 1,240 and 530, are called the addends . The total distance, 1,770 miles, is the sum.
Adding Whole Numbers without Regrouping
Adding numbers with more than one digit requires an understanding of place value . The place value of a digit is the value based on its position within the number. In the number 492, the 4 is in the hundreds place, the 9 is in the tens place, and the 2 is in the ones place. You can use a number line to add. In the example below, the blue lines represent the two quantities, 15 and 4, that are being added together. The red line represents the resulting quantity.

On the number line, the blue line segment stretches across 15 units, representing the number 15. The second blue segment shows that if you add 4 more units, the resulting number is 19.
15 + 4 = 19
You can solve the same problem without a number line, by adding vertically. When adding numbers with more than 1 digit, it is important to line up your numbers by place value, as in the example below. You must add ones to ones, tens to tens, hundreds to hundreds, and so on.
| \(\ \begin{array}{r} 15 \\ +\quad 4 \\ \hline \end{array}\) | Because 5 and 4 have the same place value, make sure they are aligned when you add. |
| \(\ \begin{array}{r} 15 \\ +\quad 4 \\ \hline 9 \end{array}\) | First, add the ones digits (the numbers on the right). The result goes in the ones place for the answer. |
| \(\ \begin{array}{r} 15 \\ +\quad 4 \\ \hline 19 \end{array}\) | Then, add the tens digits and put the result in the tens place of the answer. In this case, there is no tens digit in the second number, so the result is the same as the tens digit of the first number (1). |
This strategy of lining up the numbers is effective for adding a series of numbers as well.
1 + 2 + 3 + 2 = ?
\(\ \begin{array}{r} 1 \\2 \\ 3 \\ +2 \\ \hline 8 \end{array}\)
1 + 2 + 3 + 2 = 8
Adding Whole Numbers with Regrouping
When adding whole numbers, a place-value position can have only one digit in it. If the sum of digits in a place value position is more than 10, you have to regroup the number of tens to the next greater place value position.
When you add, make sure you line up the digits according to their place values, as in the example below. As you regroup, place the regrouped digit above the appropriate digit in the next higher place value position and add it to the numbers below it.
45 + 15 = ?
| \(\ \begin{array}{r} \color{blue}1\ \ \\ 45 \\ +15 \\ \hline \color{blue}0 \end{array}\) | Add the ones. Regroup as needed. The sum of 5 and 5 is 10. This is 1 ten and 0 ones. Write the number of ones (0) in the ones place and the 1 ten in the tens place above the 4. |
| \(\ \begin{array}{l} &\color{blue}1 \\ &45 \\ +&15 \\ \hline &{\color{blue}6}0 \end{array}\) | Add the tens, 1 + 4 + 1 is 6 tens. The final sum is 60. |
45 + 15 = 60
You must add digits in the ones place first, the digits in the tens place next, and so on. Go from right to left.
4,576 + 698 = ?
| \(\ \begin{array}{r} 4,576 \\ +\quad 698 \\ \hline \end{array}\) | First, write the problem with one addend on top of the other. Be sure you line up the place values! |
| \(\ \begin{array}{r} \color{blue}1\ \ \\ 4,576 \\ +\quad 698 \\ \hline \color{blue}4 \end{array}\) | Add the numbers, 6 and 8, in the ones place. Since the sum is 14, write the ones value (4) in the ones place of the answer. Write the 1 ten in the tens place above the 7. |
| \(\ \begin{array}{r} {\color{blue}1}1\ \ \\ 4,576 \\ +\quad 698 \\ \hline {\color{blue}7}4 \end{array}\) | Add the numbers in the tens place. Since the sum is 17 tens, regroup 17 tens as 1 hundred, 7 in the tens place in the answer and write the 1 hundred in the hundreds place above the 5. |
| \(\ \begin{array}{r} {\color{blue}1}\ \ 11\ \ \\ 4,576 \\ +\quad 698 \\ \hline {\color{blue}2}74 \end{array}\) | Add the numbers in the hundreds place, including the 1. Again, the sum is more than one digit. Rename 12 hundreds as 2 hundreds and 1 thousand. Write the 2 in the hundreds place and the 1 above the 4 in the thousands place. |
| \(\ \begin{array}{r} 1\ \ 11\ \ \\ 4,576 \\ +\quad 698 \\ \hline {\color{blue}5},274 \end{array}\) | Add the numbers in the thousands place, including the 1. The final sum is 5,274. |
4,576 + 698 = 5,274
Adding Numbers Using the Partial Sums Method
Another way to add is the partial sums method. In the example below, the sum of 23 + 46 is found using the partial sums method. In this method, you add together all the numbers with the same place value and record their values (not just a single digit). Once you have done this for each place value, add their sums together.
23 + 46 = ?
| \(\ \begin{array}{r} 23&\color{blue}20 \\ 46&\color{blue}+40\\ \hline &\color{blue}60 \end{array}\) | Let’s begin by adding the values in the tens position, the 2 and 4. The values are written as 20 and 40. |
| \(\ \begin{array}{r} 23&\color{blue}3 \\ 46&\color{blue}+6\\ \hline &\color{blue}9 \end{array}\) | Add the values in the ones place, the 3 and 6. |
| \(\ \begin{array}{r} \color{blue}60 \\ \color{blue}+\quad 9 \\ \hline \color{blue}69 \end{array}\) | Finally, add the two sums, 60 and 9, together. |
23 + 46 = 69
The next example adds a series of three numbers. Notice that hundreds is the greatest place value now, so hundreds are added before the tens. (You can add in any order that you prefer.) Also notice that in Step 3, the value in the ones column for 350 is zero, but you still add that in to make sure everything is accounted for.
225 + 169 + 350 = ?
| \(\ \begin{array}{r} {\color{blue}2}25 & \color{blue}200 \\ {\color{blue}1}69 & \color{blue}100 \\ {\color{blue}3}50 &{\color{blue}+ 300}\\ \hline &\color{blue}600 \end{array}\) | Add the values represented by the digits 2, 1, and 3 in the hundreds place first. This gives a sum of 600. |
| \(\ \begin{array}{r} 2{\color{blue}2}5 & \color{blue}20 \\ 1{\color{blue}6}9 & \color{blue}60 \\ 3{\color{blue}5}0&\color{blue}+50\\ \hline &\color{blue}130 \end{array}\) | Next, add the values from the digits in the tens place, the 2, 6, and 9. The sum is 130. |
| \(\ \begin{array}{r} 22\color{blue}5 & \color{blue}5\\ | Add the values from the digits in the ones place, the 5, 9, and 0. The sum is 14. |
| \(\ \begin{array}{r} \color{blue}600 \\ \color{blue}130 \\ \color{blue}+\quad 14 \\ \hline \color{blue}744 \end{array}\) | At this point, you have a sum for each place value. Add together these three sums, which gives a final value of 744. |
225 + 169 + 350 = 744
A local company built a playground at a park. It took the company 124 hours to plan out the playground, 243 hours to prepare the site, and 575 hours to build the playground. Find the total number of hours the company spent on the project.
- Incorrect. You probably did not add the ones correctly. The correct answer is 942 hours.
- Incorrect. You probably did not add the tens correctly. The correct answer is 942 hours.
- Incorrect. You probably did not add the hundreds correctly. The correct answer is 942 hours.
- Correct. You carried out the partial sums process effectively. The parts should be 800 + 130 + 12.
When adding multi-digit numbers, use the partial sums method or any method that works best for you.
Finding the Perimeter of a Polygon
A polygon is a many-sided closed figure with sides that are straight line segments. Triangles, rectangles, and pentagons (five-sided figures) are polygons, but a circle or semicircle is not. The perimeter of a polygon is the distance around the polygon. To find the perimeter of a polygon, add the lengths of its sides, as in the example below.
One side of a square has a length of 5cm. Find the perimeter.
| Draw the polygon and label the lengths of the sides. Since the side lengths of a square are equal, each side is 5cm. | |
| \(\ \begin{array}{r} 5 \\ 5 \\ 5 \\ +\quad 5 \\ \hline 20 \end{array}\) | Add the lengths of each side, 5 + 5 + 5 + 5. |
The perimeter is 20cm.
The key part of completing a polygon problem is correctly identifying the side lengths. Once you know the side lengths, you add them as you would in any other addition problem.
A company is planning to construct a building. Below is a diagram illustrating the shape of the building’s floor plan. The length of each side is given in the diagram. Measurements for each side are in feet. Find the perimeter of the building.
| \(\ \begin{array}{r} 50 \\ 20 \\ 20 \\ 10 \\ 10 \\ 40 \\ 40 \\ +30 \\ \hline 220 \end{array}\) | Add the lengths of each side, making sure to align all numbers according to place value. |
The perimeter is 220 feet.
Find the perimeter of the trapezoid in feet.
- Correct. You added the lengths of the sides together successfully.
- Incorrect. You probably did not add the two diagonal sides of the trapezoid. The correct answer is 2,200 feet.
- Incorrect. You probably subtracted the total length of the two sides, 1,000 feet, from the total length of the top and bottom, 1,200. The correct answer is 2,200 feet.
- Incorrect. You may have added some of the sides more than once. The correct answer is 2,200 feet.
Solving Application Problems
Addition is useful for many kinds of problems. When you see a problem written in words, look for key words that let you know you need to add numbers.
A woman preparing an outdoor market is setting up a stand with 321 papayas, 45 peaches, and 213 mangos. How many pieces of fruit in total does the woman have on her stand?
| \(\ \begin{array}{r} 321 \\ 45 \\ +213 \\ \hline \end{array}\) | The words “how many… in total” suggest that you need to add the numbers of the different kinds of fruits. Use any method you like to add the numbers. Below, the partial sums method is used. |
| \(\ \begin{array}{r} {\color{blue}3}21 & \color{blue}300\\ {\color{blue} 0}45&\color{blue}0\\ {\color{blue}2}13 &\color{blue}+200\\ \hline &\color{blue}500 \end{array}\) | Add the numbers represented by the digits in the hundreds place first, the 3, 0 and 2. This gives a sum of 500. |
| \(\ \begin{array}{r} 3{\color{blue}2}1 & \color{blue}20 \\ 0{\color{blue}4}5 & \color{blue}40 \\ 2{\color{blue}1}3 &\color{blue}+ 10\\ \hline &\color{blue}70 \end{array}\) | Next, add the numbers represented by the digits from the tens place, the 2, 4, and 1. The sum is 70. |
| \(\ \begin{array}{r} 32\color{blue}1 & \color{blue}1 \\ 04\color{blue}5 & \color{blue}5 \\ 21\color{blue}3 &+ \color{blue}3\\ \hline &\color{blue}9 \end{array}\) | Add the numbers from the ones, the 1, 5, and 3. |
| \(\ \begin{array}{r} \color{blue}500 \\ \color{blue}70 \\ \color{blue}+\quad 9 \\ \hline \color{blue}579 \end{array}\) | Add together the three previous sums. The final sum is 579. |
The woman has 579 pieces of fruit on her stand.
Lynn has 23 rock CDs, 14 classical music CDs, 8 country and western CDs, and 6 movie soundtrack CDs. How many CDs does she have in all?
| \(\ \begin{array}{r} 23 \\ 14 \\ 8 \\ +6 \\ \hline \end{array}\) | The words “how many… in all” suggest that addition is the way to solve this problem. To find how many CDs Lynn has, you need to add the number of CDs she has for each music style. |
| \(\ \begin{array}{r} 2\ \ \\ 23 \\ 14 \\ 8 \\ +\quad 6 \\ \hline 51 \end{array}\) | Use whatever method you prefer to find the sum of the numbers. |
Lynn has 51 CDs.
The following phrases also appear in problem situations that require addition.
| Add to | Jonah was planning a trip from Boston to New York City. The distance is 218 miles. His sister wanted him to visit her in Springfield, Massachusetts, on his way. Jonah knew this would 17 miles his trip. How long is his trip if he visits his sister? |
| Plus | Carrie rented a DVD and returned it one day late. The store charged $5 for a two-day rental, a $3 late fee. How much did Carrie pay for the rental? |
| Increased by | One statistic that is important for football players in offensive positions is . After four games, one player had rushed 736 yards. After two more games, the number of yards rushed by this player 352 yards. How many yards had he rushed after the six games? |
| More than | Lavonda posted 38 photos to her social network profile. Chris posted 27 photos to his Lavonda. How many photos did Chris post? |
Lena was planning a trip from her home in Amherst to the Museum of Science in Boston. The trip is 91 miles. She had to take a detour on the way, which added 13 miles to her trip. What is the total distance she traveled?
The word “added” suggests that addition is the way to solve this problem.
To find the total distance, you need to add the two distances.
\(\ \begin{array}{r} 91 \\ +\quad 13 \\ \hline 104 \end{array}\)
The total distance is 104 miles.
It can help to seek out words in a problem that imply what operation to use. See if you can find the key word(s) in the following problem that provide you clues on how to solve it.
A city was struck by an outbreak of a new flu strain in December. To prevent another outbreak, 3,462 people were vaccinated against the new strain in January. In February, 1,298 additional people were vaccinated. How many people in total received vaccinations over these two months?
- Incorrect. You probably subtracted instead of adding. The correct answer is 4,760.
- Correct. You recognized this as an addition problem and successfully carried out your addition process.
- Incorrect. You probably did not regroup to the hundreds place, or added the hundreds places incorrectly. The correct answer is 4,760.
- Incorrect. You probably did not regroup to the tens place, or added the tens place incorrectly. The correct answer is 4,760.
Drawing a diagram to solve problems is very useful in fields such as engineering, sports, and architecture.
A coach tells her athletes to run one lap around a soccer field. The length of the soccer field is 100 yards, while the width of the field is 60 yards. Find the total distance that each athlete will have run after completing one lap around the perimeter of the field.
| The words “total distance” and “perimeter” both tell you to add. Draw the soccer field and label the various sides so you can see the numbers you are working with to find the perimeter. | |
| \(\ \begin{array}{r} \color{blue}1\ \ \ \ \\ 100 \\ 100 \\ 60 \\ +\quad 60 \\ \hline 20 \end{array}\) | There is a zero in the ones place, and the sum of 6 and 6 in the tens place is 12 tens. Place 2 tens in the tens place in the answer, and regroup 10 tens as 1 hundred. |
| \(\ \begin{array}{r} \color{blue}1\ \ \ \ \\ 100 \\ 100 \\ 60 \\ +\quad 60 \\ \hline {\color{blue}3}20 \end{array}\) | By adding the 1 hundred to the other digits in the hundreds place, you end up with a 3 in the hundreds place of the answer. |
Each athlete will have run 320 yards.
You can add numbers with more than one digit using any method, including the partial sums method. Sometimes when adding, you may need to regroup to the next greater place value position. Regrouping involves grouping ones into groups of tens, grouping tens into groups of hundreds, and so on. The perimeter of a polygon is found by adding the lengths of each of its sides.

IMAGES
VIDEO
COMMENTS
Use Place Value to Write Whole Numbers. In the following exercises, write each number as a whole number using digits. six hundred two. fifteen thousand, two hundred fifty-three. three hundred forty million, nine hundred twelve thousand, sixty-one. two billion, four hundred ninety-two million, seven hundred eleven thousand, two.
Multi-step word problems with whole numbers. Google Classroom. Microsoft Teams. After collecting eggs from his chickens, Dale puts the eggs into cartons to sell. Dale fills 15 cartons and has 7 eggs left over. Each carton holds 12 eggs.
So, the required two-digit number is 42. Problem 9 : A whole number consisting of two digits is four times the sum of its digits and if 27 be added to it, the digits are reversed. Find the whole number. Solution : Let xy be the required two-digit whole number. Given : The two-digit whole is equal four times the sum of its digits. xy = 4(x + y)
The four basic operations on whole numbers are addition; subtraction; multiplication and division. We will learn about the basic operations in more detailed explanations along with the examples. Worked-out problems related to Operations on whole numbers. 1. Solve using rearrangement: = (784 + 216) + 127. = 1000 + 127. = 1127. (b) 25 × 8 × 125 ...
Singapore Maths: Primary 5 - Whole Numbers, Word Problem Q4. Learn how to use models to understand and solve word problems on whole numbers. Example: Dave and Eli bought some DVDs and paid $96 altogether. If Eli bought 10 more DVDs than Dave and paid $20 more than him, find the number of DVDs that Dave bought. Next set of videos in this series.
In this article, you will learn how to solve various problems on whole numbers in simple methods and get accurate answers. What are whole numbers? In mathematics, whole numbers are defined as the set of numbers that include positive integers and 0. In other words, whole numbers are comprised of natural numbers and 0.
Example 5: apply a property of whole numbers. Fill in the blank using your knowledge of the commutative property of multiplication to make the equation true. \rule {0.5cm} {0.15mm} \, \times 15=15 \times 3 × 15 = 15 × 3. Recall the property. Show step.
1.6 Solving problems with whole numbers Order of operations. If you use "BODMAS" or "BEDMAS" correctly to remember the order of operations, you will get the same answer. But, evaluating an expression using terms will help more with algebra later on!
Number Word Problems Worksheets and Solutions. Objective: I can solve whole number word problems. Example: At a football match, there were 11 820 spectators. 8 256 of the spectators were adults. Of the remaining spectators, there were 3 times as many teenagers as young children. How many teenagers were there?
Solving a word problem on whole numbers using models. Example: Each month Li pays bills for electricity and water. If she pays $36 a month for electricity, and $720 a year for electricity and water together, find the amount of money she pays for water each month. Show Step-by-step Solutions.
This video provides several examples of solving word problems using whole number operations.Complete Video List: http://www.mathispower4u.yolasite.com
1.3: Multiplication and Division of Whole Numbers We begin this section by discussing multiplication of whole numbers. The first order of business is to introduce the various symbols used to indicate multiplication of two whole numbers. 1.4: Prime Factorization; 1.5: Order of Operations; 1.6: Solving Equations by Addition and Subtraction; 1.7 ...
4th Grade Resources - Use the four operations with whole numbers to solve problems. Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 x 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations. Multiply or divide to ...
Practice Solving Word Problems Using Multiplication of Whole Numbers with practice problems and explanations. Get instant feedback, extra help and step-by-step explanations. Boost your Algebra ...
Multiply whole numbers by a power of 10. Use rounding to estimate products. Find the area of a rectangle. Solve application problems using multiplication. Introduction. Instead of adding the same number over and over again, an easier way to reach an answer is to use multiplication. Suppose you want to find the value in pennies of 9 nickels.
4.OA.A.3. Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation
Follow the steps here to solve a word problem involving division. Step 1: Determine the total number of objects that are being divided into groups. Step 2: Determine either (a) the number of ...
Round whole numbers word problems. The distance to the moon is an average of 384,400 kilometers. Round the distance to the nearest ten thousand. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free ...
Practice Solving a Word Problem with the Addition of Whole Numbers with practice problems and explanations. Get instant feedback, extra help and step-by-step explanations. Boost your Algebra grade ...
You will learn about different ways to express whole numbers as sums and products. You will learn about different ways of doing calculations, and different ways of recording your work when doing calculations. You will strengthen your skills to do calculations and to solve problems. Revision. Do not use a calculator at all in section 1.1.
It means, when we add or multiply two whole numbers, then the resulting value is also a whole number. If A and B are two whole numbers, then, A + B → W. A x B → W. Where W represents whole numbers. See some examples of closure property below: Closure property of Addition. Closure property of multiplication. 2 + 3 = 5.
Three Ways to Represent Division. 12 ÷ 3 = 4 ( with a division symbol; this equation is read "12 divided by 3 equals 4." 4 3\longdiv12 ( with a division or long division symbol; this expression is read "12 divided by 3 equals 4." Notice here, though, that you have to start with what is underneath the symbol.
Here you will find our selection of 1st Grade Addition Word Problems which will help your child learn to solve addition problems using numbers with a sum of up to 20. Addition Word Problems. Math Word Problems. Addition Words. Subtraction Word Problems. Math Problem Solving. Word Problem Worksheets.
In this article we will explain a number of sophisticated prompt engineering strategies, simplifying these difficult ideas through straightforward human metaphors. The techniques and their examples have been discussed to see how they resemble human approaches to problem-solving. Chaining Methods. Analogy: Solving a problem step-by-step.
Adding Whole Numbers without Regrouping. Adding numbers with more than one digit requires an understanding of place value. The place value of a digit is the value based on its position within the number. In the number 492, the 4 is in the hundreds place, the 9 is in the tens place, and the 2 is in the ones place. You can use a number line to add.