unit 12 homework 5 law of sines

Law of Sines Worksheet

Students will practice applying the law of sines to calculate side lengths and angle measurements. This worksheet includes word problems as well as challenging bonus problems.

Example Questions

Visual Aids

Other Details

This is a 5 part worksheet:

• Part I Model Problems
• Part II Practice Problems (1-6)
• Part III Practice (harder) & Word Problems (7 - 18)
• Part IV Challenge Problems
• Part V Answer Key
• Pictures of Law of Sines (triangles, formula and more..)
• Law of Sines and Cosines Worksheets

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.1.1: Laws of Sines and Cosines

• Last updated
• Save as PDF
• Page ID 4154

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Solving for parts of non-right triangles using trigonometry.

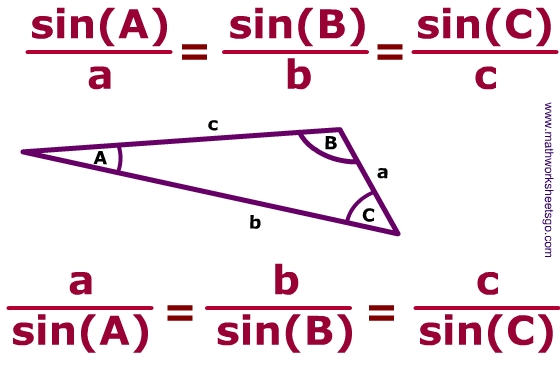
Law of Sines: If \(\Delta ABC\) has sides of length, \(a\), \(b\), and \(c\), then \(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\).

Looking at a triangle, the lengths a,b, and c are opposite the angles of the same letter.

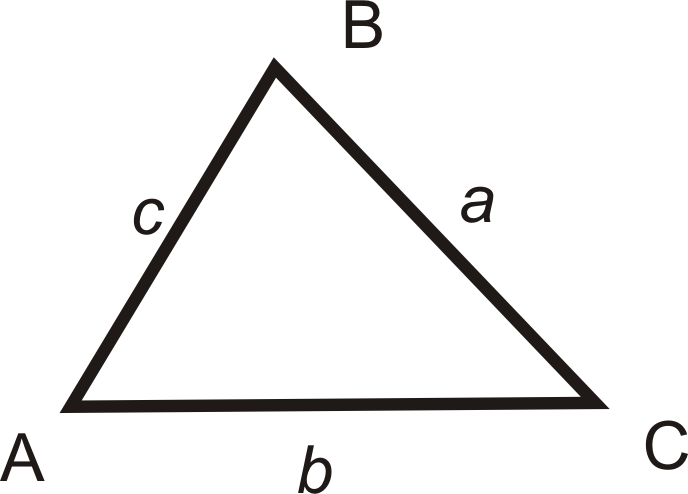
Use Law of Sines when given:

• An angle and its opposite side.
• Any two angles and one side.

Two sides and the non-included angle.

Law of Cosines: If \(\Delta ABC\) has sides of length \(a\),\(b\), and \(c\), then:

\(\begin{aligned} a^2&=b^2+c^2−2bc\cos A \\ b^2&=a^2+c^2−2ac \cos B \\ c^2&=a^2+b^2−2ab \cos C \end{aligned}\)

Even though there are three formulas, they are all very similar. First, notice that whatever angle is in the cosine, the opposite side is on the other side of the equal sign.

Use Law of Cosines when given:

• Two sides and the included angle.
• All three sides.

Using the Law of Sines

1. Solve the triangle using the Law of Sines . Round decimal answers to the nearest tenth.

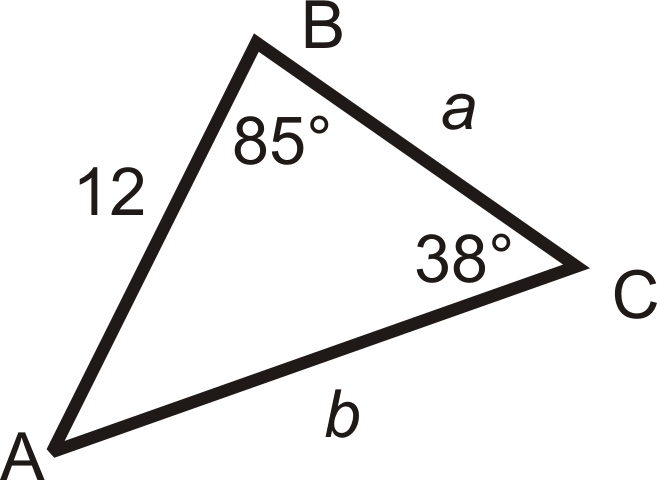
First, to find \(m\angle A\), we can use the Triangle Sum Theorem.

\(\begin{aligned} m\angle A+85^{\circ} +38^{\circ}&=180^{\circ} \\ m\angle A&=57^{\circ} \end{aligned}\)

Now, use the Law of Sines to set up ratios for \(a\) and \(b\).

\(\dfrac{\sin 57^{\circ} }{a}=\dfrac{\sin 85^{\circ} }{b}=\dfrac{\sin 38^{\circ} }{12}\)

\(\begin{aligned} \dfrac{\sin 57^{\circ}}{a} &=\dfrac{\sin 38^{\circ}}{12} & \dfrac{\sin 85^{\circ}}{b} &=\dfrac{\sin 38^{\circ}}{12} \\ a \cdot \sin 38^{\circ} &=12 \cdot \sin 57^{\circ} & b \cdot \sin 38^{\circ} &=12 \cdot \sin 85^{\circ} \\ a &=\dfrac{12 \cdot \sin 57^{\circ}}{\sin 38^{\circ}} \approx 16.4 & \quad b &=\dfrac{12 \cdot \sin 85^{\circ}}{\sin 38^{\circ}} \approx 19.4 \end{aligned}\)

2. Solve the triangle using the Law of Sines. Round decimal answers to the nearest tenth.

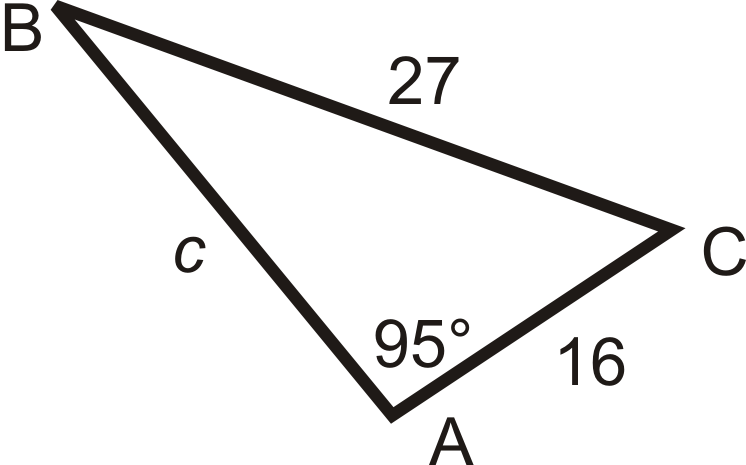
Set up the ratio for \(\angle B\) using Law of Sines.

\(\begin{aligned} \dfrac{\sin 95^{\circ} }{27}&=\dfrac{\sin B}{16} \\ 27\cdot \sin B&=16\cdot \sin 95^{\circ} \\ \sin B&=\dfrac{16\cdot \sin 95^{\circ} }{27}\rightarrow\sin ^{−1}\left(\dfrac{16\cdot \sin 95^{\circ} }{27} \right) =36.2^{\circ} \end{aligned}\)

To find \(m\angle C\) use the Triangle Sum Theorem.

\(m\angle C+95^{\circ} +36.2^{\circ} =180^{\circ} \rightarrow m\angle C=48.8^{\circ}\)

To find \(c\), use the Law of Sines again. \(\dfrac{\sin 95^{\circ} }{27}=\dfrac{\sin 48.8^{\circ} }{c}\)

\(\begin{aligned} c\cdot \sin 95^{\circ}&=27\cdot \sin 48.8^{\circ} \\ c&=27\cdot \sin 48.8^{\circ} \sin 95^{\circ} \approx 20.4 \end{aligned}\)

Using the Law of Cosines

Solve the triangle using Law of Cosines . Round your answers to the nearest hundredth.

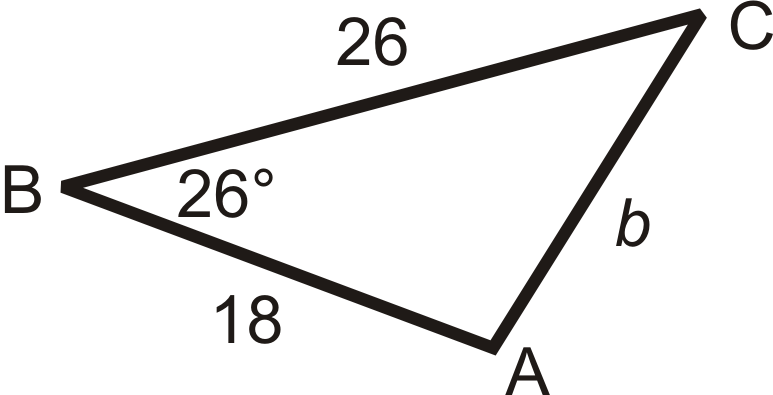
Use the second equation to solve for \(\angle B\).

\(\begin{aligned} b^2&=26^2+18^2−2(26)(18)\cos 26^{\circ} \\ b^2&=1000−936\cos 26^{\circ} \\ b^2&=158.7288 \\ b&\approx 12.60 \end{aligned}\)

To find \(m\angle A\) or \(m\angle C\), you can use either the Law of Sines or Law of Cosines . Let’s use the Law of Sines.

\(\begin{aligned} \dfrac{\sin 26^{\circ} }{12.60}&=\dfrac{\sin A}{18} \\ 12.60\cdot \sin A&=18\cdot \sin 26^{\circ} \\ \sin A&=18\cdot \sin 26^{\circ} 12.60 \end{aligned}\)

\(\sin ^{−1} \left(18\cdot \sin 26^{\circ} 12.60 \right)\approx 38.77^{\circ} \) To find \(m\angle C\), use the Triangle Sum Theorem.

\(\begin{aligned} 26^{\circ} +38.77^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=115.23^{\circ} \end{aligned}\)

Find the following angles in the triangle below. Round your answers to the nearest hundredth.

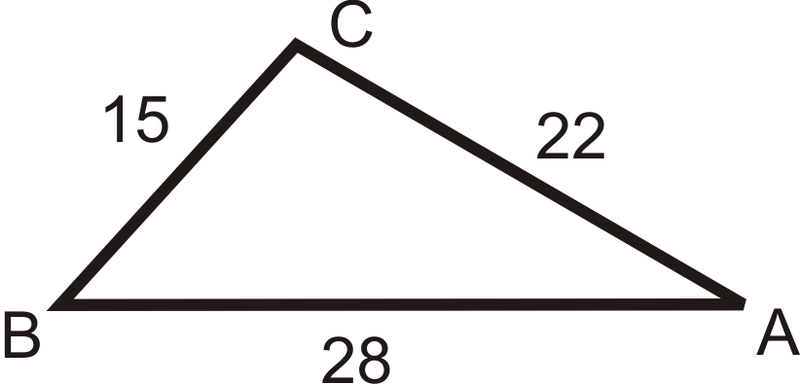
Example \(\PageIndex{1}\)

\(m\angle A\)

When you are given only the sides, you have to use the Law of Cosines to find one angle and then you can use the Law of Sines to find another.

\(\begin{aligned} 15^2&=22^2+28^2−2(22)(28)\cos A \\ 225&=1268−1232\cos A \\ −1043&=−1232\cos A \\ \dfrac{−1043}{−1232}&=\cos A \rightarrow \cos ^{−1}\left(\dfrac{1043}{1232}\right) \approx 32.16^{\circ}\end{aligned}\)

Example \(\PageIndex{2}\)

\(m\angle B\)

Now that we have an angle and its opposite side, we can use the Law of Sines.

\(\begin{aligned} \dfrac{\sin 32.16^{\circ} }{15} &=\dfrac{\sin B}{22} \\ 15\cdot \sin B &=22\cdot \sin 32.16^{\circ} \\ \sin B &=\dfrac{22\cdot \sin 32.16^{\circ} }{15} \end{aligned}\)

\(\sin ^{−1}\left(\dfrac{22\cdot \sin 32.16^{\circ} }{15}\right)\approx 51.32^{\circ} \).

Example \(\PageIndex{3}\)

\(m\angle C\)

To find \(m\angle C\), use the Triangle Sum Theorem.

\(\begin{aligned} 32.16^{\circ} +51.32^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=96.52^{\circ} \end{aligned}\)

Use the Law of Sines or Cosines to solve \(\Delta ABC\). If you are not given a picture, draw one. Round all decimal answers to the nearest tenth.

• \(m\angle A=74^{\circ} \), \(m\angle B=11^{\circ} \), \(BC=16\)
• \(m\angle A=64^{\circ} \), \(AB=29\), \(AC=34\)
• \(m\angle C=133^{\circ} \), \(m\angle B=25^{\circ} \),\(AB=48\)

Use the Law of Sines to solve \(\Delta ABC\) below.

• \(m\angle A=20^{\circ} \), \(AB=12\), \(BC=5\)

Recall that when we learned how to prove that triangles were congruent we determined that SSA (two sides and an angle not included) did not determine a unique triangle. When we are using the Law of Sines to solve a triangle and we are given two sides and the angle not included, we may have two possible triangles. Problem 14 illustrates this.

• Let’s say we have \(\Delta ABC\) as we did in problem 13. In problem 13 you were given two sides and the not included angle. This time, you have two angles and the side between them (ASA). Solve the triangle given that \(m\angle A=20^{\circ} \), \(m\angle C=125^{\circ}\), \(AC=8.4\)
• Does the triangle that you found in problem 14 meet the requirements of the given information in problem 13? How are the two different \(m\angle C\) related? Draw the two possible triangles overlapping to visualize this relationship.

Review (Answers)

To view the Review answers, open this PDF file and look for section 8.10.

Additional Resources

Video: The Law of Sines: The Basics

Chapter 3: Laws of Sines and Cosines

Exercises: 3.2 The Law of Sines

• Use the law of sines to find a side #1-6
• Use the law of sines to find an angle #7-12
• Use the law of sines to solve an oblique triangle #13-18
• Solve problems using the law of sines #19-28
• Compute distances using the parallax #29-32
• Solve problems involving the ambiguous case #33-46

Suggested homework problems

Homework 3.2

Exercise group.

For Problems 13–18, sketch the triangle and solve. Round answers to two decimal places. 13. [latex]b = 7,~ A = 23°,~ B = 42°[/latex] 14. [latex]c = 34,~ A = 53°,~ C = 26°[/latex] 15. [latex]a = 1.8,~ c = 2.1,~ C = 44°[/latex] 16. [latex]b = 8.5,~ c = 6.8,~ B = 23°[/latex] 17. [latex]c = 75,~ A = 35°,~ B = 46°[/latex] 18. [latex]a = 94,~ B = 29°,~ C = 84°[/latex]

For Problems 19–26, sketch and label a triangle to illustrate the problem. Solve the problem. 19. Maryam wants to know the height of a cliff on the other side of a ravine. The angle of elevation from her edge of the ravine to the cliff top is [latex]84.6°{.}[/latex] When she moves [latex]30[/latex] feet back from the ravine, the angle of elevation is [latex]82.5°{.}[/latex] How tall is the cliff? 20. Amir wants to know the height of a tree in the median strip of a highway. The angle of elevation from the highway shoulder to the treetop is [latex]43.5°{.}[/latex] When he moves 10 feet farther away from the tree, the angle of elevation is [latex]37.2°{.}[/latex] How tall is the tree? 21. Delbert and Francine are [latex]10[/latex] kilometers apart, both observing a satellite that passes directly over their heads. At a moment when the satellite is between them, Francine measures its angle of elevation as [latex]84.6°{,}[/latex] and Delbert measures an angle of [latex]87°{.}[/latex] How far is the satellite from Delbert? 22. Megan rows her kayak due east. When she began, she spotted a lighthouse [latex]2000[/latex] meters in the distance at an angle of [latex]14°[/latex] south of east. After traveling for an hour, the lighthouse was at an angle of [latex]83°[/latex] south of east. How far did Megan travel, and what was her average speed? 23. Chad is hiking along a straight path but needs to detour around a large pond. He turns [latex]23°[/latex] from his path until clear of the pond, then walks back to his original path, intercepting it at an angle of [latex]29°[/latex] and at a distance of [latex]2[/latex] miles from where he had left the path. How far did Chad walk in each of the two segments of his detour, and how much farther did his detour require compared with a straight line through the pond?

• Find [latex]\angle ACB{.}[/latex]
• Find[latex]\angle CAB{,}[/latex] at the top of the antenna.
• How long is [latex]BC{,}[/latex] the distance from the bottom of the antenna to [latex]C{?}[/latex]
• How tall is the hill?

28. A billboard of California’s gubernatorial candidate Angelyne is located on the roof of a building. At a distance of [latex]180[/latex] feet from the building, the angles of elevation to the bottom and top of the billboard are, respectively, [latex]39.8°[/latex] and [latex]47.3°{.}[/latex] How tall is the billboard?

For Problems 29–32, compute the following distances in astronomical units (AUs). Then convert to kilometers, using the fact that 1 AU [latex]\approx 1.5[/latex] times [latex]10^{8}[/latex] km. 29. When observed from opposite sides of Earth’s orbit, the star Alpha Centauri has a parallax of [latex]0.76^{\prime\prime}{.}[/latex] How far from the Sun is Alpha Centauri? 30. How far from the Sun is Barnard’s Star, which has a parallax of [latex]1.1^{\prime\prime}[/latex] when observed at opposite ends of Earth’s orbit? 31. How far from the Sun is Tau Ceti, which has a parallax of [latex]0.55^{\prime\prime}[/latex] when observed from opposite ends of Earth’s orbit? 32. How far from the Sun is Sirius, which has a parallax of [latex]0.75^{\prime\prime}[/latex] when observed from opposite ends of Earth’s orbit?

• Use the definition of [latex]\sin A[/latex] to solve for [latex]a[/latex] (the length of side [latex]\overline{BC}[/latex]).
• Can you draw a triangle [latex]\triangle ABC[/latex] with [latex]\angle A = 30°[/latex] and [latex]c = 3[/latex] if [latex]a \lt \dfrac{3}{2}{?}[/latex] Why or why not?
• How many triangles are possible if [latex]\dfrac{3}{2} \lt a \lt 3{?}[/latex]
• How many triangles are possible if [latex]a \gt 3{?}[/latex]

34. In this problem we show that there are two different triangles [latex]\triangle ABC[/latex] with [latex]\angle A = 30°,~ a = 2[/latex] and [latex]c = 3{.}[/latex]

• Use a protractor to draw an angle [latex]\angle A = 30°{.}[/latex] Mark point [latex]B[/latex] on one side of the angle so that [latex]\overline{AB}[/latex] is 3 inches long.
• Locate two distinct points on the other side of the angle that are each 2 inches from point [latex]B{.}[/latex] These points are both possible locations for point [latex]C{.}[/latex]
• Use the law of sines to find two distinct possible measures for [latex]\angle C{.}[/latex]

35. In [latex]\triangle ABC, \angle A = 30°[/latex] and [latex]c = 12{.}[/latex] How many triangles are possible for each of the following lengths for side [latex]a{?}[/latex] Sketch the solutions in each case.

• [latex]a = 6[/latex]
• [latex]a = 4[/latex]
• [latex]a = 9[/latex]
• [latex]a = 15[/latex]
• Express the length of the altitude in terms of [latex]\angle A[/latex] and [latex]c{.}[/latex]
• Now suppose we keep [latex]\angle A[/latex] and side [latex]c[/latex] fixed but allow [latex]a[/latex] to vary in length. What is the smallest value [latex]a[/latex] can have and still be long enough to make a triangle?
• What are the largest and smallest values that [latex]a[/latex] can have in order to produce two distinct triangles [latex]\triangle ABC[/latex] (without changing [latex]\angle A[/latex] and side [latex]c[/latex])?

37. For the triangle in Problem 36, suppose [latex]\angle A = 40°[/latex] and [latex]c = 8{.}[/latex]

• Sketch and solve the triangle if [latex]a = 12{.}[/latex]
• Sketch and solve the triangle if [latex]a = 6{.}[/latex]
• Sketch and solve the triangle if [latex]a = 4{.}[/latex]
• For what value of [latex]a[/latex] is [latex]c[/latex] the hypotenuse of a right triangle?

38. For the figure in Problem 36, suppose [latex]\angle A = 70°[/latex] and [latex]c = 20{.}[/latex]

• For what value of [latex]a[/latex] is the triangle a right triangle?
• For what values of [latex]a[/latex] are there two solutions for the triangle?
• For what values of [latex]a[/latex] is there one obtuse solution for the triangle?
• For what value of [latex]a[/latex] is there no solution?

For Problems 39–42, find the remaining angles of the triangle. Round answers to two decimal places. (These problems involve the ambiguous case.) 39. [latex]a = 66,~ c = 43,~ \angle C = 25°[/latex] 40. [latex]b = 10,~ c = 14,~ \angle B = 20°[/latex] 41. [latex]b = 100,~ c = 80,~ \angle B = 49°[/latex] 42. [latex]b = 4.7,~ c = 6.3,~ \angle C = 54°[/latex] 43. Delbert and Francine are [latex]1000[/latex] yards apart. The angle Delbert sees between Francine and a certain tree is [latex]38°{.}[/latex] If the tree is [latex]800[/latex] yards from Francine, how far is it from Delbert? (There are two possible answers.) 44. From the lookout point on Fabrick Rock, Ann can see not only the famous “Crooked Spire” in Chesterfield, which is [latex]8[/latex] miles away, but also the red phone box in the village of Alton. Chesterfield and Alton are [latex]7[/latex] miles apart. Fabrick Rock has a plaque that shows directions to famous sites, and from the plaque Ann determines that the angle between the lines to the spire and the phone box measures [latex]19°{.}[/latex] How far is Fabrick Rock from the phone box? (There are two possible answers.) 45.

• Sketch a triangle with [latex]\angle A = 25°,~ \angle B = 35°{,}[/latex] and [latex]b = 16{.}[/latex]
• Use the law of sines to find [latex]a{.}[/latex]
• Use the law of sines to find [latex]c{.}[/latex]
• Find [latex]c[/latex] without using the law of sines. (Hint: Sketch the altitude, [latex]h{,}[/latex] from [latex]\angle C[/latex] to make two right triangles. Find [latex]h{,}[/latex] then use [latex]h[/latex] to find [latex]c[/latex].)
• Sketch a triangle with [latex]\angle A = 75°[/latex], [latex]a = 15{,}[/latex] and [latex]b = 6{.}[/latex]
• Find [latex]c[/latex] without using the law of sines.

Problems 47–48 prove the law of sines using the formula for the area of a triangle. (See Section 3.1 for the appropriate formula.) 47.

• Sketch a triangle with angles [latex]\angle A, ~\angle B[/latex] and [latex]\angle C[/latex] and opposite sides of lengths respectively [latex]a,~ b[/latex] and [latex]c{.}[/latex]
• Write the area of the triangle in terms of [latex]a,~b{,}[/latex] and angle [latex]\angle C{.}[/latex]
• Write the area of the triangle in terms of [latex]a,~c{,}[/latex] and angle [latex]\angle B{.}[/latex]
• Write the area of the triangle in terms of [latex]b

48. Equate the three different expressions from Problem 47 for the area of the triangle. Multiply through by [latex]\dfrac{2}{abc}[/latex] and simplify to deduce the law of sines. 49. Here is a method for solving certain oblique triangles by dividing them into two right triangles. In the triangle shown, we know two angles, [latex]\angle A[/latex] and [latex]\angle B{,}[/latex] and the side opposite one of them, say [latex]a{.}[/latex] We would like to find side [latex]b{.}[/latex]

• Draw the altitude [latex]h[/latex] from angle [latex]\angle C{.}[/latex]
• Write an expression for [latex]b[/latex] in terms of [latex]h[/latex] and angle [latex]\angle A{.}[/latex]
• Write an expression for [latex]h[/latex] in terms of angle [latex]\angle B{.}[/latex]
• Substitute your expression for [latex]h[/latex] into your expression for [latex]b{.}[/latex]
• [latex]a \sin A = b \sin B[/latex]
• [latex]\dfrac{a}{\sin A} = \dfrac{b}{\sin B}[/latex]
• [latex]\dfrac{a}{\sin B} = \dfrac{b}{\sin A}[/latex]

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 8: Trigonometry

About this unit.

In this unit we'll start by learning all about the law of sines and the law of cosines, which can help us figure out the side lengths or angles of a triangle. We'll also get to explore the unit circle, and how it connects to trigonometric functions like sine, cosine, and tangent. Finally, we'll have some fun graphing these functions and learning how to transform them. Get ready to get triggy with it!

Law of sines

• Solving for a side with the law of sines (Opens a modal)
• Solving for an angle with the law of sines (Opens a modal)
• Proof of the law of sines (Opens a modal)
• Solve triangles using the law of sines Get 3 of 4 questions to level up!

Law of cosines

• Solving for a side with the law of cosines (Opens a modal)
• Solving for an angle with the law of cosines (Opens a modal)
• Proof of the law of cosines (Opens a modal)
• Solve triangles using the law of cosines Get 3 of 4 questions to level up!

Solving general triangles

• Trig word problem: stars (Opens a modal)
• Laws of sines and cosines review (Opens a modal)
• General triangle word problems Get 3 of 4 questions to level up!

Unit circle introduction

• Unit circle (Opens a modal)
• The trig functions & right triangle trig ratios (Opens a modal)
• Trig unit circle review (Opens a modal)
• Unit circle Get 3 of 4 questions to level up!
• Intro to radians (Opens a modal)
• Radians & degrees (Opens a modal)
• Degrees to radians (Opens a modal)
• Radians to degrees (Opens a modal)
• Radian angles & quadrants (Opens a modal)
• Radians & degrees Get 3 of 4 questions to level up!
• Unit circle (with radians) Get 3 of 4 questions to level up!

The Pythagorean identity

• Proof of the Pythagorean trig identity (Opens a modal)
• Using the Pythagorean trig identity (Opens a modal)
• Pythagorean identity review (Opens a modal)
• Use the Pythagorean identity Get 3 of 4 questions to level up!

Trigonometric values of special angles

• Trig values of π/4 (Opens a modal)
• Trig values of special angles Get 3 of 4 questions to level up!

Graphs of sin(x), cos(x), and tan(x)

• Graph of y=sin(x) (Opens a modal)
• Intersection points of y=sin(x) and y=cos(x) (Opens a modal)
• Graph of y=tan(x) (Opens a modal)

Amplitude, midline, & period

• Features of sinusoidal functions (Opens a modal)
• Midline, amplitude, and period review (Opens a modal)
• Midline of sinusoidal functions from graph Get 3 of 4 questions to level up!
• Amplitude of sinusoidal functions from graph Get 3 of 4 questions to level up!
• Period of sinusoidal functions from graph Get 3 of 4 questions to level up!

Transforming sinusoidal graphs

• Amplitude & period of sinusoidal functions from equation (Opens a modal)
• Transforming sinusoidal graphs: vertical stretch & horizontal reflection (Opens a modal)
• Transforming sinusoidal graphs: vertical & horizontal stretches (Opens a modal)
• Amplitude of sinusoidal functions from equation Get 3 of 4 questions to level up!
• Midline of sinusoidal functions from equation Get 3 of 4 questions to level up!
• Period of sinusoidal functions from equation Get 3 of 4 questions to level up!

Graphing sinusoidal functions

• Example: Graphing y=3⋅sin(½⋅x)-2 (Opens a modal)
• Example: Graphing y=-cos(π⋅x)+1.5 (Opens a modal)
• Sinusoidal function from graph (Opens a modal)
• Graph sinusoidal functions Get 3 of 4 questions to level up!
• Construct sinusoidal functions Get 3 of 4 questions to level up!
• Graph sinusoidal functions: phase shift Get 3 of 4 questions to level up!

Sinusoidal models

• Interpreting trigonometric graphs in context (Opens a modal)
• Trig word problem: modeling daily temperature (Opens a modal)
• Trig word problem: modeling annual temperature (Opens a modal)
• Trig word problem: length of day (phase shift) (Opens a modal)
• Interpreting trigonometric graphs in context Get 3 of 4 questions to level up!
• Modeling with sinusoidal functions Get 3 of 4 questions to level up!
• Modeling with sinusoidal functions: phase shift Get 3 of 4 questions to level up!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.2: The Law of Sines - The Ambiguous Case

• Last updated
• Save as PDF
• Page ID 37225

• Richard W. Beveridge
• Clatsop Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In all of the examples and problems in Section \(4.1,\) notice that we were always given two angles and one side, although we could use the Law of sines if we were given one angle and two sides (as long as one of the sides corresponded to the given angle). This is because when we use the Law of sines to find an angle, an ambiguity can arise due to the sine function being positive in Quadrant I and Quadrant II.

We saw in Chapter 3 that multiple answers arise when we use the inverse trigonometric functions. For problems in which we use the Law of sines given one angle and two sides, there may be one possible triangle, two possible triangles or no possible triangles. There are six different scenarios related to the ambiguous case of the Law of sines: three result in one triangle, one results in two triangles and two result in no triangle.

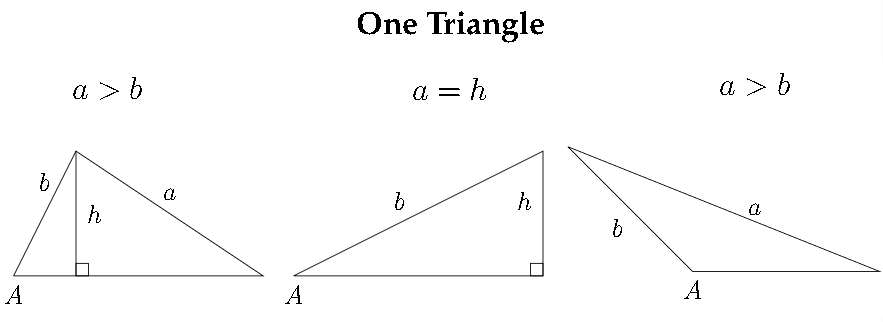
We'll look at three examples: one for one triangle, one for two triangles and one for no triangles.

Example \(\PageIndex{1}\)

Solve the triangle if: \(\angle A=112^{\circ}, \quad a=45, \quad b=24\) Round the angles and side lengths to the nearest \(10^{t h}\)

Using the Law of sines, we can say that:

\[ \begin{array}{c} \frac{\sin 112^{\circ}}{45}=\frac{\sin B}{24} \\ \frac{0.9272}{45} \approx \frac{\sin B}{24} \\ 24 * \frac{0.9272}{45} \approx \sin B \\ 0.4945 \approx \sin B \end{array} \]

Then, we find \(\sin ^{-1}(0.4945) \approx 29.6^{\circ} .\) Remember from Chapter 3 that there is a Quadrant II angle that has \(\sin \theta \approx 0.4945,\) with a reference angle of \(29.6^{\circ} . \mathrm{So}, \angle B\) could also be \(\approx 150.4^{\circ} .\) However, with \(\angle A=112^{\circ},\) there is no way that another angle of \(150.4^{\circ}\) would fit inside the same triangle. For this reason, we know then that \(\angle B\) must be \(29.6^{\circ}\)

\[ 29.6^{\circ} \approx B\]

\[ \begin{array}{c} \angle A=112^{\circ} \\ \angle B \approx 29.6^{\circ} \\ \operatorname{and} \angle C=180^{\circ}-\left(112^{\circ}+29.6^{\circ}\right)=180^{\circ}-141.6^{\circ} \approx 38.4^{\circ} \\ \angle C \approx 38.4^{\circ} \end{array}\]

We already know that \(a=45\) and \(b=24 .\) To find side \(c,\) I would recommend using the most exact values possible in the Law of sines calculation. This will provide the most accurate result in finding the length of side \(c\)

\begin{array}{cc} \frac{45}{\sin 112^{\circ}}=\frac{c}{\sin 38.4^{\circ}} \\ \frac{45}{0.9272} \approx \frac{c}{0.6211} \\ 0.6211 * \frac{45}{0.9272} \approx c \\ 30.1 \approx c \\ \angle A=112^{\circ} & a=45 \\ \angle B \approx 29.6^{\circ} & b=24 \\ \angle C \approx 38.4^{\circ} & c \approx 30.1 \end{array}

Example \(\PageIndex{2}\)

Solve the triangle if: \(\angle A=38^{\circ}, \quad a=40, \quad b=52\) Round the angles and side lengths to the nearest \(10^{\text {th }}\).

\[ \begin{array}{c} \frac{\sin 38^{\circ}}{40}=\frac{\sin B}{52} \\ \frac{0.6157}{40} \approx \frac{\sin B}{52} \\ 52 * \frac{0.6157}{40} \approx \sin B \\ 0.8004 \approx \sin B \end{array} \]

Just as in the previous example, we can find \(\sin ^{-1}(0.8004) \approx 53.2^{\circ} .\) But again, there is a Quadrant II angle whose sine has the same value \(\approx 0.8004\). The angle \(126.8^{\circ}\) has a sine \(\approx 0.8004\) and a reference angle of \(53.2^{\circ} .\) With \(\angle A=38^{\circ},\) both of these angles \(\left(53.2^{\circ} \text { and } 126.8^{\circ}\right)\) could potentially fit in the triangle with angle \(A\)

If we go back to the diagrams we looked at earlier in this section, we can see how this would happen:

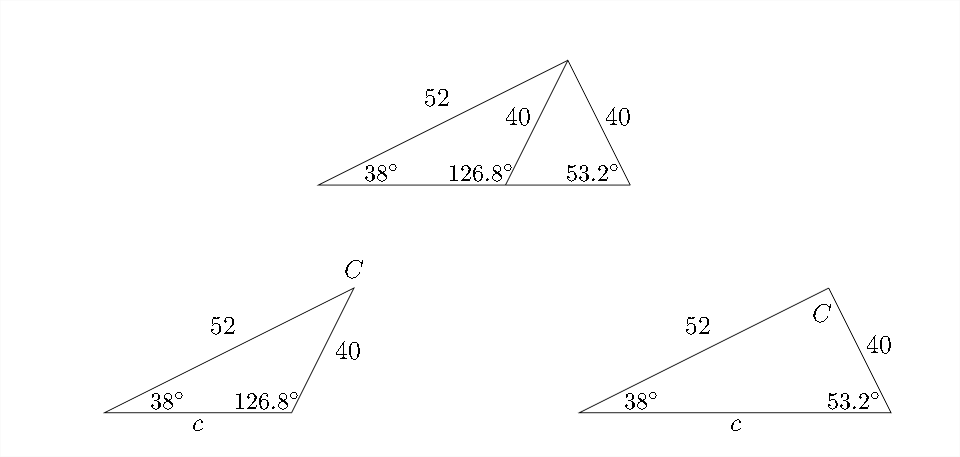
In the first possibility \(\angle C\) would be \(\approx 15.2^{\circ}\) In the second possibility \(\angle C\) would be \(\approx 88.8^{\circ}\)

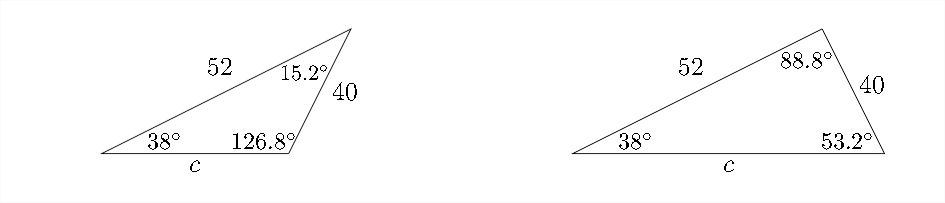
To find the two possible lengths for side \(c,\) we'll need to solve two Law of sines calculations, one with \(\angle C \approx 15.2^{\circ}\) and one with the \(\angle C \approx 88.8^{\circ}\)

\[ \begin{array}{c} \frac{40}{\sin 38^{\circ}}=\frac{c}{\sin 15.2^{\circ}} \\ \frac{40}{0.6157} \approx \frac{c}{0.2622} \\ 0.2622 * \frac{40}{0.6157} \approx c \\ 17.0 \approx c \end{array} \]

With \(\angle C \approx 88.8^{\circ}\):

\[ \frac{40}{\sin 38^{\circ}}=\frac{c}{\sin 88.8^{\circ}} \\ \frac{40}{0.6157} \approx \frac{c}{0.9998} \\ 0.9998 * \frac{40}{0.6157} \approx c \\ 65.0 \approx c \]

So, our two possible solutions would be: \[ \begin{array}{lll} \angle A=38^{\circ} & a=40 \\ \angle B \approx 126.8^{\circ} & b=52 \\ \angle C \approx 15.2^{\circ} & c \approx 17.0 \end{array} \] \(\mathrm{OR}\) \[ \angle A=38^{\circ} \quad a=40 \] \[ \begin{array}{lll} \angle B \approx 53.2^{\circ} & b=52 \\ \angle C \approx 88.8^{\circ} & c \approx 65.0 \end{array} \]

Example \(\PageIndex{3}\)

Solve the triangle if:

\[\angle B=73^{\circ}, \quad b=51, \quad a=92.\]

Round the angles and side lengths to the nearest \(10^{\text {th }}\).

\[ \frac{\sin 73^{\circ}}{51}=\frac{\sin A}{92}\]

\[ \begin{array}{c} \frac{0.9563}{51} \approx \frac{\sin A}{92} \\ 92 * \frac{0.9563}{51} \approx \sin A \\ 1.7251 \approx \sin A \end{array}\]

As we saw previously, no real-valued angle has a sine greater than \(1 .\) Therefore, no triangle is possible.

In each problem, solve the triangle. Round side lengths to the nearest \(100^{\text {th }}\) and angle measures to the nearest \(10^{\text {th }}\).

1. \(\quad \angle A=50^{\circ}, \quad b=20, \quad a=32\) 2. \(\quad \angle B=40^{\circ}, \quad b=4, \quad c=3\) 3. \(\quad \angle A=43^{\circ}, \quad a=23, \quad b=29\) 4. \(\quad \angle C=20^{\circ}, \quad c=43, \quad a=55\) 5. \(\quad \angle B=62^{\circ}, \quad b=4, \quad a=5\) 6. \(\quad \angle A=75^{\circ}, \quad b=8, \quad a=3\) 7. \(\quad \angle B=24^{\circ}, \quad a=17, \quad b=8\) 8. \(\quad \angle A=40^{\circ}, \quad a=4, \quad c=5\) 9. \(\quad \angle A=108^{\circ}, \quad a=12, \quad b=7\) 10. \(\quad \angle B=117^{\circ}, \quad b=19.6, \quad c=10.5\) 11. \(\quad \angle A=42^{\circ}, \quad a=18, \quad c=11\) 12. \(\quad \angle C=27^{\circ}, \quad a=42, \quad c=37\) 13. \(\quad \angle C=125^{\circ}, \quad c=2.7, \quad b=5.2\) 14. \(\quad \angle B=115^{\circ}, \quad b=68, \quad a=92\) 15. \(\quad \angle A=43^{\circ}, \quad a=31, \quad b=37\) 16. \(\quad \angle A=28^{\circ}, \quad b=3.5, \quad a=4.3\) 17. \(\quad \angle C=132^{\circ}, \quad c=22, \quad b=16\) 18. \(\quad \angle B=114.2^{\circ}, \quad b=87.2, \quad a=12.1\) 19. \(\quad \angle B=52^{\circ}, \quad c=82.7, \quad b=70\) 20. \(\quad \angle C=65^{\circ}, \quad b=7.6, \quad c=7.1\)

Trigonometry (Algebra 2 Curriculum - Unit 12) | All Things Algebra®

• Google Apps™

What educators are saying

Also included in.

Description

Due to the length of this Trigonometry Unit Bundle , it is divided into two parts with two unit tests. In addition to the unit tests, each part includes guided notes, homework assignments, quizzes, and study guides to cover the following topics:

Unit 12 Part I:

• Pythagorean Theorem

• Special Right Triangles

• Trigonometric Functions (sin, cos, tan, csc, sec, cot)

• Finding Side and Angle Measures

• Applications: Angle of Elevation and Depression

• Angles in Standard Position

• Converting between Degrees and Radians

• Coterminal and Reference Angles

• Trigonometric Functions in the Coordinate Plane

• The Unit Circle

• Law of Sines

• Law of Cosines

• Area of Triangles

• Applications of Law of Sines, Law of Cosines, and Area

Unit 12 Part II:

• Graphing Trigonometric Functions

• Trigonometric Identities

• Sum and Difference of Angle Identities

• Double-Angle and Half-Angle Identities

• Solving Trigonometric Equations

ADDITIONAL COMPONENTS INCLUDED:

(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice.  Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.

(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes;  this is the PDF in Google Slides.  I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead! 

This resource is included in the following bundle(s):

Algebra 2 Curriculum

More Algebra 2 Units:

Unit 1 – Equations and Inequalities

Unit 2 – Linear Functions and Systems

Unit 3 – Parent Functions and Transformations

Unit 4 – Solving Quadratics and Complex Numbers

Unit 5 – Polynomial Functions

Unit 6 – Radical Functions

Unit 7 – Exponential and Logarithmic Functions

Unit 8 – Rational Functions

Unit 9 – Conic Sections

Unit 10 – Sequences and Series

Unit 11 – Probability and Statistics

LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].

COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

© All Things Algebra (Gina Wilson), 2012-present

Questions & Answers

All things algebra.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think