trigonometry class 10 assignment pdf

CBSE NCERT Solutions

NCERT and CBSE Solutions for free

Class 10 Mathematics Trigonometry Worksheets

We have provided below free printable  Class 10 Mathematics Trigonometry Worksheets  for Download in PDF. The worksheets have been designed based on the latest  NCERT Book for Class 10 Mathematics Trigonometry . These Worksheets for Grade 10 Mathematics Trigonometry  cover all important topics which can come in your standard 10 tests and examinations.  Free printable worksheets for CBSE Class 10 Mathematics Trigonometry , school and class assignments, and practice test papers have been designed by our highly experienced class 10 faculty. You can free download CBSE NCERT printable worksheets for Mathematics Trigonometry Class 10 with solutions and answers. All worksheets and test sheets have been prepared by expert teachers as per the latest Syllabus in Mathematics Trigonometry Class 10. Students can click on the links below and download all Pdf  worksheets for Mathematics Trigonometry class 10  for free. All latest Kendriya Vidyalaya  Class 10 Mathematics Trigonometry Worksheets  with Answers and test papers are given below.

Mathematics Trigonometry Class 10 Worksheets Pdf Download

Here we have the biggest database of free  CBSE NCERT KVS  Worksheets for Class 10  Mathematics Trigonometry . You can download all free Mathematics Trigonometry worksheets in Pdf for standard 10th. Our teachers have covered  Class 10 important questions and answers  for Mathematics Trigonometry as per the latest curriculum for the current academic year. All test sheets question banks for Class 10 Mathematics Trigonometry and  CBSE Worksheets for Mathematics Trigonometry Class 10  will be really useful for Class 10 students to properly prepare for the upcoming tests and examinations. Class 10th students are advised to free download in Pdf all printable workbooks given below.

Topicwise Worksheets for Class 10 Mathematics Trigonometry Download in Pdf

Advantages of Solving Class 10 Mathematics Trigonometry Worksheets

• As we have the best collection of Mathematics Trigonometry worksheets for Grade 10, you will be able to find important questions which will come in your class tests and examinations.
• You will be able to revise all important and difficult topics given in your CBSE Mathematics Trigonometry  textbooks for Class 10 .
• All Mathematics Trigonometry worksheets for standard 10 have been provided with solutions. You will be able to solve them yourself and them compare with the answers provided by our teachers.
• Class 10 Students studying in per CBSE, NCERT and KVS schools will be able to free download all Mathematics Trigonometry chapter wise assgnments and worksheets for free in Pdf
• Class 10 Mathematics Trigonometry Workbook will help to enhance and improve subject knowledge which will help to get more marks in exams

Frequently Asked Questions by Class 10 Mathematics Trigonometry students

At https://www.cbsencertsolutions.com, we have provided the biggest database of free worksheets for Mathematics Trigonometry Class 10 which you can download in Pdf

We provide here Standard 10 Mathematics Trigonometry chapter-wise worksheets which can be easily downloaded in Pdf format for free.

You can click on the links above and get worksheets for Mathematics Trigonometry in Grade 10, all topic-wise question banks with solutions have been provided here. You can click on the links to download in Pdf.

We have provided here subject-wise Mathematics Trigonometry Grade 10 question banks, revision notes and questions for all difficult topics, and other study material.

We have provided the best quality question bank for Class 10 for all subjects. You can download them all and use them offline without the internet.

Related Posts

Class 10 French Worksheets

Class 10 Mathematics Linear Equations Worksheets

Class 10 Mathematics Triangles Worksheets

• NCERT Solutions
• NCERT Solutions for Class 10
• NCERT Solutions for Class 10 Maths
• Chapter 8: Introduction To Trigonometry

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Ncert solutions for class 10 maths chapter 8 – download free pdf.

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry is helpful for the students as it aids in understanding the concepts as well as in scoring well in CBSE Class 10 board examination. The NCERT Solutions are designed and reviewed by subject experts and cover all the questions from the textbook. These NCERT Solutions are framed as per the latest update on the CBSE Syllabus for 2023-24 and its guidelines, in accordance with the exam pattern.

Download Exclusively Curated Chapter Notes for Class 10 Maths Chapter – 8 Introduction to Trigonometry

Download most important questions for class 10 maths chapter – 8 introduction to trigonometry.

The  NCERT Solutions for Class 10 Maths provide a strong foundation for every concept across all chapters. Students can clarify their doubts and understand the fundamentals of this chapter. Also, students can solve the difficult problems in each exercise with the help of these NCERT Solutions for Class 10  Maths Chapter 8.

• Chapter 1 Real Numbers
• Chapter 2 Polynomials
• Chapter 3 Pair of Linear Equations in Two Variables
• Chapter 4 Quadratic Equations
• Chapter 5 Arithmetic Progressions
• Chapter 6 Triangles
• Chapter 7 Coordinate Geometry
• Chapter 8 Introduction to Trigonometry
• Chapter 9 Some Applications of Trigonometry
• Chapter 10 Circles
• Chapter 11 Constructions
• Chapter 12 Areas Related to Circles
• Chapter 13 Surface Areas and Volumes
• Chapter 14 Statistics
• Chapter 15 Probability

Download PDF of NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry

carouselExampleControls111

Previous Next

Access Answers to NCERT Class 10 Maths Chapter 8 – Introduction to Trigonometry

Exercise 8.1 Page: 181

1. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:

(i) sin A, cos A

(ii) sin C, cos C

In a given triangle ABC, right angled at B = ∠B = 90°

Given: AB = 24 cm and BC = 7 cm

According to the Pythagoras Theorem,

In a right- angled triangle, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides.

By applying Pythagoras theorem, we get

AC 2 =AB 2 +BC 2

AC 2  = (24) 2 +7 2

AC 2  = (576+49)

AC 2  = 625cm 2

AC = √625 = 25

Therefore, AC = 25 cm

(i) To find Sin (A), Cos (A)

We know that sine (or) Sin function is the equal to the ratio of length of the opposite side to the hypotenuse side. So it becomes

Sin (A) = Opposite side /Hypotenuse = BC/AC = 7/25

Cosine or Cos function is equal to the ratio of the length of the adjacent side to the hypotenuse side and it becomes,

Cos (A) = Adjacent side/Hypotenuse = AB/AC = 24/25

(ii) To find Sin (C), Cos (C)

Sin (C) = AB/AC = 24/25

Cos (C) = BC/AC = 7/25

2. In Fig. 8.13, find tan P – cot R

In the given triangle PQR, the given triangle is right angled at Q and the given measures are:

Since the given triangle is right angled triangle, to find the side QR, apply the Pythagorean theorem

According to Pythagorean theorem,

PR 2 = QR 2 + PQ 2

Substitute the values of PR and PQ

13 2 = QR 2 +12 2

169 = QR 2 +144

Therefore, QR 2 = 169−144

QR = √25 = 5

Therefore, the side QR = 5 cm

To find tan P – cot R:

According to the trigonometric ratio, the tangent function is equal to the ratio of the length of the opposite side to the adjacent sides, the value of tan (P) becomes

tan (P) = Opposite side /Adjacent side = QR/PQ = 5/12

Since cot function is the reciprocal of the tan function, the ratio of cot function becomes,

Cot (R) = Adjacent side/Opposite side = QR/PQ = 5/12

tan (P) – cot (R) = 5/12 – 5/12 = 0

Therefore, tan(P) – cot(R) = 0

3. If sin A = 3/4, calculate cos A and tan A.

Let us assume a right angled triangle ABC, right angled at B

Given: Sin A = 3/4

We know that, Sin function is the equal to the ratio of length of the opposite side to the hypotenuse side.

Therefore, Sin A = Opposite side /Hypotenuse= 3/4

Let BC be 3k and AC will be 4k

where k is a positive real number.

According to the Pythagoras theorem, the squares of the hypotenuse side is equal to the sum of the squares of the other two sides of a right angle triangle and we get,

AC 2 =AB 2 + BC 2

Substitute the value of AC and BC

(4k) 2 =AB 2 + (3k) 2

16k 2 −9k 2 =AB 2

Therefore, AB = √7k

Now, we have to find the value of cos A and tan A

We know that,

Cos (A) = Adjacent side/Hypotenuse

Substitute the value of AB and AC and cancel the constant k in both numerator and denominator, we get

AB/AC = √7k/4k = √7/4

Therefore, cos (A) = √7/4

tan(A) = Opposite side/Adjacent side

Substitute the Value of BC and AB and cancel the constant k in both numerator and denominator, we get,

BC/AB = 3k/√7k = 3/√7

Therefore, tan A = 3/√7

4. Given 15 cot A = 8, find sin A and sec A.

Given: 15 cot A = 8

So, Cot A = 8/15

We know that, cot function is the equal to the ratio of length of the adjacent side to the opposite side.

Therefore, cot A = Adjacent side/Opposite side = AB/BC = 8/15

Let AB be 8k and BC will be 15k

Where, k is a positive real number.

Substitute the value of AB and BC

AC 2 = (8k) 2 + (15k) 2

AC 2 = 64k 2 + 225k 2

AC 2 = 289k 2

Therefore, AC = 17k

Now, we have to find the value of sin A and sec A

Sin (A) = Opposite side /Hypotenuse

Substitute the value of BC and AC and cancel the constant k in both numerator and denominator, we get

Sin A = BC/AC = 15k/17k = 15/17

Therefore, sin A = 15/17

Since secant or sec function is the reciprocal of the cos function which is equal to the ratio of the length of the hypotenuse side to the adjacent side.

Sec (A) = Hypotenuse/Adjacent side

AC/AB = 17k/8k = 17/8

Therefore sec (A) = 17/8

5. Given sec θ = 13/12 Calculate all other trigonometric ratios

We know that sec function is the reciprocal of the cos function which is equal to the ratio of the length of the hypotenuse side to the adjacent side

sec θ =13/12 = Hypotenuse/Adjacent side = AC/AB

Let AC be 13k and AB will be 12k

Substitute the value of AB and AC

(13k) 2 = (12k) 2 + BC 2

169k 2 = 144k 2 + BC 2

BC 2 = 169k 2 – 144k 2

BC 2 = 25k 2

Therefore, BC = 5k

Now, substitute the corresponding values in all other trigonometric ratios

Sin θ = Opposite Side/Hypotenuse = BC/AC = 5/13

Cos θ = Adjacent Side/Hypotenuse = AB/AC = 12/13

tan θ = Opposite Side/Adjacent Side = BC/AB = 5/12

Cosec θ = Hypotenuse/Opposite Side = AC/BC = 13/5

cot θ = Adjacent Side/Opposite Side = AB/BC = 12/5

6. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B.

Let us assume the triangle ABC in which CD⊥AB

Give that the angles A and B are acute angles, such that

Cos (A) = cos (B)

As per the angles taken, the cos ratio is written as

AD/AC = BD/BC

Now, interchange the terms, we get

AD/BD = AC/BC

Let take a constant value

AD/BD = AC/BC = k

Now consider the equation as

AD = k BD …(1)

AC = k BC …(2)

By applying Pythagoras theorem in △CAD and △CBD we get,

CD 2 = BC 2 – BD 2 … (3)

CD 2 =AC 2 −AD 2  ….(4)

From the equations (3) and (4) we get,

AC 2 −AD 2 = BC 2 −BD 2

Now substitute the equations (1) and (2) in (3) and (4)

K 2 (BC 2 −BD 2 )=(BC 2 −BD 2 ) k 2 =1

Putting this value in equation, we obtain

∠A=∠B (Angles opposite to equal side are equal-isosceles triangle)

7. If cot θ = 7/8, evaluate :

(i) (1 + sin θ)(1 – sin θ)/(1+cos θ)(1-cos θ)

(ii) cot 2 θ

Let us assume a △ABC in which ∠B = 90° and ∠C = θ

cot θ = BC/AB = 7/8

Let BC = 7k and AB = 8k, where k is a positive real number

According to Pythagoras theorem in △ABC we get.

AC 2 = AB 2 +BC 2

AC 2 = (8k) 2 +(7k) 2

AC 2 = 64k 2 +49k 2

AC 2 = 113k 2

AC = √113 k

According to the sine and cos function ratios, it is written as

sin θ = AB/AC = Opposite Side/Hypotenuse = 8k/√113 k = 8/√113 and

cos θ = Adjacent Side/Hypotenuse = BC/AC = 7k/√113 k = 7/√113

Now apply the values of sin function and cos function:

8. If 3 cot A = 4, check whether (1-tan 2 A)/(1+tan 2 A) = cos 2 A – sin 2 A or not.

Let △ABC in which ∠B=90°

We know that, cot function is the reciprocal of tan function and it is written as

cot(A) = AB/BC = 4/3

Let AB = 4k an BC =3k, where k is a positive real number.

According to the Pythagorean theorem,

AC 2 =(4k) 2 +(3k) 2

AC 2 =16k 2 +9k 2

AC 2 =25k 2

Now, apply the values corresponding to the ratios

tan(A) = BC/AB = 3/4

sin (A) = BC/AC = 3/5

cos (A) = AB/AC = 4/5

Now compare the left hand side(LHS) with right hand side(RHS)

Since, both the LHS and RHS = 7/25

R.H.S. =L.H.S.

Hence, (1-tan 2 A)/(1+tan 2 A) = cos 2 A – sin 2 A   is proved

9. In triangle ABC, right-angled at B, if tan A = 1/√3 find the value of:

(i) sin A cos C + cos A sin C

(ii) cos A cos C – sin A sin C

Let ΔABC in which ∠B=90°

tan A = BC/AB = 1/√3

Let BC = 1k and AB = √3 k,

Where k is the positive real number of the problem

By Pythagoras theorem in ΔABC we get:

AC 2 =(√3 k) 2 +(k) 2

AC 2 =3k 2 +k 2

Now find the values of cos A, Sin A

Sin A = BC/AC = 1/2

Cos A = AB/AC = √3/2

Then find the values of cos C and sin C

Sin C = AB/AC = √ 3/2

Cos C = BC/AC = 1/2

Now, substitute the values in the given problem

(i) sin A cos C + cos A sin C = (1/2) ×(1/2 )+ √3/2 ×√3/2 = 1/4 + 3/4 = 1

(ii) cos A cos C – sin A sin C = ( √ 3/2 )(1/2) – (1/2) ( √ 3/2 ) = 0

10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P

In a given triangle PQR, right angled at Q, the following measures are

PR + QR = 25 cm

Now let us assume, QR = x

According to the Pythagorean Theorem,

PR 2 = PQ 2 + QR 2

Substitute the value of PR as x

(25- x) 2 = 5 2 + x 2

25 2 + x 2 – 50x = 25 + x 2

625 + x 2 -50x -25 – x 2 = 0

-50x = -600

x= -600/-50

x = 12 = QR

Now, find the value of PR

PR = 25- QR

Substitute the value of QR

Now, substitute the value to the given problem

(1) sin p = Opposite Side/Hypotenuse = QR/PR = 12/13

(2) Cos p = Adjacent Side/Hypotenuse = PQ/PR = 5/13

(3) tan p =Opposite Side/Adjacent side = QR/PQ = 12/5

11. State whether the following are true or false. Justify your answer.

(i) The value of tan A is always less than 1.

(ii) sec A = 12/5 for some value of angle A.

(iii)cos A is the abbreviation used for the cosecant of angle A.

(iv) cot A is the product of cot and A.

(v) sin θ = 4/3 for some angle θ.

Answer: False

Proof: In ΔMNC in which ∠N = 90∘,

MN = 3, NC = 4 and MC = 5

Value of tan M = 4/3 which is greater than 1.

The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as it will follow the Pythagoras theorem.

MC 2 =MN 2 +NC 2

5 2 =3 2 +4 2

25   =   25

(ii) sec A = 12/5 for some value of angle A

Answer: True

Justification: Let a ΔMNC in which ∠N = 90º,

MC=12k and MB=5k, where k is a positive real number.

By Pythagoras theorem we get,

(12k) 2 =(5k) 2 +NC 2

NC 2 +25k 2 =144k 2

NC 2 =119k 2

Such a triangle is possible as it will follow the Pythagoras theorem.

(iii) cos A is the abbreviation used for the cosecant of angle A.

Justification: Abbreviation used for cosecant of angle M is cosec M. cos M is the abbreviation used for cosine of angle M.

Justification: cot M is not the product of cot and M. It is the cotangent of ∠M.

Answer : False

Justification: sin θ = Opposite/Hypotenuse

We know that in a right angled triangle, Hypotenuse is the longest side.

∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.

Exercise 8.2 Page: 187

1. Evaluate the following:

(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan 2 45° + cos 2 30° – sin 2 60

First, find the values of the given trigonometric ratios

sin 30° = 1/2

cos 30° = √3/2

sin 60° = 3/2

cos 60°= 1/2

sin 60° cos 30° + sin 30° cos 60° = √3/2 ×√3/2 + (1/2) ×(1/2 ) = 3/4+1/4 = 4/4 =1

We know that, the values of the trigonometric ratios are:

sin 60° = √3/2

tan 45° = 1

Substitute the values in the given problem

2 tan 2 45° + cos 2 30° – sin 2 60 = 2(1) 2 + (√3/2) 2 -(√3/2) 2

2 tan 2 45° + cos 2 30° – sin 2 60 = 2 + 0

2 tan 2 45° + cos 2 30° – sin 2 60 = 2

(iii) cos 45°/(sec 30°+cosec 30°)

cos 45° = 1/√2

sec 30° = 2/√3

cosec 30° = 2

Substitute the values, we get

Now, multiply both the numerator and denominator by √2 , we get

Therefore, cos 45°/(sec 30°+cosec 30°) = (3√2 – √6)/8

cosec 60° = 2/√3

cos 60° = 1/2

cot 45° = 1

Substitute the values in the given problem, we get

Now, substitute the values in the given problem, we get

(5cos 2 60° + 4sec 2 30° – tan 2 45°)/(sin 2 30° + cos 2 30°)

= 5(1/2) 2 +4(2/√3) 2 -1 2 /(1/2) 2 +(√3/2) 2

  = (5/4+16/3-1)/(1/4+3/4)

= (15+64-12)/12/(4/4)

2. Choose the correct option and justify your choice : (i) 2tan 30°/1+tan 2 30° = (A) sin 60°            (B) cos 60°          (C) tan 60°            (D) sin 30° (ii) 1-tan 2 45°/1+tan 2 45° = (A) tan 90°            (B) 1                    (C) sin 45°            (D) 0 (iii)  sin 2A = 2 sin A is true when A = (A) 0°                   (B) 30°                  (C) 45°                 (D) 60°

(iv) 2tan30°/1-tan 2 30° = (A) cos 60°          (B) sin 60°             (C) tan 60°           (D) sin 30°

(i) (A) is correct.

Substitute the of tan 30° in the given equation

tan 30° = 1/√3

2tan 30°/1+tan 2 30° = 2(1/√3)/1+(1/√3) 2

= (2/√3)/(1+1/3) = (2/√3)/(4/3)

= 6/4√3 = √3/2 = sin 60°

The obtained solution is equivalent to the trigonometric ratio sin 60°

(ii) (D) is correct.

Substitute the of tan 45° in the given equation

1-tan 2 45°/1+tan 2 45° = (1-1 2 )/(1+1 2 )

The solution of the above equation is 0.

(iii) (A) is correct.

To find the value of A, substitute the degree given in the options one by one

sin 2A = 2 sin A is true when A = 0°

As sin 2A = sin 0° = 0

2 sin A = 2 sin 0° = 2 × 0 = 0

Apply the sin 2A formula, to find the degree value

sin 2A = 2sin A cos A

⇒2sin A cos A = 2 sin A

⇒ 2cos A = 2 ⇒ cos A = 1

Now, we have to check, to get the solution as 1, which degree value has to be applied.

When 0 degree is applied to cos value, i.e., cos 0 =1

Therefore, ⇒ A = 0°

(iv) (C) is correct.

2tan30°/1-tan 2 30° =  2(1/√3)/1-(1/√3) 2

= (2/√3)/(1-1/3) = (2/√3)/(2/3) = √3 = tan 60°

The value of the given equation is equivalent to tan 60°.

3. If tan (A + B) = √3 and tan (A – B) = 1/√3 ,0° < A + B ≤ 90°; A > B, find A and B.

tan (A + B) = √3

Since √3 = tan 60°

Now substitute the degree value

⇒ tan (A + B) = tan 60°

(A + B) = 60° … (i)

The above equation is assumed as equation (i)

tan (A – B) = 1/√3

Since 1/√3 = tan 30°

⇒ tan (A – B) = tan 30°

(A – B) = 30° … equation (ii)

Now add the equation (i) and (ii), we get

A + B + A – B = 60° + 30°

Cancel the terms B

Now, substitute the value of A in equation (i) to find the value of B

45° + B = 60°

B = 60° – 45°

Therefore A = 45° and B = 15°

4. State whether the following are true or false. Justify your answer.

(i) sin (A + B) = sin A + sin B.

(ii) The value of sin θ increases as θ increases.

(iii) The value of cos θ increases as θ increases.

(iv) sin θ = cos θ for all values of θ.

(v) cot A is not defined for A = 0°.

Justification:

Let us take A = 30° and B = 60°, then

Substitute the values in the sin (A + B) formula, we get

sin (A + B) = sin (30° + 60°) = sin 90° = 1 and,

sin A + sin B = sin 30° + sin 60°

= 1/2 + √3/2 = 1+√3/2

Since the values obtained are not equal, the solution is false.

According to the values obtained as per the unit circle, the values of sin are:

sin 45° = 1/√2

sin 60° = √3/2

sin 90° = 1

Thus the value of sin θ increases as θ increases. Hence, the statement is true

(iii) False.

According to the values obtained as per the unit circle, the values of cos are:

cos 60° = 1/2

cos 90° = 0

Thus, the value of cos θ decreases as θ increases. So, the statement given above is false.

sin θ = cos θ, when a right triangle has 2 angles of (π/4). Therefore, the above statement is false.

Since cot function is the reciprocal of the tan function, it is also written as:

cot A = cos A/sin A

Now substitute A = 0°

cot 0° = cos 0°/sin 0° = 1/0 = undefined.

Hence, it is true

Exercise 8.3 Page: 189

1. Evaluate :

(i) sin 18°/cos 72°        

(ii) tan 26°/cot 64°      

(iii)  cos 48° – sin 42°      

(iv)  cosec 31° – sec 59°

(i) sin 18°/cos 72°

To simplify this, convert the sin function into cos function

We know that, 18° is written as 90° – 18°, which is equal to the cos 72°.

= sin (90° – 18°) /cos 72°

Substitute the value, to simplify this equation

= cos 72° /cos 72° = 1

(ii) tan 26°/cot 64°

To simplify this, convert the tan function into cot function

We know that, 26° is written as 90° – 26°, which is equal to the cot 64°.

= tan (90° – 26°)/cot 64°

= cot 64°/cot 64° = 1

(iii) cos 48° – sin 42°

To simplify this, convert the cos function into sin function

We know that, 48° is written as 90° – 42°, which is equal to the sin 42°.

= cos (90° – 42°) – sin 42°

= sin 42° – sin 42° = 0

(iv) cosec 31° – sec 59°

To simplify this, convert the cosec function into sec function

We know that, 31° is written as 90° – 59°, which is equal to the sec 59°

= cosec (90° – 59°) – sec 59°

= sec 59° – sec 59° = 0

2.  Show that:

(i) tan 48° tan 23° tan 42° tan 67° = 1

(ii) cos 38° cos 52° – sin 38° sin 52° = 0

(i) tan 48° tan 23° tan 42° tan 67°

Simplify the given problem by converting some of the tan functions to the cot functions

We know that, tan 48° = tan (90° – 42°) = cot 42°

tan 23° = tan (90° – 67°) = cot 67°

= tan (90° – 42°) tan (90° – 67°) tan 42° tan 67°

Substitute the values

= cot 42° cot 67° tan 42° tan 67°

= (cot 42° tan 42°) (cot 67° tan 67°) = 1×1 = 1

(ii) cos 38° cos 52° – sin 38° sin 52°

Simplify the given problem by converting some of the cos functions to the sin functions

cos 38° = cos (90° – 52°) = sin 52°

cos 52°= cos (90°-38°) = sin 38°

= cos (90° – 52°) cos (90°-38°) – sin 38° sin 52°

= sin 52° sin 38° – sin 38° sin 52° = 0

3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A .

tan 2A = cot (A- 18°)

We know that tan 2A = cot (90° – 2A)

Substitute the above equation in the given problem

⇒ cot (90° – 2A) = cot (A -18°)

Now, equate the angles,

⇒ 90° – 2A = A- 18° ⇒ 108° = 3A

A = 108° / 3

Therefore, the value of A = 36°

4.  If tan A = cot B, prove that A + B = 90°.

tan A = cot B

We know that cot B = tan (90° – B)

To prove A + B = 90°, substitute the above equation in the given problem

tan A = tan (90° – B)

A = 90° – B

A + B = 90°

Hence Proved.

5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.

sec 4A = cosec (A – 20°)

We know that sec 4A = cosec (90° – 4A)

To find the value of A, substitute the above equation in the given problem

cosec (90° – 4A) = cosec (A – 20°)

Now, equate the angles

90° – 4A= A- 20°

A = 110°/ 5 = 22°

Therefore, the value of A = 22°

6. If A, B and C are interior angles of a triangle ABC, then show that

    sin (B+C/2) = cos A/2

We know that, for a given triangle, sum of all the interior angles of a triangle is equal to 180°

A + B + C = 180° ….(1)

To find the value of (B+ C)/2, simplify the equation (1)

⇒ B + C = 180° – A

⇒ (B+C)/2 = (180°-A)/2

⇒ (B+C)/2 = (90°-A/2)

Now, multiply both sides by sin functions, we get

⇒ sin (B+C)/2 = sin (90°-A/2)

Since sin (90°-A/2) = cos A/2, the above equation is equal to

sin (B+C)/2 = cos A/2

Hence proved.

7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

sin 67° + cos 75°

In term of sin as cos function and cos as sin function, it can be written as follows

sin 67° = sin (90° – 23°)

cos 75° = cos (90° – 15°)

So, sin 67° + cos 75° = sin (90° – 23°) + cos (90° – 15°)

Now, simplify the above equation

= cos 23° + sin 15°

Therefore, sin 67° + cos 75° is also expressed as cos 23° + sin 15°

Exercise 8.4 Page: 193

1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.

To convert the given trigonometric ratios in terms of cot functions, use trigonometric formulas

cosec 2 A   – cot 2 A = 1

cosec 2 A = 1 + cot 2 A

Since cosec function is the inverse of sin function, it is written as

1/sin 2 A = 1 + cot 2 A

Now, rearrange the terms, it becomes

sin 2 A = 1/(1+cot 2 A)

Now, take square roots on both sides, we get

sin A = ±1/(√(1+cot 2 A)

The above equation defines the sin function in terms of cot function

Now, to express sec function in terms of cot function, use this formula

sin 2 A = 1/ (1+cot 2 A)

Now, represent the sin function as cos function

1 – cos 2 A = 1/ (1+cot 2 A)

Rearrange the terms,

cos 2 A = 1 – 1/(1+cot 2 A)

⇒cos 2 A = (1-1+cot 2 A)/(1+cot 2 A)

Since sec function is the inverse of cos function,

⇒ 1/sec 2 A = cot 2 A/(1+cot 2 A)

Take the reciprocal and square roots on both sides, we get

⇒ sec A = ±√ (1+cot 2 A)/cotA

Now, to express tan function in terms of cot function

tan A = sin A/cos A and cot A = cos A/sin A

Since cot function is the inverse of tan function, it is rewritten as

tan A = 1/cot A

2. Write all the other trigonometric ratios of ∠A in terms of sec A. Solution:

Cos A function in terms of sec A:

sec A = 1/cos A

⇒ cos A = 1/sec A

sec A function in terms of sec A:

cos 2 A + sin 2 A = 1

Rearrange the terms

sin 2 A = 1 – cos 2 A

sin 2 A = 1 – (1/sec 2 A)

sin 2 A = (sec 2 A-1)/sec 2 A

sin A = ± √(sec 2 A-1)/sec A

cosec A function in terms of sec A:

sin A = 1/cosec A

⇒cosec A = 1/sin A

cosec A = ± sec A/√(sec 2 A-1)

Now, tan A function in terms of sec A:

sec 2 A – tan 2 A = 1

⇒ tan 2 A = sec 2 A – 1

tan A = √(sec 2 A – 1)

cot A function in terms of sec A:

⇒ cot A = 1/tan A

cot A = ±1/√(sec 2 A – 1)

3. Evaluate:

(i) (sin 2 63° + sin 2 27°)/(cos 2 17° + cos 2 73°) (ii)  sin 25° cos 65° + cos 25° sin 65°

(i) (sin 2 63° + sin 2 27°)/(cos 2 17° + cos 2 73°)

To simplify this, convert some of the sin functions into cos functions and cos function into sin function and it becomes,

= (cos 2 27°   + sin 2 27°)/(sin 2 27° + cos 2 73°)

= 1/1 =1                       (since sin 2 A + cos 2 A = 1)

Therefore, (sin 2 63° + sin 2 27°)/(cos 2 17° + cos 2 73°) = 1

(ii) sin 25° cos 65° + cos 25° sin 65°

= sin(90°-25°) cos 65° + cos (90°-65°) sin 65°

= cos 65° cos 65° + sin 65° sin 65°

= cos 2 65°   + sin 2 65° = 1 (since sin 2 A + cos 2 A = 1)

Therefore, sin 25° cos 65° + cos 25° sin 65° = 1

4. Choose the correct option. Justify your choice. (i) 9 sec 2 A – 9 tan 2 A = (A) 1                 (B) 9              (C) 8                (D) 0 (ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) (A) 0                 (B) 1              (C) 2                (D) – 1 (iii) (sec A + tan A) (1 – sin A) = (A) sec A           (B) sin A        (C) cosec A      (D) cos A

(iv) 1+tan 2 A/1+cot 2 A = 

      (A) sec 2 A                 (B) -1              (C) cot 2 A                (D) tan 2 A

(i) (B) is correct.

Take 9 outside, and it becomes

9 sec 2 A – 9 tan 2 A

= 9 (sec 2 A – tan 2 A)

= 9×1 = 9             (∵ sec2 A – tan2 A = 1)

Therefore, 9 sec 2 A – 9 tan 2 A = 9

(ii) (C) is correct

(1 + tan θ + sec θ) (1 + cot θ – cosec θ)

We know that, tan θ = sin θ/cos θ

sec θ = 1/ cos θ

cot θ = cos θ/sin θ

cosec θ = 1/sin θ

Now, substitute the above values in the given problem, we get

= (1 + sin θ/cos θ + 1/ cos θ) (1 + cos θ/sin θ – 1/sin θ)

Simplify the above equation,

= (cos θ +sin θ+1)/cos θ × (sin θ+cos θ-1)/sin θ

= (cos θ+sin θ) 2 -1 2 /(cos θ sin θ)

= (cos 2 θ + sin 2 θ + 2cos θ sin θ -1)/(cos θ sin θ)

= (1+ 2cos θ sin θ -1)/(cos θ sin θ) (Since cos 2 θ + sin 2 θ = 1)

= (2cos θ sin θ)/(cos θ sin θ) = 2

Therefore, (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =2

(iii) (D) is correct.

Sec A= 1/cos A

Tan A = sin A / cos A

(secA + tanA) (1 – sinA)

= (1/cos A + sin A/cos A) (1 – sinA)

= (1+sin A/cos A) (1 – sinA)

= (1 – sin 2 A)/cos A

= cos 2 A/cos A = cos A

Therefore, (secA + tanA) (1 – sinA) = cos A

(iv) (D) is correct.

tan 2 A =1/cot 2 A

Now, substitute this in the given problem, we get

1+tan 2 A/1+cot 2 A

= (1+1/cot 2 A)/1+cot 2 A

= (cot 2 A+1/cot 2 A)×(1/1+cot 2 A)

= 1/cot 2 A = tan 2 A

So, 1+tan 2 A/1+cot 2 A = tan 2 A

5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i) (cosec θ – cot θ) 2  = (1-cos θ)/(1+cos θ)

(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A

(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ

     [Hint : Write the expression in terms of sin θ and cos θ]

(iv) (1 + sec A)/sec A = sin 2 A/(1-cos A)  

     [Hint : Simplify LHS and RHS separately]

(v) ( cos A–sin A+1)/( cos A +sin A–1) = cosec A + cot A, using the identity cosec 2 A = 1+cot 2 A.

(vii) (sin θ – 2sin 3 θ)/(2cos 3 θ-cos θ) = tan θ (viii) (sin A + cosec A) 2  + (cos A + sec A) 2  = 7+tan 2 A+cot 2 A (ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA) [Hint : Simplify LHS and RHS separately] (x) (1+tan 2 A/1+cot 2 A) = (1-tan A/1-cot A) 2  =   tan 2 A

To prove this, first take the Left-Hand side (L.H.S) of the given equation, to prove the Right Hand Side (R.H.S)

L.H.S. = (cosec θ – cot θ) 2

The above equation is in the form of (a-b) 2 , and expand it

Since (a-b) 2 = a 2 + b 2 – 2ab

Here a = cosec θ and b = cot θ

= (cosec 2 θ + cot 2 θ – 2cosec θ cot θ)

Now, apply the corresponding inverse functions and equivalent ratios to simplify

= (1/sin 2 θ + cos 2 θ/sin 2 θ – 2cos θ/sin 2 θ)

= (1 + cos 2 θ – 2cos θ)/(1 – cos 2 θ)

= (1-cos θ) 2 /(1 – cosθ)(1+cos θ)

= (1-cos θ)/(1+cos θ) = R.H.S.

Therefore, (cosec θ – cot θ) 2  = (1-cos θ)/(1+cos θ)

(ii)  (cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A

Now, take the L.H.S of the given equation.

L.H.S. = (cos A/(1+sin A)) + ((1+sin A)/cos A)

= [cos 2 A + (1+sin A) 2 ]/(1+sin A)cos A

= (cos 2 A + sin 2 A + 1 + 2sin A)/(1+sin A) cos A

Since cos 2 A + sin 2 A = 1, we can write it as

= (1 + 1 + 2sin A)/(1+sin A) cos A

= (2+ 2sin A)/(1+sin A)cos A

= 2(1+sin A)/(1+sin A)cos A

= 2/cos A = 2 sec A = R.H.S.

L.H.S. = R.H.S.

(cos A/(1+sin A)) + ((1+sin A)/cos A) = 2 sec A

L.H.S. = tan θ/(1-cot θ) + cot θ/(1-tan θ)

We know that tan θ =sin θ/cos θ

Now, substitute it in the given equation, to convert it in a simplified form

= (1 + sin θ cos θ)/sin θ cos θ

= 1/sin θ cos θ + 1

= 1 + sec θ cosec θ = R.H.S.

Therefore, L.H.S. = R.H.S.

Hence proved

(iv)  (1 + sec A)/sec A = sin 2 A/(1-cos A)

First find the simplified form of L.H.S

L.H.S. = (1 + sec A)/sec A

Since secant function is the inverse function of cos function and it is written as

= (1 + 1/cos A)/1/cos A

= (cos A + 1)/cos A/1/cos A

Therefore, (1 + sec A)/sec A = cos A + 1

R.H.S. = sin 2 A/(1-cos A)

We know that sin 2 A = (1 – cos 2 A), we get

= (1 – cos 2 A)/(1-cos A)

= (1-cos A)(1+cos A)/(1-cos A)

Therefore, sin 2 A/(1-cos A)= cos A + 1

(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A, using the identity cosec 2 A = 1+cot 2 A.

With the help of identity function, cosec 2 A = 1+cot 2 A, let us prove the above equation.

L.H.S. = (cos A–sin A+1)/(cos A+sin A–1)

Divide the numerator and denominator by sin A, we get

= (cos A–sin A+1)/sin A/(cos A+sin A–1)/sin A

We know that cos A/sin A = cot A and 1/sin A = cosec A

= (cot A – 1 + cosec A)/(cot A+ 1 – cosec A)

= (cot A – cosec 2 A + cot 2 A + cosec A)/(cot A+ 1 – cosec A) (using cosec 2 A – cot 2 A = 1

= [(cot A + cosec A) – (cosec 2 A – cot 2 A)]/(cot A+ 1 – cosec A)

= [(cot A + cosec A) – (cosec A + cot A)(cosec A – cot A)]/(1 – cosec A + cot A)

=  (cot A + cosec A)(1 – cosec A + cot A)/(1 – cosec A + cot A)

=  cot A + cosec A = R.H.S.

Therefore, (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A

Hence Proved

First divide the numerator and denominator of L.H.S. by cos A,

We know that 1/cos A = sec A and sin A/ cos A = tan A and it becomes,

= √(sec A+ tan A)/(sec A-tan A)

Now using rationalization, we get

= (sec A + tan A)/1

= sec A + tan A = R.H.S

(vii) (sin θ – 2sin 3 θ)/(2cos 3 θ-cos θ) = tan θ

L.H.S. = (sin θ – 2sin 3 θ)/(2cos 3 θ – cos θ)

Take sin θ as in numerator and cos θ in denominator as outside, it becomes

We know that sin 2 θ = 1-cos 2 θ

= tan θ = R.H.S.

(viii) (sin A + cosec A) 2  + (cos A + sec A) 2  = 7+tan 2 A+cot 2 A

L.H.S. = (sin A + cosec A) 2  + (cos A + sec A) 2

It is of the form (a+b) 2 , expand it

(a+b) 2 =a 2 + b 2 +2ab

= (sin 2 A + cosec 2 A + 2 sin A cosec A) + (cos 2 A + sec 2 A + 2 cos A sec A)

= (sin 2 A + cos 2 A) + 2 sin A(1/sin A) + 2 cos A(1/cos A) + 1 + tan 2 A + 1 + cot 2 A

= 1 + 2 + 2 + 2 + tan 2 A + cot 2 A

= 7+tan 2 A+cot 2 A = R.H.S.

Therefore, (sin A + cosec A) 2  + (cos A + sec A) 2  = 7+tan 2 A+cot 2 A

(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)

First, find the simplified form of L.H.S

L.H.S. = (cosec A – sin A)(sec A – cos A)

Now, substitute the inverse and equivalent trigonometric ratio forms

= (1/sin A – sin A)(1/cos A – cos A)

= (cos 2 A/sin A)×(sin 2 A/cos A)

= cos A sin A

Now, simplify the R.H.S

R.H.S. = 1/(tan A+cotA)

= 1/(sin A/cos A +cos A/sin A)

(cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)

(x)  (1+tan 2 A/1+cot 2 A) = (1-tan A/1-cot A) 2  =   tan 2 A

L.H.S. = (1+tan 2 A/1+cot 2 A)

Since cot function is the inverse of tan function,

= (1+tan 2 A/1+1/tan 2 A)

Now cancel the 1+tan 2 A terms, we get

(1+tan 2 A/1+cot 2 A) = tan 2 A

(1-tan A/1-cot A) 2  =   tan 2 A

NCERT Solutions for Class 10 Chapter 8 – Introduction to Trigonometry

For the  Class 10 CBSE Maths examinations, out of the 80 marks (combined), 12 marks are assigned from the unit 5 “Trigonometry”. The paper consists of 4 parts. Each part carries different marks and the questions have been assigned with 1 mark, two marks, 3 marks and 4 marks. You can expect at least 2-3 compulsory questions from this chapter. The main topics covered in this chapter include:

8.1 Introduction

You have already studied about triangles, and in particular, right triangles, in your earlier classes. In this chapter, we will study some ratios of the sides of a right triangle with respect to its acute angles, called trigonometric ratios of the angle. We also define the trigonometric ratios for angles of measure 0 o and 90 o . We will calculate trigonometric ratios for some specific angles and establish some identities involving these ratios, called trigonometric identities.

8.2 Trigonometric Identities

You have studied the concept of ratio, in your earlier classes. We now define certain ratios involving the sides of a right triangle, and call them trigonometric ratios. The topic is explained with suitable examples by using different functions of Trigonometry.

8.3 Trigonometric Ratios of Some Specific Angles

From Geometry, you are already familiar with the construction of angles of 30 0 , 45 o , 60 o and 90 0 . In this section, we will find the values of the trigonometric ratios for these angles and for 0 o . It explains Trigonometric Ratios of 45 o , Trigonometric Ratios of 30 o and 60 0 , Trigonometric Ratios of 0 o and 90 o with suitable examples.

8.4 Trigonometric Ratios of Complementary Angles

Two angles are said to be complementary if their sum equals 90 o . The topic discusses various formulas to solve numerical problems related to trigonometric ratios.

8.5 Trigonometric Identities

You may recall that an equation is called an identity when it is true for all values of the variables involved. Similarly, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true of all values of the angles involved. In this section, we will prove one trigonometric identity, and use it further to prove other useful trigonometric identities.

8.6 Summary

Summary is the brief of concepts that includes all the important points which you need to memorize to solve numerical problems related to the chapter.

List of Exercises in Class 10 Maths Chapter 8 :

Exercise 8.1 Solutions – 11 Questions (7 short answers, 3 long answers, 1 short answer with reasoning)

Exercise 8.2 Solutions – 4 Questions ( 1 short answer, 2 long answers, 1 MCQ)

Exercise 8.3 Solutions – 7 Questions (5 short answers, 2 long answers)

Exercise 8.4 Solutions – 5 Questions ( 2 short answers, 2 long answers, 1 MCQ)

Hence, these  NCERT Solutions for Class 10 Maths  will help students understand different types of questions and their answers along with key shortcuts and diagrammatic representations. All the NCERT Solutions for Class 10 Maths Chapter 8   PDF given here are presented in simple language. Comprehending these solutions thoroughly will aid students to solve complex problems effortlessly.

The faculty have curated the NCERT Solutions for Class 10 in a lucid manner to improve the problem-solving abilities among the students. For a more clear idea about Introduction To Trigonometry, students can refer to the study materials available at BYJU’S.

• RD Sharma Solutions for Class 10 Maths Introduction To Trigonometry

Frequently Asked Questions on NCERT Solutions for Class 10 Maths Chapter 8

List out the frequently-asked topics of chapter 8 of ncert solutions in the cbse exam of class 10 maths., why should we download ncert solutions for class 10 maths chapter 8 from byju’s, is ncert solutions for class 10 maths chapter 8 important from the exam point of view, leave a comment cancel reply.

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

I can’t understand how 6/4√3=√3/2

we have, 6/4√3=√3/2 6/4√3= 3/2√3 (√3 * √3)/2√3 Since,√3/√3 = 1 we get the answer, √3/2

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Talk to our experts

1800-120-456-456

NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry

• NCERT Solutions
• Chapter 8 Introduction To Trigonometry

NCERT Solutions for Maths Chapter 8 Class 10 Introduction to Trigonometry - Free PDF Download

NCERT Solutions for Class 10 Maths Chapter 8 - Introduction to Trigonometry . Trigonometry, a fundamental branch of mathematics, explores the relationships between angles and sides of triangles. In this chapter, students delve into the basic concepts of trigonometry, such as trigonometric ratios, complementary angles, trigonometric identities, and their applications in solving problems related to heights and distances. These solutions are meticulously crafted by Vedantu’s subject expert with a clear understanding of the concepts, aiding students in mastering the fundamentals of trigonometry and preparing them for more advanced topics in mathematics.

Glance of NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry | Vedantu

Trigonometry comes from Greek words meaning " three sides " and " measure ."

The article covers the basics of Trigonometry and Trigonometric Ratios.

This chapter focuses on trigonometric ratios for acute angles (less than 90 degrees).

You will learn how to calculate these ratios for specific angles.

A table for the values of angles (0 Degree, 30 Degree, 45 Degree, 60 Degree, 90 Degree) with their corresponding trigonometric functions(sin, cos, tan, cot, sec, cosec) is provided.

There are relationships between these ratios, which you will explore (trigonometric identities).

Also, This article contains chapter notes, formulas, exercises links, and important questions for chapter 8 -Introduction to Trigonometry.

There are four exercises (27 fully solved questions) in class 10th maths chapter 8 Introduction to Trigonometry.

Access Exercise Wise NCERT Solutions for Chapter 8 Maths Class 10

Related Chapters

Exercises Under NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Exercise 8.1 - In this exercise, students are introduced to the basic trigonometric ratios - sine, cosine, and tangent, and their reciprocal functions. They learn how to find the values of these ratios for acute angles in a right triangle. The exercise also covers the concept of trigonometric identities, which are fundamental relationships between trigonometric functions.

Exercise 8.2 - This exercise deals with the application of trigonometric ratios to solve real-life problems. Students learn how to use trigonometric ratios to find the height and distance of an object, as well as the angle of elevation and depression. They also learn how to use the Pythagorean theorem to solve problems involving right triangles.

Exercise 8.3 - The final exercise covers the concept of trigonometric equations. Students learn how to solve trigonometric equations using the identities and ratios learned in the previous exercises. They also learn how to find the general solution of a trigonometric equation, which involves finding all the possible solutions. Finally, the exercise covers the concept of the period of a trigonometric function and how to find it for different functions.

Access NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry

Exercise 8.1 .

1. In $\Delta ABC$ right angled at $B$, $AB=24\text{ cm}$, $BC=7\text{ cm}$. Determine 

(i) $\sin A,\cos A$ 

Ans: Given that in the right angle triangle $\Delta ABC$, $AB=24\text{ cm}$, $BC=7\text{ cm}$.

Let us draw a right triangle $\Delta ABC$, also $AB=24\text{ cm}$, $BC=7\text{ cm}$. We get

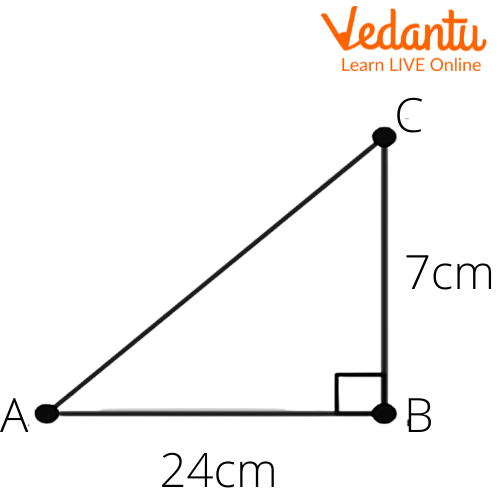
We have to find $\sin A,\cos A$.

We know that for right triangle

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and 

$\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $\Delta ABC$, by Pythagoras theorem ,

${{\left( \text{hypotenuse} \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( perpendicular \right)}^{2}}$ 

Here, $AB=24\text{ cm}$, $BC=7\text{ cm}$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$ 

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{\left( 24 \right)}^{2}}+{{\left( 7 \right)}^{2}}$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=576+49$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=625\text{ }c{{m}^{2}}$

$\Rightarrow AC=25\text{ cm}$ 

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ 

$\Rightarrow \sin A=\dfrac{BC}{AC}$ 

$\therefore \sin A=\dfrac{7}{25}$

$\Rightarrow \cos A=\dfrac{AB}{AC}$

$\therefore \cos A=\dfrac{24}{25}$

(ii) $\sin C,\cos C$ 

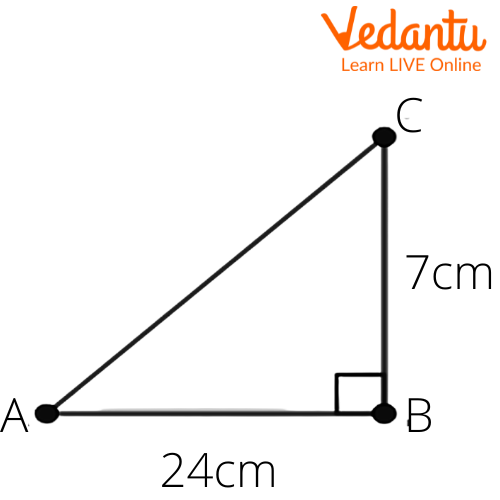
We have to find $\sin C,\cos C$.

$\Rightarrow AC=25\text{ cm}$

$\Rightarrow \sin C=\dfrac{AB}{AC}$ 

$\therefore \sin C=\dfrac{24}{25}$

$\Rightarrow \cos C=\dfrac{BC}{AC}$

$\therefore \cos A=\dfrac{7}{25}$

3. In the given figure find $\tan P-\cot R$.

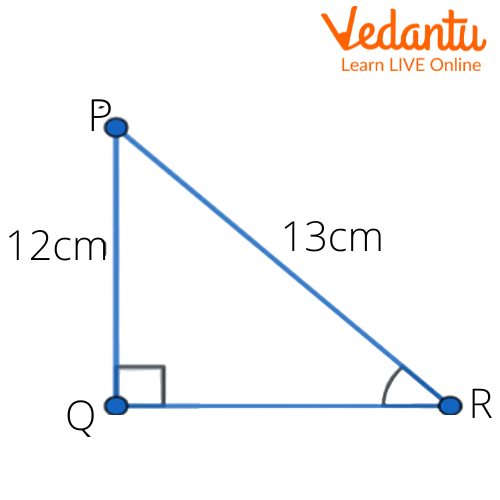
Ans: Given in the figure, 

$PQ=12\text{ cm}$ 

$PQ=13\text{ cm}$

$\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$ and 

$\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$

Now, we need to apply the Pythagoras theorem to find the measure of adjacent side/base.

In $\Delta PQR$, by Pythagoras theorem ,

$\Rightarrow {{\left( PR \right)}^{2}}={{\left( PQ \right)}^{2}}+{{\left( QR \right)}^{2}}$ 

$\Rightarrow {{\left( 13 \right)}^{2}}={{\left( 12 \right)}^{2}}+{{\left( QR \right)}^{2}}$

$\Rightarrow 169=144+{{\left( QR \right)}^{2}}$

$\Rightarrow {{\left( QR \right)}^{2}}=169-144$

$\Rightarrow {{\left( QR \right)}^{2}}=25\text{ }c{{m}^{2}}$

$\Rightarrow QR=5\text{ cm}$ 

$\tan P=\dfrac{\text{opposite side}}{\text{adjacent side}}$ 

$\Rightarrow \tan P=\dfrac{QR}{PQ}$ 

$\therefore \tan P=\dfrac{5}{12}$

$\cot R=\dfrac{\text{adjacent side}}{\text{opposite side}}$

$\Rightarrow \cot R=\dfrac{QR}{PQ}$

$\therefore \cot R=\dfrac{5}{12}$

$\Rightarrow \tan P-\cot R=\dfrac{5}{12}-\dfrac{5}{12}$

$\therefore \tan P-\cot R=0$ 

3. If $\sin A=\dfrac{3}{4}$, calculate $\cos A$ and $\tan A$.

Ans: Let us consider a right angled triangle $\Delta ABC$. We get

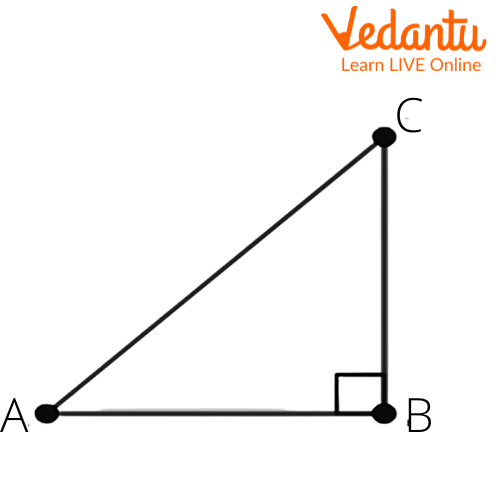
Given that $\sin A=\dfrac{3}{4}$.

We know that  $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$.

From the above figure, we get

$\sin A=\dfrac{BC}{AC}$

Therefore, we get

$\Rightarrow BC=3$ and

$\Rightarrow AC=4$ 

Now, we have to find the values of $\cos A$ and $\tan A$.

We know that $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$ and $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$.

Here, $AC=4\text{ cm}$, $BC=3\text{ cm}$

$\Rightarrow {{4}^{2}}=A{{B}^{2}}+{{3}^{2}}$

$\Rightarrow 16=A{{B}^{2}}+9$

$\Rightarrow A{{B}^{2}}=16-9$

$\Rightarrow A{{B}^{2}}=7$

$\Rightarrow AB=\sqrt{7}\text{ cm}$

Now, we get

$\cos A=\dfrac{AB}{AC}$ 

$\therefore \cos A=\dfrac{\sqrt{7}}{4}$ 

And $\tan A=\dfrac{BC}{AB}$

$\therefore \tan A=\dfrac{3}{\sqrt{7}}$

4. Given $15\cot A=8$. Find $\sin A$ and $\sec A$.

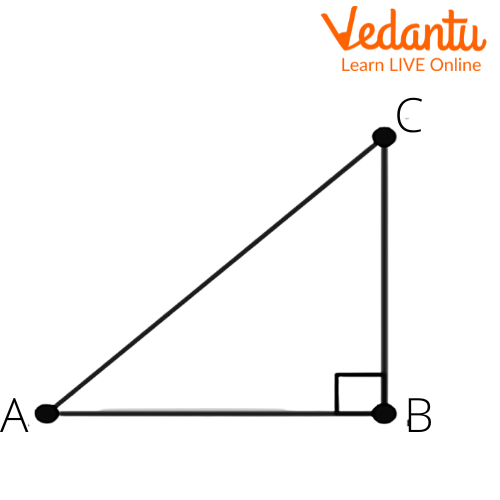
Given that $15\cot A=8$.

We get $\cot A=\dfrac{8}{15}$.

We know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$.

$\cot A=\dfrac{AB}{BC}$

$\Rightarrow BC=15$ and

$\Rightarrow AB=8$ 

Now, we have to find the values of $\sin A$ and $\sec A$.

We know that $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\sec \theta =\dfrac{\text{hypotenuse}}{\text{adjacent side}}$.

$\Rightarrow A{{C}^{2}}={{8}^{2}}+{{15}^{2}}$

$\Rightarrow A{{C}^{2}}=64+225$

$\Rightarrow A{{C}^{2}}=289$

$\Rightarrow AC=17\text{ cm}$

$\sin A=\dfrac{BC}{AC}$ 

$\therefore \sin A=\dfrac{15}{17}$ 

And $\sec A=\dfrac{AC}{AB}$

$\therefore \sec A=\dfrac{17}{8}$

5. Given $\sec \theta =\dfrac{13}{12}$, calculate all other trigonometric ratios.

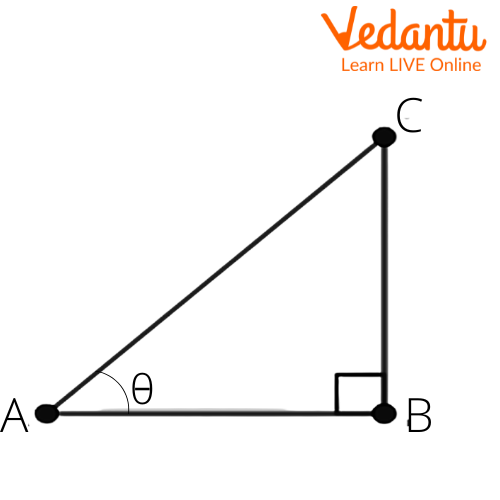
Given that $\sec \theta =\dfrac{13}{12}$.

We know that $\sec \theta =\dfrac{\text{hypotenuse}}{\text{adjacent side}}$.

$\sec \theta =\dfrac{AC}{AB}$

$\Rightarrow AC=13$ and

$\Rightarrow AB=12$ 

Now, we need to apply the Pythagoras theorem to find the measure of the perpendicular/opposite side.

$\Rightarrow {{13}^{2}}={{12}^{2}}+B{{C}^{2}}$

$\Rightarrow 169=144+B{{C}^{2}}$

$\Rightarrow B{{C}^{2}}=25$

$\Rightarrow BC=5\text{ cm}$

Now, we know that

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$

Here, $\sin \theta =\dfrac{BC}{AC}$ 

$\therefore \sin \theta =\dfrac{5}{13}$ 

We know that $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$

Here, $\cos \theta =\dfrac{AB}{AC}$ 

$\therefore \cos \theta =\dfrac{12}{13}$

We know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

Here, $\tan \theta =\dfrac{BC}{AB}$ 

$\therefore \tan \theta =\dfrac{5}{12}$

We know that $\operatorname{cosec}\theta =\dfrac{\text{hypotenuse}}{\text{opposite side}}$

Here, $\operatorname{cosec}\theta =\dfrac{AC}{BC}$

$\therefore \operatorname{cosec}\theta =\dfrac{13}{5}$

We know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$

Here, $\cot \theta =\dfrac{\text{AB}}{BC}$

\[\therefore \cot \theta =\dfrac{12}{5}\] .

6. If $\angle A$ and $\angle B$ are acute angles such that $\cos A=\cos B$, then show that $\angle A=\angle B$.

Given that $\cos A=\cos B$.

In a right triangle $\Delta ABC$, we know that 

Here, 

$\cos A=\dfrac{AC}{AB}$ 

And $\cos B=\dfrac{BC}{AB}$ 

As given $\cos A=\cos B$, we get

$\Rightarrow \dfrac{AC}{AB}=\dfrac{BC}{AB}$ 

$\Rightarrow AC=AB$ 

Now, we know that angles opposite to the equal sides are also equal in measure.

Then, we get

$\angle A=\angle B$ 

Hence proved.

7. Evaluate the following if $\cot \theta =\dfrac{7}{8}$

(i) $\dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}$ 

Now, in a right triangle we know that $\cot \theta =\dfrac{\text{adjacent side}}{\text{opposite side}}$.

Here, from the figure $\cot \theta =\dfrac{BC}{AB}$ .

$AB=8$ and 

$BC=7$ 

$\Rightarrow {{\left( \text{AC} \right)}^{2}}={{8}^{2}}+{{7}^{2}}$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=64+49$

$\Rightarrow {{\left( \text{AC} \right)}^{2}}=113$

$\Rightarrow AC=\sqrt{113}$ 

Now, we know that 

Here, we get

$\sin \theta =\dfrac{AB}{AC}=\dfrac{8}{\sqrt{113}}$ and 

$\cos \theta =\dfrac{BC}{AC}=\dfrac{7}{\sqrt{113}}$ 

Now, we have to evaluate 

$\dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}$

Applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{1-{{\sin }^{2}}\theta }{1-{{\cos }^{2}}\theta }\] 

Substituting the values, we get

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{1-{{\left( \dfrac{8}{\sqrt{113}} \right)}^{2}}}{1-{{\left( \dfrac{7}{\sqrt{113}} \right)}^{2}}}\]

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{1-\dfrac{64}{113}}{1-\dfrac{49}{113}}\]

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{\dfrac{113-64}{113}}{\dfrac{113-49}{113}}\]

\[\Rightarrow \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{\dfrac{49}{113}}{\dfrac{64}{113}}\]

\[\therefore \dfrac{\left( 1+\sin \theta  \right)\left( 1-\sin \theta  \right)}{\left( 1+\cos \theta  \right)\left( 1-\cos \theta  \right)}=\dfrac{49}{64}\]

(ii) ${{\cot }^{2}}\theta $ 

Ans: Given that $\cot \theta =\dfrac{7}{8}$.

Now, ${{\cot }^{2}}\theta ={{\left( \dfrac{7}{8} \right)}^{2}}$

$\therefore {{\cot }^{2}}\theta =\dfrac{49}{64}$ 

8. If $3\cot A=4$, check whether $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$ or not.

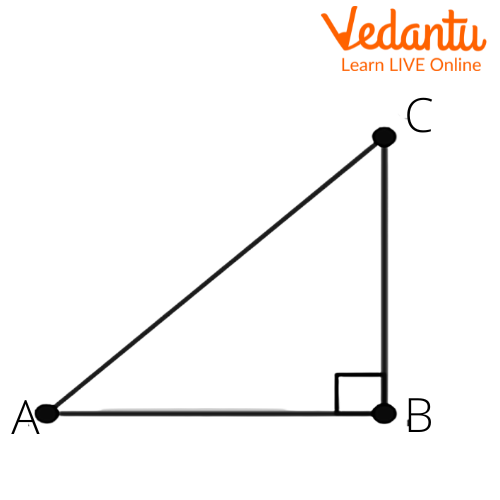
Given that $3\cot A=4$.

We get $\cot A=\dfrac{4}{3}$.

$\Rightarrow AB=4$ 

$\Rightarrow A{{C}^{2}}={{4}^{2}}+{{3}^{2}}$

$\Rightarrow A{{C}^{2}}=16+9$

$\Rightarrow A{{C}^{2}}=25$

$\Rightarrow AC=5$

Now, let us consider LHS of the expression $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$, we get

$LHS=\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}$

Now, we know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

$\tan A=\dfrac{BC}{AB}=\dfrac{3}{4}$ 

Substitute the value, we get

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{1-{{\left( \dfrac{3}{4} \right)}^{2}}}{1+{{\left( \dfrac{3}{4} \right)}^{2}}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{1-\dfrac{9}{16}}{1+\dfrac{9}{16}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{\dfrac{16-9}{16}}{\dfrac{16+9}{16}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{\dfrac{7}{16}}{\dfrac{25}{16}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}=\dfrac{7}{25}$

Now, let us consider RHS of the expression $\dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$, we get

$RHS={{\cos }^{2}}A-{{\sin }^{2}}A$

We know that $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ and $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$.

$\sin A=\dfrac{BC}{AC}=\dfrac{3}{5}$  

And $\cos A=\dfrac{AB}{AC}=\dfrac{4}{5}$

Substitute the values, we get

$\Rightarrow {{\cos }^{2}}A-{{\sin }^{2}}A={{\left( \dfrac{4}{5} \right)}^{2}}-{{\left( \dfrac{3}{5} \right)}^{2}}$

$\Rightarrow {{\cos }^{2}}A-{{\sin }^{2}}A=\dfrac{16}{25}-\dfrac{9}{25}$

$\Rightarrow {{\cos }^{2}}A-{{\sin }^{2}}A=\dfrac{7}{25}$

Hence, we get LHS=RHS

$\therefore \dfrac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A$.

9. In $ABC$, right angled at $B$. If $\tan A=\dfrac{1}{\sqrt{3}}$, find the value of 

(i) $\sin A\cos C+\cos A\sin C$ 

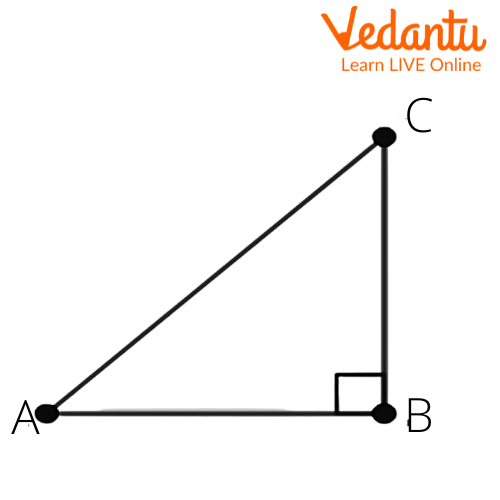
Given that $\tan A=\dfrac{1}{\sqrt{3}}$.

In a right triangle, we know that $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$

Here, from the figure we get

$\tan A=\dfrac{BC}{AB}=\dfrac{1}{\sqrt{3}}$

We get $BC=1$ and $AB=\sqrt{3}$ .

$\Rightarrow A{{C}^{2}}={{\left( \sqrt{3} \right)}^{2}}+{{1}^{2}}$

$\Rightarrow A{{C}^{2}}=3+1$

$\Rightarrow A{{C}^{2}}=4$

$\Rightarrow AC=2$

$\sin A=\dfrac{BC}{AC}=\dfrac{1}{2}$  and $\sin C=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{2}$

And $\cos A=\dfrac{AB}{AC}=\dfrac{\sqrt{3}}{2}$and $\cos C=\dfrac{BC}{AC}=\dfrac{1}{2}$

Now, we have to find the value of the expression $\sin A\cos C+\cos A\sin C$.

Substituting the values we get

$\Rightarrow \sin A\cos C+\cos A\sin C=\dfrac{1}{2}\times \dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3}}{2}$ 

$\Rightarrow \sin A\cos C+\cos A\sin C=\dfrac{1}{4}+\dfrac{3}{4}$

$\Rightarrow \sin A\cos C+\cos A\sin C=\dfrac{4}{4}$

$\therefore \sin A\cos C+\cos A\sin C=1$

(ii) $\cos A\cos C-\sin A\sin C$

Now, we have to find the value of the expression $\cos A\cos C-\sin A\sin C$.

$\Rightarrow \cos A\cos C-\sin A\sin C=\dfrac{\sqrt{3}}{2}\times \dfrac{1}{2}-\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2}$ 

$\Rightarrow \cos A\cos C-\sin A\sin C=\dfrac{\sqrt{3}}{4}-\dfrac{\sqrt{3}}{4}$

$\therefore \Rightarrow \cos A\cos C-\sin A\sin C=0$

10. In $\Delta PQR$, right angled at $Q$, $PR+QR=25\text{ cm}$ and $PQ=5\text{ cm}$. Determine the values of $\sin P,\cos P$ and $\tan P$.

Ans: Let us consider a right angled triangle $\Delta PQR$, we get

Given that $PR+QR=25\text{ cm}$ and $PQ=5\text{ cm}$.

Let $QR=25-PR$

Now, applying the Pythagoras theorem in $\Delta PQR$, we get

$\Rightarrow P{{R}^{2}}={{5}^{2}}+{{\left( 25-PR \right)}^{2}}$

$\Rightarrow P{{R}^{2}}=25+{{25}^{2}}+P{{R}^{2}}-50PR$

$\Rightarrow P{{R}^{2}}=P{{R}^{2}}+25+625-50PR$

$\Rightarrow 50PR=650$

$\Rightarrow PR=13\text{ cm}$ 

Therefore, 

$\Rightarrow QR=12\text{ cm}$ 

Now, we know that in right triangle,

$\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$, $\cos \theta =\dfrac{\text{adjacent side}}{\text{hypotenuse}}$ and $\tan \theta =\dfrac{\text{opposite side}}{\text{adjacent side}}$.

$\sin P=\dfrac{QR}{PR}$ 

$\therefore \sin P=\dfrac{12}{13}$ 

$\cos P=\dfrac{PQ}{PR}$ 

$\therefore \cos P=\dfrac{5}{13}$ 

$\tan P=\dfrac{QR}{PQ}$ 

$\therefore \tan P=\dfrac{12}{5}$

11. State whether the following are true or false. Justify your answer.

(i) The value of $\tan A$ is always less than $1$.

Ans: The given statement is false. The value of $\tan A$ depends on the length of sides of a right triangle and sides of a triangle may have any measure.

(ii) For some value of angle $A$, $\sec A=\dfrac{12}{5}$.

Ans: We know that in the right triangle $\sec A=\dfrac{\text{hypotenuse}}{\text{adjacent side of }\angle \text{A}}$ .

We know that in the right triangle the hypotenuse is the largest side.

Therefore, the value of $\sec A$ must be greater than $1$.

In the given statement $\sec A=\dfrac{12}{5}$, which is greater than $1$.

Therefore, the given statement is true.

(iii) $\cos A$ is the abbreviation used for the cosecant of angle $A$.

Ans: The given statement is false because $\cos A$ is the abbreviation used for the cosine of angle $A$. Abbreviation used for the cosecant of angle $A$ is $\operatorname{cosec}A$.

(iv) $\cot A$ is the product of $\cot $ and $A$.

Ans: $\cot A$ is the abbreviation used for the cotangent of angle $A$. Hence the given statement is false.

(v) For some angle $\theta $, $\sin \theta =\dfrac{4}{3}$.

Ans: We know that in the right triangle $\sin \theta =\dfrac{\text{opposite side}}{\text{hypotenuse}}$ .

Therefore, the value of $\sin \theta $ must be less than $1$.

In the given statement $\sin \theta =\dfrac{4}{3}$, which is greater than $1$.

Therefore, the given statement is false.

Exercise 8.2

1. Evaluate the following:

(i) $\sin 60{}^\circ \cos 30{}^\circ +\sin 30{}^\circ \cos 60{}^\circ $ 

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

We have to evaluate $\sin 60{}^\circ \cos 30{}^\circ +\sin 30{}^\circ \cos 60{}^\circ $.

Substitute the values from the above table, we get

$\Rightarrow \dfrac{\sqrt{3}}{2}\times \dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\times \dfrac{1}{2}$

$\Rightarrow \dfrac{3}{4}+\dfrac{1}{4}$ 

$\Rightarrow \dfrac{4}{4}$ 

$\therefore \sin 60{}^\circ \cos 30{}^\circ +\sin 30{}^\circ \cos 60{}^\circ =1$.

(ii) $2{{\tan }^{2}}45{}^\circ +{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ $

We have to evaluate $2{{\tan }^{2}}45{}^\circ +{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ $.

$\Rightarrow 2{{\left( 1 \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}-{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}$

$\Rightarrow 2+\dfrac{3}{4}-\dfrac{3}{4}$ 

$\Rightarrow 2$ 

$\therefore 2{{\tan }^{2}}45{}^\circ +{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ =2$.

(iii) $\dfrac{\cos 45{}^\circ }{\sec 30{}^\circ +\operatorname{cosec}30{}^\circ }$

We have to evaluate $\dfrac{\cos 45{}^\circ }{\sec 30{}^\circ +\operatorname{cosec}30{}^\circ }$.

$\Rightarrow \dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2}{\sqrt{3}}+2}$

$\Rightarrow \dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2+2\sqrt{3}}{\sqrt{3}}}$ 

\[\Rightarrow \dfrac{1}{\sqrt{2}}\times \dfrac{\sqrt{3}}{2+2\sqrt{3}}\]

Multiplying and dividing by \[\sqrt{3}-1\], we get

\[\Rightarrow \dfrac{1}{\sqrt{2}}\times \dfrac{\sqrt{3}}{2+2\sqrt{3}}\times \dfrac{\sqrt{3}-1}{\sqrt{3}-1}\]

\[\Rightarrow \dfrac{\sqrt{3}\left( \sqrt{3}-1 \right)}{\sqrt{2}\left( 2+2\sqrt{3} \right)\left( \sqrt{3}-1 \right)}\]

\[\Rightarrow \dfrac{\sqrt{3}\left( \sqrt{3}-1 \right)}{2\sqrt{2}\left( \sqrt{3}+1 \right)\left( \sqrt{3}-1 \right)}\]

\[\Rightarrow \dfrac{3-\sqrt{3}}{2\sqrt{2}\left( {{\left( \sqrt{3} \right)}^{2}}-{{1}^{2}} \right)}\]

\[\Rightarrow \dfrac{3-\sqrt{3}}{2\sqrt{2}\left( 3-1 \right)}\]

$\Rightarrow \dfrac{3-\sqrt{3}}{4\sqrt{2}}$ 

$\therefore \dfrac{\cos 45{}^\circ }{\sec 30{}^\circ +\operatorname{cosec}30{}^\circ }=\dfrac{3-\sqrt{3}}{4\sqrt{2}}$

(iv) $\dfrac{\sin 30{}^\circ +\tan 45{}^\circ -\operatorname{cosec}60{}^\circ }{\sec 30{}^\circ +\cos 60{}^\circ -\cot 45{}^\circ }$

We have to evaluate $\dfrac{\sin 30{}^\circ +\tan 45{}^\circ -\operatorname{cosec}60{}^\circ }{\sec 30{}^\circ +\cos 60{}^\circ -\cot 45{}^\circ }$.

$\Rightarrow \dfrac{\dfrac{1}{2}+1-\dfrac{2}{\sqrt{3}}}{\dfrac{2}{\sqrt{3}}+\dfrac{1}{2}+1}$

$\Rightarrow \dfrac{\dfrac{3}{2}-\dfrac{2}{\sqrt{3}}}{\dfrac{2}{\sqrt{3}}+\dfrac{3}{2}}$

$\Rightarrow \dfrac{\dfrac{3\sqrt{3}-4}{2\sqrt{3}}}{\dfrac{3\sqrt{3}+4}{2\sqrt{3}}}$

$\Rightarrow \dfrac{3\sqrt{3}-4}{3\sqrt{3}+4}$

Multiplying and dividing by \[3\sqrt{3}-4\], we get

\[\Rightarrow \dfrac{3\sqrt{3}-4}{3\sqrt{3}+4}\times \dfrac{3\sqrt{3}-4}{3\sqrt{3}-4}\]

Now, applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

\[\Rightarrow \dfrac{{{\left( 3\sqrt{3}-4 \right)}^{2}}}{{{\left( 3\sqrt{3} \right)}^{2}}-{{4}^{2}}}\]

\[\Rightarrow \dfrac{27+16-24\sqrt{3}}{27-16}\]

$\Rightarrow \dfrac{43-24\sqrt{3}}{11}$ 

$\therefore \dfrac{\sin 30{}^\circ +\tan 45{}^\circ -\operatorname{cosec}60{}^\circ }{\sec 30{}^\circ +\cos 60{}^\circ -\cot 45{}^\circ }=\dfrac{43-24\sqrt{3}}{11}$

(v) $\dfrac{5{{\cos }^{2}}60{}^\circ +4{{\sec }^{2}}30{}^\circ -{{\tan }^{2}}45{}^\circ }{{{\sec }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ }$

We have to evaluate $\dfrac{5{{\cos }^{2}}60{}^\circ +4{{\sec }^{2}}30{}^\circ -{{\tan }^{2}}45{}^\circ }{{{\sec }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ }$.

$\Rightarrow \dfrac{5{{\left( \dfrac{1}{2} \right)}^{2}}+4{{\left( \dfrac{2}{\sqrt{3}} \right)}^{2}}-{{1}^{2}}}{{{\left( \dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}}$

$\Rightarrow \dfrac{5\left( \dfrac{1}{4} \right)+4\left( \dfrac{4}{3} \right)-1}{\left( \dfrac{1}{4} \right)+\left( \dfrac{3}{4} \right)}$

$\Rightarrow \dfrac{\dfrac{15+64-12}{12}}{\dfrac{1+3}{4}}$

$\Rightarrow \dfrac{\dfrac{15+64-12}{12}}{\dfrac{4}{4}}$ 

$\Rightarrow \dfrac{\dfrac{67}{12}}{1}$ 

$\therefore \dfrac{5{{\cos }^{2}}60{}^\circ +4{{\sec }^{2}}30{}^\circ -{{\tan }^{2}}45{}^\circ }{{{\sec }^{2}}30{}^\circ +{{\cos }^{2}}30{}^\circ }=\dfrac{67}{12}$.

2. Choose the correct option and justify your choice.

(i) $\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=$ ………

(a) $\sin 60{}^\circ $ 

(b) $\cos 60{}^\circ $ 

(c) $\tan 60{}^\circ $ 

(d) $\sin 30{}^\circ $ 

Ans: The given expression is $\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$.

We know that from the trigonometric ratio table we have $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$.

Substitute the value in the given expression we get

$\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{2\left( \dfrac{1}{\sqrt{3}} \right)}{1+{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{1+\dfrac{1}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{4}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\dfrac{\sqrt{3}}{2}$

From the trigonometric table we know that 

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$ 

$\cos 60{}^\circ =\dfrac{1}{2}$ 

$\tan 60{}^\circ =\sqrt{3}$ 

$\sin 30{}^\circ =\dfrac{1}{2}$

Hence, $\dfrac{2\tan 30{}^\circ }{1+{{\tan }^{2}}30{}^\circ }=\sin 60{}^\circ $.

Therefore, option (A) is the correct answer.

(ii) $\dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=$ ………

(a) $\tan 90{}^\circ $ 

(b) $1$ 

(c) $\sin 45{}^\circ $ 

Ans: The given expression is $\dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }$.

We know that from the trigonometric ratio table we have $\tan 45{}^\circ =1$.

$\dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=\dfrac{1-{{1}^{2}}}{1+{{1}^{2}}}$

$\Rightarrow \dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=\dfrac{1-1}{1+1}$

$\Rightarrow \Rightarrow \dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=\dfrac{0}{2}$

$\therefore \dfrac{1-{{\tan }^{2}}45{}^\circ }{1+{{\tan }^{2}}45{}^\circ }=0$

Therefore, option (D) is the correct answer.

(iii) $\sin 2A=2\sin A$ is true when $A=$ ……..

(a) $0{}^\circ $ 

(b) $30{}^\circ $ 

(c) $45{}^\circ $ 

(d) $60{}^\circ $ 

Ans: The given expression is $\sin 2A=2\sin A$.

We know that from the trigonometric ratio table we have 

$\sin 0{}^\circ =0$

$\sin 45{}^\circ =\dfrac{1}{\sqrt{2}}$

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$  

$\sin 90{}^\circ =1$ 

The given statement is true when $A=0{}^\circ $.

$\Rightarrow \sin 2A=2\sin A$

$\Rightarrow \sin 2\times 0{}^\circ =2\sin 0{}^\circ $

$0=0$ 

(iv) $\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=$………

Ans: The given expression is $\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }$.

$\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\dfrac{2\left( \dfrac{1}{\sqrt{3}} \right)}{1-{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{1-\dfrac{1}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{2}{3}}$

$\Rightarrow \dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\sqrt{3}$

Hence, $\dfrac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\tan 60{}^\circ $.

Therefore, option (C) is the correct answer.

3. If $\tan \left( A+B \right)=\sqrt{3}$ and $\tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$, $0{}^\circ <A+B\le 90{}^\circ $. Find $A$ and $B$ .

Ans: Given that $\tan \left( A+ dB \right)=\sqrt{3}$ and $\tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$.

From the trigonometric ratio table we know that $\tan 60{}^\circ =\sqrt{3}$ and $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$.

Then we get

$\tan \left( A+B \right)=\sqrt{3}$

$\Rightarrow \tan \left( A+B \right)=\tan 60{}^\circ $

$\Rightarrow A+B=60{}^\circ $ ……….(1)

Also, $\tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$

$\Rightarrow \tan \left( A-B \right)=\tan 30{}^\circ $

$\Rightarrow A-B=30{}^\circ $ ……….(2)

Adding eq. (1) and (2), we get

$2A=90{}^\circ $

$\therefore A=45{}^\circ $ 

Substitute the obtained value in eq. (1), we get

$45{}^\circ +B=60{}^\circ $ 

$\Rightarrow B=60{}^\circ -45{}^\circ $ 

$\therefore B=15{}^\circ $ 

Therefore, the values of $A$ and $B$ is $45{}^\circ $ and $15{}^\circ $ respectively.

4. State whether the following are true or false. Justify your answer.

(i) $\sin \left( A+B \right)=\sin A+\sin B$.

Ans: Let us assume $A=30{}^\circ $ and $B=60{}^\circ $.

Now, let us consider LHS of the given expression, we get

$\sin \left( A+B \right)$

Substitute the assumed values in the LHS, we get

$\sin \left( A+B \right)=\sin \left( 30{}^\circ +60{}^\circ  \right)$

$\Rightarrow \sin \left( A+B \right)=\sin \left( 90{}^\circ  \right)$ 

From the trigonometric ratio table we know that $\sin 90{}^\circ =1$, we get

$\Rightarrow \sin \left( A+B \right)=1$

Now, let us consider the RHS of the given expression and substitute the values, we get

$\sin A+\sin B=\sin 30{}^\circ +\sin 60{}^\circ $

From the trigonometric ratio table we know that $\sin 30{}^\circ =\dfrac{1}{2}$ and $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$, we get

$\Rightarrow \sin A+\sin B=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}$

$\Rightarrow \sin A+\sin B=\dfrac{1+\sqrt{3}}{2}$

Thus, $LHS\ne RHS$.

(ii) The value of $\sin \theta $ increases as $\theta $ increases. 

Ans: The value of sine from the trigonometric ratio table is as follows:

$\sin 30{}^\circ =\dfrac{1}{2}=0.5$

$\sin 45{}^\circ =\dfrac{1}{\sqrt{2}}=0.707$

$\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}=0.866$  

Therefore, we can conclude that the value of $\sin \theta $ increases as $\theta $ increases. 

(iii) The value of $\cos \theta $ increases as $\theta $ increases. 

Ans: The value of cosine from the trigonometric ratio table is as follows:

$\cos 0{}^\circ =1$

$\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}=0.866$

$\cos 45{}^\circ =\dfrac{1}{\sqrt{2}}=0.707$

$\cos 60{}^\circ =\dfrac{1}{2}=0.5$  

$\cos 90{}^\circ =0$ 

Therefore, we can conclude that the value of $\cos \theta $ decreases as $\theta $ increases. 

(iv) \[\sin \theta =\cos \theta \] for all values of \[\theta \].

Ans: The trigonometric ratio table is given as follows:

From the above table we can conclude that \[\sin \theta =\cos \theta \] is true only for $\theta =45{}^\circ $.

\[\sin \theta =\cos \theta \] is not true for all values of $\theta $.

(v) $\cot A$ is not defined for $A=0{}^\circ $.

Ans: We know that $\cot A=\dfrac{\cos A}{\sin A}$ .

If $A=0{}^\circ $, then $\cot 0{}^\circ =\dfrac{\cos 0{}^\circ }{\sin 0{}^\circ }$

From trigonometric ratio table we get

$\sin 0{}^\circ =0$ and $\cos 0{}^\circ =1$

$\cot 0{}^\circ =\dfrac{1}{0}$, which is undefined.

Exercise 8.3

1. Express the trigonometric ratios $\sin A,\sec A$ and $\tan A$ in terms of $\cot A$.

Ans: For a right triangle we have an identity ${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$.

Let us consider the above identity, we get

${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$

Now, reciprocating both sides we get

$\Rightarrow \dfrac{1}{{{\operatorname{cosec}}^{2}}A}=\dfrac{1}{1+{{\cot }^{2}}A}$

Now, we know that $\dfrac{1}{{{\operatorname{cosec}}^{2}}A}={{\sin }^{2}}A$, we get

$\Rightarrow {{\sin }^{2}}A=\dfrac{1}{1+{{\cot }^{2}}A}$

$\Rightarrow \sin A=\pm \dfrac{1}{\sqrt{1+{{\cot }^{2}}A}}$

Now, we know that sine value will be negative for angles greater than $180{}^\circ $, for a triangle sine value is always positive with respect to an angle. Then we will consider only positive values.

$\therefore \sin A=\dfrac{1}{\sqrt{1+{{\cot }^{2}}A}}$ 

We know that $\tan A=\dfrac{1}{\cot A}$ 

Also, we will use the identity ${{\sec }^{2}}A=1+{{\tan }^{2}}A$, we get

${{\sec }^{2}}A=1+{{\tan }^{2}}A$

$\Rightarrow {{\sec }^{2}}A=1+\dfrac{1}{{{\cot }^{2}}A}$

$\Rightarrow {{\sec }^{2}}A=\dfrac{{{\cot }^{2}}A+1}{{{\cot }^{2}}A}$

\[\Rightarrow \sec A=\dfrac{\sqrt{{{\cot }^{2}}A+1}}{\sqrt{{{\cot }^{2}}A}}\]

\[\therefore \sec A=\dfrac{\sqrt{{{\cot }^{2}}A+1}}{\cot A}\]

2. Write all the other trigonometric ratios of $\angle A$ in terms of $\sec A$.

We know that $\cos A=\dfrac{1}{\sec A}$.

$\therefore \cos A=\dfrac{1}{\sec A}$

For a right triangle we have an identity ${{\sin }^{2}}A+{{\cos }^{2}}A=1$.

${{\sin }^{2}}A+{{\cos }^{2}}A=1$

Now, we know that $\cos A=\dfrac{1}{\sec A}$, we get

$\Rightarrow {{\sin }^{2}}A=1-{{\cos }^{2}}A$

$\Rightarrow {{\sin }^{2}}A=1-\dfrac{1}{{{\sec }^{2}}A}$

$\Rightarrow \sin A=\sqrt{1-{{\left( \dfrac{1}{\sec A} \right)}^{2}}}$

$\therefore \sin A=\dfrac{\sqrt{{{\sec }^{2}}A-1}}{\sec A}$

${{\tan }^{2}}A={{\sec }^{2}}A-1$

$\therefore \tan A=\sqrt{{{\sec }^{2}}A-1}$ 

Now, we know that $\cot A=\dfrac{\cos A}{\sin A}$, we get

$\Rightarrow \cot A=\dfrac{\dfrac{1}{\sec A}}{\dfrac{\sqrt{{{\sec }^{2}}A-1}}{\sec A}}$

$\therefore \cot A=\dfrac{1}{\sqrt{{{\sec }^{2}}A-1}}$

We know that $cosecA=\dfrac{1}{\sin A}$, we get

 $\therefore cosecA=\dfrac{\sec A}{\sqrt{{{\sec }^{2}}A-1}}$

3. Evaluate the following:

(i) $\dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }$ 

Ans: The given expression is $\dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }$.

The above expression can be written as 

$\dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=\dfrac{{{\left[ \sin \left( 90{}^\circ -27{}^\circ  \right) \right]}^{2}}+{{\sin }^{2}}27{}^\circ }{{{\left[ \cos \left( 90{}^\circ -73{}^\circ  \right) \right]}^{2}}+{{\cos }^{2}}73{}^\circ }$

Now, we can apply the identity $\cos \left( 90{}^\circ -\theta  \right)=\sin \theta $ and $\sin \left( 90{}^\circ -\theta  \right)=\cos \theta $, we get

$\Rightarrow \dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=\dfrac{{{\cos }^{2}}27{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\sin }^{2}}73{}^\circ +{{\cos }^{2}}73{}^\circ }$

Now, by applying the trigonometric identity ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=\dfrac{1}{1}$ 

$\therefore \dfrac{{{\sin }^{2}}63{}^\circ +{{\sin }^{2}}27{}^\circ }{{{\cos }^{2}}17{}^\circ +{{\cos }^{2}}73{}^\circ }=1$

(ii) $\sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ $ 

Ans: The given expression is $\sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ $ .

$\sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =\sin 25{}^\circ \cos \left( 90{}^\circ -25{}^\circ  \right)+\cos 25{}^\circ \sin \left( 90{}^\circ -25{}^\circ  \right)$

\[\Rightarrow \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =\sin 25{}^\circ \sin 25{}^\circ +\cos 25{}^\circ \cos 25{}^\circ \]

\[\Rightarrow \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ ={{\sin }^{2}}25{}^\circ +{{\cos }^{2}}25{}^\circ \]

\[\Rightarrow \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =1\] 

\[\therefore \sin 25{}^\circ \cos 65{}^\circ +\cos 25{}^\circ \sin 65{}^\circ =1\]

4. Choose the correct option and justify your choice:

(i) \[9{{\sec }^{2}}A-9{{\tan }^{2}}A=\] …….

(a) $1$ 

(c) $8$ 

Ans: The given expression is $9{{\sec }^{2}}A-9{{\tan }^{2}}A$.

The given expression can be written as 

$\Rightarrow 9{{\sec }^{2}}A-9{{\tan }^{2}}A=9\left( {{\sec }^{2}}A-{{\tan }^{2}}A \right)$

Now, we will use the identity ${{\sec }^{2}}A=1+{{\tan }^{2}}A$, we get

${{\sec }^{2}}A-{{\tan }^{2}}A=1$

$\Rightarrow 9{{\sec }^{2}}A-9{{\tan }^{2}}A=9\left( 1 \right)$

$\therefore 9{{\sec }^{2}}A-9{{\tan }^{2}}A=9$

Therefore, option (B) is the correct answer.

(ii) $\left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)$ 

Ans: The given expression is $\left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)$.

We know that the trigonometric functions have values as:

$\tan \theta =\dfrac{\sin \theta }{\cos \theta }$, $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$, $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$

Substituting these values in the given expression, we get

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\left( 1+\dfrac{\sin \theta }{\cos \theta }+\dfrac{1}{\cos \theta } \right)\left( 1+\dfrac{\cos \theta }{\sin \theta }-\dfrac{1}{\sin \theta } \right)$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\left( \dfrac{\cos \theta +\sin \theta +1}{\cos \theta } \right)\left( \dfrac{\sin \theta +\cos \theta -1}{\sin \theta } \right)$

Now, by applying the identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, we get

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{{{\left( \sin \theta +\cos \theta  \right)}^{2}}-{{1}^{2}}}{\sin \theta \cos \theta }$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta +2\sin \theta \cos \theta -1}{\sin \theta \cos \theta }$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{1+2\sin \theta \cos \theta -1}{\sin \theta \cos \theta }$

$\Rightarrow \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=\dfrac{2\sin \theta \cos \theta }{\sin \theta \cos \theta }$

$\therefore \left( 1+\tan \theta +\sec \theta  \right)\left( 1+\cot \theta -\operatorname{cosec}\theta  \right)=2$

(iii) $\left( \sec A+\tan A \right)\left( 1-\sin A \right)=$ ………

(a) $\sec A$ 

(b) $\sin A$ 

(c) $cosecA$ 

(d) $\cos A$ 

Ans: Given expression is $\left( \sec A+\tan A \right)\left( 1-\sin A \right)$.

We know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$

$\left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A} \right)\left( 1-\sin A \right)$

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{1+\sin A}{\cos A} \right)\left( 1-\sin A \right)$

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{\left( 1+\sin A \right)\left( 1-\sin A \right)}{\cos A} \right)$

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{{{1}^{2}}-{{\sin }^{2}}A}{\cos A} \right)$

Now, we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, we get

$\Rightarrow \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\left( \dfrac{{{\cos }^{2}}A}{\cos A} \right)$

$\therefore \left( \sec A+\tan A \right)\left( 1-\sin A \right)=\cos A$

(iv) $\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}$ 

(a) ${{\sec }^{2}}A$ 

(b) $-1$ 

(c) ${{\cot }^{2}}A$ 

(d) ${{\tan }^{2}}A$ 

Ans: Given expression is $\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}$.

$\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$.

$\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{1+\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}}{1+\dfrac{{{\cos }^{2}}A}{{{\sin }^{2}}A}}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{\dfrac{{{\cos }^{2}}A+{{\sin }^{2}}A}{{{\cos }^{2}}A}}{\dfrac{{{\sin }^{2}}A+{{\cos }^{2}}A}{{{\sin }^{2}}A}}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{\dfrac{1}{{{\cos }^{2}}A}}{\dfrac{1}{{{\sin }^{2}}A}}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{{{\sin }^{2}}A}{{{\cos }^{2}}A}$

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\tan }^{2}}A$

5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i) ${{\left( cosec\theta -cot\theta  \right)}^{2}}=\dfrac{1-\cos \theta }{1+\cos \theta }$ 

Ans: Given expression is ${{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{1-\cos \theta }{1+\cos \theta }$.

Let us consider the LHS of the given expression, we get

$LHS={{\left( cosec\theta -\cot \theta  \right)}^{2}}$

Now, we know that $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$ and $cosec\theta =\dfrac{1}{\sin \theta }$.

By substituting the values, we get

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}={{\left( \dfrac{1}{\sin \theta }-\dfrac{\cos \theta }{\sin \theta } \right)}^{2}}$

 $\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}={{\left( \dfrac{1-\cos \theta }{\sin \theta } \right)}^{2}}$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{{{\left( 1-\cos \theta  \right)}^{2}}}{{{\sin }^{2}}\theta }$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{{{\left( 1-\cos \theta  \right)}^{2}}}{1-{{\cos }^{2}}\theta }$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{{{\left( 1-\cos \theta  \right)}^{2}}}{\left( 1-\cos \theta  \right)\left( 1+\cos \theta  \right)}$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{\left( 1-\cos \theta  \right)}{\left( 1+\cos \theta  \right)}$

$\Rightarrow {{\left( cosec\theta -\cot \theta  \right)}^{2}}=RHS$

$\therefore {{\left( cosec\theta -\cot \theta  \right)}^{2}}=\dfrac{1-\cos \theta }{1+\cos \theta }$

Hence proved

(ii) $\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A$

Ans: Given expression is $\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A$.

$LHS=\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}$

Now, taking LCM, we get

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{{{\cos }^{2}}A+\left( 1+\sin A \right)\left( 1+\sin A \right)}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{{{\cos }^{2}}A+{{\sin }^{2}}A+2\sin A+1}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{1+2\sin A+1}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{2+2\sin A}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{2\left( 1+\sin A \right)}{\left( 1+\sin A \right)\cos A}$

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=\dfrac{2}{\cos A}$

We know that $sec\theta =\dfrac{1}{\cos \theta }$, we get

$\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A$

\[\Rightarrow \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=RHS\]

\[\therefore \dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2\sec A\]

(iii) $\dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta cosec\theta $ 

Ans: Given expression is $\dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta \operatorname{cosec}\theta $.

$LHS=\dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }$

Now, we know that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ and $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$.

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\left( \dfrac{\dfrac{\sin \theta }{\cos \theta }}{1-\dfrac{\cos \theta }{\sin \theta }}+\dfrac{\dfrac{\cos \theta }{\sin \theta }}{1-\dfrac{\sin \theta }{\cos \theta }} \right)\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\left( \dfrac{\dfrac{\sin \theta }{\cos \theta }}{\dfrac{\sin \theta -\cos \theta }{\sin \theta }}+\dfrac{\dfrac{\cos \theta }{\sin \theta }}{\dfrac{\cos \theta -\sin \theta }{\cos \theta }} \right)\]

 \[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\left( \dfrac{{{\sin }^{2}}\theta }{\cos \theta \left( \sin \theta -\cos \theta  \right)}+\dfrac{{{\cos }^{2}}\theta }{\sin \theta \left( \sin \theta -\cos \theta  \right)} \right)\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left( \dfrac{{{\sin }^{2}}\theta }{\cos \theta }+\dfrac{{{\cos }^{2}}\theta }{\sin \theta } \right)\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left( \dfrac{{{\sin }^{3}}\theta -{{\cos }^{3}}\theta }{\sin \theta \cos \theta } \right)\]

Now, by applying the identity \[{{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\], we get

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left[ \dfrac{\left( \sin \theta -\cos \theta  \right)\left( {{\sin }^{2}}\theta +{{\cos }^{2}}\theta +\sin \theta \cos \theta  \right)}{\sin \theta \cos \theta } \right]\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\left( \sin \theta -\cos \theta  \right)}\left[ \dfrac{\left( \sin \theta -\cos \theta  \right)\left( 1+\sin \theta \cos \theta  \right)}{\sin \theta \cos \theta } \right]\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{\left( 1+\sin \theta \cos \theta  \right)}{\sin \theta \cos \theta }\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\sin \theta \cos \theta }+\dfrac{\sin \theta \cos \theta }{\sin \theta \cos \theta }\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\dfrac{1}{\sin \theta \cos \theta }+1\]

We know that $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$, we get

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=\sec \theta cosec\theta +1\]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta cosec\theta \]

\[\Rightarrow \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=RHS\]

\[\therefore \dfrac{\tan \theta }{1-\cot \theta }+\dfrac{\cot \theta }{1-\tan \theta }=1+\sec \theta cosec\theta \]

(iv) $\dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{1-\cos A}$ 

Ans: Given expression is $\dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{1-\cos A}$.

$LHS=\dfrac{1+\sec A}{\sec A}$

Now, we know that $\sec \theta =\dfrac{1}{\cos \theta }$.

By substituting the value, we get

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{1+\dfrac{1}{\cos A}}{\dfrac{1}{\cos A}}\]

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{\dfrac{\cos A+1}{\cos A}}{\dfrac{1}{\cos A}}\]

 \[\Rightarrow \dfrac{1+\sec A}{\sec A}=\cos A+1\]

Multiply and divide by $\left( 1-\cos A \right)$, we get

 \[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{\left( 1+\cos A \right)\left( 1-\cos A \right)}{\left( 1-\cos A \right)}\]

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{1-{{\cos }^{2}}A}{\left( 1-\cos A \right)}\]

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{\left( 1-\cos A \right)}\]

\[\Rightarrow \dfrac{1+\sec A}{\sec A}=RHS\]

\[\therefore \dfrac{1+\sec A}{\sec A}=\dfrac{{{\sin }^{2}}A}{1-\cos A}\]

(v) $\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=cosecA+\cot A$ 

Ans: Given expression is $\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=cosecA+\cot A$.

Now, let us consider the LHS of the given expression, we get

$LHS=\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}$

Dividing numerator and denominator by $\sin A$, we get

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\dfrac{\cos A}{\sin A}-\dfrac{\sin A}{\sin A}+\dfrac{1}{\sin A}}{\dfrac{\cos A}{\sin A}+\dfrac{\sin A}{\sin A}-\dfrac{1}{\sin A}}$

Now, we know that $\cot \theta =\dfrac{\cos \theta }{\sin \theta }=\dfrac{1}{\tan \theta }$ and $cosec\theta =\dfrac{1}{\sin \theta }$, we get

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\cot A-1+\operatorname{cosec}A}{\cot A+1-\operatorname{cosec}A}$

Now, by applying the identity ${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$, substitute $1={{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A$, we get

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\cot A-\left( {{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A \right)+\operatorname{cosec}A}{\cot A+{{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A-\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\cot A-{{\cot }^{2}}A+{{\operatorname{cosec}}^{2}}A+\operatorname{cosec}A}{\cot A+{{\cot }^{2}}A-{{\operatorname{cosec}}^{2}}A-\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{{{\left( \cot A-1+\operatorname{cosec}A \right)}^{2}}}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{2{{\operatorname{cosec}}^{2}}A+2\cot A\operatorname{cosec}A-2\cot A-2\operatorname{cosec}A}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{2\operatorname{cosec}A\left( \cot A-\operatorname{cosec}A \right)-2\left( \cot A-\operatorname{cosec}A \right)}{{{\cot }^{2}}A-1+{{\operatorname{cosec}}^{2}}A+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\left( 2\operatorname{cosec}A-2 \right)\left( \cot A-\operatorname{cosec}A \right)}{1-1+2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\dfrac{\left( 2\operatorname{cosec}A-2 \right)\left( \cot A-\operatorname{cosec}A \right)}{2\operatorname{cosec}A}$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec}A+\cot A$

$\Rightarrow \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=RHS$

$\therefore \dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec}A+\cot A$ 

(vi) $\sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$ 

Ans: Given expression is $\sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$.

$LHS=\sqrt{\dfrac{1+\sin A}{1-\sin A}}$

Now, multiply and divide the expression by $\sqrt{1+\sin A}$, we get

$\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sqrt{\dfrac{\left( 1+\sin A \right)\left( 1+\sin A \right)}{\left( 1-\sin A \right)\left( 1+\sin A \right)}}$

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sqrt{\dfrac{{{\left( 1+\sin A \right)}^{2}}}{1-{{\sin }^{2}}A}}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\dfrac{1+\sin A}{\sqrt{{{\cos }^{2}}A}}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\dfrac{1+\sin A}{\cos A}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A}\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A\]

\[\Rightarrow \sqrt{\dfrac{1+\sin A}{1-\sin A}}=RHS\]

$\therefore \sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$ 

(vii) $\dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $ 

Ans: Given expression is $\dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $.

$LHS=\dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }$

Taking common terms out, we get

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 2{{\cos }^{2}}\theta -1 \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 2\left( 1-2{{\sin }^{2}}\theta  \right)-1 \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 2-2{{\sin }^{2}}\theta -1 \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta \left( 1-2{{\sin }^{2}}\theta  \right)}{\cos \theta \left( 1-2{{\sin }^{2}}\theta  \right)}$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\dfrac{\sin \theta }{\cos \theta }$

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $

$\Rightarrow \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=RHS$

$\therefore \dfrac{\sin \theta -2{{\sin }^{3}}\theta }{2\cos \theta -\cos \theta }=\tan \theta $

(viii) ${{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+secA \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A$ 

Ans: Given expression is ${{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A$.

$LHS={{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}$

Now, by applying the identity \[{{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\], we get

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}={{\sin }^{2}}A+cosec{{A}^{2}}+2\sin AcosecA+{{\cos }^{2}}A+{{\sec }^{2}}A+2\cos A\sec A\]\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}={{\sin }^{2}}A+{{\cos }^{2}}A+cosec{{A}^{2}}+{{\sec }^{2}}A+2\sin AcosecA+2\cos A\sec A\]We know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$, $cosec\theta =\dfrac{1}{\sin \theta }$ and $sec\theta =\dfrac{1}{\cos \theta }$, we get

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=1+cose{{c}^{2}}\theta +{{\sec }^{2}}\theta +2\sin A\dfrac{1}{\sin A}+2\cos A\dfrac{1}{\cos A}\] 

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=1+\left( 1+{{\cot }^{2}}A+1+{{\tan }^{2}}A \right)+2+2\]

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A\]

\[\Rightarrow {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=RHS\]

\[\therefore {{\left( \sin A+cosecA \right)}^{2}}+{{\left( \cos A+\sec A \right)}^{2}}=7+{{\tan }^{2}}A+{{\cot }^{2}}A\]

(ix) $\left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\dfrac{1}{\tan A+\cot A}$

Ans: Given expression is $\left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\dfrac{1}{\tan A+\cot A}$.

$LHS=\left( cosecA-\sin A \right)\left( \sec A-\cos A \right)$

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\left( \dfrac{1}{\sin A}-\sin A \right)\left( \dfrac{1}{\cos A}-\cos A \right)$

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\left( \dfrac{1-{{\sin }^{2}}A}{\sin A} \right)\left( \dfrac{1-{{\cos }^{2}}A}{\cos A} \right)$

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\left( \dfrac{{{\cos }^{2}}A}{\sin A} \right)\left( \dfrac{{{\sin }^{2}}A}{\cos A} \right)$

$\Rightarrow \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\sin A\cos A$

Now, consider the RHS of the given expression, we get

$RHS=\dfrac{1}{\tan A+\cot A}$

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\dfrac{1}{\dfrac{\sin A}{\cos A}+\dfrac{\cos A}{\sin A}}$

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\dfrac{1}{\dfrac{{{\sin }^{2}}A+{{\cos }^{2}}A}{\sin A\cos A}}$

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\dfrac{\sin A\cos A}{{{\sin }^{2}}A+{{\cos }^{2}}A}$

$\Rightarrow \dfrac{1}{\tan A+\cot A}=\sin A\cos A$

Here, we get LHS=RHS

$\therefore \left( cosecA-\sin A \right)\left( \sec A-\cos A \right)=\dfrac{1}{\tan A+\cot A}$ 

(x) $\left( \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A} \right)={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$

Ans: Given expression is $\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$.

$LHS=\dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}$

By applying the identities ${{\sec }^{2}}A=1+{{\tan }^{2}}A$ and ${{\operatorname{cosec}}^{2}}A=1+{{\cot }^{2}}A$, we get

$\Rightarrow \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}=\dfrac{se{{c}^{2}}A}{{{\operatorname{cosec}}^{2}}A}$

$RHS={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$

Now, we know that $\cot \theta =\dfrac{1}{\tan \theta }$, we get

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\left( \dfrac{1-\tan A}{1-\dfrac{1}{\tan A}} \right)}^{2}}$

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\left( \dfrac{1-\tan A}{\dfrac{\tan A-1}{\tan A}} \right)}^{2}}$

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\left( -\tan A \right)}^{2}}$

$\Rightarrow {{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}={{\tan }^{2}}A$

$\therefore \dfrac{1+{{\tan }^{2}}A}{1+{{\cot }^{2}}A}={{\left( \dfrac{1-\tan A}{1-\cot A} \right)}^{2}}$ 

NCERT Solutions for Class 10 Maths Chapter 8 - Summary

Introduction to trigonometry.

Trigonometry is all about triangles. It is all about right-angled triangles, triangles with one angle equal to 90 degrees, to be more precise. It's a method that helps us find a triangle's missing angles and missing sides. The ‘trigono’ word means triangle and the ‘metry’ word means to measure.

Trigonometric Ratios

In ΔABC, right-angled at ∠B, the trigonometric ratios of the ∠A are as follows:

sin A=opposite side/hypotenuse=BC/AC

cos A=adjacent side/hypotenuse=AB/AC

tan A=opposite side/adjacent side=BC/AB

cosec A=hypotenuse/opposite side=AC/BC

sec A=hypotenuse/adjacent side=AC/AB

cot A=adjacent side/opposite side=AB/BC

Standard Values of Trigonometric Ratios:

Trigonometric Identities: Trigonometric identities are essential tools in trigonometry for simplifying expressions, solving equations, and proving other mathematical statements.There are three Pythagorean trigonometric identities in trigonometry that are based on the right-triangle theorem or Pythagoras theorem.

$\sin^2(x) + \cos^2(x) = 1$

$1 + \tan^2(x) = \sec^2(x)$

$\text{cosec}^2(x) = 1 + \cot^2(x)$

Overview of Deleted Syllabus for CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry

Class 10 Maths Chapter 8: Exercise Breakdown

NCERT Solutions for Class 10 Maths Introduction to Trigonometry, provided by Vedantu, offer a comprehensive understanding of this foundational topic. By focusing on key concepts like trigonometric ratios, Pythagorean identities, and solving triangles, students can develop a strong foundation in trigonometry. Pay attention to the step-by-step solutions provided in the NCERT Solutions, as they help clarify concepts and reinforce problem-solving techniques. Understanding trigonometry is crucial as it forms the basis for more advanced topics in mathematics and has practical applications in fields like engineering, physics, and navigation. In previous years question papers, around  5-6 questions have been typically asked from this chapter.

Other Study Materials of CBSE Class 10 Maths Chapter 8

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

FAQs on NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry

1. Can I completely rely on NCERT solutions on Vedantu for exam preparation?

Yes, you may focus entirely on the NCERT Solutions provided on Vedantu for exam preparation. Many students face difficulties when searching for a reliable study-guide for several subjects. The subject-experts at Vedantu have prepared these NCERT Solutions in a simple language. You can also download the same from our app from the play store and view all the solutions in one place at any time. All solutions are developed with utmost care to ease the examination preparation. So download the NCERT solutions now and start preparing efficiently for the exams.

2. Can I find solutions for all the subjects of Class 10 on Vedantu?

You can find all the solution for all Class 10 subjects provided by Vedantu for the preparation of the exam. Many students face difficulties in finding a reliable study guide for a range of subjects. These NCERT Solutions have been prepared in a clear language by the subject experts at Vedantu. You can also download our Play Store app and view all the solutions in one location at any time. All answers are developed with the utmost care to facilitate the preparation of the examination.

3. What do you learn about trigonometry in Class 10 Maths Chapter 8?

Chapter 8 of Class 10 Maths is basically about trigonometry which is a very important topic for Class 10. It covers the introduction to the ratios and identities, trigonometric ratios of some specific angles, ratios of some complementary angles, and trigonometric identities to solve equations. Visit Vedantu’s website(vedantu.com) to take a look at the solutions for all the exercises. You can refer to Vedantu’s NCERT Solutions for Chapter 8 of Class 10 Maths Trigonometry to understand the concepts better and score high marks in exams. These solutions are available at free of cost on Vedantu website and mobile app.

4. What is the objective of Chapter 8 in Class 10 Maths Trigonometry?

The main objective of Chapter 8 of Class 10 Maths is to introduce a very important concept to students. Trigonometry is a key concept which will play a role in higher studies and also be a part of Physics numerical problems. Students should make sure that the basics of this chapter are understood well. To get an in-depth understanding of the concepts, refer to NCERT solutions, revision notes and important questions offered by Vedantu. These are available free of cost.

5. What does Exercise 8.4 of Chapter 8 Trigonometry of Class 10 Maths  deal with?

Exercise 8.4 of Chapter 8 Trigonometry of Class 10 Maths deals with trigonometric ratios of complementary angles. Complementary angles are those angles whose sum adds up to a total of 90 degrees. There are some standard formulae which are important to be memorised. Students are advised to solve every single question from this exercise and refer to Vedantu’s solutions for further answers.

6. What is important in trigonometry class 10?

The three fundamental functions of trigonometry are sine, cosine, and tangent and all other essential trigonometric functions can be built using these three basic ratios or functions: cotangent, secant, and cosecant.

7. Which is the hardest question in trigonometry class 10?

Here are some specific examples of potentially challenging questions:

Prove that (cos^2 A + sin^2 A) + (1 + tan^2 A) = sec^2 A.

In a right triangle ABC where angle B = 30° and AB = 2a, find AC without using trigonometric tables.

Prove that sin 2A ≤ 2 sin A cos A for all angles A in the interval (0°, 180°).

8. Is class 10 trigonometry hard?

Class 10 trigonometry might seem challenging at first, but with practice and understanding, it becomes manageable. It's a new concept for many students, so it's natural to find it a bit difficult initially. However, with clear explanations, practice exercises, and guidance from teachers or resources like NCERT Solutions, it becomes easier to grasp. Trigonometry involves learning new terms, formulas, and solving problems using trigonometric ratios. By breaking down the concepts into smaller steps and practicing regularly, students can overcome any difficulties and feel more confident in their abilities. Remember, persistence and patience are key to mastering trigonometry, and seeking help when needed can make the learning process smoother.

9. How many trigonometric identities are there in class 10?

There are three basic Trigonometric Identities. They are 

For Pythagorean Identities 

sin^2 (x) + cos^2 (x) = 1.

1+tan^2 (x) = sec^2 (x).

For Reciprocal Identities

csx(x) = 1/sin(x)

sec(x) = 1/cos(x)

cot(x) = 1/tan(x)

For Quotient Identities

tan(x) = sin(x)/cos(x)

cot(x) = cos(x)/sin(x)

sec(x) = 1/os(x)

10. How many marks is trigonometry class 10?

Trigonometry questions generally carry a moderate weightage, often ranging from 10% to 20% of the total marks allocated for the mathematics paper.

11. What is the easiest way to learn trigonometry class 10?

The easiest way to learn trigonometry in Class 10 is through a combination of clear explanations, practice, and real-life applications.

12. How to be perfect in trigonometry class 10?

Becoming proficient in trigonometry in Class 10 requires dedication, practice, and a systematic approach.

NCERT Solutions for Class 10 Maths

Ncert solutions for class 10.

NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry

Ncert solutions for class 10 maths chapter 8 – introduction to trigonometry pdf.

Free PDF of NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry includes all the questions provided in NCERT Books prepared by Mathematics expert teachers as per CBSE NCERT guidelines from Mathongo.com. To download our free pdf of Chapter 8 Introduction to Trigonometry Maths NCERT Solutions for Class 10 to help you to score more marks in your board exams and as well as competitive exams.

Share with friends: