linear quadratic assignment problem

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

1 Introduction
2.1 Koopmans-Beckman Mathematical Formulation
2.2.1 Parameters
2.3.1 Optimization Problem
2.4 Computational Complexity
2.5 Algorithmic Discussions
2.6 Branch and Bound Procedures
2.7 Linearizations
3.1 QAP with 3 Facilities
4.1 Inter-plant Transportation Problem
4.2 The Backboard Wiring Problem
4.3 Hospital Layout
4.4 Exam Scheduling System
5 Conclusion
6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

$F=(F_{ij})$

Inner Product

$A,B$

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

$F_{i,j}(X_{\phi }DX_{\phi }^{T})_{i,j}$

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

$\min _{X\in P}\langle F,XDX^{T}\rangle$

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

Dynamic Program
Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

$min\sum _{i=1}^{n}\sum _{j=1}^{n}c{_{\phi (i)\phi (j)}}+\sum _{i=1}^{n}b{_{\phi (i)}}$

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

$D={\begin{bmatrix}0&5&6\\5&0&3.6\\6&3.6&0\end{bmatrix}}$

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

$E=\left\{E_{1},E_{2},...,E_{n}\right\}$

as well as a set of r points

$P_{1},P_{2},...,P_{r}$

In his paper he derives the below formula:

$min\sum _{1\leq i\leq j\leq n}^{}C_{ij}(d_{s(i)s(j))})$

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

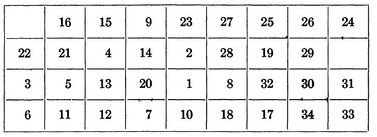
Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

$min\sum _{i,j}\sum _{k,q}f_{ik}d_{jq}y_{ij}y_{kq}$

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

$n!$

↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

Analysis of Algorithms
Backtracking
Dynamic Programming
Divide and Conquer
Geometric Algorithms
Mathematical Algorithms
Pattern Searching
Bitwise Algorithms
Branch & Bound
Randomized Algorithms
Art Gallery Problem
Transform and Conquer Technique
Implementation of Exact Cover Problem and Algorithm X using DLX
Preemptive Priority CPU Scheduling Algorithm
Introduction to Exact Cover Problem and Algorithm X
Introduction to Grover's Algorithm
Approximation Algorithms
What Does Big O(N^2) Complexity Mean?
How to develop an Algorithm from Scratch | Develop Algorithmic Thinking
Algorithm definition and meaning
Representation Change in Transform and Conquer Technique
How to write a Pseudo Code?
Print numbers 1 to N using Indirect recursion
Genetic Algorithms
The Role of Algorithms in Computing
Trial division Algorithm for Prime Factorization
Mo's Algo with update and without update
Instance Simplification Method in Transform and Conquer Technique
Make n using 1s and 2s with minimum number of terms multiple of k

Quadratic Assignment Problem (QAP)

The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.

The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.

The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.

The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.

There are various types of algorithms for different problem structures, such as:

Precise algorithms
Approximation algorithms
Metaheuristics like genetic algorithms and simulated annealing
Specialized algorithms

Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.

Facilities cost matrix:

Flow matrix:

To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.

The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.

The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.

To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.

Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.

Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

scipy.optimize.linear_sum_assignment #

Solve the linear sum assignment problem.

The cost matrix of the bipartite graph.

Calculates a maximum weight matching if true.

An array of row indices and one of corresponding column indices giving the optimal assignment. The cost of the assignment can be computed as cost_matrix[row_ind, col_ind].sum() . The row indices will be sorted; in the case of a square cost matrix they will be equal to numpy.arange(cost_matrix.shape[0]) .

for sparse inputs

The linear sum assignment problem [1] is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a ‘worker’) and vertex j of the second set (a ‘job’). The goal is to find a complete assignment of workers to jobs of minimal cost.

Formally, let X be a boolean matrix where $X[i,j] = 1$ iff row i is assigned to column j. Then the optimal assignment has cost

where, in the case where the matrix X is square, each row is assigned to exactly one column, and each column to exactly one row.

This function can also solve a generalization of the classic assignment problem where the cost matrix is rectangular. If it has more rows than columns, then not every row needs to be assigned to a column, and vice versa.

This implementation is a modified Jonker-Volgenant algorithm with no initialization, described in ref. [2] .

New in version 0.17.0.

https://en.wikipedia.org/wiki/Assignment_problem

DF Crouse. On implementing 2D rectangular assignment algorithms. IEEE Transactions on Aerospace and Electronic Systems , 52(4):1679-1696, August 2016, DOI:10.1109/TAES.2016.140952

Systems of Linear and Quadratic Equations

A System of those two equations can be solved (find where they intersect), either:

Graphically (by plotting them both on the Function Grapher and zooming in)
or using Algebra

How to Solve using Algebra

Make both equations into "y =" format

Set them equal to each other

Simplify into "= 0" format (like a standard Quadratic Equation)

Solve the Quadratic Equation!

Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers

An example will help:

Example: Solve these two equations:

y = x 2 - 5x + 7

Make both equations into "y=" format:

They are both in "y=" format, so go straight to next step

(The hardest part for me)

You can read how to solve Quadratic Equations , but here we will factor the Quadratic Equation :

Which gives us the solutions x=1 and x=6

The matching y values are (also see Graph):

for x= 1 : y = 2x+1 = 3
for x= 6 : y = 2x+1 = 13

Our solution: the two points are (1,3) and (6,13)

I think of it as three stages:

Combine into Quadratic Equation ⇒ Solve the Quadratic ⇒ Calculate the points

There are three possible cases:

No real solution (happens when they never intersect)
One real solution (when the straight line just touches the quadratic)
Two real solutions (like the example above)

Time for another example!

y - x 2 = 7 - 5x
4y - 8x = -21

First equation is: y - x 2 = 7 - 5x

Second equation is: 4y - 8x = -21

Using the Quadratic Formula from Quadratic Equations :

x = [ -b ± √(b 2 -4ac) ] / 2a
x = [ 7 ± √((-7) 2 -4×1×12.25) ] / 2×1
x = [ 7 ± √(49-49) ] / 2
x = [ 7 ± √0 ] / 2

Just one solution! (The "discriminant" is 0)

The matching y value is:

for x= 3.5 : y = 2x-5.25 = 1.75

Our solution: (3.5,1.75)

Real World Example

The cannon ball flies through the air, following a parabola:

y = 2 + 0.12x - 0.002x 2

The land slopes upward: y = 0.15x

Where does the cannon ball land?

Both equations are already in the "y =" format, so set them equal to each other:

Simplify into "= 0" format:

Solve the Quadratic Equation:

The negative answer can be ignored, so x = 25

Use the linear equation to calculate matching "y" value:

So the cannonball impacts the slope at (25, 3.75)

You can also find the answer graphically by using the Function Grapher :

Both Variables Squared

Sometimes BOTH terms of the quadratic can be squared:

Example: Find the points of intersection of

The circle x 2 + y 2 = 25

And the straight line 3y - 2x = 6

First put the line in "y=" format:

NOW, Instead of making the circle into "y=" format, we can use substitution (replace "y" in the quadratic with the linear expression):

Now it is in standard Quadratic form, let's solve it:

Now work out y-values:

So one point is (3, 4)
3y + 126/13 = 6
y + 42/13 = 2
y = 2 - 42/13 = 26/13 - 42/13 = -16/13
So the other point is (-63/13, -16/13)

Solving the quadratic assignment problem by means of general purpose mixed integer linear programming solvers

Published: 07 February 2012
Volume 207 , pages 261–278, ( 2013 )

Cite this article

Huizhen Zhang 1 , 2 ,
Cesar Beltran-Royo 1 &
Liang Ma 2

795 Accesses

18 Citations

Explore all metrics

The Quadratic Assignment Problem (QAP) can be solved by linearization, where one formulates the QAP as a mixed integer linear programming (MILP) problem. On the one hand, most of these linearizations are tight, but rarely exploited within a reasonable computing time because of their size. On the other hand, Kaufman and Broeckx formulation (Eur. J. Oper. Res. 2(3):204–211, 1978 ) is the smallest of these linearizations, but very weak. In this paper, we analyze how the Kaufman and Broeckx formulation can be tightened to obtain better QAP-MILP formulations. As shown in our numerical experiments, these tightened formulations remain small but computationally effective to solve the QAP by means of general purpose MILP solvers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

A partial Bregman ADMM with a general relaxation factor for structured nonconvex and nonsmooth optimization

Jianghua Yin, Chunming Tang, … Qiongxuan Huang

Survey on Lagrangian relaxation for MILP: importance, challenges, historical review, recent advancements, and opportunities

Mikhail A. Bragin

The Frank-Wolfe Algorithm: A Short Introduction

Sebastian Pokutta

Adams, W. P., Guignard, M., Hahn, P. M., & Hightower, W. L. (2007). A level-2 reformulation-linearization technique bound for the quadratic assignment problem. European Journal of Operational Research , 180 (3), 983–996.

Article Google Scholar

Adams, W. P., & Johnson, T. A. (1994). Improved linear programming-based lower bounds for the quadratic assignment problem. In DIMACS series in discrete mathematics and theoretical computer science (Vol. 16 , pp. 43–75), Providence: American Mathematical Society.

Google Scholar

Baotic, M. (2004). Matlab interface for CPLEX, http://control.ee.ethz.ch/~hybrid/cplexint.php .

Burkard, R. E., Dell’Amico, M., & Martello, S. (2009). Assignment problems (pp. 203–304). Philadelphia: SIAM.

Book Google Scholar

Burkard, R. E., Karisch, S. E., & Rendl, F. (1997). QAPLIB —a quadratic assignment problem library. Journal of Global Optimization , 10 (4), 391–403. http://www.seas.upenn.edu/qaplib/ .

Drezner, Z., Hahn, P. M., & Taillard, É. D. (2005). Recent advances for the quadratic assignment problem with special emphasis on instances that are difficult for meta-heuristic methods. Annals of Operations Research , 139 (1), 65–94.

Eschermann, B., & Wunderlich, H. J. (1990). Optimized synthesis of self-testable finite state machines. In 20th international symposium on fault-tolerant computing (FTCS 20) , Newcastle Upon Tyne, UK, June.

Fischetti, M., Monaci, M., & Salvagnin, D. (2012). Three ideas for the quadratic assignment problem. Operations Research , in press.

Gilmore, P. C. (1962). Optimal and suboptimal algorithms for the quadratic assignment problem. Journal of the Society for Industrial and Applied Mathematics , 10 (2), 305–313.

Hahn, P., & Grant, T. (1998). Lower bounds for the quadratic assignment problem based upon a dual formulation. Operations Research , 46 (6), 912–922.

Kaufman, L., & Broeckx, F. (1978). An algorithm for the quadratic assignment problem using Benders’ decomposition. European Journal of Operational Research , 2 (3), 204–211.

Koopmans, T. C., & Beckmann, M. J. (1957). Assignment problems and the location of economic activities. Econometrica. Journal of the Econometric Society , 25 (1), 53–76.

Lawler, E. L. (1963). The quadratic assignment problem. Management Science , 9 (4), 586–599.

Loiola, E. M., Abreu, N. M. M., Boaventura-Netto, P. O., Hahn, P., & Querido, T. (2007). A survey for the quadratic assignment problem. European Journal of Operational Research , 176 (2), 657–690.

Peng, J., Mittelmann, H., & Li, X. (2010). A new relaxation framework for quadratic assignment problems based on matrix splitting. Mathematical Programming Computation , 2 (1), 59–77.

Xia, Y., & Yuan, Y. X. (2006). A new linearization method for quadratic assignment problems. Optimization Methods and Software , 21 (5), 805–818.

Zhang, H. Z., Beltran-Royo, C., & Constantino, M. (2010). Effective formulation reductions for the quadratic assignment problem. Computers and Operations Research , 37 (11), 2007–2016.

Zhang, H. Z., Beltran-Royo, C., & Ma, L. (2010). Solving the quadratic assignment problem by means of general purpose mixed integer linear programming solvers. http://www.optimization-online.org/DB_HTML/2010/05/2622.html , pp. 1–16.

Download references

Acknowledgements

Thanks are due to the support of the National Natural Science Foundation of China (Grant No. 70871081), and to the support from MAEC-AECID fellowship from the Spanish government. We wish to thank the Faculty of Sciences of the University of Lisbon for providing the software Cplex 11.2. We also thank the support of the grant S2009/esp-1594 from the ‘Comunidad de Madrid’ (Spain) and the grant MTM2009-14039-C06-03 from the Spanish government.

Author information

Authors and affiliations.

Statistics and Operations Research, Rey Juan Carlos University, Madrid, Spain

Huizhen Zhang & Cesar Beltran-Royo

School of Management, University of Shanghai for Science and Technology, Shanghai, China

Huizhen Zhang & Liang Ma

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huizhen Zhang .

Rights and permissions

Reprints and permissions

About this article

Zhang, H., Beltran-Royo, C. & Ma, L. Solving the quadratic assignment problem by means of general purpose mixed integer linear programming solvers. Ann Oper Res 207 , 261–278 (2013). https://doi.org/10.1007/s10479-012-1079-4

Download citation

Published : 07 February 2012

Issue Date : August 2013

DOI : https://doi.org/10.1007/s10479-012-1079-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quadratic assignment problem
Mixed integer linear programming
Find a journal
Publish with us
Track your research

IMAGES

PPT
PPT
Solve Linear-Quadratic System
Algebra 2 Quadratic Equations Worksheet
Quadratic Assignment Problem Example
Solve a Linear-Quadratic System by Graphing

VIDEO

Quadratic assignment discussion 3 27 24
#Job, #Quadratic Assignment Problem |Lect-18 |Unit-IV -Analysis of Algorithm -Sem-V |by #Aryacollege
QUADRATIC QUESTION FOR JEE ADVANCED
quadratic from linear algebra
Introduction to optimization Quadratic Assignment Problem QAP
The Best Way to Solve Quadratic Word Problems

COMMENTS

Quadratic assignment problem
The quadratic assignment problem (QAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems first introduced by Koopmans and Beckmann.. The problem models the following real-life problem: There are a set of n facilities and a set of n locations.
Quadratic assignment problem
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 ... in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be ...
Quadratic Assignment Problem (QAP)
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance ...
A comprehensive review of quadratic assignment problem: variants
The quadratic assignment problem (QAP) has considered one of the most significant combinatorial optimization problems due to its variant and significant applications in real life such as scheduling, production, computer manufacture, chemistry, facility location, communication, and other fields. ... 3.1 Linear assignment problem (LAP) LAP is one ...
Quadratic Assignment Problem
The quadratic assignment problem (QAP) is a combinatorial optimization problem, that although there is a substantial amount of research devoted to it, it is still, up to this date, not well solvable in the sense that no exact algorithm can solve problems of size n > 20 in reasonable computational time. The QAP can be viewed as a natural extension of the linear assignment problem (LAP; cf. also ...
PDF The Quadratic Assignment Problem
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the ... contrast with its linear counterpart the linear assignment problem (LAP ...
Quadratic Assignment Problems
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of indivisible economical activities [].Consider the problem of allocating n facilities to n locations, with the cost being a function of the distance and flow between the facilities plus costs associated with placing a facility at a certain location.
A survey for the quadratic assignment problem
The quadratic assignment problem (QAP) is an extremely challenging NP-hard combinatorial optimization program. ... Included within this emphasis are instances which are linearizable; that is, which can be rewritten as a linear assignment problem having the property that the objective function value is preserved at all feasible solutions ...
Linear programming insights into solvable cases of the quadratic
The quadratic assignment problem is an NP-hard discrete optimization program that has been extensively studied for over 50 years. It has a variety of applications in many fields, but has proven itself extremely challenging to solve. As a result, an area of research has been to identify special cases which admit efficient solution strategies.
Assignment problem
The assignment problem is a special case of the transportation problem, which is a special case of the minimum cost flow problem, which in turn is a special case of a linear program. While it is possible to solve any of these problems using the simplex algorithm , each specialization has a smaller solution space and thus more efficient ...
PDF Exact extended formulation of the linear assignment problem (LAP
tours. It can be solved optimally using any linear programming (LP) solver, hence o ering a new (incidental) proof of the equality of the computational complexity classes \P" and \NP." The extensions of the model to the time-dependent traveling salesman problem (TDTSP) as well as the quadratic assignment problem (QAP) are straightforward.
A new exact discrete linear reformulation of the quadratic assignment
The quadratic assignment problem (QAP) is a challenging combinatorial problem. The problem is NP-hard and in addition, it is considered practically intractable to solve large QAP instances, to proven optimality, within reasonable time limits. In this paper we present an attractive mixed integer linear programming (MILP) formulation of the QAP.
The Quadratic Assignment Problem
hence the name "Quadratic Assignment Problem". The constraints are identical to those of the linear assignment problem (Burkard and Cela 1999) but the objective function is quadratic rather than linear. The QAP was proven to be NP-hard by Sahni and Gonzalez ().Even obtaining an ε-approximation for a given ε > 0 cannot be done in polynomial time unless P = NP.
PDF Computing Lower Bounds for the Quadratic Assignment Problem ...
even moderate values of n, the resulting linear programs are large, by today's standards. For example, to compute the LP-based bound for a quadratic assignment problem of dimension n = 30, requires the solution of a linear program with 52,260 constraints and 379,350 variables. To solve linear programs up to this size, we apply an
Quadratic functions & equations
Solve by completing the square: Non-integer solutions. Worked example: completing the square (leading coefficient ≠ 1) Solving quadratics by completing the square: no solution. Proof of the quadratic formula. Solving quadratics by completing the square. Completing the square review. Quadratic formula proof review.
[PDF] Solving the quadratic assignment problem by means of general
The Quadratic Assignment Problem (QAP) can be solved by linearization, where one formulates the QAP as a mixed integer linear programming (MILP) problem. On the one hand, most of these linearizations are tight, but rarely exploited within a reasonable computing time because of their size. On the other hand, Kaufman and Broeckx formulation (Eur ...
Quadratic assignment problem variants: A survey and an effective
The assignment problem, with applications in supply chains, healthcare logistics, and production scheduling, represents a prominent optimization challenge. This paper focuses on addressing the Generalized Quadratic Assignment Problem (GQAP), a well-known NP-hard combinatorial optimization problem. To tackle the GQAP, we propose an OR analytical ...
[PDF] The quadratic assignment problem: the linearization of Xia and
The quadratic assignment problem is a well-known optimization problem with numerous applications. A common strategy to solve it is to use one of its linearizations and then apply the toolbox of mixed integer linear programming methods. One measure of quality of a mixed integer formulation is the quality of its linear relaxation. In this paper, we compare two linearizations of the quadratic ...
(PDF) The Quadratic Assignment Problem
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the ...
The Quadratic Assignment Problem
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. ... Improved linear programming-based lower bounds for the quadratic assignment problem, in Quadratic Assignment and Related Problems, P. M. Pardalos and H ...
scipy.optimize.linear_sum_assignment
The linear sum assignment problem is also known as minimum weight matching in bipartite graphs. A problem instance is described by a matrix C, where each C[i,j] is the cost of matching vertex i of the first partite set (a 'worker') and vertex j of the second set (a 'job'). ... scipy.optimize.quadratic_assignment. On this page linear_sum ...
Systems of Linear and Quadratic Equations
Solve the Quadratic Equation! Use the linear equation to calculate matching "y" values, so we get (x,y) points as answers; An example will help: Example: Solve these two equations: y = x 2 - 5x + 7; y = 2x + 1 . Make both equations into "y=" format: They are both in "y=" format, so go straight to next step .
Solving the quadratic assignment problem by means of general ...
The Quadratic Assignment Problem (QAP) can be solved by linearization, where one formulates the QAP as a mixed integer linear programming (MILP) problem. On the one hand, most of these linearizations are tight, but rarely exploited within a reasonable computing time because of their size. On the other hand, Kaufman and Broeckx formulation (Eur. J. Oper. Res. 2(3):204-211, 1978) is the ...