5.2 Properties of Exponents and Scientific Notation
Learning objectives.
- Simplify expressions using the properties for exponents
- Use the definition of a negative exponent
- Use scientific notation

Be Prepared 5.2
Before you get started, take this readiness quiz.
- Simplify: ( −2 ) ( −2 ) ( −2 ) . ( −2 ) ( −2 ) ( −2 ) . If you missed this problem, review Example 1.19 .
- Simplify: 8 x 24 y . 8 x 24 y . If you missed this problem, review Example 1.24 .
- Name the decimal ( −2.6 ) ( 4.21 ) . ( −2.6 ) ( 4.21 ) . If you missed this problem, review Example 1.36 .
Simplify Expressions Using the Properties for Exponents
Remember that an exponent indicates repeated multiplication of the same quantity. For example, in the expression a m , a m , the exponent m tells us how many times we use the base a as a factor.
Let’s review the vocabulary for expressions with exponents.
Exponential Notation
This is read a to the m t h m t h power.
In the expression a m , a m , the exponent m tells us how many times we use the base a as a factor.
When we combine like terms by adding and subtracting, we need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too.
First, we will look at an example that leads to the Product Property .
Notice that 5 is the sum of the exponents, 2 and 3. We see x 2 · x 3 x 2 · x 3 is x 2 + 3 x 2 + 3 or x 5 . x 5 .
The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.
Product Property for Exponents
If a is a real number and m and n are integers, then
To multiply with like bases, add the exponents.
Example 5.12
Simplify each expression: ⓐ y 5 · y 6 y 5 · y 6 ⓑ 2 x · 2 3 x 2 x · 2 3 x ⓒ 2 a 7 · 3 a . 2 a 7 · 3 a .
Try It 5.23
Simplify each expression:
ⓐ b 9 · b 8 b 9 · b 8 ⓑ 4 2 x · 4 x 4 2 x · 4 x ⓒ 3 p 5 · 4 p 3 p 5 · 4 p ⓓ x 6 · x 4 · x 8 . x 6 · x 4 · x 8 .
Try It 5.24
ⓐ x 12 · x 4 x 12 · x 4 ⓑ 10 · 10 x 10 · 10 x ⓒ 2 z · 6 z 7 2 z · 6 z 7 ⓓ b 5 · b 9 · b 5 . b 5 · b 9 · b 5 .
Now we will look at an exponent property for division. As before, we’ll try to discover a property by looking at some examples.
Notice, in each case the bases were the same and we subtracted exponents. We see x 5 x 2 x 5 x 2 is x 5 − 2 x 5 − 2 or x 3 x 3 . We see x 2 x 3 x 2 x 3 is or 1 x . 1 x . When the larger exponent was in the numerator, we were left with factors in the numerator. When the larger exponent was in the denominator, we were left with factors in the denominator--notice the numerator of 1. When all the factors in the numerator have been removed, remember this is really dividing the factors to one, and so we need a 1 in the numerator. x x = 1 x x = 1 . This leads to the Quotient Property for Exponents.
Quotient Property for Exponents
If a is a real number, a ≠ 0 , a ≠ 0 , and m and n are integers, then
Example 5.13
Simplify each expression: ⓐ x 9 x 7 x 9 x 7 ⓑ 3 10 3 2 3 10 3 2 ⓒ b 8 b 12 b 8 b 12 ⓓ 7 3 7 5 . 7 3 7 5 .
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
Notice that when the larger exponent is in the numerator, we are left with factors in the numerator.
Notice that when the larger exponent is in the denominator, we are left with factors in the denominator.
Try It 5.25
Simplify each expression: ⓐ x 15 x 10 x 15 x 10 ⓑ 6 14 6 5 6 14 6 5 ⓒ x 18 x 22 x 18 x 22 ⓓ 12 15 12 30 . 12 15 12 30 .
Try It 5.26
Simplify each expression: ⓐ y 43 y 37 y 43 y 37 ⓑ 10 15 10 7 10 15 10 7 ⓒ m 7 m 15 m 7 m 15 ⓓ 9 8 9 19 . 9 8 9 19 .
A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like a m a m . a m a m . We know , x x = 1 , , x x = 1 , for any x ( x ≠ 0 ) x ( x ≠ 0 ) since any number divided by itself is 1.
The Quotient Property for Exponents shows us how to simplify a m a m . a m a m . when m > n m > n and when n < m n < m by subtracting exponents. What if m = n ? m = n ? We will simplify a m a m a m a m in two ways to lead us to the definition of the Zero Exponent Property . In general, for a ≠ 0 : a ≠ 0 :
We see a m a m a m a m simplifies to a 0 a 0 and to 1. So a 0 = 1 . a 0 = 1 . Any non-zero base raised to the power of zero equals 1.
Zero Exponent Property
If a is a non-zero number, then a 0 = 1 . a 0 = 1 .
If a is a non-zero number, then a to the power of zero equals 1.
Any non-zero number raised to the zero power is 1.
In this text, we assume any variable that we raise to the zero power is not zero.
Example 5.14
Simplify each expression: ⓐ 9 0 9 0 ⓑ n 0 . n 0 .
The definition says any non-zero number raised to the zero power is 1.
ⓐ 9 0 Use the definition of the zero exponent. 1 9 0 Use the definition of the zero exponent. 1
ⓑ n 0 Use the definition of the zero exponent. 1 n 0 Use the definition of the zero exponent. 1
To simplify the expression n raised to the zero power we just use the definition of the zero exponent. The result is 1.
Try It 5.27
Simplify each expression: ⓐ 11 0 11 0 ⓑ q 0 . q 0 .
Try It 5.28
Simplify each expression: ⓐ 23 0 23 0 ⓑ r 0 . r 0 .
Use the Definition of a Negative Exponent
We saw that the Quotient Property for Exponents has two forms depending on whether the exponent is larger in the numerator or the denominator. What if we just subtract exponents regardless of which is larger?
Let’s consider x 2 x 5 . x 2 x 5 . We subtract the exponent in the denominator from the exponent in the numerator. We see x 2 x 5 x 2 x 5 is x 2 − 5 x 2 − 5 or x −3 . x −3 .
We can also simplify x 2 x 5 x 2 x 5 by dividing out common factors:
This implies that x −3 = 1 x 3 x −3 = 1 x 3 and it leads us to the definition of a negative exponent . If n is an integer and a ≠ 0 , a ≠ 0 , then a − n = 1 a n . a − n = 1 a n .
Let’s now look at what happens to a fraction whose numerator is one and whose denominator is an integer raised to a negative exponent.
1 a − n Use the definition of a negative exponent, a − n = 1 a n . 1 1 a n Simplify the complex fraction. 1 · a n 1 Multiply. a n 1 a − n Use the definition of a negative exponent, a − n = 1 a n . 1 1 a n Simplify the complex fraction. 1 · a n 1 Multiply. a n
This implies 1 a − n = a n 1 a − n = a n and is another form of the definition of Properties of Negative Exponents .
Properties of Negative Exponents
If n is an integer and a ≠ 0 , a ≠ 0 , then a − n = 1 a n a − n = 1 a n or 1 a − n = a n . 1 a − n = a n .
The negative exponent tells us we can rewrite the expression by taking the reciprocal of the base and then changing the sign of the exponent.
Any expression that has negative exponents is not considered to be in simplest form. We will use the definition of a negative exponent and other properties of exponents to write the expression with only positive exponents.
For example, if after simplifying an expression we end up with the expression x −3 , x −3 , we will take one more step and write 1 x 3 . 1 x 3 . The answer is considered to be in simplest form when it has only positive exponents.
Example 5.15
Simplify each expression: ⓐ x −5 x −5 ⓑ 10 −3 10 −3 ⓒ 1 y −4 1 y −4 ⓓ 1 3 −2 . 1 3 −2 .
ⓐ x −5 Use the definition of a negative exponent, a − n = 1 a n . 1 x 5 x −5 Use the definition of a negative exponent, a − n = 1 a n . 1 x 5
ⓑ 10 −3 Use the definition of a negative exponent, a − n = 1 a n . 1 10 3 Simplify. 1 1000 10 −3 Use the definition of a negative exponent, a − n = 1 a n . 1 10 3 Simplify. 1 1000
ⓒ 1 y −4 Use the property of a negative exponent, 1 a − n = a n . y 4 1 y −4 Use the property of a negative exponent, 1 a − n = a n . y 4
ⓓ 1 3 −2 Use the property of a negative exponent, 1 a − n = a n . 3 2 Simplify. 9 1 3 −2 Use the property of a negative exponent, 1 a − n = a n . 3 2 Simplify. 9
Try It 5.29
Simplify each expression: ⓐ z −3 z −3 ⓑ 10 −7 10 −7 ⓒ 1 p −8 1 p −8 ⓓ 1 4 −3 . 1 4 −3 .
Try It 5.30
Simplify each expression: ⓐ n −2 n −2 ⓑ 10 −4 10 −4 ⓒ 1 q −7 1 q −7 ⓓ 1 2 −4 . 1 2 −4 .
Suppose now we have a fraction raised to a negative exponent. Let’s use our definition of negative exponents to lead us to a new property.
( 3 4 ) −2 Use the definition of a negative exponent, a − n = 1 a n . 1 ( 3 4 ) 2 Simplify the denominator. 1 9 16 Simplify the complex fraction. 16 9 But we know that 16 9 is ( 4 3 ) 2 . This tells us that ( 3 4 ) −2 = ( 4 3 ) 2 ( 3 4 ) −2 Use the definition of a negative exponent, a − n = 1 a n . 1 ( 3 4 ) 2 Simplify the denominator. 1 9 16 Simplify the complex fraction. 16 9 But we know that 16 9 is ( 4 3 ) 2 . This tells us that ( 3 4 ) −2 = ( 4 3 ) 2
To get from the original fraction raised to a negative exponent to the final result, we took the reciprocal of the base—the fraction—and changed the sign of the exponent.
This leads us to the Quotient to a Negative Power Property .
Quotient to a Negative Power Property
If a and b are real numbers, a ≠ 0 , b ≠ 0 a ≠ 0 , b ≠ 0 and n is an integer, then
Example 5.16
Simplify each expression: ⓐ ( 5 7 ) −2 ( 5 7 ) −2 ⓑ ( − x y ) −3 . ( − x y ) −3 .
ⓐ ( 5 7 ) −2 Use the Quotient to a Negative Exponent Property, ( a b ) − n = ( b a ) n . Take the reciprocal of the fraction and change the sign of the exponent. ( 7 5 ) 2 Simplify. 49 25 ( 5 7 ) −2 Use the Quotient to a Negative Exponent Property, ( a b ) − n = ( b a ) n . Take the reciprocal of the fraction and change the sign of the exponent. ( 7 5 ) 2 Simplify. 49 25
ⓑ ( − x y ) −3 Use the Quotient to a Negative Exponent Property, ( a b ) − n = ( b a ) n . Take the reciprocal of the fraction and change the sign of the exponent. ( − y x ) 3 Simplify. − y 3 x 3 ( − x y ) −3 Use the Quotient to a Negative Exponent Property, ( a b ) − n = ( b a ) n . Take the reciprocal of the fraction and change the sign of the exponent. ( − y x ) 3 Simplify. − y 3 x 3
Try It 5.31
Simplify each expression: ⓐ ( 2 3 ) −4 ( 2 3 ) −4 ⓑ ( − m n ) −2 . ( − m n ) −2 .
Try It 5.32
Simplify each expression: ⓐ ( 3 5 ) −3 ( 3 5 ) −3 ⓑ ( − a b ) −4 . ( − a b ) −4 .
Now that we have negative exponents, we will use the Product Property with expressions that have negative exponents.
Example 5.17
Simplify each expression: ⓐ z −5 · z −3 z −5 · z −3 ⓑ ( m 4 n −3 ) ( m −5 n −2 ) ( m 4 n −3 ) ( m −5 n −2 ) ⓒ ( 2 x −6 y 8 ) ( −5 x 5 y −3 ) . ( 2 x −6 y 8 ) ( −5 x 5 y −3 ) .
ⓐ z −5 · z −3 Add the exponents, since the bases are the same. z −5 − 3 Simplify. z −8 Use the definition of a negative exponent. 1 z 8 z −5 · z −3 Add the exponents, since the bases are the same. z −5 − 3 Simplify. z −8 Use the definition of a negative exponent. 1 z 8
ⓑ ( m 4 n −3 ) ( m −5 n −2 ) Use the Commutative Property to get like bases together. m 4 m −5 · n −2 n −3 Add the exponents for each base. m −1 · n −5 Take reciprocals and change the signs of the exponents. 1 m 1 · 1 n 5 Simplify. 1 m n 5 ( m 4 n −3 ) ( m −5 n −2 ) Use the Commutative Property to get like bases together. m 4 m −5 · n −2 n −3 Add the exponents for each base. m −1 · n −5 Take reciprocals and change the signs of the exponents. 1 m 1 · 1 n 5 Simplify. 1 m n 5
ⓒ ( 2 x −6 y 8 ) ( −5 x 5 y −3 ) Rewrite with the like bases together. 2 ( −5 ) · ( x −6 x 5 ) · ( y 8 y −3 ) Multiply the coefficients and add the exponents of each variable. −10 · x −1 · y 5 Use the definition of a negative exponent, a − n = 1 a n . −10 · 1 x · y 5 Simplify. −10 y 5 x ( 2 x −6 y 8 ) ( −5 x 5 y −3 ) Rewrite with the like bases together. 2 ( −5 ) · ( x −6 x 5 ) · ( y 8 y −3 ) Multiply the coefficients and add the exponents of each variable. −10 · x −1 · y 5 Use the definition of a negative exponent, a − n = 1 a n . −10 · 1 x · y 5 Simplify. −10 y 5 x
Try It 5.33
ⓐ z −4 · z −5 z −4 · z −5 ⓑ ( p 6 q −2 ) ( p −9 q −1 ) ( p 6 q −2 ) ( p −9 q −1 ) ⓒ ( 3 u −5 v 7 ) ( −4 u 4 v −2 ) . ( 3 u −5 v 7 ) ( −4 u 4 v −2 ) .
Try It 5.34
ⓐ c −8 · c −7 c −8 · c −7 ⓑ ( r 5 s −3 ) ( r −7 s −5 ) ( r 5 s −3 ) ( r −7 s −5 ) ⓒ ( −6 c −6 d 4 ) ( −5 c −2 d −1 ) . ( −6 c −6 d 4 ) ( −5 c −2 d −1 ) .
Now let’s look at an exponential expression that contains a power raised to a power. See if you can discover a general property.
( x 2 ) 3 What does this mean? x 2 · x 2 · x 2 ( x 2 ) 3 What does this mean? x 2 · x 2 · x 2
Notice the 6 is the product of the exponents, 2 and 3. We see that ( x 2 ) 3 ( x 2 ) 3 is x 2 · 3 x 2 · 3 or x 6 . x 6 .
We multiplied the exponents. This leads to the Power Property for Exponents.
Power Property for Exponents
To raise a power to a power, multiply the exponents.
Example 5.18
Simplify each expression: ⓐ ( y 5 ) 9 ( y 5 ) 9 ⓑ ( 4 4 ) 7 ( 4 4 ) 7 ⓒ ( y 3 ) 6 ( y 5 ) 4 . ( y 3 ) 6 ( y 5 ) 4 .
ⓒ ( y 3 ) 6 ( y 5 ) 4 Use the Power Property. y 18 · y 20 Add the exponents. y 38 ( y 3 ) 6 ( y 5 ) 4 Use the Power Property. y 18 · y 20 Add the exponents. y 38
Try It 5.35
Simplify each expression: ⓐ ( b 7 ) 5 ( b 7 ) 5 ⓑ ( 5 4 ) 3 ( 5 4 ) 3 ⓒ ( a 4 ) 5 ( a 7 ) 4 . ( a 4 ) 5 ( a 7 ) 4 .
Try It 5.36
Simplify each expression: ⓐ ( z 6 ) 9 ( z 6 ) 9 ⓑ ( 3 7 ) 7 ( 3 7 ) 7 ⓒ ( q 4 ) 5 ( q 3 ) 3 . ( q 4 ) 5 ( q 3 ) 3 .
We will now look at an expression containing a product that is raised to a power. Can you find this pattern?
( 2 x ) 3 What does this mean? 2 x · 2 x · 2 x We group the like factors together. 2 · 2 · 2 · x · x · x How many factors of 2 and of x 2 3 · x 3 ( 2 x ) 3 What does this mean? 2 x · 2 x · 2 x We group the like factors together. 2 · 2 · 2 · x · x · x How many factors of 2 and of x 2 3 · x 3
Notice that each factor was raised to the power and ( 2 x ) 3 ( 2 x ) 3 is 2 3 · x 3 . 2 3 · x 3 .
The exponent applies to each of the factors! This leads to the Product to a Power Property for Exponents .
Product to a Power Property for Exponents
If a and b are real numbers and m is a whole number, then
To raise a product to a power, raise each factor to that power.
Example 5.19
Simplify each expression: ⓐ ( −3 m n ) 3 ( −3 m n ) 3 ⓑ ( −4 a 2 b ) 0 ( −4 a 2 b ) 0 ⓒ ( 6 k 3 ) −2 ( 6 k 3 ) −2 ⓓ ( 5 x −3 ) 2 . ( 5 x −3 ) 2 .
ⓑ ( −4 a 2 b ) 0 Use Power of a Product Property, ( a b ) m = a m b m . ( −4 ) 0 ( a 2 ) 0 ( b ) 0 Simplify. 1 · 1 · 1 Multiply. 1 ( −4 a 2 b ) 0 Use Power of a Product Property, ( a b ) m = a m b m . ( −4 ) 0 ( a 2 ) 0 ( b ) 0 Simplify. 1 · 1 · 1 Multiply. 1
ⓒ ( 6 k 3 ) −2 Use the Product to a Power Property, ( a b ) m = a m b m . ( 6 ) −2 ( k 3 ) −2 Use the Power Property, ( a m ) n = a m · n . 6 −2 k −6 Use the Definition of a negative exponent, a − n = 1 a n . 1 6 2 · 1 k 6 Simplify. 1 36 k 6 ( 6 k 3 ) −2 Use the Product to a Power Property, ( a b ) m = a m b m . ( 6 ) −2 ( k 3 ) −2 Use the Power Property, ( a m ) n = a m · n . 6 −2 k −6 Use the Definition of a negative exponent, a − n = 1 a n . 1 6 2 · 1 k 6 Simplify. 1 36 k 6
ⓓ ( 5 x −3 ) 2 Use the Product to a Power Property, ( a b ) m = a m b m . 5 2 ( x −3 ) 2 Simplify. 25 · x −6 Rewrite x −6 using, a − n = 1 a n . 25 · 1 x 6 Simplify. 25 x 6 ( 5 x −3 ) 2 Use the Product to a Power Property, ( a b ) m = a m b m . 5 2 ( x −3 ) 2 Simplify. 25 · x −6 Rewrite x −6 using, a − n = 1 a n . 25 · 1 x 6 Simplify. 25 x 6
Try It 5.37
Simplify each expression: ⓐ ( 2 w x ) 5 ( 2 w x ) 5 ⓑ ( −11 p q 3 ) 0 ( −11 p q 3 ) 0 ⓒ ( 2 b 3 ) −4 ( 2 b 3 ) −4 ⓓ ( 8 a −4 ) 2 . ( 8 a −4 ) 2 .
Try It 5.38
Simplify each expression: ⓐ ( −3 y ) 3 ( −3 y ) 3 ⓑ ( −8 m 2 n 3 ) 0 ( −8 m 2 n 3 ) 0 ⓒ ( −4 x 4 ) −2 ( −4 x 4 ) −2 ⓓ ( 2 c −4 ) 3 . ( 2 c −4 ) 3 .
Now we will look at an example that will lead us to the Quotient to a Power Property.
( x y ) 3 This means x y · x y · x y Multiply the fractions. x · x · x y · y · y Write with exponents. x 3 y 3 ( x y ) 3 This means x y · x y · x y Multiply the fractions. x · x · x y · y · y Write with exponents. x 3 y 3
Notice that the exponent applies to both the numerator and the denominator.
We see that ( x y ) 3 ( x y ) 3 is x 3 y 3 . x 3 y 3 .
This leads to the Quotient to a Power Property for Exponents .
Quotient to a Power Property for Exponents
If a a and b b are real numbers, b ≠ 0 , b ≠ 0 , and m m is an integer, then
To raise a fraction to a power, raise the numerator and denominator to that power.
Example 5.20
ⓐ ( b 3 ) 4 ( b 3 ) 4 ⓑ ( k j ) −3 ( k j ) −3 ⓒ ( 2 x y 2 z ) 3 ( 2 x y 2 z ) 3 ⓓ ( 4 p −3 q 2 ) 2 . ( 4 p −3 q 2 ) 2 .
ⓒ ( 2 x y 2 z ) 3 Use Quotient to a Power Property, ( a b ) m = a m b m . ( 2 x y 2 ) 3 z 3 Use the Product to a Power Property, ( a b ) m = a m b m . 8 x 3 y 6 z 3 ( 2 x y 2 z ) 3 Use Quotient to a Power Property, ( a b ) m = a m b m . ( 2 x y 2 ) 3 z 3 Use the Product to a Power Property, ( a b ) m = a m b m . 8 x 3 y 6 z 3
ⓓ ( 4 p −3 q 2 ) 2 Use Quotient to a Power Property, ( a b ) m = a m b m . ( 4 p −3 ) 2 ( q 2 ) 2 Use the Product to a Power Property, ( a b ) m = a m b m . 4 2 ( p −3 ) 2 ( q 2 ) 2 Simplify using the Power Property, ( a m ) n = a m · n . 16 p −6 q 4 Use the definition of negative exponent. 16 q 4 · 1 p 6 Simplify. 16 p 6 q 4 ( 4 p −3 q 2 ) 2 Use Quotient to a Power Property, ( a b ) m = a m b m . ( 4 p −3 ) 2 ( q 2 ) 2 Use the Product to a Power Property, ( a b ) m = a m b m . 4 2 ( p −3 ) 2 ( q 2 ) 2 Simplify using the Power Property, ( a m ) n = a m · n . 16 p −6 q 4 Use the definition of negative exponent. 16 q 4 · 1 p 6 Simplify. 16 p 6 q 4
Try It 5.39
ⓐ ( p 10 ) 4 ( p 10 ) 4 ⓑ ( m n ) −7 ( m n ) −7 ⓒ ( 3 a b 3 c 2 ) 4 ( 3 a b 3 c 2 ) 4 ⓓ ( 3 x −2 y 3 ) 3 . ( 3 x −2 y 3 ) 3 .
Try It 5.40
ⓐ ( −2 q ) 3 ( −2 q ) 3 ⓑ ( w x ) −4 ( w x ) −4 ⓒ ( x y 3 3 z 2 ) 2 ( x y 3 3 z 2 ) 2 ⓓ ( 2 m −2 n −2 ) 3 . ( 2 m −2 n −2 ) 3 .
We now have several properties for exponents. Let’s summarize them and then we’ll do some more examples that use more than one of the properties.
Summary of Exponent Properties
If a and b are real numbers, and m and n are integers, then
Example 5.21
Simplify each expression by applying several properties:
ⓐ ( 3 x 2 y ) 4 ( 2 x y 2 ) 3 ( 3 x 2 y ) 4 ( 2 x y 2 ) 3 ⓑ ( x 3 ) 4 ( x −2 ) 5 ( x 6 ) 5 ( x 3 ) 4 ( x −2 ) 5 ( x 6 ) 5 ⓒ ( 2 x y 2 x 3 y −2 ) 2 ( 12 x y 3 x 3 y −1 ) −1 . ( 2 x y 2 x 3 y −2 ) 2 ( 12 x y 3 x 3 y −1 ) −1 .
ⓐ ( 3 x 2 y ) 4 ( 2 x y 2 ) 3 Use the Product to a Power Property, ( a b ) m = a m b m . ( 3 4 x 8 y 4 ) ( 2 3 x 3 y 6 ) Simplify. ( 81 x 8 y 4 ) ( 8 x 3 y 6 ) Use the Commutative Property. 81 · 8 · x 8 · x 3 · y 4 · y 6 Multiply the constants and add the exponents. 648 x 11 y 10 ( 3 x 2 y ) 4 ( 2 x y 2 ) 3 Use the Product to a Power Property, ( a b ) m = a m b m . ( 3 4 x 8 y 4 ) ( 2 3 x 3 y 6 ) Simplify. ( 81 x 8 y 4 ) ( 8 x 3 y 6 ) Use the Commutative Property. 81 · 8 · x 8 · x 3 · y 4 · y 6 Multiply the constants and add the exponents. 648 x 11 y 10
ⓑ ( x 3 ) 4 ( x −2 ) 5 ( x 6 ) 5 Use the Power Property, ( a m ) n = a m · n . ( x 12 ) ( x −10 ) ( x 30 ) Add the exponents in the numerator. x 2 x 30 Use the Quotient Property, a m a n = 1 a n − m . 1 x 28 ( x 3 ) 4 ( x −2 ) 5 ( x 6 ) 5 Use the Power Property, ( a m ) n = a m · n . ( x 12 ) ( x −10 ) ( x 30 ) Add the exponents in the numerator. x 2 x 30 Use the Quotient Property, a m a n = 1 a n − m . 1 x 28
ⓒ ( 2 x y 2 x 3 y −2 ) 2 ( 12 x y 3 x 3 y −1 ) −1 Simplify inside the parentheses first. ( 2 y 4 x 2 ) 2 ( 12 y 4 x 2 ) −1 Use the Quotient to a Power Property, ( a b ) m = a m b m . ( 2 y 4 ) 2 ( x 2 ) 2 ( 12 y 4 ) −1 ( x 2 ) −1 Use the Product to a Power Property, ( a b ) m = a m b m . 4 y 8 x 4 · 12 −1 y −4 x −2 Simplify. 4 y 4 12 x 2 Simplify. y 4 3 x 2 ( 2 x y 2 x 3 y −2 ) 2 ( 12 x y 3 x 3 y −1 ) −1 Simplify inside the parentheses first. ( 2 y 4 x 2 ) 2 ( 12 y 4 x 2 ) −1 Use the Quotient to a Power Property, ( a b ) m = a m b m . ( 2 y 4 ) 2 ( x 2 ) 2 ( 12 y 4 ) −1 ( x 2 ) −1 Use the Product to a Power Property, ( a b ) m = a m b m . 4 y 8 x 4 · 12 −1 y −4 x −2 Simplify. 4 y 4 12 x 2 Simplify. y 4 3 x 2
Try It 5.41
ⓐ ( c 4 d 2 ) 5 ( 3 c d 5 ) 4 ( c 4 d 2 ) 5 ( 3 c d 5 ) 4 ⓑ ( a −2 ) 3 ( a 2 ) 4 ( a 4 ) 5 ( a −2 ) 3 ( a 2 ) 4 ( a 4 ) 5 ⓒ ( 3 x y 2 x 2 y −3 ) 2 ( 9 x y −3 x 3 y 2 ) −1 . ( 3 x y 2 x 2 y −3 ) 2 ( 9 x y −3 x 3 y 2 ) −1 .
Try It 5.42
ⓐ ( a 3 b 2 ) 6 ( 4 a b 3 ) 4 ( a 3 b 2 ) 6 ( 4 a b 3 ) 4 ⓑ ( p −3 ) 4 ( p 5 ) 3 ( p 7 ) 6 ( p −3 ) 4 ( p 5 ) 3 ( p 7 ) 6 ⓒ ( 4 x 3 y 2 x 2 y −1 ) 2 ( 8 x y −3 x 2 y ) −1 . ( 4 x 3 y 2 x 2 y −1 ) 2 ( 8 x y −3 x 2 y ) −1 .
Use Scientific Notation
Working with very large or very small numbers can be awkward. Since our number system is base ten we can use powers of ten to rewrite very large or very small numbers to make them easier to work with. Consider the numbers 4,000 and 0.004.
Using place value, we can rewrite the numbers 4,000 and 0.004. We know that 4,000 means 4 × 1,000 4 × 1,000 and 0.004 means 4 × 1 1,000 . 4 × 1 1,000 .
If we write the 1,000 as a power of ten in exponential form, we can rewrite these numbers in this way:
When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than ten, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation .
- Scientific Notation
A number is expressed in scientific notation when it is of the form
It is customary in scientific notation to use as the × × multiplication sign, even though we avoid using this sign elsewhere in algebra.
If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation.
In both cases, the decimal was moved 3 places to get the first factor between 1 and 10.
The power of 10 is positive when the number is larger than 1: 4,000 = 4 × 10 3 4,000 = 4 × 10 3
The power of 10 is negative when the number is between 0 and 1: 0.004 = 4 × 10 −3 0.004 = 4 × 10 −3
To convert a decimal to scientific notation.
- Step 1. Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Step 2. Count the number of decimal places, n , that the decimal point was moved.
- greater than 1, the power of 10 will be 10 n . 10 n .
- between 0 and 1, the power of 10 will be 10 − n . 10 − n .
- Step 4. Check.
Example 5.22
Write in scientific notation: ⓐ 37,000 ⓑ 0.0052 . 0.0052 .
Try It 5.43
Write in scientific notation: ⓐ 96,000 ⓑ 0.0078.
Try It 5.44
Write in scientific notation: ⓐ 48,300 ⓑ 0.0129.
How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.
If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.
In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.
Convert scientific notation to decimal form.
- Step 1. Determine the exponent, n , on the factor 10.
- If the exponent is positive, move the decimal point n places to the right.
- If the exponent is negative, move the decimal point | n | | n | places to the left.
- Step 3. Check.
Example 5.23
Convert to decimal form: ⓐ 6.2 × 10 3 6.2 × 10 3 ⓑ −8.9 × 10 −2 . −8.9 × 10 −2 .
Try It 5.45
Convert to decimal form: ⓐ 1.3 × 10 3 1.3 × 10 3 ⓑ −1.2 × 10 −4 . −1.2 × 10 −4 .
Try It 5.46
Convert to decimal form: ⓐ −9.5 × 10 4 −9.5 × 10 4 ⓑ 7.5 × 10 −2 . 7.5 × 10 −2 .
When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
Example 5.24
Multiply or divide as indicated. Write answers in decimal form: ⓐ ( −4 × 10 5 ) ( 2 × 10 −7 ) ( −4 × 10 5 ) ( 2 × 10 −7 ) ⓑ 9 × 10 3 3 × 10 −2 . 9 × 10 3 3 × 10 −2 .
ⓐ ( −4 × 10 5 ) ( 2 × 10 −7 ) Use the Commutative Property to rearrange the factors. −4 · 2 · 10 5 · 10 −7 Multiply. −8 × 10 −2 Change to decimal form by moving the decimal two places left. −0.08 ( −4 × 10 5 ) ( 2 × 10 −7 ) Use the Commutative Property to rearrange the factors. −4 · 2 · 10 5 · 10 −7 Multiply. −8 × 10 −2 Change to decimal form by moving the decimal two places left. −0.08
ⓑ 9 × 10 3 9 × 10 −2 Separate the factors, rewriting as the product of two fractions. 9 3 × 10 3 10 −2 Divide. 3 × 10 5 Change to decimal form by moving the decimal five places right. 300,000 9 × 10 3 9 × 10 −2 Separate the factors, rewriting as the product of two fractions. 9 3 × 10 3 10 −2 Divide. 3 × 10 5 Change to decimal form by moving the decimal five places right. 300,000
Try It 5.47
Multiply or divide as indicated. Write answers in decimal form:
ⓐ ( −3 × 10 5 ) ( 2 × 10 −8 ) ( −3 × 10 5 ) ( 2 × 10 −8 ) ⓑ 8 × 10 2 4 × 10 −2 . 8 × 10 2 4 × 10 −2 .
Try It 5.48
ⓐ ; ( −3 × 10 −2 ) ( 3 × 10 −1 ) ( −3 × 10 −2 ) ( 3 × 10 −1 ) ⓑ 8 × 10 4 2 × 10 −1 . 8 × 10 4 2 × 10 −1 .
Access these online resources for additional instruction and practice with using multiplication properties of exponents.
- Properties of Exponents
- Negative exponents
Section 5.2 Exercises
Practice makes perfect.
In the following exercises, simplify each expression using the properties for exponents.
ⓐ d 3 · d 6 d 3 · d 6 ⓑ 4 5 x · 4 9 x 4 5 x · 4 9 x ⓒ 2 y · 4 y 3 2 y · 4 y 3 ⓓ w · w 2 · w 3 w · w 2 · w 3
ⓐ x 4 · x 2 x 4 · x 2 ⓑ 8 9 x · 8 3 8 9 x · 8 3 ⓒ 3 z 25 · 5 z 8 3 z 25 · 5 z 8 ⓓ y · y 3 · y 5 y · y 3 · y 5
ⓐ n 19 · n 12 n 19 · n 12 ⓑ 3 x · 3 6 3 x · 3 6 ⓒ 7 w 5 · 8 w 7 w 5 · 8 w ⓓ a 4 · a 3 · a 9 a 4 · a 3 · a 9
ⓐ q 27 · q 15 q 27 · q 15 ⓑ 5 x · 5 4 x 5 x · 5 4 x ⓒ 9 u 41 · 7 u 53 9 u 41 · 7 u 53 ⓓ c 5 · c 11 · c 2 c 5 · c 11 · c 2
m x · m 3 m x · m 3
n y · n 2 n y · n 2
y a · y b y a · y b
x p · x q x p · x q
ⓐ x 18 x 3 x 18 x 3 ⓑ 5 12 5 3 5 12 5 3 ⓒ q 18 q 36 q 18 q 36 ⓓ 10 2 10 3 10 2 10 3
ⓐ y 20 y 10 y 20 y 10 ⓑ 7 16 7 2 7 16 7 2 ⓒ t 10 t 40 t 10 t 40 ⓓ 8 3 8 5 8 3 8 5
ⓐ p 21 p 7 p 21 p 7 ⓑ 4 16 4 4 4 16 4 4 ⓒ b b 9 b b 9 ⓓ 4 4 6 4 4 6
ⓐ u 24 u 3 u 24 u 3 ⓑ 9 15 9 5 9 15 9 5 ⓒ x x 7 x x 7 ⓓ 10 10 3 10 10 3
ⓐ 20 0 20 0 ⓑ b 0 b 0
ⓐ 13 0 13 0 ⓑ k 0 k 0
ⓐ − 27 0 − 27 0 ⓑ − ( 27 0 ) − ( 27 0 )
ⓐ − 15 0 − 15 0 ⓑ − ( 15 0 ) − ( 15 0 )
In the following exercises, simplify each expression.
ⓐ a −2 a −2 ⓑ 10 −3 10 −3 ⓒ 1 c −5 1 c −5 ⓓ 1 3 −2 1 3 −2
ⓐ b −4 b −4 ⓑ 10 −2 10 −2 ⓒ 1 c −5 1 c −5 ⓓ 1 5 −2 1 5 −2
ⓐ r −3 r −3 ⓑ 10 −5 10 −5 ⓒ 1 q −10 1 q −10 ⓓ 1 10 −3 1 10 −3
ⓐ s −8 s −8 ⓑ 10 −2 10 −2 ⓒ 1 t −9 1 t −9 ⓓ 1 10 −4 1 10 −4
ⓐ ( 5 8 ) −2 ( 5 8 ) −2 ⓑ ( − b a ) −2 ( − b a ) −2
ⓐ ( 3 10 ) −2 ( 3 10 ) −2 ⓑ ( − 2 z ) −3 ( − 2 z ) −3
ⓐ ( 4 9 ) −3 ( 4 9 ) −3 ⓑ ( − u v ) −5 ( − u v ) −5
ⓐ ( 7 2 ) −3 ( 7 2 ) −3 ⓑ ( − 3 x ) −3 ( − 3 x ) −3
ⓐ ( −5 ) −2 ( −5 ) −2 ⓑ − 5 −2 − 5 −2 ⓒ ( − 1 5 ) −2 ( − 1 5 ) −2 ⓓ − ( 1 5 ) −2 − ( 1 5 ) −2
ⓐ − 5 −3 − 5 −3 ⓑ ( − 1 5 ) −3 ( − 1 5 ) −3 ⓒ − ( 1 5 ) −3 − ( 1 5 ) −3 ⓓ ( −5 ) −3 ( −5 ) −3
ⓐ 3 · 5 −1 3 · 5 −1 ⓑ ( 3 · 5 ) −1 ( 3 · 5 ) −1
ⓐ 3 · 4 −2 3 · 4 −2 ⓑ ( 3 · 4 ) −2 ( 3 · 4 ) −2
In the following exercises, simplify each expression using the Product Property.
ⓐ b 4 b −8 b 4 b −8 ⓑ ( w 4 x −5 ) ( w −2 x −4 ) ( w 4 x −5 ) ( w −2 x −4 ) ⓒ ( −6 c −3 d 9 ) ( 2 c 4 d −5 ) ( −6 c −3 d 9 ) ( 2 c 4 d −5 )
ⓐ s 3 · s −7 s 3 · s −7 ⓑ ( m 3 n −3 ) ( m −5 n −1 ) ( m 3 n −3 ) ( m −5 n −1 ) ⓒ ( −2 j −5 k 8 ) ( 7 j 2 k −3 ) ( −2 j −5 k 8 ) ( 7 j 2 k −3 )
ⓐ a 3 · a −3 a 3 · a −3 ⓑ ( u v −2 ) ( u −5 v −3 ) ( u v −2 ) ( u −5 v −3 ) ⓒ ( −4 r −2 s −8 ) ( 9 r 4 s 3 ) ( −4 r −2 s −8 ) ( 9 r 4 s 3 )
ⓐ y 5 · y −5 y 5 · y −5 ⓑ ( p q −4 ) ( p −6 q −3 ) ( p q −4 ) ( p −6 q −3 ) ⓒ ( −5 m 4 n 6 ) ( 8 m −5 n −3 ) ( −5 m 4 n 6 ) ( 8 m −5 n −3 )
p 5 · p −2 · p −4 p 5 · p −2 · p −4
x 4 · x −2 · x −3 x 4 · x −2 · x −3
In the following exercises, simplify each expression using the Power Property.
ⓐ ( m 4 ) 2 ( m 4 ) 2 ⓑ ( 10 3 ) 6 ( 10 3 ) 6 ⓒ ( x 3 ) −4 ( x 3 ) −4
ⓐ ( b 2 ) 7 ( b 2 ) 7 ⓑ ( 3 8 ) 2 ( 3 8 ) 2 ⓒ ( k 2 ) −5 ( k 2 ) −5
ⓐ ( y 3 ) x ( y 3 ) x ⓑ ( 5 x ) y ( 5 x ) y ⓒ ( q 6 ) −8 ( q 6 ) −8
ⓐ ( x 2 ) y ( x 2 ) y ⓑ ( 7 a ) b ( 7 a ) b ⓒ ( a 9 ) −10 ( a 9 ) −10
In the following exercises, simplify each expression using the Product to a Power Property.
ⓐ ( −3 x y ) 2 ( −3 x y ) 2 ⓑ ( 6 a ) 0 ( 6 a ) 0 ⓒ ( 5 x 2 ) −2 ( 5 x 2 ) −2 ⓓ ( −4 y −3 ) 2 ( −4 y −3 ) 2
ⓐ ( −4 a b ) 2 ( −4 a b ) 2 ⓑ ( 5 x ) 0 ( 5 x ) 0 ⓒ ( 4 y 3 ) −3 ( 4 y 3 ) −3 ⓓ ( −7 y −3 ) 2 ( −7 y −3 ) 2
ⓐ ( −5 a b ) 3 ( −5 a b ) 3 ⓑ ( −4 p q ) 0 ( −4 p q ) 0 ⓒ ( −6 x 3 ) −2 ( −6 x 3 ) −2 ⓓ ( 3 y −4 ) 2 ( 3 y −4 ) 2
ⓐ ( −3 x y z ) 4 ( −3 x y z ) 4 ⓑ ( −7 m n ) 0 ( −7 m n ) 0 ⓒ ( −3 x 3 ) −2 ( −3 x 3 ) −2 ⓓ ( 2 y −5 ) 2 ( 2 y −5 ) 2
In the following exercises, simplify each expression using the Quotient to a Power Property.
ⓐ ( p 2 ) 5 ( p 2 ) 5 ⓑ ( x y ) −6 ( x y ) −6 ⓒ ( 2 x y 2 z ) 3 ( 2 x y 2 z ) 3 ⓓ ( 4 p −3 q 2 ) 2 ( 4 p −3 q 2 ) 2
ⓐ ( x 3 ) 4 ( x 3 ) 4 ⓑ ( a b ) −5 ( a b ) −5 ⓒ ( 2 x y 2 z ) 3 ( 2 x y 2 z ) 3 ⓓ ( x 3 y z 4 ) 2 ( x 3 y z 4 ) 2
ⓐ ( a 3 b ) 4 ( a 3 b ) 4 ⓑ ( 5 4 m ) −2 ( 5 4 m ) −2 ⓒ ( 3 a -2 b 3 c 3 ) -2 ( 3 a -2 b 3 c 3 ) -2 ⓓ ( p -1 q 4 r -4 ) 2 ( p -1 q 4 r -4 ) 2
ⓐ ( x 2 y ) 3 ( x 2 y ) 3 ⓑ ( 10 3 q ) −4 ( 10 3 q ) −4 ⓒ ( 2 x 3 y 4 3 z 2 ) 5 ( 2 x 3 y 4 3 z 2 ) 5 ⓓ ( 5 a 3 b -1 2 c 4 ) -3 ( 5 a 3 b -1 2 c 4 ) -3
In the following exercises, simplify each expression by applying several properties.
ⓐ ( 5 t 2 ) 3 ( 3 t ) 2 ( 5 t 2 ) 3 ( 3 t ) 2 ⓑ ( t 2 ) 5 ( t −4 ) 2 ( t 3 ) 7 ( t 2 ) 5 ( t −4 ) 2 ( t 3 ) 7 ⓒ ( 2 x y 2 x 3 y −2 ) 2 ( 12 x y 3 x 3 y −1 ) −1 ( 2 x y 2 x 3 y −2 ) 2 ( 12 x y 3 x 3 y −1 ) −1
ⓐ ( 10 k 4 ) 3 ( 5 k 6 ) 2 ( 10 k 4 ) 3 ( 5 k 6 ) 2 ⓑ ( q 3 ) 6 ( q −2 ) 3 ( q 4 ) 8 ( q 3 ) 6 ( q −2 ) 3 ( q 4 ) 8
ⓐ ( m 2 n ) 2 ( 2 m n 5 ) 4 ( m 2 n ) 2 ( 2 m n 5 ) 4 ⓑ ( −2 p −2 ) 4 ( 3 p 4 ) 2 ( −6 p 3 ) 2 ( −2 p −2 ) 4 ( 3 p 4 ) 2 ( −6 p 3 ) 2
ⓐ ( 3 p q 4 ) 2 ( 6 p 6 q ) 2 ( 3 p q 4 ) 2 ( 6 p 6 q ) 2 ⓑ ( −2 k −3 ) 2 ( 6 k 2 ) 4 ( 9 k 4 ) 2 ( −2 k −3 ) 2 ( 6 k 2 ) 4 ( 9 k 4 ) 2
Mixed Practice
ⓐ 7 n −1 7 n −1 ⓑ ( 7 n ) −1 ( 7 n ) −1 ⓒ ( −7 n ) −1 ( −7 n ) −1
ⓐ 6 r −1 6 r −1 ⓑ ( 6 r ) −1 ( 6 r ) −1 ⓒ ( −6 r ) −1 ( −6 r ) −1
ⓐ ( 3 p ) −2 ( 3 p ) −2 ⓑ 3 p −2 3 p −2 ⓒ −3 p −2 −3 p −2
ⓐ ( 2 q ) −4 ( 2 q ) −4 ⓑ 2 q −4 2 q −4 ⓒ −2 q −4 −2 q −4
( x 2 ) 4 · ( x 3 ) 2 ( x 2 ) 4 · ( x 3 ) 2
( y 4 ) 3 · ( y 5 ) 2 ( y 4 ) 3 · ( y 5 ) 2
( a 2 ) 6 · ( a 3 ) 8 ( a 2 ) 6 · ( a 3 ) 8
( b 7 ) 5 · ( b 2 ) 6 ( b 7 ) 5 · ( b 2 ) 6
( 2 m 6 ) 3 ( 2 m 6 ) 3
( 3 y 2 ) 4 ( 3 y 2 ) 4
( 10 x 2 y ) 3 ( 10 x 2 y ) 3
( 2 m n 4 ) 5 ( 2 m n 4 ) 5
( −2 a 3 b 2 ) 4 ( −2 a 3 b 2 ) 4
( −10 u 2 v 4 ) 3 ( −10 u 2 v 4 ) 3
( 2 3 x 2 y ) 3 ( 2 3 x 2 y ) 3
( 7 9 p q 4 ) 2 ( 7 9 p q 4 ) 2
( 8 a 3 ) 2 ( 2 a ) 4 ( 8 a 3 ) 2 ( 2 a ) 4
( 5 r 2 ) 3 ( 3 r ) 2 ( 5 r 2 ) 3 ( 3 r ) 2
( 10 p 4 ) 3 ( 5 p 6 ) 2 ( 10 p 4 ) 3 ( 5 p 6 ) 2
( 4 x 3 ) 3 ( 2 x 5 ) 4 ( 4 x 3 ) 3 ( 2 x 5 ) 4
( 1 2 x 2 y 3 ) 4 ( 4 x 5 y 3 ) 2 ( 1 2 x 2 y 3 ) 4 ( 4 x 5 y 3 ) 2
( 1 3 m 3 n 2 ) 4 ( 9 m 8 n 3 ) 2 ( 1 3 m 3 n 2 ) 4 ( 9 m 8 n 3 ) 2
( 3 m 2 n ) 2 ( 2 m n 5 ) 4 ( 3 m 2 n ) 2 ( 2 m n 5 ) 4
( 2 p q 4 ) 3 ( 5 p 6 q ) 2 ( 2 p q 4 ) 3 ( 5 p 6 q ) 2
ⓐ ( 3 x ) 2 ( 5 x ) ( 3 x ) 2 ( 5 x ) ⓑ ( 2 y ) 3 ( 6 y ) ( 2 y ) 3 ( 6 y )
ⓐ ( 1 2 y 2 ) 3 ( 2 3 y ) 2 ( 1 2 y 2 ) 3 ( 2 3 y ) 2 ⓑ ( 1 2 j 2 ) 5 ( 2 5 j 3 ) 2 ( 1 2 j 2 ) 5 ( 2 5 j 3 ) 2
ⓐ ( 2 r −2 ) 3 ( 4 −1 r ) 2 ( 2 r −2 ) 3 ( 4 −1 r ) 2 ⓑ ( 3 x −3 ) 3 ( 3 −1 x 5 ) 4 ( 3 x −3 ) 3 ( 3 −1 x 5 ) 4
( k −2 k 8 k 3 ) 2 ( k −2 k 8 k 3 ) 2
( j −2 j 5 j 4 ) 3 ( j −2 j 5 j 4 ) 3
( −4 m −3 ) 2 ( 5 m 4 ) 3 ( −10 m 6 ) 3 ( −4 m −3 ) 2 ( 5 m 4 ) 3 ( −10 m 6 ) 3
( −10 n −2 ) 3 ( 4 n 5 ) 2 ( 2 n 8 ) 2 ( −10 n −2 ) 3 ( 4 n 5 ) 2 ( 2 n 8 ) 2
In the following exercises, write each number in scientific notation.
ⓐ 57,000 ⓑ 0.026
ⓐ 340,000 ⓑ 0.041
ⓐ 8,750,000 ⓑ 0.00000871
ⓐ 1,290,000 ⓑ 0.00000103
In the following exercises, convert each number to decimal form.
ⓐ 5.2 × 10 2 5.2 × 10 2 ⓑ 2.5 × 10 −2 2.5 × 10 −2
ⓐ −8.3 × 10 2 −8.3 × 10 2 ⓑ 3.8 × 10 −2 3.8 × 10 −2
ⓐ 7.5 × 10 6 7.5 × 10 6 ⓑ −4.13 × 10 −5 −4.13 × 10 −5
ⓐ 1.6 × 10 10 1.6 × 10 10 ⓑ 8.43 × 10 −6 8.43 × 10 −6
In the following exercises, multiply or divide as indicated. Write your answer in decimal form.
ⓐ ( 3 × 10 −5 ) ( 3 × 10 9 ) ( 3 × 10 −5 ) ( 3 × 10 9 ) ⓑ 7 × 10 −3 1 × 10 −7 7 × 10 −3 1 × 10 −7
ⓐ ( 2 × 10 2 ) ( 1 × 10 −4 ) ( 2 × 10 2 ) ( 1 × 10 −4 ) ⓑ 5 × 10 −2 1 × 10 −10 5 × 10 −2 1 × 10 −10
ⓐ ( 7.1 × 10 −2 ) ( 2.4 × 10 −4 ) ( 7.1 × 10 −2 ) ( 2.4 × 10 −4 ) ⓑ 6 × 10 4 3 × 10 −2 6 × 10 4 3 × 10 −2
ⓐ ( 3.5 × 10 −4 ) ( 1.6 × 10 −2 ) ( 3.5 × 10 −4 ) ( 1.6 × 10 −2 ) ⓑ 8 × 10 6 4 × 10 −1 8 × 10 6 4 × 10 −1
Writing Exercises
Use the Product Property for Exponents to explain why x · x = x 2 . x · x = x 2 .
Jennifer thinks the quotient a 24 a 6 a 24 a 6 simplifies to a 4 . a 4 . What is wrong with her reasoning?
Explain why − 5 3 = ( −5 ) 3 − 5 3 = ( −5 ) 3 but − 5 4 ≠ ( −5 ) 4 . − 5 4 ≠ ( −5 ) 4 .
When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After reviewing this checklist, what will you do to become confident for all goals?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra/pages/1-introduction
- Authors: Lynn Marecek
- Publisher/website: OpenStax
- Book title: Intermediate Algebra
- Publication date: Mar 14, 2017
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra/pages/5-2-properties-of-exponents-and-scientific-notation
© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Polynomials and Polynomial Functions
Properties of Exponents and Scientific Notation
Learning objectives.
By the end of this section, you will be able to:
- Simplify expressions using the properties for exponents
- Use the definition of a negative exponent
- Use scientific notation
Before you get started, take this readiness quiz.
Simplify Expressions Using the Properties for Exponents
Let’s review the vocabulary for expressions with exponents.

When we combine like terms by adding and subtracting, we need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too.
First, we will look at an example that leads to the Product Property .
The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.
If a is a real number and m and n are integers, then
To multiply with like bases, add the exponents.
Simplify each expression:
Now we will look at an exponent property for division. As before, we’ll try to discover a property by looking at some examples.
To simplify an expression with a quotient, we need to first compare the exponents in the numerator and denominator.
Notice that when the larger exponent is in the numerator, we are left with factors in the numerator.
Notice that when the larger exponent is in the denominator, we are left with factors in the denominator.
- If a is a non-zero number, then a to the power of zero equals 1.
- Any non-zero number raised to the zero power is 1.
In this text, we assume any variable that we raise to the zero power is not zero.
The definition says any non-zero number raised to the zero power is 1.
To simplify the expression n raised to the zero power we just use the definition of the zero exponent. The result is 1.
Use the Definition of a Negative Exponent
We saw that the Quotient Property for Exponents has two forms depending on whether the exponent is larger in the numerator or the denominator. What if we just subtract exponents regardless of which is larger?
Let’s now look at what happens to a fraction whose numerator is one and whose denominator is an integer raised to a negative exponent.

The negative exponent tells us we can rewrite the expression by taking the reciprocal of the base and then changing the sign of the exponent.
Any expression that has negative exponents is not considered to be in simplest form. We will use the definition of a negative exponent and other properties of exponents to write the expression with only positive exponents.
Suppose now we have a fraction raised to a negative exponent. Let’s use our definition of negative exponents to lead us to a new property.

To get from the original fraction raised to a negative exponent to the final result, we took the reciprocal of the base—the fraction—and changed the sign of the exponent.
This leads us to the Quotient to a Negative Power Property .
Now that we have negative exponents, we will use the Product Property with expressions that have negative exponents.
Now let’s look at an exponential expression that contains a power raised to a power. See if you can discover a general property.
We multiplied the exponents. This leads to the Power Property for Exponents.
To raise a power to a power, multiply the exponents.
We will now look at an expression containing a product that is raised to a power. Can you find this pattern?

The exponent applies to each of the factors! This leads to the Product to a Power Property for Exponents .
If a and b are real numbers and m is a whole number, then
To raise a product to a power, raise each factor to that power.
Now we will look at an example that will lead us to the Quotient to a Power Property.

Notice that the exponent applies to both the numerator and the denominator.
This leads to the Quotient to a Power Property for Exponents .
To raise a fraction to a power, raise the numerator and denominator to that power.
We now have several properties for exponents. Let’s summarize them and then we’ll do some more examples that use more than one of the properties.
If a and b are real numbers, and m and n are integers, then
Simplify each expression by applying several properties:
Use Scientific Notation
Working with very large or very small numbers can be awkward. Since our number system is base ten we can use powers of ten to rewrite very large or very small numbers to make them easier to work with. Consider the numbers 4,000 and 0.004.
If we write the 1,000 as a power of ten in exponential form, we can rewrite these numbers in this way:
When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than ten, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation .
A number is expressed in scientific notation when it is of the form
If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation.

In both cases, the decimal was moved 3 places to get the first factor between 1 and 10.
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, n , that the decimal point was moved.
Write in scientific notation: ⓐ 96,000 ⓑ 0.0078.
Write in scientific notation: ⓐ 48,300 ⓑ 0.0129.
How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.

If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.

In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.
- Determine the exponent, n , on the factor 10.
- If the exponent is positive, move the decimal point n places to the right.
When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
Multiply or divide as indicated. Write answers in decimal form:
Access these online resources for additional instruction and practice with using multiplication properties of exponents.
- Properties of Exponents
- Negative exponents
- Scientific Notation
Key Concepts

Practice Makes Perfect
In the following exercises, simplify each expression using the properties for exponents.
In the following exercises, simplify each expression.
In the following exercises, simplify each expression using the Product Property.
In the following exercises, simplify each expression using the Power Property.
In the following exercises, simplify each expression using the Product to a Power Property.
In the following exercises, simplify each expression using the Quotient to a Power Property.
In the following exercises, simplify each expression by applying several properties.
Mixed Practice
In the following exercises, write each number in scientific notation.
ⓐ 57,000 ⓑ 0.026
ⓐ 340,000 ⓑ 0.041
ⓐ 8,750,000 ⓑ 0.00000871
ⓐ 1,290,000 ⓑ 0.00000103
In the following exercises, convert each number to decimal form.
ⓐ 16,000,000,000
In the following exercises, multiply or divide as indicated. Write your answer in decimal form.
ⓐ 0.02 ⓑ 500,000,000
ⓐ 0.0000056 ⓑ 20,000,000
Writing Exercises
Answers will vary.
When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all goals?
Intermediate Algebra by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book
Curriculum / Math / 8th Grade / Unit 1: Exponents and Scientific Notation / Lesson 6
Exponents and Scientific Notation
Lesson 6 of 15
Criteria for Success
Tips for teachers, anchor problems, problem set, target task, additional practice.
Apply the power of powers rule and power of product rule to write equivalent, simplified exponential expressions.
Common Core Standards
Core standards.
The core standards covered in this lesson
Expressions and Equations
8.EE.A.1 — Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 3² × 3<sup>-5</sup> = 3<sup>-3</sup> = 1/3³ = 1/27.
The essential concepts students need to demonstrate or understand to achieve the lesson objective
- Investigate, determine, and apply the general rule for power of product : $${(xy)^m = x^my^m}$$ .
- Investigate, determine, and apply the general rule for power of powers : $${(x^m)^n=x^{mn}}$$ .
- Know that $${\left ( x+y \right )^{m} \neq x^m+y^m}$$ .
Suggestions for teachers to help them teach this lesson
- In terms of pacing, this lesson may be split over more than one day.
- Similar to Lesson 5, these Anchor Problems can be used in a variety of ways, including having students lead the discovery and seek out a general rule.
- Once students have experimented with the problems and found a generalization, then provide them with the name of the rule and the general form.
Unlock features to optimize your prep time, plan engaging lessons, and monitor student progress.
Problems designed to teach key points of the lesson and guiding questions to help draw out student understanding
Is the following statement true? Show your reasoning.
$${4^53^5=12^5}$$
Guiding Questions
Write an equivalent form of each of the following:
a. $${(4x)^5}$$
b. $${(-3mn)^2}$$
c. $${\left ({5x\over y} \right )^3}$$
Lucas thinks that since $${(ab)^2 = a^2b^2}$$ , then that must mean $${(a+b)^2 = a^2+b^2}$$ . Is Lucas’ reasoning correct? Explain or show why or why not.
How is $${7^27^6}$$ different from $${(7^2)^6}$$ ? What is an equivalent expression for each one?
Use your reasoning to simplify the following:
a. $${(11^5)^4}$$
b. $${-(2^3)^6}$$
c. $${((-1)^3)^{12}}$$
A set of suggested resources or problem types that teachers can turn into a problem set
Give your students more opportunities to practice the skills in this lesson with a downloadable problem set aligned to the daily objective.
A task that represents the peak thinking of the lesson - mastery will indicate whether or not objective was achieved
Simplify the following expressions:
a. $$(2^5)^7$$
b. $$(91^3\times 19\times 103^8)^4$$
c. $$(p^4q^5r)^9$$
d. $$2^7\over 3^7$$
Student Response
The following resources include problems and activities aligned to the objective of the lesson that can be used for additional practice or to create your own problem set.
- Include a mixture of problems that involve using all the rules learned so far.
- Revisit the worksheet from Lesson 4, before students learned the more general approaches and rules. Do any of the problems illustrate the rules you’ve learned?
- EngageNY Mathematics Grade 8 Mathematics > Module 1 > Topic A > Lesson 3 — Exercises and Problem Set
- Kuta Software Free Pre-Algebra Worksheets Exponents and Radicals — Powers of products and quotients
Topic A: Review of Exponents
Review exponent notation and identify equivalent exponential expressions.
Evaluate numerical and algebraic expressions with exponents using the order of operations.
Investigate patterns of exponents with positive/negative bases and even/odd bases.
Create a free account to access thousands of lesson plans.
Already have an account? Sign In
Topic B: Properties of Exponents
Investigate exponent patterns to write equivalent expressions.
Apply the product of powers rule and the quotient of powers rule to write equivalent, simplified exponential expressions.
Reason with zero exponents to write equivalent, simplified exponential expressions.
Reason with negative exponents to write equivalent, simplified exponential expressions.
Simplify and write equivalent exponential expressions using all exponent rules.
Topic C: Scientific Notation
Write large and small numbers as powers of 10.
8.EE.A.3 8.EE.A.4
Define and write numbers in scientific notation.
Compare numbers written in scientific notation.
Multiply and divide with numbers in scientific notation. Interpret scientific notation on calculators.
Add and subtract with numbers in scientific notation.
Solve multi-step applications using scientific notation and properties of exponents.
8.EE.A.1 8.EE.A.3 8.EE.A.4
Request a Demo
See all of the features of Fishtank in action and begin the conversation about adoption.
Learn more about Fishtank Learning School Adoption.
Contact Information
School information, what courses are you interested in, are you interested in onboarding professional learning for your teachers and instructional leaders, any other information you would like to provide about your school.

Effective Instruction Made Easy
Access rigorous, relevant, and adaptable math lesson plans for free

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 6: Polynomials
6.1 Working with Exponents
Exponents often can be simplified using a few basic properties, since exponents represent repeated multiplication. The basic structure of writing an exponent looks like [latex]x^y,[/latex] where [latex]x[/latex] is defined as the base and [latex]y[/latex] is termed its exponent. For this instance, [latex]y[/latex] represents the number of times that the variable [latex]x[/latex] is multiplied by itself
When looking at numbers to various powers, the following table gives the numeric value of several numbers to various powers.
[latex]\begin{array}{llllll} \text{Squares}&\text{Cubes}&4^{\text{th}}\text{ Power}&5^{\text{th}}\text{ Power}&6^{\text{th}}\text{ Power}&7^{\text{th}}\text{ Power} \\ \\ 2^2=4&2^3=8&2^4=16&2^5=32&2^6=64&2^7=128 \\ 3^2=9&3^3=27&3^4=81&3^5=243&3^6=729&3^7=2,187 \\ 4^2=16&4^3=64&4^4=256&4^5=1,024&4^6=4,096&4^7=16,384 \\ 5^2=25&5^3=125&5^4=625&5^5=3,125&5^6=15,625&5^7=78,125 \\ 6^2=36&6^3=216&6^4=1,296&6^5=7,776&6^6=46,656&6^7=279,936 \\ 7^2=49&7^3=343&7^4=2,401&7^5=16,807&7^6=117,649&7^7=823,543 \\ 8^2=64&8^3=512&8^4=4,096&8^5=32,768&8^6=262,144&8^7=2,097,152 \\ 9^2=81&9^3=729&9^4=6,561&9^5=59,049&9^6=531,441&9^7=4,782,969 \\ 10^2=100&10^3=1,000&10^4=10,000&10^5=100,000&10^6=1,000,000&10^7=10,000,000 \\ \\ 11^2=121&12^2=144&13^2=169&14^2=196&15^2=225&20^2=400 \end{array}[/latex]
For this chart, the expanded forms of the base 2 for multiple exponents is shown:
[latex]\begin{array}{lllllllllllllll} 2^2&=&2&\times &2&=&4,&&&&&&&& \\ 2^3&=&2&\times &2&\times &2&=&8,&&&&&& \\ 2^4&=&2&\times &2&\times &2&\times &2&=&16,&&&& \\ 2^5&=&2&\times &2&\times &2&\times &2&\times &2&=&32&& \\ 2^6&=&2&\times &2&\times &2&\times &2&\times &2&\times &2&=&64\hspace{0.25in} \text{and so on} \\ \end{array}[/latex]
Once there is an exponent as a base that is multiplied or divided by itself to the number represented by the exponent, it becomes straightforward to identify a number of rules and properties that can be defined.
The following examples outline a number of these rules.
Example 6.1.1
What is the value of [latex]a^2 \times a^3[/latex]?
[latex]a^2 \times a^3[/latex] means that you have [latex](a \times a) (a \times a \times a),[/latex]
which is the same as [latex](a \times a \times a \times a \times a)[/latex]
or [latex]a^5[/latex]
This means that, when there is the same base and exponent that is multiplied by the same base with a different exponent, the total exponent value can be found by adding up the exponents.
[latex]\text{Product Rule of Exponents: }x^m \times x^n = x^{m+n}[/latex]
Example 6.1.2
What is the value of [latex](a^2)^3[/latex]?
[latex](a^2)^3[/latex] means that you have [latex](a^2) \times (a^2) \times (a^2)[/latex],
which is the same as [latex](a \times a) (a \times a) (a \times a)[/latex]
or [latex](a \times a \times a \times a \times a \times a)[/latex],
which equals [latex]a^6[/latex]
When you have some base and exponent where both are multiplied by another exponent, the total exponent value can be found by multiplying the two different exponents together.
[latex]\text{Power of a Power Rule of Exponents: }(x^m)^n = x^{mn}[/latex]
Example 6.1.3
What is the value of [latex](ab)^2[/latex]?
[latex](ab)^2[/latex] means that you have [latex](ab) \times (ab)[/latex],
which is the same as [latex](a \times b) \times (a \times b)[/latex]
or [latex](a \times a \times b \times b)[/latex],
which equals [latex]a^2b^2[/latex]
[latex]\text{Power of a Product Rule of Exponents: }(xy)^n = x^ny^n[/latex]
Example 6.1.4
What is the value of [latex]\dfrac{a^5}{a^3}[/latex]?
[latex]\dfrac{a^5}{a^3}[/latex] means that you have [latex]\dfrac{a \times a \times a \times a \times a}{a \times a \times a}[/latex], or that you are multiplying [latex]a[/latex] by itself five times and dividing it by itself three times.
Multiplying and dividing by the exact same number is a redundant exercise; multiples can be cancelled out prior to doing any multiplying and/or dividing. The easiest way to do this type of a problem is to subtract the exponents, where the exponents in the denominator are being subtracted from the exponents in the numerator. This has the same effect as cancelling any excess or redundant exponents.
For this example, the subtraction looks like [latex]a^{5-3},[/latex] leaving [latex]a^2.[/latex]
[latex]\text{Quotient Rule of Exponents: }\dfrac{x^m}{x^n}=x^{m-n}\hspace{0.25in} (x \ne 0)[/latex]
Example 6.1.5
What is the value of [latex]\left(\dfrac{a}{b}\right)^3[/latex]?
Expanded, this exponent is the same as:
[latex]\dfrac{a}{b}\times \dfrac{a}{b}\times \dfrac{a}{b}[/latex]
Which is the same as:
[latex]\dfrac{a \times a \times a}{b \times b \times b} \text{ or } \dfrac{a^3}{b^3}[/latex]
One can see that this result is very similar to the power of a product rule of exponents.
[latex]\text{Power of a Quotient Rule of Exponents: }\left(\dfrac{x}{y}\right)^n = \dfrac{x^n}{y^n}\hspace{0.25in} (y \ne 0)[/latex]
Simplify the following.
- [latex]4\cdot 4^4\cdot 4^4[/latex]
- [latex]4\cdot 4^4\cdot 4^2[/latex]
- [latex]2m^4n^2\cdot 4nm^2[/latex]
- [latex]x^2y^4\cdot xy^2[/latex]
- [latex](3^3)^4[/latex]
- [latex](4^3)^4[/latex]
- [latex](2u^3v^2)^2[/latex]
- [latex](xy)^3[/latex]
- [latex]4^5 \div 4^3[/latex]
- [latex]3^7 \div 3^3[/latex]
- [latex]3nm^2 \div 3n[/latex]
- [latex]x^2y^4 \div 4xy[/latex]
- [latex](x^3y^4\cdot 2x^2y^3)^2[/latex]
- [latex][(u^2v^2)(2u^4)]^3[/latex]
- [latex][(2x)^3 \div x^3]^2[/latex]
- [latex](2a^2b^2a^7) \div (ba^4)^2[/latex]
- [latex][(2y^{17}) \div (2x^2y^4)^4]^3[/latex]
- [latex][(xy^2)(y^4)^2] \div 2y^4[/latex]
- [latex](2xy^5\cdot 2x^2y^3) \div (2xy^4\cdot y^3)[/latex]
- [latex](2y^3x^2) \div [(x^2y^4)(x^2)][/latex]
- [latex][(q^3r^2)(2p^2q^2r^3)^2] \div 2p^3[/latex]
- [latex](2x^4y^5)(2z^{10}x^2y^7) \div (xy^2z^2)^4[/latex]
Answer Key 6.1
Intermediate Algebra by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1.3: Exponents and Scientific Notation
- Last updated
- Save as PDF
- Page ID 118279
In this section, you will:
- Use the product rule of exponents.
- Use the quotient rule of exponents.
- Use the power rule of exponents.
- Use the zero exponent rule of exponents.
- Use the negative rule of exponents.
- Find the power of a product and a quotient.
- Simplify exponential expressions.
- Use scientific notation.
Mathematicians, scientists, and economists commonly encounter very large and very small numbers. But it may not be obvious how common such figures are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is 2,048 pixels by 1,536 pixels, which is a very high resolution picture. It can also perceive a color depth (gradations in colors) of up to 48 bits per pixel, and can shoot the equivalent of 24 frames per second. The maximum possible number of bits of information used to film a one-hour (3,600-second) digital film is then an extremely large number.
Using a calculator, we enter 2,048×1,536×48×24×3,6002,048×1,536×48×24×3,600 and press ENTER. The calculator displays 1.304596316E13. What does this mean? The “E13” portion of the result represents the exponent 13 of ten, so there are a maximum of approximately 1.3×10131.3×1013 bits of data in that one-hour film. In this section, we review rules of exponents first and then apply them to calculations involving very large or small numbers.
Using the Product Rule of Exponents
Consider the product x3⋅x4.x3⋅x4. Both terms have the same base, x , but they are raised to different exponents. Expand each expression, and then rewrite the resulting expression.
x3⋅x4===x⋅x⋅x3factors⋅x⋅x⋅x⋅x4factorsx⋅x⋅x⋅x⋅x⋅x⋅x7factorsx7x3⋅x4=x⋅x⋅x3factors⋅x⋅x⋅x⋅x 4factors=x⋅x⋅x⋅x⋅x⋅x⋅x7factors=x7
The result is that x3⋅x4=x3+4=x7.x3⋅x4=x3+4=x7.
Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.
am⋅an=am+nam⋅an=am+n
Now consider an example with real numbers.
23⋅24=23+4=2723⋅24=23+4=27
We can always check that this is true by simplifying each exponential expression. We find that 2323 is 8, 2424 is 16, and 2727 is 128. The product 8⋅168⋅16 equals 128, so the relationship is true. We can use the product rule of exponents to simplify expressions that are a product of two numbers or expressions with the same base but different exponents.
THE PRODUCT RULE OF EXPONENTS
For any real number aa and natural numbers mm and n,n, the product rule of exponents states that
EXAMPLE 1
Using the product rule.
Write each of the following products with a single base. Do not simplify further.
- ⓐ t5⋅t3t5⋅t3
- ⓑ (−3)5⋅(−3)(−3)5⋅(−3)
- ⓒ x2⋅x5⋅x3x2⋅x5⋅x3
TRY IT #1
- ⓐ k6⋅k9k6⋅k9
- ⓑ (2y)4⋅(2y)(2y)4⋅(2y)
- ⓒ t3⋅t6⋅t5t3⋅t6⋅t5
Using the Quotient Rule of Exponents
The quotient rule of exponents allows us to simplify an expression that divides two numbers with the same base but different exponents. In a similar way to the product rule, we can simplify an expression such as ymyn,ymyn, where m>n.m>n. Consider the example y9y5.y9y5. Perform the division by canceling common factors.
y9y5====y⋅y⋅y⋅y⋅y⋅y⋅y⋅y⋅yy⋅y⋅y⋅y⋅yy⋅y⋅y⋅y⋅y⋅y⋅y⋅y⋅yy⋅y⋅y⋅y⋅yy⋅y⋅y⋅y1y4y9y5=y⋅y⋅y⋅y⋅y⋅y⋅y⋅y⋅yy⋅y⋅y⋅y⋅y=y⋅y⋅y⋅y⋅y⋅y⋅y⋅y⋅yy⋅y⋅y⋅y⋅y=y⋅y⋅y⋅y1=y4
Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend.
aman=am−naman=am−n
In other words, when dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.
y9y5=y9−5=y4y9y5=y9−5=y4
For the time being, we must be aware of the condition m>n.m>n. Otherwise, the difference m−nm−n could be zero or negative. Those possibilities will be explored shortly. Also, instead of qualifying variables as nonzero each time, we will simplify matters and assume from here on that all variables represent nonzero real numbers.
THE QUOTIENT RULE OF EXPONENTS
For any real number aa and natural numbers mm and n,n, such that m>n,m>n, the quotient rule of exponents states that
EXAMPLE 2
Using the quotient rule.
- ⓐ (−2)14(−2)9(−2)14(−2)9
- ⓑ t23t15t23t15
- ⓒ (z2√)5z2√(z2)5z2
TRY IT #2
- ⓐ s75s68s75s68
- ⓑ (−3)6−3(−3)6−3
- ⓒ (ef2)5(ef2)3(ef2)5(ef2)3
Using the Power Rule of Exponents
Suppose an exponential expression is raised to some power. Can we simplify the result? Yes. To do this, we use the power rule of exponents . Consider the expression (x2)3.(x2)3. The expression inside the parentheses is multiplied twice because it has an exponent of 2. Then the result is multiplied three times because the entire expression has an exponent of 3.
(x2)3====(x2)⋅(x2)⋅(x2)3factors⎛⎝x⋅x2factors⎞⎠⋅⎛⎝x⋅x2factors⎞⎠⋅⎛⎝x⋅x2factors⎞⎠3factorsx⋅x⋅x⋅x⋅x⋅xx6(x2)3=(x2)⋅(x2)⋅(x2)3factors=(x⋅x︷2factors)⋅(x⋅x︷2factors)⋅(x⋅x︷2factors)3factors=x⋅x⋅x⋅x⋅x⋅x=x6
The exponent of the answer is the product of the exponents: (x2)3=x2⋅3=x6.(x2)3=x2⋅3=x6. In other words, when raising an exponential expression to a power, we write the result with the common base and the product of the exponents.
(am)n=am⋅n(am)n=am⋅n
Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.
53⋅54x5⋅x2(3a)7⋅(3a)10===Product Rule53+4x5+2(3a)7+10===57x7(3a)17butbutbut(53)4(x5)2((3a)7)10Power Rule===53⋅4x5⋅2(3a)7⋅10===512x10(3a)70Product RulePower Rule53⋅54=53+4=57but(53)4=53⋅4=512x5⋅x2=x5+2=x7but(x5)2=x5⋅2=x10(3a)7⋅(3a)10=(3a)7+10=(3a)17but((3a)7)10=(3a)7⋅10=(3a)70
THE POWER RULE OF EXPONENTS
For any real number aa and positive integers mm and n,n, the power rule of exponents states that

EXAMPLE 3
Using the power rule.
- ⓐ (x2)7(x2)7
- ⓑ ((2t)5)3((2t)5)3
- ⓒ ((−3)5)11((−3)5)11
TRY IT #3
- ⓐ ((3y)8)3((3y)8)3
- ⓑ (t5)7(t5)7
- ⓒ ((−g)4)4((−g)4)4
Using the Zero Exponent Rule of Exponents
Return to the quotient rule. We made the condition that m>nm>n so that the difference m−nm−n would never be zero or negative. What would happen if m=n?m=n? In this case, we would use the zero exponent rule of exponents to simplify the expression to 1. To see how this is done, let us begin with an example.
t8t8=t8t8=1t8t8=t8t8=1
If we were to simplify the original expression using the quotient rule, we would have
t8t8=t8−8=t0t8t8=t8−8=t0
If we equate the two answers, the result is t0=1.t0=1. This is true for any nonzero real number, or any variable representing a real number.
The sole exception is the expression 00.00. This appears later in more advanced courses, but for now, we will consider the value to be undefined.
THE ZERO EXPONENT RULE OF EXPONENTS
For any nonzero real number a,a, the zero exponent rule of exponents states that
EXAMPLE 4
Using the zero exponent rule.
Simplify each expression using the zero exponent rule of exponents.
- ⓐ c3c3c3c3
- ⓑ −3x5x5−3x5x5
- ⓒ (j2k)4(j2k)⋅(j2k)3(j2k)4(j2k)⋅(j2k)3
- ⓓ 5(rs2)2(rs2)25(rs2)2(rs2)2
TRY IT #4
- ⓐ t7t7t7t7
- ⓑ (de2)112(de2)11(de2)112(de2)11
- ⓒ w4⋅w2w6w4⋅w2w6
- ⓓ t3⋅t4t2⋅t5t3⋅t4t2⋅t5
Using the Negative Rule of Exponents
Another useful result occurs if we relax the condition that m>nm>n in the quotient rule even further. For example, can we simplify h3h5?h3h5? When m<nm<n —that is, where the difference m−nm−n is negative—we can use the negative rule of exponents to simplify the expression to its reciprocal.
Divide one exponential expression by another with a larger exponent. Use our example, h3h5.h3h5.
h3h5====h⋅h⋅hh⋅h⋅h⋅h⋅hh⋅h⋅hh⋅h⋅h⋅h⋅h1h⋅h1h2h3h5=h⋅h⋅hh⋅h⋅h⋅h⋅h=h⋅h⋅hh⋅h⋅h⋅h⋅h=1h⋅h=1h2
h3h5==h3−5h−2h3h5=h3−5=h−2
Putting the answers together, we have h−2=1h2.h−2=1h2. This is true for any nonzero real number, or any variable representing a nonzero real number.
A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the fraction bar—from numerator to denominator or vice versa.
a−n=1anandan=1a−na−n=1anandan=1a−n
We have shown that the exponential expression anan is defined when nn is a natural number, 0, or the negative of a natural number. That means that anan is defined for any integer n.n. Also, the product and quotient rules and all of the rules we will look at soon hold for any integer n.n.
THE NEGATIVE RULE OF EXPONENTS
For any nonzero real number aa and natural number n,n, the negative rule of exponents states that
a−n=1ana−n=1an
EXAMPLE 5
Using the negative exponent rule.
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
- ⓐ θ3θ10θ3θ10
- ⓑ z2⋅zz4z2⋅zz4
- ⓒ (−5t3)4(−5t3)8(−5t3)4(−5t3)8
TRY IT #5
- ⓐ (−3t)2(−3t)8(−3t)2(−3t)8
- ⓑ f47f49⋅ff47f49⋅f
- ⓒ 2k45k72k45k7
EXAMPLE 6
Using the product and quotient rules.
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
- ⓐ b2⋅b−8b2⋅b−8
- ⓑ (−x)5⋅(−x)−5(−x)5⋅(−x)−5
- ⓒ −7z(−7z)5−7z(−7z)5
TRY IT #6
- ⓐ t−11⋅t6t−11⋅t6
- ⓑ 2512251325122513
Finding the Power of a Product
To simplify the power of a product of two exponential expressions, we can use the power of a product rule of exponents, which breaks up the power of a product of factors into the product of the powers of the factors. For instance, consider (pq)3.(pq)3. We begin by using the associative and commutative properties of multiplication to regroup the factors.
(pq)3====(pq)⋅(pq)⋅(pq)3factorsp⋅q⋅p⋅q⋅p⋅qp⋅p⋅p3factors⋅q⋅q⋅q3factorsp3⋅q3(pq)3= (pq)⋅(pq)⋅(pq) 3factors=p⋅q⋅p⋅q⋅p⋅q= p⋅p⋅p 3factors⋅ q⋅q⋅q 3factors=p3⋅q3
In other words, (pq)3=p3⋅q3.(pq)3=p3⋅q3.
THE POWER OF A PRODUCT RULE OF EXPONENTS
For any real numbers aa and bb and any integer n,n, the power of a product rule of exponents states that
(ab)n=anbn(ab)n=anbn
EXAMPLE 7
Using the power of a product rule.
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
- ⓐ (ab2)3(ab2)3
- ⓑ (2t)15(2t)15
- ⓒ (−2w3)3(−2w3)3
- ⓓ 1(−7z)41(−7z)4
- ⓔ (e−2f2)7(e−2f2)7
TRY IT #7
- ⓐ (g2h3)5(g2h3)5
- ⓑ (5t)3(5t)3
- ⓒ (−3y5)3(−3y5)3
- ⓓ 1(a6b7)31(a6b7)3
- ⓔ (r3s−2)4(r3s−2)4
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at the following example.
(e−2f2)7=f14e14(e−2f2)7=f14e14
Let’s rewrite the original problem differently and look at the result.
(e−2f2)7==(f2e2)7f14e14(e−2f2)7=( f2 e2)7=f14e14
It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.
(e−2f2)7====(f2e2)7(f2)7(e2)7f2⋅7e2⋅7f14e14(e−2f2)7=(f2e2)7=(f2)7(e2)7=f2⋅7e2⋅7=f14e14
THE POWER OF A QUOTIENT RULE OF EXPONENTS
For any real numbers aa and bb and any integer n,n, the power of a quotient rule of exponents states that
EXAMPLE 8
Using the power of a quotient rule.
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
- ⓐ (4z11)3(4z11)3
- ⓑ (pq3)6(pq3)6
- ⓒ (−1t2)27(−1t2)27
- ⓓ (j3k−2)4(j3k−2)4
- ⓔ (m−2n−2)3(m−2n−2)3
TRY IT #8
- ⓐ (b5c)3(b5c)3
- ⓑ (5u8)4(5u8)4
- ⓒ (−1w3)35(−1w3)35
- ⓓ (p−4q3)8(p−4q3)8
- ⓔ (c−5d−3)4(c−5d−3)4
Simplifying Exponential Expressions
Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.
EXAMPLE 9
Simplify each expression and write the answer with positive exponents only.
- ⓐ (6m2n−1)3(6m2n−1)3
- ⓑ 175⋅17−4⋅17−3175⋅17−4⋅17−3
- ⓒ (u−1vv−1)2(u−1vv−1)2
- ⓓ (−2a3b−1)(5a−2b2)(−2a3b−1)(5a−2b2)
- ⓔ (x22–√)4(x22–√)−4(x22)4(x22)−4
- ⓕ (3w2)5(6w−2)2(3w2)5(6w−2)2
TRY IT #9
- ⓐ (2uv−2)−3(2uv−2)−3
- ⓑ x8⋅x−12⋅xx8⋅x−12⋅x
- ⓒ (e2f−3f−1)2(e2f−3f−1)2
- ⓓ (9r−5s3)(3r6s−4)(9r−5s3)(3r6s−4)
- ⓔ (49tw−2)−3(49tw−2)3(49tw−2)−3(49tw−2)3
- ⓕ (2h2k)4(7h−1k2)2(2h2k)4(7h−1k2)2
Using Scientific Notation
Recall at the beginning of the section that we found the number 1.3×10131.3×1013 when describing bits of information in digital images. Other extreme numbers include the width of a human hair, which is about 0.00005 m, and the radius of an electron, which is about 0.00000000000047 m. How can we effectively work read, compare, and calculate with numbers such as these?
A shorthand method of writing very small and very large numbers is called scientific notation , in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10. Count the number of places n that you moved the decimal point. Multiply the decimal number by 10 raised to a power of n . If you moved the decimal left as in a very large number, nn is positive. If you moved the decimal right as in a small large number, nn is negative.
For example, consider the number 2,780,418. Move the decimal left until it is to the right of the first nonzero digit, which is 2.
We obtain 2.780418 by moving the decimal point 6 places to the left. Therefore, the exponent of 10 is 6, and it is positive because we moved the decimal point to the left. This is what we should expect for a large number.
2.780418×1062.780418×106
Working with small numbers is similar. Take, for example, the radius of an electron, 0.00000000000047 m. Perform the same series of steps as above, except move the decimal point to the right.
Be careful not to include the leading 0 in your count. We move the decimal point 13 places to the right, so the exponent of 10 is 13. The exponent is negative because we moved the decimal point to the right. This is what we should expect for a small number.
4.7×10−134.7×10−13
SCIENTIFIC NOTATION
A number is written in scientific notation if it is written in the form a×10n,a×10n, where 1≤|a|<101≤| a |<10 and nn is an integer.
EXAMPLE 10
Converting standard notation to scientific notation.
Write each number in scientific notation.
ⓐDistance to Andromeda Galaxy from Earth: 24,000,000,000,000,000,000,000 m
ⓑDiameter of Andromeda Galaxy: 1,300,000,000,000,000,000,000 m
ⓒNumber of stars in Andromeda Galaxy: 1,000,000,000,000
ⓓDiameter of electron: 0.00000000000094 m
ⓔProbability of being struck by lightning in any single year: 0.00000143
Observe that, if the given number is greater than 1, as in examples a–c, the exponent of 10 is positive; and if the number is less than 1, as in examples d–e, the exponent is negative.
TRY IT #10
- ⓐU.S. national debt per taxpayer (April 2014): $152,000
- ⓑWorld population (April 2014): 7,158,000,000
- ⓒWorld gross national income (April 2014): $85,500,000,000,000
- ⓓTime for light to travel 1 m: 0.00000000334 s
- ⓔProbability of winning lottery (match 6 of 49 possible numbers): 0.0000000715
Converting from Scientific to Standard Notation
To convert a number in scientific notation to standard notation, simply reverse the process. Move the decimal nn places to the right if nn is positive or nn places to the left if nn is negative and add zeros as needed. Remember, if nn is positive, the absolute value of the number is greater than 1, and if nn is negative, the absolute value of the number is less than one.
EXAMPLE 11
Converting scientific notation to standard notation.
Convert each number in scientific notation to standard notation.
- ⓐ 3.547×10143.547×1014
- ⓑ −2×106−2×106
- ⓒ 7.91×10−77.91×10−7
- ⓓ −8.05×10−12−8.05×10−12
TRY IT #11
- ⓐ 7.03×1057.03×105
- ⓑ −8.16×1011−8.16×1011
- ⓒ −3.9×10−13−3.9×10−13
- ⓓ 8×10−68×10−6
Using Scientific Notation in Applications
Scientific notation, used with the rules of exponents, makes calculating with large or small numbers much easier than doing so using standard notation. For example, suppose we are asked to calculate the number of atoms in 1 L of water. Each water molecule contains 3 atoms (2 hydrogen and 1 oxygen). The average drop of water contains around 1.32×10211.32×1021 molecules of water and 1 L of water holds about 1.22×1041.22×104 average drops. Therefore, there are approximately 3⋅(1.32×1021)⋅(1.22×104)≈4.83×10253⋅(1.32×1021)⋅(1.22×104)≈4.83×1025 atoms in 1 L of water. We simply multiply the decimal terms and add the exponents. Imagine having to perform the calculation without using scientific notation!
When performing calculations with scientific notation, be sure to write the answer in proper scientific notation. For example, consider the product (7×104)⋅(5×106)=35×1010.(7×104)⋅(5×106)=35×1010. The answer is not in proper scientific notation because 35 is greater than 10. Consider 35 as 3.5×10.3.5×10. That adds a ten to the exponent of the answer.
(35)×1010=(3.5×10)×1010=3.5×(10×1010)=3.5×1011(35)×1010=(3.5×10)×1010=3.5×(10×1010)=3.5×1011
EXAMPLE 12
Perform the operations and write the answer in scientific notation.
- ⓐ (8.14×10−7)(6.5×1010)(8.14×10−7)(6.5×1010)
- ⓑ (4×105)÷(−1.52×109)(4×105)÷(−1.52×109)
- ⓒ (2.7×105)(6.04×1013)(2.7×105)(6.04×1013)
- ⓓ (1.2×108)÷(9.6×105)(1.2×108)÷(9.6×105)
- ⓔ (3.33×104)(−1.05×107)(5.62×105)(3.33×104)(−1.05×107)(5.62×105)
TRY IT #12
- ⓐ (−7.5×108)(1.13×10−2)(−7.5×108)(1.13×10−2)
- ⓑ (1.24×1011)÷(1.55×1018)(1.24×1011)÷(1.55×1018)
- ⓒ (3.72×109)(8×103)(3.72×109)(8×103)
- ⓓ (9.933×1023)÷(−2.31×1017)(9.933×1023)÷(−2.31×1017)
- ⓔ (−6.04×109)(7.3×102)(−2.81×102)(−6.04×109)(7.3×102)(−2.81×102)
EXAMPLE 13
Applying scientific notation to solve problems.
In April 2014, the population of the United States was about 308,000,000 people. The national debt was about $17,547,000,000,000. Write each number in scientific notation, rounding figures to two decimal places, and find the amount of the debt per U.S. citizen. Write the answer in both scientific and standard notations.
TRY IT #13
An average human body contains around 30,000,000,000,000 red blood cells. Each cell measures approximately 0.000008 m long. Write each number in scientific notation and find the total length if the cells were laid end-to-end. Write the answer in both scientific and standard notations.
Access these online resources for additional instruction and practice with exponents and scientific notation.
- Exponential Notation
- Properties of Exponents
- Zero Exponent
- Simplify Exponent Expressions
- Quotient Rule for Exponents
- Scientific Notation
- Converting to Decimal Notation
1.2 Section Exercises
Is 2323 the same as 32?32? Explain.
When can you add two exponents?
What is the purpose of scientific notation?
Explain what a negative exponent does.
For the following exercises, simplify the given expression. Write answers with positive exponents.
15−215−2
32×3332×33
44÷444÷4
(22)−2(22)−2
(5−8)0(5−8)0
113÷114113÷114
65×6−765×6−7
5−2÷525−2÷52
For the following exercises, write each expression with a single base. Do not simplify further. Write answers with positive exponents.
42×43÷4−442×43÷4−4
(123×12)10(123×12)10
106÷(1010)−2106÷(1010)−2
7−6×7−37−6×7−3
(33÷34)5(33÷34)5
For the following exercises, express the decimal in scientific notation.
148,000,000
For the following exercises, convert each number in scientific notation to standard notation.
1.6×10101.6×1010
9.8×10−99.8×10−9
mn2m−2mn2m−2
(b3c4)2(b3c4)2
(x−3y2)−5(x−3y2)−5
ab2÷d−3ab2÷d−3
(w0x5)−1(w0x5)−1
y−4(y2)2y−4(y2)2
p−4q2p2q−3p−4q2p2q−3
(l×w)2(l×w)2
(y7)3÷x14(y7)3÷x14
(a23)2(a23)2
(25m)÷(50m)(25m)÷(50m)
(16x√)2y−1(16x)2y−1
23(3a)−223(3a)−2
(ma6)21m3a2(ma6)21m3a2
(b−3c)3(b−3c)3
(x2y13÷y0)2(x2y13÷y0)2
(9z3)−2y(9z3)−2y
Real-World Applications
To reach escape velocity, a rocket must travel at the rate of 2.2×1062.2×106 ft/min. Rewrite the rate in standard notation.
A dime is the thinnest coin in U.S. currency. A dime’s thickness measures 1.35×10−31.35×10−3 m. Rewrite the number in standard notation.
The average distance between Earth and the Sun is 92,960,000 mi. Rewrite the distance using scientific notation.
A terabyte is made of approximately 1,099,500,000,000 bytes. Rewrite in scientific notation.
The Gross Domestic Product (GDP) for the United States in the first quarter of 2014 was $1.71496×1013.$1.71496×1013. Rewrite the GDP in standard notation.
One picometer is approximately 3.397×10−113.397×10−11 in. Rewrite this length using standard notation.
The value of the services sector of the U.S. economy in the first quarter of 2012 was $10,633.6 billion. Rewrite this amount in scientific notation.
For the following exercises, use a graphing calculator to simplify. Round the answers to the nearest hundredth.
(123m334−3)2(123m334−3)2
173÷152x3173÷152x3
(32a3)−2(a422)2(32a3)−2(a422)2
(62−24)2÷(xy)−5(62−24)2÷(xy)−5
m2n3a2c−3⋅a−7n−2m2c4m2n3a2c−3⋅a−7n−2m2c4
(x6y3x3y−3⋅y−7x−3)10(x6y3x3y−3⋅y−7x−3)10
((ab2c)−3b−3)2((ab2c)−3b−3)2
Avogadro’s constant is used to calculate the number of particles in a mole. A mole is a basic unit in chemistry to measure the amount of a substance. The constant is 6.0221413×1023.6.0221413×1023. Write Avogadro’s constant in standard notation.
Planck’s constant is an important unit of measure in quantum physics. It describes the relationship between energy and frequency. The constant is written as 6.62606957×10−34.6.62606957×10−34. Write Planck’s constant in standard notation.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 1.1: Exponents and Scientific Notation
Learning objectives.
In this section students will:
- Use the product rule of exponents.
- Use the quotient rule of exponents.
- Use the power rule of exponents.
- Use the zero exponent rule of exponents.
- Use the negative rule of exponents.
- Find the power of a product and a quotient.
- Simplify exponential expressions.
- Use scientific notation.
Mathematicians, scientists, and economists commonly encounter very large and very small numbers. But it may not be obvious how common such figures are in everyday life. For instance, a pixel is the smallest unit of light that can be perceived and recorded by a digital camera. A particular camera might record an image that is 2,048 pixels by 1,536 pixels, which is a very high resolution picture. It can also perceive a color depth (gradations in colors) of up to 48 bits per frame, and can shoot the equivalent of 24 frames per second. The maximum possible number of bits of information used to film a one-hour (3,600-second) digital film is then an extremely large number.
Using the Product Rule of Exponents
Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents.
Now consider an example with real numbers.
The Product Rule of Exponents
Using the Product Rule
Write each of the following products with a single base. Do not simplify further.
Use the product rule to simplify each expression.
At first, it may appear that we cannot simplify a product of three factors. However, using the associative property of multiplication, begin by simplifying the first two.
Notice we get the same result by adding the three exponents in one step.
Using the Quotient Rule of Exponents
Notice that the exponent of the quotient is the difference between the exponents of the divisor and dividend.
In other words, when dividing exponential expressions with the same base, we write the result with the common base and subtract the exponents.
The Quotient Rule of Exponents
Using the Quotient Rule
Use the quotient rule to simplify each expression.
Using the Power Rule of Exponents
Be careful to distinguish between uses of the product rule and the power rule. When using the product rule, different terms with the same bases are raised to exponents. In this case, you add the exponents. When using the power rule, a term in exponential notation is raised to a power. In this case, you multiply the exponents.
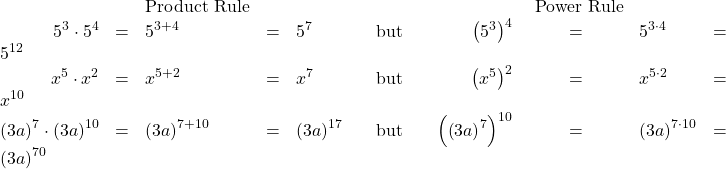
The Power Rule of Exponents
Using the power rule.
Use the power rule to simplify each expression.
Using the Zero Exponent Rule of Exponents
If we were to simplify the original expression using the quotient rule, we would have
The Zero Exponent Rule of Exponents
Using the Zero Exponent Rule
Simplify each expression using the zero exponent rule of exponents.
Use the zero exponent and other rules to simplify each expression.
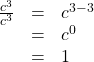
Using the Negative Rule of Exponents
A factor with a negative exponent becomes the same factor with a positive exponent if it is moved across the fraction bar—from numerator to denominator or vice versa.
The Negative Rule of Exponents
Using the Negative Exponent Rule
Write each of the following quotients with a single base. Do not simplify further. Write answers with positive exponents.
Using the Product and Quotient Rules
Write each of the following products with a single base. Do not simplify further. Write answers with positive exponents.
Finding the Power of a Product
The Power of a Product Rule of Exponents
Using the Power of a Product Rule
Simplify each of the following products as much as possible using the power of a product rule. Write answers with positive exponents.
Use the product and quotient rules and the new definitions to simplify each expression.
Finding the Power of a Quotient
To simplify the power of a quotient of two expressions, we can use the power of a quotient rule, which states that the power of a quotient of factors is the quotient of the powers of the factors. For example, let’s look at the following example.
Let’s rewrite the original problem differently and look at the result.
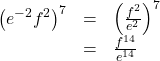
It appears from the last two steps that we can use the power of a product rule as a power of a quotient rule.

The Power of a Quotient Rule of Exponents
Using the Power of a Quotient Rule
Simplify each of the following quotients as much as possible using the power of a quotient rule. Write answers with positive exponents.
Simplifying Exponential Expressions
Recall that to simplify an expression means to rewrite it by combing terms or exponents; in other words, to write the expression more simply with fewer terms. The rules for exponents may be combined to simplify expressions.
Simplify each expression and write the answer with positive exponents only.
Using Scientific Notation
For example, consider the number 2,780,418. Move the decimal left until it is to the right of the first nonzero digit, which is 2.

We obtain 2.780418 by moving the decimal point 6 places to the left. Therefore, the exponent of 10 is 6, and it is positive because we moved the decimal point to the left. This is what we should expect for a large number.
Working with small numbers is similar. Take, for example, the radius of an electron, 0.00000000000047 m. Perform the same series of steps as above, except move the decimal point to the right.

Be careful not to include the leading 0 in your count. We move the decimal point 13 places to the right, so the exponent of 10 is 13. The exponent is negative because we moved the decimal point to the right. This is what we should expect for a small number.
- Scientific Notation
Converting Standard Notation to Scientific Notation
Write each number in scientific notation.
- Distance to Andromeda Galaxy from Earth: 24,000,000,000,000,000,000,000 m
- Diameter of Andromeda Galaxy: 1,300,000,000,000,000,000,000 m
- Number of stars in Andromeda Galaxy: 1,000,000,000,000
- Diameter of electron: 0.00000000000094 m
- Probability of being struck by lightning in any single year: 0.00000143

Observe that, if the given number is greater than 1, as in examples a–c, the exponent of 10 is positive; and if the number is less than 1, as in examples d–e, the exponent is negative.
- U.S. national debt per taxpayer (April 2014): $152,000
- World population (April 2014): 7,158,000,000
- World gross national income (April 2014): $85,500,000,000,000
- Time for light to travel 1 m: 0.00000000334 s
- Probability of winning lottery (match 6 of 49 possible numbers): 0.0000000715
Converting from Scientific to Standard Notation
Converting scientific notation to standard notation.
Convert each number in scientific notation to standard notation.
Using Scientific Notation in Applications
Perform the operations and write the answer in scientific notation.
Applying Scientific Notation to Solve Problems
In April 2014, the population of the United States was about 308,000,000 people. The national debt was about $17,547,000,000,000. Write each number in scientific notation, rounding figures to two decimal places, and find the amount of the debt per U.S. citizen. Write the answer in both scientific and standard notations.
To find the amount of debt per citizen, divide the national debt by the number of citizens.
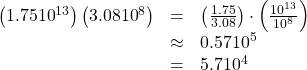
An average human body contains around 30,000,000,000,000 red blood cells. Each cell measures approximately 0.000008 m long. Write each number in scientific notation and find the total length if the cells were laid end-to-end. Write the answer in both scientific and standard notations.
Access these online resources for additional instruction and practice with exponents and scientific notation.
- Exponential Notation
- Properties of Exponents
- Zero Exponent
- Simplify Exponent Expressions
- Quotient Rule for Exponents
- Converting to Decimal Notation
Key Equations
Key concepts.
- Products of exponential expressions with the same base can be simplified by adding exponents. See (Figure) .
- Quotients of exponential expressions with the same base can be simplified by subtracting exponents. See (Figure) .
- Powers of exponential expressions with the same base can be simplified by multiplying exponents. See (Figure) .
- An expression with exponent zero is defined as 1. See (Figure) .
- An expression with a negative exponent is defined as a reciprocal. See (Figure) and (Figure) .
- The power of a product of factors is the same as the product of the powers of the same factors. See (Figure) .
- The power of a quotient of factors is the same as the quotient of the powers of the same factors. See (Figure) .
- The rules for exponential expressions can be combined to simplify more complicated expressions. See (Figure) .
- Scientific notation uses powers of 10 to simplify very large or very small numbers. See (Figure) and (Figure) .
- Scientific notation may be used to simplify calculations with very large or very small numbers. See (Figure) and (Figure) .
Section Exercises
2. When can you add two exponents?
3. What is the purpose of scientific notation?
It is a method of writing very small and very large numbers.
4. Explain what a negative exponent does.
For the following exercises, simplify the given expression. Write answers with positive exponents.
For the following exercises, write each expression with a single base. Do not simplify further. Write answers with positive exponents.
For the following exercises, express the decimal in scientific notation.
21. 0.0000314
22. 148,000,000
For the following exercises, convert each number in scientific notation to standard notation.
16,000,000,000
Real-World Applications
46. The average distance between Earth and the Sun is 92,960,000 mi. Rewrite the distance using scientific notation.
47. A terabyte is made of approximately 1,099,500,000,000 bytes. Rewrite in scientific notation.
0.00000000003397 in.
51. The value of the services sector of the U.S. economy in the first quarter of 2012 was $10,633.6 billion. Rewrite this amount in scientific notation.
52. For the following exercises, use a graphing calculator to simplify. Round the answers to the nearest hundredth.
0.000000000000000000000000000000000662606957
Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Module 1: Exponents and Radicals
Summary: exponents, scientific notation and square roots, key concepts.
- Exponential Notation

- If [latex]a,b[/latex] are real numbers and [latex]m,n[/latex] are integers, then [latex]\begin{array}{cccc}\mathbf{\text{Product Property}}\hfill & & & {a}^{m}\cdot {a}^{n}={a}^{m+n}\hfill \\ \mathbf{\text{Power Property}}\hfill & & & {\left({a}^{m}\right)}^{n}={a}^{m\cdot n}\hfill \\ \mathbf{\text{Power of a Product Property}}\hfill & & & {\left(ab\right)}^{m}={a}^{m}{b}^{m}\hfill \\ \mathbf{\text{Quotient Property}}\hfill & & & {\Large\frac{{a}^{m}}{{a}^{n}}}={a}^{m-n},a\ne 0\hfill \\ \mathbf{\text{Zero Exponent Property}}\hfill & & & {a}^{0}=1,a\ne 0\hfill \\ \mathbf{\text{Power of a Quotient Property}}\hfill & & & {\left({\Large\frac{a}{b}}\right)}^{m}={\Large\frac{{a}^{m}}{{b}^{m}}},b\ne 0\hfill \\ \mathbf{\text{Definition of Negative Exponent}}\hfill & & & {a}^{-n}={\Large\frac{1}{{a}^{n}}}\hfill \end{array}[/latex]
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places, [latex]n[/latex] , that the decimal point was moved.
- If the original number is greater than [latex]1[/latex], the power of [latex]10[/latex] will be [latex]{10}^{n}[/latex] .
- If the original number is between [latex]0[/latex] and [latex]1[/latex], the power of [latex]10[/latex] will be [latex]{10}^{n}[/latex] .
- Determine the exponent, [latex]n[/latex] , on the factor [latex]10[/latex].
- If the exponent is positive, move the decimal point [latex]n[/latex] places to the right.
- If the exponent is negative, move the decimal point [latex]|n|[/latex] places to the left.

- Square Roots and Area If the area of the square is A square units, the length of a side is [latex]\sqrt{A}[/latex] units.
- Square Roots and Gravity On Earth, if an object is dropped from a height of [latex]h[/latex] feet, the time in seconds it will take to reach the ground is found by evaluating the expression [latex]{\Large\frac{\sqrt{h}}{4}}[/latex].
- Square Roots and Accident Investigations Police officers investigating car accidents measure the length of the skid marks on the pavement. Then they use square roots to determine the speed, in miles per hour, a car was going before applying the brakes. According to some formulas, if the length of the skid marks is [latex]d[/latex] feet, then the speed of the car can be found by evaluating [latex]\sqrt{24d}[/latex]. .
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Write a complete sentence that answers the question.
Contribute!
Improve this page Learn More
- Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Skip to main content
- Skip to primary sidebar
EVERYTHING YOU NEED FOR THE YEAR >>> ALL ACCESS
Maneuvering the Middle
Student-Centered Math Lessons
Teaching Scientific Notation and Exponents

Let’s chat about scientific notation and exponents ! I have found that the simplest skills in math are often the most miscalculated and confusing for students. Exponents and scientific notation can fall into this trap.
Vertical Alignment

Exponent Tips
It is important with both exponents and scientific notation that students understand that they show a different way to represent a value.
Before even showing an exponent, start by showing the expanded form like 7*7*7*7*7. You can start by asking students:
- Is this the most efficient way to write this?
- Would 7*5 give you the same result? Why or why not?
Tip: I have learned the hard way to NEVER use 2^2 in any of your early examples because it will just confuse students into thinking you multiply the base and exponent.
Easy, no-plan activity idea: A fun way for students to practice exponents is by using concentric circles. The inside circle is the base and the outside circle is the exponent. Assign students numbers 1-10 and have them rotate to a new partner each round. Students pair up, write down the exponent form, the expanded form, and then calculate the standard form. Keep rotating until your time is up.

Laws of Exponents
The laws of exponents are so fun! I love how students can build on their previous knowledge to come up with the laws themselves. For example:
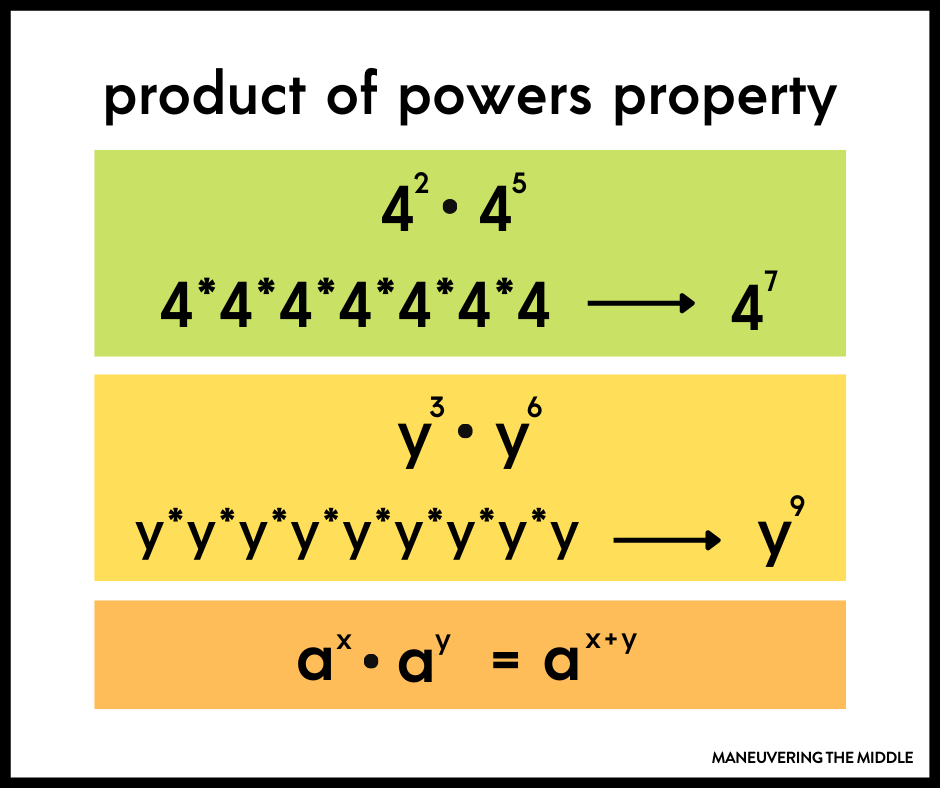
On a Facebook thread, I recently saw a teacher say, “When in doubt, expand it out.” If a student forgets a law, all they need to do is expand it and calculate to discover the law again. That is something a student is more likely to do if you are modeling it consistently.
Because the laws are so accessible, this content really shines as a discovery-based lesson. Your students could also participate in a jigsaw. Each group becomes experts at their assigned law, then they present the law, the proof, and examples to their peers.
If you go the traditional teaching route, I recommend splitting this skill up over at least 2 days. Maneuvering the Middle 8th grade curriculum covers multiplying/dividing like bases, power to power, and product to power on day one. Negative and zero exponents are covered on day two.
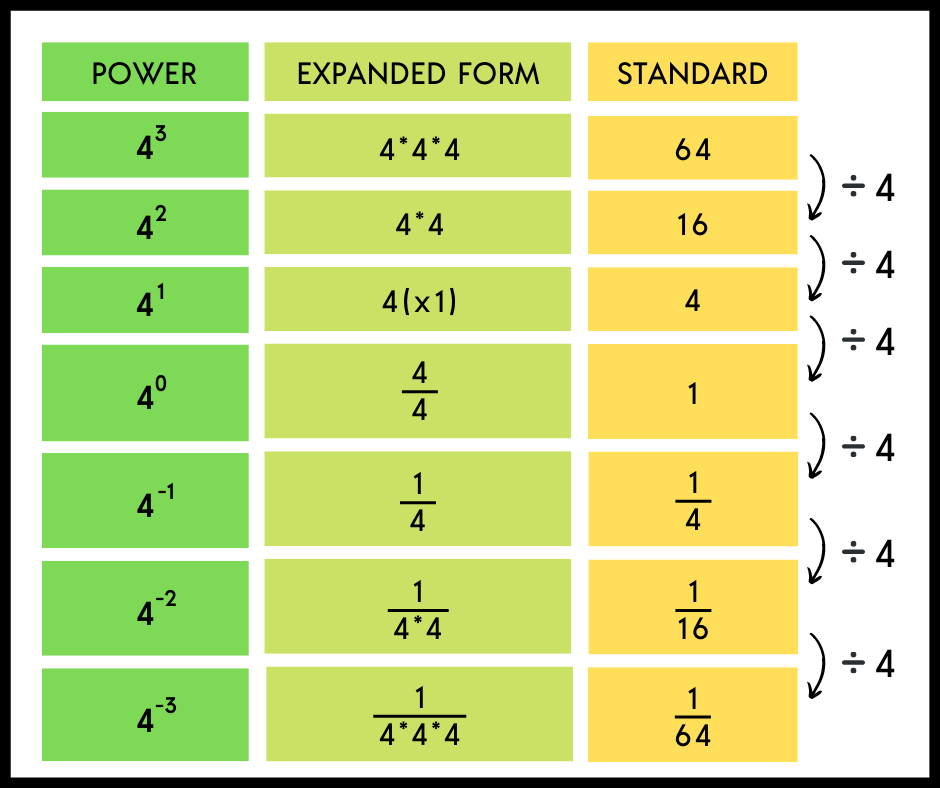
I highly recommend an anchor chart with all of the laws for easy reference. Sometimes in my last class on a Friday, my brain needed to look at an anchor chart to give it the boost it needed (and I am the teacher).
Scientific Notation
Like I said before, scientific notation is just a different way to represent a value. Here is a great way to introduce why we might use scientific notation. Write down the mass of Earth and Mars on your whiteboard or project it. Make sure students will have to copy it down themselves since that is part of your point.

Start by asking students to read the numbers to you. You will get some funny responses. Then ask students to add them or subtract the masses. As students write and count all of the zeros and inevitably miscalculate or miscount the number of zeros, you can introduce why we used scientific notation. (Less room for error, more efficient) Scientific notation is similar to typing TTYL instead of typing “talk to you later.”
Tips for Scientific Notation
Avoid using right or left when describing the direction to move the decimal. Instead, emphasize that smaller numbers will have negative exponents and larger numbers will have positive exponents. This re-enforces the negative exponent law.
Speaking of exponent laws, scientific notation operations reinforce the laws of exponents. If you look at the vertical alignment, scientific notation only shows up in 8th grade (in TEKS and CCSS), so at least, it reinforces other important concepts that students will use in Algebra 1 and 2.
I have never (and will never) teach Science, but it did occur to me to look up the Texas Science standards, and take a look at this chemistry standard –
“C.2(G) express and manipulate chemical quantities using scientific conventions and mathematical procedures, including dimensional analysis, scientific notation , and significant figures”
An opportunity for cross curricular?! Wahoo! If this is something that has peaked your interest, here is a NASA themed exploration lesson with resources for practicing scientific notation. This demos activity is also a great science based activity.
What tips do you have for teaching exponents and scientific notation?

Free Digital Math Activities
Digital Activities for 6th - 8th grade Math & Algebra 1 interactive | easy-to-use with Google Slides | self-grading Google Forms exit ticket
Check Out These Related Products From My Shop

If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Math (NSDC) - Hinglish
Course: math (nsdc) - hinglish > unit 7.
- Unit test Exponents
Exponents and Scientific Notation Unit | Properties of Exponents 8th Grade Notes

- Google Apps™
Description
A 10 day CCSS-Aligned Exponents and Scientific Notation Unit includes properties of exponents, integer exponents, scientific notations, adding and subtracting with scientific notation, and multiplying and dividing with scientific notation.
Students will practice with both skill-based problems, real-world application questions, and error analysis to support higher level thinking skills. You can reach your students and teach the standards without all of the prep and stress of creating materials!
Standards: 8.EE.1, 8.EE.2, 8.EE.3, 8.EE.4; Texas Teacher? Scientific Notation has been included in the TEKS-Aligned Real Number System Unit . Please don’t purchase both as there is overlapping content.
Learning Focus:
- evaluate square and cube roots
- know and apply the properties of exponents
- perform operations with numbers in scientific notation, including estimating quantities
More details on what is included:
1. Unit Overviews
- Streamline planning with unit overviews that include essential questions, big ideas, vertical alignment, vocabulary, and common misconceptions.
- A pacing guide and tips for teaching each topic are included to help you be more efficient in your planning.
2. Student Handouts
- Student-friendly guided notes are scaffolded to support student learning.
- Available as a PDF and the student handouts/homework/study guides have been converted to Google Slides™ for your convenience.
3. Independent Practice
- Daily homework is aligned directly to the student handouts and is versatile for both in class or at home practice.
4. Assessments
- 1-2 quizzes, a unit study guide, and a unit test allow you to easily assess and meet the needs of your students.
- The Unit Test is available as an editable PPT, so that you can modify and adjust questions as needed.
5. Answer Keys
- All answer keys are included.
***Please download a preview to see sample pages and more information.***
How to use this resource:
- Use as a whole group, guided notes setting
- Use in a small group, math workshop setting
- Chunk each student handout to incorporate whole group instruction, small group practice, and independent practice.
- Incorporate our Exponent and Scientific Notation Activity Bundle for hands-on activities as additional and engaging practice opportunities.
Time to Complete:
- Each student handout is designed for a single class period. However, feel free to review the problems and select specific ones to meet your student needs. There are multiple problems to practice the same concepts, so you can adjust as needed.
Is this resource editable?
- The unit test is editable with Microsoft PPT. The remainder of the file is a PDF and not editable.
Looking for hands-on classroom activities?
- Check out the corresponding Exponent and Scientific Notation Activity Bundle , which includes activities like scavenger hunts, find it and fix its, mazes and more to allow students to engage and practice the concepts. Win-win!
More 8th Grade Units:
Unit 1: Real Number System
Unit 2: Exponents and Scientific Notation
Unit 3: Linear Equations
Unit 4: Linear Relationships
Unit 5: Functions
Unit 6: Systems of Equations
Unit 7: Transformations
Unit 8: Angle Relationships
Unit 9: Pythagorean Theorem
Unit 10: Volume Unit 11: Scatter Plots and Data
More 8th Grade Activity Bundles:
Looking for more helpful teaching tips, ideas, and support? Check out Maneuveringthemiddle.com and join our online FB community MTM VIPS!
Try out a FREE math resource! Grab your freebie here!
Licensing:
This file is a license for ONE teacher and their students. Please purchase the appropriate number of licenses if you plan to use this resource with your team. Thank you!
Customer Service:
If you have any questions, please feel free to reach out for assistance . We aim to provide quality resources to help teachers and students alike, so contact me before leaving feedback if you have a need.
Maneuvering the Middle ® Terms of Use
Products by Maneuvering the Middle®, LLC may be used by the purchaser for their classroom use only. This is a single classroom license only. All rights reserved. Resources may only be posted online in an LMS such as Google Classroom, Canvas, or Schoology. Students should be the only ones able to access the resources. It is a copyright violation to upload the files to school/district servers or shared Google Drives. See more information on our terms of use here .
If you are interested in a personalized quote for campus and district licenses, please click here .
©Maneuvering the Middle® LLC, 2012-present
Questions & Answers
Maneuvering the middle.
- We're hiring
- Help & FAQ
- Privacy policy
- Student privacy
- Terms of service
- Tell us what you think

IMAGES
VIDEO
COMMENTS
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of \(10\). To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between \(1\) and \(10\).
The result is that x3 ⋅ x4 = x3 + 4 = x7. Notice that the exponent of the product is the sum of the exponents of the terms. In other words, when multiplying exponential expressions with the same base, we write the result with the common base and add the exponents. This is the product rule of exponents. am ⋅ an = am + n.
When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
To multiply with like bases, add the exponents. Quotient Property for Exponents. If a is a real number, a ≠ 0, and m and n are integers, then. am an = am − n, m > n and am an = 1 an − m, n > m. Zero Exponent. If a is a non-zero number, then a0 = 1. If a is a non-zero number, then a to the power of zero equals 1.
Unit 2 Dilations, similarity, and introducing slope. Unit 3 Linear relationships. Unit 4 Linear equations and linear systems. Unit 5 Functions and volume. Unit 6 Associations in data. Unit 7 Exponents and scientific notation. Unit 8 Pythagorean theorem and irrational numbers. Course challenge. Test your knowledge of the skills in this course.
Unit 5 Exponents intro and order of operations. Unit 6 Variables & expressions. Unit 7 Equations & inequalities introduction. Unit 8 Percent & rational number word problems. Unit 9 Proportional relationships. Unit 10 One-step and two-step equations & inequalities. Unit 11 Roots, exponents, & scientific notation. Unit 12 Multi-step equations.
Rule 2. 1 a − n = an. Rule 3. (a b) − n = (b a)n. Negative exponents are combined in several different ways. As a general rule, in a fraction, a base with a negative exponent moves to the other side of the fraction bar as the exponent changes sign.
Exponent properties review. Google Classroom. Review the common properties of exponents that allow us to rewrite powers in different ways. For example, x²⋅x³ can be written as x⁵. Property. Example. x n ⋅ x m = x n + m. . 2 3 ⋅ 2 5 = 2 8.
If a is a real number and m and n are integers, then. To multiply with like bases, add the exponents. Quotient Property for Exponents. If is a real number, and m and n are integers, then. Zero Exponent. If a is a non-zero number, then. If a is a non-zero number, then a to the power of zero equals 1.
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10.
Core Standards. 8.EE.A.1 — Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 3² × 3-5 = 3-3 = 1/3³ = 1/27. Expressions and Equations. 8.EE.A.1 — Know and apply the properties of integer exponents to generate equivalent numerical expressions.
6.3 Scientific Notation (Homework Assignment) 6.4 Basic Operations Using Polynomials. ... 6.1 Working with Exponents Exponents often can be simplified using a few basic properties, since exponents represent repeated multiplication. The basic structure of writing an exponent looks like [latex]x^y,[/latex] where [latex]x[/latex] is defined as the ...
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10.
Exponents and Scientific Notation Extra Practice Sheets. Rules of Exponents (Notes,not Practice Problems) Simplifying Exponents (Easier) Simplifying Exponents (Harder) Writing Numbers in Scientific Notation. Multiplying & Dividing Scientific Notation.
Exponents and Scientific Notation Notes Packet. Homework #1. Homework #2. Homework #3. Homework #4 Unit 1 Homework Calendar: 9/4 (Tuesday) - First Day of School 9/5 (Wednesday) - Get Welcome Letter Signed and Finish About Me 9/6 (Thursday) - 9/7 (Friday) - Welcome Letter and About Me Due!
"This year begins with students extending the properties of exponents to integer exponents in Module 1. They use the number line model to support their understanding of the rational numbers and the number system. The number system is revisited at the end of the year (in Module 7) to develop the real number line through a detailed study of irrational numbers.
Use the Quotient Property, a m a n = 1 a n − m. 1 b 5 − 3. Simplify. 1 7 2 or 1 49. A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like a m a m . We know, x x = 1 , for any x ( x ≠ 0) since any number divided by itself is 1.
A shorthand method of writing very small and very large numbers is called scientific notation, in which we express numbers in terms of exponents of 10. To write a number in scientific notation, move the decimal point to the right of the first digit in the number. Write the digits as a decimal number between 1 and 10.
Convert from Decimal Notation to Scientific Notation: To convert a decimal to scientific notation: Move the decimal point so that the first factor is greater than or equal to 1 but less than 10. Count the number of decimal places, n. \displaystyle n n , that the decimal point was moved. Write the number as a product with a power of.
Tips for Scientific Notation. Avoid using right or left when describing the direction to move the decimal. Instead, emphasize that smaller numbers will have negative exponents and larger numbers will have positive exponents. This re-enforces the negative exponent law. Speaking of exponent laws, scientific notation operations reinforce the laws ...
Unit test. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
CCSS 8.EE.A.1. Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example, 3² × (3⁻⁵) = (3⁻³) = 1/3³ = 1/27. CCSS 8.EE.A.2. Use square root and cube root symbols to represent solutions to equations of the form 𝘹² = 𝘱 and 𝘹³ = 𝘱, where 𝘱 is a positive rational number.
Study with Quizlet and memorize flashcards containing terms like 1. Simplify. 5⁻¹(3⁻²), 2. Simplify. mn⁻⁴/p⁰q⁻², 3. Write in scientific notation. 0.0042 and more.