random assignment random sampling measures of central tendency

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 6.

• Statistical significance of experiment

Random sampling vs. random assignment (scope of inference)

• Conclusions in observational studies versus experiments
• Finding errors in study conclusions
• (Choice A)   Just the residents involved in Hilary's study. A Just the residents involved in Hilary's study.
• (Choice B)   All residents in Hilary's town. B All residents in Hilary's town.
• (Choice C)   All residents in Hilary's country. C All residents in Hilary's country.
• (Choice A)   Yes A Yes
• (Choice B)   No B No
• (Choice A)   Just the residents in Hilary's study. A Just the residents in Hilary's study.

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.8: When to use each measure of Central Tendency

• Last updated
• Save as PDF
• Page ID 16240

By now, everyone should know how to calculate mean, median and mode. They each give us a measure of Central Tendency (i.e. where the center of our data falls), but often give different answers. So how do we know when to use each? Here are some general rules:

•  Mean is the most frequently used measure of central tendency and generally considered the best measure of it. However, there are some situations where either median or mode are preferred.
•  There are a few extreme scores in the distribution of the data. (NOTE: Remember that a single outlier can have a great effect on the mean). b.
• There are some missing or undetermined values in your data. c.
• There is an open ended distribution (For example, if you have a data field which measures number of children and your options are 0, 1, 2, 3, 4, 5 or “6 or more,” then the “6 or more field” is open ended and makes calculating the mean impossible, since we do not know exact values for this field) d.
• You have data measured on an ordinal scale.
• Mode is the preferred measure when data are measured in a nominal ( and even sometimes ordinal) scale.
• When to use each measure of Central Tendency?. Authored by : Paul Jones. Provided by : Columbia Basin College. License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.1: Measures of Central Tendency and Dispersion (Ungrouped Data)

• Last updated
• Save as PDF
• Page ID 139602

Learning Objectives

• Recognize, describe, and calculate the measures of the center of data.
• Recognize, describe, and calculate the measures of the spread of data.
• Use the Empirical rule to interpret the mean and standard deviation.

Measures of the Center of the Data

The "center" of a data set is also a way of describing the location. The two most widely used measures of the "center" of the data are the mean (average) and the median . To calculate the mean weight of 50 people, add the 50 weights together and divide by 50. To find the median weight of the 50 people, order the data and find the number that splits the data into two equal parts. The median is generally a better measure of the center when there are extreme values or outliers because it is not affected by the precise numerical values of the outliers. The mean is the most common measure of the center. 

The letter used to represent the sample mean is an \(x\) with a bar over it (pronounced “\(x\) bar”): \(\overline{x}\). The Greek letter \(\mu\) (pronounced "mew") represents the population mean . One of the requirements for the sample mean to be a good estimate of the population mean is for the sample taken to be truly random.

You can quickly find the location of the median by using the expression

\[\dfrac{n+1}{2}\]

The letter \(n\) is the total number of data values in the sample. If \(n\) is an odd number, the median is the middle value of the ordered data (ordered smallest to largest). If \(n\) is an even number, the median is equal to the average of the two middle values after the data has been ordered. For example, if the total number of data values is 97, then

\[\dfrac{n+1}{2} = \dfrac{97+1}{2} = 49.\]

The median is the 49 th value in the ordered data. If the total number of data values is 100, then

\[\dfrac{n+1}{2} = \dfrac{100+1}{2} = 50.5.\]

The median occurs midway between the 50 th and 51 st values. The location of the median and the value of the median are not the same. The upper case letter \(M\) is often used to represent the median. The next example illustrates the location of the median and the value of the median.

Example \(\PageIndex{1}\)

 The following dataset is in order from smallest to largest:

3; 4; 8; 8; 10; 11; 12; 13; 14; 15; 15; 16; 16; 17; 17; 18; 21; 22; 22; 24; 24; 25; 26; 26; 27; 27; 29; 29; 31; 32; 33; 33; 34; 34; 35; 37; 40; 44; 44; 47

Calculate the mean and the median.

The calculation for the mean is:

\[\bar{x} = \dfrac{[3+4+(8)(2)+10+11+12+13+14+(15)(2)+(16)(2)+...+35+37+40+(44)(2)+47]}{40} = 23.6\]

\[\dfrac{n+1}{2} = \dfrac{40+1}{2} = 20.5\]

Starting at the smallest value, the median is located between the 20 th and 21 st values (the two 24s):

\[M = \dfrac{24+24}{2} = 24\]

Exercise \(\PageIndex{1}\)

The following dataset is ordered from smallest to largest. Calculate the mean and median.

3; 4; 5; 7; 7; 7; 7; 8; 8; 9; 9; 10; 10; 10; 10; 10; 11; 12; 12; 13; 14; 14; 15; 15; 17; 17; 18; 19; 19; 19; 21; 21; 22; 22; 23; 24; 24; 24; 24

Mean: \(3 + 4 + 5 + 7 + 7 + 7 + 7 + 8 + 8 + 9 + 9 + 10 + 10 + 10 + 10 + 10 + 11 + 12 + 12 + 13 + 14 + 14 + 15 + 15 + 17 + 17 + 18 + 19 + 19 + 19 + 21 + 21 + 22 + 22 + 23 + 24 + 24 + 24 = 544\)

\[\dfrac{544}{39} = 13.95\]

Median: Starting at the smallest value, the median is the 20 th term, which is 13.

Interactive Exercise \(\PageIndex{1}\)

Another measure of the center is the mode. The mode is the most frequent value. There can be more than one mode in a data set as long as those values have the same frequency and that frequency is the highest. If there are no repeats in a dataset, meaning each value occurs exactly one time, there is no mode.

Example \(\PageIndex{2}\)

Statistics exam scores for 20 students are as follows:

50; 53; 59; 59; 63; 63; 72; 72; 72; 72; 72; 76; 78; 81; 83; 84; 84; 84; 90; 93

Find the mode.

The most frequent score is 72, which occurs five times. Mode = 72.

Exercise \(\PageIndex{2}\)

The number of books checked out from the library from 25 students are as follows:

0; 0; 0; 1; 2; 3; 3; 4; 4; 5; 5; 7; 7; 7; 7; 8; 8; 8; 8; 10; 10; 11; 11; 12; 12

There is a tie for the most frequent value: 7 and 8 both occur four times. Mode = 7 and 8.

Interactive Exercise \(\PageIndex{2}\)

Interactive exercise \(\pageindex{3}\), measures of variation of the data.

One of the differences between the two data sets that any measure of center doesn't capture is the variety of data within the set. To describe the variation quantitatively, we use measures of variation or measures of spread . Just as there are several different measures of center, there are also several different measures of variation. In this section, we examine two of the most frequently used measures of variation: the range and standard deviation.

Definition: Range

The range of a data set is the difference between the maximum (largest) and minimum (smallest) observations.

Example \(\PageIndex{4}\)

Find the range of the data:

The range of the data is the difference between the largest and the smallest values in the data set: 14−6=8

Interactive Exercise \(\PageIndex{4}\)

Definition: the standard deviation.

The range only measures the total variation and doesn't capture any variation between the minimum and maximum observed values. In contrast to the range, the standard deviation takes into account all the observations. It is the preferred measure of variation when the mean is used as the measure of center. Roughly speaking, the standard deviation measures variation by indicating how far, on average, the observations are from the mean. For a data set with a large amount of variation, the observations will, on average, be far from the mean; so the standard deviation will be large. For a data set with a small amount of variation, the observations will, on average, be close to the mean; so the standard deviation will be small.

Calculating the Standard Deviations

If \(x\) is a number, then the difference "\(x\) – mean" is called its deviation . In a data set, there are as many deviations as there are items in the data set. The deviations are used to calculate the standard deviation. If the numbers belong to a population, in symbols a deviation is \(x - \mu\). For sample data, in symbols a deviation is \(x - \bar{x}\).

The procedure to calculate the standard deviation depends on whether the numbers are the entire population or are data from a sample. The calculations are similar, but not identical. Therefore the symbol used to represent the standard deviation depends on whether it is calculated from a population or a sample. The lower case letter s represents the sample standard deviation and the Greek letter \(\sigma\) (sigma, lower case) represents the population standard deviation. If the sample has the same characteristics as the population, then s should be a good estimate of \(\sigma\).

To calculate the standard deviation, we need to calculate the variance first. The variance is the average of the squares of the deviations (the \(x - \bar{x}\) values for a sample, or the \(x - \mu\) values for a population). The symbol \(\sigma^{2}\) represents the population variance; the population standard deviation \(\sigma\) is the square root of the population variance. The symbol \(s^{2}\) represents the sample variance; the sample standard deviation s is the square root of the sample variance. You can think of the standard deviation as a special average of the deviations.

If the numbers come from a census of the entire population and not a sample, when we calculate the average of the squared deviations to find the variance, we divide by \(N\), the number of items in the population. If the data are from a sample rather than a population, when we calculate the average of the squared deviations, we divide by n – 1 , one less than the number of items in the sample.

Formulas for the Sample Standard Deviation

\[s = \sqrt{\dfrac{\sum(x-\bar{x})^{2}}{n-1}} \label{eq1}\]

\[s = \sqrt{\dfrac{\sum f (x-\bar{x})^{2}}{n-1}} \label{eq2}\]

For the sample standard deviation, the denominator is \(n - 1\), that is one less than the sample size.

Example \(\PageIndex{5}\)

Calculate the sample standard deviation for the following dataset.

5; 6; 10; 10; 14

First we calculate the mean:

\[\bar{x} = \dfrac{5+6+10+10+14}{5} = 9 \nonumber\]

The mean is 9.

The variance may be calculated by using a table. Then the standard deviation is calculated by taking the square root of the variance. We will explain the parts of the table after calculating s .

The sample variance , \(s^{2}\), is equal to the sum of the last column (52) divided by the total number of data values minus one (5 – 1):

\[s^{2} = \dfrac{52}{5-1} = 13 \nonumber\]

The sample standard deviation s is equal to the square root of the sample variance:

\[s = \sqrt{13} = 3.605551275 \nonumber\]

and this is rounded to two decimal places, \(s = 3.61\).

Interactive Exercise \(\PageIndex{5.1}\)

Interactive exercise \(\pageindex{5.2}\).

In practice, USE A CALCULATOR OR COMPUTER SOFTWARE TO CALCULATE THE STANDARD DEVIATION such as this one :

Descriptive Statistics Calculator

Regardless of the tool that you use, you still need to be aware of the context and use the appropriate notation for standard deviation \(\sigma\) or \(s\).

Interpreting the Mean and Standard Deviation Together

The empirical rule.

For data having a distribution that is BELL-SHAPED and SYMMETRIC:

• Approximately 68% of the data is within one standard deviation of the mean.
• Approximately 95% of the data is within two standard deviations of the mean.
• More than 99% of the data is within three standard deviations of the mean.

The empirical rule is also known as the 68-95-99.7 rule. We will learn more about this when studying the "Normal" or "Gaussian" probability distribution in later chapters.

Example \(\PageIndex{6}\)

Suppose \(x\) is from a population with mean 50 and standard deviation 6 with bell-shape distribution.

• About 68% of the x values lie within one standard deviation of the mean. Therefore, about 68% of the x values lie between –1σ = (–1)(6) = –6 and 1σ = (1)(6) = 6 of the mean 50. The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation from the mean 50.
• About 95% of the x values lie within two standard deviations of the mean. Therefore, about 95% of the x values lie between –2σ = (–2)(6) = –12 and 2σ = (2)(6) = 12. The values 50 – 12 = 38 and 50 + 12 = 62 are within two standard deviations from the mean 50.
• About 99.7% of the x values lie within three standard deviations of the mean. Therefore, about 99.7% of the x values lie between –3σ = (–3)(6) = –18 and 3σ = (3)(6) = 18 from the mean 50. The values 50 – 18 = 32 and 50 + 18 = 68 are within three standard deviations of the mean 50.

Exercise \(\PageIndex{6}\)

The population of scores on a college entrance exam have an approximate bell-shape distribution with mean, \(\mu = 52\) points and a standard deviation, \(\sigma = 11\) points.

• About 68% of the \(y\) values lie between what two values? These values are ________________.
• About 95% of the \(y\) values lie between what two values? These values are ________________.
• About 99.7% of the \(y\) values lie between what two values? These values are ________________.

a. About 68% of the values lie between the values 41 and 63.

b. About 95% of the values lie between the values 30 and 74.

c.  About 99.7% of the values lie between the values 19 and 85.

Interactive Exercise \(\PageIndex{6}\)

It is important to note that the Empirical Rule only applies when the shape of the distribution of the data is bell-shaped and symmetric thus allowing us to sketch the following shape of the distribution based only on the two numbers: the mean and the standard deviation:

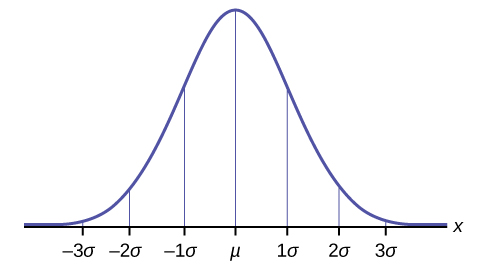
Figure \(\PageIndex{A}\)

Interactive Exercise \(\PageIndex{7}\)

3.2 – Measures of Central Tendency

Introduction.

• Other “means”
• How to calculate these other means
• Do try on your own!

Other measures of central tendency

Why the median may be a better middle than the mean, scaling and transformation of data, r operators, creating objects in r, r code calculate central tendency, chapter 3 contents.

For a sample of observations we can begin the summary by identifying the “typical” value. Various statistics are used to describe the middle and collectively these are referred to as measures of central tendency . The mean , the median , and the mode are the most common measures of central tendency. In the situation in which we work with data from a population census , we would calculate population descriptive statistics — not inferential statistics ; because we more often work with samples from populations, we report sample descriptive statistics .

First we review the familiar arithmetic mean and introduce the weighted mean. Next we introduce “other means,” which you may not be as familiar with.

There are several means beyond the simple arithmetic average or mean. Here we review a few. We use this topic also to start introducing standard notation we will use throughout the book.

The population mean , μ (pronounced “mu”) is given by

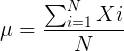
X i , an observation on the i -th individual

Σ, or “sigma,” which instructs you to add them up (the X’s), from i = 1 (the first observation) to i = N (the last observation).

Note: Parameters (aka random variables ) get Greek letters and sample variables get Roman letters . See Chapter 3.4

Weighted arithmetic mean

In some cases you may have several samples from the same population. If the sample sizes are the same, you can calculate the average of averages without any fuss — just take all of the sample means and add them up, then divide by the total number of samples. If the sample sizes differ, then you needs to weight (W) each sample mean by its sample size. Simply divide each sample mean by its appropriate sample size, then add all of these up. That is the weighted average.

More generally, we can write

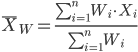
For example, consider a variable containing the following observations

Table 1. A sample of observations

The observation “4” was observed four times; the observation “5” was observed twice, and so on for a total of 15 observations.

What is the arithmetic mean of these 15 observations? To solve this, well, you have a couple of choices. You could copy the numbers down as often as they appear and then calculate the mean in the usual way.

Other “means”

The arithmetic average (illustrated above) is not the only way to estimate the mean.

The trimmed mean , also called the truncated mean , is a useful approach when data is widely dispersed — data spread away from the middle (see Chapter 3.3 ). Thus, the trimmed mean will be less influenced compared to the arithmetic mean by outlier data points , i.e., data far from other data points in the set.

You would use the trimmed mean to describe the middle of a data set in which a plot shows most of the values are clumped together around a middle – and yet you see a few values that are much smaller or much greater. A specified percentage of the smallest and largest values are removed from the data set and then the simple arithmetic mean is calculated for the trimmed data set. For example, given a data set of daily rainfall for different cities, you might wish to remove the driest 5% and wettest 5% of the days in order to better compare the rainfall trends for the cities.

Calculating the trimmed mean is straight-forward in R: use the same built-in function, mean() , but add some options.

This is a good point to remind you how to get help with R commands . Do you recall how to get help in R? 

At the R prompt type

The R Documentation page for mean() will pop up (assuming you allowed R to install help pages as html). Figure 1 shows a screenshot of a portion of the help page for mean()

Figure 1. A portion of the R help page about the function mean.

From the help page (Fig. 1) we can see that we can specify a trimmed mean by adding options to the mean(x, ...) command. For our x variable defined above, get the trimmed mean after 25% of the data are removed.

Note from the help page that the only required option you need to feed the mean command is the name of the variable, in this case, “x” (it can be, of course, any name provided the data are attached). In this case we removed 25% of the values – 12.5% of the smallest values and 12.5% of the largest values – that’s also called the interquartile mean.

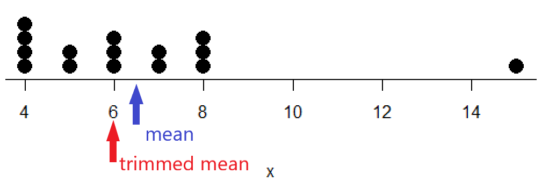
Figure 2. Dot plot of our x variable with locations of the mean (blue) and the trimmed mean (red).  The Dotplot(x) function in package RcmdrMisc was used in Rcmdr to make this graphic. Arrows were added by hand. Dotplot() example code presented in Chapter 3.4 .

If we recalculate a trimmed mean after dropping 10% of the points, or even 40% of the points, we get the same mean value of 6. The trimmed mean is an example of a robust estimator ; it’s resistant to the influence of outliers.

Another useful descriptor of the middle is the geometric mean . The geometric mean is useful for calculating the average of ratios.  Geometric mean would be used when you want to compare central tendency for different variables, each differing in scale. For example, gene expression results, reported as fold-changes, for different genes often shows tremendous differences among genes and would be best described by logarithmic scale, not arithmetic scale. Geometric mean expression values would be better choice for central tendency. Other examples are found in economics: for example, calculating compound interest or interest. The geometric mean applies whenever the scale is multiplicative and not additive

The geometric mean is given by the equation

The geometric mean (gm) is equivalent to log-transforming your data, then calculating the arithmetic mean, and transforming the result back (with the antilog exponent.) As you recall, for our simple data set the arithmetic mean was 6.2. The geometric mean for this data was 5.977. Taking the natural log for each of the values from our simple data set, then calculating the arithmetic mean we have 1.788. 

The antilog of this value is

Another frequently encountered mean is the harmonic mean , which is defined by the equation

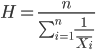
Harmonic mean is appropriate for averaging rates. For example, what is the average speed traveled if you travel 30 miles per hour (mph) between point A and B, then on the return trip, your speed was 40 mph? If you think (30 + 40)/2 = 35 mph, then this would be incorrect — after all, the distance covered has not changed, just the time. The harmonic mean returns 34.2 mph. Let

The harmonic mean returns 34.2 mph (see below “How to calculate these other means”)

Both harmonic and geometric means apply for values greater than zero.

How to calculate these “other” means

In Microsoft Excel, calculate geometric mean via the function GEOMEAN() ; calculate harmonic mean via the function HARMEAN() .

The base R (and Rcmdr) doesn’t have built in functions for these, although you could download and install some R packages which do (e.g., package psych , geometric.mean(variable) , harmonic.mean(variable) ). It is quicker to just to calculate these by submitting a snippet of code into the script window

For geometric mean of variable “x” at the R prompt type

For harmonic mean of variable “x” at the R prompt type

where is the base of the natural logarithm, Euler’s number , and log is the natural logarithm (in R, to get log to other bases you can use log10 for base 10 logarithm or log2 for base 2 logarithm , or   log(x, base = n ) for any base n of the variable x , and variable is the name of the variable you wish to do the calculations on.

R code: Do try on your own!

Here’s some numbers to try your hand. For example, create a variable containing a few numbers, any numbers. and write it to the variable named z

Now, calculate the arithmetic mean, the geometric mean, and the harmonic mean for the variable z . You should get Table 4.2)}

Table 2. Comparison of different means for z .

Try three more. In R (or R Commander script window), create three new variables.

Now, calculate the arithmetic mean, geometric mean, and harmonic mean for each variable.

For the simple arithmetic mean

For the geometric mean, use the formula above

For the harmonic mean, use the formula above

What did you get?

odd number of measurements minus the middle value minus even number of measurements minus average of the 2 middle values

Or, more succinctly, we have

To get the median in R type at the R prompt

and of course, replace variable with the name of the variable containing the numbers. For our x variable created earlier, the function median returns in R

[Note that the median for x was the same as the trimmed mean for x , which is consistent with with our view that the trimmed mean is a robust estimator of the middle of a data set.

Mode is another way to express the middle and it refers to the most frequent occurring measurement. Use of mode makes most sense for discrete or countable numbers. For a normal distribution, the mean, median and mode will be the same value. Note that a data set may have more than one mode. For example, what is the mode for the variable  we created earlier?

For this small data set we see that “4” is the most frequent with a count of four occurrences in the set.

Mode would seem like a straightforward function in R. However, it turns out there is not a mode function in the base package.

A little explanation is in order. In R, typing  mode at the R prompt like so

Not the answer we were expecting. In R, mode command is used to tell you what the mode (i.e., way or manner in which some task is accomplished) of storage is for the variables.

In order to get the statistical mode we want, we either hunt down a package that contains mode estimation (e.g., install the package modeest use the  mfv function), or we can write a little code.

Note: Although the  modeest  package is available from the typical repositories, the  genefilter  dependency required by  modeest  is available through  Bioconductor . Bioconductor is an R repository dedicated to R packages for genomic data analysis.

A quick Google search found a number of answers at stackoverflow.com (e.g., question 2547402 ). The simplest response was to use names and max commands like so

Comparing the two measures of central tendency can tell you without plotting how your data are distributed about the middle. Sample distributions are discussed in Chapter 6 . 

• When the distribution of the data is symmetric or normally distributed (discussed in Chapter 6.7 ) then the mean and the median will be about the same value
• When data are right-skewed (a few large values), then the mean will be greater than the median.
• When the data are left-skewed (a few small values), then the mean will be less than the median.

Here’s an illustration (Fig. 3). I sampled 100 points from a random normal distribution with mean zero and standard deviation 0ne and another 100 points from a log-normal distribution also with mean zero and standard deviation one. In Figure 3, the histograms (see Chapter 4.2 – Histograms ), along with summary statistics (see Note below). Means are indicated with red arrows and medians are indicated with blue arrows.

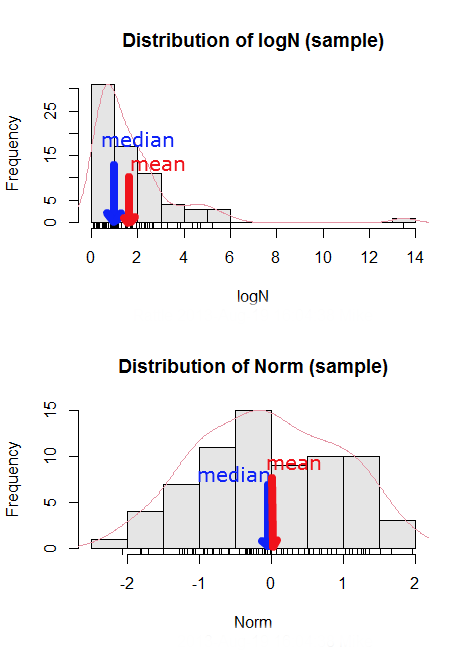
Figure 3. Normal and lognormal distributions with mean (red) and median (blue) noted for comparison.

So the median is a better descriptor or the central tendency of a sample distribution when the distribution is NOT normally distributed.

Note: “Summary statistics” refers to reporting of one or more descriptive statistics on a data set. The mean, median, standard deviation, range are common reported statistics. R Commander provides a menu to select from descriptive statistics, returning a table of the estimates. Rcmdr: Statistics → Summaries → Numerical summaries…

Sometimes it is useful to standardize your data so that the variables all have the same scale. One algorithm for standardization is called normalization . Normalization implies that you correct the data so that data has a mean, μ, of zero, and a standard deviation, σ, of 1 (unit variance). There are several ways to standardize, each with strengths and limitations. To normalize we use the Z-score equation (see Chapter 6.7 for other uses of Z score).

where  X i  is each observation in your data set.

Normalization will make outliers , the few points in a data set that are noticeably different from the central tendency of the rest of the data, smaller and less influential. When you normalize multiple sets of data, then each will have the same mean (0) and variance (unit variance), but the ranges will differ. An example of this is the simple product moment correlation — by standardizing you change the variances for the different variables to have the same unit variance.

As we will see later in class it is also useful to expand or contract the variability of the data or to change the shape of the distribution (if the data is not normally distributed). For example, if you compare individuals of a population for many morphological traits (e.g. body size, growth rate), the spread of points (called a distribution) will look more like a Poisson distribution (not symmetrical about the mean, a few individuals may be much larger…). This is partly due to the way in which morphological traits are measured. We normally measure body size on a linear scale (inches or centimeters). However, body size is affected by physiological processes that are more related to volume. Therefore, the more appropriate scale of measurement is on a log scale. We can transform the data measured on a linear scale to a log scale. For morphological traits this can produce a distribution that is normally distributed (bell shape). There are many more statistical procedures for data that is normally distributed than there are statistical procedures for Poisson distributions or any other type of distribution. Additional discussion about data transformation is introduced in Chapter 13.3 .

You can always uncode  or unstandardize  your data after performing the statistical procedures and return to the original scale. In fact, when reporting descriptive statistics you should report the untransformed, uncoded data. Moreover, you will find it useful to report means adjusted for other variables (e.g., from ANOVA or regression); if the ANOVA or regression equations are performed on transformed or coded data you would want to back calculate to the original scale after applying the ANOVA or regression adjustments. This advise will make more sense after we’ve discussed ANOVA ( Chapter 12 ) and linear regression ( Chapter 17 ).

The  names command can be used to retrieve the names contained in the variable (if text types) or to set the names of the observations, which is what we are using it for here. We set the numbers to text names “4”, “5”, etc. then find the maximum count of named items in the temp table. The double equals operator (==) is used to tell R to find the object that is “equal to” something we specify, in this case, the max value (R Language Definition 2014). Table 3 shows common operators in R.

Table 3. Common arithmetic* and comparison** operators

The R package modeest has a number of algorithms for calculating the mode, depending on the kind of data you are working with. After installing the package and its dependencies, type at the R prompt 

Everything in R is an object (Chambers 2008). Create the variable in R by assigning the vector x , either directly at the R prompt or in a script window (Rcmdr, RStudio), like so

The function c() , which stands for combine  is used to combine the set of numbers into the object, x . For small sets like this you may find it convenient to enter the values one by one and let R store it into the vector for you. Use the scan() function and your keyboard. Careful! Make sure that you remember to assign the results from scan to a vector.

I’ll create the object tryScan just to distinguish it from x , although I will enter the same values. Until R receives an interrupt signal from you, it will prompt you to enter numbers one row at a time. When you’ve reached the end, use the keyboard combination Ctrl+q ( Command + q on Macs) to interrupt keyboard input. 

The function tryScan is a very useful command, with many options, and can be used for more than keyboard entry. For example, you can paste from your computer’s clipboard a column of numbers from your spreadsheet.

Once we have the vector x , calculate the mean by entering at the R prompt

and you should get the answer of 6.466667

And of course, you don’t type in the R prompt > , right?

Or, for the better option, create two variables, one containing the list of observed numbers and the second that contains the frequency for each observed number in the series. You would then use the command for weighted mean.

Note — you can check that the frequencies sum to 1 by using the sum command like so

For the weighted mean, the command is

and, the answer returned is 6.466667 , the same as before.

• Find the help page in R for the median function. How does the function handle missing values?
• For a simple data set like the following y <- c(1,1,3,6) you should now be able to calculate, by hand, the • mean • median • mode
• If the observations for a ratio scale variable are normally (symmetrically) distributed, which statistic of central tendency is best (e.g., less sensitive to outlier values)?
• In the names() command, what do you think the result will be if you replace max in the command with  min ?
• If data are right skewed, what will be the order of the mean, median, and mode?
• Calculate the sample mean, median, and mode for the following data sets • Basal 5 hour fasting plasma glucose-to-insulin ratio of four inbred strains of mice, x <- c(44, 100, 105, 107) #(data from Berglund et al 2008) • Height in inches of mothers, mom <- c(67, 66.5, 64, 58.5, 68, 66.5) #(data from GaltonFamilies in R package HistData) and fathers, dad <- c(78.5, 75.5, 75, 75, 74, 74) #(data from GaltonFamilies in R package HistData) • Carbon dioxide (CO 2 ) readings from Mauna Loa for the month of December for demi-decade 1960 – 2020 years <-c (1960, 1965, 1970, 1975, 1980, 1985, 1990, 1995, 2000, 2005, 2010, 2015, 2020) #obviously, do not calculate statistics on years; you can use to make a plot co2 <- c(316.19, 319.42, 325.13, 330.62, 338.29, 346.12, 354.41, 360.82, 396.83, 380.31, 389.99, 402.06, 414.26) #data from Dr. Pieter Tans, NOAA/GML ( gml.noaa.gov/ccgg/trends/ ) and Dr. Ralph Keeling, Scripps Institution of Oceanography ( scrippsco2.ucsd.edu/ ) • Body mass of Rhinella marina (formerly Bufo marinus , Fig. 4), bufo <- c(71.3, 71.4, 74.1, 85.4, 85.4, 86.6, 97.4, 99.6, 107, 115.7, 135.7, 156.2)

Figure 4. Female Rhinella marina (formerly Bufo marinus ), Chaminade University campus. Body length 23.5 cm.

• Exploring data
• Measures of Central Tendency
• Measures of dispersion
• Estimating parameters
• Statistics of error
• References and suggested readings

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

1.4 - measures of central tendency.

  The ability to visually summarize data is effective, but someone like Maria will probably need to present some numerical summaries of her data to use in her reporting. The most common measures to describe data are measures of central tendency.

Mean, Median, Mode Section  

A measure of central tendency is an important aspect of quantitative data. It is an estimate of a “typical” value. Maria may be asked for the typical number of children seen per month.

Three of the many ways to measure central tendency are the mean, median and mode.

There are other measures, such as a trimmed mean, that we do not discuss here.

NOTE: At this point, we are going to start to use some basic notation to represent numbers as we present formulas and ways of calculating.  When you read "Let (some confusing symbols) represent" we are trying to convey the formula in a "generic" way.  If this gets confusing, skim over the formulas and pay more attention to the detailed example below!)

Let \(x_1, x_2, \ldots, x_n\) be our sample.  (As per the previous note, all we are doing is having the  \(x_1, x_2, \ldots, x_n\) represent numbers.  We could have easily illustrated this with real values such as (1,2,3,4 and 5)

The sample mean is usually denoted by \(\bar{x}\)  (If you are following this correctly, for the values of 1,2,3,4, and 5)\(\bar{x}\)  would be 3!)

\(\bar{x}=\sum_{i=1}^n \dfrac{x_i}{n}=\dfrac{1}{n}\sum_{i=1}^n x_i\)

where n is the sample size and \(x_i\) are the measurements. One may need to use the sample mean to estimate the population mean since usually only a random sample is drawn and we don't know the population mean.

Is this notation confusing you?  Don't let it get to you.  If this is not intuitive focus on the concepts of what the formulas are doing.  (in this example, we are adding all of the numbers (represented by the big squiggly E) and dividing by the total number of observations!

Quite simply, Maria would simply calculate the average number of children per month.

What if we say we used \(y_i\) for our measurements instead of \(x_i\)? Is this a problem? No. The formula would simply look like this: \(\bar{y}=\sum_{i=1}^n \dfrac{y_i}{n}=\dfrac{1}{n}\sum_{i=1}^n y_i\)

The formulas are exactly the same. The letters that you select to denote the measurements are up to you. For instance, many textbooks use \(y\) instead of \(x\) to denote the measurements. The point is to understand how the calculation that is expressed in the formula works. In this case, the formula is calculating the mean by summing all of the observations and dividing by the number of observations. There is some notation that you will come to see as standards, i.e, n will always equal sample size. We will make a point of letting you know what these are. However, when it comes to the variables, these labels can (and do) vary.

The median is the middle value of the ordered data. Maria might be asked to report the median if she had one or two months with extremely larger or small numbers of children seen at the agency.

The most important step in finding the median is to first order the data from smallest to largest.

Steps to finding the median for a set of data:

• Arrange the data in increasing order, i.e. smallest to largest.
• Find the location of the median in the ordered data by \(\frac{n+1}{2}\), where n is the sample size.
• The value that represents the location found in Step 2 is the median.

Example 1-2: SAT Data

From an SAT data set, we get the following participation rates for the nine South Atlantic states (Region is SA): 74, 79, 65, 75, 71, 74, 64, 73, and 20. In order to find the median we must first rank the data from smallest to largest:

20, 64, 65, 71, 73, 74, 74, 75, 79

To find the middle point we take the number of observations plus one and divide by two. Mathematically this looks like this where n is the number of total observations:

\(\dfrac{n+1}{2}=\dfrac{9+1}{2}=5\)

Returning to the ordered string of data, the fifth observation is 73. Thus the median of this distribution is 73. The interpretation of the median is that 50% of the observations fall at or below this value and 50% fall at or above this value. In this example, this would mean that 50% of the observations are at or below 73 and 50% are at or above 73. If another value was observed, say 88, this would bring the number of observations to ten. Using the formula above to find the middle point would be at 5.5 (10 plus 1 divided by 2). Here we would find the median by taking the average of the fifth and sixth observations which would be the average of 73 and 74. The new median for these ten observations would be 73.5. As you can see, the median value is not always an observed value of the data set.

To find the mean, we simply add all of the numbers and then divide this total by total numbers summed. Mathematically this looks like this where again n is the number of observations:

\(\bar{x}=\dfrac{\sum^n_{i=1}x_i}{n}=\dfrac{74+79+65+75+71+74+64+73+20}{9}=66.11\)

Effects of Outliers Section  

One shortcoming of the mean is that means are easily affected by extreme values. Measures that are not that affected by extreme values are called  resistant . Measures that are affected by extreme values are called  sensitive . As stated, Maria would use the median if she felt her numbers were could be impacted by outliers because the median is resistant to outliers.

Adding and Multiplying Constants Section  

What happens to the mean and median if we add or multiply each observation in a data set by a constant?

Consider for example if an instructor curves an exam by adding five points to each student’s score. What effect does this have on the mean and the median? The result of adding a constant to each value has the intended effect of altering the mean and median by the constant.

For example, if in the above example where we have 9 participation rates for the South Atlantic states, if 5 was added to each participation rate the mean of this new data set would be 71.11 (the original mean of 66.11 plus 5) and the new median would be 78 (the original median of 73 plus 5).

Similarly, if each observed data value was multiplied by a constant, the new mean and median would change by a factor of this constant. Returning to the 9 participation rates, if all of the original rates were multiplied by 1.20 (a 20 percent increase), then the new mean and new median would be found by multiplying the original mean and median by 1.20. As we will learn shortly, the effect is not the same on the variance!

Shape and Central Tendency Section  

The shape of the data helps us to determine the most appropriate measure of central tendency. The three most important descriptions of shape are Symmetric, Left-skewed, and Right-skewed. Skewness is a measure of the degree of asymmetry of the distribution. Maria might want to examine the shape of the distribution of the number of children seen.

• mean, median, and mode are all the same here
• no skewness is apparent
• the distribution is described as symmetric

Left-Skewed or Skewed Left

• mean < median
• long tail on the left

Right-skewed or Skewed Right

• mean > median
• long tail on the right

Uses and Abuses of Summaries Section  

  Descriptive statistics allow Maria to show her data using pictures, however as pointed out with the pie chart, not all presentations accurately portray the data. Since Maria is also balancing her reporting obligations to her funding needs, she might be tempted to present her data to convey very high usage rates or successes for her services. To avoid the temptation to misuse or misrepresent data, Maria needs to consider some of the ethics in statistics.