mcq questions on assignment problem

How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

• Subtract the smallest entry in each row from all the entries of the row.
• Subtract the smallest entry in each column from all the entries of the column.
• Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
• Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

• Emp 1 to Task 3
• Emp 2 to Task 2
• Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

• Machine Learning Decision Tree – Solved Problem (ID3 algorithm)
• Poisson Distribution | Probability and Stochastic Process
• Conditional Probability | Joint Probability
• Solved assignment problems in communicaion |online Request
• while Loop in C++

EngineersTutor

Solved assignment problems – algorithms and flowcharts.

An algorithm is defined as sequence of steps to solve a problem (task) . The steps must be finite, well defined and unambiguous. Writing algorithm requires some thinking. Algorithm can also be defined as a plan to solve a problem and represents its logic. Note that an algorithm is of no use if it does not help us arrive at the desired solution

Algorithm characteristics

• It should have finite number of steps . No one can be expected to execute infinite number of steps.
• The steps must be in order and simple
• Each step should be defined clearly i.e. without un-ambiguity (without doubtfulness)
• Must include all required information
• Should exhibit at least one output

A flowchart is a pictorial (graphical) representation of an algorithm . A flowchart is drawn using different kinds of symbols. A symbol is used for a specific purpose. Each symbol has name.

Different algorithms have different performance characteristics to solve the same problem. Some algorithms are fast. Some are slow. Some occupy more memory space. Some occupy less memory space. Some are complex and some algorithms are simple.

Logically algorithm, flowchart and program are the same.

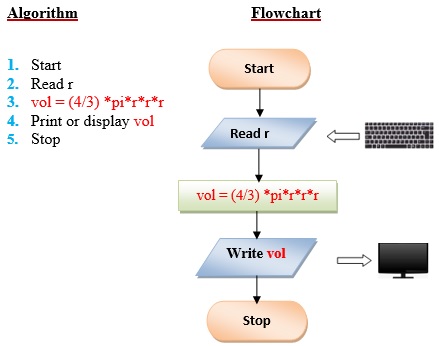
Q1 . Create a program to compute the volume of a sphere. Use the formula: V = (4/3) *pi*r 3 where pi is equal to 3.1416 approximately. The r is the radius of sphere.  Display the result.

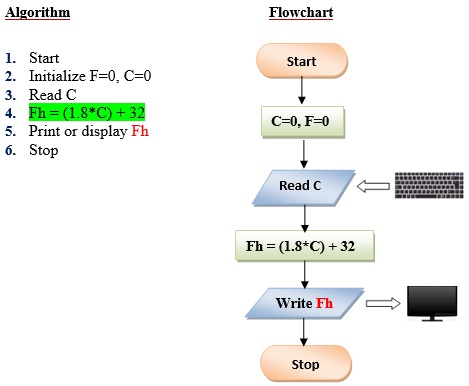
Q2 . Write a program the converts the input Celsius degree into its equivalent Fahrenheit degree. Use the formula: F = (9/5) *C+32.

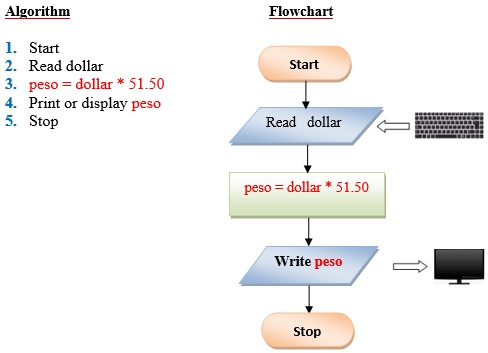
Q3 . Write a program that converts the input dollar to its peso exchange rate equivalent.  Assume that the present exchange rate is 51.50 pesos against the dollar. Then display the peso equivalent exchange rate.

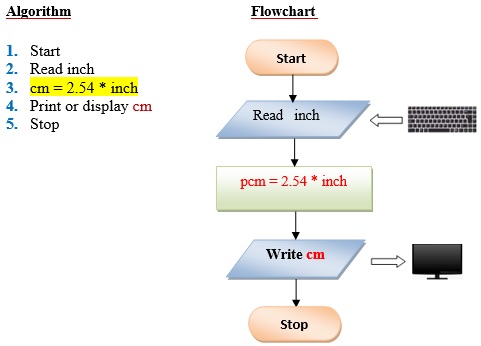
Q4 . Write a program that converts an input inch(es) into its equivalent centimeters. Take note that one inch is equivalent to 2.54cms.

Q5 . Write a program that exchanges the value of two variables: x and y.  The output must be: the value of variable y will become the value of variable x, and vice versa.

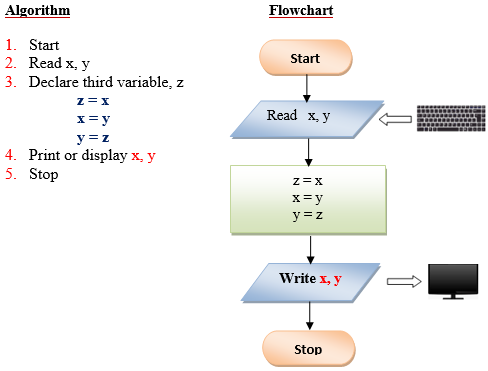
Q6 . Design a program to find the circumference of a circle. Use the formula: C=2πr, where π is approximately equivalent 3.1416.

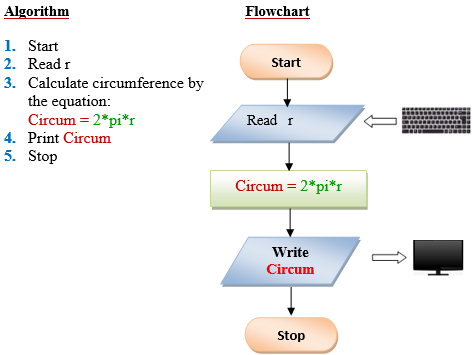
Q7 . Write a program that takes as input the purchase price of an item (P), its expected number of years of service (Y) and its expected salvage value (S). Then outputs the yearly depreciation for the item (D). Use the formula: D = (P – S) Y.

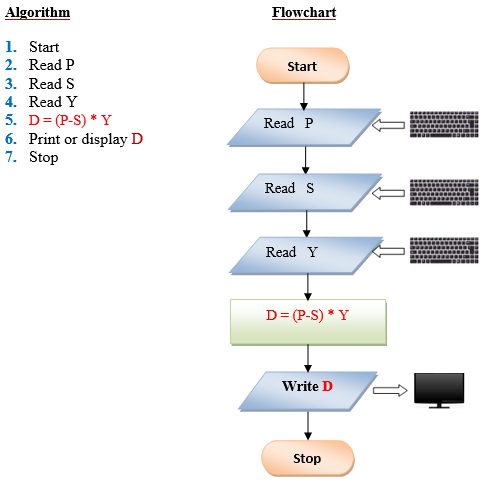
Q8 . Swapping of 2 variables without using temporary (or 3 rd variable).

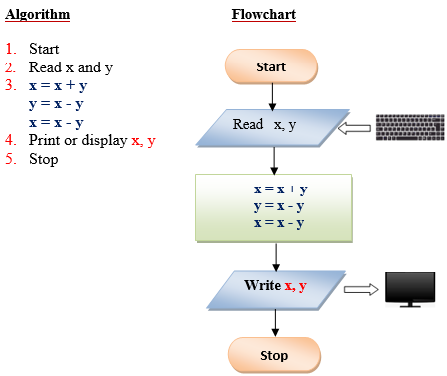
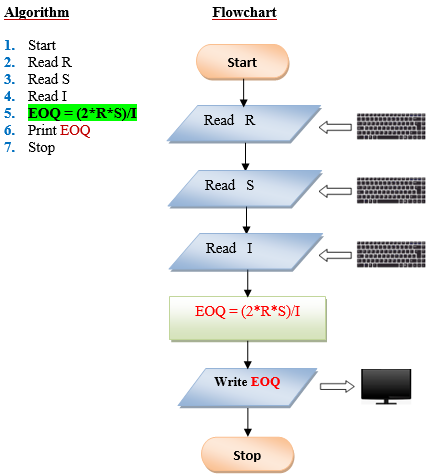
Q9 . Determine the most economical quantity to be stocked for each product that a manufacturing company has in its inventory: This quantity, called economic order quantity (EOQ) is calculated as follows: EOQ=2rs/1 where: R= total yearly production requirement S=set up cost per order I=inventory carrying cost per unit.

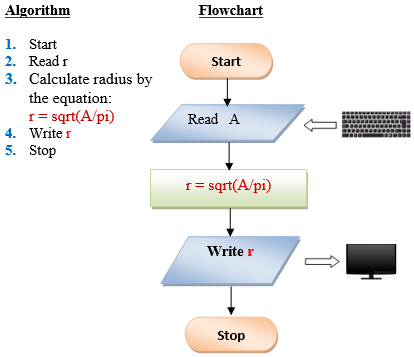
Q10 . Write a program to compute the radius of a circle. Derive your formula from the given equation: A=πr², then display the output.

• ← Solved Assignment Problems in Java (with Algorithm and Flowchart)
• Simple if statement in C →

Gopal Krishna

Hey Engineers, welcome to the award-winning blog,Engineers Tutor. I'm Gopal Krishna. a professional engineer & blogger from Andhra Pradesh, India. Notes and Video Materials for Engineering in Electronics, Communications and Computer Science subjects are added. "A blog to support Electronics, Electrical communication and computer students".

You May Also Like

Binary search example step by step, solved assignment problems in java (with algorithm and flowchart), programming languages, leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Data Science Questions and Answers – Clustering

This set of Data Science Multiple Choice Questions & Answers (MCQs) focuses on “Clustering”.

2. Point out the correct statement. a) The choice of an appropriate metric will influence the shape of the clusters b) Hierarchical clustering is also called HCA c) In general, the merges and splits are determined in a greedy manner d) All of the mentioned View Answer Answer: d Explanation: Some elements may be close to one another according to one distance and farther away according to another.

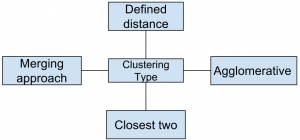
3. Which of the following is finally produced by Hierarchical Clustering? a) final estimate of cluster centroids b) tree showing how close things are to each other c) assignment of each point to clusters d) all of the mentioned View Answer Answer: b Explanation: Hierarchical clustering is an agglomerative approach.

4. Which of the following is required by K-means clustering? a) defined distance metric b) number of clusters c) initial guess as to cluster centroids d) all of the mentioned View Answer Answer: d Explanation: K-means clustering follows partitioning approach.

5. Point out the wrong statement. a) k-means clustering is a method of vector quantization b) k-means clustering aims to partition n observations into k clusters c) k-nearest neighbor is same as k-means d) none of the mentioned View Answer Answer: c Explanation: k-nearest neighbor has nothing to do with k-means.

6. Which of the following combination is incorrect? a) Continuous – euclidean distance b) Continuous – correlation similarity c) Binary – manhattan distance d) None of the mentioned View Answer Answer: d Explanation: You should choose a distance/similarity that makes sense for your problem.

7. Hierarchical clustering should be primarily used for exploration. a) True b) False View Answer Answer: a Explanation: Hierarchical clustering is deterministic.

8. Which of the following function is used for k-means clustering? a) k-means b) k-mean c) heatmap d) none of the mentioned View Answer Answer: a Explanation: K-means requires a number of clusters.

9. Which of the following clustering requires merging approach? a) Partitional b) Hierarchical c) Naive Bayes d) None of the mentioned View Answer Answer: b Explanation: Hierarchical clustering requires a defined distance as well.

10. K-means is not deterministic and it also consists of number of iterations. a) True b) False View Answer Answer: a Explanation: K-means clustering produces the final estimate of cluster centroids.

Sanfoundry Global Education & Learning Series – Data Science.

Here’s the list of Best Books in Data Science.

• Apply for Data Science Internship
• Apply for Computer Science Internship
• Check Data Science Books
• Practice Computer Science MCQs
• Check Programming Books

Recommended Articles:

• SQL Server Questions and Answers – Clustering
• Data Science Questions and Answers – Graphics Devices – 1
• Data Mining Questions and Answers – Data Reduction – Set 2
• Data Science Questions and Answers – caret – 3
• Data Science Questions and Answers – Pandas – 1
• Data Science Questions and Answers – Summarizing and Merging Data
• Data Science Questions and Answers – Basics of Data Science
• Spring Questions and Answers – Clustering Object State Using Terracotta and Execution to a Grid
• Data Science Questions and Answers – Reading from Web and APIs – 2
• Data Science Questions and Answers – Shiny
• Data Science MCQ Questions
• Data Structures in C
• Data Structures in Java
• Data Structures in C++
• Data Structure MCQ Questions
• Tree Programs in Java
• Python Programs on Trees
• Information Science Questions and Answers
• Computer Science MCQ Questions
• C Programming Examples on Trees

Problem Questions with Answer, Solution | Operations Research - Exercise 10.1: Transportation Problem | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research, exercise 10.1: transportation problem.

Exercise 10.1

1. What is transportation problem?

2. Write mathematical form of transportation problem.

3. what is feasible solution and non degenerate solution in transportation problem?

4. What do you mean by balanced transportation problem?

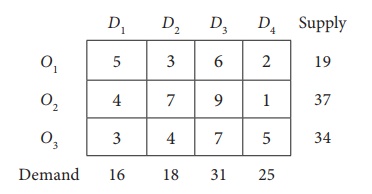
5. Find an initial basic feasible solution of the following problem using north west corner rule.

6. Determine an initial basic feasible solution of the following transportation problem by north west corner method

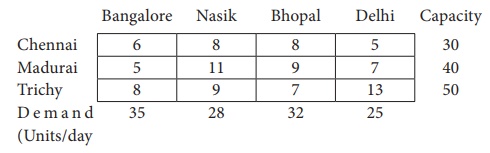
7. Obtain an initial basic feasible solution to the following transportation problem by using least- cost method.

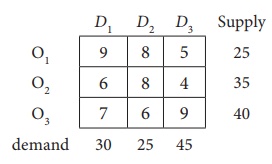
8. Explain Vogel’s approximation method by obtaining initial feasible solution of the following transportation problem

9. Consider the following transportation problem

Determine initial basic feasible solution by VAM

10. Determine basic feasible solution to the following transportation problem using North west Corner rule.

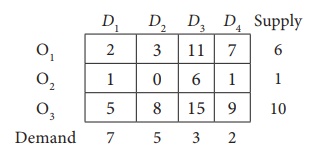
11. Find the initial basic feasible solution of the following transportation problem:

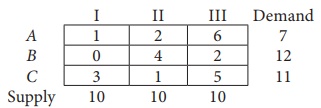
Using (i) North West Corner rule

(ii) Least Cost method

(iii) Vogel’s approximation method

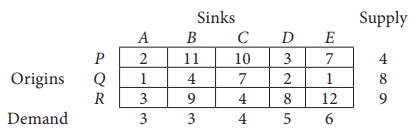
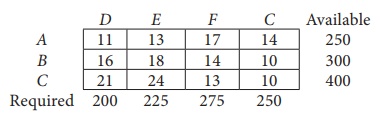
12. Obtain an initial basic feasible solution to the following transportation problem by north west corner method.

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2023 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Operations Research

31. Using ______________ method, we can never have an unbounded solution

• Dual simplex

32. The customers of high priority are given service over the low priority customers is ______________.

• Pre emptive

33. A queuing system is said to be a ______________ when its operating characteristic are independent upon time

• pure birth model
• pure death model
• transient state
• steady state

34. An activity which does not consume neither any resource nor time is known as ______________.

• predecessor activity
• successor activity
• dummy activity

35. The difference between total and free float is ______________.

• independent
• interference

36. The number of time estimates involved in Program Evaluation Review Technique problem is ______________.

37. The assignment problem is always a ______________matrix.

38. The slack variables indicate ______________.

• excess resource available.
• shortage of resource
• nil resource
• idle resource

39. If the net evaluation corresponding to any non -basic variable is zero, it is an indication of the existence of an ______________.

• initial basic feasible solution
• optimum basic feasible solution
• optimum solution.
• alternate optimum solution.

40. Mathematical model of linear programming problem is important because ______________.

• it helps in converting the verbal description and numerical data into mathematical expression
• decision makers prefer to work with formal models
• it captures the relevant relationship among decision factors
• it enables the use of algebraic technique

Search MBA MCQ.com

TRANSPORTATION PROBLEM Solved MCQs

Date: My name: Section ID: E-mail address: Format: Me: '); } else { document.write(' '); } } else { document.write(' '); } --> My Instructor: '); } else { document.write(' '); } } else { document.write(' '); } --> My TA: '); } else { document.write(' '); } } else { document.write(' '); } --> Other: '); } else { document.write(' '); } } else { document.write(' '); } --> To learn more about the book this website supports, please visit its . and . is one of the many fine businesses of . You must be a registered user to view the in this website. If you already have a username and password, enter it below. If your textbook came with a card and this is your first visit to this site, you can to register. Username: Password: '); document.write(''); } // --> ( ) .'); } else{ document.write('This form changes settings for this website only.'); } //--> Send mail as: '); } else { document.write(' '); } } else { document.write(' '); } // --> '); } else { document.write(' '); } } else { document.write(' '); } document.write(' TA email: '); } else { document.write(' '); } } else { document.write(' '); } // --> Other email: '); } else { document.write(' '); } } else { document.write(' '); } // --> "Floating" navigation? '); } else if (floatNav == 2) { document.write(' '); } else { document.write(' '); } // --> Drawer speed: '; theseOptions += (glideSpeed == 1) ? ' ' : ' ' ; theseOptions += (glideSpeed == 2) ? ' ' : ' ' ; theseOptions += (glideSpeed == 3) ? ' ' : ' ' ; theseOptions += (glideSpeed == 4) ? ' ' : ' ' ; theseOptions += (glideSpeed == 5) ? ' ' : ' ' ; theseOptions += (glideSpeed == 6) ? ' ' : ' ' ; document.write(theseOptions); // --> 1. (optional) Enter a note here: 2. (optional) Select some text on the page (or do this before you open the "Notes" drawer). 3. Highlighter Color: 4. Search for: Search in: Course-wide Content Quizzes More Resources Instructor Resources Course-wide Content Instructor Resources WatElectronics.com Operational Amplifier Question & Answers June 5, 2021 By WatElectronics This article lists 100+ Operational Amplifier MCQs for engineering students . All the O perational Amplifier Questions & Answers given below include a hint and wherever possible link to the relevant topic. This is helpful for users who are preparing for their exams, interviews, or professionals who would like to brush up their fundamentals on the Operational Amplifier topic. An operational amplifier also called OP-Amp and is a basic building block of analog-type electronic circuits. IC 741 is an op-amp invented by Karl D in 1967. It has 2 input terminals which are of differential voltage, where one of its input terminals is called inverting terminal represented as –V and another input terminal as +V, and a single output terminal Vout, which can be a source current and voltage or sink. The output obtained from an op-amp is an amplified value of the input signal. There are 4 types of gain in op-amps namely, voltage gain, current gain, transconductance gain, and trans resistance gain. Op-amp can perform operations such as logic and arithmetic. The advantage of an op-amp is it occupies less area, more reliable, low cost, low power consumption. The disadvantage of the Op-amp is designed for low-power operation only, not suitable for high output, and requires passive components. The applications of the op-amp are voltage comparator , Schmitt trigger , triangle wave oscillator, differentiator , and integrator. Read more about Operational Amplifier . Read more about Instrumentation Amplifier . Operational Amplifier MCQs for Interviews Read more about Isolation Amplifier . Read more about MOSFET . Operational Amplifier Exam Questions & Answers Read more about IGBT . Read more about Types of MOSFET . Read more about 741 Op-amp . Operational Amplifier Important Questions for Interviews Operational amplifier mcqs with answers. Test: Transportation & Assignment Model - Mechanical Engineering MCQ 10 questions mcq test - test: transportation & assignment model. 1 Crore+ students have signed up on EduRev. Have you? Which of the following is needed to use the transportation model? Capacity of the sources Demand of the destinations Unit shipping cost All of these Which method usually gives a very good solution to the assignment problem? Northwest corner rule Vogel's approximation method MODI method Stepping-stone method In applying Vogel’s approximation method to a profit maximation problem, row and column penalties are determined by finding the largest unit cost in each row or column. finding the sum of the unit costs in each row or column. finding the difference between the two highest unit costs in each row and column. finding the difference between the two lowest unit costs in each row and column. The concept of Vogel’s Approximation Method can be well understood through an illustration given below :  The difference between two least cost cells are calculated for each row and column, which can be seen in the iteration given for each row and column. Which one of the following is riot the solution method of transportation method? Hungarian method North west corner method Least cost method Vogel’s approximate method The matrix in assignment model is square maxtrix rectangular matrix diagonal matrix unit matrix Assignment model can be solved by conventional linear programming approach or transportation model approach, it is square matrix, having equal number of rows and columns. The objective is to assign one item from row to one item from column so that total cost of assignement is minimum. In order for a transportation matrix which has six rows and four columns not to degenerate, what is the number of occupied cells, in the matrix? Number of cells for non-degenerate solution  = 6 + 4 - 1 = 9 Consider the following statements: 1. For the application of optimally test in case of transportation model, the number of allocations should be equal to (m + n) where m is the number of rows and n is the number of columns. 2. Transportation problem is a special case of a linear programming problem. 3. In case of assignment problem, the first step is to dummy row or a matrix by adding a dummy row or a dummy column. Which of these statements is/are correct? 1 and 2 only 2 and 3 only Consider the following statements on transportation problem: 1. In Vogel’s approximation method, priority allotment is made in the cell with the lowest cost. 2. The North-west corner method ensures faster optimal solution. 3. If the total demand is higher than the supply, transportation problem cannot be solved. 4. A feasible solution may not be an optimal solution. Which of these statements are correct? Penalty cost method is North West corner method Vogel’s approximation method None of the above One disadvantage of using North-West Corner Rule to find initial solution to the transportation problem is that it is complicated to use it does not ’take into account cost of transportation it leads to a degenerate initial solution all of the above --> and get INR 200 additional OFF Top Courses for Mechanical Engineering Important Questions for Transportation & Assignment Model Transportation & assignment model mcqs with answers, online tests for transportation & assignment model. cation olution Join the 10M+ students on EduRev Welcome Back Create your account for free. Forgot Password Have an account? Transportation and Assignment Problem Mathematics. 5 questions Introducing new   Paper mode No student devices needed.   Know more The north- west corner rule is used to find Initial feasible solution An optimum solution Non- optimum solution None of these An assignment problem is a Non- integer programming problem Integer programming problem Transportation problem Which is true for assignment problem? The number of rows equals the number of columns All circled values in a stone are one All rim requirements are one All are true In a balanced transportation problem with m origins and n destinations the number of linearly independent constraints is In an unbalanced transportation problem with m- sources and n- destinations the number of basic variables is Explore all questions with a free account Continue with email Continue with phone 339 IMAGES MCQ Assignment More MCQ Practice Problems Questions Sample MCQ questions and answers How to create Multiple Choice Question (MCQS) Paper in ms word 2016 in two column MCQ Assignment Mcq sheet 4 VIDEO September 16, 2021 Assignment problem| Part 2 Interview Sample Questions Assignment Questions on Assignment Problem Innovation and Entrepreneurship interview questions Assignment 3 Part B Assignment problem question bank, random questions, assignment and grades in moodle COMMENTS Assignment MCQ [Free PDF] Assignment Question 10. An assignment problem is solved to minimize the total processing time of four jobs (1, 2, 3 and 4) on four different machines such that each job is processed exactly by one machine and each machine processes exactly one job. The minimum total processing time is found to be 500 minutes. MCQ Assignment Chapter 1: Assignment Problem. Multiple Choice Questions (MCQ) The application of assignment problems is to obtain _____. a. only minimum cost. b. only maximum profit. c. minimum cost or maximum profit. d. assign the jobs. The assignment problem is said to be unbalanced if _____. a. number of rows is greater than number of columns. b. 270+ Operations Research solved MCQs with PDF download Solved MCQs for Operations Research, ... When a maximization assignment problem is converted in minimization problem, the resulting matrix is called matrix. A. cost: B. regret: C. profit: D. dummy ... , Operations Research multiple choice questions and answers , Operations ... Problem Solving MCQ [Free PDF] Problem Solving Question 1: Arrange the stages of the problem-solving process in the correct order: A. Identifying the problem. B. Generating potential solutions. C. Implementing the chosen solution. D. Evaluating the outcomes. E. Analyzing the available information. Transportation and assignment MCQs Transportation and assignment Multiple Choice Questions. Operations research (OR) is an analytical method of problem-solving and decision-making that is useful. Skip to document. University; High School; ... The assignment problem will have alternate solutions when _____ (a) at least one zero in each row and column (b) when all rows have two ... How to Solve the Assignment Problem: A Complete Guide Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively. Linear Programming MCQ [Free PDF] Get Linear Programming Multiple Choice Questions (MCQ Quiz) with answers and detailed solutions. Download these Free Linear Programming MCQ Quiz Pdf and prepare for your upcoming exams Like Banking, SSC, Railway, UPSC, State PSC. ... The assignment problem is a special case of transportation problem when each origin is associated with one and ... Solved Assignment Problems Program. An algorithm is defined as sequence of steps to solve a problem (task). A flowchart is pictorial (graphical) representation of an algorithm. Set of instructions. Instruction is a command to the computer to do some task. Algorithm can also be defined as a plan to solve a problem and represents its logic. A picture is worth of 1000 words. PDF OPERATIONS RESEARCH Multiple Choice Questions a, b, and c are independent. a, b, and d are independent. d c. are independentb and d are i. dependent38. Consider the linear equation 2 x1 + 3 x2 - 4 x3 + 5 x4 = 10 How many basic and non. One variable is basic, three variables are non-basic. Two variables are basic, two variables are non-basic. e i. MCQ OR Multiple Choice Questions. Operations research is the application of _____methods to arrive at the optimal Solutions to the problems. A. economical B. scientific C. a and b both D. artistic. In operations research, the -----are prepared for situations. ... An assignment problem is a special case of transportation problem, where A. Number of ... Assignment Problems Assignment problems (AP) are a unique form of linear programming issues that are focused on the assigning of different types of merchandise. The goal of assignment problems are to find the optimal assignment, minimizing the expenses and the like. Assignment problems emerge on the grounds that accessible assets, for example, men, machines and so on. PDF ASSIGNMENT PROBLEM introduction to assignment problem matrix form of assignenmt problem mathematical formulation of an assignment problem difference between transportation problem and assigment problem assigment algorithm (or) hungarian method example of assigment problems question to answer mcq questions with answer k.bharathi,scsvmv. assignment problem 2 / 55 Clustering View Answer. 2. Point out the correct statement. a) The choice of an appropriate metric will influence the shape of the clusters. b) Hierarchical clustering is also called HCA. c) In general, the merges and splits are determined in a greedy manner. d) All of the mentioned. View Answer. 3. Exercise 10.1: Transportation Problem 5. Find an initial basic feasible solution of the following problem using north west corner rule. 6. Determine an initial basic feasible solution of the following transportation problem by north west corner method . 7. Obtain an initial basic feasible solution to the following transportation problem by using least- cost method. 8. Operations Research Multiple choice Questions and Answers. Page 4 Multiple choice Questions on Operations Research. Practice for BBA or MBA exams using these MCQ. Page 4. ... The assignment problem is always a _____matrix. circle; square; rectangle; triangle; View answer. Correct answer: (B) ... Mathematical model of linear programming problem is important because _____. TRANSPORTATION PROBLEM Solved MCQs with PDF Download An alternative optimal solution to a minimization transportation problem exists whenever opportunity cost corresponding to unused route of transportation is: A. positive & greater than zero. B. positive with at least one equal to zero. C. negative with at least one equal to zero. D. Operations Research MCQ [Free PDF] Get Operations Research Multiple Choice Questions (MCQ Quiz) with answers and detailed solutions. Download these Free Operations Research MCQ Quiz Pdf and prepare for your upcoming exams Like Banking, SSC, Railway, UPSC, State PSC. Multiple Choice Quiz The correct answer for each question is indicated by a . 1: Transportation and assignment problems can be solved by simplex method though special purpose algorithms offer an easier solution procedure. A) True: B) False: 2: The total supply must equal total demand in a transportation problem in order to solve it by the transportation algorithm ... 100+ Operational Amplifier Multiple Choice Questions (MCQ) with Answers This article lists 100+ Operational Amplifier MCQs for engineering students.All the Operational Amplifier Questions & Answers given below include a hint and wherever possible link to the relevant topic. This is helpful for users who are preparing for their exams, interviews, or professionals who would like to brush up their fundamentals on the Operational Amplifier topic. Transportation and Assignment Model Free MCQ Practice Test with Test: Transportation & Assignment Model - Question 8. Save. Consider the following statements on transportation problem: 1. In Vogel's approximation method, priority allotment is made in the cell with the lowest cost. 2. The North-west corner method ensures faster optimal solution. 3. MCQ 9. The Hungarian method is a. a way to develop an initial solution to a transportation problem. b. used to solve assignment problems. c. also called Vogel's approximation method. d. only used for problems in which the objective is to maximize profit. 10. In an assignment problem, it may be necessary to add more than one row to the table. a ... Transportation Model MCQ [Free PDF] Get Transportation Model Multiple Choice Questions (MCQ Quiz) with answers and detailed solutions. Download these Free Transportation Model MCQ Quiz Pdf and prepare for your upcoming exams Like Banking, SSC, Railway, UPSC, State PSC. ... The assignment problem is a special case of transportation problem when each origin is associated with one ... Transportation and Assignment Problem 2 minutes. 1 pt. An assignment problem is a. Non- integer programming problem. Integer programming problem. Transportation problem. None of these. 3. Multiple Choice. assignment essay homework paper phd report review speech thesis