case study of sensitivity analysis

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 18 May 2022

Sensitivity analysis in clinical trials: three criteria for a valid sensitivity analysis

• Sameer Parpia 1 , 2 ,
• Tim P. Morris 3 ,
• Mark R. Phillips   ORCID: orcid.org/0000-0003-0923-261X 2 ,
• Charles C. Wykoff 4 , 5 ,
• David H. Steel   ORCID: orcid.org/0000-0001-8734-3089 6 , 7 ,
• Lehana Thabane   ORCID: orcid.org/0000-0003-0355-9734 2 , 8 ,
• Mohit Bhandari   ORCID: orcid.org/0000-0001-9608-4808 2 , 9 &
• Varun Chaudhary   ORCID: orcid.org/0000-0002-9988-4146 2 , 9

for the Retina Evidence Trials InterNational Alliance (R.E.T.I.N.A.) Study Group

Eye volume  36 ,  pages 2073–2074 ( 2022 ) Cite this article

13k Accesses

6 Citations

26 Altmetric

Metrics details

• Outcomes research

What is a sensitivity analysis?

Randomized clinical trials are a tool to generate high-quality evidence of efficacy and safety for new interventions. The statistical analysis plan (SAP) of a trial is generally pre-specified and documented prior to seeing outcome data, and it is encouraged that researchers follow the pre-specified analysis plan. The process of pre-specification of the primary analysis involves making assumptions about methods, models, and data that may not be supported by the final trial data. Sensitivity analysis examines the robustness of the result by conducting the analyses under a range of plausible assumptions about the methods, models, or data that differ from the assumptions used in the pre-specified primary analysis. If the results of the sensitivity analyses are consistent with the primary results, researchers can be confident that the assumptions made for the primary analysis have had little impact on the results, giving strength to the trial findings. Recent guidance documents for statistical principles have emphasized the importance of sensitivity analysis in clinical trials to ensure a robust assessment of the observed results [ 1 ].

When is a sensitivity analysis valid?

While the importance of conducting sensitivity analysis has been widely acknowledged, what constitutes a valid sensitivity analysis has been unclear. To address this ambiguity, Morris et al. proposed a framework to conduct such analysis [ 2 ] and suggest that a particular analysis can be classified as a sensitivity analysis if it meets the following criteria: (1) the proposed analysis aims to answer the same question as to the primary analysis, (2) there is a possibility that the proposed analysis will lead to conclusions that differ from those of the primary analysis, and (3) there would be uncertainty as to which analysis to believe if the proposed analysis led to different conclusions than the primary analysis. These criteria can guide the conduct of sensitivity analysis and indicate what to consider when interpreting sensitivity analysis.

Criterion 1: do the sensitivity and primary analysis answer the same question?

The first criterion aims to ascertain whether the question being answered by the two analyses is the same. If the analysis addresses a different question than the primary question, then it should be referred to as a supplementary (or secondary) analysis. This may seem obvious, but it is important to consider, as if the questions being answered are different, the results could lead to unwarranted uncertainty regarding the robustness of the primary conclusions.

This misconception is commonly observed in trials where a primary analysis according to intention-to-treat (ITT) principle is followed by a per-protocol (PP) analysis, which many consider a sensitivity analysis. The ITT analysis considers the effect of a decision to treat regardless of if the treatment was received, while the PP analysis considers the effect of actually receiving treatment as intended. While the results of the PP analysis may be of value to certain stakeholders, the PP analysis is not a sensitivity analysis to a primary ITT analysis. Because the analyses address two distinct questions, it would not be surprising if the results differ. However, failure to appreciate that they ask different questions could lead to confusion over the robustness of the primary conclusions.

Criterion 2: could the sensitivity analysis yield different results than the primary analysis?

The second criterion relates to the assumptions made for the sensitivity analysis; if these assumptions will always lead to conclusions that are equivalent to the primary analysis, then we have learned nothing about the true sensitivity of the trial conclusion. Thus, a sensitivity analysis must be designed under a reasonable assumption that the findings could potentially differ from the primary analysis.

Consider the sensitivity analysis utilized in the LEAVO trial that assessed the effect of aflibercept and bevacizumab versus ranibizumab for patients with macular oedema secondary to central retinal vein occlusion [ 3 ]. The primary outcome of this study evaluated best-corrected visual acuity (BCVA) change from baseline for aflibercept, or bevacizumab, versus ranibizumab. At the end of the study, the primary outcome of the trial, BCVA score, was missing in some patients. For the purposes of imputation of the missing data, the investigators considered a range of values (from −20 to 20) as assumed values for the mean difference in BCVA scores between patients with observed and missing data. An example of this criterion not being met would be if a mean difference of 0 was used to impute BCVA scores for the missing patients, as it would be equivalent to re-running the primary analysis, leading to similar conclusions as to the primary analysis. This would provide a misleading belief in the robustness of results, as the “sensitivity” analysis conducted did not actually fulfill the appropriate criterion to be labeled as such.

On the other hand, modifying the assumptions to differ from the primary analysis by varying mean difference from −20 to 20 provides a useful analysis to assess the sensitivity of the primary analysis under a range of possible values that the missing participants may have had. One could reasonably postulate that assuming a mean change in BCVA scores of −20 to 20 to impute missing data could impact the primary analysis findings, as these values range from what one might consider a “best” and “worst” case scenario for the results observed among participants with missing data. In the LEAVO trial the authors demonstrated that, under these scenarios, the results of the sensitivity analysis support the primary conclusions of the trial.

Criterion 3: what should one believe if the sensitivity and primary analyses differ?

The third criterion assesses whether there would be uncertainty as to which analysis is to be believed if the proposed analysis leads to a different conclusion than the primary analysis. If one analysis will always be believed over another, then it is not worthwhile performing the analysis that will not be believed as it is impossible for that analysis to change our understanding of the outcome. Consider a trial in which an individual is randomized to intervention or control, and the primary outcome is measured for each eye. Because the results from each eye within a given patient are not independent, if researchers perform analyses both accounting for and not accounting for this dependence, it is clear that the analysis accounting for the dependence will be preferred. This is not a proper sensitivity analysis. In this situation, the analysis accounting for the dependence should be the primary analysis and the analysis not accounting for the dependence should not be performed, or be designated a secondary outcome.

Conclusions

Sensitivity analyses are important to perform in order to assess the robustness of the conclusions of the trial. It is critical to distinguish between sensitivity and supplementary or other analysis, and the above three criteria can inform an understanding of what constitutes a sensitivity analysis. Often, sensitivity analyses are underreported in published reports, making it difficult to assess whether appropriate sensitivity analyses were performed. We recommend that sensitivity analysis be considered a key part of any clinical trial SAP and be consistently and clearly reported with trial outcomes.

Food and Drug Administration. E9 (R1) statistical principles for clinical trials: addendum: estimands and sensitivity analysis in clinical trials. Guidance for Industry. May 2021.

Morris TP, Kahan BC, White IR. Choosing sensitivity analyses for randomised trials: principles. BMC Med Res Methodol. 2014;14:1–5. https://doi.org/10.1186/1471-2288-14-11 .

Article   CAS   Google Scholar  

Hykin P, Prevost AT, Vasconcelos JC, Murphy C, Kelly J, Ramu J, et al. Clinical effectiveness of intravitreal therapy with ranibizumab vs aflibercept vs bevacizumab for macular edema secondary to central retinal vein occlusion: a randomized clinical trial. JAMA Ophthalmol. 2019;137:1256–64. https://doi.org/10.1001/jamaophthalmol.2019.3305 .

Article   PubMed   PubMed Central   Google Scholar  

Download references

Author information

Authors and affiliations.

Department of Oncology, McMaster University, Hamilton, ON, Canada

Sameer Parpia

Department of Health Research Methods, Evidence, and Impact, McMaster University, Hamilton, ON, Canada

Sameer Parpia, Mark R. Phillips, Lehana Thabane, Mohit Bhandari & Varun Chaudhary

MRC Clinical Trials Unit, University College London, London, UK

Tim P. Morris

Retina Consultants of Texas (Retina Consultants of America), Houston, TX, USA

Charles C. Wykoff

Blanton Eye Institute, Houston Methodist Hospital, Houston, TX, USA

Sunderland Eye Infirmary, Sunderland, UK

David H. Steel

Biosciences Institute, Newcastle University, Newcastle Upon Tyne, UK

Biostatistics Unit, St. Joseph’s Healthcare-Hamilton, Hamilton, ON, Canada

Lehana Thabane

Department of Surgery, McMaster University, Hamilton, ON, Canada

Mohit Bhandari & Varun Chaudhary

NIHR Moorfields Biomedical Research Centre, Moorfields Eye Hospital, London, UK

Sobha Sivaprasad

Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

Peter Kaiser

Retinal Disorders and Ophthalmic Genetics, Stein Eye Institute, University of California, Los Angeles, CA, USA

David Sarraf

Department of Ophthalmology, Mayo Clinic, Rochester, MN, USA

Sophie J. Bakri

The Retina Service at Wills Eye Hospital, Philadelphia, PA, USA

Sunir J. Garg

Center for Ophthalmic Bioinformatics, Cole Eye Institute, Cleveland Clinic, Cleveland, OH, USA

Rishi P. Singh

Cleveland Clinic Lerner College of Medicine, Cleveland, OH, USA

Department of Ophthalmology, University of Bonn, Bonn, Germany

Frank G. Holz

Singapore Eye Research Institute, Singapore, Singapore

Tien Y. Wong

Singapore National Eye Centre, Duke-NUD Medical School, Singapore, Singapore

Centre for Eye Research Australia, Royal Victorian Eye and Ear Hospital, East Melbourne, VIC, Australia

Robyn H. Guymer

Department of Surgery (Ophthalmology), The University of Melbourne, Melbourne, VIC, Australia

You can also search for this author in PubMed   Google Scholar

• Varun Chaudhary
• , Mohit Bhandari
• , Charles C. Wykoff
• , Sobha Sivaprasad
• , Lehana Thabane
• , Peter Kaiser
• , David Sarraf
• , Sophie J. Bakri
• , Sunir J. Garg
• , Rishi P. Singh
• , Frank G. Holz
• , Tien Y. Wong
•  & Robyn H. Guymer

Contributions

SP was responsible for writing, critical review, and feedback on the manuscript. TPM was responsible for writing, critical review, and feedback on the manuscript. MRP was responsible for conception of idea, writing, critical review, and feedback on the manuscript. CCW was responsible for critical review and feedback on the manuscript. DHS was responsible for critical review and feedback on the manuscript. LT was responsible for critical review and feedback on the manuscript. MB was responsible for conception of idea, critical review, and feedback on the manuscript. VC was responsible for conception of idea, critical review, and feedback on the manuscript.

Corresponding author

Correspondence to Varun Chaudhary .

Ethics declarations

Competing interests.

SP: nothing to disclose. TPM: nothing to disclose. MRP: nothing to disclose. CCW: consultant: Acuela, Adverum Biotechnologies, Inc, Aerpio, Alimera Sciences, Allegro Ophthalmics, LLC, Allergan, Apellis Pharmaceuticals, Bayer AG, Chengdu Kanghong Pharmaceuticals Group Co, Ltd, Clearside Biomedical, DORC (Dutch Ophthalmic Research Center), EyePoint Pharmaceuticals, Gentech/Roche, GyroscopeTx, IVERIC bio, Kodiak Sciences Inc, Novartis AG, ONL Therapeutics, Oxurion NV, PolyPhotonix, Recens Medical, Regeneron Pharmaceuticals, Inc, REGENXBIO Inc, Santen Pharmaceutical Co, Ltd, and Takeda Pharmaceutical Company Limited; research funds: Adverum Biotechnologies, Inc, Aerie Pharmaceuticals, Inc, Aerpio, Alimera Sciences, Allergan, Apellis Pharmaceuticals, Chengdu Kanghong Pharmaceutical Group Co, Ltd, Clearside Biomedical, Gemini Therapeutics, Genentech/Roche, Graybug Vision, Inc, GyroscopeTx, Ionis Pharmaceuticals, IVERIC bio, Kodiak Sciences Inc, Neurotech LLC, Novartis AG, Opthea, Outlook Therapeutics, Inc, Recens Medical, Regeneron Pharmaceuticals, Inc, REGENXBIO Inc, Samsung Pharm Co, Ltd, Santen Pharmaceutical Co, Ltd, and Xbrane Biopharma AB—unrelated to this study. DHS: consultant: Gyroscope, Roche, Alcon, BVI; research funding for IIS: Alcon, Bayer, DORC, Gyroscope, Boehringer-Ingelheim—unrelated to this study. LT: nothing to disclose. MB: research funds: Pendopharm, Bioventus, Acumed—unrelated to this study. VC: advisory board member: Alcon, Roche, Bayer, Novartis; Grants: Bayer, Novartis—unrelated to this study.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Parpia, S., Morris, T.P., Phillips, M.R. et al. Sensitivity analysis in clinical trials: three criteria for a valid sensitivity analysis. Eye 36 , 2073–2074 (2022). https://doi.org/10.1038/s41433-022-02108-0

Download citation

Received : 06 May 2022

Revised : 09 May 2022

Accepted : 12 May 2022

Published : 18 May 2022

Issue Date : November 2022

DOI : https://doi.org/10.1038/s41433-022-02108-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Addressing Uncertainty in MultiSector Dynamics Research documentation

Sensitivity analysis: the basics, 3. sensitivity analysis: the basics ¶, 3.1. global versus local sensitivity ¶.

Out of the several definitions for sensitivity analysis presented in the literature, the most widely used has been proposed by Saltelli et al. [ 38 ] as “the study of how uncertainty in the output of a model (numerical or otherwise) can be apportioned to different sources of uncertainty in the model input”. In other words, sensitivity analysis explores the relationship between the model’s \(N\) input variables, \(x=[x_1,x_2,...,x_N]\) , and \(M\) output variables, \(y=[y_1,y_2,...,y_M]\) with \(y=g(x)\) , where \(g\) is the model that maps the model inputs to the outputs [ 39 ] .

Historically, there have been two broad categories of sensitivity analysis techniques: local and global. Local sensitivity analysis is performed by varying model parameters around specific reference values, with the goal of exploring how small input perturbations influence model performance. Due to its ease-of-use and limited computational demands, this approach has been widely used in literature, but has important limitations [ 40 , 41 ] . If the model is not linear, the results of local sensitivity analysis can be heavily biased, as they are strongly influenced by independence assumptions and a limited exploration of model inputs (e.g., Tang et al. [ 42 ] ). If the model’s factors interact, local sensitivity analysis will underestimate their importance, as it does not account for those effects (e.g., [ 43 ] ). In general, as local sensitivity analysis only partially and locally explores a model’s parametric space, it is not considered a valid approach for nonlinear models [ 44 ] . This is illustrated in Fig. 3.1 (a-b), presenting contour plots of a model response ( \(y\) ) with an additive linear model (a) and with a nonlinear model (b). In a linear model without interactions between the input terms \(x_1\) and \(x_2\) , local sensitivity analysis (assuming deviations from some reference values) can produce appropriate sensitivity indices ( Fig. 3.1 (a)). If however, factors \(x_1\) and \(x_2\) interact, the local and partial consideration of the space can not properly account for each factor’s effects on the model response ( Fig. 3.1 (b)), as it is only informative at the reference value where it is applied. In contrast, a global sensitivity analysis varies uncertain factors within the entire feasible space of variable model responses ( Fig. 3.1 (c)). This approach reveals the global effects of each parameter on the model output, including any interactive effects. For models that cannot be proven linear, global sensitivity analysis is preferred and this text is primarily discussing global sensitivity analysis methods. In the text that follows, whenever we use the term sensitivity analysis we are referring to its global application.

Fig. 3.1 Treatment of a two-dimensional space of variability by local (panels a-b) and global (panel c) sensitivity analyses. Panels depict contour plots with the value of a model response ( \(y\) ) changing with changes in the values of input terms \(x_1\) and \(x_2\) . Local sensitivity analysis is only an appropriate approach to sensitivity in the case of linear models without interactions between terms, for example in panel (a), where \(y=3x_1+5x_2\) . In the case of more complex models, for example in panels (b-c), where \(y={1 \above 1pt e^{x^2_1+x^2_2}} + {50 \above 1pt e^{(0.1x_1)^2+(0.1x_2)^3}}\) , local sensitivity will miscalculate sensitivity indices as the assessed changes in the value \(y\) depend on the assumed base values chose for \(x_1\) and \(x_2\) (panel (b)). In these cases, global sensitivity methods should be used instead (panel (c)). The points in panel (c) are generated using a uniform random sample of \(n=50\) , but many other methods are available. ¶

3.2. Why Perform Sensitivity Analysis ¶

It is important to understand the many ways in which a SA might be of use to your modeling effort. Most commonly, one might be motivated to perform sensitivity analysis for the following reasons:

Model evaluation : Sensitivity analysis can be used to gauge model inferences when assumptions about the structure of the model or its parameterization are dubious or have changed. For instance, consider a numerical model that uses a set of calibrated parameter values to produce outputs, which we then use to inform decisions about the real-world system represented. One might like to know if small changes in these parameter values significantly change this model’s output and the decisions it informs or if, instead, our parameter inferences yield stable model behavior regardless of the uncertainty present in the specific parameterized processes or properties. This can either discredit or lend credence to the model at hand, as well as any inferences drawn that are founded on its accurate representation of the system. Sensitivity analysis can identify which uncertain model factors cause this undesirable model behavior.

Model simplification : Sensitivity analysis can also be used to identify factors or components of the model that appear to have limited effects on direct outputs or metrics of interest. Consider a model that has been developed in an organization for the purposes of a specific research question and is later used in the context of a different application. Some processes represented in significant detail might no longer be of the same importance while consuming significant data or computational resources, as different outputs might be pertinent to the new application. Sensitivity analysis can be used to identify unimportant model components and simplify them to nominal values and reduced model forms. Model complexity and computational costs can therefore be reduced.

Model refinement : Alternatively, sensitivity analysis can reveal the factors or processes that are highly influential to the outputs or metrics of interest, by assessing their relative importance. In the context of model evaluation, this can inform which model components warrant additional investigation or measurement so the uncertainty surrounding them and the resulting model outputs or metrics of interest can be reduced.

Exploratory modeling : When sufficient credence has been established in the model, sensitivity analysis can be applied to a host of other inquiries. Inferences about the factors and processes that most (or least) control a model’s outputs of interest can be extrapolated to the real system they represent and be used in a heuristic manner to inform model-based inferences. On this foundation, a model paired with the advanced techniques presented in this text can be used to “discover” decision relevant and highly consequential outcomes (i.e., scenario discovery, discussed in more detail in Chapter 4.3 [ 36 , 45 ] ).

The nature and context of the model shapes the specific objectives of applying a sensitivity analysis, as well as methods and tools most appropriate and defensible for each application setting [ 35 , 38 , 46 ] . The three most common sensitivity analysis modes ( Factor Prioritization , Factor Fixing , and Factor Mapping ) are presented below, but the reader should be aware that other uses have been proposed in the literature (e.g., [ 47 , 48 ] ).

Factor prioritization : This sensitivity analysis application mode (also referred to as factor ranking ) refers to when one would like to identify the uncertain factors that have the greatest impact on the variability of the output, and which, when fixed to their true value (i.e., if there were no uncertainty regarding their value), would lead to the greatest reduction in output variability [ 49 ] . Information from this type of analysis can be crucial to model improvement as these factors can become the focus of future measurement campaigns or numerical experiments so that uncertainty in the model output can be reduced. The impact of each uncertain input on the variance of the model output is often used as the criterion for factor prioritization. Fig. 3.2 (a) shows the effects of three uncertain variables ( \(X_1\) , \(X_2\) , and \(X_3\) ) on the variance of output \(Y\) . \(V(E(Y|X_i))\) indicates the variance in \(Y\) if factor \(X_i\) is left to vary freely while all other factors remain fixed to nominal values. In this case, factor \(X_2\) makes the largest contribution to the variability of output \(Y\) and it should therefore be prioritized. In the context of risk analysis, factor prioritization can be used to reduce output variance to below a given tolerable threshold (also known as variance cutting).

Factor fixing : This mode of sensitivity analysis (also referred to as factor screening ) aims to identify the model components that have a negligible effect or make no significant contributions to the variability of the outputs or metrics of interest (usually referred to as non-influential [ 49 ] ). In the stylized example of Fig. 3.2 (a), \(X_1\) makes the smallest contribution to the variability of output \(Y\) suggesting that the uncertainty in its value could be negligible and the factor itself fixed in subsequent model executions. Eliminating these factors or processes in the model or fixing them to a nominal value can help reduce model complexity as well as the unnecessary computational burden of subsequent model runs, results processing, or other sensitivity analyses (the fewer uncertain factors considered, the fewer runs are necessary to illuminate their effects on the output). Significance of the outcome can be gauged in a variety of manners, depending on the application. For instance, if applying a variance-based method, a minimum threshold value of contribution to the variance could be considered as a significance ‘cutoff’, and factors with indices below that value can be considered non-influential. Conclusions about factor fixing should be made carefully, considering all of the effects a factor has, individually and in interaction with other factors (explained in more detail in the Chapter 3.4.5 ).

Factor mapping : Finally, factor mapping can be used to pinpoint which values of uncertain factors lead to model outputs within a given range of the output space [ 49 ] . In the context of model diagnostics, it is possible that the model’s output changes in ways considered impossible based on the represented processes, or other observed evidence. In this situation, factor mapping can be used to identify which uncertain model factors cause this undesirable model behavior by ‘filtering’ model runs that are considered ‘non-behavioral’ [ 50 , 51 , 52 ] . In Fig. 3.2 (b), region \(B\) of the output space \(Y\) denotes the set of behavioral model outcomes and region \(\bar{B}\) denotes the set of non-behavioral outcomes, resulting from the entirety of input space \(X\) . Factor mapping refers to the process of tracing which factor values of input space \(X\) produce the behavioral model outcomes in the output space.

Fig. 3.2 Factor prioritization, factor fixing and factor mapping settings of sensitivity analysis. ¶

The language used above reflects a use of sensitivity analysis for model fidelity evaluation and refinement. However, as previously mentioned, when a model has been established as a sufficiently accurate representation of the system, sensitivity analysis can produce additional inferences (i.e., exploratory modeling and scenario discovery). For instance, under the factor mapping use, the analyst can now focus on undesirable system states and discover which factors are most responsible for them: for instance, “population growth of above 25% would be responsible for unacceptably high energy demands”. Factor prioritization and factor fixing can be used to make equivalent inferences, such as “growing populations and increasing temperatures are the leading factors for changing energy demands” (prioritizing of factors) or “changing dietary needs are inconsequential to increasing energy demands for this region” (a factor that can be fixed in subsequent model runs). All these inferences hinge on the assumption that the real system’s stakeholders consider the model states faithful enough representations of system states. As elaborated in Chapter 2.2 , this view on sensitivity analysis is founded on a relativist perspective on modeling, which tends to place more value on model usefulness rather than strict accuracy of representation in terms of error. As such, sensitivity analysis performed with decision-making relevance in mind will focus on model outputs or metrics that are consequential and decision relevant (e.g., energy demand in the examples above).

3.3. Design of Experiments ¶

Before conducting a sensitivity analysis, the first element that needs to be clarified is the uncertainty space of the model [ 51 , 53 ] . In other words, how many and which factors making up the mathematical model are considered uncertain and can potentially affect the model output and the inferences drawn from it. Uncertain factors can be model parameters, model structures, inputs, or alternative model resolution levels (scales), all of which can be assessed through the tools presented in this text. Depending on the kind of factor, its variability can be elicited through various means: expert opinion, values reported in the literature, historical observations, its physical meaning (e.g., population values in a city can never be negative), or through the use of more formal UQ methods ( Chapter A ). The model uncertainty space represents the entire space of variability present in each of the uncertain factors of a model. The complexity of most real-world models means that the response function, \(y=g(x)\) , mapping inputs to outputs, is hardly ever available in an analytical form and therefore analytically computing the sensitivity of the output to each uncertain factor becomes impossible. In these cases, sensitivity analysis is only feasible through numerical procedures that employ different strategies to sample the uncertainty space and calculate sensitivity indices.

A sampling strategy is often referred to as a design of experiments and represents a methodological choice made before conducting any sensitivity analysis. Experimental design was first introduced by Fisher [ 54 ] in the context of laboratory or field-based experiments. Its application in sensitivity analysis is similar to setting up a physical experiment in that it is used to discover the behavior of a system under specific conditions. An ideal design of experiments should provide a framework for the extraction of all plausible information about the impact of each factor on the output of the model. The design of experiments is used to set up a simulation platform with the minimum computational cost to answer specific questions that cannot be readily drawn from the data through analytical or common data mining techniques. Models representing coupled human-natural systems usually have a large number of inputs, state variables and parameters, but not all of them exert fundamental control over the numerical process, despite their uncertainty, nor have substantial impacts on the model output, either independently or through their interactions. Each factor influences the model output in different ways that need to be discovered. For example, the influence of a parameter on model output can be linear or non-linear and can be continuous or only be active during specific times or at particular states of the system [ 55 , 56 ] . An effective and efficient design of experiments allows the analyst to explore these complex relationships and evaluate different behaviors of the model for various scientific questions [ 57 ] . The rest of this section overviews some of the most commonly used designs of experiments. Table 1 summarizes the designs discussed.

There are a few different approaches to the design of experiments, closely related to the chosen sensitivity analysis approach, which is in turn shaped by the research motivations, scientific questions, and computational constraints at hand (additional discussion of this can be found at the end of Chapter 3 ). For example, in a sensitivity analysis using perturbation and derivatives methods, the model input parameters vary from their nominal values one at a time, something that the design of experiments needs to reflect. If, instead, one were to perform sensitivity analysis using a multiple-starts perturbation method, the design of experiments needs to consider that multiple points across the factor space are used. The design of experiments specifically defines two key characteristics of samples that are fed to the numerical model: the number of samples and the range of each factor.

Generally, sampling can be performed randomly or by applying a stratifying approach. In random sampling, such as Monte Carlo [ 58 ] , samples are randomly generated by a pseudo-random number generator with an a-priori assumption about the distribution of parameters and their possible ranges. Random seeds can also be used to ensure consistency and higher control over the random process. However, this method could leave some gaps in the parameter space and cause clustering in some spaces, especially for a large number of parameters [ 59 ] . Most sampling strategies use stratified sampling to mitigate these disadvantages. Stratified sampling techniques divide the domain of each factor into subintervals, often of equal lengths. From each subinterval, an equal number of samples is drawn randomly, or based on the specific locations within the subintervals [ 49 ] .

3.3.1. One-At-a-Time (OAT) ¶

In this approach, only one model factor is changed at a time while all others are kept fixed across each iteration in a sampling sequence. The OAT method assumes that model factors of focus are linearly independent (i.e., there are no interactions) and can analyze how factors individually influence model outputs or metrics of interest. While popular given its ease of implementation, OAT is ultimately limited in its exploration of a model’s sensitivities [ 49 ] . It is primarily used with local sensitivity techniques with similar criticisms: applying this sampling scheme on a system with nonlinear and interactive processes will miss important information on the effect uncertain factors have on the model. OAT samplings can be repeated multiple times in a more sophisticated manner and across different locations of the parameter space to overcome some of these challenges, which would increase computational costs and negate the main reasons for its selection. Given these limitations OAT methods could be used as preliminary, low-cost analyses of the factors’ individual effects, but should ultimately be complemented with more sophisticated methods.

3.3.2. Full and Fractional Factorial Sampling ¶

In full factorial sampling each factor is treated as being discrete by considering two or more levels (or intervals) of its values. The sampling process then generates samples within each possible combination of levels, corresponding to each parameter. This scheme produces a more comprehensive sampling of the factors’ variability space, as it accounts for all candidate combinations of factor levels ( Fig. 3.3 (a)). If the number of levels is the same across all factors, the number of generated samples is estimated using \(n^k\) , where \(n\) is the number of levels and \(k\) is the number of factors. For example, Fig. 3.3 (a) presents a full factorial sampling of three uncertain factors \((x_1,\) \(x_2,\) and \(x_3)\) , each considered as having four discrete levels. The total number of samples necessary for such an experiment is \(4^3=64\) . As the number of factors increases, the number of simulations necessary will also grow exponentially, making full factorial sampling computationally burdensome ( Fig. 3.3 (b)). As a result, it is common in the literature to apply full factorial sampling at only two levels per factor, typically the two extremes [ 60 ] . This significantly reduces computational burden but is only considered appropriate in cases where factors can indeed only assume two discrete values (e.g., when testing the effects of epistemic uncertainty and comparing between model structure A and model structure B). In the case of physical parameters on continuous distributions (e.g., when considering the effects of measurement uncertainty in a temperature sensor), discretizing the range of a factor to only extreme levels can bias its estimated importance.

Fractional factorial sampling is a widely used alternative to full factorial sampling that allows the analyst to significantly reduce the number of simulations by focusing on the main effects of a factor and seeking to avoid model runs that yield redundant response information [ 49 ] . In other words, if one can reasonably assume that higher-order interactions are negligible, information about the most significant effects and lower-order interactions (e.g., effects from pairs of factors) can be obtained using a fraction of the full factorial design. Traditionally, fractional factorial design has also been limited to two levels [ 60 ] , referred to as Fractional Factorial designs 2k-p [ 61 ] . Recently, Generalized Fractional Factorial designs have also been proposed that allow for the structured generation of samples at more than two levels per factor [ 62 ] . Consider a case where the modeling team dealing with the problem in Fig. 3.3 (a) cannot afford to perform 64 simulations of their model. They can afford 32 runs for their experiment and instead decide to fractionally sample the variability space of their factors. A potential design of such a sampling strategy is presented in Fig. 3.3 (c).

Fig. 3.3 Alternative designs of experiments and their computational costs for three uncertain factors \((x_1,\) \(x_2,\) and \(x_3)\) . (a) Full factorial design sampling of three factors at four levels, at a total of 64 samples; (b) exponential growth of necessary number of samples when applying full factorial design at four levels; (c) fractional factorial design of three factors at four levels, at a total of 32 samples; and (d) Latin Hypercube sample of three factors with uniform distributions, at a total of 32 samples. ¶

3.3.3. Latin Hypercube Sampling (LHS) ¶

Latin hypercube sampling (LHS) [ 63 ] is one of the most common methods in space-filling experimental designs. With this sampling technique, for \(N\) uncertain factors, an \(N\) -dimensional hypercube is generated, with each factor divided into an equal number of levels depending on the total number of samples to be generated. Equal numbers of samples are then randomly generated at each level, across all factors. In this manner, latin hypercube design guarantees sampling from every level of the variability space and without any overlaps. When the number of samples generated is much larger than the number of uncertain factors, LHS can be very effective in examining the effects of each factor [ 49 ] . LHS is an attractive technique, because it guarantees a diverse coverage of the space, through the use of subintervals, without being constrained to discrete levels for each factor - compare Fig. 3.3 (c) with Fig. 3.3 (d) for the same number of samples.

LHS is less effective when the number of samples is not much larger than the number of uncertain factors, and the effects of each factor cannot be appropriately distinguished. The samples between factors can also be highly correlated, biasing any subsequent sensitivity analysis results. To address this, the sampling scheme can be modified to control for the correlation in parameters while maximizing the information derived. An example of such modification is through the use of orthogonal arrays [ 64 ] .

3.3.4. Low-Discrepancy Sequences ¶

Low-discrepancy sequences is another sampling technique that employs a pseudo-random generator for Monte Carlo sampling [ 65 , 66 ] . These quasi-Monte Carlo methods eliminate ‘lumpiness’ across samples (i.e, the presence of gaps and clusters) by minimizing discrepancy across the hypercube samples. Discrepancy can be quantitatively measured using the deviations of sampled points from a uniform distribution [ 65 , 67 ] . Low-discrepancy sequences ensure that the number of samples in any subspace of the variability hypercube is approximately the same. This is not something guaranteed by Latin Hypercube sampling, and even though its design can be improved through optimization with various criteria, such adjustments are limited to small sample sizes and low dimensions [ 67 , 68 , 69 , 70 , 71 ] . In contrast, the Sobol sequence [ 72 , 73 ] , one of the most widely used sampling techniques, utilizes the low-discrepancy approach to uniformly fill the sampled factor space. A core advantage of this style of sampling is that it takes far fewer samples (i.e., simulations) to attain a much lower level of error in estimating model output statistics (e.g., the mean and variance of outputs).

Put this into practice! Click the following link to try out an interactive tutorial which uses Sobol sequence sampling for the purposes of a Sobol sensitivity analysis: Sobol SA using SALib Jupyter Notebook

3.3.5. Other types of sampling ¶

The sampling techniques mentioned so far are general sampling methods useful for a variety of applications beyond sensitivity analysis. There are however techniques that have been developed for specific sensitivity analysis methods. Examples of these methods include the Morris One-At-a-Time [ 74 ] , Fourier Amplitude Sensitivity Test (FAST; [ 75 ] ), Extended FAST [ 76 ] , and Extended Sobol methods [ 77 ] . For example, the Morris sampling strategy builds a number of trajectories (usually referred to as repetitions and denoted by \(r\) ) in the input space each composed of \(N+1\) factor points, where \(N\) is the number of uncertain factors. The first point of the trajectory is selected randomly and the subsequent \(N\) points are generated by moving one factor at a time by a fixed amount. Each factor is perturbed once along the trajectory, while the starting points of all of the trajectories are randomly and uniformly distributed. Several variations of this strategy also exist in the literature; for more details on each approach and their differences the reader is directed to Pianosi et al. [ 51 ] .

3.3.6. Synthetic generation of input time series ¶

Models often have input time series or processes with strong temporal and/or spatial correlations (e.g., streamflow, energy demand, pricing of commodities, etc.) that, while they might not immediately come to mind as factors to be examined in sensitivity analysis, can be treated as such. Synthetic input time series are used for a variety of reasons, for example, when observations are not available or are limited, or when past observations are not considered sufficiently representative to capture rare or extreme events of interest [ 78 , 79 ] . Synthetic generation of input time series provides a valuable tool to consider non-stationarity and incorporate potential stressors, such as climate change impacts into input time series [ 80 ] . For example, a century of record will be insufficient to capture very high impact rare extreme events (e.g., persistent multi-year droughts). A large body of statistical literature exists focusing on the topics of synthetic weather [ 81 , 82 ] and streamflow [ 83 , 84 ] generation that provides a rich suite of approaches for developing history-informed, well-characterized stochastic process models to better estimate rare individual or compound (hot, severe drought) extremes. It is beyond the scope of this text to review these methods, but readers are encouraged to explore the studies cited above as well as the following publications for discussions and comparisons of these methods: [ 78 , 80 , 85 , 86 , 87 , 88 , 89 ] . The use of these methods for the purposes of exploratory modeling, especially in the context of well-characterized versus deep uncertainty, is further discussed in Chapter 4.3 .

3.4. Sensitivity Analysis Methods ¶

In this section, we describe some of the most widely applied sensitivity analysis methods along with their mathematical definitions. We also provide a detailed discussion on applying each method, as well as a comparison of and their features and limitations.

3.4.1. Derivative-based Methods ¶

Derivative-based methods explore how model outputs are affected by perturbations in a single model input around a particular input value. These methods are local and are performed using OAT sampling. For simplicity of mathematical notations, let us assume that the model \(g(X)\) only returns one output. Following [ 90 ] and [ 51 ] , the sensitivity index, \(S_i\) , of the model’s i -th input factor, \(x_i\) , can be measured using the partial derivative evaluated at a nominal value, \(\bar{x}\) , of the vector of inputs:

where c i is the scaling factor. In most applications however, the relationship \(g(X)\) is not fully known in its analytical form, and therefore the above partial derivative is usually approximated:

Using this approximation, the i -th input factor is perturbed by a magnitude of \(\Delta_i\) , and its relative importance is calculated. Derivative-based methods are some of the oldest sensitivity analysis methods as they only require \(N+1\) model evaluations to estimate indices for \(N\) uncertain factors. As described above, being computationally very cheap comes at the cost of not being able to explore the entire input space, but only (local) perturbations to the nominal value. Additionally, as these methods examine the effects of each input factor one at a time, they cannot assess parametric interactions or capture the interacting nature of many real systems and the models that abstract them.

3.4.2. Elementary Effect Methods ¶

Elementary effect (EE) SA methods provide a solution to the local nature of the derivative-based methods by exploring the entire parametric range of each input parameter [ 91 ] . However, EE methods still use OAT sampling and do not vary all input parameters simultaneously while exploring the parametric space. The OAT nature of EEs methods therefore prevents them from properly capturing the interactions between uncertain factors. EEs methods are computationally efficient compared to their All-At-a-Time (AAT) counterparts, making them more suitable when computational capacity is a limiting factor, while still allowing for some inferences regarding factor interactions. The most popular EE method is the Method of Morris [ 74 ] . Following the notation by [ 51 ] , this method calculates global sensitivity using the mean of the EEs (finite differences) of each parameter at different locations:

with \(r\) representing the number of sample repetitions (also refered to as trajectories) in the input space, usually set between 4 and 10 [ 38 ] . Each \(x_j\) represents the points of each trajectory, with \(j=1,…, r\) , selected as described in the sampling strategy for this method, found above. This method also produces the standard deviation of the EEs:

which is a measure of parametric interactions. Higher values of \(\sigma_i\) suggest model responses at different levels of factor \(x_i\) are significantly different, which indicates considerable interactions between that and other uncertain factors. The values of \(\mu_i^*\) and \(\sigma_i\) for each factor allow us to draw several different conclusions, illustrated in Fig. 3.4 , following the example by [ 91 ] . In this example, factors \(x_1\) , \(x_2\) , \(x_4\) , and \(x_5\) can be said to have an influence on the model outputs, with \(x_1\) , \(x_4\) , and \(x_5\) having some interactive or non-linear effects. Depending on the orders of magnitude of \(\mu_i^*\) and \(\sigma_i\) one can indirectly deduce whether the factors have strong interactive effects, for example if a factor \(\sigma_i << \mu_i^*\) then the relationship between that factor and the output can be assumed to be largely linear (note that this is still an OAT method and assumptions on factor interactions should be strongly caveated). Extensions of the Method of Morris have also been developed specifically for the purposes of factor fixing and explorations of parametric interactions (e.g., [ 48 , 92 , 93 ] ).

Fig. 3.4 Illustrative results of the Morris Method. Factors \(x_1\) , \(x_2\) , \(x_4\) , and \(x_5\) have an influence on the model outputs, with \(x_1\) , \(x_4\) , and \(x_5\) having interactive or non-linear effects. Whether or not a factor should be considered influential to the output depends on the output selected and is specific to the research context and purpose of the analysis, as discussed in Chapter 3.2 . ¶

3.4.3. Regression-based Methods ¶

Regression analysis is one of the oldest ways of investigating parametric importance and sensitivity [ 38 ] . Here, we describe some of the most popular regression-based sensitivity indices. One of the main sensitivity indices of this category is the standardized regression coefficient (SRC). To calculate SRC, a linear regression relationship needs to be fitted between the input vector, \(x\) , and the model output of interest by using a least-square minimizing method:

where \(b_0\) and \(b_i\) (corresponding to the i -th model input) are regression coefficients. The following relationship can then be used to calculate the SRCs for different input values:

where \(\sigma_i\) and \(\sigma_y\) are standard deviations of i -th model input and output, respectively.

Several other regression-based indices explore the correlation between input and output parameters as a proxy to model parametric sensitivity [ 91 , 94 , 95 ] . The Pearson correlation coefficient (PCC) can be used when a linear relationship exists between an uncertain factor, \(x_i\) , and the output \(y\) :

In cases when there are outliers in the data or the relationship between the uncertain factors and the output is not linear, rank-based correlation coefficients are preferred, for example, Spearman’s rank correlation coefficient (SRCC):

where the raw values of \(x_i\) and \(y\) and converted to ranks \(rx_i\) and \(ry\) respectively, which instead represent a measurement of the strength of the monotonic relationship, rather than linear relationship, between the input and output. Other regression-based metrics include the partial correlations coefficient, the partial rank correlations coefficient, and the Nash-Sutcliffe coefficient, more discussion on which can be found in [ 39 , 91 ] .

Tree-based regression techniques have also been used for sensitivity analysis in an effort to address the challenges faced with nonlinear models [ 96 ] . Examples of these methods include the Patient Rule Induction Method (PRIM; [ 97 ] ) and Classification And Regression Trees (CART; [ 98 ] ). CART-based approaches also include boosting and bagging extensions [ 99 , 100 ] . These methods are particularly useful when sensitivity analysis is used for factor mapping (i.e., when trying to identify which uncertain model factors produce a certain model behavior). Chapter 4.3 elaborates on the use of these methods. Regression-based sensitivity analysis methods are global by nature and can explore the entire space of variables. However, the true level of comprehensiveness depends on the design of experiments and the number of simulations providing data to establish the regression relationships. Although they are usually computationally efficient, they do not produce significant information about parametric interactions [ 38 , 39 ] .

3.4.4. Regional Sensitivity Analysis ¶

Another method primarily applied for basic factor mapping applications is Regional Sensitivity Analysis (RSA; [ 101 ] ). RSA is a global sensitivity analysis method that is typically implemented using standard sampling methods such as latin hypercube sampling. It is performed by specifying a condition on the output space (e.g., an upper threshold) and classifying outputs that meet the condition as behavioral and the ones that fail it as non-behavioral (illustrated in Fig. 3.2 (b)). Note that the specified threshold depends on the nature of the problem, model, and the research question. It can reflect model-performance metrics (such as errors) or consequential decision-relevant metrics (such as unacceptable system outcomes). The behavioral and non-behavioral outputs are then traced back to their originating sampled factors, where differences between the distributions of samples can be used to determine their significance in producing each part of the output. The Kolmogorov-Smirnov divergence is commonly used to quantify the difference between the distribution of behavioral and non-behavioral parameters [ 51 ] :

where \(Y_b\) represents the set of behavioral outputs, and \(F_{x_i|y_b}\) is the empirical cumulative distribution function of the values of \(x_i\) associated with values of \(y\) that belong in the behavioral set. The \(nb\) notation indicates the equivalent elements related to the non-behavioral set. Large differences between the two distributions indicate stronger effects by the parameters on the respective part of the output space.

Used in a factor mapping setting, RSA can be applied for scenario discovery [ 102 , 103 ] , the Generalized Likelihood Uncertainty Estimation method (GLUE; [ 18 , 104 , 105 ] ) and other hybrid sensitivity analysis methods (e.g., [ 106 , 107 ] ). The fundamental shortcomings of RSA are that, in some cases, it could be hard to interpret the difference between behavioral and non-behavioral sample sets, and that insights about parametric correlations and interactions cannot always be uncovered [ 38 ] . For more elaborate discussions and illustrations of the RSA method, readers are directed to Tang et al. [ 42 ], Saltelli et al. [ 49 ], Young [ 108 ] and references therein.

3.4.5. Variance-based Methods ¶

Variance-based sensitivity analysis methods hypothesize that various specified model factors contribute differently to the variation of model outputs; therefore, decomposition and analysis of output variance can determine a model’s sensitivity to input parameters [ 38 , 77 ] . The most popular variance-based method is the Sobol method, which is a global sensitivity analysis method that takes into account complex and nonlinear factor interaction when calculating sensitivity indices, and employs more sophisticated sampling methods (e.g., the Sobol sampling method). The Sobol method is able to calculate three types of sensitivity indices that provide different types of information about model sensitivities. These indices include first-order, higher-order (e.g., second-, third-, etc. orders), and total-order sensitivities.

The first-order sensitivity index indicates the percent of model output variance contributed by a factor individually (i.e., the effect of varying \(x_i\) alone) and is obtained using the following [ 77 , 109 ] :

with \(E\) and \(V\) denoting the expected value and the variance, respectively. \(x_{\sim i}\) denotes all factors expect for \(x_i\) . The first-order sensitivity index ( \(S_i^1\) ) can therefore also be thought of as the portion of total output variance ( \(V_y\) ) that can be reduced if the uncertainty in factor \(x_i\) is eliminated [ 110 ] . First-order sensitivity indices are usually used to understand the independent effect of a factor and to distinguish its individual versus interactive influence. It would be expected for linearly independent factors that they would only have first order indices (no interactions) that should correspond well with sensitivities obtained from simpler methods using OAT sampling.

Higher-order sensitivity indices explore the interaction between two or more parameters that contribute to model output variations. For example, a second-order index indicates how interactions between a pair of factors can lead to change in model output variance and is calculated using the following relationship:

with \(i \ne j\) . Higher order indices can be calculated by similar extensions (i.e., fixing additional operators together), but it is usually computationally expensive in practice.

The total sensitivity analysis index represents the entire influence of an input factor on model outputs including all of its interactions with other factors [ 111 ] . In other words, total-order indices include first-order and all higher-order interactions associated with each factor and can be estimated calculated using the following:

This index reveals the expected portion of variance that remains if uncertainty is eliminated in all factors but \(x_i\) [ 110 ] . The total sensitivity index is the overall best measure of sensitivity as it captures the full individual and interactive effects of model factors.

Besides the Sobol method, there are some other variance-based sensitivity analysis methods, such as the Fourier amplitude sensitivity test (FAST; [ 75 , 112 ] ) and extended-FAST [ 113 , 114 ] , that have been used by the scientific community. However, Sobol remains by far the most common method of this class. Variance-based techniques have been widely used and have proved to be powerful in a variety of applications. Despite their popularity, some authors have expressed concerns about the methods’ appropriateness in some settings. Specifically, the presence of heavy-tailed distributions or outliers, or when model outputs are multimodal can bias the sensitivity indices produced by these methods [ 115 , 116 , 117 ] . Moment-independent measures, discussed below, attempt to overcome these challenges.

Put this into practice! Click the following link to try out an interactive tutorial which demonstrates the application of a Sobol sensitivity analysis: Sobol SA using SALib Jupyter Notebook

3.4.6. Analysis of Variance (ANOVA) ¶

Analysis of Variance (ANOVA) was first introduced by Fisher and others [ 118 ] and has since become a popular factor analysis method in physical experiments. ANOVA can be used as a sensitivity analysis method in computational experiments with a factorial design of experiment (referred to as factorial ANOVA). Note that Sobol can also be categorized as an ANOVA sensitivity analysis method, and that is why Sobol is sometimes referred to as a functional ANOVA [ 119 ] . Factorial ANOVA methods are particularly suited for models and problems that have discrete input spaces, significantly reducing the computational time. More information about these methods can be found in [ 119 , 120 , 121 ] .

3.4.7. Moment-Independent (Density-Based) Methods ¶

These methods typically compare the entire distribution (i.e., not just the variance) of input and output parameters in order to determine the sensitivity of the output to a particular input variable. Several moment-independent sensitivity analysis methods have been proposed in recent years. The delta ( \(\delta\) ) moment-independent method calculates the difference between unconditional and conditional cumulative distribution functions of the output. The method was first introduced by [ 122 , 123 ] and has become widely used in various disciplines. The \(\delta\) sensitivity index is defined as follows:

where \(f_y(y)\) is the probability density function of the entire model output \(y\) , and \(f_{y|x_i}(y)\) is the conditional density of \(y\) , given that factor \(x_i\) assumes a fixed value. The \(\delta_i\) sensitivity indicator therefore represents the normalized expected shift in the distribution of \(y\) provoked by \(x_i\) . Moment-independent methods are advantageous in cases where we are concerned about the entire distribution of events, such as when uncertain factors lead to more extreme events in a system [ 13 ] . Further, they can be used with a pre-existing sample of data, without requiring a specific sampling scheme, unlike the previously reviewed methods [ 124 ] . The \(\delta\) sensitivity index does not include interactions between factors and it is therefore akin to the first order index produced by the Sobol method. Interactions between factors can still be estimated using this method, by conditioning the calculation on more than one uncertain factor being fixed [ 123 ] .

3.5. How To Choose A Sensitivity Analysis Method: Model Traits And Dimensionality ¶

Fig. 3.5 , synthesized from variants found in [ 51 , 91 ] , presents a graphical synthesis of the methods overviewed in this section, with regards to their appropriateness of application based on the complexity of the model at hand and the computational limits on the number of model evaluations afforded. The bars below each method also indicate the sensitivity analysis purposes they are most appropriate to address, which are in turn a reflection of the motivations and research questions the sensitivity analysis is called to address. Computational intensity is measured as a multiple of the number of model factors that are considered uncertain ( \(d\) ). Increasing model complexity mandates that more advanced sensitivity analysis methods are applied to address potential nonlinearities, factor interactions, and discontinuities. Such methods can only be performed at increasing computational expense. For example, computationally cheap linear regression should not be used to assess factors’ importance if the model cannot be proven linear and the factors independent, because important relationships will invariably be missed (recall the example in Fig. 3.5 ). When computational limits do constrain applications to make simplified assumptions and sensitivity techniques, any conclusions in such cases should be delivered with clear statements of the appropriate caveats.

Fig. 3.5 Classification of the sensitivity analysis methods overviewed in this section, with regards to their computational cost (horizontal axis), their appropriateness to model complexity (vertical axis), and the purpose they can be used for (colored bars). d: number of uncertain factors considered; ANOVA: Analysis of Variance; FAST: Fourier Amplitude Sensitivity Test; PRIM: Patient Rule Induction Method; CART: Classification and Regression Trees; SRCC: Spearman’s rank correlation coefficient: NSE: Nash–Sutcliffe efficiency; SRC: standardized regression coefficient; PCC: Pearson correlation coefficient. This figure is synthesized from variants found in [ 51 , 91 ] . ¶

The reader should also be aware that the estimates of computational intensity that are given here are indicative of magnitude and would vary depending on the sampling technique, model complexity and the level of information being asked. For example, a Sobol sensitivity analysis typically requires a sample of size \(n * d+2\) to produce first- and total-order indices, where \(d\) is the number of uncertain factors and \(n\) is a scaling factor, selected ad hoc, depending on model complexity [ 46 ] . The scaling factor \(n\) is typically set to at least 1000, but it should most appropriately be set on the basis of index convergence. In other words, a prudent analyst would perform the analysis several times with increasing \(n\) and observe at what level the indices converge to stable values [ 125 ] . The level should be the minimum sample size used in subsequent sensitivity analyses of the same system. Furthermore, if the analyst would like to better understand the degrees of interaction between factors, requiring second-order indices, the sample size would have to increase to \(n * 2d+2\) [ 46 ] .

Another important consideration is that methods that do not require specific sampling schemes can be performed in conjunction with others without requiring additional model evaluations. None of the regression-based methods, for example, require samples of specific structures or sizes, and can be combined with other methods for complementary purposes. For instance, one could complement a Sobol analysis with an application of CART, using the same data, but to address questions relating to factor mapping (e.g., we know factor \(x_i\) is important for a model output, but we would like to also know which of its values specifically push the output to undesirable states). Lastly, comparing results from different methods performed together can be especially useful in model diagnostic settings. For example, [ 13 ] used \(\delta\) indices, first-order Sobol indices, and \(R^2\) values from linear regression, all performed on the same factors, to derive insights about the effects on factors on different moments of the output distribution and about the linearity of their relationship.

3.6. Software Toolkits ¶

This section presents available open source sensitivity analysis software tools, based on the programming language they use and the methods they support Fig. 3.6 . Our review covers five widely used programming languages: R, MATLAB, Julia, Python, and C++, as well as one tool that provides a graphical user interface (GUI). Each available SA tool was assessed on the number of SA methods and design of experiments methods it supports. For example, the sensobol package in R only supports the variance-based Sobol method. However, it is the only package we came across that calculates third-order interactions among parameters. On the other side of the spectrum, there are SA software packages that contain several popular SA methods. For example, SALib in Python [ 126 ] supports seven different SA methods. The DifferentialEquations package is a comprehensive package developed for Julia, and GlobalSensitivityAnalysis is another Julia package that has mostly adapted SALib methods. Fig. 3.6 also identifies the SA packages that have been updated since 2018, indicating active support and development.

Fig. 3.6 Sensitivity analysis packages available in different programming language platforms (R, Python, Julia, MATLAB, and C++), with the number of methods they support. Packages supporting more than five methods are indicated in pink. Packages updated since 2018 are indicated with asterisks. ¶

The following articles are suggested as fundamental reading for the information presented in this section:

Wagener, T., Pianosi, F., 2019. What has Global Sensitivity Analysis ever done for us? A systematic review to support scientific advancement and to inform policy-making in earth system modelling. Earth-Science Reviews 194, 1–18. https://doi.org/10.1016/j.earscirev.2019.04.006

Pianosi, F., Beven, K., Freer, J., Hall, J.W., Rougier, J., Stephenson, D.B., Wagener, T., 2016. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environmental Modelling & Software 79, 214–232. https://doi.org/10.1016/j.envsoft.2016.02.008

The following articles can be used as supplemental reading:

Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., Saisana, M., Tarantola, S., 2008. Global Sensitivity Analysis: The Primer, 1st edition. ed. Wiley-Interscience, Chichester, England ; Hoboken, NJ.

Montgomery, D.C., 2017. Design and analysis of experiments. John Wiley & Sons.

Iooss, B., Lemaître, P., 2015. A Review on Global Sensitivity Analysis Methods, in: Dellino, G., Meloni, C. (Eds.), Uncertainty Management in Simulation-Optimization of Complex Systems: Algorithms and Applications, Operations Research/Computer Science Interfaces Series. Springer US, Boston, MA, pp. 101–122. https://doi.org/10.1007/978-1-4899-7547-8_5

2. Diagnostic Modeling Overview and Perspectives

4. Sensitivity Analysis: Diagnostic & Exploratory Modeling

Title: A comprehensive evaluation of various sensitivity analysis methods: A case study with a hydrological model

• Full Record
• References ( 49 )
• Cited by ( 40 )
• Other Related Research

Sensitivity analysis (SA) is a commonly used approach for identifying important parameters that dominate model behaviors. We use a newly developed software package, a Problem Solving environment for Uncertainty Analysis and Design Exploration (PSUADE), to evaluate the effectiveness and efficiency of ten widely used SA methods, including seven qualitative and three quantitative ones. All SA methods are tested using a variety of sampling techniques to screen out the most sensitive (i.e., important) parameters from the insensitive ones. The Sacramento Soil Moisture Accounting (SAC-SMA) model, which has thirteen tunable parameters, is used for illustration. The South Branch Potomac River basin near Springfield, West Virginia in the U.S. is chosen as the study area. The key findings from this study are: (1) For qualitative SA methods, Correlation Analysis (CA), Regression Analysis (RA), and Gaussian Process (GP) screening methods are shown to be not effective in this example. Morris One-At-a-Time (MOAT) screening is the most efficient, needing only 280 samples to identify the most important parameters, but it is the least robust method. Multivariate Adaptive Regression Splines (MARS), Delta Test (DT) and Sum-Of-Trees (SOT) screening methods need about 400–600 samples for the same purpose. Monte Carlo (MC), Orthogonal Array (OA) and Orthogonal Array more » based Latin Hypercube (OALH) are appropriate sampling techniques for them; (2) For quantitative SA methods, at least 2777 samples are needed for Fourier Amplitude Sensitivity Test (FAST) to identity parameter main effect. McKay method needs about 360 samples to evaluate the main effect, more than 1000 samples to assess the two-way interaction effect. OALH and LPτ (LPTAU) sampling techniques are more appropriate for McKay method. For the Sobol' method, the minimum samples needed are 1050 to compute the first-order and total sensitivity indices correctly. These comparisons show that qualitative SA methods are more efficient but less accurate and robust than quantitative ones. « less

• Beijing Normal Univ., Beijing (China)
• Lawrence Livermore National Lab. (LLNL), Livermore, CA (United States)
• Univ. of California, Irvine, CA (United States)

Citation Formats

• CSV / Excel

Works referenced in this record:

A manifesto for the equifinality thesis journal , March 2006

• Beven, Keith
• Journal of Hydrology, Vol. 320, Issue 1-2
• DOI: 10.1016/j.jhydrol.2005.07.007

The future of distributed models: Model calibration and uncertainty prediction journal , July 1992

• Beven, Keith; Binley, Andrew
• Hydrological Processes, Vol. 6, Issue 3
• DOI: 10.1002/hyp.3360060305

Scale issues in hydrological modelling: A review journal , April 1995

• Blöschl, G.; Sivapalan, M.
• Hydrological Processes, Vol. 9, Issue 3-4
• DOI: 10.1002/hyp.3360090305

Model emulation and moment-independent sensitivity analysis: An application to environmental modelling journal , June 2012

• Borgonovo, E.; Castaings, W.; Tarantola, S.
• Environmental Modelling & Software, Vol. 34
• DOI: 10.1016/j.envsoft.2011.06.006

Some New Three Level Designs for the Study of Quantitative Variables journal , November 1960

• Box, G. E. P.; Behnken, D. W.
• Technometrics, Vol. 2, Issue 4
• DOI: 10.1080/00401706.1960.10489912

Toward improved calibration of hydrologic models: Combining the strengths of manual and automatic methods journal , December 2000

• Boyle, Douglas P.; Gupta, Hoshin V.; Sorooshian, Soroosh
• Water Resources Research, Vol. 36, Issue 12
• DOI: 10.1029/2000WR900207

An effective screening design for sensitivity analysis of large models journal , October 2007

• Campolongo, Francesca; Cariboni, Jessica; Saltelli, Andrea
• Environmental Modelling & Software, Vol. 22, Issue 10
• DOI: 10.1016/j.envsoft.2006.10.004

BART: Bayesian additive regression trees journal , March 2010

• Chipman, Hugh A.; George, Edward I.; McCulloch, Robert E.
• The Annals of Applied Statistics, Vol. 4, Issue 1
• DOI: 10.1214/09-AOAS285

Pursuing the method of multiple working hypotheses for hydrological modeling: HYPOTHESIS TESTING IN HYDROLOGY journal , September 2011

• Clark, Martyn P.; Kavetski, Dmitri; Fenicia, Fabrizio
• Water Resources Research, Vol. 47, Issue 9
• DOI: 10.1029/2010WR009827

Correlation and Regression journal , November 2006

• Crawford, Sybil L.
• Circulation, Vol. 114, Issue 19
• DOI: 10.1161/CIRCULATIONAHA.105.586495

Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory journal , October 1973

• Cukier, R. I.; Fortuin, C. M.; Shuler, K. E.
• The Journal of Chemical Physics, Vol. 59, Issue 8
• DOI: 10.1063/1.1680571

Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops journal , March 2006

• Duan, Q.; Schaake, J.; Andréassian, V.
• DOI: 10.1016/j.jhydrol.2005.07.031

Optimal use of the SCE-UA global optimization method for calibrating watershed models journal , June 1994

• Duan, Qingyun; Sorooshian, Soroosh; Gupta, Vijai K.
• Journal of Hydrology, Vol. 158, Issue 3-4
• DOI: 10.1016/0022-1694(94)90057-4

Effective and efficient global optimization for conceptual rainfall-runoff models journal , April 1992

• Duan, Qingyun; Sorooshian, Soroosh; Gupta, Vijai
• Water Resources Research, Vol. 28, Issue 4
• DOI: 10.1029/91WR02985

Multivariate Adaptive Regression Splines journal , March 1991

• Friedman, Jerome H.
• The Annals of Statistics, Vol. 19, Issue 1
• DOI: 10.1214/aos/1176347963

Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information journal , April 1998

• Gupta, Hoshin Vijai; Sorooshian, Soroosh; Yapo, Patrice Ogou
• Water Resources Research, Vol. 34, Issue 4
• DOI: 10.1029/97WR03495

Using and comparing two nonparametric methods (CART and MARS) to model the potential distribution of gullies journal , December 2009

• Gutiérrez, Álvaro Gómez; Schnabel, Susanne; Lavado Contador, J. Francisco
• Ecological Modelling, Vol. 220, Issue 24
• DOI: 10.1016/j.ecolmodel.2009.06.020

Importance measures in global sensitivity analysis of nonlinear models journal , April 1996

• Homma, Toshimitsu; Saltelli, Andrea
• Reliability Engineering & System Safety, Vol. 52, Issue 1
• DOI: 10.1016/0951-8320(96)00002-6

How much complexity is warranted in a rainfall-runoff model? journal , August 1993

• Jakeman, A. J.; Hornberger, G. M.
• Water Resources Research, Vol. 29, Issue 8
• DOI: 10.1029/93WR00877

Ancient numerical daemons of conceptual hydrological modeling: 2. Impact of time stepping schemes on model analysis and prediction journal , October 2010

• Kavetski, Dmitri; Clark, Martyn P.
• Water Resources Research, Vol. 46, Issue 10
• DOI: 10.1029/2009WR008896

Semidistributed hydrological modeling: A “saturation path” perspective on TOPMODEL and VIC: SEMIDISTRIBUTED HYDROLOGICAL MODELING journal , September 2003

• Kavetski, Dmitri; Kuczera, George; Franks, Stewart W.
• Water Resources Research, Vol. 39, Issue 9
• DOI: 10.1029/2003WR002122

Computer experiments: a review journal , December 2010

• Levy, Sigal; Steinberg, David M.
• AStA Advances in Statistical Analysis, Vol. 94, Issue 4
• DOI: 10.1007/s10182-010-0147-9

Exploring parameter sensitivities of the land surface using a locally coupled land-atmosphere model: EXPLORING PARAMETER SENSITIVITIES journal , November 2004

• Liu, Yuqiong; Gupta, Hoshin V.; Sorooshian, Soroosh
• Journal of Geophysical Research: Atmospheres, Vol. 109, Issue D21
• DOI: 10.1029/2004JD004730

Choosing the Sample Size of a Computer Experiment: A Practical Guide journal , November 2009

• Loeppky, Jason L.; Sacks, Jerome; Welch, William J.
• Technometrics, Vol. 51, Issue 4
• DOI: 10.1198/TECH.2009.08040

The Monte Carlo Method journal , September 1949

• Metropolis, Nicholas; Ulam, S.
• Journal of the American Statistical Association, Vol. 44, Issue 247
• DOI: 10.1080/01621459.1949.10483310

Factorial Sampling Plans for Preliminary Computational Experiments journal , May 1991

• Morris, Max D.
• Technometrics, Vol. 33, Issue 2
• DOI: 10.1080/00401706.1991.10484804

Finding the Embedding Dimension and Variable Dependencies in Time Series journal , May 1994

• Pi, Hong; Peterson, Carsten
• Neural Computation, Vol. 6, Issue 3
• DOI: 10.1162/neco.1994.6.3.509

The Design of Optimum Multifactorial Experiments journal , January 1946

• Plackett, R. L.; Burman, J. P.
• Biometrika, Vol. 33, Issue 4
• DOI: 10.1093/biomet/33.4.305

State Dependent Parameter metamodelling and sensitivity analysis journal , December 2007

• Ratto, Marco; Pagano, Andrea; Young, Peter
• Computer Physics Communications, Vol. 177, Issue 11
• DOI: 10.1016/j.cpc.2007.07.011

Understanding predictive uncertainty in hydrologic modeling: The challenge of identifying input and structural errors: IDENTIFIABILITY OF INPUT AND STRUCTURAL ERRORS journal , May 2010

• Renard, Benjamin; Kavetski, Dmitri; Kuczera, George
• Water Resources Research, Vol. 46, Issue 5
• DOI: 10.1029/2009WR008328

Design and Analysis of Computer Experiments journal , November 1989

• Sacks, Jerome; Welch, William J.; Mitchell, Toby J.
• Statistical Science, Vol. 4, Issue 4
• DOI: 10.1214/ss/1177012413

Making best use of model evaluations to compute sensitivity indices journal , May 2002

• Saltelli, Andrea
• Computer Physics Communications, Vol. 145, Issue 2
• DOI: 10.1016/S0010-4655(02)00280-1

A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output journal , February 1999

• Saltelli, A.; Tarantola, S.; Chan, K. P. -S.
• Technometrics, Vol. 41, Issue 1
• DOI: 10.1080/00401706.1999.10485594

Variance-based sensitivity analysis of model outputs using surrogate models journal , June 2011

• Shahsavani, D.; Grimvall, A.
• Environmental Modelling & Software, Vol. 26, Issue 6
• DOI: 10.1016/j.envsoft.2011.01.002

Quasi-Monte Carlo methods journal , January 1990

• Soboĺ, I. M.
• Progress in Nuclear Energy, Vol. 24, Issue 1-3
• DOI: 10.1016/0149-1970(90)90022-W

Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates journal , February 2001

• Sobol′, I. M.
• Mathematics and Computers in Simulation, Vol. 55, Issue 1-3
• DOI: 10.1016/S0378-4754(00)00270-6

Automatic calibration of conceptual rainfall-runoff models: The question of parameter observability and uniqueness journal , February 1983

• Sorooshian, Soroosh; Gupta, Vijai Kumar
• Water Resources Research, Vol. 19, Issue 1
• DOI: 10.1029/WR019i001p00260

The Proof and Measurement of Association between Two Things journal , January 1904

• Spearman, C.
• The American Journal of Psychology, Vol. 15, Issue 1
• DOI: 10.2307/1412159

Orthogonal Array-Based Latin Hypercubes journal , December 1993

• Tang, Boxin
• Journal of the American Statistical Association, Vol. 88, Issue 424
• DOI: 10.1080/01621459.1993.10476423

Comparing sensitivity analysis methods to advance lumped watershed model identification and evaluation journal , January 2007

• Tang, Y.; Reed, P.; Wagener, T.
• Hydrology and Earth System Sciences, Vol. 11, Issue 2
• DOI: 10.5194/hess-11-793-2007

A global sensitivity analysis tool for the parameters of multi-variable catchment models journal , June 2006

• van Griensven, A.; Meixner, T.; Grunwald, S.
• Journal of Hydrology, Vol. 324, Issue 1-4
• DOI: 10.1016/j.jhydrol.2005.09.008

Characterization of watershed model behavior across a hydroclimatic gradient: WATERSHED MODEL BEHAVIOR journal , January 2008

• van Werkhoven, Kathryn; Wagener, Thorsten; Reed, Patrick
• Water Resources Research, Vol. 44, Issue 1
• DOI: 10.1029/2007WR006271

Multicriteria Analysis in Engineering book , January 2002

• Statnikov, Roman B.; Matusov, Joseph B.
• Springer Link
• DOI: 10.1007/978-94-015-9968-9

The proof and measurement of association between two things journal , October 2010

• International Journal of Epidemiology, Vol. 39, Issue 5
• DOI: 10.1093/ije/dyq191
• All References
• journal (48)

Works referencing / citing this record:

Assessment of Wind Parameter Sensitivity on Extreme and Fatigue Wind Turbine Loads conference , January 2018

• Robertson, Amy; Sethuraman, Latha; Jonkman, Jason M.
• 2018 Wind Energy Symposium
• DOI: 10.2514/6.2018-1728

Remediation of Diesel-Contaminated Soil by Ultrasonic Solvent Extraction journal , July 2018

• Maceiras, Rocio; Alfonsin, Victor; Martinez, Javier
• International Journal of Environmental Research, Vol. 12, Issue 5
• DOI: 10.1007/s41742-018-0121-z

Analysis of policy scenarios for achieving renewable energy sources targets: A fuzzy TOPSIS approach journal , December 2016

• Papapostolou, Aikaterini; Karakosta, Charikleia; Doukas, Haris
• Energy & Environment, Vol. 28, Issue 1-2
• DOI: 10.1177/0958305x16685474

Updating the neural network sediment load models using different sensitivity analysis methods: a regional application journal , March 2020

• Asheghi, Reza; Hosseini, Seyed Abbas; Saneie, Mojtaba
• Journal of Hydroinformatics
• DOI: 10.2166/hydro.2020.098

Assessing Parameter Importance of the Weather Research and Forecasting Model Based On Global Sensitivity Analysis Methods journal , May 2018

• Ji, Dong; Dong, Wenjie; Hong, Tao
• Journal of Geophysical Research: Atmospheres, Vol. 123, Issue 9
• DOI: 10.1002/2017jd027348

Trends in Modeling, Design, and Optimization of Multiphase Systems in Minerals Processing journal , December 2019

• Cisternas, Luis; Lucay, Freddy; Botero, Yesica
• Minerals, Vol. 10, Issue 1
• DOI: 10.3390/min10010022

A two- stage sensitivity analysis for parameter identification and calibration of a physically-based distributed model in a river basin text , January 2019

• Sreedevi, S.; Eldho, T. I.
• Taylor & Francis
• DOI: 10.6084/m9.figshare.7936643.v1

Comprehensive Evaluation of Coal-Fired Power Units Using Grey Relational Analysis and a Hybrid Entropy-Based Weighting Method journal , March 2018

• Wu, Dianfa; Wang, Ningling; Yang, Zhiping
• Entropy, Vol. 20, Issue 4, p. 215
• DOI: 10.3390/e20040215

Downscaling SMAP Radiometer Soil Moisture Over the CONUS Using an Ensemble Learning Method journal , January 2019

• Abbaszadeh, Peyman; Moradkhani, Hamid; Zhan, Xiwu
• Water Resources Research, Vol. 55, Issue 1
• DOI: 10.1029/2018wr023354

Quantitative Microbial Risk Assessment for Workers Exposed to Bioaerosol in Wastewater Treatment Plants Aimed at the Choice and Setup of Safety Measures journal , July 2018

• Carducci, Annalaura; Donzelli, Gabriele; Cioni, Lorenzo
• International Journal of Environmental Research and Public Health, Vol. 15, Issue 7
• DOI: 10.3390/ijerph15071490

Sensitivity Analysis in a Complex Marine Ecological Model journal , May 2015

• Mateus, Marcos; Franz, Guilherme
• Water, Vol. 7, Issue 12
• DOI: 10.3390/w7052060

Watershed System Model: The Essentials to Model Complex Human-Nature System at the River Basin Scale journal , March 2018

• Li, Xin; Cheng, Guodong; Lin, Hui
• Journal of Geophysical Research: Atmospheres, Vol. 123, Issue 6
• DOI: 10.1002/2017jd028154

Nonlinear variable selection algorithms for surrogate modeling journal , May 2019

• Zhai, Jianyuan; Boukouvala, Fani
• AIChE Journal, Vol. 65, Issue 8
• DOI: 10.1002/aic.16601

Mathematical modeling of the relocation of the divalent metal transporter DMT1 in the intestinal iron absorption process journal , June 2019

• Cegarra, Layimar; Colins, Andrea; Gerdtzen, Ziomara P.
• PLOS ONE, Vol. 14, Issue 6
• DOI: 10.1371/journal.pone.0218123

Multi-objective parameter optimization of common land model using adaptive surrogate modeling journal , January 2015

• Gong, W.; Duan, Q.; Li, J.
• Hydrology and Earth System Sciences, Vol. 19, Issue 5
• DOI: 10.5194/hess-19-2409-2015

Global Sensitivity Analysis Methods Applied to Hydrologic Modeling with the Sac-Sma Model journal , February 2019

• Uliana, Eduardo M.; Silva, Demetrius D. da; Moreira, Michel C.
• Engenharia Agrícola, Vol. 39, Issue 1
• DOI: 10.1590/1809-4430-eng.agric.v39n1p65-74/2019

An automatic and effective parameter optimization method for model tuning journal , January 2015

• Zhang, T.; Li, L.; Lin, Y.
• Geoscientific Model Development, Vol. 8, Issue 11
• DOI: 10.5194/gmd-8-3579-2015

Sensitivity Analysis Methods book , January 2018

• Gan, Yanjun; Duan, Qingyun
• Handbook of Hydrometeorological Ensemble Forecasting
• DOI: 10.1007/978-3-642-40457-3_65-1

Modeling sea cage outputs for data-scarce areas: application to red drum (Sciaenops ocellatus) aquaculture in Mayotte, Indian Ocean journal , March 2019

• Chary, Killian; Fiandrino, Annie; Covès, Denis
• Aquaculture International, Vol. 27, Issue 3
• DOI: 10.1007/s10499-019-00351-z

Practical Experience of Sensitivity Analysis: Comparing Six Methods, on Three Hydrological Models, with Three Performance Criteria journal , May 2019

• Wang, Anqi; Solomatine, Dimitri P.
• Water, Vol. 11, Issue 5
• DOI: 10.3390/w11051062

A Robust Gauss‐Newton Algorithm for the Optimization of Hydrological Models: From Standard Gauss‐Newton to Robust Gauss‐Newton journal , November 2018

• Qin, Youwei; Kavetski, Dmitri; Kuczera, George
• Water Resources Research, Vol. 54, Issue 11
• DOI: 10.1029/2017wr022488

Principle of maximum entropy in the estimation of suspended sediment concentration journal , January 2017

• Martins, Patrícia Diniz; Poleto, Cristiano
• RBRH, Vol. 22, Issue 0
• DOI: 10.1590/2318-0331.011716058

Extending sensitivity analysis using regression to effectively disseminate life cycle assessment results journal , August 2019

• Di Lullo, Giovanni; Gemechu, Eskinder; Oni, Abayomi Olufemi
• The International Journal of Life Cycle Assessment, Vol. 25, Issue 2
• DOI: 10.1007/s11367-019-01674-y

Spatial Pattern Oriented Multicriteria Sensitivity Analysis of a Distributed Hydrologic Model journal , September 2018

• Demirel, Mehmet; Koch, Julian; Mendiguren, Gorka
• Water, Vol. 10, Issue 9
• DOI: 10.3390/w10091188

Review of statistical model calibration and validation—from the perspective of uncertainty structures journal , May 2019

• Lee, Guesuk; Kim, Wongon; Oh, Hyunseok
• Structural and Multidisciplinary Optimization, Vol. 60, Issue 4
• DOI: 10.1007/s00158-019-02270-2

Uncertainty propagation and sensitivity analysis in composite manufacturing cost estimation: ALPHA-framework and cost tool development journal , April 2019

• Hueber, Christian; Schwingshandl, Nikolaus; Schledjewski, Ralf
• Advanced Manufacturing: Polymer & Composites Science, Vol. 5, Issue 2
• DOI: 10.1080/20550340.2019.1599536

How parameter specification of an Earth system model of intermediate complexity influences its climate simulations journal , June 2019

• Shi, Yuhan; Gong, Wei; Duan, Qingyun
• Progress in Earth and Planetary Science, Vol. 6, Issue 1
• DOI: 10.1186/s40645-019-0294-x

Assessment and Reduction of the Physical Parameterization Uncertainty for Noah‐MP Land Surface Model journal , July 2019

• Gan, Yanjun; Liang, Xin‐Zhong; Duan, Qingyun
• Water Resources Research, Vol. 55, Issue 7
• DOI: 10.1029/2019wr024814

Investigating the Behaviour of Human Thermal Indices under Divergent Atmospheric Conditions: A Sensitivity Analysis Approach journal , September 2019

• Charalampopoulos, Ioannis; Santos Nouri, Andre
• Atmosphere, Vol. 10, Issue 10
• DOI: 10.3390/atmos10100580

Sobol Global Sensitivity Analysis of a Coupled Surface/Subsurface Water Flow and Reactive Solute Transfer Model on a Real Hillslope journal , December 2019

• Gatel, Laura; Lauvernet, Claire; Carluer, Nadia
• Water, Vol. 12, Issue 1
• DOI: 10.3390/w12010121

Sensitivity Analysis Methods book , January 2019

• DOI: 10.1007/978-3-642-39925-1_65

A two-stage sensitivity analysis for parameter identification and calibration of a physically-based distributed model in a river basin text , January 2019

• DOI: 10.6084/m9.figshare.7936643.v2
• DOI: 10.6084/m9.figshare.7936643

A two-stage sensitivity analysis for parameter identification and calibration of a physically-based distributed model in a river basin journal , April 2019

• Hydrological Sciences Journal, Vol. 64, Issue 6
• DOI: 10.1080/02626667.2019.1602730

Ranking of mechanisms governing the phytoavailability of cadmium in agricultural soils using a mechanistic model journal , September 2015

• Lin, Zhongbing; Schneider, André; Sterckeman, Thibault
• Plant and Soil, Vol. 399, Issue 1-2
• DOI: 10.1007/s11104-015-2663-6

Impact of DEM Resolution and Spatial Scale: Analysis of Influence Factors and Parameters on Physically Based Distributed Model journal , January 2016

• Zhang, Hanchen; Li, Zhijia; Saifullah, Muhammad
• Advances in Meteorology, Vol. 2016
• DOI: 10.1155/2016/8582041

Sensitivity Analysis of the Integral Quality Monitoring System® Using Monte Carlo Simulation journal , January 2017

• Oderinde, Oluwaseyi M.; du Plessis, F. C. P.
• Computational and Mathematical Methods in Medicine, Vol. 2017
• DOI: 10.1155/2017/7025281

Parameter sensitivity analysis of a 1-D cold region lake model for land-surface schemes journal , January 2017

• Guerrero, Jose-Luis; Pernica, Patricia; Weather, Howard
• Hydrology and Earth Systems Sciences Discussions
• DOI: 10.5194/hess-2017-5
• All Cited By
• conference (1)
• journal (34)

Similar Records in DOE PAGES and OSTI.GOV collections:

• Similar Records

• Search Search Please fill out this field.
• Corporate Finance
• Financial Analysis

Sensitivity Analysis Definition

What Is Sensitivity Analysis?

Sensitivity analysis determines how different values of an independent variable affect a particular dependent variable under a given set of assumptions. In other words, sensitivity analyses study how various sources of uncertainty in a mathematical model contribute to the model's overall uncertainty. This technique is used within specific boundaries that depend on one or more input variables.

Sensitivity analysis is used in the business world and in the field of economics . It is commonly used by financial analysts and economists and is also known as a what-if analysis.

Key Takeaways

• Sensitivity analysis determines how different values of an independent variable affect a particular dependent variable under a given set of assumptions.
• This model is also referred to as a what-if or simulation analysis.
• Sensitivity analysis can be used to help make predictions in the share prices of publicly traded companies or how interest rates affect bond prices.
• Sensitivity analysis allows for forecasting using historical, true data.
• While sensitivity analysis determines how variables impact a single event, scenario analysis is more useful to determine many different outcomes for more broad situations.

Investopedia / Lara Antal

How Sensitivity Analysis Works

Sensitivity analysis is a financial model that determines how target variables are affected based on changes in other variables known as input variables. It is a way to predict the outcome of a decision given a certain range of variables. By creating a given set of variables, an analyst can determine how changes in one variable affect the outcome.

Both the target and input—or independent and dependent—variables are fully analyzed when sensitivity analysis is conducted. The person doing the analysis looks at how the variables move as well as how the target is affected by the input variable.

Sensitivity analysis can be used to help make predictions about the share prices of public companies . Some of the variables that affect stock prices include company earnings, the number of shares outstanding, the debt-to-equity ratios (D/E), and the number of competitors in the industry. The analysis can be refined about future stock prices by making different assumptions or adding different variables. This model can also be used to determine the effect that changes in interest rates have on bond prices. In this case, the interest rates are the independent variable, while bond prices are the dependent variable.

Sensitivity analysis allows for forecasting using historical, true data. By studying all the variables and the possible outcomes, important decisions can be made about businesses, the economy, and making investments.

Investors can also use sensitivity analysis to determine the effects different variables have on their investment returns.

Usefulness of Sensitivity Analysis

Financial models that incorporate sensitivity analysis can provide management a range of feedback that is useful in many different scenarios. The breadth of the usefulness of sensitivity analysis includes but is not limited to:

• Understanding influencing factors. This includes what and how different external factors interact with a specific project or undertaking. This allows management to better understand what input variables may impact output variables.
• Reducing uncertainty. Complex sensitivity analysis models educate users on different elements impacting a project; this in turn informs members on the project what to be alert for or what to plan in advance for.
• Catching errors. The original assumptions for the baseline analysis may have had some uncaught errors. By performing different analytical iterations, management may catch mistakes in the original analysis.
• Simplifying the model. Overly complex models may make it hard to analyze the inputs. By performing sensitivity analysis, users can better understand what factors don't actually matter and can be removed from the model due to its lack of materiality.
• Communicating results. Upper management may already be defensive or inquisitive about an undertaking. Compiling analysis on different situations helps inform decision-makers of other outcomes they may be interested in knowing about.
• Achieving goals. Management may lay long-term strategic plans that must meet specific benchmarks. By performing sensitivity analysis, a company can better understand how a project may change and what conditions must be present for the team to meet its metric targets.

Because sensitivity analysis answers questions such as "What if XYZ happens?", this type of analysis is also called what-if analysis.

Sensitivity vs. Scenario Analysis

In finance, a sensitivity analysis is created to understand the impact a range of variables has on a given outcome. It is important to note that a sensitivity analysis is not the same as a scenario analysis . As an example, assume an equity analyst wants to do a sensitivity analysis and a scenario analysis around the impact of earnings per share (EPS) on a company's relative valuation by using the price-to-earnings (P/E) multiple.

The sensitivity analysis is based on the variables that affect valuation, which a financial model can depict using the variables' price and EPS. The sensitivity analysis isolates these variables and then records the range of possible outcomes.

On the other hand, for a scenario analysis, an analyst determines a certain scenario such as a stock market crash or change in industry regulation. The analyst then changes the variables within the model to align with that scenario. Put together, the analyst has a comprehensive picture and now knows the full range of outcomes, given all extremes, and has an understanding of what the outcomes would be, given a specific set of variables defined by real-life scenarios.

Advantages and Limitations of Sensitivity Analysis

Conducting sensitivity analysis provides a number of benefits for decision-makers. First, it acts as an in-depth study of all the variables. Because it's more in-depth, the predictions may be far more reliable. Secondly, It allows decision-makers to identify where they can make improvements in the future. Finally, it allows for the ability to make sound decisions about companies, the economy, or their investments.

There are some disadvantages to using a model such as this. The outcomes are all based on assumptions because the variables are all based on historical data. Very complex models may be system-intensive, and models with too many variables may distort a user's ability to analyze influential variables.

Provides management different output situations based on risk or changing variables

May help management target specific inputs to achieve more specific results

May easily communicate areas to focus on or greatest risks to control

May identify mistakes in the original benchmark

Generally reduces the uncertainty and unpredictability of a given undertaking

Heavily relies on assumptions that may not become true in the future

May burden computer systems with complex, intensive models

May become overly complicated which distorts an analysts ability to

May not accurately integrate independent variables (as one variable may not accurately the impact of another variable)

Example of Sensitivity Analysis

Assume Sue is a sales manager who wants to understand the impact of customer traffic on total sales. She determines that sales are a function of price and transaction volume. The price of a widget is $1,000, and Sue sold 100 last year for total sales of $100,000.

Sue also determines that a 10% increase in customer traffic increases transaction volume by 5%. This allows her to build a financial model and sensitivity analysis around this equation based on what-if statements. It can tell her what happens to sales if customer traffic increases by 10%, 50%, or 100%.

Based on 100 transactions today, a 10%, 50%, or 100% increase in customer traffic equates to an increase in transactions by 5%, 25%, or 50% respectively. The sensitivity analysis demonstrates that sales are highly sensitive to changes in customer traffic.

What Is Sensitivity Analysis in NPV?

Sensitivity analysis in NPV analysis is a technique to evaluate how the profitability of a specific project will change based on changes to underlying input variables. Though a company may have calculated the anticipated NPV of a project, it may want to better understand how better or worse conditions will impact the return the company receives. 

How Do You Calculate Sensitivity Analysis?

Sensitivity analysis is often performed in analysis software, and Excel has built in functions to help perform the analysis. In general, sensitivity analysis is calculated by leveraging formulas that reference different input cells. For example, a company may perform NPV analysis using a discount rate of 6%. Sensitivity analysis can be performed by analyzing scenarios of 5%, 8%, and 10% discount rates as well by simply maintaining the formula but referencing the different variable values. 

What Are the Two Main Types of Sensitivity Analysis?

The two main types of sensitivity analysis are local sensitivity analysis and global sensitivity analysis. Local sensitivity analysis assesses the effect of a single parameter at a time while holding all other parameters constant, while global sensitivity analysis is a more broad analysis used in more complex modeling scenarios such as Monte Carlo techniques.

What Is the Difference Between Sensitivity Analysis and Scenario Analysis?

Sensitivity analysis is the technique of taking a single event and determining different outcomes of that event. For example, a company may analyze its valuation based on several factors that may influence the calculation. On the other hand, scenario analysis relates to more broad conditions where the outcome is not known. For this example, imagine economists trying to project macroeconomic conditions 18 months from now. 

The Bottom Line

When a company wants to determine different potential outcomes for a given project, it may consider performing a scenario analysis. Scenario analysis entails manipulating independent variables to see the resulting financial impacts. Companies perform scenario analysis to identify opportunities, mitigate risk, and communicate decisions to upper management.

Stanford University, Department of Aeronautics and Astronautics. " Chapter 4, Sensitivity Analysis ," Pages 77.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• Open access
• Published: 21 May 2024

Hyperkalemia in chronic kidney disease patients with and without heart failure: an Italian economic modelling study

• Ewa Stawowczyk 1 ,
• Thomas Ward 1 , 2 ,
• Ernesto Paoletti 3 ,
• Michele Senni 4 &
• Antonio Ramirez de Arellano 5  

Cost Effectiveness and Resource Allocation volume  22 , Article number:  42 ( 2024 ) Cite this article

Metrics details

Hyperkalemia (HK) is frequently present in chronic kidney disease (CKD). Risk factors for HK among CKD patients include comorbidities and renin–angiotensin–aldosterone system inhibitor (RAASi) treatment. Current standard of care (SoC) often necessitates RAASi down-titration or discontinuation, resulting in poorer cardiorenal outcomes, hospitalization and mortality. This study evaluates the cost-effectiveness of patiromer for HK in CKD patients with and without heart failure (HF) in an Italian setting.

A lifetime Markov cohort model was developed based on OPAL-HK to assess the health economic impact of patiromer therapy in comparison to SoC after accounting for the effects of HK and RAASi use on clinical events. Outcomes included accumulated clinical events, number needed to treat (NNT) and the incremental cost-effectiveness ratio (ICER). Subgroup analysis was conducted in CKD patients with and without HF.

Patiromer was associated with an incremental discounted cost of €4,660 and 0.194 quality adjusted life years (QALYs), yielding an ICER of €24,004. Per 1000 patients, patiromer treatment prevented 275 moderate/severe HK events, 54 major adverse cardiovascular event, 246 RAASi discontinuation and 213 RAASi up-titration/restart. Subgroup analysis showed patiromer was more effective in preventing clinical events in CKD patients with HF compared to those without; QALY gains were greater in CKD patients without HF versus those with HF (0.267 versus 0.092, respectively). Scenario analysis and sensitivity analysis results support base-case conclusions.

Patiromer is associated with QALY gains in CKD patients with and without HF compared to SoC in Italy. Patiromer prevented HK events, enabled RAASi therapy maintenance and reduced cardiovascular event risk.

Introduction

Hyperkalemia (HK) (serum potassium concentration > 5.0 mmol/l) is associated with increased risk of cardiac arrhythmias, muscle weakness/paralysis and mortality [ 1 , 2 ]. HK occurs due to potassium homeostasis dysfunction and frequently presents in patients with chronic kidney disease (CKD); the presence of other comorbidities (including heart failure (HF), diabetes mellitus and hypertension [ 3 , 4 , 5 ]) heightens risk of HK. A retrospective analysis investigating the association between HK prevalence and comorbidities reported that HK events were more frequent in patients with CKD and/or HF versus patients without these comorbidities [ 6 ].

An additional risk factor for HK includes renin–angiotensin–aldosterone system inhibitor (RAASi) use, including angiotensin-converting enzyme inhibitors and angiotensin-receptor blockers, the current mainstay treatment options for cardiorenal patients [ 7 ]. Optimal RAASi dosing offers renal and cardiovascular protection in patients with CKD and HF, reducing the risk of cardiovascular events, kidney failure and all-cause mortality [ 5 ]. Despite the clinical benefits of RAASi, its use in cardiorenal patients is often compromised through discontinuation/down-titration, due to increased HK incidence rates and the requirement to manage potassium levels; resulting in an increased risk of poorer cardiorenal outcomes, hospitalization and mortality [ 5 ].

Treatments for HK, such as dietary interventions, loop diuretic therapy, and RAASi discontinuation/down-titration, are not effective long-term. Consequently, HK management in CKD patients with and without HF remains inadequate and further therapeutic development is needed in this clinical setting.

Patiromer, a non-absorbed polymer which binds to potassium within the gastrointestinal tract reducing serum potassium levels, has been approved for the treatment of HK by the European Medicines Agency [ 8 ], and reimbursed in five European countries including Italy [ 9 ]. Clinical trials, including OPAL-HK, PEARL-HF, AMETHYST-DN, DIAMOND and AMBER, have demonstrated the effectiveness and safety of long-term patiromer use in reducing serum potassium levels in cardiorenal patients receiving RAASi [ 10 , 11 , 12 , 13 , 14 ]. Patiromer therapy could address some of the unmet need in chronic HK management in cardiorenal patients.

In Italy, current HK management is insufficient, with approximately one-third of CKD patients in nephrology clinics remaining with or developing HK annually [ 15 , 16 , 17 ]. Although approved in the EU for treating HK in patients with CKD with or without HF [ 8 ], economic evaluation of patiromer introduction in an Italian setting is lacking. The objective of this study is to estimate the cost-effectiveness of patiromer for the treatment of HK in patients with CKD with or without HF in Italy, and to explore the influence of HF on outcomes.

A previously published lifetime Markov cohort model was adapted to assess the economic impact of patiromer therapy in comparison to standard of care (SoC), in controlling HK in CKD patients with and without HF, from a payer’s perspective [ 18 ]. The model was designed to predict the natural history of CKD and HF and quantify the direct medical costs and benefits associated with patiromer use for serum potassium management in patients in Italy. As CKD and HF are chronic progressive diseases associated with increased risk of mortality, a lifetime horizon was modelled in line with technology assessment guidelines, and a monthly cycle length was adopted [ 19 ]. A discount rate of 3% was applied to both costs and utilities.

Model structure

Patients enter the model with either CKD alone or CKD and HF. CKD disease progression was modelled through advanced CKD stages to end-stage renal disease (ESRD), comprising of separate dialysis and transplant health states. In CKD patients with HF, HF disease progression was modelled via transitions between New York Heart Association (NYHA) classifications (I to IV). CKD and HF were modelled independently, with progression through health states in one not impacting progression through health states in the other, except for those exiting the model in the death health state. As a simplifying assumption, patients without HF at model initiation were assumed to not develop HF throughout the modelled time horizon. The distribution of patients among health states at model initiation, alongside baseline age and sex input parameters, were based on the OPAL-HK trial [ 10 ] and are presented in Table  1 . Disease progression and long-term outcomes, sourced from published literature, are described in Additional file 1 .

As the simulated cohort progresses through the model, the value of alternative treatments is captured through the occurrence of HK events, changes in RAASi use and treatment discontinuation. The likelihood of clinical events (major adverse cardiac events (MACE), hospitalization and mortality) was predicted and impacted directly by a patient’s health state (e.g., CKD and HF), RAASi use and HK incidence (i.e., potassium level).

Patiromer use was compared against current SoC. Modelling SoC is challenging due to the considerable heterogeneity associated with HK pathogenesis, methods to correct/manage potassium levels (particularly non-pharmacological interventions, and variable levels of adherence to pharmacological methods), and patient responses to such interventions. Accordingly, the broad definition of SoC used in OPAL-HK was adopted and comprised lifestyle interventions for the background maintenance of potassium (e.g., dietary intervention and modification of concomitant medications) and acute management for the correction of potassium. This aligns with current clinical HK management in Italy [ 17 ].

Clinical event incidence

HK was classified as a serum potassium level > 5 mmol/l, consistent with definitions used in OPAL-HK and the broader HK literature [ 21 , 22 ]. Events were further stratified by severity (i.e., of 5-5.5 mmol/l [mild HK], 5.5-6 mmol/l [moderate HK] and > 6 mmol/l [severe HK]). During the first three cycles of the modelled time horizon, incident HK events were based on data from OPAL-HK [ 21 , 23 ]. For the remaining timeframe, HK annual rates were sourced from European data from Humphrey et al. [ 24 ] and applied to the SoC arm [ 25 ]. The effect of patiromer use on the rate of HK was obtained from OPAL-HK and incorporated into the model. Table  2 summarizes the applied HK event probabilities. Increased potassium levels negatively impact the occurrence of MACE, hospitalization, and death; the magnitude of these impacts is further described in additional file 2 .

All patients are assumed to be using a maximal RAASi dose upon entering the model. Patients may reduce their RAASi dose or discontinue RAASi treatment (from any dose) at any point in the model. Continuous RAASi use is known to favorably impact on CKD progression and the incidence of MACE, hospitalization and death, and negatively impact on the incidence of HK. The relationships between these events are further described in additional files 1 and 2 . The effect of RAASi dose on clinical events has previously been investigated in CKD and HF patients; for the purposes of defining an optimal versus sub-optimal RAASi dose level, we utilize the definition reported within this study (i.e., < 50% and ≥ 50% of the guideline-recommended RAASi dose for sub-optimal and optimal RAASi dose levels, respectively) [ 5 ].

The proportion of patients still on RAASi one month after patiromer and SoC initiation is based on data reported from OPAL-HK [ 10 ]. For the patiromer arm, this proportion relates only to those that have achieved response; patients not responding to treatment were assumed to receive RAASi therapy in line with the SoC arm. Rates of RAASi discontinuation and down-titration were taken from OPAL-HK for months 2 and 3 [ 20 ]. For the remaining timeframe of the model, RAASi discontinuation and down-titration rates were dependent on potassium levels, based on data from Linde et al., and applied to the SoC arm [ 5 ]. The effects of patiromer on RAASi discontinuation/down-titration compared to SoC were obtained from OPAL-HK and incorporated into the model [ 10 ]. To reflect transient changes in RAASi regimen, patients were allowed to return to optimal RAASi use, independent of their potassium level, with a monthly probability of 3.51% [ 5 ]. Due to a lack of relevant data, patients who down-titrated RAASi use were assumed not to return to maximum use. Rates of RAASi discontinuation and down-titration used in the model are detailed in additional file 1 .

Treatment discontinuation

Patients initiated on patiromer could discontinue treatment after one month, depending on their response to treatment. In accordance with OPAL-HK, patients responding to patiromer within the first month continued to receive patiromer and were subject to the associated event risks. Those not responding to patiromer discontinued treatment and incurred a risk of events in line with SoC (i.e., assuming no legacy effect of patiromer treatment). In the comparator arm, treatment with SoC could not be discontinued. Beyond the first month, patients receiving patiromer discontinued treatment at a constant monthly probability of 10.33%, or if they reached ESRD, subsequently incurring event risk in line with the SoC arm. Patients in the patiromer arm repeated treatment if their potassium levels were equal to or exceeded 5.5-6 mmol/l in the months following discontinuation.

Clinical events

MACE comprised of hospitalizations due to coronary heart disease, HF, ischemic stroke, and peripheral arterial disease as defined in Go et al. [ 26 ]. Hospitalization related to all-cause hospitalization. The probability of MACE, hospitalization and mortality, stratified by disease severity, were estimated for a CKD-only and HF-only patient; the higher value was then applied in the CKD cohort with HF. In both cohorts, where all-cause mortality estimates from Italian-specific life Table [ 27 ] exceeded mortality estimates based on comorbidities and RAASi use, the greater mortality rate was utilized.

A targeted literature search was carried out to identify studies reporting on the rate of cardiovascular events, hospitalization, and mortality in Italian patients with CKD or HF and HK. The search was carried out in Medline (PubMed) and Google Advanced Search; and was supported with snowballing on relevant articles. Search terms used were grouped into health state concepts (CKD or HF-related), HK-related terms and a search filter for studies conducted in Italy. The best available evidence, identified by relevance of the population, sample size and study robustness, was used to inform model parameters. Event rates are described in additional file 1 .

Direct medical costs included HK and disease management costs, costs of RAASi use and dose titrations, and one-off event costs of MACE, hospitalization, death and ESRD events (dialysis, transplantation). All costs were reported in 2020/21 Euros.

Healthcare utilization for HK management was primarily derived from Italian guidelines [ 17 ] and multicenter prospective observational studies in non-dialysis [ 16 , 25 ] and dialysis patients [ 28 ]. RAASi use was based on OPAL-HK [ 20 ] and dose optimization was aligned with technology appraisal guidance from National Institute for Health and Care Excellence (NICE) for sodium zirconium cyclosilicate in treating HK [ 29 ]. HK-related hospitalization cost data was taken from Italian diagnostic-related-groups (DRGs) [ 30 ]. Drug costs were primarily obtained from the list of class A medicines [ 31 ]. Resource utilization and the costing of disease management and clinical events was primarily informed by published literature [ 28 , 32 , 33 , 34 ]. All costs are summarized in Table  3 and detailed in additional file 3 .

Health utilities

Health utilities (and disutilities) applied to modelled health states (and events) are presented in additional file 4 [ 37 , 38 , 39 , 40 , 41 , 42 ]. Utility estimates measured with the EQ-5D were broadly informed by a recent NICE technology appraisal [ 29 ]. A targeted literature search carried out in Medline (PubMed) and Google Advanced Search did not identify any Italian-specific studies reporting on quality of life that could be deemed more appropriate than those informed by the NICE technology appraisal.

The costs, life years and quality-adjusted life years (QALYs) accumulated by each treatment arm were reported. Comparisons between treatments were made utilizing the incremental cost-effectiveness ratio (ICER). The number of clinical events occurring throughout the modelled time horizon and the number of patients needed to treat (NNT) with patiromer to prevent one additional case of HK, MACE, hospitalization and RAASi discontinuation/down-titration were calculated. In sub-group analysis, these calculations were repeated in CKD patients with and without HF, where all other model input parameters were assumed to remain the same as in the base case analysis.

In scenario analysis, the effect of RAASi use on clinical events (i.e., MACE and hospitalization) was incorporated into the model using an alternative definition of optimal RAASi use reported in Italian-specific studies [ 43 , 44 ]. Within these data sources, persons with > 80% proportion of days covered (PDC) with RAASi were defined as adherent, and subsequently informed risk in the optimal RAASi use group in the model. Conversely, those with ≤ 80% PDC were assumed to represent those not receiving RAASi in the model. PDC is one of the most reliable methods for measuring medication adherence in chronic therapies; a threshold of 80% is indicative of achieving maximum clinical benefit [ 45 ].

Italian-specific data were also incorporated into scenario analysis, including alternative assumptions around the baseline distribution of patients among health states, the proportion of patients with HF and baseline demographic and clinical risk factors. Further details on the data applied in scenario analyses are presented in additional file 5 .

Sensitivity analysis

One-way sensitivity analysis was undertaken to assess the impact of individual model parameters on the ICER; the most influential and uncertain input parameters were incorporated in the analysis. The discount rate was varied between 0% and 5%, as required by Italian guidelines [ 19 ]. Probabilistic sensitivity analysis was undertaken, with parameter values sampled independently across 5,000 model iterations. Patient characteristics were sampled using a normal distribution; probabilities and health utilities were sampled using a beta distribution; and costs, hazard ratios and odds ratios were sampled using a gamma distribution.

Base-case analysis

Base-case results are presented in Table  4 . Treatment with patiromer was associated with an additional discounted €4,660 and 0.194 QALYs, yielding an ICER of €24,004. Compared to SoC, life expectancy was extended by 0.256 life years. Differences in costs were primarily driven by patiromer treatment and CKD/ESRD disease management. Compared to SoC, patiromer use was associated with higher CKD management costs and renal replacement therapy (RRT) costs, with patients spending more time in pre-dialysis disease stages (due to reduced CKD progression) and observing greater life expectancy. Costs associated with HK events and MACE were also reduced in the patiromer arm. Furthermore, the distribution of costs relating to RAASi use and titration indicates more persons remain on RAASi treatment when receiving patiromer.

Patients received patiromer treatment for an average of 10.4 months. The number of incremental events accrued by patients over the modelled time horizon are illustrated in Fig.  1 . Per 1,000 patients, 224 moderate HK (5.5-6 mmol/l) events and 51 severe HK (≥ 6 mmol/l) events were avoided with patiromer use. The NNT with patiromer to avoid an additional case of HK was 4.5 and 19.4 for moderate and severe HK, respectively. Compared to SoC, there were fewer cases of MACE and RAASi discontinuation and subsequent up-titration with patiromer use. The NNT with patiromer to prevent one additional case of MACE and RAASi discontinuation was 45.6 and 4.7 patients, respectively. Event counts of RAASi down-titration, hospitalization, dialysis and transplant were similar between arms.

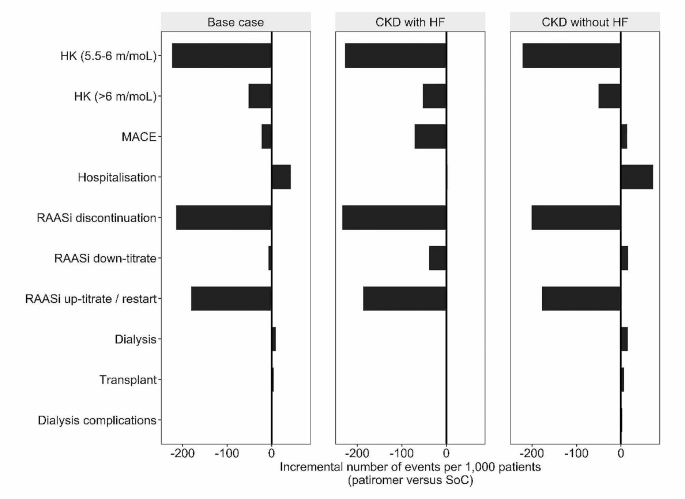
Incremental number of lifetime clinical events per 1,000 patients (patiromer versus SoC). Abbreviations: CKD: chronic kidney disease; HF: heart failure; HK: hyperkalemia; MACE: major adverse cardiac event; RAASi: renin?angiotensin?aldosterone system inhibitor; SoC: standard of care

Subgroup analysis

Patiromer was associated with incremental costs and survival and QALY gains in patients with CKD and HF and in patients with CKD alone. Discounted incremental costs were €2,838 in those with CKD and HF and €5,969 in those with CKD alone, while discounted QALY gains were 0.092 and 0.267, respectively (Table  4 ). Differences in outcomes were predominantly driven by the greater rate of mortality amongst patients with comorbid HF. Over the modelled time horizon, patients with CKD and HF in the patiromer arm observed an average life expectancy of 9.8 years (SoC: 9.6 years), while those without HF observed an average life expectancy of 13.7 years (SoC: 13.3 years).

Whilst the total number of clinical events was lower in the CKD and HF subgroup compared to CKD alone (Additional file 6 ), the number of HK events (≥ 5.5 mmol/l) avoided with patiromer, NNT and associated costs were similar across sub-groups and base-case results. The need to discontinue RAASi therapy was substantially reduced with patiromer in both subgroups, although this reduction was more pronounced in the CKD and HF subgroup. Across subgroups, 4–5 patients would need to be treated with patiromer to avoid one additional case of RAASi discontinuation. The number of events avoided through patiromer use for each subgroup are presented in Fig.  1 . Cost savings were realized through reductions in the number of HK events, MACE events (although only in the cohort with HF) and RAASi discontinuation episodes in both subgroups. Patiromer was associated with 272 fewer moderate and severe HK events, 14 additional MACE events and 201 fewer RAASi discontinuation episodes in the CKD without HF subgroup per 1,000 patients. For the CKD with HF subgroup, the number of events avoided were 280 moderate and severe HK events, 71 MACE events and 234 RAASi discontinuation episodes, per 1,000 patients. This equated to a NNT of 3.6–3.7 to avoid one HK event, 14 to avoid one MACE event (in the subgroup with HF), and 4.3-5.0 to avoid one RAASi discontinuation episode. The extension of life associated with patiromer in patients with CKD without HF resulted in an additional 73 hospitalizations and 22 RRT events per 1,000 patients, and an additional 3 hospitalization and 2 RRT events per 1,000 patients with CKD with HF.

Changing the discount rate applied to costs and benefits, respectively, resulted in ICER estimates varying from €20,618 to €31,924 and €18,163 to €28,194 under base case assumptions. In wider-ranging one-way sensitivity analyses, the most influential parameters were the model discount rates, the patiromer discontinuation rate, the cost of patiromer, the influence of RAASi use on CKD disease progression rates and RAASi discontinuation and baseline patient age. The sensitivity analysis tornado plot is shown in Additional file 7 .

Results of probabilistic sensitivity analyses, presented in Fig.  2 , support the deterministic base case analysis. Under base case assumptions, the discounted incremental cost and QALY gains were €4,887 and 0.191, respectively, resulting in an ICER of €25,553. Patiromer was estimated to have a 49.1% and 94.0% probability of cost-effectiveness, compared to SoC, at willingness-to-pay thresholds of €25,000 and €40,000, respectively.

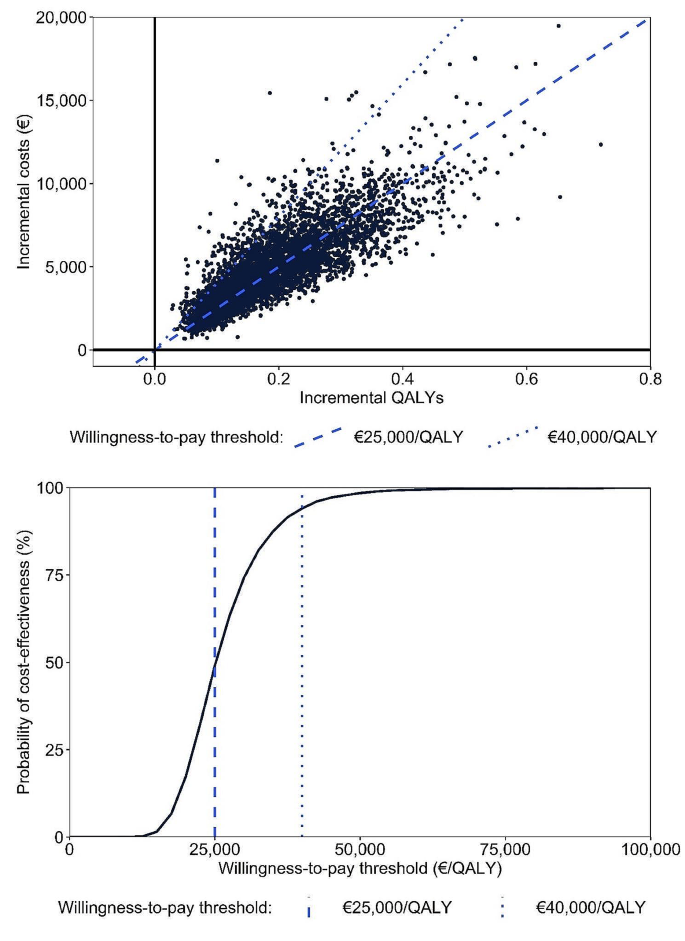
Results of probabilistic sensitivity analysis. Upper figure shows the scatterplot of incremental costs and QALYs. Lower figure displays the cost-effectiveness acceptability curve. Abbreviations : QALY: quality-adjusted life years

Scenario analysis

Utilizing alternative sources of RAASi influence on transient events (i.e., different definitions of optimal RAASi use, approximated through estimates of adherence) increased discounted incremental cost and QALY outcomes to €5,326 and 0.216, respectively, resulting in an ICER of €24,693. The average increase in life expectancy associated with patiromer use was estimated to be 0.407 years.

The introduction of alternative Italian-specific baseline patient data to the model increased discounted incremental costs and QALY outcomes to €5,244 and 0.191, respectively, yielding an ICER of €27,506. Patiromer use was associated with an average life expectancy gain of 0.343 years.

Our results demonstrate that HK treatment with patiromer in CKD patients with and without HF increases quality of life outcomes compared to SoC in Italy. From a healthcare payer’s perspective, the model estimated that the introduction of patiromer was associated with an incremental discounted lifetime benefit of 0.194 QALYs, with an incremental discounted cost of €4,660, yielding an ICER of €24,004 per QALY in comparison to SoC. Despite a small incremental cost associated with patiromer use, attributable to both initial patiromer treatment and increased CKD and ESRD management costs, cost-offsets were made through reductions in MACE and HK costs. Patiromer was able to prevent future HK events; enabling patients to maintain RAASi therapy and reduce their risk of cardiovascular events. Subsequently, patients progressed at a slower rate to RRT and had more time to accrue CKD-related healthcare costs. In our subgroup analyses, the beneficial effects of patiromer are observed in both CKD patients with and without HF, and are most pronounced in patients with CKD alone, due to their longer life expectancy and longer time available to accrue the benefit of patiromer use. Together with scenario and sensitivity analyses, our results highlight the importance of continuous RAASi therapy in CKD patients both with and without HF.

In Italy, HK presents a significant clinical and economic burden, with increased HK prevalence in CKD and HF populations associated with worsening outcomes and lower RAASi use [ 15 , 16 , 17 , 44 , 46 ]. A community database study of 12 million inhabitants investigated the prevalence of HK in the general Italian population; although HK prevalence was low among the general population (0.035%), more than half of those affected were hospitalized over a one year period, with tripling costs to the Italian healthcare system [ 46 ]. This study also examined the burden and prevalence of HK in patients with HF, using data from the Italian Network on Heart Failure (IN-HF) registry [ 46 ]. Authors reported that HK was frequent in patients with CKD and/or HF and was associated with decreased RAASi use compared to patients with normokalemia. Furthermore, an Italian observational study assessed outcomes and determinants of HK in 2,446 CKD patients across 46 nephrology clinics, and found that HK (mild to moderate) was prevalent amongst 37% of CKD patients with an associated risk of ESRD progression [ 16 ]. These studies highlight the unmet need for better treatment options for HK in CKD patients with and without HF in Italy.

The clinical benefits of reducing potassium levels are paramount in allowing CKD patients with and without HF to maintain RAASi therapy. Enabling optimal dosage of RAASi therapy is associated with improvement of cardiovascular and renal outcomes, including attenuation of disease progression [ 16 , 43 ] and improved survival [ 16 , 43 , 44 , 47 ] in CKD and/or HF patients.

Whilst RAASi enablement is important for reducing the rate of events in HF, a patient’s ability to realize this gain is limited due to the significantly reduced life expectancy in CKD patients with HF. In the elderly population, whom are most at risk of developing comorbid CKD and HF, there is a significant increased risk associated with cardiovascular-related hospitalizations and mortality [ 48 ]. Since there were greater reductions in hospitalizations in the CKD with HF group compared to CKD alone, in this instance, a treatment which enables optimal use of RAASi therapy would greatly reduce hospitalization. Patiromer therapy was associated with an incremental gain of 0.256 LY in the base-case analysis and 0.145 LY for the CKD with HF group. These are clinically meaningful increases (2.8% and 1.9%) over their respective control arms; for the CKD with HF cohort, this is approximately equivalent to 53 days.

Our cost-effectiveness analysis was based on OPAL-HK, which had its limitations. Long-term outcomes for patiromer are not yet available, hence extrapolation of treatment outcomes, measured over 3 months in OPAL-HK, were required to approximate the longer-term impact of patiromer, introducing uncertainty to estimates of long-term cost-effectiveness. The design of the trial (i.e., a two-part, single-blind study) may have contributed to an underestimation in the relative benefit of patiromer compared to SoC, as patients in the SoC arm initially received patiromer, which was then withdrawn over subsequent months. The RAASi discontinuation algorithm utilized in OPAL-HK may not accurately represent discontinuation in all healthcare settings and may have overestimated the proportion of patients discontinuing RAASi therapy in the SoC arm. Both limitations are considered in one-way sensitivity analyses. OPAL-HK enrolled patients from different countries, with only a small fraction from Italy, hence there may be discrepancies between trial and real-world Italian outcomes.

Until the publication of the DIAMOND study [ 49 ], studies evaluating the association between HK, RAASi and clinical outcomes in CKD patients with and without HF have been limited. Hence, a targeted literature search attempted to identify the best available evidence to inform disease progression and clinical outcomes. Inconsistencies in HK definitions between studies limited the utilization of Italian-specific data in the model, although the UK studies used to inform rates are believed to be representative. A further data limitation concerns the use of the Framingham risk equation for HF mortality, which while utilized widely in contemporary health economic evaluations, is derived from an old data source and is US-specific, potentially overestimating mortality risk. It is likely that this results in an underestimation of the true lifetime benefit of patiromer. Finally, due to limited data availability, hospitalization, MACE, and death were modelled independently; the ability to more accurately relate these clinical events to each would likely improve the real-world validity of the model. Despite these limitations, the methodology applied is rigorous and the data sources represent appropriate approximations of real-world practice and outcomes; this study can be viewed as an indicative first step towards the health economic evaluation of patiromer for the treatment of HK in patients with CKD with and without HF, a complicated and multi-faceted disease area.

To conclude, our results indicate the health economic value of patiromer for the treatment of HK in CKD patients with and without HF in an Italian setting, with cost savings and QALY gains. Improving HK management in Italy by expanding treatment options has the potential to greatly benefit CKD patients with or without HF by enabling optimal RAASi therapy and reducing risk of hospitalization and mortality.

Data availability

The data that support the findings of this study are available from CSL Vifor but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Data are however available from the authors upon reasonable request and with permission of CSL Vifor.

Clase CM, Carrero J-J, Ellison DH, Grams ME, Hemmelgarn BR, Jardine MJ, et al. Potassium homeostasis and management of dyskalemia in kidney diseases: conclusions from a kidney disease: improving global outcomes (KDIGO) Controversies Conference. Kidney Int. 2020;97(1):42–61.

An JN, Lee JP, Jeon HJ, Kim DH, Oh YK, Kim YS, et al. Severe hyperkalemia requiring hospitalization: predictors of mortality. Crit Care. 2012;16(6):1–14.

Article   Google Scholar  

Kovesdy CP. Management of hyperkalemia: an update for the internist. Am J Med. 2015;128(12):1281–7.

Article   PubMed   Google Scholar  

Pitt B, Bakris GL. New potassium binders for the treatment of hyperkalemia: current data and opportunities for the future. Hypertension. 2015;66(4):731–8.

Article   CAS   PubMed   Google Scholar  

Linde C, Bakhai A, Furuland H, Evans M, McEwan P, Ayoubkhani D, et al. Real-World associations of renin-angiotensin-aldosterone system inhibitor dose, Hyperkalemia, and adverse clinical outcomes in a cohort of patients with New-Onset chronic kidney disease or heart failure in the United Kingdom. J Am Heart Assoc. 2019;8(22):e012655.

Article   PubMed   PubMed Central   Google Scholar  

Latts L, Reaven N, Funk S, McGaughey K, Adamson R. Hyperkalemia is highly prevalent in patients with cardiorenal comorbidities compared to patients without these comorbidities. Value Health. 2015;18(3):A135.

Xie X, Liu Y, Perkovic V, Li X, Ninomiya T, Hou W, et al. Renin-angiotensin system inhibitors and kidney and Cardiovascular outcomes in patients with CKD: a bayesian network Meta-analysis of Randomized clinical trials. Am J Kidney Dis. 2016;67(5):728–41.

European Medicines Agency. EPAR summary for the public: Veltessa. 2017.

Vifor Pharma Annual Report. 2021 2021 [ https://www.viforpharma.com/sites/vifor-corp/files/reports-and-presentations/vifor-pharma-annual-report-2021-full-version-en.pdf .

Weir MR, Bakris GL, Bushinsky DA, Mayo MR, Garza D, Stasiv Y, et al. Patiromer in patients with kidney disease and hyperkalemia receiving RAAS inhibitors. N Engl J Med. 2015;372(3):211–21.

Pitt B, Weir M, Bushinsky D, Mayo M, Garza D, Stasiv Y, et al. Patiromer reduces serum K + in hyperkalemic patients with HF and CKD on RAAS inhibitors: results from OPAL-HK and AMETHYST-DN. J Card Fail. 2015;21(8):S107–8.

Pitt B, Anker SD, Bushinsky DA, Kitzman DW, Zannad F, Huang I-Z. Evaluation of the efficacy and safety of RLY5016, a polymeric potassium binder, in a double-blind, placebo-controlled study in patients with chronic heart failure (the PEARL-HF) trial. Eur Heart J. 2011;32(7):820–8.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Agarwal R, Rossignol P, Romero A, Garza D, Mayo MR, Warren S, et al. Patiromer versus placebo to enable spironolactone use in patients with resistant hypertension and chronic kidney disease (AMBER): a phase 2, randomised, double-blind, placebo-controlled trial. Lancet. 2019;394(10208):1540–50.

Rossignol P, Williams B, Mayo MR, Warren S, Arthur S, Ackourey G, et al. Patiromer versus placebo to enable spironolactone use in patients with resistant hypertension and chronic kidney disease (AMBER): results in the pre-specified subgroup with heart failure. Eur J Heart Fail. 2020;22(8):1462–71.

Borrelli S, De Nicola L, Minutolo R, Conte G, Chiodini P, Cupisti A, et al. Current management of hyperkalemia in non-dialysis CKD: longitudinal study of patients receiving stable nephrology care. Nutrients. 2021;13(3):942.

Provenzano M, De Francesco M, Iannazzo S, Garofalo C, Andreucci M, Genualdo R, et al. Cost-analysis of persistent hyperkalaemia in non-dialysis chronic kidney disease patients under nephrology care in Italy. Int J Clin Pract. 2020;74(5):e13475.

Bianchi S, Aucella F, De Nicola L, Genovesi S, Paoletti E, Regolisti G. Management of hyperkalemia in patients with kidney disease: a position paper endorsed by the Italian Society of Nephrology. J Nephrol. 2019;32(4):499–516.

Ward T, Brown T, Lewis RD, Kliess MK, de Arellano AR, Quinn CM. The cost effectiveness of Patiromer for the Treatment of Hyperkalaemia in patients with chronic kidney disease with and without heart failure in Ireland. PharmacoEconomics-Open. 2022;6(5):757–71.

Guidelines. and procedures for submitting to AIFA applications for reimbursement and pricing by pharmaceutical companies. Version 1.0.2020 4 April 2022. https://www.aifa.gov.it/en/negoziazione-e-rimborsabilit%C3%A0 .

Vifor Pharma. OPAL-HK CSR. Data on file.; 2014.

Weir MR, Bakris GL, Bushinsky DA, Mayo MR, Garza D, Stasiv Y, et al. Patiromer in patients with kidney disease and hyperkalemia receiving RAAS inhibitors. N Engl J Med. 2014;372(3):211–21.

Viera AJ, Wouk N. Potassium disorders: Hypokalemia and Hyperkalemia. Am Fam Physician. 2015;92(6):487–95.

PubMed   Google Scholar  

Weir MR, Mayo MR, Garza D, Arthur SA, Berman L, Bushinsky D, et al. Effectiveness of patiromer in the treatment of hyperkalemia in chronic kidney disease patients with hypertension on diuretics. J Hypertens. 2017;35(1Suppl 1):S57–63.

Humphrey T, Davids MR, Chothia M-Y, Pecoits-Filho R, Pollock C, James G. How common is hyperkalaemia? A systematic review and meta-analysis of the prevalence and incidence of hyperkalaemia reported in observational studies. Clin Kidney J. 2022;15(4):727–37.

Borrelli S, De Nicola L, Minutolo R, Conte G, Chiodini P, Cupisti A et al. Current management of Hyperkalemia in Non-dialysis CKD: longitudinal study of patients receiving stable Nephrology Care. Nutrients. 2021;13(3).

Go AS, Chertow GM, Fan D, McCulloch CE, Hsu C-y. Chronic kidney Disease and the risks of Death, Cardiovascular events, and hospitalization. N Engl J Med. 2004;351(13):1296–305.

Life Table 2020. Istituto Nazionale di Statistica; 2020.

Roggeri A, Roggeri DP, Zocchetti C, Bersani M, Conte F, ReNe, et al. Healthcare costs of the progression of chronic kidney disease and different dialysis techniques estimated through administrative database analysis. J Nephrol. 2017;30(2):263–9.

Technology appraisal guidance [TA599]. Sodium zirconium cyclosilicate for treating hyperkalaemia.2019 4 April 2022. https://www.nice.org.uk/guidance/ta599 .

Rapporto annuale sull’attività di ricovero ospedaliero. Dati SDO 2019.2020 4 April 2022. http://www.salute.gov.it/portale/temi/p2_4.jsp?lingua=italiano&tema=Assistenza,%20ospedale%20e%20territorio&area=ricoveriOspedalieri .

List of Class A and. Class H medicinal products. editor.: Italian Medicines Agency (AIFA); 2021. ingredient LoCAmpba.

Jommi C, Armeni P, Battista M, di Procolo P, Conte G, Ronco C, et al. The cost of patients with chronic kidney failure before Dialysis: results from the IRIDE Observational Study. Pharmacoecon Open. 2018;2(4):459–67.

Roggeri DP, Roggeri A, Zocchetti C, Cozzolino M, Rossi C, Conte F. Real-world data on healthcare resource consumption and costs before and after kidney transplantation. Clin Transpl. 2019;33(10):e13728.

Riccio E, Sabbatini M, Capuano I, Pellegrino AM, Petruzzelli LA, Pisani A. Oral Sucrosomial(R) iron versus intravenous iron for recovering iron deficiency anaemia in ND-CKD patients: a cost- minimization analysis. BMC Nephrol. 2020;21(1):57.

Corrao G, Ghirardi A, Ibrahim B, Merlino L, Maggioni AP. Burden of new hospitalization for heart failure: a population-based investigation from Italy. Eur J Heart Fail. 2014;16(7):729–36.

Roggeri DP, Roggeri A, Salomone M. Chronic kidney disease: evolution of healthcare costs and resource consumption from predialysis to dialysis in Piedmont Region, Italy. Adv Nephrol. 2014;2014.

Gorodetskaya I, Zenios S, Mcculloch CE, Bostrom A, Hsu C-Y, Bindman AB, et al. Health-related quality of life and estimates of utility in chronic kidney disease. Kidney Int. 2005;68(6):2801–8.

Lee AJ, Morgan CL, Conway P, Currie CJ. Characterisation and comparison of health-related quality of life for patients with renal failure. Curr Med Res Opin. 2005;21(11):1777–83.

Göhler A, Geisler BP, Manne JM, Kosiborod M, Zhang Z, Weintraub WS, et al. Utility estimates for decision–Analytic modeling in Chronic Heart failure—health states based on New York Heart Association Classes and Number of Rehospitalizations. Value Health. 2009;12(1):185–7.

Kent S, Briggs A, Eckermann S, Berry C. Are value of information methods ready for prime time? An application to alternative treatment strategies for NSTEMI patients. Int J Technol Assess Health Care. 2013;29(04):435–42.

National Institute for Health and Care Excellence. Clinical guideline [CG125]: Chronic kidney disease (stage 5): peritoneal dialysis 2011 08 December 2016. https://www.nice.org.uk/guidance/cg125 .

Sennfalt K, Magnusson M, Carlsson P. Comparison of hemodialysis and peritoneal dialysis–a cost-utility analysis. Perit Dial Int. 2002;22(1):39–47.

Santoro A, Perrone V, Giacomini E, Sangiorgi D, Alessandrini D, Degli Esposti L. Association between hyperkalemia, RAASi non-adherence and outcomes in chronic kidney disease. J Nephrol. 2021.

Volterrani M, Perrone V, Sangiorgi D, Giacomini E, Iellamo F, Degli Esposti L, et al. Effects of hyperkalaemia and non-adherence to renin-angiotensin-aldosterone system inhibitor therapy in patients with heart failure in Italy: a propensity-matched study. Eur J Heart Fail. 2020;22(11):2049–55.

Raebel MA, Schmittdiel J, Karter AJ, Konieczny JL, Steiner JF. Standardizing terminology and definitions of medication adherence and persistence in research employing electronic databases. Med Care. 2013;51(8 Suppl 3):S11–21.

Maggioni AP, Dondi L, Andreotti F, Calabria S, Iacoviello M, Gorini M, et al. Prevalence, clinical impact and costs of hyperkalaemia: special focus on heart failure. Eur J Clin Invest. 2021;51(8):e13551.

Rossignol P, Lainscak M, Crespo-Leiro MG, Laroche C, Piepoli MF, Filippatos G, et al. Unravelling the interplay between hyperkalaemia, renin-angiotensin-aldosterone inhibitor use and clinical outcomes. Data from 9222 chronic heart failure patients of the ESC-HFA-EORP heart failure Long-Term Registry. Eur J Heart Fail. 2020;22(8):1378–89.

Shiba N, Shimokawa H. Chronic kidney disease and heart failure—bidirectional close link and common therapeutic goal. J Cardiol. 2011;57(1):8–17.

Butler J, Anker SD, Lund LH, Coats AJ, Filippatos G, Siddiqi TJ, et al. Patiromer for the management of hyperkalemia in heart failure with reduced ejection fraction: the DIAMOND trial. Eur Heart J. 2022;43(41):4362–73.

Italy -The World Bank. Italian consumer price index 2021 [ https://data.worldbank.org/country/IT .

Download references

Acknowledgements

The authors thank Melodi Kosaner-Kließ and Ruth D Lewis of Health Economics and Outcomes Research Ltd. for assisting study conceptualization and design, and for providing medical writing and editorial support, respectively.

This work was supported by CSL Vifor who provided support for data analysis, model development and medical writing for this study, in accordance with Good Publication Practice (GPP3) guidelines ( http://www.ismpp.org/gpp3 ).

Author information

Authors and affiliations.

Health Economics and Outcomes Research Ltd, Cardiff, UK

Ewa Stawowczyk & Thomas Ward

Health Economics Group, College of Medicine and Health, University of Exeter, Exeter, UK

Thomas Ward

Nephrology, Dialysis and Transplantation, University of Genoa and Policlinico, San Martino Genoa, Italy

Ernesto Paoletti

Cardiovascular Department and Cardiology Unit, Papa Giovanni XXIII Hospital, Bergamo, Italy

Michele Senni

HEOR, CSL Vifor, Glattbrugg, Switzerland

Antonio Ramirez de Arellano

You can also search for this author in PubMed   Google Scholar

Contributions

A.R.dA conceptualized and designed the study. T.W was responsible for data analysis. E.S, T.W, E.P, M.S and A.R.dA contributed to interpretation of the results, preparation and review of the manuscript, and approval of the final manuscript for publication.

Corresponding author

Correspondence to Ewa Stawowczyk .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests.

A.R.dA is an employee of CSL Vifor At the time of original drafts, T.W was an employee of HEOR Ltd. E.S is an employee of HEOR Ltd. HEOR Ltd received fees from CSL Vifor in relation to this study. M.S reports consultancy fees from CSL Vifor, Novartis, Merck, Bayer, Abbott, Boehringer Ingelheim, AstraZeneca, Bioventrix, Servier, Novo Nordisk, and Cardurion, AnaCardio. E.P reports consultancy fees from CSL Vifor, AstratZeneca, Astellas, and Novartis.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Additional file 1

: Disease progression. Provides details of the disease progression data utilized in the model

Additional file 2

: Disease progression and events. Provides details of the disease progression and events utilized in the model

Additional file 3

: Costs. Provides detail of cost data stylized in the model. All costs are presented in 2021 EUR

Additional file 4

: Utility and disutility. Provides details of utility and disutility input parameters utilized in the model

Additional file 5

: Scenario analysis. Provides additional data utilized in scenario analyses

Additional file 6

: Subgroup analysis. Provides details of cumulative clinical events in patients with CKD and HK versus CKD alone

Additional file 7

: Sensitivity analysis tornado. Provides results of deterministic sensitivity analysis

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Stawowczyk, E., Ward, T., Paoletti, E. et al. Hyperkalemia in chronic kidney disease patients with and without heart failure: an Italian economic modelling study. Cost Eff Resour Alloc 22 , 42 (2024). https://doi.org/10.1186/s12962-024-00547-y

Download citation

Received : 14 July 2023

Accepted : 18 April 2024

Published : 21 May 2024

DOI : https://doi.org/10.1186/s12962-024-00547-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Cost-effectiveness
• Heart failure
• Chronic kidney disease
• Hyperkalemia

Cost Effectiveness and Resource Allocation

ISSN: 1478-7547

• General enquiries: [email protected]

• Open access
• Published: 16 July 2013

A tutorial on sensitivity analyses in clinical trials: the what, why, when and how

• Lehana Thabane 1 , 2 , 3 , 4 , 5 ,
• Lawrence Mbuagbaw 1 , 4 ,
• Shiyuan Zhang 1 , 4 ,
• Zainab Samaan 1 , 6 , 7 ,
• Maura Marcucci 1 , 4 ,
• Chenglin Ye 1 , 4 ,
• Marroon Thabane 1 , 8 ,
• Lora Giangregorio 9 ,
• Brittany Dennis 1 , 4 ,
• Daisy Kosa 1 , 4 , 10 ,
• Victoria Borg Debono 1 , 4 ,
• Rejane Dillenburg 11 ,
• Vincent Fruci 12 ,
• Monica Bawor 13 ,
• Juneyoung Lee 14 ,
• George Wells 15 &
• Charles H Goldsmith 1 , 4 , 16  

BMC Medical Research Methodology volume  13 , Article number:  92 ( 2013 ) Cite this article

277k Accesses

452 Citations

115 Altmetric

Metrics details

Sensitivity analyses play a crucial role in assessing the robustness of the findings or conclusions based on primary analyses of data in clinical trials. They are a critical way to assess the impact, effect or influence of key assumptions or variations—such as different methods of analysis, definitions of outcomes, protocol deviations, missing data, and outliers—on the overall conclusions of a study.

The current paper is the second in a series of tutorial-type manuscripts intended to discuss and clarify aspects related to key methodological issues in the design and analysis of clinical trials.

In this paper we will provide a detailed exploration of the key aspects of sensitivity analyses including: 1) what sensitivity analyses are, why they are needed, and how often they are used in practice; 2) the different types of sensitivity analyses that one can do, with examples from the literature; 3) some frequently asked questions about sensitivity analyses; and 4) some suggestions on how to report the results of sensitivity analyses in clinical trials.

When reporting on a clinical trial, we recommend including planned or posthoc sensitivity analyses, the corresponding rationale and results along with the discussion of the consequences of these analyses on the overall findings of the study.

Peer Review reports

The credibility or interpretation of the results of clinical trials relies on the validity of the methods of analysis or models used and their corresponding assumptions. An astute researcher or reader may be less confident in the findings of a study if they believe that the analysis or assumptions made were not appropriate. For a primary analysis of data from a prospective randomized controlled trial (RCT), the key questions for investigators (and for readers) include:

How confident can I be about the results?

Will the results change if I change the definition of the outcome (e.g., using different cut-off points)?

Will the results change if I change the method of analysis?

Will the results change if we take missing data into account? Will the method of handling missing data lead to different conclusions?

How much influence will minor protocol deviations have on the conclusions?

How will ignoring the serial correlation of measurements within a patient impact the results?

What if the data were assumed to have a non-Normal distribution or there were outliers?

Will the results change if one looks at subgroups of patients?

Will the results change if the full intervention is received (i.e. degree of compliance)?

The above questions can be addressed by performing sensitivity analyses—testing the effect of these “changes” on the observed results. If, after performing sensitivity analyses the findings are consistent with those from the primary analysis and would lead to similar conclusions about treatment effect, the researcher is reassured that the underlying factor(s) had little or no influence or impact on the primary conclusions. In this situation, the results or the conclusions are said to be “robust”.

The objectives of this paper are to provide an overview of how to approach sensitivity analyses in clinical trials. This is the second in a series of tutorial-type manuscripts intended to discuss and clarify aspects related to some key methodological issues in the design and analysis of clinical trials. The first was on pilot studies [ 1 ]. We start by describing what sensitivity analysis is, why it is needed and how often it is done in practice. We then describe the different types of sensitivity analyses that one can do, with examples from the literature. We also address some of the commonly asked questions about sensitivity analysis and provide some guidance on how to report sensitivity analyses.

Sensitivity Analysis

What is a sensitivity analysis in clinical research.

Sensitivity Analysis (SA) is defined as “a method to determine the robustness of an assessment by examining the extent to which results are affected by changes in methods, models, values of unmeasured variables, or assumptions” with the aim of identifying “results that are most dependent on questionable or unsupported assumptions” [ 2 ]. It has also been defined as “a series of analyses of a data set to assess whether altering any of the assumptions made leads to different final interpretations or conclusions” [ 3 ]. Essentially, SA addresses the “what-if-the-key-inputs-or-assumptions-changed”-type of question. If we want to know whether the results change when something about the way we approach the data analysis changes, we can make the change in our analysis approach and document the changes in the results or conclusions. For more detailed coverage of SA, we refer the reader to these references [ 4 – 7 ].

Why is sensitivity analysis necessary?

The design and analysis of clinical trials often rely on assumptions that may have some effect, influence or impact on the conclusions if they are not met. It is important to assess these effects through sensitivity analyses. Consistency between the results of primary analysis and the results of sensitivity analysis may strengthen the conclusions or credibility of the findings. However, it is important to note that the definition of consistency may depend in part on the area of investigation, the outcome of interest or even the implications of the findings or results.

It is equally important to assess the robustness to ensure appropriate interpretation of the results taking into account the things that may have an impact on them. Thus, it imperative for every analytic plan to have some sensitivity analyses built into it.

The United States (US) Food and Drug Administration (FDA) and the European Medicines Association (EMEA), which offer guidance on Statistical Principles for Clinical Trials, state that “it is important to evaluate the robustness of the results and primary conclusions of the trial.” Robustness refers to “the sensitivity of the overall conclusions to various limitations of the data, assumptions, and analytic approaches to data analysis” [ 8 ]. The United Kingdom (UK) National Institute of Health and Clinical Excellence (NICE) also recommends the use of sensitivity analysis in “exploring alternative scenarios and the uncertainty in cost-effectiveness results” [ 9 ].

How often is sensitivity analysis reported in practice?

To evaluate how often sensitivity analyses are used in medical and health research, we surveyed the January 2012 editions of major medical journals (British Medical Journal, New England Journal of Medicine, the Lancet, Journal of the American Medical Association and the Canadian Medical Association Journal) and major health economics journals (Pharmaco-economics, Medical Decision making, European Journal of Health Economics, Health Economics and the Journal of Health Economics). From every article that included some form of statistical analyses, we evaluated: i) the percentage of published articles that reported results of some sensitivity analyses; and ii) the types of sensitivity analyses that were performed. Table  1 provides a summary of the findings. Overall, the point prevalent use of sensitivity analyses is about 26.7% (36/135) —which seems very low. A higher percentage of papers published in health economics than in medical journals (30.8% vs. 20.3%) reported some sensitivity analyses. Among the papers in medical journals, 18 (28.1%) were RCTs, of which only 3 (16.6%) reported sensitivity analyses. Assessing robustness of the findings to different methods of analysis was the most common type of sensitivity analysis reported in both types of journals. Therefore despite their importance, sensitivity analyses are under-used in practice. Further, sensitivity analyses are more common in health economics research—for example in conducting cost-effectiveness analyses, cost-utility analyses or budget-impact analyses—than in other areas of health or medical research.

Types of sensitivity analyses

In this section, we describe scenarios that may require sensitivity analyses, and how one could use sensitivity analyses to assess the robustness of the statistical analyses or findings of RCTs. These are not meant to be exhaustive, but rather to illustrate common situations where sensitivity analyses might be useful to consider (Table  2 ). In each case, we provide examples of actual studies where sensitivity analyses were performed, and the implications of these sensitivity analyses.

Impact of outliers

An outlier is an observation that is numerically distant from the rest of the data. It deviates markedly from the rest of the sample from which it comes [ 14 , 15 ]. Outliers are usually exceptional cases in a sample. The problem with outliers is that they can deflate or inflate the mean of a sample and therefore influence any estimates of treatment effect or association that are derived from the mean. To assess the potential impact of outliers, one would first assess whether or not any observations meet the definition of an outlier—using either a boxplot or z-scores [ 16 ]. Second, one could perform a sensitivity analysis with and without the outliers.

In a cost–utility analysis of a practice-based osteopathy clinic for subacute spinal pain, Williams et al. reported lower costs per quality of life year ratios when they excluded outliers [ 17 ]. In other words, there were certain participants in the trial whose costs were very high, and were making the average costs look higher than they probably were in reality. The observed cost per quality of life year was not robust to the exclusion of outliers, and changed when they were excluded.

A primary analysis based on the intention-to-treat principle showed no statistically significant differences in reducing depression between a nurse-led cognitive self-help intervention program compared to standard care among 218 patients hospitalized with angina over 6 months. Some sensitivity analyses in this trial were performed by excluding participants with high baseline levels of depression (outliers) and showed a statistically significant reduction in depression in the intervention group compared to the control. This implies that the results of the primary analysis were affected by the presence of patients with baseline high depression [ 18 ].

Impact of non-compliance or protocol deviations

In clinical trials some participants may not adhere to the intervention they were allocated to receive or comply with the scheduled treatment visits. Non-adherence or non-compliance is a form of protocol deviation. Other types of protocol deviations include switching between intervention and control arms (i.e. treatment switching or crossovers) [ 19 , 20 ], or not implementing the intervention as prescribed (i.e. intervention fidelity) [ 21 , 22 ].

Protocol deviations are very common in interventional research [ 23 – 25 ]. The potential impact of protocol deviations is the dilution of the treatment effect [ 26 , 27 ]. Therefore, it is crucial to determine the robustness of the results to the inclusion of data from participants who deviate from the protocol. Typically, for RCTs the primary analysis is based on an intention-to-treat (ITT) principle—in which participants are analyzed according to the arm to which they were randomized, irrespective of whether they actually received the treatment or completed the prescribed regimen [ 28 , 29 ]. Two common types of sensitivity analyses can be performed to assess the robustness of the results to protocol deviations: 1) per-protocol (PP) analysis—in which participants who violate the protocol are excluded from the analysis [ 30 ]; and 2) as-treated (AT) analysis—in which participants are analyzed according to the treatment they actually received [ 30 ]. The PP analysis provides the ideal scenario in which all the participants comply, and is more likely to show an effect; whereas the ITT analysis provides a “real life” scenario, in which some participants do not comply. It is more conservative, and less likely to show that the intervention is effective. For trials with repeated measures, some protocol violations which lead to missing data can be dealt with alternatively. This is covered in more detail in the next section.

A trial was designed to investigate the effects of an electronic screening and brief intervention to change risky drinking behaviour in university students. The results of the ITT analysis (on all 2336 participants who answered the follow-up survey) showed that the intervention had no significant effect. However, a sensitivity analysis based on the PP analysis (including only those with risky drinking at baseline and who answered the follow-up survey; n = 408) suggested a small beneficial effect on weekly alcohol consumption [ 31 ]. A reader might be less confident in the findings of the trial because of the inconsistency between the ITT and PP analyses—the ITT was not robust to sensitivity analyses. A researcher might choose to explore differences in the characteristics of the participants who were included in the ITT versus the PP analyses.

A study compared the long-term effects of surgical versus non-surgical management of chronic back pain. Both the ITT and AT analyses showed no significant difference between the two management strategies [ 32 ]. A reader would be more confident in the findings because the ITT and AT analyses were consistent—the ITT was robust to sensitivity analyses.

Impact of missing data

Missing data are common in every research study. This is a problem that can be broadly defined as “missing some information on the phenomena in which we are interested” [ 33 ]. Data can be missing for different reasons including (1) non-response in surveys due to lack of interest, lack of time, nonsensical responses, and coding errors in data entry/transfer; (2) incompleteness of data in large data registries due to missing appointments, not everyone is captured in the database, and incomplete data; and (3) missingness in prospective studies as a result of loss to follow up, dropouts, non-adherence, missing doses, and data entry errors.

The choice of how to deal with missing data would depend on the mechanisms of missingness. In this regard, data can be missing at random (MAR), missing not at random (MNAR), or missing completely at random (MCAR). When data are MAR, the missing data are dependent on some other observed variables rather than any unobserved one. For example, consider a trial to investigate the effect of pre-pregnancy calcium supplementation on hypertensive disorders in pregnancy. Missing data on the hypertensive disorders is dependent (conditional) on being pregnant in the first place. When data are MCAR, the cases with missing data may be considered a random sample drawn from all the cases. In other words, there is no “cause” of missingness. Consider the example of a trial comparing a new cancer treatment to standard treatment in which participants are followed at 4, 8, 12 and 16 months. If a participant misses the follow up at the 8th and 16th months and these are unrelated to the outcome of interest, in this case mortality, then this missing data is MCAR. Reasons such as a clinic staff being ill or equipment failure are often unrelated to the outcome of interest. However, the MCAR assumption is often challenging to prove because the reason data is missing may not be known and therefore it is difficult to determine if it is related to the outcome of interest. When data are MNAR, missingness is dependent on some unobserved data. For example, in the case above, if the participant missed the 8th month appointment because he was feeling worse or the 16th month appointment because he was dead, the missingness is dependent on the data not observed because the participant was absent. When data are MAR or MCAR, they are often referred to as ignorable (provided the cause of MAR is taken into account). MNAR on the other hand, is nonignorable missingness. Ignoring the missingness in such data leads to biased parameter estimates [ 34 ]. Ignoring missing data in analyses can have implications on the reliability, validity and generalizability of research findings.

The best way to deal with missing data is prevention, by steps taken in the design and data collection stages, some of which have been described by Little et al. [ 35 ]. But this is difficult to achieve in most cases. There are two main approaches to handling missing data: i) ignore them—and use complete case analysis; and ii) impute them—using either single or multiple imputation techniques. Imputation is one of the most commonly used approaches to handling missing data. Examples of single imputation methods include hot deck, cold deck method, mean imputation, regression technique, last observation carried forward (LOCF) and composite methods—which uses a combination of the above methods to impute missing values. Single imputation methods often lead to biased estimates and under-estimation of the true variability in the data. Multiple imputation (MI) technique is currently the best available method of dealing with missing data under the assumption that data are missing at random (MAR) [ 33 , 36 – 38 ]. MI addresses the limitations of single imputation by using multiple imputed datasets which yield unbiased estimates, and also accounts for the within- and between-dataset variability. Bayesian methods using statistical models that assume a prior distribution for the missing data can also be used to impute data [ 35 ].

It is important to note that ignoring missing data in the analysis would be implicitly assuming that the data are MCAR, an assumption that is often hard to verify in reality.

There are some statistical approaches to dealing with missing data that do not necessarily require formal imputation methods. For example, in studies using continuous outcomes, linear mixed models for repeated measures are used for analyzing outcomes measured repeatedly over time [ 39 , 40 ]. For categorical responses or count data, generalized estimating equations [GEE] and random-effects generalized linear mixed models [GLMM] methods may be used [ 41 , 42 ]. In these models it is assumed that missing data are MAR. If this assumption is valid, then the complete-case analysis by including predictors of missing observations will provide consistent estimates of the parameter.

The choice of whether to ignore or impute missing data, and how to impute it, may affect the findings of the trial. Although one approach (ignore or impute, and if the latter, how to impute) should be made a priori, a sensitivity analysis can be done with a different approach to see how “robust” the primary analysis is to the chosen method for handling missing data.

A 2011 paper reported the sensitivity analyses of different strategies for imputing missing data in cluster RCTs with a binary outcome using the community hypertension assessment trial (CHAT) as an example. They found that variance in the treatment effect was underestimated when the amount of missing data was large and the imputation strategy did not take into account the intra-cluster correlation. However, the effects of the intervention under various methods of imputation were similar. The CHAT intervention was not superior to usual care [ 43 ].

In a trial comparing methotrexate with to placebo in the treatment of psoriatic arthritis, the authors reported both an intention-to-treat analysis (using multiple imputation techniques to account for missing data) and a complete case analysis (ignoring the missing data). The complete case analysis, which is less conservative, showed some borderline improvement in the primary outcome (psoriatic arthritis response criteria), while the intention-to-treat analysis did not [ 44 ]. A reader would be less confident about the effects of methotrexate on psoriatic arthritis, due to the discrepancy between the results with imputed data (ITT) and the complete case analysis.

Impact of different definitions of outcomes (e.g. different cut-off points for binary outcomes)

Often, an outcome is defined by achieving or not achieving a certain level or threshold of a measure. For example in a study measuring adherence rates to medication, levels of adherence can be dichotomized as achieving or not achieving at least 80%, 85% or 90% of pills taken. The choice of the level a participant has to achieve can affect the outcome—it might be harder to achieve 90% adherence than 80%. Therefore, a sensitivity analysis could be performed to see how redefining the threshold changes the observed effect of a given intervention.

In a trial comparing caspofungin to amphotericin B for febrile neutropoenic patients, a sensitivity analysis was conducted to investigate the impact of different definitions of fever resolution as part of a composite endpoint which included: resolution of any baseline invasive fungal infection, no breakthrough invasive fungal infection, survival, no premature discontinuation of study drug, and fever resolution for 48 hours during the period of neutropenia. They found that response rates were higher when less stringent fever resolution definitions were used, especially in low-risk patients. The modified definitions of fever resolution were: no fever for 24 hours before the resolution of neutropenia; no fever at the 7-day post-therapy follow-up visit; and removal of fever resolution completely from the composite endpoint. This implies that the efficacy of both medications depends somewhat on the definition of the outcomes [ 45 ].

In a phase II trial comparing minocycline and creatinine to placebo for Parkinson’s disease, a sensitivity analysis was conducted based on another definition (threshold) for futility. In the primary analysis a predetermined futility threshold was set at 30% reduction in mean change in Unified Parkinson’s Disease Rating Scale (UPDRS) score, derived from historical control data. If minocycline or creatinine did not bring about at least a 30% reduction in UPDRS score, they would be considered as futile and no further testing will be conducted. Based on the data derived from the current control (placebo) group, a new threshold of 32.4% (more stringent) was used for the sensitivity analysis. The findings from the primary analysis and the sensitivity analysis both confirmed that that neither creatine nor minocycline could be rejected as futile and should both be tested in Phase III trials [ 46 ]. A reader would be more confident of these robust findings.

Impact of different methods of analysis to account for clustering or correlation

Interventions can be administered to individuals, but they can also be administered to clusters of individuals, or naturally occurring groups. For example, one might give an intervention to students in one class, and compare their outcomes to students in another class – the class is the cluster. Clusters can also be patients treated by the same physician, physicians in the same practice center or hospital, or participants living in the same community. Likewise, in the same trial, participants may be recruited from multiple sites or centers. Each of these centers will represent a cluster. Patients or elements within a cluster often have some appreciable degree of homogeneity as compared to patients between clusters. In other words, members of the same cluster are more likely to be similar to each other than they are to members of another cluster, and this similarity may then be reflected in the similarity or correlation measure, on the outcome of interest.

There are several methods of accounting or adjusting for similarities within clusters, or “clustering” in studies where this phenomenon is expected or exists as part of the design (e.g., in cluster randomization trials). Therefore, in assessing the impact of clustering one can build into the analytic plans two forms of sensitivity analyses: i) analysis with and without taking clustering into account—comparing the analysis that ignores clustering (i.e. assumes that the data are independent) to one primary method chosen to account for clustering; ii) analysis that compares several methods of accounting for clustering.

Correlated data may also occur in longitudinal studies through repeat or multiple measurements from the same patient, taken over time or based on multiple responses in a single survey. Ignoring the potential correlation between several measurements from an individual can lead to inaccurate conclusions [ 47 ].

Here are a few references to studies that compared the outcomes that resulted when different methods were/were not used to account for clustering. Noteworthy, is the fact that the analytical approaches for cluster-RCTs and multi-site RCTs are similar.

Ma et al. performed sensitivity analyses of different methods of analysing cluster RCTs [ 48 ]. In this paper they compared three cluster-level methods (un-weighted linear regression, weighted linear regression and random-effects meta-regression) to six individual level analysis methods (standard logistic regression, robust standard errors approach, GEE, random effects meta-analytic approach, random-effects logistic regression and Bayesian random-effects regression). Using data from the CHAT trial, in this analysis, all nine methods provided similar results, re-enforcing the hypothesis that the CHAT intervention was not superior to usual care.

Peters et al. conducted sensitivity analyses to compare different methods—three cluster-level (un-weighted regression of practice log odds, regression of log odds weighted by their inverse variance and random-effects meta-regression of log odds with cluster as a random effect) and five individual-level methods (standard logistic regression ignoring clustering, robust standard errors, GEE, random-effects logistic regression and Bayesian random-effects logistic regression.)—for analyzing cluster randomized trials using an example involving a factorial design [ 13 ]. In this analysis, they demonstrated that the methods used in the analysis of cluster randomized trials could give varying results, with standard logistic regression ignoring clustering being the least conservative.

Cheng et al. used sensitivity analyses to compare different methods (six models for clustered binary outcomes and three models for clustered nominal outcomes) of analysing correlated data in discrete choice surveys [ 49 ]. The results were robust to various statistical models, but showed more variability in the presence of a larger cluster effect (higher within-patient correlation).

A trial evaluated the effects of lansoprazole on gastro-esophageal reflux disease in children from 19 clinics with asthma. The primary analysis was based on GEE to determine the effect of lansoprazole in reducing asthma symptoms. Subsequently they performed a sensitivity analysis by including the study site as a covariate. Their finding that lansoprazole did not significantly improve symptoms was robust to this sensitivity analysis [ 50 ].

In addition to comparing the performance of different methods to estimate treatment effects on a continuous outcome in simulated multicenter randomized controlled trials [ 12 ], the authors used data from the Computerization of Medical Practices for the Enhancement of Therapeutic Effectiveness (COMPETE) II [ 51 ] to assess the robustness of the primary results (based on GEE to adjust for clustering by provider of care) under different methods of adjusting for clustering. The results, which showed that a shared electronic decision support system improved care and outcomes in diabetic patients, were robust under different methods of analysis.

Impact of competing risks in analysis of trials with composite outcomes

A competing risk event happens in situations where multiple events are likely to occur in a way that the occurrence of one event may prevent other events from being observed [ 48 ]. For example, in a trial using a composite of death, myocardial infarction or stroke, if someone dies, they cannot experience a subsequent event, or stroke or myocardial infarction—death can be a competing risk event. Similarly, death can be a competing risk in trials of patients with malignant diseases where thrombotic events are important. There are several options for dealing with competing risks in survival analyses: (1) to perform a survival analysis for each event separately, where the other competing event(s) is/are treated as censored; the common representation of survival curves using the Kaplan-Meier estimator is in this context replaced by the cumulative incidence function (CIF) which offers a better interpretation of the incidence curve for one risk, regardless of whether the competing risks are independent; (2) to use a proportional sub-distribution hazard model (Fine & Grey approach) in which subjects that experience other competing events are kept in the risk set for the event of interest (i.e. as if they could later experience the event); (3) to fit one model, rather than separate models, taking into account all the competing risks together (Lunn-McNeill approach) [ 13 ]. Therefore, the best approach to assessing the influence of a competing risk would be to plan for sensitivity analysis that adjusts for the competing risk event.

A previously-reported trial compared low molecular weight heparin (LMWH) with oral anticoagulant therapy for the prevention of recurrent venous thromboembolism (VTE) in patients with advanced cancer, and a subsequent study presented sensitivity analyses comparing the results from standard survival analysis (Kaplan-Meier method) with those from competing risk methods—namely, the cumulative incidence function (CIF) and Gray's test [ 52 ]. The results using both methods were similar. This strengthened their confidence in the conclusion that LMWH reduced the risk of recurrent VTE.

For patients at increased risk of end stage renal disease (ESRD) but also of premature death not related to ESRD, such as patients with diabetes or with vascular disease, analyses considering the two events as different outcomes may be misleading if the possibility of dying before the development of ESRD is not taken into account [ 49 ]. Different studies performing sensitivity analyses demonstrated that the results on predictors of ESRD and death for any cause were dependent on whether the competing risks were taken into account or not [ 53 , 54 ], and on which competing risk method was used [ 55 ]. These studies further highlight the need for a sensitivity analysis of competing risks when they are present in trials.

Impact of baseline imbalance in RCTs

In RCTs, randomization is used to balance the expected distribution of the baseline or prognostic characteristics of the patients in all treatment arms. Therefore the primary analysis is typically based on ITT approach unadjusted for baseline characteristics. However, some residual imbalance can still occur by chance. One can perform a sensitivity analysis by using a multivariable analysis to adjust for hypothesized residual baseline imbalances to assess their impact on effect estimates.

A paper presented a simulation study where the risk of the outcome, effect of the treatment, power and prevalence of the prognostic factors, and sample size were all varied to evaluate their effects on the treatment estimates. Logistic regression models were compared with and without adjustment for the prognostic factors. The study concluded that the probability of prognostic imbalance in small trials could be substantial. Also, covariate adjustment improved estimation accuracy and statistical power [ 56 ].

In a trial testing the effectiveness of enhanced communication therapy for aphasia and dysarthria after stroke, the authors conducted a sensitivity analysis to adjust for baseline imbalances. Both primary and sensitivity analysis showed that enhanced communication therapy had no additional benefit [ 57 ].

Impact of distributional assumptions

Most statistical analyses rely on distributional assumptions for observed data (e.g. Normal distribution for continuous outcomes, Poisson distribution for count data, or binomial distribution for binary outcome data). It is important not only to test for goodness-of-fit for these distributions, but to also plan for sensitivity analyses using other suitable distributions. For example, for continuous data, one can redo the analysis assuming a Student-T distribution—which is symmetric, bell-shaped distribution like the Normal distribution, but with thicker tails; for count data, once can use the Negative-binomial distribution—which would be useful to assess the robustness of the results if over-dispersion is accounted for [ 52 ]. Bayesian analyses routinely include sensitivity analyses to assess the robustness of findings under different models for the data and prior distributions [ 58 ]. Analyses based on parametric methods—which often rely on strong distributional assumptions—may also need to be evaluated for robustness using non-parametric methods. The latter often make less stringent distributional assumptions. However, it is essential to note that in general non-parametric methods are less efficient (i.e. have less statistical power) than their parametric counter-parts if the data are Normally distributed.

Ma et al. performed sensitivity analyses based on Bayesian and classical methods for analysing cluster RCTs with a binary outcome in the CHAT trial. The similarities in the results after using the different methods confirmed the results of the primary analysis: the CHAT intervention was not superior to usual care [ 10 ].

A negative binomial regression model was used [ 52 ] to analyze discrete outcome data from a clinical trial designed to evaluate the effectiveness of a pre-habilitation program in preventing functional decline among physically frail, community-living older persons. The negative binomial model provided an improved fit to the data than the Poisson regression model. The negative binomial model provides an alternative approach for analyzing discrete data where over-dispersion is a problem [ 59 ].

Commonly asked questions about sensitivity analyses

Q: Do I need to adjust the overall level of significance for performing sensitivity analyses?

A: No. Sensitivity analysis is typically a re-analysis of either the same outcome using different approaches, or different definitions of the outcome—with the primary goal of assessing how these changes impact the conclusions. Essentially everything else including the criterion for statistical significance needs to be kept constant so that we can assess whether any impact is attributable to underlying sensitivity analyses.

Q: Do I have to report all the results of the sensitivity analyses?

A: Yes, especially if the results are different or lead to different a conclusion from the original results—whose sensitivity was being assessed. However, if the results remain robust (i.e. unchanged), then a brief statement to this effect may suffice.

Q: Can I perform sensitivity analyses posthoc?

A: It is desirable to document all planned analyses including sensitivity analyses in the protocol a priori . Sometimes, one cannot anticipate all the challenges that can occur during the conduct of a study that may require additional sensitivity analyses. In that case, one needs to incorporate the anticipated sensitivity analyses in the statistical analysis plan (SAP), which needs to be completed before analyzing the data. Clear rationale is needed for every sensitivity analysis. This may also occur posthoc .

Q: How do I choose between the results of different sensitivity analyses? (i.e. which results are the best?)

A: The goal of sensitivity analyses is not to select the “best” results. Rather, the aim is to assess the robustness or consistency of the results under different methods, subgroups, definitions, assumptions and so on. The assessment of robustness is often based on the magnitude, direction or statistical significance of the estimates. You cannot use the sensitivity analysis to choose an alternate conclusion to your study. Rather, you can state the conclusion based on your primary analysis, and present your sensitivity analysis as an example of how confident you are that it represents the truth. If the sensitivity analysis suggests that the primary analysis is not robust, it may point to the need for future research that might address the source of the inconsistency. Your study cannot answer the question which results are best? To answer the question of which method is best and under what conditions, simulation studies comparing the different approaches on the basis of bias, precision, coverage or efficiency may be necessary.

Q: When should one perform sensitivity analysis?

A: The default position should be to plan for sensitivity analysis in every clinical trial. Thus, all studies need to include some sensitivity analysis to check the robustness of the primary findings. All statistical methods used to analyze data from clinical trials rely on assumptions—which need to either be tested whenever possible, with the results assessed for robustness through some sensitivity analyses. Similarly, missing data or protocol deviations are common occurrences in many trials and their impact on inferences needs to be assessed.

Q: How many sensitivity analyses can one perform for a single primary analysis?

A: The number is not an important factor in determining what sensitivity analyses to perform. The most important factor is the rationale for doing any sensitivity analysis. Understanding the nature of the data, and having some content expertise are useful in determining which and how many sensitivity analyses to perform. For example, varying the ways of dealing with missing data is unlikely to change the results if 1% of data are missing. Likewise, understanding the distribution of certain variables can help to determine which cut points would be relevant. Typically, it is advisable to limit sensitivity analyses to the primary outcome. Conducting multiple sensitivity analysis on all outcomes is often neither practical, nor necessary.

Q: How many factors can I vary in performing sensitivity analyses?

A: Ideally, one can study the impact of all key elements using a factorial design—which would allow the assessment of the impact of individual and joint factors. Alternatively, one can vary one factor at a time to be able to assess whether the factor is responsible for the resulting impact (if any). For example, in a sensitivity analysis to assess the impact of the Normality assumption (analysis assuming Normality e.g. T-test vs. analysis without assuming Normality e.g. Based on a sign test) and outlier (analysis with and without outlier), this can be achieved through 2x2 factorial design.

Q: What is the difference between secondary analyses and sensitivity analyses?

A: Secondary analyses are typically analyses of secondary outcomes. Like primary analyses which deal with primary outcome(s), such analyses need to be documented in the protocol or SAP. In most studies such analyses are exploratory—because most studies are not powered for secondary outcomes. They serve to provide support that the effects reported in the primary outcome are consistent with underlying biology. They are different from sensitivity analyses as described above.

Q: What is the difference between subgroup analyses and sensitivity analyses?

A: Subgroup analyses are intended to assess whether the effect is similar across specified groups of patients or modified by certain patient characteristics [ 60 ]. If the primary results are statistically significant, subgroup analyses are intended to assess whether the observed effect is consistent across the underlying patient subgroups—which may be viewed as some form of sensitivity analysis. In general, for subgroup analyses one is interested in the results for each subgroup, whereas in subgroup “sensitivity” analyses, one is interested in the similarity of results across subgroups (ie. robustness across subgroups). Typically subgroup analyses require specification of the subgroup hypothesis and rationale, and performed through inclusion of an interaction term (i.e. of the subgroup variable x main exposure variable) in the regression model. They may also require adjustment for alpha—the overall level of significance. Furthermore, most studies are not usually powered for subgroup analyses.

Reporting of sensitivity analyses

There has been considerable attention paid to enhancing the transparency of reporting of clinical trials. This has led to several reporting guidelines, starting with the CONSORT Statement [ 61 ] in 1996 and its extensions [ http://www.equator-network.org ]. Not one of these guidelines specifically addresses how sensitivity analyses need to be reported. On the other hand, there is some guidance on how sensitivity analyses need to be reported in economic analyses [ 62 ]—which may partly explain the differential rates of reporting of sensitivity analyses shown in Table  1 . We strongly encourage some modifications of all reporting guidelines to include items on sensitivity analyses—as a way to enhance their use and reporting. The proposed reporting changes can be as follows:

In Methods Section: Report the planned or posthoc sensitivity analyses and rationale for each.

In Results Section: Report whether or not the results of the sensitivity analyses or conclusions are similar to those based on primary analysis. If similar, just state that the results or conclusions remain robust. If different, report the results of the sensitivity analyses along with the primary results.

In Discussion Section: Discuss the key limitations and implications of the results of the sensitivity analyses on the conclusions or findings. This can be done by describing what changes the sensitivity analyses bring to the interpretation of the data, and whether the sensitivity analyses are more stringent or more relaxed than the primary analysis.

Some concluding remarks

Sensitivity analyses play an important role is checking the robustness of the conclusions from clinical trials. They are important in interpreting or establishing the credibility of the findings. If the results remain robust under different assumptions, methods or scenarios, this can strengthen their credibility. The results of our brief survey of January 2012 editions of major medical and health economics journals that show that their use is very low. We recommend that some sensitivity analysis should be the default plan in statistical or economic analyses of any clinical trial. Investigators need to identify any key assumptions, variations, or methods that may impact or influence the findings, and plan to conduct some sensitivity analyses as part of their analytic strategy. The final report must include the documentation of the planned or posthoc sensitivity analyses, rationale, corresponding results and a discussion of their consequences or repercussions on the overall findings.

Abbreviations

• Sensitivity analysis

United States

Food and Drug Administration

European Medicines Association

United Kingdom

National Institute of Health and Clinical Excellence

Randomized controlled trial

Intention-to-treat

Per-protocol

Last observation carried forward

Multiple imputation

Missing at random

Generalized estimating equations

Generalized linear mixed models

Community hypertension assessment trial

Prostate specific antigen

Cumulative incidence function

End stage renal disease

Instrumental variable

Analysis of covariance

Statistical analysis plan

Consolidated Standards of Reporting Trials.

Thabane L, Ma J, Chu R, Cheng J, Ismaila A, Rios LP, Robson R, Thabane M, Giangregorio L, Goldsmith CH: A tutorial on pilot studies: the what, why and how. BMC Med Res Methodol. 2010, 10: 1-10.1186/1471-2288-10-1.

Article   PubMed   PubMed Central   Google Scholar  

Schneeweiss S: Sensitivity analysis and external adjustment for unmeasured confounders in epidemiologic database studies of therapeutics. Pharmacoepidemiol Drug Saf. 2006, 15 (5): 291-303. 10.1002/pds.1200.

Article   PubMed   Google Scholar  

Viel JF, Pobel D, Carre A: Incidence of leukaemia in young people around the La Hague nuclear waste reprocessing plant: a sensitivity analysis. Stat Med. 1995, 14 (21–22): 2459-2472.

Article   CAS   PubMed   Google Scholar  

Goldsmith CH, Gafni A, Drummond MF, Torrance GW, Stoddart GL: Sensitivity Analysis and Experimental Design: The Case of Economic Evaluation of Health Care Programmes. Proceedings of the Third Canadian Conference on Health Economics 1986. 1987, Winnipeg MB: The University of Manitoba Press

Google Scholar  

Saltelli A, Tarantola S, Campolongo F, Ratto M: Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. 2004, New York, NY: Willey

Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, Saisana M, Tarantola S: Global Sensitivity Analysis: The Primer. 2008, New York, NY: Wiley-Interscience

Hunink MGM, Glasziou PP, Siegel JE, Weeks JC, Pliskin JS, Elstein AS, Weinstein MC: Decision Making in Health and Medicine: Integrating Evidence and Values. 2001, Cambridge: Cambridge University Press

USFDA: International Conference on Harmonisation; Guidance on Statistical Principles for Clinical Trials. Guideline E9. Statistical principles for clinical trials. Federal Register, 16 September 1998, Vol. 63, No. 179, p. 49583. [ http://www.fda.gov/downloads/RegulatoryInformation/Guidances/UCM129505.pdf ],

NICE: Guide to the methods of technology appraisal. [ http://www.nice.org.uk/media/b52/a7/tamethodsguideupdatedjune2008.pdf ],

Ma J, Thabane L, Kaczorowski J, Chambers L, Dolovich L, Karwalajtys T, Levitt C: Comparison of Bayesian and classical methods in the analysis of cluster randomized controlled trials with a binary outcome: the Community Hypertension Assessment Trial (CHAT). BMC Med Res Methodol. 2009, 9: 37-10.1186/1471-2288-9-37.

Peters TJ, Richards SH, Bankhead CR, Ades AE, Sterne JA: Comparison of methods for analysing cluster randomized trials: an example involving a factorial design. Int J Epidemiol. 2003, 32 (5): 840-846. 10.1093/ije/dyg228.

Chu R, Thabane L, Ma J, Holbrook A, Pullenayegum E, Devereaux PJ: Comparing methods to estimate treatment effects on a continuous outcome in multicentre randomized controlled trials: a simulation study. BMC Med Res Methodol. 2011, 11: 21-10.1186/1471-2288-11-21.

Kleinbaum DG, Klein M: Survival Analysis – A-Self Learning Text. 2012, Springer, 3

Barnett V, Lewis T: Outliers in Statistical Data. 1994, John Wiley & Sons, 3

Grubbs FE: Procedures for detecting outlying observations in samples. Technometrics. 1969, 11: 1-21. 10.1080/00401706.1969.10490657.

Article   Google Scholar  

Thabane L, Akhtar-Danesh N: Guidelines for reporting descriptive statistics in health research. Nurse Res. 2008, 15 (2): 72-81.

Williams NH, Edwards RT, Linck P, Muntz R, Hibbs R, Wilkinson C, Russell I, Russell D, Hounsome B: Cost-utility analysis of osteopathy in primary care: results from a pragmatic randomized controlled trial. Fam Pract. 2004, 21 (6): 643-650. 10.1093/fampra/cmh612.

Zetta S, Smith K, Jones M, Allcoat P, Sullivan F: Evaluating the Angina Plan in Patients Admitted to Hospital with Angina: A Randomized Controlled Trial. Cardiovascular Therapeutics. 2011, 29 (2): 112-124. 10.1111/j.1755-5922.2009.00109.x.

Morden JP, Lambert PC, Latimer N, Abrams KR, Wailoo AJ: Assessing methods for dealing with treatment switching in randomised controlled trials: a simulation study. BMC Med Res Methodol. 2011, 11: 4-10.1186/1471-2288-11-4.

White IR, Walker S, Babiker AG, Darbyshire JH: Impact of treatment changes on the interpretation of the Concorde trial. AIDS. 1997, 11 (8): 999-1006. 10.1097/00002030-199708000-00008.

Borrelli B: The assessment, monitoring, and enhancement of treatment fidelity in public health clinical trials. J Public Health Dent. 2011, 71 (Suppl 1): S52-S63.

Article   PubMed Central   Google Scholar  

Lawton J, Jenkins N, Darbyshire JL, Holman RR, Farmer AJ, Hallowell N: Challenges of maintaining research protocol fidelity in a clinical care setting: a qualitative study of the experiences and views of patients and staff participating in a randomized controlled trial. Trials. 2011, 12: 108-10.1186/1745-6215-12-108.

Ye C, Giangregorio L, Holbrook A, Pullenayegum E, Goldsmith CH, Thabane L: Data withdrawal in randomized controlled trials: Defining the problem and proposing solutions: a commentary. Contemp Clin Trials. 2011, 32 (3): 318-322. 10.1016/j.cct.2011.01.016.

Horwitz RI, Horwitz SM: Adherence to treatment and health outcomes. Arch Intern Med. 1993, 153 (16): 1863-1868. 10.1001/archinte.1993.00410160017001.

Peduzzi P, Wittes J, Detre K, Holford T: Analysis as-randomized and the problem of non-adherence: an example from the Veterans Affairs Randomized Trial of Coronary Artery Bypass Surgery. Stat Med. 1993, 12 (13): 1185-1195. 10.1002/sim.4780121302.

Montori VM, Guyatt GH: Intention-to-treat principle. CMAJ. 2001, 165 (10): 1339-1341.

CAS   PubMed   PubMed Central   Google Scholar  

Gibaldi M, Sullivan S: Intention-to-treat analysis in randomized trials: who gets counted?. J Clin Pharmacol. 1997, 37 (8): 667-672. 10.1002/j.1552-4604.1997.tb04353.x.

Porta M: A dictionary of epidemiology. 2008, Oxford: Oxford University Press, Inc, 5

Everitt B: Medical statistics from A to Z. 2006, Cambridge: Cambridge University Press, 2

Book   Google Scholar  

Sainani KL: Making sense of intention-to-treat. PM R. 2010, 2 (3): 209-213. 10.1016/j.pmrj.2010.01.004.

Bendtsen P, McCambridge J, Bendtsen M, Karlsson N, Nilsen P: Effectiveness of a proactive mail-based alcohol internet intervention for university students: dismantling the assessment and feedback components in a randomized controlled trial. J Med Internet Res. 2012, 14 (5): e142-10.2196/jmir.2062.

Brox JI, Nygaard OP, Holm I, Keller A, Ingebrigtsen T, Reikeras O: Four-year follow-up of surgical versus non-surgical therapy for chronic low back pain. Ann Rheum Dis. 2010, 69 (9): 1643-1648. 10.1136/ard.2009.108902.

McKnight PE, McKnight KM, Sidani S, Figueredo AJ: Missing Data: A Gentle Introduction. 2007, New York, NY: Guilford

Graham JW: Missing data analysis: making it work in the real world. Annu Rev Psychol. 2009, 60: 549-576. 10.1146/annurev.psych.58.110405.085530.

Little RJ, D'Agostino R, Cohen ML, Dickersin K, Emerson SS, Farrar JT, Frangakis C, Hogan JW, Molenberghs G, Murphy SA, et al: The Prevention and Treatment of Missing Data in Clinical Trials. New England Journal of Medicine. 2012, 367 (14): 1355-1360. 10.1056/NEJMsr1203730.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Little RJA, Rubin DB: Statistical Analysis with Missing Data. 2002, New York NY: Wiley, 2

Rubin DB: Multiple Imputation for Nonresponse in Surveys. 1987, John Wiley & Sons, Inc: New York NY

Schafer JL: Analysis of Incomplete Multivariate Data. 1997, New York: Chapman and Hall

Son H, Friedmann E, Thomas SA: Application of pattern mixture models to address missing data in longitudinal data analysis using SPSS. Nursing research. 2012, 61 (3): 195-203. 10.1097/NNR.0b013e3182541d8c.

Peters SA, Bots ML, den Ruijter HM, Palmer MK, Grobbee DE, Crouse JR, O'Leary DH, Evans GW, Raichlen JS, Moons KG, et al: Multiple imputation of missing repeated outcome measurements did not add to linear mixed-effects models. J Clin Epidemiol. 2012, 65 (6): 686-695. 10.1016/j.jclinepi.2011.11.012.

Zhang H, Paik MC: Handling missing responses in generalized linear mixed model without specifying missing mechanism. J Biopharm Stat. 2009, 19 (6): 1001-1017. 10.1080/10543400903242761.

Chen HY, Gao S: Estimation of average treatment effect with incompletely observed longitudinal data: application to a smoking cessation study. Statistics in medicine. 2009, 28 (19): 2451-2472. 10.1002/sim.3617.

Ma J, Akhtar-Danesh N, Dolovich L, Thabane L: Imputation strategies for missing binary outcomes in cluster randomized trials. BMC Med Res Methodol. 2011, 11: 18-10.1186/1471-2288-11-18.

Kingsley GH, Kowalczyk A, Taylor H, Ibrahim F, Packham JC, McHugh NJ, Mulherin DM, Kitas GD, Chakravarty K, Tom BD, et al: A randomized placebo-controlled trial of methotrexate in psoriatic arthritis. Rheumatology (Oxford). 2012, 51 (8): 1368-1377. 10.1093/rheumatology/kes001.

Article   CAS   Google Scholar  

de Pauw BE, Sable CA, Walsh TJ, Lupinacci RJ, Bourque MR, Wise BA, Nguyen BY, DiNubile MJ, Teppler H: Impact of alternate definitions of fever resolution on the composite endpoint in clinical trials of empirical antifungal therapy for neutropenic patients with persistent fever: analysis of results from the Caspofungin Empirical Therapy Study. Transpl Infect Dis. 2006, 8 (1): 31-37. 10.1111/j.1399-3062.2006.00127.x.

A randomized, double-blind, futility clinical trial of creatine and minocycline in early Parkinson disease. Neurology. 2006, 66 (5)): 664-671.

Song P-K: Correlated Data Analysis: Modeling, Analytics and Applications. 2007, New York, NY: Springer Verlag

Pintilie M: Competing Risks: A Practical Perspective. 2006, New York, NY: John Wiley

Tai BC, Grundy R, Machin D: On the importance of accounting for competing risks in pediatric brain cancer: II. Regression modeling and sample size. Int J Radiat Oncol Biol Phys. 2011, 79 (4): 1139-1146. 10.1016/j.ijrobp.2009.12.024.

Holbrook JT, Wise RA, Gold BD, Blake K, Brown ED, Castro M, Dozor AJ, Lima JJ, Mastronarde JG, Sockrider MM, et al: Lansoprazole for children with poorly controlled asthma: a randomized controlled trial. JAMA. 2012, 307 (4): 373-381.

Holbrook A, Thabane L, Keshavjee K, Dolovich L, Bernstein B, Chan D, Troyan S, Foster G, Gerstein H: Individualized electronic decision support and reminders to improve diabetes care in the community: COMPETE II randomized trial. CMAJ: Canadian Medical Association journal = journal de l’Association medicale canadienne. 2009, 181 (1–2): 37-44.

Hilbe JM: Negative Binomial Regression. 2011, Cambridge: Cambridge University Press, 2

Forsblom C, Harjutsalo V, Thorn LM, Waden J, Tolonen N, Saraheimo M, Gordin D, Moran JL, Thomas MC, Groop PH: Competing-risk analysis of ESRD and death among patients with type 1 diabetes and macroalbuminuria. J Am Soc Nephrol. 2011, 22 (3): 537-544. 10.1681/ASN.2010020194.

Grams ME, Coresh J, Segev DL, Kucirka LM, Tighiouart H, Sarnak MJ: Vascular disease, ESRD, and death: interpreting competing risk analyses. Clin J Am Soc Nephrol. 2012, 7 (10): 1606-1614. 10.2215/CJN.03460412.

Lim HJ, Zhang X, Dyck R, Osgood N: Methods of competing risks analysis of end-stage renal disease and mortality among people with diabetes. BMC Med Res Methodol. 2010, 10: 97-10.1186/1471-2288-10-97.

Chu R, Walter SD, Guyatt G, Devereaux PJ, Walsh M, Thorlund K, Thabane L: Assessment and implication of prognostic imbalance in randomized controlled trials with a binary outcome–a simulation study. PLoS One. 2012, 7 (5): e36677-10.1371/journal.pone.0036677.

Bowen A, Hesketh A, Patchick E, Young A, Davies L, Vail A, Long AF, Watkins C, Wilkinson M, Pearl G, et al: Effectiveness of enhanced communication therapy in the first four months after stroke for aphasia and dysarthria: a randomised controlled trial. BMJ. 2012, 345: e4407-10.1136/bmj.e4407.

Spiegelhalter DJ, Best NG, Lunn D, Thomas A: Bayesian Analysis using BUGS: A Practical Introduction. 2009, New York, NY: Chapman and Hall

Byers AL, Allore H, Gill TM, Peduzzi PN: Application of negative binomial modeling for discrete outcomes: a case study in aging research. J Clin Epidemiol. 2003, 56 (6): 559-564. 10.1016/S0895-4356(03)00028-3.

Yusuf S, Wittes J, Probstfield J, Tyroler HA: Analysis and interpretation of treatment effects in subgroups of patients in randomized clinical trials. JAMA: the journal of the American Medical Association. 1991, 266 (1): 93-98. 10.1001/jama.1991.03470010097038.

Altman DG: Better reporting of randomised controlled trials: the CONSORT statement. BMJ. 1996, 313 (7057): 570-571. 10.1136/bmj.313.7057.570.

Mauskopf JA, Sullivan SD, Annemans L, Caro J, Mullins CD, Nuijten M, Orlewska E, Watkins J, Trueman P: Principles of good practice for budget impact analysis: report of the ISPOR Task Force on good research practices–budget impact analysis. Value Health. 2007, 10 (5): 336-347. 10.1111/j.1524-4733.2007.00187.x.

Pre-publication history

The pre-publication history for this paper can be accessed here: http://www.biomedcentral.com/1471-2288/13/92/prepub

Download references

Acknowledgements

This work was supported in part by funds from the CANNeCTIN programme.

Author information

Authors and affiliations.

Department of Clinical Epidemiology and Biostatistics, McMaster University, Hamilton, ON, Canada

Lehana Thabane, Lawrence Mbuagbaw, Shiyuan Zhang, Zainab Samaan, Maura Marcucci, Chenglin Ye, Marroon Thabane, Brittany Dennis, Daisy Kosa, Victoria Borg Debono & Charles H Goldsmith

Departments of Pediatrics and Anesthesia, McMaster University, Hamilton, ON, Canada

Lehana Thabane

Center for Evaluation of Medicine, St Joseph’s Healthcare Hamilton, Hamilton, ON, Canada

Biostatistics Unit, Father Sean O’Sullivan Research Center, St Joseph’s Healthcare Hamilton, Hamilton, ON, Canada

Lehana Thabane, Lawrence Mbuagbaw, Shiyuan Zhang, Maura Marcucci, Chenglin Ye, Brittany Dennis, Daisy Kosa, Victoria Borg Debono & Charles H Goldsmith

Population Health Research Institute, Hamilton Health Sciences, Hamilton, ON, Canada

Department of Psychiatry and Behavioral Neurosciences, McMaster University, Hamilton, ON, Canada

Zainab Samaan

Population Genomics Program, McMaster University, Hamilton, ON, Canada

GSK, Mississauga, ON, Canada

Marroon Thabane

Department of Kinesiology, University of Waterloo, Waterloo, ON, Canada

Lora Giangregorio

Department of Nephrology, Toronto General Hospital, Toronto, ON, Canada

Department of Pediatrics, McMaster University, Hamilton, ON, Canada

Rejane Dillenburg

Michael G. DeGroote School of Medicine, McMaster University, Hamilton, ON, Canada

Vincent Fruci

McMaster Integrative Neuroscience Discovery & Study (MiNDS) Program, McMaster University, Hamilton, ON, Canada

Monica Bawor

Department of Biostatistics, Korea University, Seoul, South Korea

Juneyoung Lee

Department of Clinical Epidemiology, University of Ottawa, Ottawa, ON, Canada

George Wells

Faculty of Health Sciences, Simon Fraser University, Burnaby, BC, Canada

Charles H Goldsmith

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Lehana Thabane .

Additional information

Competing interests.

The authors declare that they have no competing interests.

Authors’ contributions

LT conceived the idea and drafted the outline and paper. GW, CHG and MT commented on the idea and draft outline. LM and SZ performed literature search and data abstraction. ZS, LG and CY edited and formatted the manuscript. MM, BD, DK, VBD, RD, VF, MB, JL reviewed and revised draft versions of the manuscript. All authors reviewed several draft versions of the manuscript and approved the final manuscript.

Rights and permissions

This article is published under license to BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Reprints and permissions

About this article

Cite this article.

Thabane, L., Mbuagbaw, L., Zhang, S. et al. A tutorial on sensitivity analyses in clinical trials: the what, why, when and how. BMC Med Res Methodol 13 , 92 (2013). https://doi.org/10.1186/1471-2288-13-92

Download citation

Received : 11 December 2012

Accepted : 10 July 2013

Published : 16 July 2013

DOI : https://doi.org/10.1186/1471-2288-13-92

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Clinical trials

BMC Medical Research Methodology

ISSN: 1471-2288

• General enquiries: [email protected]

Advertisement

Landslide susceptibility mapping and sensitivity analysis using various machine learning models: a case study of Beas valley, Indian Himalaya

• Original Paper
• Published: 13 May 2024
• Volume 83 , article number  228 , ( 2024 )

Cite this article

• Ramandeep Kaur 1 , 2 ,
• Vikram Gupta 1 , 3 &
• B. S. Chaudhary 2  

108 Accesses

Explore all metrics

Landslide is one of the most destructive hazards in the Upper Beas valley of the Himalayan region of India. Landslide susceptibility mapping is an important and preliminary task in order to prospect the spatial variability of landslide prone zones in the area. As the use of machine learning algorithms has increased the success rate in susceptibility studies, the performance of the four machine learning models, namely Naïve Bayes (NB), K-Nearest Neighbor (KNN), Random Forest (RF) and Extreme Gradient Boosting (XGBoost) were initially tested for landslide susceptibility mapping in the area. Landslide inventory containing both landslide and non-landslide data and thirteen landslide conditioning factors were considered to train the models. The models were optimized using hyperparameter optimization and input factors selection based on variable importance. Among the four models, Extreme Gradient Boosting (XGBoost), an advanced ensemble-based machine learning algorithm, demonstrated superior performance (AUC = ~ 0.91) followed by RF, NB and KNN with AUC values of ~ 0.88, ~ 0.87, and ~ 0.82. Therefore, XGboost model was selected for detailed study, including sensitivity analysis. The results depict that 44% of the total area falls under high and very high susceptible zones. Southward facing slopes having inclination between 31˚-50˚ located at an elevation of 2001–3000 m in the vicinity of road and drainage network contain most of the landslide susceptible zones. Sensitivity analysis has provided an in-depth understanding of the factors’ relation with the model as the XGBoost model is most sensitive to factors such as slope inclination, distance to thrust and road, elevation, TWI and slope aspect.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price excludes VAT (USA) Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Can geomorphic flood descriptors coupled with machine learning models enhance in quantifying flood risks over data-scarce catchments? Development of a hybrid framework for Ganga basin (India)

Urban flood susceptibility mapping using frequency ratio and multiple decision tree-based machine learning models

Application of ensemble fuzzy weights of evidence-support vector machine (Fuzzy WofE-SVM) for urban flood modeling and coupled risk (CR) index for ward prioritization in NCT Delhi, India

Data availability.

All data included in this study are available upon request by contact with the corresponding author.

Achour Y, Pourghasemi HR (2020) How do machine learning techniques help in increasing accuracy of landslide susceptibility maps? Geosci Front 11(3):871–883

Article   Google Scholar  

Achour Y, Saidani Z, Touati R, Pham QB, Pal SC, Mustafa F, Balik Sanli F (2021) Assessing landslide susceptibility using a machine learning-based approach to achieving land degradation neutrality. Environ Earth Sci 80:1–20

Akgun A (2012) A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: a case study at İzmir, Turkey. Landslides 9(1):93–106

Aktas H, San BT (2019) Landslide susceptibility mapping using an automatic sampling algorithm based on two level random sampling. Comput Geosci 133:104329

Article   CAS   Google Scholar  

Alcántara-Ayala I (2002) Geomorphology, natural hazards, vulnerability and prevention of natural disasters in developing countries. Geomorphology 47(2–4):107–124

Ali SA, Parvin F, Vojteková J, Costache R, Linh NT, Pham QB, Vojtek M, Gigović L, Ahmad A, Ghorbani MA (2021) GIS-based landslide susceptibility modeling: a comparison between fuzzy multi-criteria and machine learning algorithms. Geosci Front 12(2):857–876

Althuwaynee OF, Pradhan B, Park HJ, Lee JH (2014) A novel ensemble decision tree-based CHi-squared Automatic Interaction Detection (CHAID) and multivariate logistic regression models in landslide susceptibility mapping. Landslides 11:1063–1078

Ambraseys N, Bilham R (2000) A note on the Kangra M s = 7.8 earthquake of 4 April 1905. Curr Sci 79(1):45–50

Arabameri A, Cerda A, Pradhan B, Tiefenbacher JP, Lombardo L, Bui DT (2000) (2020) A methodological comparison of head-cut based gully erosion susceptibility models: Combined use of statistical and artificial intelligence. Geomorphology 359:107–136

Google Scholar  

Bizimana H, Sönmez O (2015) Landslide occurrences in the hilly areas of Rwanda, their causes and protection measures. Disaster Sci Eng 1(1):1–7

Breiman L (2001) Random forests. Mach Learn 45(1):5–32

Breiman L (2002) Manual on setting up, using, and understanding Random Forests V3.1. https://www.stat.berkeley.edu/~breiman/Using_random_forests_V3.1.pdf . Accessed 11 Jan 2022

Budetta P (2004) Assessment of rockfall risk along roads. Nat Hazards Earth Syst Sci 4(1):71–81

Can R, Kocaman S, Gokceoglu C (2021) A comprehensive assessment of XGBoost algorithm for landslide susceptibility mapping in the upper basin of Ataturk dam, Turkey. Appl Sci 11(11):4993

Chahal P, Rana N, Bisht P, Bagri DS, Wasson RJ, Sundriyal Y (2017) Identification of landslide-prone zones in the geomorphically and climatically sensitive Mandakini valley, (central Himalaya), for disaster governance using the weights of evidence method. Geomorphology 284:41–52

Chen T, He T, Benesty M, Khotilovich V, Tang Y, Cho H, Chen K, Mitchell R, Cano I, Zhou T (2015) Xgboost: extreme gradient boosting. R package version 0.4-2 1(4):1–4

Chen XL, Liu CG, Chang ZF, Zhou Q (2016) The relationship between the slope angle and the landslide size derived from limit equilibrium simulations. Geomorphology 253:547–550

Chen W, Xie X, Wang J, Pradhan B, Hong H, Bui DT, Duan Z, Ma J (2017) A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 151:147–160

Chowdhuri I, Pal SC, Chakrabortty R, Malik S, Das B, Roy P, Sen K (2021) Spatial prediction of landslide susceptibility using projected storm rainfall and land use in himalayan region. Bull Eng Geol Environ 80:5237–5258

Clarke BA, Burbank DW (2010) Bedrock fracturing, threshold hillslopes, and limits to the magnitude of bedrock landslides. Earth Planet Sci Lett 297(3–4):577–586

Cover T, Hart P (1967) Nearest neighbor pattern classification. IEEE Trans Inf Theory 13(1):21–27

Das G, Lepcha K (2019) Application of logistic regression (LR) and frequency ratio (FR) models for landslide susceptibility mapping in Relli Khola river basin of Darjeeling Himalaya, India. SN Appl Sci 1(11):1–22

Devkota KC, Regmi AD, Pourghasemi HR, Yoshida K, Pradhan B, Ryu IC, Dhital MR, Althuwaynee OF (2013) Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat Hazards 65:135–165

Dhiman RK, Thakur M (2021) Rockfall Hazard Assessment using RAMMS for the SE facing escarpment of Manikaran, Himachal Pradesh, India. In: Rai PK, Singh P, Mishra VN (eds) Recent Technologies for Disaster Management and Risk Reduction. Earth and Environmental Sciences Library. Springer, Cham, pp 57–74

Chapter   Google Scholar  

Di Napoli M, Carotenuto F, Cevasco A, Confuorto P, Di Martire D, Firpo M, Pepe G, Raso E, Calcaterra D (2020) Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 17(8):1897–1914

Drid I, Achour Y, Zighmi K, Nouioua T, Khababa O, Rahmani S, Ouadfel O, Atoui B (2022) Designing gully erosion susceptibility maps (GESM) in the Algerian Eastern tell: a case study of the K’sob River watershed. Arab J Geosci 15(14):1264

Feizizadeh B, Jankowski P, Blaschke T (2014) A GIS based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis. Comput Geosci 64:81–95

Gokceoglu C, Sezer E (2009) A statistical assessment on international landslide literature (1945–2008). Landslides 6:345–351

Guha-Sapir D, Below R, Hoyois P (2020) EM-DAT: the CRED/OFDA international disaster database. Centre for Research on the Epidemiology of Disasters (CRED), Université Catholique de Louvain, Brussels

Gupta V, Sah MP, Virdi NS, Bartarya SK (1993) Landslide hazard zonation in the upper Satluj valley, District Kinnaur, Himachal Pradesh. J Himal Geol 4(1):81–93

Gupta V, Bhasin RK, Kaynia AM, Tandon RS, Venkateshwarlu B (2016) Landslide hazard in the Nainital township, Kumaun Himalaya, India: the case of September 2014 Balia Nala landslide. Nat Hazards 80:863–877

Gupta V, Paul A, Kumar S, Dash B (2021) Spatial distribution of landslides vis-à-vis epicentral distribution of earthquakes in the vicinity of the Main Central Thrust Zone, Uttarakhand Himalaya. India Curr Sci 120(12):1927–1932

Gupta V, Kumar S, Kaur R, Tandon RS (2022) Regional-scale landslide susceptibility assessment for the hilly state of Uttarakhand, NW Himalaya, India. J Earth Syst Sci 131(1):2

He K, Ma G, Hu X, Luo G, Mei X, Liu B, He X (2019) Characteristics and mechanisms of coupled road and rainfall-induced landslide in Sichuan China. Geomatics, Nat Hazards Risk 10(1):2313–2329

https://bhukosh.gsi.gov.in / (n.d.) Accessed 13 May 2020

https://chrsdata.eng.uci.edu/  (n.d.) Accessed 11 June 2020

Huang Y, Zhao L (2018) Review on landslide susceptibility mapping using support vector machines. Catena 165:520–529

Huang F, Cao Z, Guo J, Jiang SH, Li S, Guo Z (2020) Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 191:104580

Ilia I, Tsangaratos P (2016) Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map. Landslides 13(2):379–397

Jennifer JJ, Saravanan S (2022) Artificial neural network and sensitivity analysis in the landslide susceptibility mapping of Idukki district, India. Geocarto Int 37(19):5693–5715

Johnson D (2019) R Random Forest tutorial with example. GURU99. https://www.guru99.com/r-random-forest-tutorial.html . Accessed 11 Jan 2022

Karakas G, Can R, Kocaman S, Nefeslioglu HA, Gokceoglu C (2020) Landslide susceptibility mapping with random forest model for Ordu, Turkey. ISPRS - Int Arch Photogram Remote Sens Spat Info Sci XLIII-B3-2020:1229–1236

Keesstra SD, Bouma J, Wallinga J, Tittonell P, Smith P, Cerdà A, Montanarella L, Quinton JN, Pachepsky Y, Van Der Putten WH, Bardgett RD (2016) The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2(2):111–128

Khanna R, Dubey RK (2021) Comparative assessment of slope stability along road-cuts through rock slope classification systems in Kullu Himalayas, Himachal Pradesh, India. Bull Eng Geol Environ 80:993–1017

Kumar R, Anbalagan R (2016) Landslide susceptibility mapping using analytical hierarchy process (AHP) in Tehri reservoir rim region, Uttarakhand. J Geol Soc India 87:271–286

Kumar S, Gupta V (2021) Evaluation of spatial probability of landslides using bivariate and multivariate approaches in the Goriganga valley, Kumaun Himalaya, India. Nat Hazards 109:2461–2488

Kumar A, Sharma RK, Bansal VK (2018) Landslide hazard zonation using analytical hierarchy process along National Highway-3 in mid Himalayas of Himachal Pradesh, India. Environ Earth Sci 77:1–19

Local (2023) LOCAL Situation Report – 012/2023 (16/08/2023). Local organisations’ coalition for advancing localisation. https://reliefweb.int/report/india/local-situation-report-0122023-16082023 . Accessed 15 Sept 2023

Manzo G, Tofani V, Segoni S, Battistini A, Catani F (2013) GIS techniques for regional-scale landslide susceptibility assessment: the Sicily (Italy) case study. Int J Geogr Inf Sci 27(7):1433–1452

Meena SR, Mishra BK, Tavakkoli Piralilou S (2019) A hybrid spatial multi-criteria evaluation method for mapping landslide susceptible areas in kullu valley, himalayas. Geosciences 9(4):156

Mehta BS, Parti RA, Sharma RK (2010) Landslide hazard analysis and zonation on National Highway-21 from Panasra to Manali, HP, India. Int J Earth Sci Eng 3(3):376–381

Merghadi A, Yunus AP, Dou J, Whiteley J, ThaiPham B, Bui DT, Avtar R, Abderrahmane B (2020) Machine learning methods for landslide susceptibility studies: a comparative overview of algorithm performance. Earth-Sci Rev 207:103225

Micheletti N, Foresti L, Robert S, Leuenberger M, Pedrazzini A, Jaboyedoff M, Kanevski M (2014) Machine learning feature selection methods for landslide susceptibility mapping. Math Geosci 46(1):33–57

Misra DK, Tewari VC (1988) Tectonics and sedimentation of the rocks between Mandi and Rohtang, Beas valley, Himachal Pradesh, India. Geosci J 9(2):53–172

Neaupane KM, Piantanakulchai M (2006) Analytic network process model for landslide hazard zonation. Eng Geo 85(3–4):281–294

Nseka D, Kakembo V, Bamutaze Y, Mugagga F (2019) Analysis of topographic parameters underpinning landslide occurrence in Kigezi highlands of southwestern Uganda. Nat Hazards 99(2):973–989

Peterson LE (2009) K-nearest neighbor. Scholarpedia 4(2):1883

Petley D (2012) Global patterns of loss of life from landslides. Geology 40(10):927–930

Pham BT, Jaafari A, Prakash I, Bui DT (2019) A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull Eng Geol Environ 78(4):2865–2886

Pham QB, Achour Y, Ali SA, Parvin F, Vojtek M, Vojteková J, Al-Ansari N, Achu AL, Costache R, Khedher KM, Anh DT (2021) A comparison among fuzzy multi-criteria decision making, bivariate, multivariate and machine learning models in landslide susceptibility mapping. Geomatics, Nat Hazards Risk 12(1):1741–1777

Postance B, Hillier J, Dijkstra T, Dixon N (2017) Extending natural hazard impacts: an assessment of landslide disruptions on a national road transportation network. Environ Res Lett 12(1):014010

Poudyal CP, Chang C, Oh HJ, Lee S (2010) Landslide susceptibility maps comparing frequency ratio and artificial neural networks: a case study from the Nepal Himalaya. Environ Earth Sci 61(5):1049–1064

Pourghasemi HR, Teimoori Yansari Z, Panagos P, Pradhan B (2018) Analysis and evaluation of landslide susceptibility: a review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arab J Geosci 11(9):1–12

Pradhan AM, Kim YT (2014) Relative effect method of landslide susceptibility zonation in weathered granite soil: a case study in Deokjeok-Ri Creek, South Korea. Nat Hazards 72(2):1189–1217

Pradhan SP, Panda SD, Roul AR, Thakur M (2019) Insights into the recent Kotropi landslide of August 2017, India: a geological investigation and slope stability analysis. Landslides 16(8):1529–1537

Prasad AS, Pandey BW, Leimgruber W, Kunwar RM (2016) Mountain hazard susceptibility and livelihood security in the upper catchment area of the river Beas, Kullu Valley, Himachal Pradesh, India. Geoenvironmental Disasters 3(1):1–7

Rabby YW, Hossain MB, Abedin J (2020) Landslide susceptibility mapping in three Upazilas of Rangamati hill district Bangladesh: application and comparison of GIS-based machine learning methods. Geocarto Int 37(12):3371–3396

Ram P, Gupta V, Devi M, Vishwakarma N (2020) Landslide susceptibility mapping using bivariate statistical method for the hilly township of Mussoorie and its surrounding areas, Uttarakhand Himalaya. J Earth Syst Sci 129(1):1–18

Sabokbar HF, Roodposhti MS, Tazik E (2014) Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 226:15–24

Sah MP, Mazari RK (1998) Anthropogenically accelerated mass movement, Kulu Valley, Himachal Pradesh, India. Geomorphology 26(1–3):123–138

Sah MP, Mazari RK (2007) An overview of the geoenvironmental status of the Kullu Valley, Himachal Pradesh, India. J Mt Sci 4(1):003–023

Sahin EK (2020) Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. SN Appl Sci 2(7):1–17

Saraswat M (2020) Beginners Tutorial on XGBoost and Parameter Tuning in R. hackerearth. https://www.hackerearth.com/practice/machine-learning/machine-learning-algorithms/beginners-tutorial-on-xgboost-parameter-tuning-r/tutorial/ . Accessed 11 Jan 2022

Scheingross JS, Minchew BM, Mackey BH, Simons M, Lamb MP, Hensley S (2013) Fault-Zone controls on the spatial distribution of slow-moving landslides. Geol Soc Am Bull 125(3–4):473–489

Shahabi H, Shirzadi A, Ghaderi K, Omidvar E, Al-Ansari N, Clague JJ, Geertsema M, Khosravi K, Amini A, Bahrami S, Rahmati O (2020) Flood detection and susceptibility mapping using sentinel-1 remote sensing data and a machine learning approach: hybrid intelligence of bagging ensemble based on k-nearest neighbor classifier. Remote Sens 12(2):266

Solanki A, Gupta V, Joshi M (2022) Application of machine learning algorithms in landslide susceptibility mapping, Kali Valley, Kumaun Himalaya, India. Geocarto Int 1–26. https://doi.org/10.1080/10106049.2022.2120546

Srivastava T (2020) How to use XGBoost algorithm in R in easy steps. Analytics Vidhya. https://www.analyticsvidhya.com/blog/2016/01/xgboost-algorithm-easy-steps/ . Accessed 11 Jan 2022

Stead D, Wolter A (2015) A critical review of rock slope failure mechanisms: the importance of structural geology. J Struct Geol 74:1–23

Tien Bui D, Ho TC, Pradhan B, Pham BT, Nhu VH, Revhaug I (2016) GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ Earth Sci 75(14):1101

Tiwari A, Sain K, Kumar A, Tiwari J, Paul A, Kumar N, Haldar C, Kumar S, Pandey CP (2022) Potential seismic precursors and surficial dynamics of a deadly himalayan disaster: an early warning approach. Sci Rep 12(1):1–13

Van Westen CJ, Rengers N, Soeters R (2003) Use of geomorphological information in indirect landslide susceptibility assessment. Nat Hazards 30(3):399–419

Varnes DJ (1978) Slope movements, type and processes. In: Schuster RL, Krizek RJ (eds) Landslide analysis and control, Transportation Research Board. National Academy Sciences, Washington, DC, pp 11–33 (Special report 176)

Versain LD, Banshtu RS, Pandey DD (2019) Comparative evaluation of GIS based landslide hazard zonation maps using different approaches. J Geol Soc India 93(6):684–692

Vijay R, Kushwaha VK, Chaudhury AS, Naik K, Gupta I, Kumar R, Wate SR (2016) Assessment of tourism impact on land use/land cover and natural slope in Manali, India: a geospatial analysis. Environ Earth Sci 75(1):1–9

Webb GI, Keogh E, Miikkulainen R (2010) Naïve Bayes. Encycl Mach Learn 15:713–714

Wu X, Ren F, Niu R (2014) Landslide susceptibility assessment using object mapping units, decision tree, and support vector machine models in the Three Gorges of China. Environ Earth Sci 71(11):4725–4738

Wu Y, Ke Y, Chen Z, Liang S, Zhao H, Hong H (2020) Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 187:104396

Youssef AM, Pourghasemi HR (2021) Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci Front 12(2):639–655

Yu X, Zhang K, Song Y, Jiang W, Zhou J (2021) Study on landslide susceptibility mapping based on rock–soil characteristic factors. Sci Rep 11(1):1–27

Zhao P, Masoumi Z, Kalantari M, Aflaki M, Mansourian A (2022) A GIS-Based landslide susceptibility mapping and variable importance analysis using Artificial Intelligent Training-based methods. Remote Sens 14(1):211

Download references

Acknowledgements

The authors thank the Director, Wadia Institute of Himalayan Geology, Dehradun for his constant encouragement and providing necessary facilities to carry out the work. RK acknowledges the financial assistance in the form of fellowship from Council of Scientific and Industrial Research (CSIR), New Delhi. Dr. Bikash Ram and Ambar Solanki are also thanked for their precious assistance in writing the article. The article bears the Wadia Institute contribution number WIHG/0248.

Author information

Authors and affiliations.

Wadia Institute of Himalayan Geology, Dehradun, Uttarakhand, India

Ramandeep Kaur & Vikram Gupta

Department of Geophysics, Kurukshetra University, Kurukshetra, Haryana, India

Ramandeep Kaur & B. S. Chaudhary

Department of Geology, Sikkim University, Gangtok, Sikkim, India

Vikram Gupta

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Vikram Gupta .

Ethics declarations

Competing interest.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Kaur, R., Gupta, V. & Chaudhary, B.S. Landslide susceptibility mapping and sensitivity analysis using various machine learning models: a case study of Beas valley, Indian Himalaya. Bull Eng Geol Environ 83 , 228 (2024). https://doi.org/10.1007/s10064-024-03712-y

Download citation

Received : 10 May 2022

Accepted : 28 April 2024

Published : 13 May 2024

DOI : https://doi.org/10.1007/s10064-024-03712-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Susceptibility
• Beas valley
• Extreme Gradient Boosting
• Sensitivity analysis
• Find a journal
• Publish with us
• Track your research

Is an active hospital microbiology laboratory cost-effective in a resource-limited setting? - a case study from Timor-Leste

• Find this author on Google Scholar
• Find this author on PubMed
• Search for this author on this site
• For correspondence: [email protected]
• Info/History
• Preview PDF

Maintaining an active hospital microbiology laboratory allows definitive antibiotic treatment for bacterial infections to be given in a timely manner. This would be expected to improve patient outcomes and shorten length of hospital stay. However, many hospitals in low- and middle-income countries lack access to microbiology services, and the cost-effectiveness of an active microbiology service is unknown. We constructed a decision tree and performed a cost-effectiveness model analysis to determine whether maintaining an active microbiology laboratory service would be cost-effective in Timor-Leste, a lower middle-income country. The analysis was informed by local microbiology data, local patient treatment costs, results of an expert elicitation exercise and data from literature reviews. The results indicate that there is a high probability that maintaining an active microbiology laboratory is a cost-effective intervention that would both improve patient outcomes and reduce net costs (due to reduced intensive care admissions and potential costs of resistant infections) compared to no microbiological testing, especially for the hospitalised paediatric patients with suspected primary bacteraemia. This remained true under various one-way sensitivity analyses, including when accuracy of microbiological testing is low, prevalence of bacterial infection among patients with suspected bloodstream infection was high, and prevalence of antibiotic resistance was high.

Competing Interest Statement

The authors have declared no competing interest.

Funding Statement

This study was funded by the Fleming Fund Country Grant to Timor-Leste. The Fleming Fund is a UK Aid fund administered by the UK Government's Department of Health and Social Care, which supports antimicrobial resistance surveillance activities in at least 25 countries around the world.

Author Declarations

I confirm all relevant ethical guidelines have been followed, and any necessary IRB and/or ethics committee approvals have been obtained.

I confirm that all necessary patient/participant consent has been obtained and the appropriate institutional forms have been archived, and that any patient/participant/sample identifiers included were not known to anyone (e.g., hospital staff, patients or participants themselves) outside the research group so cannot be used to identify individuals.

I understand that all clinical trials and any other prospective interventional studies must be registered with an ICMJE-approved registry, such as ClinicalTrials.gov. I confirm that any such study reported in the manuscript has been registered and the trial registration ID is provided (note: if posting a prospective study registered retrospectively, please provide a statement in the trial ID field explaining why the study was not registered in advance).

I have followed all appropriate research reporting guidelines, such as any relevant EQUATOR Network research reporting checklist(s) and other pertinent material, if applicable.

Funding: This study was funded by the Fleming Fund Country Grant to Timor-Leste. The Fleming Fund is a UK Aid fund administered by the UK Government’s Department of Health and Social Care, which supports antimicrobial resistance surveillance activities in at least 25 countries around the world.

Data Availability

All data produced in the present work are contained in the manuscript

View the discussion thread.

Thank you for your interest in spreading the word about medRxiv.

NOTE: Your email address is requested solely to identify you as the sender of this article.

Citation Manager Formats

• EndNote (tagged)
• EndNote 8 (xml)
• RefWorks Tagged
• Ref Manager
• Tweet Widget
• Facebook Like
• Google Plus One

Subject Area

• Health Economics
• Addiction Medicine (324)
• Allergy and Immunology (628)
• Anesthesia (165)
• Cardiovascular Medicine (2383)
• Dentistry and Oral Medicine (289)
• Dermatology (207)
• Emergency Medicine (380)
• Endocrinology (including Diabetes Mellitus and Metabolic Disease) (839)
• Epidemiology (11777)
• Forensic Medicine (10)
• Gastroenterology (703)
• Genetic and Genomic Medicine (3751)
• Geriatric Medicine (350)
• Health Economics (635)
• Health Informatics (2401)
• Health Policy (935)
• Health Systems and Quality Improvement (900)
• Hematology (341)
• HIV/AIDS (782)
• Infectious Diseases (except HIV/AIDS) (13323)
• Intensive Care and Critical Care Medicine (769)
• Medical Education (366)
• Medical Ethics (105)
• Nephrology (398)
• Neurology (3513)
• Nursing (198)
• Nutrition (528)
• Obstetrics and Gynecology (675)
• Occupational and Environmental Health (665)
• Oncology (1825)
• Ophthalmology (538)
• Orthopedics (219)
• Otolaryngology (287)
• Pain Medicine (233)
• Palliative Medicine (66)
• Pathology (446)
• Pediatrics (1035)
• Pharmacology and Therapeutics (426)
• Primary Care Research (422)
• Psychiatry and Clinical Psychology (3181)
• Public and Global Health (6150)
• Radiology and Imaging (1281)
• Rehabilitation Medicine and Physical Therapy (749)
• Respiratory Medicine (828)
• Rheumatology (379)
• Sexual and Reproductive Health (372)
• Sports Medicine (323)
• Surgery (402)
• Toxicology (50)
• Transplantation (172)
• Urology (146)

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Gates Foundation Open Access

Standardized Sensitivity Analysis in BCA: An Education Case Study

Elina pradhan.

1 Elina Pradhan, The World Bank Group, Health, Nutrition and Population Global Practice, Washington, DC 20433, USA

Dean T. Jamison

2 Dean T. Jamison: University of California, San Francisco, CA 94143, USA

Benefit-cost analyses of education policies in low- and middle-income countries have historically used the effect of education on future wages to estimate benefits. Strong evidence also points to female education reducing both the under-five mortality rates of their children and adult mortality rates. A more complete analysis would thus add the value of mortality risk reduction to wage increases. This paper estimates how net benefits and benefit-cost ratios respond to the values used to estimate education’s mortality-reducing impact including variation in these estimates. We utilize a ‘standardized sensitivity analysis’ to generate a range of valuations of education’s impact on mortality risks. We include alternative ways of adjusting these values for income and age differences. Our analysis is for one additional year of schooling in lower-middle-income countries, incremental to the current mean. Our analysis shows a range of benefit-cost ratios ranging from 3.2 to 6.7, and net benefits ranging from $2,800 to $7,300 per student. Benefits from mortality risk reductions account for 40% to 70% of the overall benefits depending on the scenario. Thus, accounting for changes in mortality risks in addition to wage increases noticeably enhances the value of already attractive education investments.

1 Introduction

In 2016 the International Commission on Financing Global Education Opportunity published its report, The Learning Generation: Investing in Education for a Changing World ( The International Commission on Financing Global Education Opportunity, 2016 ). The Commission, chaired by former UK Prime Minister Gordon Brown, utilized benefit-cost analyses (BCAs) to underpin its conclusion that a major acceleration of education is now warranted. Standard BCA methods were used to show large incremental benefits as compared to incremental costs, weighing costs of schooling, including opportunity costs of student time, against estimates of health benefits and education-related wage gain over the individual’s working lifetime ( Psacharopoulos et al., 2017 ).

The Commission pointed to a diverse and substantial literature relating higher levels of education to lower levels of premature mortality, and to improved health more generally ( Filmer & Pritchett, 1999 ; Gakidou et al., 2010 ; Baird et al., 2012 ; Kuruvilla et al., 2014 ; Wang et al., 2014 ; Jamison et al., 2016 ). The Commission requested that a team (assembled by SEEK Development in Berlin) utilize this literature to extend standard approaches to BCA in education to include explicit valuation of reasonable estimates of the impact of education on mortality. The Commission then featured the results of that assessment in the executive summary of their report. Pradhan et al. (2018) report those findings – and the methods on which they are based – in detail.

A notable difficulty facing the Pradhan et al. (2018) team concerned how to value small changes in mortality risk using monetary measures (derived from the revealed or stated preferences of individuals and conventionally reported as the value per statistical life, VSL). By now, a substantial empirical literature reports findings from different approaches to estimate monetary value of mortality risk reductions in low- and middle-income countries ( Narain & Sall, 2016 ; Viscusi & Masterman, 2017 a , b ). That said, huge variation remains in how one might plausibly apply existing results in a broad range of contexts, particularly in low-income or high-mortality environments. The Pradhan et al. study selected reasonable values of parameters from the literature, but other analysts could have plausibly chosen different parameters. This indeterminateness limits the utility of most BCAs for two reasons:

• (i) It can be hard to judge how sensitive the study’s findings are to parameters chosen; and
• (ii) Individual BCA results cannot be easily compared across sectors and over time to generate a solid corpus of comparable findings. (This problem applies equally to the valuation of mortality risk reductions when assessing the economic burden of diseases or risk factors.)

Analysts from several governmental and international organizations and researchers have proposed varying approaches for increasing standardization. Chang et al. (2018) provide a brief account of some options that have been considered. The Bill & Melinda Gates Foundation has funded development of a BCA reference case ( Robinson et al., 2019 a ) to address these problems in a way broadly consistent with a cost-effectiveness reference case that the Gates Foundation had previously funded ( Wilkinson et al., 2016 ). This education case study was prepared to support and illustrate the development of the BCA reference case.

One suggested approach to improving credibility and comparability was that of developing a ‘standardized sensitivity analysis’ (SSA) to be reported routinely within BCAs. The analyst might choose to highlight a particular value from the SSA as the best estimate in the analysis undertaken. Or, for any of a variety of reasons, the analyst might choose to headline a different approach but to undertake the SSA as well. The SSA would both enable judgement on the robustness of the findings of the analysis and enable comparison of those findings with an accumulating literature. The value of developing a reference case lies in enabling this comparability.

Our purpose in this case study is to illustrate how SSAs might reasonably be done. The analysis assesses the costs and benefits of education investments in lower-middle-income countries (LMCs) 1 from a perspective where we estimate the economic returns to education from the value of reductions in under-five and adult mortality risks in addition to any increases in earnings. We develop a case study that starts with the Pradhan et al. (2018) findings, but then reanalyse those findings using estimates of the value of mortality risk reduction that vary by income and age. An important output from Pradhan et al. (2018) was assessment of the benefits of quality of education as well as years of schooling. Not surprisingly, quality proves important. For simplicity, this paper illustrates the results of the SSA using only the estimated effects of years of schooling on mortality risks.

Before proceeding to the main body of the paper, we discuss how the purposes of a BCA affect the way(s) it might most usefully be reported. Perhaps the most important and typical use of BCA is to assist with determinations of how (and whether) specific major projects or regulations should be undertaken. The present value of the net benefits (PVNBs) of options considered provides the key input to decision makers, and its calculation and reporting is a central task for the analyst.

Less often – but still importantly – the BCA’s purpose is to contribute to an evolving literature about what works (and what does not) and in general to convey how attractive certain classes of investments tend to be. The analysis reported in this paper falls squarely in this latter, evaluative category. The intention is to add to a literature that provides conclusions relevant to a broad range of contexts. Benefit-cost ratios (BCRs) can be understood as relevant to many scales and contexts thereby providing useful (if only broad brush) policy guidance. Both PVNB and the BCR require an exogenously-given discounting procedure and may be (usually are) quite sensitive to choice of procedure as we shall see later in this paper.

The economics of education literature borrows from the finance literature in generally reporting the results of its BCAs as internal rates of return (IRRs). The IRR is that value of a constant discount rate that solves the equation equilibrating the time streams of benefits and costs. (A problem is that this equation may have multiple solutions although this does not appear to be a problem in practice in the education literature.) An advantage is that the discount rate is an output from rather than an input to the IRR and, like the BCR, it shows relative attractiveness independent of scale enabling comparison of economic attractiveness across studies. However, like the BCR but unlike PVNB, the IRR gives no indication of absolute attractiveness.

A standardized sensitivity analysis serves the purpose of accumulating knowledge across studies. Hence in this paper we explore the SSA by way of BCRs and – since the topic is education (and we seek to relate to that literature) – we also report IRRs as well as PVNB.

The case study proceeds as follows. The next section describes our approach to the SSA. Following the SSA methods section, section C describes the BCA undertaken for the Brown Commission ( Pradhan et al., 2018 ); in particular the analysis estimating BCR, PVNB and IRR in LMCs for one year of schooling incremental to the current mean of 7 years. Section D presents results of the SSA, and section E discusses the findings and study limitations.

Our methods begin with those standard in the economics of education literature which construct time streams over individual lifetimes of education costs and benefits, where benefits are the estimated earnings increases associated with the increment in education being considered (here one-year incremental to 7 years). We add to that the estimated value of mortality reduction in the cohort associated with that one-year increment in education. The methods discussion that follows concerns how we translate an estimated reduction in numbers of deaths into a dollar benefit. The short answer is to multiply the number of deaths estimated to be averted by the ‘value of a statistical life’ or VSL. Operationalizing that short answer in the current context is the subject of the next few pages.

We vary the value of mortality risk reductions on income and age dimensions. The first dimension is concerned with how the analysis treats variation across country income levels, based on how the ratio of the value of a unit of mortality risk reduction to gross national income (GNI) per capita (purchasing power parity (PPP) adjusted) varies with income. We report our SSA using three alternatives recommended by Robinson et al. (2019 b ) – (i) the ratio of VSL-to-GNI per capita remains constant at 160, using U.S. values as a starting point and an income elasticity of 1.0; (ii) the ratio of VSL-to-GNI per capita remains constant at 100, using OECD values as the starting point and an income elasticity of 1.0; and (iii) the ratio of VSL-to-GNI per capita has an income elasticity of 1.5, using the U.S. ratio of 160 as a starting point.

The first two income variants are included to facilitate comparisons with existing research that uses these alternative approaches. The third option, which Robinson et al. (2019 b ) propose as the featured variant, reflects the expectation that the VSL-to-GNI per capita ratio will be smaller in LMCs than in a high-income country (the United States in this case), given the need to preserve more limited income for essential expenditures. These three variants demonstrate uncertainties in the VSL estimates, given that few empirical studies have been conducted in LMCs.

Application of the first two variants is straightforward. For the third variant, we calculate the ratio of VSL-to-GNI per capita starting with the formula from Hammitt and Robinson (2011) : V S L = V S L t × ( G N I p e r c a p i t a G N I p e r c a p i t a r ) e l a s t i c i t y , where VSL r is the recommended reference value, in this case from the United States.

We reformulate this as the VSL-to-GNI per capita ratio (VSLR) = VSL/GNI per capita where,

Here, GNI per capita US = $57,900, GNI per capita LMCs = $6,430, VSL US = 160 × $57,900, and elasticity = 1.5.

Therefore, VSLR LMCs = 54.

The second dimension is concerned with how the analysis values mortality risk reductions at different ages, and we select the two alternative approaches discussed in Robinson et al. (2019 b ) : (i) the value does not vary with age; and (ii) the value is proportional to remaining life expectancy. The second age variant suggests estimating a constant value per statistical life year (VSLY) based on each of the population-average VSLs estimated using the approaches referenced above. The VSL is divided by undiscounted remaining life expectancy at midpoint of the approximate life expectancy at birth for the region of interest (age 35 in this case). The resulting VSLY is then multiplied by change in the future life expectancy of the population affected. Note that in the first scenario where the VSL does not vary with age, VSL is a population-average estimate that is applied to all beneficiaries of the intervention. The empirical research upon which these estimates are based relies largely on samples of working-age adults. Whether these values are appropriate for younger or older populations is uncertain ( Hammitt, 2007 ) even in high-income countries; little is known about the relationship of the VSL to age or life expectancy in LMCs. As Robinson et al. (2019 b ) note, although not robustly supported by available research, the second age variant of assuming a constant VSLY provides a rough proxy for the effects of age and life expectancy.

Table 1 summarizes these approaches, including three income variants combined with two age variants.

a Our case study is for LMCs as a group. Their per capita GNI in 2015 was $6,430 in PPP (current international $) (WDI 2017). With the income per capita of the case study region, we can fill in the relevant values of column 1 of Table 1 (since values in column 1 are independent of the age distribution of mortality changes). The outputs are the value of the benefits of the intervention as specified in (2) below. The SSA scenarios are based on recommendations from Robinson et al. (2019 b ).

b L ( a ) is life expectancy at age a, and L(35) is remaining life expectancy at midpoint of the approximate life expectancy at birth for LMCs (age 35 in this case).

In addition to the SSA comparisons above, we perform a sensitivity analysis across discount rates, and for SSA scenario (3,1), we evaluate the sensitivity of the BCA estimates across a wider range of income elasticities.

More generally, if δ(a) deaths/year is the annual age-specific benefit of the intervention in mortality risk reduction (at age a ), y = income, and η(a) is the age distribution of the population to which the intervention applies, then:

3 Cost-benefit analysis of additional schooling

Analyses prior to Pradhan et al. (2018) have estimated the returns to education using household and labour market survey data, and mainly focus on the private and ‘social’ returns to years of schooling in terms of earnings. IRR for education investments is the discount rate at which net present benefits of the education investments are zero. The ‘social’ IRR incorporates the full cost of schooling and pretax earnings, whereas private IRR estimates assume after-tax earnings and that the cost of schooling is borne by the government, and the only cost of schooling to the individual is the opportunity cost of time associated with attending school. Both these estimates traditionally only consider the wage benefits of increased schooling, with the private returns considering after-tax wages.

Pradhan et al. (2018) expand on the traditional approach to BCAs by including health gains to increased schooling in addition to the earnings return, and estimate the PVNBs, IRRs and BCRs of investing US$1 in education in low-, lower-middle-, and upper-middle-income countries from a societal perspective. This case study presents a proposed set of standard sensitivity analysis on BCRs of an additional year of schooling in LMCs. We also updated our data sources for our analysis as compared to Pradhan et al. (2018) , as tabulated in the Appendix .

The methods for BCA of additional schooling are briefly summarized below:

3.1 Benefits of additional schooling

Pradhan et al. (2018) use a hierarchical linear model to estimate the impact of increased female schooling on under-five mortality, adult male mortality and adult female mortality controlling for technological progress (proxied by time-period categories) and income. Further, we allow the impact of technological progress to vary every five years, hence allowing a country-specific impact of technological progress on health. We replicate the different approaches to estimating the macro-level impact of education on health found in the literature, and choose the model with the most robust controls, resulting in an estimate that is a lower bound of the range used in the same paper and in this case study.

From these regression results, we estimate the level of reductions in (1) adult female mortality, (2) adult male mortality, and (3) under-five mortality (from mother’s education) resulting from one more year of female schooling as was done in Pradhan et al. (2018) . Since the average years of schooling in LMCs is seven years, the BCR calculations estimate the benefits and costs of increasing schooling from seven years on average, to eight years per pupil.

The mortality reductions are then valued using base VSL-to-GNI per capita ratio of 160, another ratio of 100, and discount rates including 1%, 5% and 8.4% with the ratio of 160. The main analysis discounts future costs and benefits at 3%. We combine the expected health value with the earning benefit of increased schooling using smoothed age-earnings profiles received from Psacharopoulos et al. (2017) . The education to earnings link accounts for increased productivity, but it could also account for increased life expectancy or reduced morbidity which would also improve lifetime earnings.

Note that the impact of increasing schooling on earnings is estimated for both male and female pupils – we use the regional average increase in earnings by increasing one year of secondary schooling. The mortality effect of male education appears to be minimal. The costs in our BCA include costs for educating both male and female students.

3.2 Costs of additional schooling

The direct cost data was provided by International Commission on Financing Global Education Opportunity, which is the cost of teacher time, facilities rent and consumable items such as textbooks, and the opportunity cost of student time was derived from the age-earnings profile. The opportunity cost is the earnings forgone by the additional year of schooling, such that the earnings for the age of entry for additional year of schooling is negative. The direct cost of schooling is only incurred in the additional year; it is zero for ages higher than the age at which the additional schooling occurs. Similar to direct costs, the opportunity cost of schooling at ages higher than the age of additional year of schooling is also zero.

3.3 Health-inclusive benefits and costs of additional schooling

The health-inclusive IRR (hPVNR(r h )) is the value of annual IRR (r h ) such that the health-inclusive PVNB of an additional year of schooling is zero. The education literature typically reports the results of BCAs as IRRs for two reasons. One is to avoid selecting a discount rate from the sea of alternatives. The second is that, like the BCR and unlike the PVNBs – many believe the IRR provides an easily understood and cross-intervention compatible metric of attractiveness. We also report PVNBs, because only reporting a ratio can obscure the relative magnitude of the effects.

As described above, we consider annual direct costs c 1 (a) and opportunity costs of schooling c 2 (a) , and the health (mortality risk reduction) benefits hv(a) and earnings benefit ev(a) when estimating the rate of return. Equation (3) gives the net present value of health-inclusive costs and benefits of an additional year of schooling for ages A through 65. Age A is the age of entry for the additional year of schooling at the mean years of schooling (7th grade), which is at 14 years for LMCs.

Hence, the health-inclusive IRR is the value of r h where the net present value (hPVNR(r h )) equals zero. Across a range of reasonable values, inclusion of the benefits from reduced mortality increases IRRs for education by over 40%. For example, in the specific calculation reported in Pradhan et al. (2018) for LMCs, the estimated IRR increased from 7.0% to 9.3% when the value of mortality reduction was included.

Similarly, the BCR is estimated by applying an annual discount rate ( r ) to all costs and benefits. For annual costs and benefits described above, equation (4) shows the health-inclusive BCR (hBCR) and equation (5) the health-inclusive PVNB of one additional year of schooling.

The details of the estimation process of benefit and cost streams are explained in supplement section A, and supplement section D details the age- and income-adjusted benefit streams used for the SSA.

4 Results of BCA for education: standardized sensitivity analysis

Table 2a shows the present dollar value of reduction in mortality risk per student due to an additional year of schooling in LMCs, with varying assumptions of the dependency of the VSL on (i) the base VSL-to-GNI per capita estimate and the income elasticity, and (ii) age of the population groups affected; table 2b shows the BCRs, IRRs and PVNBs for the same. Note that our models assume that the health benefits accrue only to females who receive additional schooling but that the wage benefits accrue to both males and females. Hence, the estimate of the dollar value of health benefits is a weighted average with the weight depending on the fraction of the educated cohort that is female. The calculations assume the cohort is 50 percent female.

a Intervention is one additional year at the current mean of 7 years. Future benefits discounted at the rate of 3% per year.

b Since income is $6,430 per year, VSLR is 54 given an income elasticity of 1.5.

a Intervention is one additional year at the current mean of 7 years.

b BCRs calculated using a discount rate of 3% per year.

c Since income is $6,430 per year, VSL-to-GNI per capita ratio is 54 given an income elasticity of 1.5.

d PVNB in 2015 US$.

We find that the present dollar value of mortality risk reduction is 180% higher if we assume the VSL-to-GNI per capita ratio is constant at 160 (an income elasticity of 1.0), as compared to when we use this U.S. ratio as the starting point and assume that VSL is income-elastic (with an elasticity of 1.5). In the first two income variant scenarios where the VSL-to-GNI per capita ratios are 160 and 100, the present dollar value of mortality reduction benefits exceeds the value of increased earnings. Additionally, if we assume that the value of mortality benefits is age-dependent, then the present dollar value of mortality reduction benefits increases by about 25%, as compared to assuming that mortality reduction benefits are independent of age.

Our results show that using the age-adjusted VSLs rather than the population-average VSLs yields higher values of mortality reduction benefits, BCRs and IRRs, because the benefits accrue to those who are younger than the population average. Every dollar invested in schooling in LMCs would return $5.8 in earnings and reductions in under-five and adult mortality when not adjusting the VSL for age (and when assuming the ratio of VSL-to-GNI per capita is constant at 160). However, adjusting the VSLs for years of life lost, the BCR is 17% higher, at $6.7 in benefits accrued per dollar spent on schooling. We also find that adjusting VSL for income elasticity of 1.5 yields lower IRRs, BCRs and PVNB for LMCs because the income of the reference country is about 8 times higher than the GNI per capita of LMCs at $6,430.

Figure 1 presents the sensitivity of BCRs to income elasticity of VSL, using the U.S. value of 160 as the base estimate for the VSL-to-GNI per capita ratio. This scenario assumes that VSL is independent of age, and the future benefits and costs are discounted at the rate of 3%. BCRs and IRRs for LMCs decrease when we assume VSL is income elastic as the income per capita of the reference country (United States) is higher than the income per capita of LMCs. We find that the BCRs range from 2.4 to 5.8 when changing the income elasticity of VSL from 2.0 to 1.0. Note that elasticity of 2.0 is quite high given discussions and recommendations from Robinson et al. (2019 b ) – given that the two elasticities recommended are 1.0 and 1.5 with 1.5 recommended as the main one, we simply wanted to estimate the BCRs on the high end as well.

We also test the sensitivity of our results to four discount rates. The first is a rate of 3 percent, consistent with the International Decision Support Initiative (iDSI) Reference Case ( Wilkinson et al., 2016 ) recommendations as well as common practices. We also report our results for discount rate approximately twice the GDP per capita growth rate in LMCs ( Table 3 ), motivated by the Ramsey rule 2 (see Claxton et al., 2019 ). The BCR with a discount rate twice the per capita growth rate seen in LMCs ( r = 8.4%) is three times lower than at the standard rate of 3%. Additionally, the lower discount rate of 1% might be of particular importance because we assume that for each student affected, the increase in earnings accrues from age 14 (average age of entry for the additional year of schooling) to 65 (retirement age), and the mortality risk reduction accrues over 51 years. Comparing the age-unadjusted, income variant 1 scenario across the discount rate of 1% with the standard rate of 3%, we find that the lower discount rate yields a substantially higher BCR at $9.4 in benefits for every dollar spent in schooling in LMCs – this estimate is 62% higher than the BCR estimated at 3%.

b PVNB in 2015 US$.

c r = annual discount rate.

d Since income is $6,430 per year, VSLR is 54 given an income elasticity of 1.5.

e Since 2015 GDP per capita growth rate for LMCs was 4.2%, this discount rate reflects twice the near-term growth rate.

5 Discussion

BCAs in education weigh future education-associated wage increases against the current costs of providing schooling and the opportunity costs of students’ time. Female education is reliably estimated to reduce both child and adult mortality rates, and estimates reported in this paper, although at the bottom of the published range, prove quantitatively significant. The paper explores a standardized approach to valuing those mortality reductions, then adds those values to wage benefits to generate more robust BCAs for education investments. Before discussing those SSAs, it is worth making our subject and conclusions concrete. The investment we assess is to add one year to the current average of seven years of education in LMCs (as defined by the World Bank). For 10,000 students, a reasonable estimate of costs is $13 million (in 2015 US$). This increase in (female) education would, over the next half century, result in an estimated reduction in 31 deaths under age five and 64 deaths between ages 15 and 60. It would result in an (undiscounted) increase in earnings of about $60 million assuming no trend increase in wages (or, discounted at 3% per year, a $25 million increase). This is the starting point for the SSA.

This case study applies a standard sensitivity analysis that values the impact of increased education on longevity and earnings. We find that the mortality risk reduction is a sizeable fraction of the benefits of education – perhaps 40–70% of the total including increased earnings. BCRs are highly sensitive to the discount rates used and the VSL assumptions. For example, with a VSL-to-GNI per capita ratio of 160 and income elasticity 1.5, BCRs at a 1% discount rate are twice as high as the estimates at 3% discount rate, and five times higher than the estimates at 8.4%. Those caveats noted, we conclude that investing in an additional year of schooling is likely to have a BCR of greater than 2. Regardless of the SSA scenario, at least a third of the benefits result from the estimated effect of female education on the adult and under-five mortality risks.

We find that every dollar invested in schooling in LMCs would return between $3.2 to $6.7 in benefits in increased earnings and mortality risk reductions, testing the sensitivity of the BCR to differing assumptions regarding the value of mortality risk reductions and its variation by age. Zooming in on the health returns of increased schooling, the sensitivity analysis finds that the present dollar value of mortality risk reduction benefits of increasing one year of schooling ranges from $1,600 to $6,100 per student.

Another sensitivity analysis we performed was around the income elasticity of VSL. We find that the BCR decreases by 58% when we start with the U.S. VSL-to-GNI per capita ratio and change income elasticity of VSL from 1 to 2. Additionally, we find that BCR estimates are sensitive to the discount rates used – in one scenario of BCR estimation, changing the discount rate from the standard 3% to 1% results in a 62% higher BCR.

This case study estimates the direct longevity and earnings effects of increasing schooling. However, income affects health, and education affects both health and income. Further work needs to be done to estimate these indirect effects of education on health as mediated through income. Our statistical model in effect holds income constant while estimating the magnitude of education’s effect on mortality. It is this (conservative) estimate that we report. We do know, in addition, that education has an important effect on income and income has a (modest) effect on mortality. Further research should quantify all channels of education’s effects on mortality. When that research agenda has been completed, we believe our estimate will be shown to have been an underestimate, albeit a modest one. One additional question is the extent to which the VSL includes the effects of mortality risk reductions on earnings. Presumably, VSL reflects individuals’ current earnings expectations, not their expectations conditional on increased education. The interaction of these two mechanisms of education benefits while estimating a comprehensive BCR is an important area of future research.

Another limitation of the study is that we do not adjust the VSL for real income growth over time – including the increase in earnings that results from additional education and the increase that is likely to occur over time for the full population assuming economic growth.

Our BCA for incremental investment in education reflects current recommendations for valuing mortality risk reductions based on available literature, as discussed in Robinson et al. (2019 b ) . Those recommendations include both alternative estimates of the population-average VSL and of the use of VSLY estimates to adjust for the age of those affected. More research in LMCs is needed to improve these estimates.

This paper estimates the impact of increasing average years of schooling in LMCs by a year. However, (i) the impact of one additional year at the primary level is likely different from the impact of an additional year at high school or in college; and (ii) the impact of increasing schooling by a year across the different countries in the lower-middle-income group could also be different – the heterogeneous impact of increased schooling while important, is beyond the scope of this study and is another noteworthy topic for future research. Additionally, sensitivity analysis around costs is also out of the scope of the study, and is another area of further research along with additional primary data collection on education costs in low- and middle-income countries.

Further sensitivity analyses could consider other parameter values – for example, varying the impact of female schooling on mortality, or to estimating the impact of schooling on both mortality and morbidity. The mortality risk reduction benefits estimated in this study constitute an underestimate of the benefits because the study (i) does not consider the impact of education on decreasing morbidity; (ii) uses the lower bound estimate of the impact of education on mortality; (iii) fails to include stillbirths averted; and (iv) fails to include a broad range of favourable social impact (for example reduced incarceration rates). Additionally, various controls and model specifications could change the regression estimate of the impact of schooling on mortality. Pradhan et al. (2018) perform this sensitivity analysis at the regression level to estimate the impact of education on mortality using different controls and specifications in the literature, and we use the lower bound of the range of those estimates in this case study. As these points in our discussion make clear, more research will, in this case as in others, add to the confidence and generality of our findings. That said, we nonetheless would judge our broad findings robust and in general conservative.

Acknowledgments:

We wish to acknowledge very helpful comments from Lisa Robinson, James Hammitt, and from four discussants for the paper at a November 2017 workshop held at Harvard University – Anil Deolalikar, Lynn Karoly, Roger Perman and George Psacharopoulos. Two anonymous Journal of Benefit-Cost Analysis reviewers provided additional helpful guidance. The Bill & Melinda Gates Foundation provided financial support through a grant [OPP1160057] to the Harvard Center for Health Decision Science at the Harvard T.H. Chan School of Public Health. More information on the project is available at https://sites.sph.harvard.ed u/bcaguidelines/ .

The views and opinions in this case study are those of the authors and are not endorsed by the Gates Foundation or the project team or by the organizations with whom the authors are affiliated.

1 As defined by the World Bank.

2 Please note that we are assuming a social rate of time preference of zero and an elasticity of the marginal utility of consumption of 2.

Supplementary material

For supplementary material accompanying this paper, please visit https://doi.org/10.1017/bca.2019.5 .

• Baird Sarah J., Garfein Richard S., McIntosh Craig T., and Özler Berk. 2012. “Effect of a Cash Transfer Programme for Schooling on Prevalence of HIV and Herpes Simplex Type 2 in Malawi: A Cluster Randomised Trial.” The Lancet , 379 ( 9823 ): 1320–1329. [ PubMed ] [ Google Scholar ]
• Barro Robert J. and Jong Wha Lee.. 2013. “A New Data Set of Educational Attainment in the World, 1950–2010.” Journal of Development Economics , 104 : 184–198. [ Google Scholar ]
• Chang Angela, Horton Sue, and Jamison Dean T.. 2018. “Benefit-Cost Analysis in Disease Control Priorities, Third Edition.” Disease Control Priorities, Third Edition (DCP3): Volume 9. Improving Health and Reducing Poverty . Washington, D.C.: The World Bank. [ Google Scholar ]
• Claxton Karl, Asaria Miqdad, Chansa Collins, Jamison Julian, Lomas James, Ochalek Jessica, and Paulden Michael. 2019. “Accounting for Timing when Assessing Health-Related Policies.” Journal of Benefit-Cost Analysis , 10 ( S1 ): doi: 10.1017/bca.2018.29. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Filmer Deon and Pritchett Lant. 1999. “The Impact of Public Spending on Health: Does Money Matter?” Social Science & Medicine , 49 ( 10 ): 1309–1323. [ PubMed ] [ Google Scholar ]
• Gakidou Emmanuela, Cowling Krycia, Lozano Rafael, and Murray Christopher J. L.. 2010. “Increased Educational Attainment and Its Effect on Child Mortality in 175 Countries between 1970 and 2009: A Systematic Analysis.” The Lancet , 376 ( 9745 ): 959–974. [ PubMed ] [ Google Scholar ]
• Hammitt James K. 2007. “Valuing Changes in Mortality Risk: Lives Saved versus Life Years Saved.” Review of Environmental Economics and Policy , 1 ( 2 ): 228–240. [ Google Scholar ]
• Hammitt James K. 2017. “Extrapolating the Value Per Statistical Life Between Populations: Theoretical Implications.” Journal of Benefit-Cost Analysis , January, 8 ( 2 ): 1–11. 10.1017/bca.2017.13. [ CrossRef ] [ Google Scholar ]
• Hammitt James K. and Robinson Lisa A.. 2011. “The Income Elasticity of the Value per Statistical Life: Transferring Estimates between High and Low Income Populations.” Journal of Benefit-Cost Analysis , 2 ( 1 ): Art. 1. [ Google Scholar ]
• Jamison Dean T., Murphy Shane M., and Sandbu. Martin E.. 2016. “Why Has Under-5 Mortality Decreased at Such Different Rates in Different Countries?” Journal of Health Economics , 48 (July)): 16–25. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Kuruvilla Shyama, Schweitzer Julian, Bishai David, Chowdhury Sadia, Caramani Daniele, Frost Laura, and Cortez Rafael et al.. 2014. “Success Factors for Reducing Maternal and Child Mortality.” Bulletin of the World Health Organization , 92 ( 7 ): 533–544. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Lindhjem H., Navrud S., Biausque V., and Braathen N. A.. 2012. Mortality Risk Valuation in Environment, Health and Transport Policies . Paris: OECD. [ Google Scholar ]
• Narain Urvashi and Sall Chris. 2016. Methodology for Valuing the Health Impacts of Air Pollution: Discussion of Challenges and Proposed Solutions . World Bank. [ Google Scholar ]
• Pradhan Elina, Suzuki Elina M., Martínez Sebastián, Schäferhoff Marco, and Jamison Dean T.. 2018. “The Effect of Education Quantity and Quality on Child and Adult Mortality: Its Magnitude and Its Value.” Disease Control Priorities, Third Edition (DCP3): Volume 8. Child and Adolescent Health and Development . Washington, D.C.: The World Bank. [ PubMed ] [ Google Scholar ]
• Psacharopoulos George, Montenegro Claudio, and Patrinos Harry Anthony. 2017. “Education Financing Priorities in Developing Countries.” Journal of Educational Planning and Administration , XXXI ( 1 ): 5–16. [ Google Scholar ]
• Robinson Lisa A., Hammitt James K., Jamison Dean T., and Walker Damian G.. 2019a. “Conducting Benefit-Cost Analysis in Low- and Middle-Income Countries: Introduction to the Special Issue.” Journal of Benefit-Cost Analysis , 10 ( S1 ): doi: 10.1017/bca.2019.4. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Robinson Lisa A., Hammitt James K., and O’Keeffe Lucy. 2019b. “Valuing Mortality Risk Reductions in Global Benefit-Cost Analysis.” Journal of Benefit-Cost Analysis , 10 ( S1 ): doi: 10.1017/bca.2018.26. [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• The International Commission on Financing Global Education Opportunity 2016. The Learning Generation: Investing in Education for a Changing World .
• United Nations, Department of Economic and Social Affairs, Population Division 2017. World Population Prospects: The 2017 Revision, DVD Edition .
• Viscusi W. Kip. 2015. “The Role of Publication Selection Bias in Estimates of the Value of a Statistical Life.” American Journal of Health Economics , 1 ( 1 ): 27–52. [ Google Scholar ]
• Viscusi W. Kip and Masterman Clayton. 2017a. “Anchoring Biases in International Estimates of the Value of a Statistical Life.” Journal of Risk and Uncertainty , 54 ( 2 ): 103–128. [ Google Scholar ]
• Viscusi W. Kip and Masterman Clayton J.. 2017b. “Income Elasticities and Global Values of a Statistical Life.” Journal of Benefit-Cost Analysis , 8 ( 2 ): 226–250. [ Google Scholar ]
• Wang Wenjuan, Winner Michelle, Burgert Clara, and Colston Josh. 2014. “Influence of Service Readiness on Use of Facility Delivery Care: A Study Linking Health Facility Data and Population Data in Haiti.” DHS Working Papers No. 114 Rockville, Maryland, USA: ICF International; http://dhsprogram.com/pubs/pdf/WP114/WP114.pdf . [ Google Scholar ]
• Wilkinson Thomas, Sculpher Mark J., Claxton Karl, Revill Paul, Briggs Andrew, Cairns John A., and Teerawattananon Yot et al.. 2016. “The International Decision Support Initiative Reference Case for Economic Evaluation: An Aid to Thought.” Value in Health , 19 ( 8 ): 921–928. [ PubMed ] [ Google Scholar ]
• World Bank 2017. World Development Indicators . World Bank Publications. [ Google Scholar ]