problem solving and mental arithmetic

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving 

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.  

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations. 

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies: 

• Draw a model
• Use different approaches
• Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better. 

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem. 

Here are 20 strategies to help students develop their problem-solving skills. 

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand: 

• The context
• What the key information is
• How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information. 

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords 

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed.  For example, if the word problem asks how many are left, the problem likely requires subtraction.  Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary.  Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer.  Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it.  The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer.  Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem 

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process.  It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives .  When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts.  The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution.  This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71.  Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved.  It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve.   Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution 

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense. 

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions. 

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work. 

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable.  Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten.  For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10.  When the estimate is clear the two numbers are close. This means your answer is reasonable. 

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables.  To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly.   Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills.  If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.  

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems. 

Polya’s 4 steps include:

• Understand the problem
• Devise a plan
• Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall. 

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom. 

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving 

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking. 

Explore the range of problem solving resources for 2nd to 8th grade students. 

One-on-one tutoring 

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards. 

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice. 

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra. 

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

READ MORE : 8 Common Core math examples

There are many different strategies for problem-solving; Here are 5 problem-solving strategies: • draw a model  • act it out  • work backwards  • write a number sentence • use a formula

Here are 10 strategies of problem-solving: • Read the problem aloud • Highlight keywords • Summarize the information • Determine the unknown • Make a plan • Draw a model  • Act it out  • Work backwards  • Write a number sentence • Use a formula

1. Understand the problem 2. Devise a plan 3. Carry out the plan 4. Look back

Some strategies you can use to solve challenging math problems are: breaking the problem into smaller parts, using diagrams or models, applying logical reasoning, and trying different approaches.

Related articles

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

5 Math Mastery Strategies To Incorporate Into Your 4th and 5th Grade Classrooms

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

• NUMERACY SKILLS

Mental Arithmetic – Basic Mental Maths Hacks

Search SkillsYouNeed:

Numeracy Skills:

• A - Z List of Numeracy Skills
• How Good Are Your Numeracy Skills? Numeracy Quiz
• Money Management and Financial Skills
• Real-World Maths
• Numbers | An Introduction
• Special Numbers and Mathematical Concepts
• Systems of Measurement
• Common Mathematical Symbols and Terminology
• Apps to Help with Maths
• Subtraction -
• Multiplication ×
• Positive and Negative Numbers
• Ordering Mathematical Operations - BODMAS
• Ratio and Proportion
• Percentages %
• Percentage Calculators
• Percentage Change | Increase and Decrease
• Calculating with Time
• Estimation, Approximation and Rounding
• Introduction to Geometry: Points, Lines and Planes
• Introduction to Cartesian Coordinate Systems
• Polar, Cylindrical and Spherical Coordinates
• Properties of Polygons
• Simple Transformations of 2-Dimensional Shapes
• Circles and Curved Shapes
• Perimeter and Circumference
• Calculating Area
• Three-Dimensional Shapes
• Net Diagrams of 3D Shapes
• Calculating Volume
• Area, Surface Area and Volume Reference Sheet
• Graphs and Charts
• Averages (Mean, Median & Mode)
• Simple Statistical Analysis
• Statistical Analysis: Types of Data
• Understanding Correlations
• Understanding Statistical Distributions
• Significance and Confidence Intervals
• Developing and Testing Hypotheses
• Multivariate Analysis
• Introduction to Algebra
• Simultaneous and Quadratic Equations
• Introduction to Trigonometry
• Introduction to Probability

Subscribe to our FREE newsletter and start improving your life in just 5 minutes a day.

You'll get our 5 free 'One Minute Life Skills' and our weekly newsletter.

We'll never share your email address and you can unsubscribe at any time.

Mental arithmetic is the invaluable maths skill of doing calculations in your head, without the use of any tools, such as a calculator or pen and paper, or fingers! It can come in handy in countless everyday situations, from working out the best multi-buy deal in the supermarket, to calculating how long you will need to wait for the next train.

People who need to use maths in their jobs, whether accountancy, retail or engineering for example, often do quite complex and fast estimations in their heads, so that they have a good idea of what the answer will be before they take the time to do a more complex calculation.

Mental arithmetic also helps to develop a real understanding of the mathematical methods of arithmetic, rather than just doing calculations through a process of memorization.

Practising mental arithmetic might seem like hard work, and to some people who find maths difficult it might even seem like a scary prospect. But as with all things, the more you do it, the easier it gets. This page gives you some helpful hints and tips to make the process quicker, easier and a whole lot less scary.

Everyone can learn mental maths hacks! They are not just for maths wizards.

Multiplying numbers by 10, 100 and 1000 and their multiples

To do simple multiplications, you need to have a basic understanding of place value . For more on this, see our page on Numbers . Two things to remember here are:

• Zeros are important
• Decimal points always separate the whole numbers from the ‘bits’.

To mentally multiply any number by 10:

Keep the decimal point where it is. In your head, move all the digits one place to the left and add a zero to the end if needed.

24 × 10 = 24.0 × 10 = 240 175 × 10 = 175.0 × 10 = 1750 3.56 × 10 = 35.6

You can move the decimal point instead of the digits, but only do one or the other!

Some people find it easier to think of the decimal point moving, rather than the digits moving. In the example above, the decimal point stays in the same place and all of the digits shift to the left.

This is the same as moving the decimal point to the right !

To multiply any number by 100:

Either Keep the decimal point where it is. Move the digits two places to the left , adding zeros to the end if needed: 845 × 100 = 845.00 ×100 = 84500 37.64 × 100 = 3764

OR Move the decimal point two places to the right: 56.734 × 100 = 5673.4

To multiply any number by 1000:

Use either of the two methods as before and move three places : Move the digits to the left: 23.476 × 1000 = 23476 Or move the decimal point to the right: 8.45692 × 1000 = 8456.92

Multiplying by multiples of tens, hundreds and thousands or more:

The basic idea: If you need to multiply a number by 200, multiply by 2 first, then move the digits. You can do this with any quantity. For example, if you need to multiply something by 5000, multiply your number by 5 first, then move three decimal places.

The number of places you move is always the same as the number of zeros.

For example, multiply 25 by 5000. This seems quite hard to do in your head, but the trick is to break it down into easy calculations.

First multiply 25 by 5: 25 × 5 = 125

Then move the digits three places to the left (or the decimal point three places to the right): 125 × 1000 = 125000.

Dividing by 10, 100, 1000 and multiples

This process is exactly the same as with multiplication, but in reverse.

To divide by 10 you either

keep the decimal point where it is and move your digits one place to the right,

move your decimal point one place to the left.

For 100, you move two places. For 1000, you move three places, and so on.

785 ÷ 100 = 7.85 56 ÷ 1000 = 0.056

Remember there must always be a zero to the left of your decimal point if your answer is less than 1.0

450 ÷ 1000 = 0.450 = 0.45

You can remove any zeros to the right of the numbers after the decimal point. However, you CANNOT do this if the zeros come before the decimal point, or between the decimal point and other numbers.

Diving by multiples of tens, hundreds or thousands (or more):

The basic idea: If you need to divide by 7000, first divide by 7, then move your digits three spaces.

For example, 56 ÷ 7000: 56 ÷ 7 = 8 8 ÷ 1000 = 0.008

Is your answer what you would expect?

If you are worried you won’t remember whether you are mentally moving your digits left or right, take a look at your answer.

If you are multiplying your original number by number greater than 1, then you would expect your answer to be larger than the number you started with.

Likewise, if you are dividing by a number greater than 1, then your answer will be smaller. If it isn’t, then you know you’ve got it the wrong way round!

Adding and subtracting in your head

In the same way as you did with mental multiplication and mental division, you can learn some tricks for making mental addition and subtraction easier.

As before, these tricks don’t involve any maths wizardry, it is simply a case of breaking the problem down into smaller parts that are easier to tackle in your head.

The best way to do this is with some examples.

Splitting the subtraction into hundreds, tens and units (or more).

Calculate 352 – 13 in your head. Split this into two easier subtractions: Taking away 13 is the same as taking away 10, then taking away 3. 352 – 10 = 342 342 – 3 = 339

You can apply the same principle as illustrated in Example 1 to a harder subtraction:

Calculate 4583 – 333 in your head. First take away 300, then 30, then 3: 4583 – 300 = 4283 4283 – 30 = 4253 4253 – 3 = 4250

Dealing with awkward numbers that are close to 10:

Calculate 77 – 9 in your head. Taking away 9 is the same as taking away 10, then adding 1. 77 – 10 = 67 67 + 1 = 68

Dealing with awkward numbers that are close to 100:

Calculate 737 + 96 in your head. Adding 96 is the same as adding 100, then taking away 4. 737 + 100 = 837 837 – 4 = 833

Dealing with awkward numbers that are close to 1000 (or even bigger):

Calculate 5372 – 985 in your head.

This one looks even harder than the others, but no matter how large the numbers involved, you can still break the calculation down in to simple chunks.

Subtracting 985 is the same as subtracting 1000, then adding 15 (because 1000 – 985 = 15). You can even add the 15 in stages, by adding 10 then adding 5.

5372 – 1000 = 4372 4372 + 10 = 4382 4382 + 5 = 4387

Adding and multiplying in your head

Sometimes you might have a really tricky calculation to do in your head and it just seems impossible. However, if you look at how it can be split up using the skills you have learned in the examples above, something really tricky can become much simpler.

For example, calculate 97 × 7 in your head .

There are two ways you could tackle this one and you might find one way easier than the other:

97 is the same as (100 − 3), so you can think of the calculation as 7 × (100-3) This is the same as (7 × 100) – (7 × 3)

Now you have replaced the difficult multiplication with two simple multiplications and a subtraction:

7 × 100 = 700 7 × 3 = 21 700 – 21 = 700 – 20 – 1 = 679

Therefore 97 × 7 = 679

97 is almost 100, so you can begin by working out 7 × 100 = 700. The next step is to take account of the difference between 97 and 100, which is 3. So 7 lots of 3 is 21.

700 – 21 = 679

Applying Mental Maths Skills to Money and Percentages

As you have found out from the examples above, mental maths skills are all about breaking a problem down into numbers that are easy to deal with in your head. Sometimes we need to turn the calculation around and think of it in a different way.

Two examples of when you might need your mental maths skills are when you are dealing with money, or when you need to calculate a percentage, both of which occur often when you are out shopping.

When dealing with money, it can help to round the amount up to the nearest whole pound, then deal with the pennies separately. You often see prices marked in a way to make you think they are cheaper than they actually are. £24.99 for example, is only one penny away from £25, but the seller wants you to think that it’s nearer £24. When you are doing mental maths calculations, £25 is a lot easier to deal with than £24.99.

A useful mental maths hack for percentages is to remember that they are reversible, so 16% of 25 is the same as 25% of 16. Invariably, one of those will be much easier to work out in your head… try it!

Mental arithmetic can seem quite scary, but with practice, you can use these mental maths hacks to break a difficult problem down into smaller chunks that are easier to think about. There is no wizardry involved, it is just a matter of seeing the problem in a different way.

Further Reading from Skills You Need

Fundamentals of Numeracy Part of The Skills You Need Guide to Numeracy

This eBook provides worked examples and easy-to-understand explanations to show you how to use basic mathematical operations and start to manipulate numbers. It also includes real-world examples to make clear how these concepts are useful in real life.

Whether you want to brush up on your basics, or help your children with their learning, this is the book for you.

Continue to: Multiplication Division

See also: BODMAS Decimals Estimation

What is mental math?

What is mental math, and how can we use it to solve the problems in front of us? Let’s take a look!

Author Christina Levandowski

Expert Reviewer Jill Padfield

Published: September 5, 2023

• Key takeaways

Mental calculation is important – While it’s important to learn how to show your work on paper, doing math in your head (or mental math) is a helpful, lifelong skill. 

Practice makes perfect – Don’t be afraid to start your practice with “training wheels” — and don’t be afraid to make mistakes! Use paper, your fingers, and other tools to help nail down concepts before practicing mental math. 

Don’t make it complicated – There are multiple ways to get to the right answer. The “best way” is what is most intuitive for your child. Don’t make the learning process complicated or stressful!

Table of contents

• What is mental math
• Basic strategies for mental math
• Mental math at home
• Tools for mental math

Mental math is a huge part of one’s daily life. In fact, we often find ourselves doing it subconsciously or automatically! 

Many parents and caregivers often wonder how to teach their children mental math skills — and we’re here to show you that with the right techniques, it doesn’t have to be difficult. 

Read on to discover what mental math is, strategies to master core skills (such as calculations), and methods you can use to encourage an attitude of lifelong learning in your child.

Mental math refers to the steps and techniques we use in our daily lives to solve both basic and advanced math problems in our head., From calculating sale prices to balancing our checkbooks, mental math calculations help us make “number sense” of our environment — and the mental processes we use are often much easier than the paper methods we’re taught in the classroom.

Why is mental math so important?​

This form of math helps kids and adults navigate everyday math challenges! Mental math often helps us get faster, more accurate answers, and the techniques used to master a mental math skill can help us improve our ability to reason. 

Basic strategies for successful mental calculations

Everyone’s journey to mastering mental math starts differently. For example: Many might start by focusing instead on fact fluency, mental math exercises (like learning the concepts that go into solving square roots or cube roots), or more complex calculations. 

The concept of mental math usually comes into a child’s life in primary school (or elementary school), and often looks like memorization. Think about the addition facts, multiplication tables, and other basic functions you still remember from childhood; these were all taught to you to help you with mental math later in life. Teachers can inspire this journey for students using games, songs, and other strategies to reinforce the concepts. 

Here are a few common mental math tricks and steps for you to consider as your child begins their learning journey! 

Using multiples of 10​

Basic arithmetical calculations (like using multiples of 10) are part of a core group of skills essential to every learner. 

Using multiples of 10 can help with rounding, pricing, budgeting and more — and they can also help a student learn their multiplication facts. 

Many teachers use cards to teach these math facts, or they might use song or rhythmic beats,  giving students something to remember when it’s time to use the multiplication facts on a test or in real life. 

To do this mental math, simply add 10 to whatever 10s-based multiplication table you’re working with. For example: 

10 x 2 = 20

10 x 3 = 30

10 x 4 = 40

We see that each ascending multiple of 10 is the multiple itself with a 0 at the end. This confirms that 10 x 5 = 50, 10 x 6 = 60 and so on.

Subtracting large numbers

Subtracting larger sums can be difficult for some learners. However, mental math can make this process much easier. 

We can use the power of mental math in two different ways: visualization and estimation. 

Using visualization, we can “see” lines separating each column of a subtraction problem in our mind’s eye. For many, this might look something like the problem below: 

– | 2 | 3 

—————-

We can then solve it as we normally would on paper.

The second method uses estimation. This option relies on logic and a solid grasp on which numbers are “near” other numbers.

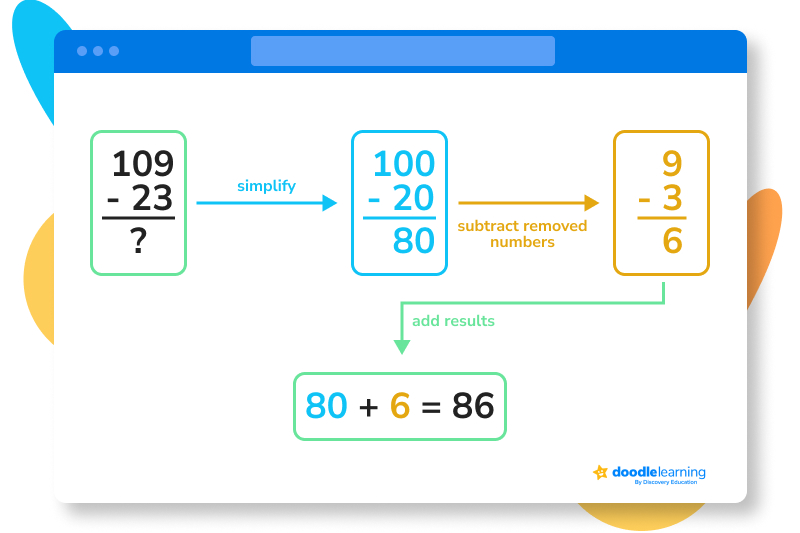
We can simplify 109 – 23 in seconds using mental math concepts. Instead of seeing 109 – 23, we can use estimation instead with an easier subtraction problem: such as 100 – 20. 

We know that 100 – 20 = 80. We then subtract 3 from 9, adding the difference to the total answer. This gives us 86. 

You can check your work on paper as you practice — and you’ll see that 109 – 23 does, indeed, equal 86.

Quick trick for multiplying by 5

Multiplying by fives can be helpful for those looking to master telling the time, estimation, and more. It can be done simply using mental math techniques. 

Before we begin, we have to understand a simple rule: Your answers, when counting by 5s, will only ever end in 0 or 5. Using this rule, you can easily determine if you are skip counting correctly (or not!) 

Knowing this, you can then prompt your child to begin multiplying and memorizing the tables. You’ll both find that: 

5 x 2 = 10 

5 x 3 = 15 

…and so on. 

You can then check their work simply, adding “5” to whatever number you leave off with (so long as it ends in 5 or 0). 

You can also have them begin learning this skill on their hands, counting by fives to the next correct integer (i.e., counting five to ten).

Addition by rounding up or down

Addition by rounding works similarly as subtraction by estimation does — as shown above! 

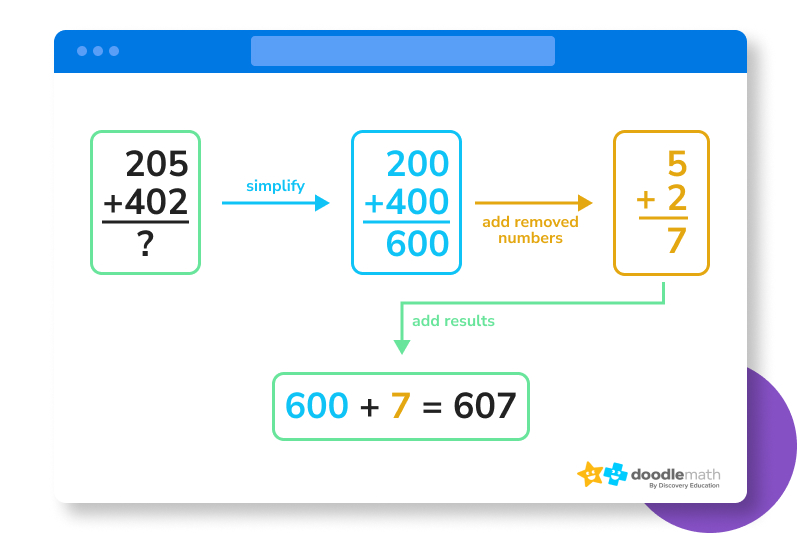
Mental math and estimation skills can be especially helpful if you’re working to add larger numbers. For example: 

While we can solve this using paper, it can be easier, faster, and more convenient to do it in our heads. Using estimation, we can rewrite the equation above as: 200 + 400 — which gives us a sum of 600. 

We can then add 5 + 2 (which equals 7), adding 7 to our total sum of 600. 

This gives us 607. 

We can check our work using paper methods, confirming that 402 + 205 does equal 607. 

Way to encourage mental math at home and in the classroom

Mental math might not be an intuitive skill for some learners — and that’s completely okay! Every student learns at their own pace and in their own ways. However, there are some tips and tricks you can use with your learner to help them take interest in developing these skills, no matter what confidence level they’re operating at. 

Reduce the use of calculators​

Calculators can become a crutch if they’re used too often. While it’s true your learner will eventually have a calculator in their pocket (i.e. their cellphones), it’s not something they should rely on. 

Your student will also be exposed to mathematical concepts and “problems” in their everyday life — such as budgeting, pricing, and estimation) — where a calculator may not be available. Mastering these skills now can give your student the confidence they need to thrive, no matter what situation they might find themselves in. 

The solution to calculator dependency is simple: remove the calculator from the learning experience. 

As you do this, you can offer your student a range of learning strategies and methods to help get them started as they build mental math skills. After your student begins to take interest and master the concepts, you can begin to reintroduce the tool for more complicated computations. 

Use it out in the real world​

A possible barrier to mastering mental math could be determining how and when to use it. You can address this by “striking first,” being purposeful about finding opportunities for mental math when you’re out and about. 

Certain scenarios where mental math might be used/could be talked about include: 

• Counting up 
• Estimating grocery store totals 

Do it with them/model it​

Some students may hesitate to learn mental math due to a fear of failure. Parents and caregivers can address this by jumping into the “deep end” and digging in with the student. 

Modeling can be an ideal way to learn mental math, speaking to a student’s learning style while addressing any fears or insecurities they might have. It also allows the parent, caregiver, or teacher to step in and ensure that the student is getting the right answer(s) as a result of the process they’re using.

Start basic and work from there

It can be easy to dive right in and overwhelm the student with too many advanced concepts. Mental math skills give students the opportunity to go back and master the fundamentals, truly solidifying their mathematical skill and understanding. Don’t be afraid to start (extra) simple, using it as a jumping-off point for future learning. 

Tools to help with mental math

Ready to start your mental math journey?

Here are some tools to consider based on your student’s unique needs: 

• DoodleMath: Our math app offers an engaging, adaptive learning experience tailored to individual needs, helping students sharpen their mental math skills through fun exercises and interactive challenges. With its gamified approach and diverse question formats, it makes mastering mental math both enjoyable and effective.
• Physical math toys, games, and learning supplies: Items created by Lakeshore or similar companies can give students a way to learn on their own terms, in a way that’s the most natural — through play.

Sign up for the DoodleMath app today!

Turn math into an adventure when you sign up for DoodleMath.

Click here to get started for free!

FAQs about mental math

We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!

Practice makes perfect when it comes to improving mental math skills. Some effective ways to enhance mental math abilities include practicing simple arithmetic operations (addition, subtraction, multiplication, and division) daily, memorizing key mathematical facts and tables, breaking down complex problems into smaller, more manageable parts, using visualization techniques, and participating in mental math games or exercises. 

Yes, mental math can be highly beneficial for students of all ages! It not only helps them develop a quicker and more accurate approach to solving math problems, but it also improves their overall math comprehension and confidence. 

Mental math can be especially helpful during exams or timed assessments when a calculator may not be allowed. Furthermore, students who excel in mental math often find it easier to grasp advanced mathematical concepts, and perform better in higher-level math courses.

Yes, there are several online resources available to practice mental math skills. Many websites and mobile applications offer interactive mental math games, quizzes, and exercises suitable for learners of all ages and levels. 

Some popular platforms include Math Playground, Math Games, Khan Academy, and MentalUP. These resources often provide real-time feedback and progress tracking, making it easier for users to measure their improvement over time. Simply search for “online mental math practice” or “mental math games” to find a wide range of options to suit your needs.

Related Posts

How to Make Math Fun

15 Math Tricks for Kids

Math Strategies for Kids

Lesson credits

Christina Levandowski

Christina has written for hundreds of clients from small businesses to Indeed.com. She has extensive experience working with marketing strategy and social media marketing, and has her own business creating assets for clients in the space. She enjoys being an entrepreneur and has also started pursuing investment opportunities as time permits.

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

What we offer

Quick links

All rights reserved. 

Are you a parent, teacher or student?

Get started for free!

Maths information pack

We ask for your contact info so we can send our info pack directly to your inbox for your convenience, exam prep information pack, case studies information pack.

Book a chat with our team

I’m new to Doodle

My school is already using Doodle

Information pack

We ask for your contact info so that our education consultants can get in touch with you and let you know a bit more about doodle., student login, which programme would you like to use.

DoodleMaths

DoodleTables

DoodleEnglish

DoodleSpell

If you’d like to use Doodle’s browser version, please visit this page on a desktop.

To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:

Mental Math Practice

This is a page where you can practice your mental math skills to your heart's desire (for free!)

What problems should I select to solve?

When engaging with our tool, you're encouraged to tackle math problems that you find most challenging or want to improve upon. Whether it's basic operations like addition and subtraction, or more complex calculations involving multiplication and division, the choice is yours. Tailoring your practice to areas where you feel less confident not only enhances your skills but also builds confidence in your abilities. Explore a variety of arithmetic problems to discover which ones you'd like to master or need more help with.

Why is mental math considered an essential skill to develop?

Math is more than just a school subject; it's a critical life skill that aids in daily decision-making and problem-solving. Whether you're calculating change, comparing prices, budgeting for expenses, or estimating time, the ability to quickly perform calculations in your head is invaluable. In the business world, mental arithmetic can help you analyze data, manage finances, and make strategic decisions swiftly. By improving your mental math skills, you're not just learning numbers; you're enhancing your ability to think critically and make informed decisions in everyday life and professional settings.

How often should I practice to improve my skills?

The amount of math practice needed to enhance your arithmetic skills varies depending on your goals and current proficiency. The key is consistent practicing and striving for continuous improvement. Whether you engage in mental math practices daily or at a pace that fits your schedule, it's essential to keep challenging yourself and to recognize progress, no matter how small. If you find yourself hitting a plateau or seeking more structured guidance, our lessons page offers additional resources and drills to further develop your skills. Remember, the journey to improvement is personal, and continuing to see progress is what truly matters!

Is there a fact or principle that makes math practice easier?

Indeed, math practice becomes more manageable when you understand the underlying principles and strategies that simplify calculations. Our lessons page is a treasure trove of such techniques, designed to strengthen your number sense and enhance your ability to solve math exercises more efficiently. From reinforcing basic facts to developing shortcuts for complex calculations, these principles (and each subsequent drill) are fundamental to becoming proficient. By familiarizing yourself with these strategies through our lessons, you'll find that approaching and solving mental math exercises becomes easier and more intuitive.

• Prodigy Math
• Prodigy English
• Is a Premium Membership Worth It?
• Promote a Growth Mindset
• Help Your Child Who's Struggling with Math
• Parent's Guide to Prodigy
• Assessments
• Math Curriculum Coverage
• English Curriculum Coverage
• Game Portal

12 Mental Math Practices to Improve the Skills of Students of All Ages

Written by Marcus Guido

Did you know?

Prodigy Math is a standards-aligned game that makes math practice fun and engaging!

• Teaching Strategies
• Introduce mnemonic devices
• Read math books
• Provide relevant word problems
• Play estimation games in class
• Play fact fluency games in class
• Encourage the use of math apps and websites
• Round up when multiplying by 9
• Double and halve
• Cover-copy-compare
• Use the Taped-Problem approach
• Building blocks
• Number talks

Mental math isn’t explicitly part of most curricula, but students who can’t answer relatively-simple equations in their heads with speed or automaticity will likely struggle with harder content.

But before answering the question, “How can I improve my mental math?”, it’s helpful to know the definition(s) of mental math.

The Manitoba Association of Mathematics Teachers defines mental math as:

A combination of cognitive strategies that enhances flexible thinking and number sense. It is calculating mentally without the use of external memory aids. It improves computational fluency by developing efficiency, accuracy, and flexibility.

Or, from students’ perspectives, it’s:

• Math done in your head
• Math that is done in the mind, quickly and efficiently
• Warming up your head with math
• To do math instantly, without the effort put into operations and processes
• Math that you understand so well that you don’t need to write anything down to do calculations/find the answer

Prince Edward Island’s Department of Education believes “mental mathematics must be a consistent part of instruction in computation from primary through the elementary and middle grades.”

Wayne Watts, educator and author of numerous math textbooks, once said: “Number sense cannot be taught. It can only be developed.”

The science behind it is convincing, too.

Research-backed benefits of mental math

Credit: Jinx!

For example, an oft-cited study of a 1st grade class found that students who quickly recall addition facts had more cognitive resources to learn other skills and concepts.

In the journal Cogent Education , researchers ran another study with 118 students in 5th grade exploring how mental computation and mathematical reasoning affect each other.

The evidence was fascinating:

[There] is a significant positive correlation between mental computation and mathematical reasoning. It is noteworthy that rather than exposing students to familiar classical problems, students need to be enabled to deal with exceptional/non-routine problems, and especially young children should be encouraged to do mental computing in order for developing both skills.

Duke researchers published a study in Clinical Psychological Science about mental math -- from a health perspective.

After brain-scanning 186 undergraduates, results suggested engaging the brain’s prefrontal cortex during mental math exercises is linked to better emotional health.

Thankfully, you’re already helping students build core mental math skills when you teach rounding, estimating and fact fluency -- developing number sense, as well as how they remember and reproduce steps and solutions.

It's mental math practice time!

To improve how your students build and practice these mental math skills, try the 12 strategies below. Use the ones that best work for you.

1. Introduce mnemonic devices

Students who struggle with basic fact fluency can improve by using mnemonic devices -- cues such as rhymes and acronyms to help recall information.

In her master’s thesis, Teaching Through Mnemonics in Elementary School Classrooms , Arianne Waite-McGough found teachers understand the positive impact this device can have on students within and “beyond the classroom walls.”

Current research shows that singing, moving and overall enjoyment of a subject enhances the learning process and long term recall of material. All of these requirements are present when using mnemonics in the classroom. My research proved similar findings. All of the teachers that I surveyed noted higher levels of learning, engagement and fun while singing songs based on the core content material.

Take this mnemonic device for a multiplication fact as an example: I need to be 16 years old to drive a 4x4 pickup truck.

Because they must be easy to remember, it helps if the cues involve:

• Tangible objects or scenarios
• Quick stories that distill larger chunks of information

Although you can think of mnemonic devices yourself and share them with students, it’s beneficial if you run an activity that gets them to make their own.

They’ll likely find it easier to remember mnemonic devices they create. 

2. Read math books

There are many math books that effectively contextualize the processes behind solving equations, helping students commit them to memory.

Depending on student age, consider:

• Each Orange Had 8 Slices  --  This book focuses on counting and addition, presenting problems in easy-to-process sentences. It sets a new scene, complete with questions, with each turn of the page.
• The Grapes of Math  --  Containing basic multiplication problems, this book is a series of illustrated riddles. Each riddle offers clues and secrets to solving a specific equation, helping students improve reading comprehension along with math skills.
• Sir Cumference  --  Set in medieval times, this book series focuses on measurement and geometry. With occasional help from his son and wife, Radius and Lady Di of Amater, the knight Sir Cumference must solve math-related challenges that pose threats to his family and kingdom.
• Secrets of Mental Math  --  As opposed to a children’s book, this guide promises to “have you thinking like a math genius in no time” with the help of “mathemagician” Arthur Benjamin. Since it’s 200+ pages long, you might find more success in selecting key excerpts and reading -- and applying -- the mental math tricks with your students. There’s also a foreword by Bill Nye the Science Guy!

As you read books out loud, your students can practice their mental math. Alternatively, you may use books as a way to leverage the benefits of peer teaching .

Just pause after identifying an equation, giving them time to work through the problems in their heads. After they share their responses, read on to discover the answer.

3. Provide relevant word problems

Many students will be more receptive to math drills and practice if the material is engaging.

David Kember, a professor in curriculum methods and pedagogy, and his team published an article in Active Learning in Higher Education about the motivators of student learning.

Upon interviewing 36 undergraduate students, Kember concluded:

Teaching abstract theory alone was demotivating.  Relevance could be established through: showing how theory can be applied in practice, establishing relevance to local cases, relating material to everyday applications, or finding applications in current newsworthy issues.

In other words, if students don’t find your math lesson relevant, their motivation to learn will greatly diminish.

A straightforward, yet effective, way of enlivening content is by creating math word problems . This is because you can tailor questions to students.

For example, you can:

• Reference Student Interests --  By framing your word problems with student interests, you should grab attention. If most of your class loves baseball, a measurement problem could involve the throwing distance of a famous outfielder. Using cross-cultural and cross-curricular connections with help strengthen students’ neural loops.
• Make Questions Topical --  Word problems based on current events or issues can engage students by providing clear, tangible ways to apply knowledge. Not only will students find your lessons more interesting, they’ll believe it’s worth knowing.
• Include Student Names --  Naming a question’s characters after your students is an easy way make it relatable, motivating your class to tackle the problem.

By capturing interest, student motivation should increase when practicing skills important for mental math.

Note : If they struggle with world problems, teach the mnemonic, “ STAR ”:

S earch the word problem  T ranslate the words into an equation  A nswer the problem  R eview the solution

4. Play estimation games in class

Estimation games are fun math activities that encourage students to develop skills and techniques they can use to simplify equations in their heads.

Easy to run but challenging to play, a popular estimation game in many classrooms involves only two dice and a sheet of paper that’s divided into two columns. One column lists the values on each dice face, whereas the other contains numbers of your choosing.

For example:

To play, pair students together. Taking turns rolling the dice, they must add the corresponding numbers together in their heads. For example, if a student rolls five and six, the equation is 878 + 777. Without pencil, paper or calculator, the student must solve the equation. If he or she is within a range of five numbers -- verifying the solution with a calculator -- the answer is considered correct.

The first student to answer five questions right wins.

For more advanced classes, you can simplify the numbers but require multiplication instead of addition.

5. Play fact fluency games in class

A fun alternative to flashcards, fact fluency games allow students to build recall and reproduction skills important for mental math.

Engaging options for 1st to 8th grade classes include:

• Math Facts Bingo --  Create bingo cards that contain answers to different equations. Then, hand them out to students. Instead of calling numbers, state equations such as 8 x 7. After determining the product is 56, they can check off the number if it’s on their cards.
• Stand Up, Sit Down --  Pick a number and share it with students. Then, read equations out loud. Sitting in a circle, students must stand if the answer matches the number you picked. If they incorrectly stand or remain seated, eliminate them until one student remains.
• 101 and Out --  As the name implies, the goal is to score as close to 101 points as possible without going over. Start by dividing your class into groups, giving each a die along with paper and a pencil. Groups take turns rolling the die, deciding if it’s best to count the number at face value or multiply it by 10. After each roll, the number is added to the group’s total. The game ends when a group hits 101 points or goes over -- whichever comes first.

As skill-building as they are engaging, your students’ improvement in fact fluency should be clear after playing a few rounds of these math games .

6. Encourage the use of math apps and websites

An alternative or supplement to drills and worksheets, consider using a digital program that features a range of problems aligned with different skills.

Such math apps and websites prompt students to continuously answer questions in an often-engaging environment, building a range of skills important for mental math.

Popular options include:

• Prodigy Math  --  Aligned with math curriculum from across the English-speaking world, Prodigy automatically differentiates content and gives adaptive feedback tailored to each student. Teachers like you can also make in-game assignments to deliver custom content.
• NRICH  --  An ongoing project by the University of Cambridge, this website features math games, articles and problems. It divides resources by United Kingdom key stages and United States grade levels, allowing your students to easily access the right content.
• Math Is Fun  --  This website contains content suitable for younger students, using concise sentences and cartoon characters. On top of exercises that cover essential math skills, there are games and puzzles.

Because all students need is a computer or mobile device to use these programs, it’s likely some will voluntarily practice at home.

Free educational content, aligned to your curriculum

Make mental math practice fun with our safe, standards-aligned math adventure!

7. Round up when multiplying by 9

There are simple ways to alter difficult equations, making them easier to solve with mental math.

Students can use existing rounding and fact fluency skills when multiplying by 9, 99, 999 and any number that follows this pattern.

First, tell students to round up the 9 to 10. Second, after solving the new equation, teach them to subtract the number they just multiplied by 10 from the answer.

For example, 67 x 9 will lead to the same answer as 67 x 10 - 67. Following the order of operations will give a result of 603. Similarly, 67 x 99 is the same as 67 x 100 - 67.

Despite more steps, altering the equation this way is usually faster and allows students complete it in their heads.

8. Double and halve

When mastering multiplication beyond basics, students can quickly use mental math skills to multiply two integers when one is an even number.

They just need to halve the even number and double the other number. They stop this process when the even integer cannot be halved, or when the equation becomes manageable.

Using 33 x 48 as an example, here’s the process:

The only prerequisite to this mental math trick is understanding the 2-times table.

9. Cover-copy-compare

Normally used as an intervention tactic, Cover-Copy-Compare can have a place in most fact fluency lessons.

There are three steps to this mental math practice, which are:

• Creating a Math Fact Sheet --  Divide a sheet into two columns, writing about 10 math facts pertaining the same skill in the left column. Include number-sentences and answers. In the right column, write “Responses.” Distribute copies of the sheet to students.
• Running the Exercise --  The goal for students is to study the math facts in the left column, correctly reproducing them in the “Responses” column. To do so, give them time to study the facts. After, they fold the paper to cover the left column while writing -- from memory -- the first fact in the “Responses” column. If correct, the student can move onto the next fact. If incorrect, the student tries again until he or she has properly reproduced the math fact.
• Recording Mastered Skills --  Once a student has completed a certain number of sheets related to a common skill, you can award him or her a badge that denotes skill mastery. This  gamification strategy  can make the exercise more engaging.

To go beyond basic fact fluency, you can make sheets that focus on rounding, memorizing steps to complex equations and more.

10. Use the Taped-Problem approach

A useful  active learning strategy , the taped-problem approach is one of the most effective ways for students to build fact fluency, indicates a 2004 study that pioneered the strategy.

First, obtain or make an audio recording of basic math problems that has short pauses between stating the problem and revealing the answer. Second, provide each student with a pencil and paper.

As you play the recording, students must write out each equation and try to solve it before the answer is revealed. If the student cannot solve the question, he or she writes down the correct answer. If the student reaches an incorrect answer, he or she crosses it out and writes the right response.

You can lengthen the pauses so students don’t depend on hearing the answers, whereas you can shorten them to encourage automaticity.

11. Building blocks

Wondering how to improve mental math speed across your class? Familiarize students with building blocks such as multiplication tables or fractions, decimal, and percent equivalents.

The more your students become familiar how multiplication tables or equivalents look, the quicker they’ll be able to recognize and solve problems in and outside the classroom.

A study in the Journal of Neuro science titled, “Why mental arithmetic counts: Brain activation during single digit arithmetic predicts high school math scores”, tested 33 high school students on their ability to solve addition and subtraction equations.

All of them performed well, which correlated to their math PSAT scores. Interestingly, as neurobiologist Dr. Susan Barry outlined :

Those students with higher math PSAT scores engaged parts of the brain, the left supramarginal gyrus and bilateral anterior cingulate cortex, which have been associated with arithmetic fact retrieval. In contrast, those students with lower math PSAT scores engaged the right intraparietal sulcus, a region involved with processing numerical quantity. In completing the test in the scanner then,  students with the higher math PSAT scores relied more on their memory of arithmetic facts .

12. Number talks

Ruth Parker, the CEO of the Mathematics Education Collaborative, and Kathy Richardson, one of the nation’s leading educators of elementary mathematics, developed this mental math practice.

To start, pose an abstract math problem. Take 18 x 5 as an example problem and ask your students to try and solve it in their heads.

Naturally, in a class of 20+ students, you’ll likely find they answered correctly -- but differently.

Number talks are a perfect way to illustrate that there’s creativity in math. They’re also a great way to begin your math lesson or encourage parents to do with their kids!

In the article “Fluency Without Fear: Research Evidence on the Best Ways to Learn Math Facts”, professor of mathematics education and co-founder of Stanford University’s you cubed , Jo Boaler, writes :

Research tells us that the best mathematics classrooms are those in which students learn number facts and number sense through engaging activities that focus on mathematical understanding rather than rote memorization.

So, we trust these activities will help your students’ mental math practice this school year and beyond.

Ready to share these mental math secrets?

Okay, they’re not really secrets. But u

sing these mental math practices should help your students build rounding, estimating and fact fluency skills -- allowing them to solve many equations with ease and automaticity, preparing them to tackle tougher content.

Armed with increased confidence, you may notice an uptick in student engagement and motivation.

These benefits, in and of themselves, make a strong case for practicing mental math.

Create or log in to your teacher account on Prodigy Math , the online math platform designed to help students build mental math skills through an engaging game-based learning environment.

Reset password New user? Sign up

Existing user? Log in

Mental Math Tricks

Already have an account? Log in here.

Recommended Course

Algebra through puzzles.

Supercharge your algebraic intuition and problem solving skills!

• Aareyan Manzoor
• Andrew Ellinor
• Mahindra Jain
• A Former Brilliant Member
• Pranshu Gaba
• Xuming Liang
• Nihar Mahajan
• Ashish Menon
• Kartik Kulkarni
• Manojkumar P
• Prajwal Kavad
• Christopher Williams
• Rishik Jain
• Zachary Salls
• Sravanth C.
• Raakin Kabir

Mental math tricks are a collection of techniques, some based on algebraic manipulation and some on visualization, that aid in large arithmetic computations. They are useful for increasing the speed at which one can do these computations, but they also serve as a useful verification mechanism to help reduce computational errors (as results reached by multiple methods are less likely to be in error).

Addition and Subtraction Tricks

Multiplication and division tricks, dividing by numbers ending in 9, product of numbers close to 100, fractions and decimals tricks, squaring numbers, finding the next square, estimating square roots, calculating integer roots, miscellaneous tricks.

For the most part, the key to addition/subtraction tricks is as follows:

The order of additions is irrelevant, so a given sum can be rearranged in any desired way.

The usual application of this is to hunt for numbers in the sum that add up to a multiple of 10, as those are easy to visualize and work with.

Determine the value of \[3 + 8 + 6 + 2 + 17 + 3 + 5 + 1 + 2 + 4.\] The addition can certainly be carried out directly without too much trouble, but this process is relatively tedious and susceptible to error. A cleaner method is to rearrange the terms: \[\begin{align*} \color{blue}{3} + \color{red}{8}+\color{green}{6}+\color{red}{2}+\color{blue}{17}+\color{skyblue}{3}+\color{skyblue}{5}+1+\color{skyblue}{2}+\color{green}{4} &=\color{blue}{3}+\color{blue}{17}+\color{red}{8}+\color{red}{2}+\color{green}{6}+\color{green}{4}+\color{skyblue}{3}+\color{skyblue}{5}+\color{skyblue}{2}+1 \\ &=20 + 10 + 10 + 10 + 1 \\ &=51. \ _\square \end{align*}\]

Take number 1000 and then add 20 to it. Now add 1000 one more time. Now add 30. Now add 1000 one more time. Now add 40. Now add 1000 one more time. Now add 10.

Determine the value of

\[ 1+9+18+3+5+2+17+15+2+8.\]

• Mental Math Tricks wiki
• Check out the set.

Given the number 100, you are tasked to do the following:

• First, add 7 to the number
• Second, add 10 to the number
• Third, add 6 to the number
• Fourth, add 10 to the number
• Fifth, add 14 to the number
• Sixth, add 10 to the number
• Lastly, add 13 to the number

What is the result?

Another technique is useful in finding the sum of series following some pattern, usually arithmetic progressions or geometric progressions . The general technique is to manipulate the sum into another, related sum, and use the two together to cancel terms and/or achieve the desired repetition. Here is an example:

Gauss's teacher has asked him to add up all the integers between 1 and 100, inclusive. What is this sum? The key realization is to rearrange the terms to pair up the numbers: \[\begin{align} S &= 1 + 2 + 3 + \cdots + 98 + 99 + 100\\ &= (1 + 100) + (2 + 99) + (3 + 98) + \cdots + (50 + 51)\\ &= 101 \times 50 \\ &= 5050. \ _\square \end{align}\]

This technique works well when there is an even number of terms. When there is an odd number of terms, the technique is essentially the same, but with a slightly more clever implementation:

Now Gauss's teacher has asked him to add up all the integers between 1 and 101, inclusive. What is this sum? The "pairing up the terms" intuition can be formalized: \[\begin{align} S = &1 + 2 + 3 + \cdots + 99 + 100 + 101\\ = &101 + 100 + 99 + \cdots + 3 + 2 + 1\\\\ 2S = &(1 + 101) + (2 + 100) + \cdots + (50 + 52) \\&+ (51 + 51) + (52 + 50) \cdots + (100 + 2) + (101 + 1) \\ = &102 \times 101\\\\ \Rightarrow S =&51 \cdot 101 \\ =& 5151.\ _\square \end{align}\]

This leads to the general result:

An \(n\)-term arithmetic series with first term \(A\) and last term \(B\) has sum \[\frac{n(A+B)}{2}.\ _\square\]

What is \( \displaystyle\sum _{ n=0 }^{ 2000 }{ n }?\)

A geometric series can be dealt with in a similar way. Here is an example:

Gauss's teacher has now asked him to find the sum of the first 10 non-negative powers of 2. What is this sum? Similar to before, compute \[\begin{align} S &= 2^0 + 2^1 + \cdots + 2^9\\ 2S &= 2^1 + 2^2 + \cdots + 2^{10}\\\\ \Rightarrow S &= 2S - S \\ &= 2^{10}-2^{0} \\ &= 1023, \end{align}\] where the general strategy is to multiply by the common ratio and then subtract. \(_\square\)

An \(n\)-term geometric series with first term \(a\) and common ratio \(r\) has sum \[a \cdot \frac{r^n-1}{r-1}.\ _\square\]

Consider a geometric progression with common ratio \(4.\) If the sum of the first \(5\) terms is \(1023,\) what is the initial term?

Firstly, it is important to note that multiplying and dividing by powers of 10 is quite easy, as multiplication and division by \(10^n\) is equivalent to moving the decimal point \(n\) steps to the right (in the case of multiplication) or left (in the case of division).

What is \(1024.276 \times 10^{5}?\) The decimal is moved 5 steps to the right, so the result is 102427600. \(_\square\)

As in addition,

The order of multiplications is irrelevant, so a given sum can be rearranged in any desired way.

The usual application of this is to hunt for numbers in the product that multiply to a power of 10, as those are easy to visualize and work with (as shown above).

Compute the value of \[2 \cdot 3 \cdot 5 \cdot 3 \cdot 2 \cdot 3 \cdot 5.\] The addition can certainly be carried out directly without too much trouble, but this process is relatively tedious and susceptible to error. A cleaner method is to rearrange the terms: \[\begin{align*} \color{red}{2} \cdot \color{green}{3} \cdot \color{red}{5} \cdot \color{green}{3} \cdot \color{blue}{2} \cdot \color{green}{3} \cdot \color{blue}{5} &=\color{red}{2}\cdot \color{red}{5}\cdot \color{blue}{2}\cdot \color{blue}{5} \cdot \color{green}{3} \cdot \color{green}{3} \cdot \color{green}{3} \\ &= 10 \cdot 10 \cdot 27 \\ &= 2700. \ _\square \end{align*}\]

Basic multiplication can also be done visually using multiplication by lines :

There are also various time-saving tricks available in special cases, as the following sections show.

Dividing by integers ending in 9, i.e. 19, 29, 39, etc., can be easily done with the help of geometric series. The general approach is shown by the below example:

What is the value of \(\frac{6}{19}\) to five decimal places? Firstly, take the numerator, in this case \(6\). Divide the numerator by \(2\) and write the result as \( \color{red}{n} \text{ remainder r}\), in this case \(\color{red}{n}=3\) and \(r=0\). Now divide \((10r+\color{red}{n})\) by \(2\). Write the result below your first calculation, expressing the result in the same format. Repeat these steps until the required accuracy is achieved (if you need 5 decimal places, do 5+1=6 lines of working): \[\begin{align}&&\dfrac{6}{2} \quad \, \, &=& \color{red}{3} \text{ remainder 0} \\ \\ \dfrac{10(0)+3}{2} \quad &=& \dfrac{3}{2} \quad \, \, &=& \color{red}{1} \text{ remainder 1} \\ \\ \dfrac{10(1)+1}{2} \quad &=& \dfrac{11}{2} \quad &=& \color{red}{5} \text{ remainder 1} \\ \\ \dfrac{10(1)+5}{2} \quad &=& \dfrac{15}{2} \quad &=& \color{red}{7} \text{ remainder 1} \\ \\ \dfrac{10(1)+7}{2} \quad &=& \dfrac{17}{2} \quad &=& \color{red}{8} \text{ remainder 1} \\ \\ \dfrac{10(1)+8}{2} \quad &=& \dfrac{18}{2} \quad &=& \color{red}{9} \text{ remainder 0} &. \end{align} \] Here's where the magic happens. List the values of \(\color{red}{n}\) for each line, and this is the decimal expansion of \(\frac{6}{19}\). Therefore we can say \(\frac{6}{19}=0. \color{red}{315789}= \color{green}{\boxed{0.31579 \, \text{(5 d.p.)}}}\). \(_\square\)

Dividing by larger numbers, such as 29, 39, etc., can be done in a similar method: to divide by \(10n+9\), divide by \(n+1\) (rather than 2) at each step in the above process. It is also worth noting that this trick demonstrates that the resulting decimal expansion is periodic .

Unsurprisingly, this trick doesn't simply work by magic; there is a much deeper reason why it holds:

Consider the following: \[\dfrac{x}{19}=\dfrac{x}{20-1}=\dfrac{\frac{x}{20}} {1-\frac1{20}}.\] By the geometric sum , we can write this as \[\begin{align} \dfrac{\frac{x}{20}}{1-\frac1{20}} &=\left(\dfrac{x}{20}\right)\left(1+\dfrac{1}{20}+\dfrac{1}{20^2}+\cdots\right)\\ &=\dfrac{\hspace{3mm} \frac{x}{2^1}\hspace{3mm} }{10^1}+\dfrac{\hspace{3mm} \frac{x}{2^2}\hspace{3mm} }{10^2}+\dfrac{\hspace{3mm} \frac{x}{2^3}\hspace{3mm} }{10^3}+\cdots. \end{align}\] We see two consecutive terms satisfy \[\dfrac{\hspace{3mm} \frac{x}{2^n}\hspace{3mm} }{10^n}+\dfrac{\hspace{3mm} \frac{x}{2^{n+1}}\hspace{3mm} }{10^{n+1}}=\dfrac{\hspace{3mm} \frac{x}{2^n}\hspace{3mm} }{10^n}+\dfrac{\hspace{3mm} \frac{\hspace{3mm} \frac{x}{2^n}\hspace{3mm} }2\hspace{3mm} }{10^{n+1}},\] which means the next digit will be the previous divided by 2 and, in case of remainder, we will take common denominator with the next term which has \( {10}^{n+2} \), so we multiply the remainder by 10. \(_\square\)

What is the value of \(\frac{41}{29}\) to 5 decimal places?

Hint: Read the Mental Math Tricks wiki.

When two numbers are sufficiently close to 100, their product can be easily calculated "component-wise." In other words, multiplying out the product \((100-a)(100-b)\) results in terms too far apart to affect one another, so they give the digits of the product. More formally,

Let \(a,b\) be integers such that \(a,b<100\). The result of \((100-a)(100-b)\) is formed as follows: the first two digits are \(100-(a+b)\), and the last two digits are the product of \(a\) and \(b\).

This is better demonstrated by examples:

What is \(94 \times 98?\) We have 2 numbers, 98 and 94. Now, to calculate this rather hard-looking product, we use a trick. First, find the difference between this and 100: \(100-94=6\) and \(100-98=2\). Now notice that \(94-2=98-6=92.\) (This will always be true for any number choice.) Our Last 2 digits are \(6\times 2=12\) and the first two are \(92\), so the answer is \(94 \times 98=9212\). \(_\square\)

What is \(97 \times 94?\) We have 2 numbers, 97 and 94. Now, to calculate this rather hard looking product, we use a trick. First, find the difference between this and 100: \(100-94=6\) and \(100-97=3\). Now notice that \(94-3=97-6=91\). Our Last 2 digits are \(6\times 3=18\) and the first two are \(91\), so the answer is \(94 \times 97=9118\). \(_\square\)

Without using a calculator, compute this:

\[ 91 \times \ 98. \]

This problem is part of the set Near 100 multiplication .

If you are interested in the proof, check this below:

Assumption : When saying the integer is close to 100, in this example, it means the integers from 91 to 99, so their product will always be 4 digits. Let both \(a\) and \(b\) be some integers from 1 to 9, then we have \[\begin{align} (100-a)(100-b) &= 10000-100(a+b)+ab\\\\ &=\underbrace{100\big(100-(a+b)\big)}_{\text{first two digits due to multiplication by 100}}+\underbrace{ab}_{\text{last two digits}}.\ _\square \end{align}\]

Turning recurring decimals into fractions

If \[0.12341234\ldots=\dfrac{a}{b}\] with \(a\) and \(b\) being coprime positive integers, find \(a\) and \(b.\) We need the number before the decimal: \(0\) the number before recurrence starts and after the decimal point: \(1234\) the length of that number: \(4.\) Then we have \[0.12341234\ldots=0+\dfrac{1234}{10^{4}-1}=\dfrac{1234}{9999}.\] So, \(a=1234\) and \(b=9999\). \(_\square\)

True or False?

\[0.9999 \ldots = 1\]

\(\) Note: The "\(\ldots\)" indicates that there are infinitely many 9's.

If a number can be written as \(0.aaaaa\ldots\) with a length of \(n,\) then it can be written as \[\sum_{k=1}^\infty \dfrac{a}{10^{kn}}.\] Using the infinite geometric progression sum, this is \[\dfrac{a}{10^n-1}.\ _\square\]

Numbers that end in 5:

What is \({75}^{2}?\) In order to square a number ending in 5, take the digits before the 5 (in this case it's 7, but let's call it \(\color{red}{X}\) so we can generalize the rule). The square number is equal to \(100\color{red}{X}(\color{red}{X}+1) + 25\). In other words, you take \(\color{red}{X}\), multiply it by \(\color{red}({X}+1)\) and write \(25\) at the end of that number. Using the rule we just read, we can write \(75^2\) as \(100 \times 7 \times 8 + 25 = \color{green}{\boxed{5625}}\). \(_\square\)

As always, there's no magic involved here; some algebraic expansion shows why this result is generally true:

Let the number we are trying to square be an \((n+1)\)-digit number of the form \(\overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { X }_{ n }5 }. \) Then our goal is to prove that \[{ \left( \overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { X }_{ n }5 } \right) }^{ 2 }=100\left( \overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { X }_{ n } } \right) \left( \overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { { X }_{ n } } } +1 \right) +25,\] where \({ X }_{ 1 },{ X }_{ 2 },{ X }_{ 3 },\dots ,{ X }_{ n }\) represent digits. Let \(\overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { X }_{ n } }=n\). Then we have \[\begin{align} {\left( \overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { X }_{ n }5 } \right) }^{ 2 } &={(10n+5)}^{2}\\ &=100n(n+1)+25 \\ &= 100\left( \overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { X }_{ n } } \right) \left( \overline { { X }_{ 1 }{ X }_{ 2 }{ X }_{ 3 }\dots { { X }_{ n } } } +1 \right) +25, \end{align}\] which is the required result and completes the proof. \(_\square\)

Compute \(165^2\).

\[\] Squaring numbers up to 25:

When \(n\) is this small, the following procedure returns \(n^2\):

• Add the units digit of \(n\) to itself \((\)e.g. if \(n=13\), the result here is \(13+3=16).\)
• Multiply by 10 \((\)e.g. if \(n=13\), the result here is \(10 \cdot 16 = 160)\) or 20, depending on the tens digit of the number.
• Add the square of the units digit \((\)e.g. if \(n=13\), the result here is \(160 + 3^2 = 169).\)

Indeed, 169 is equal to \(13^2\).

Find \(\ 24^2.\) We follow the procedure above: Add the units digit to the number: \(24+4=28.\) Multiply it by 20: \(28\times 20=560.\) Add the square of the units digit to the number: \(560+4^2=576. \ _\square\)

We have \[\begin{align} n^2 &=10\big(n+(n-10)\big)+(n-10)^2\\ &=20n-100+n^2-20n+100\\ &=n^2\\ \\ n^2&=20\big(n+(n-20)\big)+(n-20)^2\\ &=40n-400+n^2-40n+400\\ &=n^2. \ _\square \end{align}\]

\[\] Squaring numbers between 25 and 75:

For these numbers, a slightly different procedure can be followed:

• Find the difference between the number and 25 and multiply it by 100.
• Find the difference between the number and 50 and square it, using the procedure from the last section (squaring numbers below 25) if necessary.
• Add the two numbers.

Find \({39}^{2}.\) We follow the above procedure: Find the difference between 25 and the number and multiply by 100: \((39-25)\times 100=1400.\) Find the difference between the number and 50 and square it: \((50-39)^2=11^2=121.\) Add all these: \(1400+121=1521=39^2.\ _\square\)

We have \[n^2=100(n-25)+(n-50)^2=100n-2500+n^2-100n+2500=n^2.\ _\square\]

\[\] Squaring numbers between 75 and 125:

Finally, these numbers can be squared according to the following procedure:

• Find the difference between the number and 100
• Subtract this result from the original number and multiply by 100
• Square the result from step 1, using the section on squaring numbers below 25 if necessary.
• Add the results from steps 2 and 3.

Find \({109}^{2}.\) We follow the procedure below to obtain Find the difference with 100: \(100-109=-9.\) Subtract this from the original number and multiply by 100: \(100\times\big(109-(-9)\big)=11800.\) Square step 1: \((-9)^2=81.\) Add step 2 and 3: \(109^2=11800+81=11881. \ _\square\)

We have \[n^2=100\big(n-(100-n)\big)+(100-n)^2=200n-10000+n^2-200n+10000=n^2.\ _\square\]

To find \( (n + 1 ) ^{2} \) when \( n^{2} \) is known, the identity

\[ (n + 1)^{2} = n^2+2n+1 = n^{2} + n + (n + 1 ) \]

is incredibly useful.

For example, if \( 85 ^{2} = 7225\), what is \( 86 ^{2}?\) We have

\[\begin{align} 86 ^{2} &= 85^{2} + 85 + 86 \\ \phantom{86^{2}}&= 7225 + 85 + 86 \\ \phantom{86^{2}} &= 7396. \end{align}\]

This is especially useful, for instance, in calculating squares of numbers that don't end in 5: since numbers ending in 5 can be easily squared (see the previous section), it may be easier to square a multiple of 5 near the desired number, and then continually find the next square until the desired result is reached.

It is given that \(572^2=327184\). What is the value of \(574^2?\)

Estimating square roots is useful for a variety of reasons, especially in geometry where approximating lengths (which often involves square roots by virtue of the Pythagorean theorem ) is useful. One general procedure gives a fairly good approximation (certainly good enough for "by hand" use):

• Find the closest square to the number being rooted, \(n\).
• Divide \(n\) by the square root of the closest square.
• Take the average of the result and the square root of the closest square.

Find an approximation for \(\sqrt{\color{red}{123}}\). We follow the above procedure: Take the closest square: \(121.\) Divide \(\color{red}{123}\) by the square root of the closest square: \[\dfrac{123}{11}=11+\dfrac{2}{11}=11.1818.\] Use the repeating decimals into fractions trick backwards! Take the average of the answer above and the square root of the closest square: \[\dfrac{(11+11.1818)}{2}=11.0909=\color{green}{11.091}.\] We now have a good estimate for \(\sqrt{123}\). \(_\square\) Note: \(\sqrt{123}=11.090536506\ldots=\color{green}{11.091},\) so we achieved an accuracy of 3 decimal places!

To 2 decimal places, approximate

\[\sqrt { 3+\sqrt { 3+\sqrt { 3+\sqrt { 3+\cdots} } } }.\]

This problem is part of the set Hard Equations.

Square Roots:

A. The trick to working with square roots is to know what range the square root is in. Since squaring numbers ending in 0 and squaring numbers ending in 5 are both easy, the answer can be calculated within a range of 5 relatively easily.

B. If the number is known to be a perfect square, then the ending digit can be determined by looking at the last digit of the number. More specifically, if the number ends in a

• 0, then the ending digit is a 0;
• 1, then the ending digit is 1 or 9;
• 4, then the ending digit is 2 or 8;
• 5, then the ending digit is a 5;
• 6, then the ending digit is 4 or 6;
• 9, then the ending digit is 3 or 7.

C. After finding the last digit (or possibility between two digits), mentally chop off the last two digits and focus on the remaining digits.

D. Now, try to find a range of 5 that the number (in step C) is in. Once you do this, you know the answer using step B. First, find a range of 10, then find out if the answer is in the upper half of the range (i.e. it ends in 5, 6, 7, 8, or 9) or if the answer is in the lower half of the range (i.e. it ends in 0, 1, 2, 3, or 4) by squaring the middle number (the number in the range that ends in 5).

\[\] Cube Roots:

Each units digit of a perfect cube is the same as the units digit of the number being cubed, (except for 2, 3, 7, and 8 which end in 8, 7, 3, and 2, respectively). Using this schema, you can quickly identify the units digit of the cube root given. Then, examine the block of numbers to the left of the hundreds digit. Identify the largest perfect cube that is smaller than this block and take its cube root. Take the result and place the units digit found earlier on the end to get the result.

Quickly compute \(\sqrt[3]{226981}\). The last digit is 1. Therefore, \(\sqrt[3]{226981}\) ends in 1. The block of digits to the left of the hundreds place is 226. The largest perfect cube smaller than 226 is 216, which is 6 cubed. Therefore, \(\sqrt[3]{226981}\) begins with 6. We conclude that \(\sqrt[3]{226981} = 61. \ _\square\)

Quickly compute \(\sqrt[3]{148877}\). Here, 7 is in the last digit, which means \(\sqrt[3]{148877}\) ends in a 3. The block of digits on the left form 148. Since 125 is the largest perfect cube smaller than 148, the leading digit is 5. Therefore, \(\sqrt[3]{148877} = 53. \ _\square\)

Add square numbers of a particular form:

Adding square numbers of the form \((10a + b)^2+ \big[10(b-1) + (10-a)\big]^2 = 101\big(a^2+ b^2\big):\)

A. This method is simple once we reduce to this form:

\[(10a + b)^2+ \big[10(b-1) + (10-a)\big]^2 = 101\big(a^2+ b^2\big).\]

B. Using numbers instead of variables, we get the following:

• Square the ones digit on the left number.
• Square the tens digit on the left number.
• Add up the results of step 1 and step 2.
• Multiply the result of step 3 by 101 for the answer. See multiplying by 101.

C. This method is sometimes hard to recognize. If the inside numbers subtract to 1 and the outside numbers add to 10, then you can use this method.

For example,

\[97^2+61^2=101(9^2+7^2)=13130.\]

Master concepts like these

Learn more in our Algebra through Puzzles course, built by experts for you.

Problem Loading...

Note Loading...

Set Loading...

• Search Menu
• Sign in through your institution
• Browse content in Arts and Humanities
• Browse content in Archaeology
• Anglo-Saxon and Medieval Archaeology
• Archaeological Methodology and Techniques
• Archaeology by Region
• Archaeology of Religion
• Archaeology of Trade and Exchange
• Biblical Archaeology
• Contemporary and Public Archaeology
• Environmental Archaeology
• Historical Archaeology
• History and Theory of Archaeology
• Industrial Archaeology
• Landscape Archaeology
• Mortuary Archaeology
• Prehistoric Archaeology
• Underwater Archaeology
• Zooarchaeology
• Browse content in Architecture
• Architectural Structure and Design
• History of Architecture
• Residential and Domestic Buildings
• Theory of Architecture
• Browse content in Art
• Art Subjects and Themes
• History of Art
• Industrial and Commercial Art
• Theory of Art
• Biographical Studies
• Byzantine Studies
• Browse content in Classical Studies
• Classical History
• Classical Philosophy
• Classical Mythology
• Classical Literature
• Classical Reception
• Classical Art and Architecture
• Classical Oratory and Rhetoric
• Greek and Roman Epigraphy
• Greek and Roman Law
• Greek and Roman Archaeology
• Greek and Roman Papyrology
• Late Antiquity
• Religion in the Ancient World
• Digital Humanities
• Browse content in History
• Colonialism and Imperialism
• Diplomatic History
• Environmental History
• Genealogy, Heraldry, Names, and Honours
• Genocide and Ethnic Cleansing
• Historical Geography
• History by Period
• History of Agriculture
• History of Education
• History of Emotions
• History of Gender and Sexuality
• Industrial History
• Intellectual History
• International History
• Labour History
• Legal and Constitutional History
• Local and Family History
• Maritime History
• Military History
• National Liberation and Post-Colonialism
• Oral History
• Political History
• Public History
• Regional and National History
• Revolutions and Rebellions
• Slavery and Abolition of Slavery
• Social and Cultural History
• Theory, Methods, and Historiography
• Urban History
• World History
• Browse content in Language Teaching and Learning
• Language Learning (Specific Skills)
• Language Teaching Theory and Methods
• Browse content in Linguistics
• Applied Linguistics
• Cognitive Linguistics
• Computational Linguistics
• Forensic Linguistics
• Grammar, Syntax and Morphology
• Historical and Diachronic Linguistics
• History of English
• Language Acquisition
• Language Variation
• Language Families
• Language Evolution
• Language Reference
• Lexicography
• Linguistic Theories
• Linguistic Typology
• Linguistic Anthropology
• Phonetics and Phonology
• Psycholinguistics
• Sociolinguistics
• Translation and Interpretation
• Writing Systems
• Browse content in Literature
• Bibliography
• Children's Literature Studies
• Literary Studies (Asian)
• Literary Studies (European)
• Literary Studies (Eco-criticism)
• Literary Studies (Modernism)
• Literary Studies (Romanticism)
• Literary Studies (American)
• Literary Studies - World
• Literary Studies (1500 to 1800)
• Literary Studies (19th Century)
• Literary Studies (20th Century onwards)
• Literary Studies (African American Literature)
• Literary Studies (British and Irish)
• Literary Studies (Early and Medieval)
• Literary Studies (Fiction, Novelists, and Prose Writers)
• Literary Studies (Gender Studies)
• Literary Studies (Graphic Novels)
• Literary Studies (History of the Book)
• Literary Studies (Plays and Playwrights)
• Literary Studies (Poetry and Poets)
• Literary Studies (Postcolonial Literature)
• Literary Studies (Queer Studies)
• Literary Studies (Science Fiction)
• Literary Studies (Travel Literature)
• Literary Studies (War Literature)
• Literary Studies (Women's Writing)
• Literary Theory and Cultural Studies
• Mythology and Folklore
• Shakespeare Studies and Criticism
• Browse content in Media Studies
• Browse content in Music
• Applied Music
• Dance and Music
• Ethics in Music
• Ethnomusicology
• Gender and Sexuality in Music
• Medicine and Music
• Music Cultures
• Music and Religion
• Music and Culture
• Music and Media
• Music Education and Pedagogy
• Music Theory and Analysis
• Musical Scores, Lyrics, and Libretti
• Musical Structures, Styles, and Techniques
• Musicology and Music History
• Performance Practice and Studies
• Race and Ethnicity in Music
• Sound Studies
• Browse content in Performing Arts
• Browse content in Philosophy
• Aesthetics and Philosophy of Art
• Epistemology
• Feminist Philosophy
• History of Western Philosophy
• Metaphysics
• Moral Philosophy
• Non-Western Philosophy
• Philosophy of Science
• Philosophy of Action
• Philosophy of Law
• Philosophy of Religion
• Philosophy of Language
• Philosophy of Mind
• Philosophy of Perception
• Philosophy of Mathematics and Logic
• Practical Ethics
• Social and Political Philosophy
• Browse content in Religion
• Biblical Studies
• Christianity
• East Asian Religions
• History of Religion
• Judaism and Jewish Studies
• Qumran Studies
• Religion and Education
• Religion and Health
• Religion and Politics
• Religion and Science
• Religion and Law
• Religion and Art, Literature, and Music
• Religious Studies
• Browse content in Society and Culture
• Cookery, Food, and Drink
• Cultural Studies
• Customs and Traditions
• Ethical Issues and Debates
• Hobbies, Games, Arts and Crafts
• Natural world, Country Life, and Pets
• Popular Beliefs and Controversial Knowledge
• Sports and Outdoor Recreation
• Technology and Society
• Travel and Holiday
• Visual Culture
• Browse content in Law
• Arbitration
• Browse content in Company and Commercial Law
• Commercial Law
• Company Law
• Browse content in Comparative Law
• Systems of Law
• Competition Law
• Browse content in Constitutional and Administrative Law
• Government Powers
• Judicial Review
• Local Government Law
• Military and Defence Law
• Parliamentary and Legislative Practice
• Construction Law
• Contract Law
• Browse content in Criminal Law
• Criminal Procedure
• Criminal Evidence Law
• Sentencing and Punishment
• Employment and Labour Law
• Environment and Energy Law
• Browse content in Financial Law
• Banking Law
• Insolvency Law
• History of Law
• Human Rights and Immigration
• Intellectual Property Law
• Browse content in International Law
• Private International Law and Conflict of Laws
• Public International Law
• IT and Communications Law
• Jurisprudence and Philosophy of Law
• Law and Politics
• Law and Society
• Browse content in Legal System and Practice
• Courts and Procedure
• Legal Skills and Practice
• Primary Sources of Law
• Regulation of Legal Profession
• Medical and Healthcare Law
• Browse content in Policing
• Criminal Investigation and Detection
• Police and Security Services
• Police Procedure and Law
• Police Regional Planning
• Browse content in Property Law
• Personal Property Law
• Study and Revision
• Terrorism and National Security Law
• Browse content in Trusts Law
• Wills and Probate or Succession
• Browse content in Medicine and Health
• Browse content in Allied Health Professions
• Arts Therapies
• Clinical Science
• Dietetics and Nutrition
• Occupational Therapy
• Operating Department Practice
• Physiotherapy
• Radiography
• Speech and Language Therapy
• Browse content in Anaesthetics
• General Anaesthesia
• Neuroanaesthesia
• Browse content in Clinical Medicine
• Acute Medicine
• Cardiovascular Medicine
• Clinical Genetics
• Clinical Pharmacology and Therapeutics
• Dermatology
• Endocrinology and Diabetes
• Gastroenterology
• Genito-urinary Medicine
• Geriatric Medicine
• Infectious Diseases
• Medical Oncology
• Medical Toxicology
• Pain Medicine
• Palliative Medicine
• Rehabilitation Medicine
• Respiratory Medicine and Pulmonology
• Rheumatology
• Sleep Medicine
• Sports and Exercise Medicine
• Clinical Neuroscience
• Community Medical Services
• Critical Care
• Emergency Medicine
• Forensic Medicine
• Haematology
• History of Medicine
• Browse content in Medical Dentistry
• Oral and Maxillofacial Surgery
• Paediatric Dentistry
• Restorative Dentistry and Orthodontics
• Surgical Dentistry
• Medical Ethics
• Browse content in Medical Skills
• Clinical Skills
• Communication Skills
• Nursing Skills
• Surgical Skills
• Medical Statistics and Methodology
• Browse content in Neurology
• Clinical Neurophysiology
• Neuropathology
• Nursing Studies
• Browse content in Obstetrics and Gynaecology
• Gynaecology
• Occupational Medicine
• Ophthalmology
• Otolaryngology (ENT)
• Browse content in Paediatrics
• Neonatology
• Browse content in Pathology
• Chemical Pathology
• Clinical Cytogenetics and Molecular Genetics
• Histopathology
• Medical Microbiology and Virology
• Patient Education and Information
• Browse content in Pharmacology
• Psychopharmacology
• Browse content in Popular Health
• Caring for Others
• Complementary and Alternative Medicine
• Self-help and Personal Development
• Browse content in Preclinical Medicine
• Cell Biology
• Molecular Biology and Genetics
• Reproduction, Growth and Development
• Primary Care
• Professional Development in Medicine
• Browse content in Psychiatry
• Addiction Medicine
• Child and Adolescent Psychiatry
• Forensic Psychiatry
• Learning Disabilities
• Old Age Psychiatry
• Psychotherapy
• Browse content in Public Health and Epidemiology
• Epidemiology
• Public Health
• Browse content in Radiology
• Clinical Radiology
• Interventional Radiology
• Nuclear Medicine
• Radiation Oncology
• Reproductive Medicine
• Browse content in Surgery
• Cardiothoracic Surgery
• Gastro-intestinal and Colorectal Surgery
• General Surgery
• Neurosurgery
• Paediatric Surgery
• Peri-operative Care
• Plastic and Reconstructive Surgery
• Surgical Oncology
• Transplant Surgery
• Trauma and Orthopaedic Surgery
• Vascular Surgery
• Browse content in Science and Mathematics
• Browse content in Biological Sciences
• Aquatic Biology
• Biochemistry
• Bioinformatics and Computational Biology
• Developmental Biology
• Ecology and Conservation
• Evolutionary Biology
• Genetics and Genomics
• Microbiology
• Molecular and Cell Biology
• Natural History
• Plant Sciences and Forestry
• Research Methods in Life Sciences
• Structural Biology
• Systems Biology
• Zoology and Animal Sciences
• Browse content in Chemistry
• Analytical Chemistry
• Computational Chemistry
• Crystallography
• Environmental Chemistry
• Industrial Chemistry
• Inorganic Chemistry
• Materials Chemistry
• Medicinal Chemistry
• Mineralogy and Gems
• Organic Chemistry
• Physical Chemistry
• Polymer Chemistry
• Study and Communication Skills in Chemistry
• Theoretical Chemistry
• Browse content in Computer Science
• Artificial Intelligence
• Computer Architecture and Logic Design
• Game Studies
• Human-Computer Interaction
• Mathematical Theory of Computation
• Programming Languages
• Software Engineering
• Systems Analysis and Design
• Virtual Reality
• Browse content in Computing
• Business Applications
• Computer Security
• Computer Games
• Computer Networking and Communications
• Digital Lifestyle
• Graphical and Digital Media Applications
• Operating Systems
• Browse content in Earth Sciences and Geography
• Atmospheric Sciences
• Environmental Geography
• Geology and the Lithosphere
• Maps and Map-making
• Meteorology and Climatology
• Oceanography and Hydrology
• Palaeontology
• Physical Geography and Topography
• Regional Geography
• Soil Science
• Urban Geography
• Browse content in Engineering and Technology
• Agriculture and Farming
• Biological Engineering
• Civil Engineering, Surveying, and Building
• Electronics and Communications Engineering
• Energy Technology
• Engineering (General)
• Environmental Science, Engineering, and Technology
• History of Engineering and Technology
• Mechanical Engineering and Materials
• Technology of Industrial Chemistry
• Transport Technology and Trades
• Browse content in Environmental Science
• Applied Ecology (Environmental Science)
• Conservation of the Environment (Environmental Science)
• Environmental Sustainability
• Environmentalist Thought and Ideology (Environmental Science)
• Management of Land and Natural Resources (Environmental Science)
• Natural Disasters (Environmental Science)
• Nuclear Issues (Environmental Science)
• Pollution and Threats to the Environment (Environmental Science)
• Social Impact of Environmental Issues (Environmental Science)
• History of Science and Technology
• Browse content in Materials Science
• Ceramics and Glasses
• Composite Materials
• Metals, Alloying, and Corrosion
• Nanotechnology
• Browse content in Mathematics
• Applied Mathematics
• Biomathematics and Statistics
• History of Mathematics
• Mathematical Education
• Mathematical Finance
• Mathematical Analysis
• Numerical and Computational Mathematics
• Probability and Statistics
• Pure Mathematics
• Browse content in Neuroscience
• Cognition and Behavioural Neuroscience
• Development of the Nervous System
• Disorders of the Nervous System
• History of Neuroscience
• Invertebrate Neurobiology
• Molecular and Cellular Systems
• Neuroendocrinology and Autonomic Nervous System
• Neuroscientific Techniques
• Sensory and Motor Systems
• Browse content in Physics
• Astronomy and Astrophysics
• Atomic, Molecular, and Optical Physics
• Biological and Medical Physics
• Classical Mechanics
• Computational Physics
• Condensed Matter Physics
• Electromagnetism, Optics, and Acoustics
• History of Physics
• Mathematical and Statistical Physics
• Measurement Science
• Nuclear Physics
• Particles and Fields
• Plasma Physics
• Quantum Physics
• Relativity and Gravitation
• Semiconductor and Mesoscopic Physics
• Browse content in Psychology
• Affective Sciences
• Clinical Psychology
• Cognitive Neuroscience
• Cognitive Psychology
• Criminal and Forensic Psychology
• Developmental Psychology
• Educational Psychology
• Evolutionary Psychology
• Health Psychology
• History and Systems in Psychology
• Music Psychology
• Neuropsychology
• Organizational Psychology
• Psychological Assessment and Testing
• Psychology of Human-Technology Interaction
• Psychology Professional Development and Training
• Research Methods in Psychology
• Social Psychology
• Browse content in Social Sciences
• Browse content in Anthropology
• Anthropology of Religion
• Human Evolution
• Medical Anthropology
• Physical Anthropology
• Regional Anthropology
• Social and Cultural Anthropology
• Theory and Practice of Anthropology
• Browse content in Business and Management
• Business Strategy
• Business History
• Business Ethics
• Business and Government
• Business and Technology
• Business and the Environment
• Comparative Management
• Corporate Governance
• Corporate Social Responsibility
• Entrepreneurship
• Health Management
• Human Resource Management
• Industrial and Employment Relations
• Industry Studies
• Information and Communication Technologies
• International Business
• Knowledge Management
• Management and Management Techniques
• Operations Management
• Organizational Theory and Behaviour
• Pensions and Pension Management
• Public and Nonprofit Management
• Strategic Management
• Supply Chain Management
• Browse content in Criminology and Criminal Justice
• Criminal Justice
• Criminology
• Forms of Crime
• International and Comparative Criminology
• Youth Violence and Juvenile Justice
• Development Studies
• Browse content in Economics
• Agricultural, Environmental, and Natural Resource Economics
• Asian Economics
• Behavioural Finance
• Behavioural Economics and Neuroeconomics
• Econometrics and Mathematical Economics
• Economic Systems
• Economic Methodology
• Economic History
• Economic Development and Growth
• Financial Markets
• Financial Institutions and Services
• General Economics and Teaching
• Health, Education, and Welfare
• History of Economic Thought
• International Economics
• Labour and Demographic Economics
• Law and Economics
• Macroeconomics and Monetary Economics
• Microeconomics
• Public Economics
• Urban, Rural, and Regional Economics
• Welfare Economics
• Browse content in Education
• Adult Education and Continuous Learning
• Care and Counselling of Students
• Early Childhood and Elementary Education
• Educational Equipment and Technology
• Educational Strategies and Policy
• Higher and Further Education
• Organization and Management of Education
• Philosophy and Theory of Education
• Schools Studies
• Secondary Education
• Teaching of a Specific Subject
• Teaching of Specific Groups and Special Educational Needs
• Teaching Skills and Techniques
• Browse content in Environment
• Applied Ecology (Social Science)
• Climate Change
• Conservation of the Environment (Social Science)
• Environmentalist Thought and Ideology (Social Science)
• Natural Disasters (Environment)
• Social Impact of Environmental Issues (Social Science)
• Browse content in Human Geography
• Cultural Geography
• Economic Geography
• Political Geography
• Browse content in Interdisciplinary Studies
• Communication Studies
• Museums, Libraries, and Information Sciences
• Browse content in Politics
• African Politics
• Asian Politics
• Chinese Politics
• Comparative Politics
• Conflict Politics
• Elections and Electoral Studies
• Environmental Politics
• European Union
• Foreign Policy
• Gender and Politics
• Human Rights and Politics
• Indian Politics
• International Relations
• International Organization (Politics)
• International Political Economy
• Irish Politics
• Latin American Politics
• Middle Eastern Politics
• Political Methodology
• Political Communication
• Political Philosophy
• Political Sociology
• Political Theory
• Political Behaviour
• Political Economy
• Political Institutions
• Politics and Law
• Politics of Development
• Public Administration
• Public Policy
• Quantitative Political Methodology
• Regional Political Studies
• Russian Politics
• Security Studies
• State and Local Government
• UK Politics
• US Politics
• Browse content in Regional and Area Studies
• African Studies
• Asian Studies
• East Asian Studies
• Japanese Studies
• Latin American Studies
• Middle Eastern Studies
• Native American Studies
• Scottish Studies
• Browse content in Research and Information
• Research Methods
• Browse content in Social Work
• Addictions and Substance Misuse
• Adoption and Fostering
• Care of the Elderly
• Child and Adolescent Social Work
• Couple and Family Social Work
• Direct Practice and Clinical Social Work
• Emergency Services
• Human Behaviour and the Social Environment
• International and Global Issues in Social Work
• Mental and Behavioural Health
• Social Justice and Human Rights
• Social Policy and Advocacy
• Social Work and Crime and Justice
• Social Work Macro Practice
• Social Work Practice Settings
• Social Work Research and Evidence-based Practice
• Welfare and Benefit Systems
• Browse content in Sociology
• Childhood Studies
• Community Development
• Comparative and Historical Sociology
• Economic Sociology
• Gender and Sexuality
• Gerontology and Ageing
• Health, Illness, and Medicine
• Marriage and the Family
• Migration Studies
• Occupations, Professions, and Work
• Organizations
• Population and Demography
• Race and Ethnicity
• Social Theory
• Social Movements and Social Change
• Social Research and Statistics
• Social Stratification, Inequality, and Mobility
• Sociology of Religion
• Sociology of Education
• Sport and Leisure
• Urban and Rural Studies
• Browse content in Warfare and Defence
• Defence Strategy, Planning, and Research
• Land Forces and Warfare
• Military Administration
• Military Life and Institutions
• Naval Forces and Warfare
• Other Warfare and Defence Issues
• Peace Studies and Conflict Resolution
• Weapons and Equipment

• < Previous chapter
• Next chapter >

9 Arithmetic Word Problem Solving and Mental Representations

Catherine Thevenot, University of Geneva

Pierre Barrouillet, University of Geneva

• Published: 04 August 2014
• Cite Icon Cite
• Permissions Icon Permissions

Arithmetic word problem solving is considered as a testing ground of mathematical achievement, but remains the area of mathematics in which students experience the greatest difficulties. In this chapter, we review recent theoretical and empirical work that could shed light on these difficulties. We first describe the most frequently used classifications of word problems and assess their psychological relevance. Then, we present the main hypotheses concerning the nature of the representations involved in word problems. Some theories assume that problem solving relies on the instantiation of schemas abstracted from recurrently encountered problems of the same relational structure, whereas other theories propose that ad hoc transient mental representations are constructed for each problem encountered. A third part is devoted to the impact of individual differences in calculation, reading comprehension, and more general factors, such as working memory capacity. Finally, we address the issue of enhancing performance in word problem solving.

Introduction

Arithmetic word problems, also called verbal or story problems, are verbal descriptions of numerically quantified situations involving one or several explicit questions. It is tacitly assumed that the answer to these questions must correspond to a numerical value that has to be reached after one or a series of arithmetic operations has been carried out. Arithmetic word problems are of particular importance because they are often considered and used as a privileged pedagogical situation in which students are expected to show their understanding and mastery of previously learned mathematical procedures and concepts. In some sense, world problem solving is seen as the testing ground of mathematical achievement. However, as testified by several international surveys (see for example Fayol, Barrouillet, & Camos, 1997 ), this school exercise remains the area of mathematics in which students experience the greatest difficulties, word problem solving lagging far behind others domains such as the mastery of computational algorithms. In this chapter, we review recent theoretical and empirical studies that have been conducted to classify the different additive and multiplicative problems that can be constructed, to describe the representations and processes involved in their solution, to identify the characteristics of the problems, as well as the individual factors that modulate performance, and to design intervention tools for enhancing performance. As we will see, these studies allow researchers to better understand the difficulties encountered by children and provide practitioners with tools to help children in overcoming them.

To anticipate, a consensus has developed among researchers that a large part of the difficulties children encounter in solving word problems arise from an underlying difficulty in understanding the situation that the text describes. Indeed, solving a word problem does not simply consist in successfully performing arithmetic calculations, but anteriorly in understanding the relational structure in which the numerical values are embedded. In this respect, we will see that the way the text is formulated and presented has a strong impact on the ease with which children and adults grasp this structure and solve the problems. It is the reason why word problems have been traditionally classified according to their semantic characteristics, and more precisely to the relational structure of the situation they refer to. According to this view, even when they require the same arithmetic operation, solving problems that refer to quantities that undergo some transformation would not involve the same cognitive processes as solving problems that refer to comparisons between unchanged quantities. In the first part of this chapter, we describe the most frequently used classifications, and we report the empirical evidence that have been gathered in order to attest for their psychological relevance. The second part of the chapter is devoted to the question of the nature of the representations involved in word problem solving. Do problem solvers progressively extract through practice schematic abstract representations that match the most frequent relational structures and then instantiate these representations with the numerical values of the problem at hand, or do they construct in working memory ad hoc transient mental representations for each word problem encountered? This is of importance because the strategies used probably depend on the nature of the representation constructed. Empirical evidence from developmental and adult studies that favor these opposite conceptions will be reviewed. Of course, performance in arithmetic word problem solving does not entirely depend on the semantic characteristics of the problems, but also on the characteristics of the problem solvers themselves. In a third part, we focus on the impact on performance of individual differences in those abilities that are directly involved in word problem solving, such as calculation and text comprehension, but also in more general cognitive resources, such as working memory capacity. Finally, we address the studies that have focused on methods for enhancing performance in word problem solving, either by making clearer the semantic aspects of the text or by providing students with more appropriate knowledge and strategies. We conclude by pointing what we consider as the main pending questions and suggesting some leads for future research.

Semantic Characteristics of Word Problems

The most famous classification of addition problems has been proposed by Riley, Greeno and Heller (1983) . It is based on the type of semantic relations described in the text. Thus, according to the authors, many problems can be classified into three semantic types: Change, Combine, and Comparison problems. Note that, as acknowledge by Riley et al. (1983) , these categories have been used by several other investigators sometimes using different names ( Nesher, 1981 ; Vergnaud, 1982 ). Change problems describe actions that cause increases or decreases in quantities and the unknown is either the resulting amount (John has 6 marbles. Tom gives him 3 more marbles. How many marbles does John have now?), the amount of the change (John had 4 marbles. Tom gave him some more marbles. Now, John has 6 marbles. How many marbles did Tom give him?), or the starting amount (John had some marbles. Tom gave him 5 marbles. Now, John has 7 marbles. How many marbles did John have at the beginning?). In contrast to such dynamic problems, Combine and Comparison problems are relative to static situations. Combine problems describe two quantities that have to be considered in combination to produce the answer. The question can be relative to the total amount (John has 2 marbles. Peter has 4 marbles. How many marbles do John and Tom have altogether?) or to the amount in one of the subsets (Joe and Tom have 8 marbles altogether. Joe has 3 marbles. How many marbles does Tom have?). Finally, in Compare problems, a Comparison is made between two quantities using the expressions ‘more than’ and ‘less than’. The unknown is either the difference between the two quantities (John has 3 marbles. Tom has 5 marbles. How many marbles does John have less than Tom?), the compared quantity (John has 3 marbles. Tom has 5 more marbles than John. How many marbles does Tom have?), or the referent (John has 3 marbles. He has 5 more marbles less than Tom. How many marbles does Tom have?).

The ecological relevance of this classification is attested by the fact that different problem types are not of equal difficulty, even when they require the same arithmetic operation for solution ( Riley et al., 1983 ). Besides, an improvement in performance for each category of problem is observed through development and education. More concretely, Change problems are easier for Grade 2 and 3 children than for kindergarteners and Grade 1 children. When the question of the problem is relative to the resulting state, problems are quite easy, even for young children. In contrast, when the question is about the starting quantity, children experience more difficulties and successful performance for this category of problems only reach a satisfactory rate in Grade 2 (75%). Similarly, Combine problems are easy for young children when the unknown is the sum of the sets but, when the unknown is one of these sets, children experience great difficulties (only 30% of successful solving in kindergarten and Grade 1). Finally, Compare problems are more difficult than Combine and Change problems.

If Riley et al.’s classification is limited to addition problems, Vergnaud (1983) conducted semantic analyses of multiplication problems. Three different forms of relations between the problem elements are described by the author. The first form (or structure) is called ‘isomorphism of measures’ and consists in direct and simple proportions between two measures or quantities (e.g. Linda wants to share her 12 cakes with her two friends. How many cakes each of the three little girls have?). The second form called ‘product of measures’ describes situations where three measures are involved and the third measure is the product of the first two, as in calculating surfaces or volumes (e.g. What is the surface of a room that is 27 feet long and 12 feet large?). The third form of relations is called ‘multiple proportions’ and corresponds to situations that are essentially similar to the isomorphism of measures structure, but in which several variables are involved (e.g. One cow produces an average of 30 liters of milk per day, each liter of milk costs $1.05. How much will the farmer earn over a 2-week period?).

Greer (1992) also proposed a classification of problems wherein a distinction is made between situations that are psychologically commutative and non-commutative. In non-commutative situations, the multiplier and the multiplicand can be distinguished. In other words, one of the quantities involved in multiplication (i.e. multiplier) is conceptualized as operating on the other (i.e. the multiplicand) to produce the result. Concerning division problems, this implies that two types of divisions can be distinguished: division by multiplier (e.g. A college passed the top 3/5 of its students in an exam. If 48 passed, how many students sat the exam?) and division by multiplicand (e.g. A college passed the top 48 out of 80 students who sat the exam. What fraction of the students passed?). In commutative situations, it is impossible to distinguish between multiplier and multiplicand and, consequently, between the two types of division.

Contrary to addition problems, the ecological validity of multiplication problem classifications has not yet been systematically investigated. This is probably due to the dissimilarities in the classification schemata used by different researchers. However, Vergnaud (1983) showed that children master scalar problems, wherein there is a number of groups or objects having the same number in each group (e.g. 3 children have 4 cookies each. How many cookies do they have altogether?) before Cartesian-product problems (e.g. In the ballroom there are 5 boys and 4 girls. If all the boys dance with all the girls, how many couples will be constituted?) or problems involving conversion of measures (e.g. A foot is 0.3 meters. How many meters are 3 feet?). Therefore, as addition problems, the difficulty of multiplication problems does not simply depend on the nature of the operation that has to be performed. The nature and the structure of the semantic situation in which the problem is embedded play a crucial role in individuals’ performance. This is due to the fact that these factors determine the structure, nature, and complexity of the mental representation that has to be constructed to reach the solution.

The Nature of The Mental Representations in Word Problem Solving

It is generally admitted that children struggle with arithmetic word problems when they experience difficulties in constructing the adequate mental representation of the situation that the text describes ( De Corte & Verschaffel, 1985 ). For instance, Change problems are relatively straightforward because they describe dynamic situations that can be easily mentally simulated. What is represented by children is a sequence of events ordered in time in a unidirectional manner ( Nesher, Greeno, & Riley, 1982 ). In contrast, Compare problems are difficult for children because they are not familiar with the expressions ‘more than’ and ‘less than’ ( De Corte & Verschaffel, 1985 ). Interestingly, if the problem ‘There are 5 birds and 3 worms. How many more birds than worms are there?’ leads to only 25% of correct responses in kindergarten children, reformulating the question into ‘How many birds won’t get a worm?’ leads to 96% of correct responses in children at the same level ( Hudson, 1983 ). Again, compared with the first version, the second version of the problem is easier to represent because the birds and the worms can be concretely or mentally matched to form a correspondence between the two sets. However, as stated above, some non-semantic factors modulate these patterns of results. The situation is more difficult to represent when the amount of change is unknown ( Ibarra & Lindvall, 1982 ) and even more when the start set is unknown ( Garcia, Jimenez, & Hess, 2006 ; Riley et al., 1983 ). The lack of knowledge of the first or intermediate quantity would severely hinder the solving process because problems cannot be represented directly by models.

Interestingly, the semantic characteristics of the problems play a role on children’s performance before and after formal instruction. Indeed, it has been shown that some preschool children can solve arithmetic word problem before any explicit instruction by using informal strategies based on their understanding of the situation described in the text of the problem ( Carpenter & Moser, 1982 ; De Corte & Verschaffel, 1987 ; Ibarra & Lindvall, 1982 ). Children who are successful in solving verbal problems have this ability to develop physical models to serve as an aid to solution ( Lindvall & Ibarra, 1980 ). Carpenter and Moser (1984) showed that the semantic characteristics of subtraction problems strongly shape the way the models are constructed. More precisely, problems such as ‘John has 8 cookies. He gives 3 cookies to his friend Leo. How many cookies does John have left?’ is likely to be solved by young children by a counting down strategy, which consists, in our example, in counting backwards three times from the starting amount of 8. This strategy perfectly models the decrease Change situation described in the problem. In contrast, a problem such as ‘Trudy has 3 cookies. How many more cookies does she have to get so that she has 8 cookies altogether?’ is likely to be solved by a counting up strategy from 3 to 8, which is derived from a model that mimics the situation of joining the missing addend. The answer to the problem is the number of counting words in the sequence. Whereas Carpenter and Moser did not find evidence for a relationship between the semantic structure of addition problems and children’s strategies, it was done by De Corte and Verschaffel (1987) . The authors showed that Change problems such as ‘Lynn has 2 cinema tickets. Her friend Sara gives her 2 more tickets. How many tickets does Lynn have now?’ is likely to be solved through an adding procedure. In this case, the child constructs a set of blocks corresponding to the first number in the problem, then adds to this set a number of blocks corresponding to the second number, and finally counts the total number of blocks. In contrast the Combine problem ‘John has 3 bottles of soda. Tom has 4 bottles. How many bottles do they have altogether’ is more likely to be solved by a joining or a no move strategy, where the child constructs two sets corresponding to the two given numbers and either counts the total number of blocks without physically moving the sets (i.e. no move strategy) or moves the sets together with both hands and finally counts the total number of blocks (i.e. joining strategy).

These studies clearly showed that the semantic of the problems determines the strategy used by young children. Nonetheless, even after instruction and practice, semantic factors still determine strategies. Indeed, it is assumed that through practice, problem schemata would be progressively abstracted from and associated with different semantic categories and would determine the procedures used by individuals to solve the problems.

Schemata and Word Problems

Riley et al. (1983) suggest that schemata have the form of semantic network structures that consist of elements and relations between those elements. For example, a Change problem schema would contain an initial quantity that represents a start set, an event that changes the start set (increase or decrease), and an unknown final quantity or result set. The empty slots in the schema are filled in progressively as soon as the relevant information is read in the text of the problem. When all the empty slots are filled in, specific expressions or propositions triggers a second type of schema (i.e. higher order schemata) that contains the procedure required to solve the problem ( Kintsch & Greeno, 1985 ). For example, in Compare problems, ‘more than’ and ‘less than’ propositions would trigger the More-than and Less-than schemata, respectively, which include a large-set, a small-set and a difference variables to be instantiated by numerical values. Both schemata also include a Difference strategy triggered by the same propositions that allows the comparisons of the two sets by the appropriate arithmetic operation of subtraction.

Arguments in favor of the use of arithmetic word problem schemata have been provided by Lewis and Mayer (1987) . These authors focused on the study of two forms of Compare problems, namely consistent and inconsistent problems. In consistent problems, the unknown variable is the subject of the second sentence that contains a relational term consistent with the necessary arithmetic operation. For example, in the consistent problem ‘John has 3 marbles. Tom has 5 more marbles than Joe. How many marbles does Tom have?’, the expression ‘has more’ is consistent with the fact that an addition is required to solve the problem. In contrast, in inconsistent problems, the unknown variable is the object of the second sentence and the relational term conflicts with the necessary arithmetic operation. In the problem ‘Joe has 3 marbles. He has 5 marbles less than Tom. How many marbles does Tom have?’ the term ‘less’ is inconsistent with the addition that has to be performed to solve the problem. According to the authors, problem solvers come to the task with a set of schemata associated to Compare problems. When the form of the given relational sentence is not consistent with the problem solver’s schema, she or he must mentally rearrange the information. The fact that inconsistent problems are more error prone and take longer to solve than consistent problems is coherent with the author’s interpretation. These findings were extended by Fuson, Carroll, and Landis (1996) who showed that the capacity to solve inconsistent problems represents the fourth level of a progression in conceptualizing and solving Compare problems in first and second graders. In a first level, children can only identify who has more or less without being able to quantify the difference. In a second level, they strongly rely on language cues and solve consistent problems (‘John has 3 marbles. Tom has 5 more marbles than Joe. How many marbles does Tom have?’) better than inconsistent problems and even problems requiring to calculate the difference (‘John has 9 marbles. Tom has 7 marbles. How many marbles does John have more than Tom?’). In a third level, children solve these two kinds of problems, but not yet the tricky inconsistent problems. This slow progression indicates how problems inducing the wrong schemata from misleading language cues are difficult to solve.

This sketchy presentation of the schemata-based approach makes clear that schemas are abstract general frames in which the quantitative elements of the problem (numerical values and relations) constitute the only relevant information needed for successful problem solving. However, the abstract nature of these representational frames makes that the schema approach encounters difficulties in accounting for content and context effects ubiquitous in word problem solving. This limitation prompted the emergence of theories that postulate the construction of representations, such as situation models or mental models, which bring to bear a rich real-word experience that makes them more appropriate to grasp semantic content and context.

Situation Model and Word Problem

Reusser (1989 ; Staub & Reusser, 1995 ) postulates the existence of an Episodic Situation Model that includes functional and temporal features of the story problem. This qualitative model would be activated by the solver before a more logico-mathematical representation of the problem corresponding to the schemas described above. Evidence for the construction of such qualitative model during the solving process has been collected through several studies. Coquin-Viennot and Moreau (2003) showed that a problem such as ‘For a prize-giving the florist prepares for each of the 14 candidates 5 roses and 7 tulips. How many flowers does the florist use in total?’ is likely to be solved by children with a distributed strategy consisting in performing (14 × 5) + (14 × 7). However, when formulated as ‘For a prize-giving, the florist prepares for each of the 14 candidates a bouquet composed of 5 roses and 7 tulips. How many flowers does the florist use in total?’ the problem is more likely to be solved with a factorized strategy, by performing 14 × (5 + 7). In the second formulation of the problem, the term ‘bouquet’ plays a structuring role in the organization of the elements contained in the mental representation constructed by children to solve the problem. This result is difficult to interpret within the schema framework, and Coquin-Viennot and Moreau concluded that less formal representations based on real-world knowledge necessarily come into play during the resolution. Similar results were obtained by Bassok, Chase, and Martin (1998) who showed that, when college students construct mathematical problems, they align the mathematical relations between arguments of arithmetic operations with the semantic relations that are evoked by the pairs of objects they are asked to include in the problems. More concretely, division involves an asymmetric mathematical relation between dividend and divisor (a/b ≠ b/a). Bassok et al.’s participants applied this asymmetric operation to object sets that readily evoked functionally asymmetric semantic relations (e.g. a apples and b baskets), but refrained from dividing object sets that did not evoke functionally asymmetric relations (e.g. a apples and b oranges). Instead, they usually related such functionally symmetric sets with the mathematically symmetric operation of addition ( a + b = b + a ).

In addition to real-world knowledge, it has also been shown that characteristics, such as the size of numbers used in the problem can affect the strategies selected by individuals. Thevenot and Oakhill (2005) presented adults with segmented problems such as ‘How many marbles does John have more than Tom and Paul altogether?/John has 49 marbles./Tom has 24 marbles./Paul has 17 marbles./(the ‘/’s represent the boundaries of the segment)’. When a segment appeared, the previous one disappeared. The strategy preferred by adults to solve the problem was to calculate: 49 – (24 + 17), whereas an alternative sequential strategy that is far less demanding could have been possible to implement, namely (49 – 24) – 17. Nevertheless, when three-digit instead or two-digit numbers were used in the text (How many marbles does John have more than Tom and Paul altogether? / John has 649 marbles./Tom has 324 marbles./ Paul has 217 marbles./’), the alternative strategy consisting in two successive subtractions was preferred by participants. Obviously, the difficulty of the task pushed individuals to construct an alternative representation to the one directly induced by the wording of the problem. Again, these results are difficult to reconcile with a pure schema-based approach in which the use of different strategies for a specific type of problem is difficult to interpret. Still, as stated above, it is not to say that schemata did not play any role in the course of the solution process, but rather that a transitional representation between the text problem and a pure mathematical mental representation comes into play.

Mental Models and Word Problems

Nevertheless, some studies might more fundamentally question the systematic resort to problem schema in children and adults. It was shown that placing the question before a story problem rather than classically presenting it at the end facilitates problem solution in children. In the seminal studies, this finding was first attributed to mobilization by problem solvers of the appropriate schema ( Devidal, Fayol, & Barrouillet, 1997 ; Fayol, Abdi, & Gombert, 1987 ). In a standard word problem, the question often contains all the information needed to describe the relations between the different elements of the text as well as specific linguistic expressions. Therefore, according to Devidal et al. (1997) , the question placed at the beginning of the text, via the specific information it contains, directly triggers the appropriate schema (e.g. the expression ‘less than’ will trigger a Comparison schema). This early activation allows the numerical data to be integrated into the schema as soon as they are encountered, and the calculations can be achieved during reading. The resulting release of working memory resources would explain the improvement in performance. However, Thevenot, Barrouillet, and Fayol (2004) confirmed the facilitatory effect of the question at the beginning, but showed that this effect is observable whether or not the calculations are achieved during reading. Consequently, the increase in the number of successful resolutions when the question is placed before, rather than after, the text cannot be attributable only to the on-line integration of the numerical data into the activated schema. The authors proposed that the aid provided by the position of the question before the text would only be due to its facilitatory effect on the construction of the representation required to solve the problem. Just like a title before a narrative text ( Rawson & Kintsch, 2002 ), the question before an arithmetic problem would facilitate the subsequent encoding and integration of the information in the representation. This interpretation is alternative to the one formulated within the Schema framework and is compatible with an approach that considers the representation as a specific and temporary mental structure constructed in working memory, such as the Situation Model approach described above ( Reusser, 1989 ) or the Mental Model theoretical framework ( Johnson-Laird, 1983 ).

This interpretation was confirmed by Thevenot, Devidal, Barrouillet, and Fayol (2007) who showed that the facilitatory effect of the question before the text was more pronounced for children with poor abilities in mathematics. These results are not compatible with the schema framework. If the facilitatory effect of the question before the text was due to the early activation of the appropriate schema, high-skilled children would be those who are more likely to benefit from this effect. Indeed, these children are more often successful in solving problems and, consequently, are more likely to have extracted schemas. As stated above, the reverse result was obtained: it were the low-skilled children who benefited more from the position of the question before the problem. While the simple fact that high-skilled children are not those who benefit more from the position of the question before the text is sufficient to rule out the Schema interpretation, the fact that the inverse result is obtained supports the Mental Model theory. We know that low-skilled children are those children who experience the highest difficulty in the construction of the Mental Model of the situation ( Cain & Oakhill, 1999 ; Oakhill, 1996 ; Oakhill, Cain, & Yuill, 1998 ; Yuill, Oakhill, & Parkin, 1989 ). Therefore, it seems natural that they are the same children who benefit more from an aid to the construction of the representation. Moreover, Thevenot et al. (2007) showed that the facilitatory effect of the question before the text was more pronounced for difficult than easier problems. Again, this result was not compatible with the Schema theory. Difficult problems, which by definition are often failed, are less likely to be associated with the appropriate schema than easier problems, which are often correctly solved. Therefore, the higher facilitatory effect for difficult problems cannot be attributable to the early activation of a problem schema.

The relative relevance of Mental Model and Schemas in the domain of story problems was also directly tested by Thevenot (2010) . In her experiment, adults were asked to solve Compare problems wherein the question took a form such as ‘How many marbles does Louis have more than Jean?’ After the solving phase, an unexpected task of problem recognition was proposed to participants. They were presented either with the original problems, with inconsistent problems that had never been solved, or with paraphrases that respected the relational structure of the original problems, but not their exact wording. These paraphrases were constructed by inverting the terms and the linguistic expressions in the original problems (our example became ‘How many marbles does Jean have less than Louis?). Inconsistent problems were constructed by keeping the same relational terms as in the original problem, but by inverting the names of the protagonists (i.e. ‘How many marbles does Jean have more than Louis’). Whereas the literal form of paraphrastic problems bore the least resemblance to original problems, paraphrastic problems were associated to higher recognition rates than inconsistent problems. These results provided strong evidence that it is the structure of the arithmetic word problem and not its exact wording or its propositional level of representation that is mentally represented by individuals engaged in a resolution task. This is perfectly coherent with the mental model theory proposed by Johnson-Laird (1983 ; see Mani & Johnson-Laird, 1982 , for a similar demonstration in the domain of spatial reasoning), and at odds with the approach postulating that the relational expression (‘have more’ in our example) plays a crucial role in triggering the appropriate schema or procedure.

These results also fit nicely with the Situation Strategy First framework proposed by Brissiaud and Sander (2010) , which posits that the initial mental representation constructed from a problem text activates a situation-based strategy even after instruction (see also Brissiaud, 1994 ). It would be only when it is not efficient for providing the solution that the representation would be modified so that the relevant arithmetic knowledge might be used. For example, the situation-based strategy for a problem such as ‘Luc is playing with 42 marbles. During the game, he loses 39 marbles. How many marbles does Luc have now?’ would consist in counting backward from 42, which is cognitively demanding. In order to gain in efficiency, children would have to ‘re-represent’ the problem in order to apply a mental arithmetic strategy consisting in counting forward from 39 to 42. In accordance with their Situation Strategy First model, the authors show that such problems are indeed more difficult for 7 – and 8-year-old children than problems where the situation-based strategy directly corresponds to the most economic strategy (i.e. ‘Luc is playing with 42 marbles. During the game he loses 3 marbles. How many marbles does Luc have now?’).

This series of works, which provides evidence that schemata do not always constitute the core of the mental representation constructed by individuals, questions assumptions relative to the source of age-related increase in performance. According to Judd and Bilsky (1989) , young children experience difficulties with word problems because they do not yet have a repertoire of highly automatized schemata for representing the different problem types. However, it seems that schemata are not always necessarily convoked to solve familiar problems. Thus, other sources of difficulties have to be considered, such as limited working memory capacities, reading and text comprehension difficulties, or insufficient mastery of number facts and calculation procedures.

Individuals’ Factors Impacting Arithmetic Word Problem Performance

We have seen that arithmetic word problem solving is a complex activity that requires a series of cognitive processes involving the comprehension of a text, the instantiation of abstract representations with current information or the construction of ad hoc mental models, as well as reasoning activities to select appropriate arithmetic operations. Once these operations have been identified, calculation of the answers often requires selection, running, and control of algorithmic procedures that necessitate retrieval of relevant arithmetic facts from long-term memory and temporary storage of intermediary results. These activities thus involve manipulation and maintenance of verbal, but also visuospatial information, as well as the selection and control of procedures. Thus, arithmetic problem solving is a complex cognitive activity that would involve all the components of working memory. Accordingly, several studies have investigated the role of working memory in word problem solving and how individual differences in working memory capacity affect performance.

Working Memory

The relationship between mathematical cognition and working memory has been extensively studied, especially in the domain of arithmetic problem solving (see DeStefano & LeFevre, 2004 ; LeFevre, DeStefano, Coleman, & Shanahan, 2005 , for reviews). In the same way, several studies have provided support for the importance of working memory (WM) in word problem solving. Most of them used the theoretical framework provided by Baddeley’s (1986) multi-component model and aimed at identifying the specific contribution of the central executive, which is considered to be primarily responsible for coordinating activity within the cognitive system, the phonological loop that assumes the storage of verbal material, and the visuospatial sketchpad devoted to the maintenance of visual and spatial information. Among these components, the phonological loop can be expected to play a crucial role in solving arithmetic problems presented through text. Accordingly, Passolunghi and Siegel (2001) showed that 9-year-old children (Grade 4) who are poor at problem solving have difficulties with digit span, which is often used as a measure of the phonological loop. Rasmussen and Bisanz (2005) further supported the notion that, for school-age children, phonological WM is what differentiates between poor and good verbal arithmetic performers. However, Passolunghi and Siegel (2001) also identified difficulties with central executive tests of WM in children who are poor at problem solving. Several other studies by Passolunghi shed light on the role of the central executive. For example, Passolunghi, Cornoldi, and De Liberto (1999) found that Grade 4 children who present difficulties in arithmetic word problem solving also present difficulties in working memory tasks that require the inhibition of irrelevant information. Passolunghi and Pazzaglia (2004) investigated the role of memory-updating, a central process needed to active the relevant information while removing no longer relevant information from WM (this capacity is, for example, assessed by asking children to recall the five smallest animals at the end of the following list of items presented successively: hare , tiger, game, type, mole, fly , fox, return, mosquito , idea, answer, and spider ). They observed that a group of fourth-graders with high memory-updating ability performed better in problem solving compared with a group of low memory-updating ability. Andersson (2007) extended these results by demonstrating that three different measures related with the central executive contributed unique variance to word problem solving in children in grades 2, 3, and 4 – the capacity to coordinate processing and storage, to shift attention from one task to another, and to access knowledge from long-term memory. This relation holds even when the influence of reading, age, and IQ were controlled. The involvement of central executive does not seem to be restricted to arithmetic word problems and several studies have found that this component of WM also contributes significant variance in predicting algebraic word problem solving in older children ( Lee, Ng, & Ng, 2009 ; Lee, Ng, Ng, & Lim, 2004 ).

Studies that have addressed the possible implication of the visuospatial sketchpad are rarer. Nonetheless, Passolunghi and Mammarella (2010) observed that fourth graders who are poor problem solvers exhibited specific difficulties in spatial WM assessed through a Corsi block and a spatial matrix tasks, but not visual working memory. It is worth noting that, in this study, the authors did not found any relation with verbal memory. A more extensive investigation has recently been conducted by Zheng, Swanson, and Marcoulides (2011) who assessed the three components of WM along with reading and mathematical achievement in a large sample of 310 children in grades 2, 3, and 4. The results indicated that the three components predicted word-problem solving performance. Interestingly, reading and calculation proficiency mediated the effect of verbal WM and central executive, whereas academic achievement did not mediate the relationship between visuospatial WM and word problem solving, a result that echoes Passolunghi and Mammarella’s (2010) observation.

In summary, there is a strong consensus that WM plays a crucial role in word problem solving and that individual differences in WM capacity underlie at least a part of individual differences in performance. Importantly, the three components of WM have been identified as having a specific impact, though reading abilities could act as a moderating factor, a point that will be addressed below. Although the studies reported here do not leave many doubts about the involvement of WM in the complex activity that word problem solving is, they have also the common characteristic of assessing correlations between abilities and capacities measured at a given moment in development. As such, they provide only indirect evidence concerning the question of the role of WM in the development of problem solving abilities. Interestingly, Swanson (2011) addressed the question of whether the development in problem solving abilities is related to growth in WM capacity. The results showed that WM performance in Grade 1 contributes approximately 26% of the variance to problem-solving accuracy in Grade 3. The significant contribution of WM to word problem-solving accuracy was maintained when measures of attention and long-term memory capacities were entered into the regression analysis. Swanson’s results also showed that Grade 1 performance on measures of naming speed (see also Kail, 2007 , for similar results) and inhibition (see Passolunghi et al., 1999 ) contribute unique variance to Grade 3 problem-solving performance. Finally, the growth curve analysis showed that growth on the executive component of WM was related to growth in word problem solving. Thus, the executive system (controlled attention) and not measures of storage (phonological loop) were related to growth in word problem solving, suggesting that this skill and its development strongly solicits the central cognitive system in charge of coordinating cognitive activities.

Reading and Text Comprehension Abilities

When thinking about the capacities needed to solve arithmetic word problems, reading comprehension and calculation skills are among the first abilities that come to mind. Indeed, solving word problems requires, as a minimum, comprehending the text, storing facts during solution, and performing calculations on the stored numbers. Thus, along with WM, reading comprehension and calculation skills should be among the main determinants of word problem-solving performance. Accordingly, several studies have reported a role of these factors. For example, Kail and Hall (1999) measured reading skills, arithmetic knowledge, and short-term memory span in 8–12-year-old children who were asked to solve Change, Equalize, Combine, and Compare problems. Not surprisingly, knowledge of basic arithmetic facts had a strong impact on word problem performance, but reading abilities contributed also consistently and strongly, although these abilities were assessed through a simple word recognition task, whereas memory was a less consistent predictor of word-problem performance. This latter finding has been reported in several studies. For example Swanson, Cooney, and Brok (1993) observed that the correlation between WM and word-problem performance became non significant when reading comprehension was partialed out. This suggests that reading comprehension takes precedence over memory, a phenomenon also observed by Fuchs and colleagues ( Fuchs, Fuchs, Compton, Powell, Seethaler, Capizzi, et al., 2006 ) who found that, when word-reading proficiency is entered in the regression model, WM no longer plays a significant role in predicting children’s word problem accuracy (see Lee et al., 2004 , for similar findings in the domain of algebraic word problems).

A number of following studies confirmed the impact of reading comprehension skills on problem solving. We mentioned above the study by Andersson (2007) who assessed a variety of WM capacities in relation with word problem-solving performance, but also arithmetic calculation and reading skills. Although the main conclusion of the authors were related with the unique contribution of WM capacities, the best predictor of arithmetic word-problem solving was, as Kail and Hall (1999) observed, arithmetic calculation ( r = 0.69) immediately followed by reading ability ( r = 0.56). In the same way, Zheng et al., (2011) investigated the specific role of several components of WM as we reported above, but they also assessed calculation capacities and reading comprehension. Once more, arithmetic calculation was the best predictor of word problem solving, followed by reading comprehension. Interestingly, this study also revealed that all the components of WM predict word problem performance, but that reading abilities can compensate for some of the influence of WM in children. It is worth to note that comprehension per se is the key aspect of the relationship between reading abilities and word problem solving. Pinperton and Nation (2010) studied the mathematical profile of 7–8-year-old poor comprehenders, who are children who show significant deficits in reading comprehension despite average, or above-average, word-reading ability. When compared with controls showing age-appropriate reading comprehension abilities, poor comprehenders showed a deficit in mathematical reasoning assessed through verbally presented problems, whereas they did not differ from their controls in solving numerical operations.

Although the relationship between reading comprehension and word problem solving seems straightforward, it could be more complex than expected. A first interpretation could be that better reading comprehension facilitates the construction of a correct representation of the situation the problem describes, a correct representation which is necessary for solving the problem. However, as Kail and Hall (1999 , p. 667) noted, another interpretation could be that because reading and mathematics achievement are correlated ( Geary, 1993 ; Jordan, Kaplan, & Hanish, 2002 ), reading comprehension may simply be a proxy for general mathematical skills, including word problem solving. This latter interpretation is reinforced by Lerkkanen, Rasku-Puttonen, Aunola, and Nurmi (2005) . They observed in a longitudinal study that mathematics and reading comprehension are highly associated during the first and second years of primary school, but, surprisingly, it appeared that mathematical performance predicted reading comprehension rather than vice versa. Though Lerkkanen et al. (2005) did not assess word problem solving performance, their finding suggests that the correlation observed by Kail and Hall (1999) does not necessarily reveal a causal relationship from reading comprehension to word problem solving performance.

Surprisingly, some studies focusing on groups of children suffering from learning disabilities have reached the same temperate conclusions. Vukovic, Lesaux, and Siegel (2010) studied mathematical skills of third graders who present two types of reading difficulties, either a dyslexia or specific reading comprehension difficulties. When contrasted with a large control group, the two groups presenting reading difficulties performed lower than the control group on word problems. However, once mastery of arithmetic facts was controlled, children with reading difficulties performed in the average range, suggesting that reading difficulties have no effect per se in word problem-solving performance. Nonetheless, as the authors note, the problems were read to the children, eliminating the reading demand of the task and, despite this aid, children with reading difficulties performed lower than the control group. In fact, several studies have shown that children who have difficulties in both mathematics and reading perform worse in word problems than children who have difficulties in mathematics only ( Jordan & Hanish, 2000 ; Jordan & Montani, 1997 ).

To summarize, many studies have established that, after fluency in arithmetic fact and calculation abilities, reading comprehension is a strong predictor of word problem-solving performance. Even if the directionality of the causal link remains uncertain and the specific contribution of reading comprehension is difficult to isolate, reading difficulties contribute to a lower achievement in word problem solving. Alternatively, it seems that reading abilities can compensate for the influence of more general cognitive traits like WM capacity. In the next section, we address the studies that have explicitly focused on those factors susceptible to improve performance.

Enhancing Word Problem Performance

Schema-based instruction (sbi).

As noted by Jitendra, Griffin, Deatline-Buchman, and Sczesniak (2007) , traditional instruction teaches students to use keywords in order to solve verbal problems. For example, ‘all’ suggests addition, whereas ‘share’ suggests division. This approach is limited because many problems do not have keywords. Moreover, as already noted when commenting on inconsistent problems, basing the solving process on keywords can be misleading and does not help students to make sense of problem situations. In order to better promote elementary students’ mathematical problem solving skills, Jitendra and her colleagues (e.g. Jitendra et al., 2007 ; Jitendra & Hoff, 1996 ; Jitendra & Star, 2011 ) designed an intervention tool called the schema-based instruction (SBI). SBI promotes the explicit analysis of the problem schema (e.g. part-part-whole) and the relationships between its different elements (e.g. parts make up the whole). The rationale behind SBI is that understanding these relationships is crucial in selecting appropriate operations needed to solve the problems. In fact, ‘SBI allows students to approach the problem by focusing on the underlying problem structure, thus facilitating conceptual understanding and adequate word-problem-solving skills’ ( Jitendra et al., 2007 , p. 286). The instruction program consists of asking children to read and retell the problem to discover its type (Change, Combine, or Comparison, for example, for addition problems), to underline and map important information onto a schematic diagram, to decide which operation has to be performed, to write the mathematical sentence and the answer, and finally to check it. Such program conducted in low – and high-ability, as well as special education classrooms revealed performance improvement from pretest to posttest on word problem solving and computation fluency measures.

Using Manipulatives

As seen above, capacities in WM can be related to word problem performance. Therefore, decreasing the WM demand of a problem by using external aids such as manipulatives could help children to solve it. Manipulative materials, such as Cuisenaire rods or craft sticks, are concrete models that incorporate mathematical concepts, and that can be touched and moved around by students. They can be used by children in order to represent the objects and their relationships described in the text. Then, using manipulatives may be beneficial in constructing an adequate situation or mental model of the problem. Indeed, providing kindergarten children with manipulatives enable them to solve simple word problem ( Carpenter, Hiebert, & Moser, 1983 ). However, Stellingwerf and Van Lieshout (1999) showed that 11-year-old children from schools for special education do not improve their performance on word problem after a training in which only manipulatives were used. The authors conclude that, whereas young children are helped by the use of manipulatives ( Carpenter et al., 1983 ), older ones do not benefit any longer from such instructional tools. Stellingwerf and Van Lieshout also demonstrated the existence of a transitional stage (i.e. between the age of 6 and 11) in which manipulatives are helpful when used in combination with other educational tools such as the use of number sentences (e.g. a +? = c ).

Rewording The Problems

As already stated above, reformulating the problem can dramatically improve children performance. We saw that whereas the problem ‘There are 5 birds and 3 worms. How many more birds than worms are there?’ leads to only 25% of correct response in kindergarten children, a reformulation into ‘How many birds won’t get a worm?’ leads to 96% of correct response in children at the same level ( Hudson, 1983 ). According to Staub and Reusser (1995) , the two versions of the problem refer to different episodic situation models. Whereas the first version describes a static and abstract situation, the second version describes a dynamic and more concrete situation. As a consequence, everyday and real-world knowledge can easily be applied during the course of the comprehension and solving processes, hence the improvement in performance. Likewise, Stern and Lehrndofer (1992) recorded better results on Compare problems when they added qualitative information to the text. For example, in a problem such as ‘How many fewer pencils does Laura have than Peter?’, adding that Peter is the older brother and, as such, enjoys a number of advantage, helps children in their understanding of the problem. However, other studies failed to obtain such effects. Cummins, Kintsch, Reusser, & Weimer (1988) compared second graders’ comprehension and solution of standard word problems with enriched problems embedded into little stories showing plausible and realistic situations. For example, the problem ‘Joe has 8 dollars. He has 5 more dollars than Tom. How many dollars does Tom have?’ was reformulated into ‘Joe and Tom play tennis together twice a week. They both always try hard to beat each other. Both of them decided to buy new tennis balls. So far Joe has saved 8 dollars for his balls. He has saved 5 dollars more than Tom. How many dollars has Tom saved?’ Contrary to the author’s expectations, the reworded problems did not elicit significantly higher solution performance than the standard ones.

As a matter of fact, Vicente, Orrantia, and Verschaffel (2007) have shown recently that such situational rewordings are, indeed, not always very efficient. In contrast, conceptual rewording, which consists of the enhancement of the underlying semantic structure of the problem, more systematically elicits positive effects. It is the case in De Corte, Verschaffel, and de Win’s study (1985) , where the semantic relationship between the sets implied in the problem are stated more transparently. First and second graders were asked to solve Change, Combine, and Compare problems, either in their classical form, or in a reworded way. The problems were reformulated in such a way that the relations between the given and the unknown sets were made more explicit. However, the underlying mathematical structure of the problems was not affected. For example, a sentence relative to the initial situation was added at the beginning of Change problems (‘Joe had some marbles. He won 3 more marbles. Now he has 5 marbles. How many marbles did Joe have at the beginning?’) or the part-whole relation was made explicit in Combine problems (‘Tom and Ann have 9 nuts altogether. Three nuts belong to Tom. The rest belong to Ann. How many marbles does Ann have?’). Such conceptual rewordings facilitated the solving process in both age groups, but especially in younger children. The interpretation of Verschaffel, De Corte, and De Win (1985) was that their reformulations helped children in constructing the adequate mental representation of the problem, especially in children whose canonical schemata are not fully developed and, therefore, depend more on text-driven (bottom-up) processing to construct their mental representation.

Using Pictures, Graphs, and Figures

Using pictures or self-generated drawings tends to facilitate the solution of word problems. Willis and Fuson (1988) showed that asking children to choose a schematic drawing that matches the situational structure of a given problem, then to fill the problem numbers into appropriate locations in the drawing and, finally, to use the drawing in order to decide the solution procedure is an efficient mean to improve performance in second-graders. Children from high and average-achieving classrooms were generally accurate in choosing the correct drawing for Combine, Change, and Compare problems. According to the authors, this technique is useful because it helps children to grasp the semantic structure of the problem situation. Sprinthall and Nolan (1991) added that the structure of Combine problems is made even more salient when different objects are introduced within the pictures. For example, it is more efficient to present first-grade children with pictures representing 5 tulips and 2 roses than representing the same objects: 5 tulips and 2 tulips. The pictures or drawing representing different objects would present clearer visual arrays, which would allow students to form contrasting perceptions of the quantities in each set and, consequently, would help them to grasp more easily the semantic structure of the problem.

However, as for rewording, Vicente, Orrantia, and Verschaffel (2008) showed that only conceptual (mathematical) drawings and not situational ones are efficient. Conceptual drawings make salient the mathematical organization, whereas situational drawings highlight the components of the situation such as the temporal sequence of events or the context in which the story is embedded. Vicente et al. (2008) asked children with high and low abilities in arithmetic to solve easy and difficult problems. The former could be solved following the time sequence described in the text, whereas for the latter it was necessary to solve the second part of the problem before its first part in order to reach the solution (e.g. ‘Laura had 47 beads. She bought some more beads. She used 126 beads and she was left with 11 beads. How many beads did she buy?’). The problems could be presented in their standard form (as in the example), with extra mathematical information that highlighted the part-whole relation described in the problem (‘Laura had 47 beads. She bought some more beads and put them together with the beads she already had. From the total amount of beads she had after buying some , she used 126 beads and she was left with 11 beads. How many beads did she buy?’), or with extra situational information that emphasized the temporal sequence of events described in the problem (‘ Two days ago , Laura had 47 beads. Yesterday , she bought some more beads. This morning she decided to make a collar for her mother. To do so , she used 126 beads and, when she finished , she was left with 11 beads. How many beads did she buy?’). The problems could be presented by themselves or along with a drawing. Drawings that were presented with standard problems did not contribute to the understanding of the conceptual or mathematical situation of the problem but merely represented the protagonist(s) and the objects described in the problem. The mathematical drawing represented the part-whole relation described in the problem. It was constituted of two pictures, one for each part of the Change situation. The first picture depicted the reunion of the two parts into the whole, for example, Figure 9.1 .

Each part of the Change situation.

The second picture showed that the initial total amount of objects can be portioned into two parts, for example, Figure 9.2 .

Finally, situational drawings corresponded to a kind of comic strip in which each of the frames represented a temporal window described in the problem. In line with previous research (see the above section about rewording), the authors showed that when no drawing was presented with the problems, the situational and the mathematical versions of the problems elicited more correct answers than the standard versions. This was especially true for difficult problems. More importantly for our purpose, when the problem was accompanied with a mathematical drawing, children’s rate of correct answers was greater compared with a situation in which a standard or situational drawing was presented. However, and interestingly, only children with higher abilities in mathematics benefited from the presentation of mathematical drawings. The interpretation of the authors concerning this last finding was that only children with high abilities have the necessary skills and cognitive resources to process the mathematical drawing efficiently.

Initial total amount of objects portioned into two parts.

Conclusions and Directions

The main conclusion that could be drawn from this rapid survey of the literature on arithmetic word problem solving during the last decades is that this research domain has progressively moved towards an increasing emphasis of the role of semantically rich and complex representations. If the seminal works on this domain and the first semantic classifications could lend credence to a word problem-solving activity relying on a restricted and finite number of definite schemas progressively abstracted through repeated exposition with problems, the difficulties that this view encountered in accounting for ubiquitous effects of content and context brought about the necessity of envision more complex representations and associated cognitive processes. Instead of retrieving abstract schemata from long-term memory that would be readily instantiated with the available numerical values before running the associated calculation, problems solvers seem to construct ad hoc transient representations (mental models or situation models) that involve a fairly rich real-world knowledge. However, the level of abstractness of representations and procedures remains a controversial issue in research on numerical and arithmetic processes (see Cohen Kadosh & Walsh, 2009 ; Landy & Goldstone, 2007 ), and the widespread use of context-bound representations does not mean that more abstract mathematical representations cannot emerge from these initial representations and direct further calculation. Nonetheless, empirical evidence indicates that semantic and pragmatic aspects influence the entire process of problem solving. The difficulty of constructing these complex representations from text reading, and the necessity to maintain them in an active state, while selecting and performing appropriate calculations, probably explains why, along with trivial factors, such as calculation proficiency and reading comprehension, working memory capacities are so good predictors of performance. This is also probably why, among the variety of interventions and tutorials that have been imagined and tested, such as rewordings or use of drawings, those that emphasize the conceptual characteristics of the problems are the most efficient. Arithmetic word problem solving thus appears as a highly complex cognitive activity that mobilizes a variety of conceptual knowledge and procedural skills, and it does not come as a surprise that it constitutes the domain in which pupils experience their main difficulties.

As other high-level cognitive activities, such as reasoning, decision making, or expertise acquisition, the complexity of the activity of arithmetic word problem solving makes its study especially arduous for cognitive and educational psychologists. However, we would like to conclude by suggesting some leads for future research. The present review of the literature made probably clear that developmental studies have up to now focused on relatively restricted ranges of ages and degrees. Nonetheless, studies that would encompass the complete developmental era or the educational curriculum, say from kindergarten age to adulthood, would be of interest. Indeed, very little is known about how strategies and their underlying representations evolve in the long run. It is possible that the use of manipulatives to model problem situations in young children is progressively interiorized into some mental schemas that would coexist with the use of semantic representations like mental or situation models, enriching children’s toolbox. It is also possible that these semantic representations evolve themselves into more abstract representations that could direct problem solving, in the same way as experts in several domains have memorized an impressive list of strategies in response to a variety of recurrent situations. It cannot be excluded that these developmental changes interact with content and contexts, rendering developmental trends even more complex. For example, contents that facilitate the construction of mental images, such as problems involving count nouns, could more easily elicit mental models than problems involving mass nouns that could more efficiently trigger schema retrieval due to their low level of imageability. In other words, it might be that problem solvers mobilize at each developmental level a variety of strategies varying in representational format and level of abstraction, in the same way as children and adults use a variety of strategies, even for solving very simple arithmetic problems such as elementary additions or subtractions ( Siegler, 1996 ). Another necessary extension of the current research concerns the variety of the problems studied. As the present review made clear, and apart from rare attempts, the range of the problems studied has up to now remained restricted to the simplest forms of the additive problems. The ecological and psychological validity of more extended and complex classifications requires to be established. More complex problems might reveal even more elaborated strategies involving an increased variety of representational formats. Finally, psychologists should not forget that arithmetic word problem solving is not only a complex cognitive activity that constitutes a privileged tool for exploring high-level cognitive processes, but also a school activity and one of the main pedagogical tools for mathematics teaching. In this respect, a better understanding of the underlying factors that make this activity so difficult, and of the determinants of individual difficulties is needed that could help to promote more rational teaching curricula and more efficient intervention programs.

Andersson, U. ( 2007 ). The contribution of working memory to children’s mathematical word problem solving.   Applied Cognitive Psychology, 21, 1201–1216.

Google Scholar

Baddeley, A. ( 1986 ). Working Memory. New York: Oxford University Press.

Google Preview

Bassok, M. , Chase, V.M. , & Martin, S.A. ( 1998 ). Adding apples and oranges: alignment of semantic and formal knowledge.   Cognitive Psychology, 35, 99–134.

Brissiaud, R. ( 1994 ). Teaching and development: solving ‘missing addend’ problems using subtraction.   European Journal of Psychology of Education, 4, 343–365.

Brissiaud, R. , & Sander, E. ( 2010 ). Arithmetic word problem solving: a Situation Strategy First Framework.   Developmental Science, 13(1), 92–107.

Cain, K. , & Oakhill, J. ( 1999 ). Inference making ability and its relation to comprehension failure in young children.   Reading and Writing, 11, 489–503.

Carpenter, T.P. , Hiebert, J. , & Moser, J.M. ( 1983 ). Problem structure and first-grade-children’s initial solution processes for simple addition and subtraction problems.   Journal for Research in Mathematics Education, 12, 27–39.

Carpenter, T.P. , & Moser, J.M. ( 1982 ). The development of addition and subtraction problem-solving skills. In T. P Carpenter , J. M. Moser , & T. A. Romberg (Eds), Addition and Subtraction: A Cognitive Perspective (pp. 9–25). Hillsdale: Erlbaum.

Carpenter, T.P. , & Moser, J.M. ( 1984 ). The acquisition of addition and subtraction concepts in grades one through three.   Journal for Research in Mathematics Education, 15, 179–202.

Cohen Kadosh, R. , & Walsh, V ( 2009 ). Numerical representation in the parietal lobes: abstract or not abstract?   Behavioral and Brain Sciences, 32(3–4): 313–28.

Coquin-Viennot, D. , & Moreau, S. ( 2003 ). Highlighting the role of the episodic situation model in the solving of arithmetical problems.   European Journal of Psychology of Education, 18, 267–279.

Cummins, D. , Kintsch, W. , Reusser, K. , & Weimer, R. ( 1988 ). The role of understanding in solving word problems.   Cognitive Psychology, 20, 405–438.

De Corte, E. , & Verschaffel, L. ( 1985 ). Beginning first graders’ initial representation of arithmetic word problems.   Journal of Mathematical Behavior, 4, 3–21.

De Corte, E. , & Verschaffel, L. ( 1987 ). The effect of semantic structure on first grader’s strategies for solving addition and subtraction word problems.   Journal for Research in Mathematics Education, 18, 363–381.

De Corte, E. , Verschaffel, L. , & De Win, L. ( 1985 ). Influence of rewording verbal problems on children’s problem representations and solutions.   Journal of Educational Psychology, 77, 460–470.

DeStefano, D. , & LeFevre, J. ( 2004 ). The role of working memory in mental arithmetic.   European Journal of Cognitive Psychology, 16, 353–386.

Devidal, M. , Fayol, M. & Barrouillet, P. ( 1997 ). Stratégies de lecture et résolution de problèmes arithmétiques.   L’Année Psychologique, 97, 9–31.

Fayol, M. , Abdi, H. , & Gombert, J.E. ( 1987 ). Arithmetic problem formulation and working memory load.   Cognition and Instruction, 4, 183–202.

Fayol, M. , Barrouillet, P. , & Camos, V. ( 1997 ). Early mathematics learning: what can research tell us, Report for the DG 22 of the European Community, Brussels. Brussels: EU.

Fuchs, L.S. , Fuchs, D. , Compton, D.L. , Powell, S.R. , Seethaler, P.M. , Capizzi, A.M. , Schatschneider, C. , & Fletcher, J.M. ( 2006 ). The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems.   Journal of Educational Psychology, 98, 29–43.

Fuson, K.C. , Carroll, W.M. , & Landis, J. ( 1996 ). Levels in conceptualizing and solving addition and subtraction compare word problems.   Cognition and Instruction, 14, 345–371.

Garcia, A.I. , Jimenez, J.E. , & Hess, S. ( 2006 ). Solving arithmetic word problems: an analysis of classification as a function of difficulty in children with and without arithmetic LD.   Journal of Learning Disabilities, 39, 270–281.

Geary, D.C. ( 1993 ). Mathematical disabilities: cognitive, neuropsychological, and genetic components.   Psychological Bulletin, 114, 345–362.

Greer, B. ( 1992 ). Multiplication and division as models of situations. In D. A. Grouws (Ed.) Handbook of Research in Mathematics Teaching and Learning (pp. 276–295). New York: Macmillan.

Hudson, T. ( 1983 ). Correspondences and numerical differences between disjoint set.   Child Development, 54, 84–90.

Ibarra, C. , & Lindvall, C. ( 1982 ). Factors associated with the ability of kindergarten children to solve simple arithmetic story problems.   Journal of Educational Research, 75, 149–155.

Jitendra, A, K. , Griffin, C. C. , Deatline-Buchman, A. , & Sczesniak, E. ( 2007 ). Mathematical word problem solving in third-grade classrooms.   Journal of Educational Research, 100, 283–302.

Jitendra, A.K. , & Hoff, K. ( 1996 ). The effects of schema-based instruction on the mathematical word-problem solving performance of students with learning disabilities.   Journal of Learning Disabilities, 29, 422–431.

Jitendra, A.K. , & Star, J.R. ( 2011 ). Meeting the needs of students with learning disabilities in inclusive mathematics classrooms: the role of schema-based instruction on mathematical problem-solving.   Theory into Practice, 50, 12–19.

Johnson-Laird, P.N. ( 1983 ). Mental Models: Towards a Cognitive Science of Language, Inference, and Consciousness. Cambridge, MA: Harvard University Press/Cambridge: Harvard University Press.

Jordan, N.C. , & Hanish, L.B. ( 2000 ). Mathematical thinking in second-grade children with different forms of LD.   Journal of Learning Disabilities, 33, 567–578.

Jordan, N.C. , Kaplan, D. , & Hanish, L.B. ( 2002 ). Achievement growth in children with learning difficulties in mathematics: findings of a two-year longitudinal study.   Journal of Educational Psychology, 94, 586–597.

Jordan, N.C. , & Montani, T.O. ( 1997 ). Cognitive arithmetic and problem solving: a comparison of children with specific and general mathematics difficulties.   Journal of Learning Disabilities, 30, 624–634.

Judd, T.P. , & Bilsky, L.H. ( 1989 ). Comprehension and memory in the solution of verbal arithmetic problems by mentally retarded and nonretarded individuals.   Journal of Educational Psychology, 81, 541–546.

Kail, R.V. ( 2007 ). Longitudinal evidence that increases in processing speed and working memory enhance children’s reasoning.   Psychological Science, 18, 312–313.

Kail, R. , & Hall, L.K. ( 1999 ). Sources of developmental change in children’s word problem performance.   Journal of Educational Psychology, 91, 660–668.

Kintsch, W. , & Greeno, J.G. ( 1985 ). Understanding and solving word arithmetic problems.   Psychological Review, 92, 109–129.

Landy, D. , & Goldstone, R.L. ( 2007 ). How abstract is symbolic thought?   Journal of Experimental Psychology: Learning, Memory and Cognition, 33(4), 720–733.

Lee, K. , Ng, S.F. , & Ng, E.L. ( 2009 ). The contributions of working memory and executive functioning to problem representation and solution generation in algebraic word problems.   Journal of Educational Psychology, 101, 373–387.

Lee, K. , Ng, S.F. , Ng, E.L. , & Lim, Z.Y. ( 2004 ). Working memory and literacy as predictors of performance on algebraic word problem.   Journal of Experimental Child Psychology, 89, 140–158.

LeFevre, J. , DeStefano, D. , Coleman, B. , & Shanahan, T. ( 2005 ). Mathematical cognition and working memory. In J. I. D. Campbell (Ed.), Handbook of Mathematical Cognition (pp. 361–377). New York: Psychology Press.

Lerkkanen, M.-K. , Rasku-Puttonen, H. , Aunola, K. , & Nurmi, J-E. ( 2005 ). Mathematical performance predicts progress in reading comprehension among 7-year olds.   European Journal of the Psychology of Education, 20, 121–137.

Lewis, A. , & Mayer, R.E. ( 1987 ). Students’ miscomprehension of relational statements in arithmetic word problems.   Journal of Educational Psychology, 79, 363–371.

Lindvall, C.M. , & Ibarra, C.G. ( 1980 ). Incorrect procedure used by primary grade pupils in solving open addition and subtraction sentences.   Journal for Research in Mathematics Education, 11, 50–62.

Mani, K. , & Johnson-Laird, P.N. ( 1982 ). The mental representation of spatial description.   Memory & Cognition, 10, 181–187.

Nesher, P. ( 1981 ). Levels of description in the analysis of addition and subtraction. In T. P. Carpenter , J. M. Moser , & T. A. Romberg (Eds), Addition and Subtraction: Developmental Perspective (pp. 25–38). Hillsdale, NJ: Lawrence Erlbaum.

Nesher, P. , Greeno, J.G. , & Riley, M.S. ( 1982 ). The development of semantics categories for addition and subtraction.   Educational Studies in Mathematics, 13, 373–394.

Oakhill, J. ( 1996 ). Mental models in children’s text comprehension. In J. Oakhill & A. Garnham (Eds), Mental Models in Cognitive Science (pp. 77–94). Hove: Psychology Press.

Oakhill, J. , Cain, K. , & Yuill, N. ( 1998 ). Individual differences in children’s comprehension skill: Toward an integrated model. In C. Hulme & R. M. Joshi (Eds), Reading and Spelling: Development and Disorders (pp. 343–367). Mahwah, NJ: Lawrence Erlbaum Associates, Publishers.

Passolunghi, M.C. , Cornoldi, C. , & De Liberto, S. ( 1999 ). Working memory and intrusions of irrelevant information in a group of specific poor problem solvers.   Memory & Cognition, 27, 779–790.

Passolunghi, M.C. , & Mammarella, I.C. ( 2010 ). Spatial working memory impairments in children with difficulties in arithmetic word problem-solving.   European Journal of Cognitive Psychology, 22, 944–963.

Passolunghi, M.C. , & Pazzaglia, F. ( 2004 ). Individual differences in memory updating in relation to arithmetic problem solving.   Learning and Individual Differences, 14, 219–230.

Passolunghi, M.C. , & Siegel, L.S. ( 2001 ). Short-term memory, working memory, and inhibitory control in children with difficulties in arithmetic problem solving.   Journal of Experimental Child Psychology, 80, 44–57.

Pinperton, H. , & Nation, K. ( 2010 ). Understanding words, understanding numbers: an exploration of the mathematical profiles of poor comprehenders.   British Journal of Educational Psychology, 80, 255–268.

Rasmussen, C. , & Bisanz, J. ( 2005 ). Representation and working memory in early arithmetic.   Journal of Experimental Child Psychology, 91, 137–157.

Rawson, K.A. , & Kintsch, W. ( 2002 ). How does background information improve memory for test content?   Memory & Cognition, 30 (5), 768–778.

Reusser, K. ( 1989 ). Textual and Situational Factors in Solving Mathematical Word Problems. Bern: University of Bern.

Riley, M.S. , Greeno, J.G. , & Heller, J.I. ( 1983 ). Development of children’s problem solving ability in arithmetic. In H. P. Ginsburg (Ed.), The Development of Mathematical Thinking. New York: Academic Press.

Siegler, R.S. ( 1996 ). Emerging Minds: The Process of Change in Children’s Thinking. Oxford: Oxford University Press.

Sprinthall, R.C. , & Nolan, T.E. ( 1991 ). Efficacy of representing quantities with different pictures in solving arithmetic word problems.   Perceptual and Motor Skills, 72, 274–274.

Staub, F.C. , & Reusser, K. ( 1995 ). The role of presentational structures in understanding and solving mathematical word problems. In C. A. Weaver , S. Mannes , & C. R. Fletcher (Eds), Discourse Comprehension. Essays in Honor of Walter Kintsch (pp. 285–305). Hillsdale, NJ: Lawrence Erlbaum.

Stellingwerf, B.P. , & Van Lieshout, E.C.D.M. ( 1999 ). Manipulatives and number sentences in computer aided arithmetic word problem solving.   Instructional Science, 27, 459–476.

Stern, E. , & Lehrndorfer, A. ( 1992 ). The role of situational context in solving word problems.   Cognitive Development, 2, 259–268.

Swanson, H.L. ( 2011 ). Working memory, attention, and mathematical problem solving: a longitudinal study of elementary school children.   Journal of Educational Psychology, 103, 821–837.

Swanson, H.L. , Cooney, J.B. , & Brock, S. ( 1993 ). The influence of working memory and classification ability on children’s word problem solution.   Journal of Experimental Child Psychology, 55, 374–395.

Thevenot, C. ( 2010 ). Arithmetic word problem solving: evidence for the construction of a mental model.   Acta Psychologica, 133, 90–95.

Thevenot, C. , Barrouillet, P. , & Fayol, M. ( 2004 ). Mental representation and procedures in arithmetic word problems: The effect of the position of the question.   L’Année Psychologique, 104 (4), 683–699.

Thevenot, C. , Devidal, M. , Barrouillet, P. , & Fayol, M. ( 2007 ). Why does placing the question before an arithmetic word problem improve performance? A situation model account.   Quarterly Journal of Experimental Psychology, 60, 43–56.

Thevenot, C. , & Oakhill, J. ( 2005 ). The strategic use of alternative representation in arithmetic word problem solving.   Quarterly Journal of Experimental Psychology – A, 58, 1311–1323.

Verschaffel, L. , De Corte, E. , & De Win, L. ( 1985 ). Influence of rewording verbal problems on children’s problem representations and solutions.   Journal of Educational Psychology, 77, 460–470.

Vergnaud, G. ( 1982 ). A classification of cognitive tasks and operations of thought involved in addition and subtraction problems. In T. P. Carpenter , J. M. Moser , & T. A Romberg (Eds), Addition and Subtraction: A Cognitive Perspective (pp. 39–59). Hillsdale: Erlbaum.

Vergnaud, G. ( 1983 ). Multiplicative structures. In R. Lesh , & M. Landau (Eds), Acquisition of Mathematic Concepts and Processes. New York: Academic Press.

Vicente, S. , Orrantia, J. , & Verschaffel, L. ( 2007 ). Influence of situational and conceptual rewording on word problem solving.   British Journal of Educational Psychology, 77, 829–848.

Vicente, S. , Orrantia, J. , & Verschaffel, L. ( 2008 ). Influence of mathematical and situational knowledge on arithmetic word problem solving: textual and graphical aids.   Infancia y Aprendizare, 31, 463–483.

Vukovic, R.K. , Lesaux, N.K. , & Siegel, L.S. ( 2010 ). The mathematics skills of children with reading difficulties.   Learning and Individual Differences, 20, 639–643.

Willis, G.B. , & Fuson, K.C. ( 1988 ). Teaching children to use schematic drawings to solve addition and subtraction word problems.   Journal of Educational Psychology, 80, 192–201.

Yuill, N. , Oakhill, J. , & Parkin, A. ( 1989 ). Working memory, comprehension ability and the resolution of text anomaly.   British Journal of Psychology, 80, 351–61.

Zheng, X. , Swanson, H.L. , & Marcoulides, G.A. ( 2011 ). Working memory components as predictors of children’s mathematical word problem solving.   Journal of Experimental Child Psychology, 110, 481–498.

• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Think Quickly and Calculate Quicker: Mental Arithmetic Skills Hacks

Without the use of a calculator or paper and pencil, mental arithmetic is a method for performing calculations mentally. It is a helpful ability to possess, particularly in circumstances where a calculator or a pen and paper are not easily accessible. We will go over the advantages of mental arithmetic, the methods employed to do it, and how to hone your mental arithmetic abilities in this guide.

Advantages of mental arithmetic

Among the advantages of mental computation are:

Memory Gain: Mental arithmetic is a brain activity that assists with memory retention.

Increased Speed and Accuracy: Mental arithmetic improves calculating speed and accuracy, which helps you finish tasks more quickly

Improved Problem-Solving Skills: Mental arithmetic aids in the development of problem-solving abilities, which make it possible for you to tackle complicated issues more quickly.

Improved Concentration: Mental arithmetic calls for a lot of concentration, which helps you focus and concentrate better.

Techniques for Mental Arithmetic

There are several techniques used to perform mental arithmetic. Some of these techniques include:

Addition and Subtraction

The most basic mental arithmetic technique involves adding and subtracting numbers in your head. This technique involves breaking down numbers into smaller parts and adding or subtracting them.

Let's say you need to add 37 and 22 in your head.

To use the mental arithmetic technique of breaking down numbers into smaller parts, you could:

Break down 37 into 30 and 7, and then add 22 to each part separately:

30 + 20 = 50

Then, you would add those two answers together:

50 + 9 = 59

So the answer to 37 + 22 is 81.

Multiplication and Division

Multiplication and division can also be performed mentally using techniques such as grouping and halving.

Let's say you need to multiply 25 by 8 in your head.

To use the mental arithmetic technique of grouping, you could:

Group the number 25 into two smaller numbers that are easier to work with, such as 20 and 5.

Then, you can use the distributive property of multiplication to break down the multiplication into simpler operations:

25 x 8 = (20 + 5) x 8

25 x 8 = 20 x 8 + 5 x 8

Multiply each smaller number by 8:

20 x 8 = 160

Add the two answers together:

160 + 40 = 200

So the answer to 25 x 8 is 200.

To use the mental arithmetic technique of halving, let's say you need to divide 48 by 6 in your head.

Start by halving the dividend (48) and divisor (6) until you get a smaller, easier-to-work-with problem. Keep halving until you get to a point where you can solve the problem mentally.

Divide the dividend by the divisor:

48 ÷ 6 = (24 ÷ 3) = (8 ÷ 1) = 8

So the answer to 48 ÷ 6 is 8.

Dividing by 10, 100, 1000, and multiples:

Let's say you need to divide 245 by 10 in your head.

o use the mental arithmetic technique of dividing by 10, you simply move the decimal point one place to the left:

245 ÷ 10 = 24.5

So the answer to 245 ÷ 10 is 24.5.

Now, let's say you need to divide 1320 by 100 in your head.

To use the mental arithmetic technique of dividing by 100, you move the decimal point two places to the left:

1320 ÷ 100 = 13.20

So the answer to 1320 ÷ 100 is 13.20.

Multiplying numbers by 10, 100, and 1000, and their multiples:

Let's say you need to multiply 48 by 100 in your head.

To use the mental arithmetic technique of multiplying by 100, you move the decimal point two places to the right:

48 x 100 = 4800

So the answer to 48 x 100 is 4800.

Now, let's say you need to multiply 76 by 1000 in your head.

To use the mental arithmetic technique of multiplying by 1000, you move the decimal point three places to the right:

76 x 1000 = 76,000

So the answer to 76 x 1000 is 76,000.

Read more "Making Math Fun: 4 Exciting Ways to Improve Your Child's Mental Math Abilities"

Squaring and Cubing

Squaring and cubing involve multiplying a number by itself or by itself twice, respectively. Techniques such as adding and subtracting squares or cubes can be used to perform these calculations mentally.

Let's say we want to find the square of 16 in our head. We can recognize that 16 is close to (10+6)^2, and use the reduced multiplication formula:

16^2=(10+6)^2=10^2+2*10*6+6^2=100+120+36=256

The reduced multiplication formula is used (a+b)^2=a^2+2ab+b^2

Developing Your Mental Calculation Skills

Practice and commitment are necessary to improve your mental arithmetic abilities. Here are some pointers to help you sharpen your mental computation abilities:

Practice Every Day : To hone your abilities and boost your speed and accuracy, practice mental arithmetic every day.

Break Down Numbers : To make calculations easier, divide large numbers into smaller components.

Utilise memory tricks : To remember numbers and calculations, use memory tricks like visualisation or mnemonics.

Discover shortcuts : To boost your speed, learn shortcuts for simple mathematics like dividing by two or multiplying by ten. A vital talent to have is mental arithmetic, which can boost problem-solving abilities, speed and accuracy, and memory. Utilising the methods and advice in this manual can help you develop your mental math abilities and make calculations more quickly and accurately.

We hope this article has been helpful in educating you on mental arithmetic and how to hone your abilities. Contact us at any time if you have any inquiries or comments.

Caroline Milne - plays a crucial role in our blog as an articles writer, forming a strong and valuable connection with our Company. Hailing from the United Kingdom, her unique perspective and expertise greatly contribute to the content she creates for our website.

With a background in primary education, Caroline brings a wealth of knowledge and experience to her writing, ensuring that the articles she produces resonate with our target audience. Her dedication to delivering high-quality and engaging content has made her an indispensable member of our team. Caroline's exceptional work has not only enhanced the reputation of our blog but also solidified the bond between her and our Company, making her an invaluable asset to our organization.

https://www.linkedin.com/in/caroline-milne-b60441a7/

Sign Up For Lessons

Get your present!

Please complete the form below

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Peer-reviewed

Research Article

Improving mental arithmetic ability of primary school students with schema teaching method: An experimental study

Roles Conceptualization, Formal analysis, Funding acquisition, Methodology, Writing – original draft, Writing – review & editing

Affiliation College of Teacher Education, Hubei University of Education, Wuhan, China

Roles Conceptualization, Methodology, Writing – original draft, Writing – review & editing

* E-mail: [email protected]

Affiliation College of Mathematics and Statistics, Hubei University of Education, Wuhan, China

Roles Methodology, Writing – review & editing

Affiliation Brain Science and Learning Science Committee ofs Hubei Teachers Education Association, Wuhan, China

Roles Funding acquisition, Writing – review & editing

• Dawei Liu, 
• Xin Tan, 
• Huifen Yan, 

• Published: April 16, 2024
• https://doi.org/10.1371/journal.pone.0297013
• Reader Comments

Skillful utilization of mental arithmetic can significantly improve students’ mathematical computation ability. However, it was observed that primary school students often resort to reiterating the process of written arithmetic in their minds during mental arithmetic, which is not conducive to their numerical ability improvement. This paper devises a set of graphic teaching aids for primary school students’ mental arithmetic improvement based on mental arithmetic strategies, schema theory, and working memory. To validate the effectiveness of schema teaching in enhancing mental arithmetic ability among primary school students, a controlled experiment was conducted with two groups of third-grade students randomly selected from a primary school in Jingshan City. The results, obtained through descriptive statistical analysis and the multitrait—multimethod approach (MTMM), indicated that the experimental group (n = 52) demonstrated significant improvements in speed, accuracy, and stability in mental addition and subtraction after a 14-day instruction period in schema teaching. This study offers a potent mental arithmetic teaching strategy for elementary mathematics education, which can lead to a comprehensive enhancement of students’ mental calculation abilities. It also holds promise for inspiring innovative teaching methodologies in primary and secondary mathematics education in the future.

Citation: Liu D, Tan X, Yan H, Li W (2024) Improving mental arithmetic ability of primary school students with schema teaching method: An experimental study. PLoS ONE 19(4): e0297013. https://doi.org/10.1371/journal.pone.0297013

Editor: Michael B. Steinborn, Julius-Maximilians-Universität Würzburg, GERMANY

Received: September 6, 2023; Accepted: December 27, 2023; Published: April 16, 2024

Copyright: © 2024 Liu et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Data Availability: All relevant data are within the manuscript and its Supporting information files.

Funding: This research was funded by Hubei Provincial Education Science Planning 2022 Special Funding Project grant number 2022ZB23 and the key project of the 2022 Teacher Education Research Plan (No.HBJSJY2022-001). This funding was obtained by the first author DL in 2022. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Competing interests: The authors have declared that no competing interests exist.

1. Introduction

Numerical ability is fundamental to math learning. However, primary school students often perform poorly in the calculation, which is very likely to cause a series of problems. For example, in classroom teaching, slow calculation speed or low correct rate of students may not only affect the quality of individual mathematics learning, but also leads to a slower teaching pace of the overall teaching, which in turn affects the learning quality of the entire class. Richard Cowan (2011) pointed out that there is a high correlation between the calculation skills of simple addition and subtraction and the performance of mathematics among primary school students. In addition, numerical ability differs from mathematical ability in that the former can extend the application of mathematics to everyday situations, such as the counting of items in production activities, the sale of goods, and purchasing. And good numerical skills are very helpful in accomplishing these tasks [ 1 ].

Although “numerical skills” herein are discussed in the context of primary-school mathematics teaching, the teaching of it is not just a separate part from the teaching of mathematics, but rather an integral reflection on the ways in which mathematics is learned and its application to students’ lives. However, math teachers in Chinese primary schools often resort to simply explaining arithmetic rules and over-intensifying students’ calculation practice in an attempt to make their students’ numerical skills stand out through excessive exercises, especially in rural and township schools. McIntosh (2002) points out that traditional methods for numerical teaching are not sufficient to develop the numerical skills of primary school students in lower grades, and some of them may even receive counterproductive results. In the mathematics teaching process of these schools, mathematics is perceived as an arithmetic course with no meaningful pedagogical method, a view that has existed for decades [ 2 , 3 ].

LG Guthrie (2015) points out that when faced with arithmetic tasks, people often reorganize their physical displays by interacting with the environment, for example, perhaps moving coins around while counting money, taking notes with a pen, or gesturing, pointing or counting with their hands [ 4 ]. Obviously, all of these numerical behaviors affect calculation speed and correctness to varying degrees. But there is a more appropriate way, mental arithmetic. Mental arithmetic is a calculation method that relies on thinking and memory to arrive at an answer directly without the use of external tools, i.e., "oral arithmetic" commonly referred to. And it is an important thinking activity in daily activities [ 5 ], and closely related to working memory [ 6 ].

Existing research has found that multi-digit mental arithmetic plays an important role in teaching children how numbers work [ 7 ], how to decide on procedures, and how to create different strategies to solve math problems and promote a better understanding of number structure and its properties [ 8 ]. This body of research centers around the value of mental arithmetic skills to a child’s development, yet there is little current research on how to improve mental arithmetic skills. James R. Olsen (2015) also noted in his study that there are various reasons for this, for instance, mental arithmetic is often perceived to be based on an individual’s innate abilities, or there is no effective method to teach it but rigid extensive practice, with limited advancement as result [ 8 , 9 ].

Based on the theory of mental arithmetic strategy and the schema theory, this paper proposes a schema teaching method, which utilizes its unique coding advantages and is supplemented by targeted explanations for mental arithmetic training. The schema teaching method is characterized by intuitive operation, which allows students to actively recognize, think and construct codes in the process of operation. In order to test its effectiveness, this paper will use the experimental method to compare the advantages of the schema teaching method and the traditional teaching method in improving the mental arithmetic ability of primary school students.

2. Schema teaching method

2.1. mental arithmetic strategies.

A strategy comprises procedures aimed at achieving higher-level goals or tasks [ 10 ]. Generally, primary school students can employ two math calculation strategies: written and mental calculations. The written calculation involves using a pen on paper to achieve an answer, while mental arithmetic is performing operations mentally without external tools [ 11 ]. Mental arithmetic strategies entail computational procedures without external tools, relying on thought and memory [ 12 ]. They are of great significance to proficiency and personal performance in mental calculation.

The mental arithmetic strategies used by primary school students can be broadly categorized into three types: N10, 1010, and pen-and-paper mental image. In the N10 strategy, the second number in the expression of an addition/subtraction problem is divided into units and tens, which are then added or subtracted; whereas the 1010 strategy divides the two numbers into units, adds/subtracts units with tens, then reassembles the final result [ 13 ]. Pen-and-paper mental image strategy reflects that written calculation mentally, which is considered to be inefficient [ 14 ].

Facing varied calculations, primary students progress from counting to written, then combined calculations. In China, addition, subtraction, multiplication, and division are performed in vertical form with all calculations coming down to mental arithmetic up to 10 finally. Thus the higher the grade, the more mental arithmetic is emphasized [ 15 ]. And more research focuses on mental arithmetic’s impact on students’ success.

According to Campbell (1987), the general framework for understanding multiplication fact retrieval in speeded arithmetic posits two parallel processes: a fact-retrieval process based on memory, and a calculation-based process that employs algorithmic procedures. Both processes operate in parallel and are in competition with each other. In the context of multiplication calculations, an individual is capable of directly retrieving answers from pre-existing memory, or alternatively, employing mental calculation strategies based on addition to solve multiplication problems [ 16 ]. Logan (1988) also put forward a similar point of view, when a person wants to solve the arithmetic project, the strategy based on calculation and the strategy purely based on memory retrieval will compete with each other, implying that each unique trial is resolved either through retrieval from memory or through an algorithmic operation. Performance is considered automatic when it relies on direct-route retrieval of results from memory, a single-act process. Conversely, performance is considered controlled when it is dependent on algorithmic processing techniques such as counting, adding, memorising, borrowing, or negating a logical term [ 17 , 18 ].

Some empirical findings in the field of mental arithmetic can also prove the importance of memory retrieval strategies in mental arithmetic. The first one is the problem-size effect, which pertains to the finding that larger arithmetic problems (e.g., 9 + 8) generally take longer time to solve than smaller ones (e.g., 2 + 3) and that the relationship is linear in slope. The assumed reason is that smaller numbers are more frequently used by people. The second one is the tie-effect, which refers to the observation that arithmetic problems involving identical operands (e.g., 4 + 4 or 3 + 3) can be solved more quickly than equivalent non-ties (e.g., 4 + 3 or 3 + 2). Although there is no accepted reason for this, it is true that the sum of two identical numbers is visually more impressive than the sum of two different numbers to remember. The third one is the “carry-over to 10” effect, which relates to the additional cognitive effort required when performing an arithmetic operation that results in a carry-over to the next tens place (e.g., 7 + 6 = 13). The cognitive load increases because of the two-step process: adding the units and then carrying over the extra value to the next tens place [ 19 , 20 ].

Willis (1992) advocated that mental arithmetic should be the primary form of calculation, with written arithmetic as memory support [ 21 ]. However, the facts contradict the idea. Existing research shows that students often neglect learned strategies when solving math problems [ 22 ]. For this phenomenon, Blöte et al. (2000) identified the factors affecting their strategy preferences: lack of strategy awareness, weak recognition of strategy value, poor effort management on a strategy, and classroom atmosphere [ 23 ]. Considering Hiebert and Wearne’s emphasis on instruction (1996), mathematics instruction may be a key point in children’s choice of numerical strategies [ 14 ].

In light of the preceding analysis, this study advocates for an innovative mental arithmetic teaching method. It entails the development of novel instructional aids and a paradigm shift in the teaching method to mathematical mental computation. It also focuses on augmenting the consolidation of mnemonic schemas among primary education students via iterative exercises, and having unadulterated mnemonic retrieval mechanisms take the dominant position during mental calculation tasks, which helps facilitate a progressive shift from algorithmic to mnemonic processing modalities, thereby improving the speed and precision in mental arithmetic practice eventually.

2.2. Working memory and schema theory

Cognitive psychology suggests mental arithmetic comprises encoding, arithmetic, and response i.e., encoding information presented externally and then obtaining the answer through internal arithmetic knowledge extraction or arithmetic operations [ 24 ]. Hibbert and Lefebvre (1992) explain that primary students’ reluctance to use mental arithmetic is due to difficulty in encoding relationships and inadequate knowledge of placeholder values [ 25 ].

Concerning the knowledge base, this paper argues that primary school students lack working memory for some basic arithmetic formulas so that they cannot quickly complete operations that require rounding. And it is suggested that relationships or expressions between numbers be linked to them so that students can quickly extract their working memory when performing arithmetic operations. Difficulty in coding reflects the inability of primary school students to make abstract connections between numbers and understand the relationships and variations between numbers in the arithmetic process. It can be solved through a medium that is easy to comprehend and memorize.

The biggest challenge at this point is to find a numerical training means that can aptly address these two issues. During the encoding stage, information can be input into the information channel in different representations (e.g., visual or auditory forms), and it has been found that differences in the form of input not only have an impact on the encoding stage, but also on the extraction process of mental arithmetic [ 26 ]. Different ways of presenting mental arithmetic tasks can trigger different information representations of individuals. And reading arithmetic, compared with the visual arithmetic commonly used in previous teaching, may process the topic information more adequately by inputting it through both visual and auditory representations, which may help children in the lower grades to obtain better performance in simple mental arithmetic [ 27 ]. This implies that applying a schema-based approach to teaching can probably build the basis of this desired training means.

Stijn De Rammelaere (1999) pointed out that existing research has revealed two major determinants of mental arithmetic effects, namely, the organization of simple arithmetic facts in long-term memory and the processing of information in working memory. The first one has attracted many researcheres and quite extensive relevant results have been made (e.g., Anderson, 1983). However, the role of working memory in arithmetic has received little attention yet [ 28 , 29 ].

Working memory is a cognitive system with a limited memory capacity that is used to store information temporarily. But it has important implications for reasoning and guiding decisions and behavior. As part of memory, working memory stores recorded information temporarily so that it can be further included in or compared to long-term memory. It has been shown that working memory is crucial to mental arithmetic as all three components of it—the central executive, the phonological loop, and the visuospatial palette—play a role in mental arithmetic under different conditions. LG Guthrie (2015) explains the relationship more deeply. He put that mental arithmetic tasks often require strategic thinking and thoughtful information processing which needs enough time and effort. Beyond basic, well-rehearsed sums, the calculation is often considered to place a relatively high burden on an individual’s internal resources, such as working memory [ 30 ]. Through working memory and relevant executive functions, numbers are deposited, added, and manipulated to solve problems. The load on working memory varies with the complexity of the problem and domain-specific expertise (contribution of long-term memory). To reduce the load on internal resources, cognitive processes migrate to wherever it is easiest to perform “computation” and extend to external resources in dynamically distributed cognitive systems [ 31 ]. Individuals’ physical behaviors in their environments are not only integral to distributing the working memory load, but they also provide a scaffolding that allows for the development of new strategies and the expansion of cognitive scope [ 4 , 32 ,].

Furthermore, it has been pointed out that due to the limited capacity of working memory, people tend to organize recurring or interrelated information into chunks by recoding it in order to expand storage capacity [ 33 ]. Research on information chunking first originated in short-term memory, which pointed out that the main function of chunking is to store information [ 34 ]. Other research suggests that relative to short-term memory, chunking in working memory has an extra function of temporarily processing of information [ 35 ]. Therefore, the study of working memory also necessarily involves the process of chunking information [ 36 ]. Schema is exactly a kind of image that chunks and encodes information.

A schema is a cognitive or knowledge structure that exists in memory, abstracted from what the learner has in his or her life [ 37 ]. Gilboa (2017) put in his study that schemas are higher-level knowledge structures that organize lower-level representations from long-term memory. As generic reference templates, schemas can be compared with new information, and bind multiple features that appear consistently and simultaneously. Given their non-specific elements, commonalities between experiences can be reflected with considerable overlap and correlation. It should be noted that schemas are dynamic structures that can constantly evolve into new experiences and memories in a process of assimilation and conditioning [ 38 ].

The concept of memory as a dynamic, constructive process, with schemas as cognitive organizers, is widely accepted. Schemas are now fundamental in cognitive psychology, used not only in memory research but also for understanding complex cognitive processes.

Concept maps are a type of graph introduced by Novak et al. based on Ausubel’s meaningful learning theory as a mental tool to help learners construct and represent knowledge [ 39 , 40 ]. They consist of nodes and links representing learners’ understanding of a topic. The key concepts are called nodes. While being connected by different paths and relationships, they form propositions. According to Ausubel’s cognitive assimilation learning theory, meaningful learning occurs when learners organize new knowledge into hierarchies while exploring possible connections between different pieces of knowledge. Elaborative strategies, represented by concept mapping, are dominant in today’s educational psychology community, highly regarded among educators, and considered effective strategies for facilitating meaningful learning [ 41 ].

It is clear that schema-based memory efficiently connects elemental representations, aiding in forming working memory and understanding arithmetic relationships in a more visualized and clear way. The paper hypothesizes that a schema-based numerical training method effectively enhances students’ mental arithmetic ability.

2.3. Development and application of schema method

In cognitive development theory, Simonton (2022) posits that mental schema plays a vital role in cognitive processes. It is not merely a simple construction of past experiences; rather, it actively filters, screens, and organizes external stimuli in novel contexts, transforming them into a structured modular knowledge framework. By drawing upon existing knowledge and experiences, individuals understand objective objects and obtain the emotional experience of what kind of symbolic significance the objects "should" have and how they "should" be understood [ 42 , 43 ].

Based on the above theory, schema-based training aids were devised for subsequent experiments. These aids visually represent the fundamental building blocks of mental arithmetic. The initial step involves encoding numbers into visual symbols or phonetics, like representing "7" as a "sickle," "9" as a "balloon," and "16" as "shí liu" (pomegranate in Chinese). The following step is to merge these coded images into a coherent narrative, focusing on creating a proportional visual representation, where the sum’s image is noticeably larger than the addends’ images., For example, in equation 7+9 = 16, the images for "sickle" and "balloon" are smaller compared to the image for "pomegranate." This step then combines with the story "a sickle from the huge pomegranate dug out a balloon" to interlink these images. The final graphic aids were thus developed. We have developed a total of 45 diagrams (see S1 Appendix ) ranging from 1+1 = 2 to 9+9 = 18, covering all single-digit addition equations. In addition, because each graphic aid distinguishes between "addition" and "sum" by the size of the picture, each graphic actually represents four equations, e.g., Fig 1 represents 7+9 = 16, 9+7 = 16, 16–7 = 9, and 16–9 = 7. Compared to traditional methods, schema-based instruction offers lower cognitive strain, increased engagement of students, and a multi-sensory approach integrating kinesthetic sense, five senses, and images characterized by interesting and unique, fostering stronger connections between working memory and long-term memory and transforming working memory to long-term memory, thus improving the retention of memory. Additionally, the approach is more reliable and helpful for addressing persistent errors.

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

https://doi.org/10.1371/journal.pone.0297013.g001

Implementing this form of graphic teaching aids for mental arithmetic is straightforward. First, students familiarize themselves with and memorize the number codes from 1 to 18. Then, the schemas are introduced, encouraging students to create their narratives based on the images to deepen their understanding. Next, relying on the image categories and proportions, the students have to convert the schemas to arithmetic equations. Finally, calculation training was given to enhance students’ proficiency in translating schemas into arithmetic equations and vice versa.

As shown in Fig 1 , the schema uses a red flag, a sickle, and a ladder to represent the numbers "4", "7" and "11", respectively, with the red flag and the sickle geometrically connected to each other acting together on the ladder—representing the equation 4+7 = 11. The schema in Fig 2 has the gourd representing the number "8" and the pomegranate representing the number "16". The two gourds together are connected to the pomegranate—representing the equation 8+8 = 16.

https://doi.org/10.1371/journal.pone.0297013.g002

3. Research methods

3.1. participants.

In this study, the experiment locale was determined by randomly selecting one township from all those within Jingshan County of Jingmen City located in Hubei Province, P.R. China. Subsequently, a single primary school was randomly chosen within this township to serve as the study site, and the third-grade pupils served as the subject source. From this institution, four out of six third-grade classes were randomly selected. Within these selected classes, a cohort of 104 students was randomly invited for participation in the study. These participants were then randomly allocated into either an experimental group or a control group. The control group consisted of 28 male and 24 female students, with a mean age of 9 years. Similarly, the experimental group included 25 male and 27 female students, with the same mean age. The study was conducted in line with the ethical principles of the Declaration of Helsinki and of the American Psychological Association(APA). The study was approved by the ethics committee of the Ethics Professional Committee of Brain Science and Learning Science Committee of Hubei Teachers Education Association(Numbering: S2023-027-2). All procedures were in accordance with the approved guidelines and regulations. Subjects were compensated for their participation.

3.2. Procedure

The instruction of mental arithmetic necessitates students to possess not only problem-solving abilities but also proficiency in performing arithmetic calculations swiftly to meet stipulated time standards. In our fieldwork, we observed that a majority of teachers primarily emphasize the accuracy of calculation outcomes during arithmetic instruction, with the requirement for speed being vaguely defined. However, some research demonstrated a significant and positive correlation between mental arithmetic competence and working memory, processing speed, as well as executive function. Overlooking training in processing speed and executive function, as revealed by their study, detrimentally impacts the execution of the mental arithmetic computational process. Insufficient processing speed is manifested in mental arithmetic as delayed response, impaired executive function, and inability to simultaneously memorize and output [ 44 ]. Therefore, we adopted both the temporal and accuracy dimensions of mental arithmetic as indicators for gauging mental arithmetic proficiency in our experimentation.

Within this study, mental arithmetic refers to the presentation of questions in a visual form, where the subjects peruse the queries on the test paper and transcribe the answers on the test paper after calculating in their mind without recourse to any penmanship or other computational tools [ 45 ]. In order to ensure the accurate reflection of students’ mental arithmetic ability, the students are required to write down the answers as promptly as possible, thereby confirming their utilization of working memory within their long-term memory framework.

The experiment design followed a pretest and post-test structure employing the pre-addition and pre-subtraction scales, drawn from the Center for Brain Science and Learning Power Research of Hubei Second Teachers College. Each of these scales encompassed 44 addition test questions and 44 subtraction test questions, respectively, each scales incorporated an exhaustive set of single-digit addition or subtraction questions. The sequence of these questions was systematically randomized to ensure a non-repetitive and scrambled arrangement, precluding any duplication of mathematical expressions. detailed in the S2 Appendix .

Prior to the commencement of the experiment, a pretest was administered to both the experimental and control groups, with the time taken and error rates in addition and subtraction tests recorded as baseline data. Research suggests that under instructions emphasizing speed, students are more likely to employ memory retrieval strategies for arithmetic tasks [ 46 ]. Therefore, during testing, participants were also instructed to “calculate at their fastest speed”, thereby ensuring the predominant use of such strategies. In post instruction, a controlled experimental approach was adopted. Over a continuous period of 14 days, within the control group, assistant teachers organized supervised traditional calculation drills, encompassing 20-minute sessions of one- and two-digit addition and subtraction practice. Next, an additional 10-minute period was allocated for the explanation and analysis of common error-prone problems with pre-recorded online lessons. Conversely, students in the experimental group watched a 20-minute instructional video on the schema-based mental arithmetic method uniformly every day for the first 7 days. The video provides a vivid analysis of each set of computational schema composition, followed by a 10-minute review of previously covered schemas each time, with the help of the pre-recorded instructional video. The videos were consistently presented by the same volunteer teacher to avoid variances out of teacher in teaching. The last 7 days consisted of 20-minute sessions of one- and two-digit addition and subtraction arithmetic exercises, which required students to associate the corresponding schemas when solving the problems. Following 14 days of training, the mental arithmetic skills of both control and experimental students were tested on the 15th day, by means of uniform addition and subtraction post-test scales. Similarly, students were instructed to work out the results as quickly as possible, with their single test duration and scores being recorded as post-test data. To maintain experimental integrity, the experimental and control groups were segregated into different classrooms for the post-tests, each with teacher supervision to prevent inter-group communication. This segregation effectively concealed perception of group differences among the participants, ensuring a placebo effect in the experimental design.

3.3. Data collection and analysis

Each experiment requires the integrated coordination of elemental acts. The rationale proposed by the Individual Differences in Response Time (IDRT) model [ 47 ] and the multitrait—multimethod (MTMM) approach [ 48 , 49 ] was applied as a heuristic method to assess the convergent and discriminant validity of competing performance measures. Subsequently, following the completion of each test, a descriptive statistical analysis was initially conducted with Excel tool for response times (RT) and error percentages (ER) of each participant in both the experimental and control groups. Then, with the help of SPSS software, the descriptive statistics for pretest and post-test data of the two groups were computed, encompassing measures such as the average response time (RTM), average error rate (ERM), variance (SD), skewness (Skew), and the Mann-Whitney U test was conducted to derive the corresponding p-values. Following this, leveraging the descriptive statistical data, we utilized Python to compute the correlation between pretest and post-test RT and ER, thereby establishing a Multitrait-multimethod-matrix to evaluate the reliability, as well as convergent and discriminant correlations, of the alternative performance indices in the self-paced speed tests.

4.1 Descriptive statistical analysis of the experimental and control groups

As depicted in Table 1 , the addition test duration was 103.8 seconds for the control group and 103.1 seconds for the experimental group. These two means demonstrate a high degree of proximity, and the Mann-Whitney U test indicated that there was no significant difference between the results of the two groups (p = 0.899>0.05). Likewise, the subtraction test time was 104.2 seconds for the control group and 104.9 seconds for the experimental group. Once again, no significant difference was evident (p = 0.534>0.05). Therefore, there exists no significant difference between the control and the experimental groups in terms of the time spent on addition and subtraction tests.

https://doi.org/10.1371/journal.pone.0297013.t001

In contrast to the pretest findings, a significant difference emerged in the post-test durations between the experimental and control groups. Specifically, the mean addition post-test duration was 94.7 seconds for the control group and 87.7 seconds for the experimental group, resulting in a significant difference of 7.02 seconds (p = 0.003<0.05). Similarly, the mean subtraction duration was 98.6 seconds for the control group and 91.8 seconds for the experimental group, showing a significant gap of 6.8 seconds (p = 0.044<0.05). For the same set of problems, a shorter time taken indicates a faster mental calculation speed. Participants who underwent schema training exhibited superior speed in both addition and subtraction compared to the control group.

The data were analyzed from the perspective of standard deviation. The standard deviation of the addition and subtraction pretesting time of the control group was 11.86 and 12.59 respectively, and that of the experimental group was 12.86 and 12.31 respectively. This indicates a comparable level of dispersion between the two groups. On the other hand, the standard deviation of addition and subtraction post-testing time of the control group was 8.16 and 14.22 respectively, and that of the experimental group was 15.59 and 15.73 respectively. It can be concluded that there is a greater difference in the testing durations of students trained with the schema teaching method compared to the traditionally trained students, which might be closely related to learning efficiency, attitudes during the learning process, and adaptation to the novel instructional approach.

Table 2 presents the differences in error rates between pretest and post-test assessments for the control and experimental groups. As indicated in the tables, there were no significant differences in pretest error rates for addition between the two groups (p = 0.073>0.05). Similarly, no significant differences were observed in pretest error rates for subtraction (p = 0.243>0.05). Thus, there were no significant differences in error rates for addition and subtraction pretests between them. In contrast, the mean error rate for addition post-tests in the control group was 0.08, while the experimental group exhibited a mean error rate of 0.01, indicating a significant difference (p = 0.00*<0.05). For subtraction post-tests, the control group had a mean error rate of 0.05, whereas the experimental group had that of 0.03, also showing a significant difference (p = 0.00*<0.05). This suggests that students in the experimental group, who underwent schema training, demonstrated higher accuracy in both addition and subtraction compared to the control group.

https://doi.org/10.1371/journal.pone.0297013.t002

From the perspective of standard deviation, statistical analysis of the standard deviations of error rates in addition and subtraction tests for the control and experimental groups revealed noteworthy patterns. On one hand, the standard deviations for all post-tests were smaller than those for pretests, indicating a reduction in the variability of error rates among students after the assessments. On the other hand, the standard deviation for addition post-tests in the experimental group (0.01) was significantly smaller than that in the control group (0.06). Similarly, the standard deviation for subtraction post-tests in the experimental group (0.03) was smaller than that in the control group (0.05). These results suggest that experimental group exhibited lower variability in error rates and its students showed greater stability in mental calculation accuracy compared to their counterparts in the control group.

The aforementioned findings underscore a significant increase in students’ calculation speed and accuracy after training of the schema teaching method. This improvement can be attributed to the achievement of automatization in arithmetic skills. An individual can directly extract the answers to arithmetic problems from long-term memory without conscious cognitive manipulation, a process known as automated extraction [ 50 , 51 ]. Arithmetic units composed of basic arithmetic knowledge that has been repeatedly practiced and experienced to the extent of automated extraction [ 18 , 52 ] transform into arithmetic automata [ 53 ].

In summary, comparing the results of test duration and test error rates, it is evident that the schema teaching method is more conducive to enhancing students’ mental calculation abilities. Regarding test duration, the effectiveness of the method is pronounced, as the experimental group took significantly shorter testing times compared to the control group after training. In terms of test error rates, there were significant differences between the post-test error rates of the experimental group and the control group, with the former performing better than the latter. Therefore, the schema-based calculation training method is of the potential to accelerate, improve, and stabilize learners’ mental arithmetic abilities.

4.2 Correlation analysis of the experimental and control groups

Retest reliability..

Reliability coefficients are presented on the main diagonal of the correlation matrix ( Table 3 ), illustrating the correlations between pretest and post-test administrations. The reaction time (RT) for addition in the control group (r = 0.886), subtraction in the control group (r = 0.983), addition in the experimental group (r = 0.980), and subtraction in the experimental group (r = 0.991) demonstrate high reliability. Additionally, the error rates (ER) for addition in the control group (r = 0.967), subtraction in the control group (r = 0.907), addition in the experimental group (r = 0.854), and subtraction in the experimental group (r = 0.860) exhibit good reliability. It is noteworthy that considering the generally low or insufficient reliability of error scores in most mental calculation tasks (Maloney et al., 2010; Steinborn et al., 2016, 2018; Hedge et al., 2018, for an overview), the obtained reliabilities for error rates are substantial [ 54 – 56 ].

https://doi.org/10.1371/journal.pone.0297013.t003

Correlational structure.

In the tests for addition and subtraction in both the control and experimental groups, the correlations between average response time (RTM) and error rate (ER) are consistently low, with correlation coefficients (r values) generally below 0.1 ( Table 3 ). This suggests a lack of association between RTM and ER during mental calculation processes. This conclusion further supports the notion that the schema-based mental arithmetic training method enables the learners to enhance both their calculation speed and accuracy.

Obviously, the schema teaching method effectively solves the problems faced by students during mental arithmetic exercises. Additionally, it allows students to transcend reliance on pen-and-paper mental image calculation. The advantage of graphical teaching lies in the seamless integration of multiple encoded graphs, forming a coherent memory structure, which is exactly the right match for the two-digit addition and subtraction involving three elements, consequently leading to notable enhancements in calculation speed and accuracy, thus achieving instructional objectives. The outcomes of this test confirm the conjecture presented in this paper that the schema training method is an effective training method for augmenting students’ mental arithmetic ability.

At the end of the post-test, a survey was conducted to ascertain the calculation strategies adopted by students in the experimental group during the test. An overwhelming 83% of the students responded that they employed the “schematic coding" approach independently, while only 17% continued to use the method of "working with numbers in their head". This finding implies that this study’s teaching method, rooted in schemas, effectively addresses students’ inclination to circumvent the utilization of mental arithmetic strategies.

5. Conclusion and prospect

5.1 conclusion.

In response to the current state of mental arithmetic practice of elementary school students, numerous scholars have suggested that children should be encouraged to develop their own mental arithmetic strategies [ 57 ]. However, in practice, teachers and students often equate "computational ability" with "computational skills," failing to create effective and generally accessible mental arithmetic strategies [ 14 ]. This study conducts experimental research with schema encoding viewed as a memory support for mental arithmetic expressions.

The results of the study robustly demonstrate a significant improvement in students’ mental arithmetic abilities through schema-based mental arithmetic training. In both addition and subtraction tests for the control and experimental groups, schema training exhibited out-standing effectiveness in terms of Response Time (RTM) and Error Rate (ER) (in the addition and subtraction tests, with the pretest RTM almost being equal between the control and experimental groups, reduction of the post-test duration time in the experimental group was 1.69 times that of the control group for addition and 2.34 times for subtraction. In terms of ER, with the pretest ER almost being equal between the two groups, the post-test ER reduction in the experimental group was 2 times for addition and 1.43 times for subtraction compared to the control group). Additionally, the stability and reliability of the results was confirmed. These findings indicate together that through schema-based teaching, students can effectively enhance mental arithmetic speed and accuracy, overcoming the issues of speed and accuracy faced in traditional mental arithmetic processes.

The low correlation between RTM and ER in both the control and experimental groups further supports the effectiveness of schema training. This suggests that students under schema training can independently use schema encoding to obtain answers, other than overly relying on traditional pen-and-paper mental imagery algorithms. This not only enhances the efficiency of mental arithmetic but also indicates that schema training enables students to confidently tackle mental arithmetic tasks, lifting them out of dependence on external tools.

5.2 Contributions and significance of the study

The major contribution of this research lies in revealing the outstanding effects of schema-based mental arithmetic training in improving students’ mental arithmetic speed and accuracy. Systematic experimentation demonstrates that schema training is not only theoretically feasible but also yields significant educational outcomes in practical applications. This discovery provides an innovative and viable teaching method for the field of mental arithmetic education, simultaneously offering students a more effective learning path.

The significance of the study extends beyond uncovering the positive impact of schema training on mental arithmetic abilities; it also provides an innovative teaching method for mental arithmetic education. Traditional mental arithmetic teaching often neglects students’ avoidance of mental arithmetic strategies, but this study effectively addresses this issue through schema-based teaching, offering new perspectives for the future development of mental arithmetic education. Future research and practice can draw upon the teaching method employed in this study to further explore the applicability of schema training in different backgrounds and conditions, better serving the learning needs of diverse students, eventually to make a positive contribution to driving innovative development in the education sector.

5.3 Recommendations

Based on the outcomes of this research, it is recommended to actively promote schema training as an effective means of mental arithmetic education in schools and educational institutions. By leveraging modern technological tools, such as smartphone applications and online learning platforms, to integrate schema training into digital education, teaching flexibility and accessibility can be enhanced, allowing more students to benefit from schema training. Educators can expand the adoption of this innovative teaching method by providing relevant training and teaching resources.

It has to be admitted, this experiment has its limitations. For instance, the sample in the experiment is relatively small, with the participants concentrated in rural schools in a specific region. Subsequent research can expand the source and increase the quantity of participants, and prolong the testing period for further validation. Further investigation into the applicability of schema training across different age groups and academic disciplines is warranted, which would contribute to a more comprehensive understanding of the educational potential of schema training and provide guidance for tailoring more specific teaching strategies. Additionally, exploring whether students trained with schema can exhibit outstanding performance in mathematical application abilities, innovation, and metacognition should also be a subject for further exploration.

Supporting information

https://doi.org/10.1371/journal.pone.0297013.s001

https://doi.org/10.1371/journal.pone.0297013.s002

S1 Appendix. Appendix A.

https://doi.org/10.1371/journal.pone.0297013.s003

S2 Appendix. Appendix B.

https://doi.org/10.1371/journal.pone.0297013.s004

Acknowledgments

The authors are grateful for the support of the Hubei University of Education and Brain Science and Learning Science Committee of Hubei Teachers Education Association.

• View Article
• Google Scholar
• PubMed/NCBI
• 24. Handbook of mathematical cognition[M]. Psychology Press, 2005.
• 25. Sowder J T. Making sense of numbers in school mathematics[M]. Analysis of arithmetic for mathematics teaching. Routledge, 2020: 1–51.

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Mental Math Worksheets Hub Page

Welcome to our Mental Math worksheets for developing quick and accurate mental arithmetic skills.

On this page are links to our collection of worksheets which will help your child improve their mental calculation and problem solving skills and learn their Math facts.

We also have links to our Math fact resources and online practice zones to help develop mental arithmetic.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

• This page contains links to other Math webpages where you will find a range of activities and resources.
• If you can't find what you are looking for, try searching the site using the Google search box at the top of each page.

Mental Math Worksheets

The best way to improve your mental arithmetic is to practise regularly. Even 5 minutes daily practise can make a huge difference in a matter of weeks.

Below you will find links to many different webpages containing mental math worksheets as well as mental arithmetic sheets for each of the 4 operations: addition, subtraction, multiplication and division.

There are also some links to printable math games which you can print and play at home, and watch as your child progresses.

Mental Math Tests / Quizzes

Here you will find a range of printable mental math quizzes to help your child revise their math facts and problem solving skills.

The tests/quizzes are perfect for general practice, or for keeping skills sharp.

Each quiz tests the children on a range of math topics from number facts and mental arithmetic to geometry, fraction and measures questions.

A great way to revise topics, or use as a weekly math quiz!

• First Grade Mental Math
• Mental Math Worksheets 2nd Grade
• Mental Math 3rd Grade
• Mental Math Worksheets 4th Grade
• Mental Math 5th Grade
• Mental Math Worksheets 6th Grade

UK Mental Maths Worksheets

Here you will find a range of printable mental math worksheets for children in the UK to enjoy.

The language and maths skills have been adapted to support learning for primary age children.

• Mental Maths Worksheets UK

Mental Arithmetic Resources

Here you will find our selection of free resources such as flashcards and 100 squares to help your child to count and learn their addition facts.

• Math Fact Resources

Here you will find a selection of number bond sheets designed to help your child improve their recall of their number bond facts.

Online Number Bonds Practice

In our Number Bonds Practice area, you can practice your number bonds to a variety of numbers. Test your numbers bonds to 10, 20 , 100 or even 1000. Want to try decimals - you can do that too!

Select the numbers you want to practice with, and print out your results when you have finished.

You can also use the practice zone for benchmarking your performance, or using it with a group of children to gauge progress.

• Number Bonds Practice Zone

Number Bond Sheets

• Number Bonds to 10 and 12
• Number Bonds to 20
• Number Bonds to 50 and 100

Addition Mental Math Sheets

Here you will find a selection of mental math worksheets designed to help your child improve their recall of Addition Facts.

• Addition Practice Zone

Here is our online learning math addition zone, where you can practice a range of integer addition calculations.

Test yourself on the following addition facts:

• up to 5+5, 10+10, 20+20, 50+50, 100+100, or 1000+1000;
• 2 digit numbers adding ones;
• 2 digit numbers adding tens;
• 3 digit numbers adding hundreds;

Addition Worksheet Generator

Here is our free generator for addition worksheets.

This easy-to-use generator will create randomly generated addition worksheets for you to use.

Each sheet comes complete with answers if required.

The areas the generator covers includes:

• addition with numbers up to 10, 15, 20, 50, 100 and 1000;
• addition by 10s with 2 digit numbers;
• addiiton by 100s with 3 digit numbers;
• addition with numbers to 10 with one decimal place;
• addition with numbers to 1 with 2 decimal places.

These generated sheets can be used in a number of ways to help your child with their addition fact learning.

• Free Addition Worksheets (randomly generated)

Adding to 10 Sheets

Here you will find a selection of mental math worksheets designed to help your child improve their adding up to a total of 10.

Using these sheets will help your child learn to:

• add numbers up to a total of 10.
• Addition Math Worksheets to 10

Adding to 12+12

Here you will find a range of mental math worksheets designed to help you child to learn their Addition facts to 12+12.

• Addition Fact Practice to 12
• Addition Facts to 20 Worksheets
• First Grade Addition and Subtraction to 12

Addition to 20+20

Here you will find a range of Addition Sheets designed to help you child to learn their Addition facts to 20+20.

• Math Addition Facts to 20

Addition to 100+100

The following mental math worksheets develop children's knowledge of practicing their Addition facts up to 100+100.

• Third Grade Addition Facts Worksheets to 100+100

Decimal Addition Facts

The following sheets develop children's understanding of place value and decimals as well as applying their addition fact knowledge of to work out their decimal addition facts.

• Decimal Math Worksheets

Subtraction Fact Sheets

Here you will find a selection of Mental Subtraction sheets designed to help your child improve their recall of Subtraction Facts.

Online Subtraction Practice Zone

Here is our online learning math subtraction practice area where you can test yourself on your subtracting skills.

Test yourself on the following integer subtraction facts:

• up to 10, 15, 20, 50, 100, 200, 500 or 1000;
• 2 digit subtract ones;
• 2 digit subtract tens;
• 3 digit subtract hundreds.
• Subtraction Practice Zone

Subtraction Worksheet Generator

Here is our free generator for subtraction worksheets.

This easy-to-use generator will create randomly generated subtraction worksheets for you to use.

• subtraction with numbers up to 10, 15, 20, 50, 100 and 1000;
• subtraction by 10s from 2 digit numbers;
• subtraction by 100s from 3 digit numbers;
• subtraction with numbers to 10 with one decimal place;
• subtraction with numbers to 1 with 2 decimal places;
• subtraction involving negative numbers.
• Free Subtraction Worksheets (randomly generated)

Subtracting to 10 Sheets

Here you will find a selection of Subtraction sheets designed to help your child learn their Subtraction facts up to 10.

• Kindergarten Subtraction Worksheets (easier)
• Subtraction to 10 Worksheets (harder)
• Subtraction Facts to 12

Here you will find a range of Free Printable First Grade Subtraction Sheets designed to help you child to learn their Subtraction facts to 12.

Subtraction Facts to 20

Here you will find a range of Free Printable 2nd Grade Subtraction Sheets designed to help you child to learn their Subtraction facts to 20.

• Subtraction Facts to 20 Worksheets

Subtraction Facts to 100

The following sheets develop children's knowledge of their Subtraction facts up to 100.

• Third Grade Subtraction Worksheets to 100

Decimal Subtraction Facts

The following sheets develop children's understanding of place value and decimals as well as applying their Subtraction fact knowledge to work out their decimal Subtraction facts.

• Subtracting Decimals Worksheets (mental)

Multiplication Times Tables Sheets

Here you will find a selection of Mental Multiplication sheets designed to help your child improve their mental recall of Multiplication Facts and learn their times tables.

Online Multiplication Test

Here is our online learning math practice zone for multiplication facts.

Using this zone is a great way to test yourself on your facts and see how many you can do in a minute.

Then re-test yourself and see if you can improve your score.

Using this zone, you can:

• choose tables up to 5x5, 10x10 or 12x12 to test yourself on;
• select one or more tables to test yourself on;
• practice multiplying whole numbers by 10 or 100.
• Online Multiplication Zone

Multiplication Worksheet Generator

Here is our free generator for multiplication worksheets.

This easy-to-use generator will create randomly generated multiplication worksheets for you to use.

• Multiplying with numbers to 5x5;
• Multiplying with numbers to 10x10;
• Multiplying with numbers to 12x12;
• Practicing a single times table;
• Practicing selected times tables;

These generated sheets can be used in a number of ways to help your child with their times table learning.

• Times Tables Worksheets (randomly generated)

Tiimes Table Graded Sheets

As your child progresses through the grades, they will learn their multiplication table to 5x5 and eventually to 10x10, or 12x12.

Once they know their multiplication facts, they can start to learn related facts, e.g. if 3 x 4 = 12, then 30 x 4 = 120 and $300 x 4 = $1200.

• Math Times Table Worksheets

Multiplication by 10s and 100s

These Multiplication Printable Worksheets below are designed to help your child improve their ability to multiply a range of numbers by multiples of 10 and 100 mentally.

• Multiplying by Multiples of 10 and 100

Mental Multiplication Decimals

These Multiplication Printable Worksheets below involve children using their multiplication table facts to answer related questions involving decimals.

• Multiplying Decimals by Whole Numbers

Division Fact Sheets

Here you will find a selection of Mental Division sheets designed to help your child improve their recall of Division Facts and to apply their facts to answer related questions.

Online Division Practice Area

Here is our free division practice area.

If you want to practice your division facts, or take a timed division test, then this is the place for you.

In this area, we cover the following division facts:

• division facts up to 5x5, up to 10x10 or up to 12x12;
• division facts linked to individual tables facts;
• dividing by 10 and 100.
• Division Practice Zone

Division Worksheet Generator

Here is our free generator for division worksheets.

This easy-to-use generator will create randomly generated division worksheets for you to use.

• Dividing with numbers to 5x5;
• Dividing with numbers to 10x10;
• Dividing with numbers to 12x12;
• Dividing with a single times table;
• Practicing division with selected times tables;

These generated sheets can be used in a number of ways to help your child with their division table learning.

• Division Facts Worksheets (randomly generated)

Division Facts to 10x10 Sheets

Here you will find a selection of Division sheets designed to help your child learn their Division facts up to 10x10.

Example: if a child knows that 5 x 4 = 20, then they should also know that 20 ÷ 5 = 4 and 20 ÷ 4 = 5.

• Division Facts to 10x10 Worksheets

Division Related Facts 10s and 100s

Here you will find a selection of Division sheets designed to help your child learn to use their Division facts up to 10x10 to answer related questions.

Example: if you know that 42 ÷ 6 = 7, then you also know that 420 ÷ 6 = 70 or 420 ÷ 70 = 6, etc.

• Divding by Multiples of 10 and 100 Worksheets

Math Fact Games

Here you will find a range of Free Printable Math Fact Games.

The following games develop a range of mental Math skills in a fun and motivating way.

Using these sheets will help your child to:

• learn their Math facts;
• develop their strategic thinking skills.
• Math Addition Games
• Subtraction Games
• Multiplication Math Games
• Math Division Games

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return from Mental Math Worksheets to Math Salamanders Home Page

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Uncovering the interplay between drawings, mental representations, and arithmetic problem-solving strategies in children and adults

• Published: 12 February 2024

Cite this article

• Hippolyte Gros   ORCID: orcid.org/0000-0002-4151-0715 1 ,
• Jean-Pierre Thibaut 2 &
• Emmanuel Sander 3  

361 Accesses

59 Altmetric

Explore all metrics

There is an ongoing debate in the scientific community regarding the nature and role of the mental representations involved in solving arithmetic word problems. In this study, we took a closer look at the interplay between mental representations, drawing production, and strategy choice. We used dual-strategy isomorphic word problems sharing the same mathematical structure, but differing in the entities they mentioned in their problem statement. Due to the non-mathematical knowledge attached to these entities, some problems were believed to lead to a specific (cardinal) encoding compatible with one solving strategy, whereas other problems were thought to foster a different (ordinal) encoding compatible with the other solving strategy. We asked 59 children and 52 adults to solve 12 of those arithmetic word problems and to make a diagram of each problem. We hypothesized that the diagrams of both groups would display prototypical features indicating either a cardinal representation or an ordinal representation, depending on the entities mentioned in the problem statement. Joint analysis of the drawing task and the problem-solving task showed that the cardinal and ordinal features of the diagrams are linked with the hypothesized semantic properties of the problems and, crucially, with the choice of one solving strategy over another. We showed that regardless of their experience, participants’ strategy use depends on their problem representation, which is influenced by the non-mathematical information in the problem statement, as revealed in their diagrams. We discuss the relevance of drawing tasks for investigating mental representations and fostering mathematical development in school.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Similar content being viewed by others

Interpreting young children’s multiplicative strategies through their drawn representations

Model method drawing acts as a double-edged sword for solving inconsistent word problems

Unpacking associations among children’s spatial skills, mathematics, and arithmetic strategies: decomposition matters

Data availability.

All data and materials for this study are available online at https://osf.io/nhp4e/?view_only=6a5e4fd4dedb4811a994030b988033a8 .

Agrell, B., & Dehlin, O. (1998). The clock-drawing test. Age and ageing, 27 (3), 399–404. https://doi.org/10.1093/ageing/afs149

Article   Google Scholar  

Anderson, S. F., & Kelley, K. (2018), BUCSS: Bias and Uncertainty Corrected Sample Size [computer software and manual]. R package version 1.2.1, https://CRAN.R-project.org/package=BUCSS

Anderson, S. F., Kelley, K., & Maxwell, S. E. (2017). Sample-size planning for more accurate statistical power: A method adjusting sample effect sizes for publication bias and uncertainty. Psychological Science, 28 (11), 1547–1562

Article   PubMed   Google Scholar  

Baccaglini-Frank, A., Carotenuto, G., & Sinclair, N. (2020). Eliciting preschoolers’ number abilities using open, multi-touch environments. ZDM, 52 , 779–791.

Bagnoud, J., Burra, N., Castel, C., Oakhill, J., & Thevenot, C. (2018). Arithmetic word problems describing discrete quantities: EEG evidence for the construction of a situation model. Acta Psychologica, 190 , 116–121.

Bainbridge, W. A. (2022). A tutorial on capturing mental representations through drawing and crowd-sourced scoring. Behavior Research Methods, 54 (2), 663–675.

Bainbridge, W. A., Hall, E. H., & Baker, C. I. (2019). Drawings of real-world scenes during free recall reveal detailed object and spatial information in memory. Nature communications, 10 (1), 5.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Bakar, K. A., Way, J., & Bobis, J. (2016). Young children’s drawings in problem solving . Mathematics Education Research Group of Australasia.

Google Scholar  

Barrios, F. M. G., & Martínez, E. C. (2014). Diagrams produced by secondary students in multiplicative comparison word problems. Journal of Mathematics and System Science, 4 (2), 83.

Bassok, M. (2001). Semantic alignments in mathematical word problems. In D. Gentner, K. J. Holyoak, & B. N. Kokinov (Eds.), The analogical mind: Perspectives from cognitive science (pp. 401–433). MIT Press.

Chapter   Google Scholar  

Berkum, J. J. V., Hagoort, P., & Brown, C. M. (1999). Semantic integration in sentences and discourse: Evidence from the N400. Journal of Cognitive Neuroscience, 11 (6), 657–671.

Bermejo, V. (1996). Cardinality development and counting. Developmental Psychology, 32 (2), 263–268.

Burgess, A. W., & Hartman, C. R. (1993). Children’s drawings. Child Abuse & Neglect, 17 (1), 161–168.

Article   CAS   Google Scholar  

Carruthers, E., & Worthington, M. (2003). Children’s mathematics: making marks, making meaning . Sage.

Chamberlain, R., & Wagemans, J. (2016). The genesis of errors in drawing. Neuroscience & Biobehavioral Reviews, 65 , 195–207.

Cheung, C. N., & Lourenco, S. F. (2019). Does 1+ 1= 2nd? The relations between children’s understanding of ordinal position and their arithmetic performance. Journal of Experimental Child Psychology, 187 , 104651.

Colomé, À., & Noël, M. P. (2012). One first? Acquisition of the cardinal and ordinal uses of numbers in preschoolers. Journal of Experimental Child Psychology, 113 (2), 233–247.

Coquin-Viennot, D., & Moreau, S. (2003). Highlighting the role of episodic model in the solving of arithmetical problems. European Journal of Psychology and Education, 18 , 267–279.

Cox, R. (1999). Representation construction, externalised cognition and individual differences. Learning and Instruction, 9 (4), 343–363.

Crespo, S. M., & Kyriakides, A. O. (2007). Research, Reflection, Practice: To Draw or Not to Draw: Exploring Children’s Drawings for Solving Mathematics Problems. Teaching Children Mathematics, 14 (2), 118–125.

Csíkos, C., Szitányi, J., & Kelemen, R. (2012). The effects of using drawings in developing young children’s mathematical word problem solving: A design experiment with third-grade Hungarian students. Educational Studies in Mathematics, 81 (1), 47–65.

Cummins, D. D. (1991). Children’s interpretations of arithmetic word problems. Cognition and Instruction, 8 (3), 261–289.

Dantzig, T. (1945). Number the language of science. A critical survey written for the cultured non-mathematician . The Macmillan Company.

Daroczy, G., Wolska, M., Meurers, W. D., & Nuerk, H. C. (2015). Word problems: A review of linguistic and numerical factors contributing to their difficulty. Frontiers in Psychology, 6 , 348.

Article   PubMed   PubMed Central   Google Scholar  

Dauben, J. W. (1990). Georg Cantor: His mathematics and philosophy of the infinite . Princeton University Press.

De Bock, D., & Verschaffel, Janssens D. (1998). The predominance of linear model in secondary students’ solutions of word problems involving length and area of similar plane figures. Education Studies in Mathematics, 35 (1), 65–83.

De Bock, D., Verschaffel, L., Janssens, D., Van Dooren, W., & Claes, K. (2003). Do realistic contexts and graphical representations always have a beneficial impact on students’ performance? Negative evidence from a study on modelling non-linear geometry problems. Learning and Instruction, 13 (4), 441–463.

De Corte, E., Verschaffel, L., & De Win, L. (1985). Influence of rewording verbal problems on children’s problem representations and solution. Journal of Educational Psychology, 77 , 460–470.

Draschkow, D., Wolfe, J. M., & Vo, M. L. H. (2014). Seek and you shall remember: Scene semantics interact with visual search to build better memories. Journal of Vision, 14 (8), 10–10.

Edens, K., & Potter, E. (2007). The relationship of drawing and mathematical problem solving: Draw for math tasks. Studies in Art Education, 48 (3), 282–298.

Edens, K., & Potter, E. (2008). How students “unpack” the structure of a word problem: Graphic representations and problem solving. School Science and Mathematics, 108 (5), 184–196.

Ericsson, K. A., & Simon, H. A. (1980). Verbal reports as data. Psychological Review, 87 (3), 215.

Fan, J. E. (2015). Drawing to learn: How producing graphical representations enhances scientific thinking. Translational Issues in Psychological Science, 1 (2), 170.

Fan, J. E., Hawkins, R. D., Wu, M., & Goodman, N. D. (2020). Pragmatic inference and visual abstraction enable contextual flexibility during visual communication. Computational Brain & Behavior, 3 , 86–101.

Fischer, F. E., & Beckey, R. D. (1990). Beginning kindergarteners’ perception of number. Perceptual and Motor Skills, 70 (2), 419–425.

Article   CAS   PubMed   Google Scholar  

Fischer, J. P., Sander, E., Sensevy, G., Vilette, B., & Richard, J. F. (2019). Can young students understand the mathematical concept of equality? A whole-year arithmetic teaching experiment in second grade. European Journal of Psychology of Education, 34 (2), 439–456.

Fourtassi, M., Rode, G., & Pisella, L. (2017). Using eye movements to explore mental representations of space. Annals of Physical and Rehabilitation Medicine, 60 (3), 160–163.

Freeman, N. H., & Janikoun, R. (1972). Intellectual realism in children’s drawings of a familiar object with distinctive features. Child Development, 1116–1121. https://doi.org/10.2307/1127668

Frege, G. (1984). The Foundations of Arithmetic  (J. Austin, Trans.) Northwestern University Press.

Fuhrman, O., & Boroditsky, L. (2010). Cross-cultural differences in mental representations of time: Evidence from an implicit nonlinguistic task. Cognitive Science, 34 (8), 1430–1451.

Gainotti, G., & Trojano, L. (2018). Constructional apraxia. Handbook of Clinical Neurology, 151 , 331–348.

Gamo, S., Sander, E., & Richard, J.-F. (2010). Transfer of strategy use by semantic recoding in arithmetic problem solving. Learning and Instruction, 20 (5), 400–410.

Geary, D. C. (2018). Growth of symbolic number knowledge accelerates after children understand cardinality. Cognition, 177 , 69–78.

Geary, D. C., vanMarle, K., Chu, F. W., Rouder, J., Hoard, M. K., & Nugent, L. (2018). Early conceptual understanding of cardinality predicts superior school-entry number-system knowledge. Psychological science, 29 (2), 191–205.

Goffin, C., & Ansari, D. (2016). Beyond magnitude: Judging ordinality of symbolic number is unrelated to magnitude comparison and independently relates to individual differences in arithmetic. Cognition, 150 , 68–76.

Gros, H., & Gvozdic, K. (2022). Context, content effects and flexibility. In E. Clément (Eds.), Cognitive Flexibility: The Cornerstone of Learning  (pp. 203–232). https://doi.org/10.1002/9781119902737.ch8

Gros, H., Sander, E., & Thibaut, J. P. (2019). When masters of abstraction run into a concrete wall: Experts failing arithmetic word problems. Psychonomic Bulletin & Review , https://doi.org/10.3758/s13423-019-01628-3 online first.

Gros, H., Sander, E., & Thibaut, J. P. (2020a). Are content effects out of sight? An eye-tracking study of arithmetic problem solving. In S. Denison., M. Mack, Y. Xu, & B. C. Armstrong (Eds.), Proceedings of the 42nd Annual Conference of the Cognitive Science Society . Cognitive Science Society.

Gros, H., Thibaut, J. P., & Sander, E. (2020b). Semantic congruence in arithmetic: A new conceptual model for word problem solving. Educational Psychologist, 55 (2), 69–87.

Gros, H., Thibaut, J. P., & Sander, E. (2021). What we count dictates how we count: A tale of two encodings. Cognition, 212 , 104665.

Gvozdic, K., & Sander, E. (2020). Learning to be an opportunistic word problem solver: Going beyond informal solving strategies. ZDM, 52 (1), 111–123.

Hebart, M. N., Zheng, C. Y., Pereira, F., & Baker, C. I. (2020). Revealing the multidimensional mental representations of natural objects underlying human similarity judgements. Nature Human Behaviour, 4 (11), 1173–1185.

Hegarty, M., & Kozhevnikov, M. (1999). Types of visual–spatial representations and mathematical problem solving. Journal of Educational Psychology, 91 (4), 684.

Hobson, S. M., Trundle, K. C., & Saçkes, M. (2010). Using a planetarium software program to promote conceptual change with young children. Journal of Science Education and Technology, 19 , 165–176.

Hudson, T. (1983). Correspondences and numerical differences between disjoint sets. Child Development, 54 (1), 84–90. https://doi.org/10.2307/112986

Hund, A. M., Kannass, K. N., Bove, R., Fairweather, L., Maydew, M., & Monla, A. (2021). Young children’s understanding of ordinal and spatial labels. Cognitive Development, 58 , 101041.

Iacono, E., Gros, H., & Clément, E. (2022). Training flexible categorization to improve arithmetic problem solving: A school-based intervention with 5th graders. In Culbertson, J., Perfors, A., Rabagliati, H. & Ramenzoni, V. (Eds.), Proceedings of the 44th Annual Conference of the Cognitive Science Society . Cognitive Science Society (Vol. 44).

Jitendra, A. K., & Hoff, K. (1996). The effects of schema-based instruction on the mathematical word-problem solving performance of students with learning disabilities. Journal of Learning Disabilities, 29 , 422–432.

Johnson-Laird, P. N. (2010). Mental models and human reasoning. Proceedings of the National Academy of Sciences, 107 (43), 18243–18250. https://doi.org/10.1073/pnas.1012933107

Kintsch, W., & Greeno, J. G. (1985). Understanding and solving word arithmetic problems. Psychological Review, 92 (1), 109.

Kosslyn, S. M., Murphy, G. L., Bemesderfer, M. E., & Feinstein, K. J. (1977). Category and continuum in mental comparisons. Journal of Experimental Psychology: General, 106 (4), 341.

Lakoff, G., & Núñez, R. E. (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. AMC, 10 (12), 720–733.

Landis, J. R., & Koch, G. G. (1977). The measurement of observer agreement for categorical data. Biometrics, 33 (1), 159–174. https://doi.org/10.2307/2529310

Larkin, J. H., & Simon, H. A. (1987). Why a diagram is (sometimes) worth ten thousand words. Cognitive Science, 11 , 65–99.

Le Corre, M., & Carey, S. (2007). One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition, 105 (2), 395–438.

Lenth, R. V., Buerkner, P., Herve, M., Love, J., Riebl, H., & Singmann, H. (2023). Emmeans: Estimated Marginal Means, Aka Least-Squares Means ; R Package Version 1.8.9; 2023.

Lewis-Peacock, J. A., Drysdale, A. T., & Postle, B. R. (2015). Neural evidence for the flexible control of mental representations. Cerebral Cortex, 25 (10), 3303–3313.

Long, B., Fan, J. E., & Frank, M. C. (2018). Drawings as a window into developmental changes in object representations. In Kalish, C., Rau, M., Zhu, J., & Rogers, T. T. (Eds.), Proceedings of the 40th Annual Conference of Cognitive Science Society (pp. 708–713). Madison, WI: Cognitive Science Society.

Makuuchi, M., Kaminaga, T., & Sugishita, M. (2003). Both parietal lobes are involved in drawing: a functional MRI study and implications for constructional apraxia. Cognitive Brain Research, 16 (3), 338–347.

Martin, S. A., & Bassok, M. (2005). Effects of semantic cues on mathematical modeling: Evidence from word-problem solving and equation construction tasks. Memory & Cognition, 33 , 471–478.

Meade, M. E., Wammes, J. D., & Fernandes, M. A. (2018). Drawing as an encoding tool: Memorial benefits in younger and older adults. Experimental Aging Research, 44 (5), 369–396.

Meyer, C., Barbiers, S., & Weerman, F. (2016). Order and Ordinality: The Acquisition of Cardinals and Ordinals in Dutch. Boston University Conference on Language Development (BUCLD) (40th ed.). Cascadilla.

Mikkilä-Erdmann, M., Södervik, I., Vilppu, H., Kääpä, P., & Olkinuora, E. (2012). First-year medical students’ conceptual understanding of and resistance to conceptual change concerning the central cardiovascular system. Instructional Science, 40 , 745–754.

Miller, S. E., Marcovitch, S., Boseovski, J. J., & Lewkowicz, D. J. (2015). Young children’s ability to use ordinal labels in a spatial search task. Merrill-Palmer Quarterly, 61 (3), 345–361.

Miller, K., Major, S. M., Shu, H., & Zhang, H. (2000). Ordinal knowledge: Number names and number concepts in Chinese and English. Canadian Journal of Experimental Psychology/Revue canadienne de psychologie expérimentale, 54 (2), 129.

Ng, S.-F., & Lee, K. (2005). How primary five pupils use the model method to solve word problems. The Mathematics Educator, 9 (1), 60–83.

Orrantia, J., & Múñez, D. (2013). Arithmetic word problem solving: evidence for a magnitude-based mental representation. Memory & Cognition, 41 , 98–108.

Pearson, J., & Kosslyn, S. M. (2015). The heterogeneity of mental representation: Ending the imagery debate. Proceedings of the National Academy of Sciences, 112 (33), 10089–10092.

Pinnegar, S., Mangelson, J., Reed, M., & Groves, S. (2011). Exploring preservice teachers’ metaphor plotlines. Teaching and Teacher Education, 27 (3), 639–647.

Reeve, R. A. (1996). The Referential Adequacy of Students’ Visual Analogies of Fractions. Mathematical Cognition, 2 (2), 137–169. https://doi.org/10.1080/135467996387507

Rellensmann, J., Schukajlow, S., & Leopold, C. (2017). Make a drawing. Effects of strategic knowledge, drawing accuracy, and type of drawing on students’ mathematical modelling performance. Educational Studies in Mathematics, 95 , 53–78.

Reusser, K. (1990). From text to situation to equation: Cognitive simulation of understanding and solving mathematical word problems. In H. Mandl, E. De Corte, N. Bennet, & H. F. Friedrich (Eds.), Learning and Instruction, European Research in an International Context (II). Pergamon Press.

Riley, M. S., Greeno, J. G., & Heller, J. 1. (1983). Development of children’s problem-solving ability in arithmetic. The Development of Mathematical Thinking (pp. 153–196). New York: Academic Press.

Roberts, B. R., & Wammes, J. D. (2021). Drawing and memory: Using visual production to alleviate concreteness effects. Psychonomic Bulletin & Review, 28 , 259–267.

Russell, B. (1919). Introduction to mathematical philosophy . Allen & Unwin.

Sarnecka, B. W., & Lee, M. D. (2009). Levels of number knowledge during early childhood. Journal of Experimental Child Psychology, 103 (3), 325–337.

Scheibling-Sève, C., Pasquinelli, E., & Sander, E. (2020). Assessing conceptual knowledge through solving arithmetic word problems. Educational Studies in Mathematics, 103 (3), 293–311.

Scheibling-Sève, C., Gvozdic, K., Pasquinelli, E., & Sander, E. (2022). Enhancing cognitive flexibility through a training based on multiple categorization: Developing proportional reasoning in primary school. Journal of Numerical Cognition, 8 (3), 443–472.

Schmeck, A., Mayer, R. E., Opfermann, M., Pfeiffer, V., & Leutner, D. (2014). Drawing pictures during learning from scientific text: Testing the generative drawing effect and the prognostic drawing effect. Contemporary Educational Psychology, 39 (4), 275–286.

Sharp, E., & Shih Dennis, M. (2017). Model drawing strategy for fraction word problem solving of fourth-grade students with learning disabilities. Remedial and Special Education, 38 (3), 181–192.

Shepard, R. N., & Metzler, J. (1971). Mental rotation of three-dimensional objects. Science, 171 (3972), 701–703.

Shulman, K. I. (2000). Clock-drawing: is it the ideal cognitive screening test? International Journal of Geriatric Psychiatry, 15 (6), 548–561.

Shusterman, A., Slusser, E., Halberda, J., & Odic, D. (2016) Acquisition of the cardinal principle coincides with improvement in approximate number system acuity in preschoolers. PLOS ONE, 11(4), e0153072. https://doi.org/10.1371/journal.pone.0153072

Silver, R. (2009). Identifying children and adolescents with depression: Review of the stimulus drawing task and draw a story research. Art Therapy, 26 (4), 174–180.

Suppes, P. (1972). Axiomatic set theory . Dover Publications.

Thevenot, C. (2010). Arithmetic word problem solving: Evidence for the construction of a mental model. Acta Psychologica, 133 (1), 90–95.

Thevenot, C., & Barrouillet, P. (2015). Arithmetic word problem solving and mental representations. In R. C. Kadosh & A. Dowker (Eds.), The Oxford handbook of numerical cognition (pp. 158–179).

Thevenot, C., & Oakhill, J. (2005). The strategic use of alternative representations in arithmetic word problem solving. The Quarterly Journal of Experimental Psychology Section A, 58 (7), 1311–1323.

Thevenot, C., & Oakhill, J. (2006). Representations and strategies for solving dynamic and static arithmetic word problems: The role of working memory capacities. European Journal of Cognitive Psychology, 18 (5), 756–775.

Thom, J. S., & McGarvey, L. M. (2015). The act and artifact of drawing (s): observing geometric thinking with, in, and through children’s drawings. ZDM, 47 , 465–481.

Thomas, G. V., & Jolley, R. P. (1998). Drawing conclusions: A re-examination of empirical and conceptual bases for psychological evaluation of children from their drawings. British Journal of Clinical Psychology, 37 (2), 127–139.

Trundle, K., Atwood, R., & Christopher, J. (2007). Fourth-grade elementary students’ conceptions of standards-based lunar concepts. International Journal of Science Education, 29 (5), 595–616.

Tunç-Pekkan, Z. (2015). An analysis of elementary school children’s fractional knowledge depicted with circle, rectangle, and number line representations. Educational Studies in Mathematics, 89 , 419–441.

Ucar, S., Trundle, K. C., & Krissek, L. (2011). Inquiry-based instruction with archived, online data: An intervention study with preservice teachers. Research in Science Education, 41 , 261–282.

Uesaka, Y., Manalo, E., & Ichikawa, S. I. (2010). The effects of perception of efficacy and diagram construction skills on students’ spontaneous use of diagrams when solving math word problems. Diagrams 2010, Portland, OR, USA, August 9-11, 2010 (pp. 197–211). Springer Berlin Heidelberg.

Van Essen, G. V., & Hamaker, C. (1990). Using self-generated drawings to solve arithmetic word problems. The Journal of Educational Research, 83 (6), 301–312.

Van Garderen, D., & Montague, M. (2003). Visual-spatial representation, mathematical problem solving, and students of varying abilities. Learning Disabilities Research & Practice, 18 (4), 246–254.

Van Meter, P., & Garner, J. (2005). The promise and practice of learner-generated drawing: Literature review and synthesis. Educational psychology review, 17 , 285–325.

Verschaffel, L. (2016). Get the picture? On the role of graphical representations in the solution of mathematical word problems. In  Plenary lecture at the Conference of the EARLI SIG 2, Comprehension of Text and Graphics, University of Geneva, Geneva, Switzerland .

Verschaffel, L., De Corte, E., & Vierstraete, H. (1999). Upper elementary school pupils’ difficulties in modeling and solving nonstandard additive word problems involving ordinal numbers. Journal for Research in Mathematics Education, 30 (3), 265–285.

Verschaffel, L., Schukajlow, S., Star, J., & Van Dooren, W. (2020). Word problems in mathematics education: A survey. ZDM, 52 , 1–16.

Vosniadou, S., & Brewer, W. F. (1992). Mental models of the earth: A study of conceptual change in childhood. Cognitive Psychology, 24 (4), 535–585.

Wammes, J. D., Meade, M. E., & Fernandes, M. A. (2016). The drawing effect: Evidence for reliable and robust memory benefits in free recall. Quarterly Journal of Experimental Psychology, 69 (9), 1752–1776.

Wammes, J. D., Meade, M. E., & Fernandes, M. A. (2017). Learning terms and definitions: Drawing and the role of elaborative encoding. Acta Psychologica, 179 , 104–113.

Wammes, J. D., Meade, M. E., & Fernandes, M. A. (2018). Creating a recollection-based memory through drawing. Journal of Experimental Psychology: Learning, Memory, and Cognition, 44 (5), 734.

PubMed   Google Scholar  

Wasner, M., Moeller, K., Fischer, M. H., & Nuerk, H. C. (2015). Related but not the same: Ordinality, cardinality and 1-to-1 correspondence in finger-based numerical representations. Journal of Cognitive Psychology, 27 (4), 426–441.

Wechsler, D. (2009). WMS-IV: Wechsler memory scale (4th ed.). Pearson.

Weinman, J., Petrie, K. J., Moss-Morris, R., & Horne, R. (1996). The illness perception questionnaire: a new method for assessing the cognitive representation of illness. Psychology and Health, 11 (3), 431–445.

Westenskow, A., Moyer-Packenham, P., Anderson-Pence, K., Shumway, J., & Jordan, K. (2014). Cute drawings? The disconnect between students’ pictorial representations and their mathematics responses to fraction questions. Revista Internacional de Pesquisa em Educação Matemática, 4 (1), 81–105.

Wu, S. P., & Rau, M. A. (2019). How students learn content in science, technology, engineering, and mathematics (STEM) through drawing activities. Educational Psychology Review, 31 , 87–120.

Wynn, K. (1992). Addition and subtraction by human infants. Nature, 358 (6389), 749–750.

Yoshida, H., & Shinmachi, Y. (1999). The influence of instructional intervention on children’s understanding of fractions. Japanese Psychological Research, 41 (4), 218–228.

Download references

This research was supported by grants from the Regional Council of Burgundy, Paris Feder Grants (20159201AAO050S02982 & 20169201AAO050S01845), the Experimental Fund for the Youth and French Ministry of Education (HAP10-CRE-EXPE-S1), and from the French Ministry of Education and Future Investment Plan (CS-032-15-836-ARITHM-0).

Author information

Authors and affiliations.

CY Cergy Paris University, Paragraphe Lab, Gennevilliers, France

Hippolyte Gros

Université de Bourgogne, LEAD-CNRS UMR 5022, Dijon, France

Jean-Pierre Thibaut

University of Geneva, IDEA Lab, Geneva, Switzerland

Emmanuel Sander

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Hippolyte Gros .

Ethics declarations

Conflicts of interest.

We have no conflicts of interest to disclose.

Ethics approval

This research was approved by the ethics committee of the University of Geneva (decision n° PSE.20181104.18).

Consent to participate

All participants gave informed consent to participate in the study.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Open Practices Statement

All data and materials for this study are available online on OSF at https://osf.io/nhp4e/?view_only=6a5e4fd4dedb4811a994030b988033a8 .

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (DOCX 2195 KB)

Rights and permissions.

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Gros, H., Thibaut, JP. & Sander, E. Uncovering the interplay between drawings, mental representations, and arithmetic problem-solving strategies in children and adults. Mem Cogn (2024). https://doi.org/10.3758/s13421-024-01523-w

Download citation

Accepted : 14 January 2024

Published : 12 February 2024

DOI : https://doi.org/10.3758/s13421-024-01523-w

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Context effects
• Mathematical cognition
• Mental models
• Problem solving
• Find a journal
• Publish with us
• Track your research

May 31, 2024

10 min read

Math Can Help Solve Social Justice Problems

Mathematicians are working on ways to use their field to tackle major social issues, such as social inequality and the need for gender equity

By Rachel Crowell & Nature magazine

MicroStockHub/Getty Images

When Carrie Diaz Eaton trained as a mathematician, they didn’t expect their career to involve social-justice research. Growing up in Providence, Rhode Island, Diaz Eaton first saw social justice in action when their father, who’s from Peru, helped other Spanish-speaking immigrants to settle in the United States.

But it would be decades before Diaz Eaton would forge a professional path to use their mathematical expertise to study social-justice issues. Eventually, after years of moving around for education and training, that journey brought them back to Providence, where they collaborated with the Woonasquatucket River Watershed Council on projects focused on preserving the local environment of the river’s drainage basin, and bolstering resources for the surrounding, often underserved communities.

By “thinking like a mathematician” and leaning on data analysis, data science and visualization skills, they found that their expertise was needed in surprising ways, says Diaz Eaton, who is now executive director of the Institute for a Racially Just, Inclusive, and Open STEM Education at Bates College in Lewiston, Maine.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

For example, the council identified a need to help local people to better connect with community resources. “Even though health care and education don’t seem to fall under the purview of a watershed council, these are all interrelated issues,” Diaz Eaton says. Air pollution can contribute to asthma attacks, for example. In one project, Diaz Eaton and their collaborators built a quiz to help community members to choose the right health-care option, depending on the nature of their illness or injury, immigration status and health-insurance coverage.

“One of the things that makes us mathematicians, is our skills in logic and the questioning of assumptions”, and creating that quiz “was an example of logic at play”, requiring a logic map of cases and all of the possible branches of decision-making to make an effective quiz, they say.

Maths might seem an unlikely bedfellow for social-justice research. But applying the rigour of the field is turning out to be a promising approach for identifying, and sometimes even implementing, fruitful solutions for social problems.

Mathematicians can experience first-hand the messiness and complexity — and satisfaction — of applying maths to problems that affect people and their communities. Trying to work out how to help people access much-needed resources, reduce violence in communities or boost gender equity requires different technical skills, ways of thinking and professional collaborations compared with breaking new ground in pure maths. Even for an applied mathematician like Diaz Eaton, transitioning to working on social-justice applications brings fresh challenges.

Mathematicians say that social-justice research is difficult yet fulfilling — these projects are worth taking on because of their tremendous potential for creating real-world solutions for people and the planet.

Data-driven research

Mathematicians are digging into issues that range from social inequality and health-care access to racial profiling and predictive policing. However, the scope of their research is limited by their access to the data, says Omayra Ortega, an applied mathematician and mathematical epidemiologist at Sonoma State University in Rohnert Park, California. “There has to be that measured information,” Ortega says.

Fortunately, data for social issues abound. “Our society is collecting data at a ridiculous pace,” Ortega notes. Her mathematical epidemiology work has examined which factors affect vaccine uptake in different communities. Her work has found, for example, that, in five years, a national rotavirus-vaccine programme in Egypt would reduce disease burden enough that the cost saving would offset 76% of the costs of the vaccine. “Whenever we’re talking about the distribution of resources, there’s that question of social justice: who gets the resources?” she says.

Lily Khadjavi’s journey with social-justice research began with an intriguing data set.

About 15 years ago, Khadjavi, a mathematician at Loyola Marymount University in Los Angeles, California, was “on the hunt for real-world data” for an undergraduate statistics class she was teaching. She wanted data that the students could crunch to “look at new information and pose their own questions”. She realized that Los Angeles Police Department (LAPD) traffic-stop data fit that description.

At that time, every time that LAPD officers stopped pedestrians or pulled over drivers, they were required to report stop data. Those data included “the perceived race or ethnicity of the person they had stopped”, Khadjavi notes.

When the students analysed the data, the results were memorable. “That was the first time I heard students do a computation absolutely correctly and then audibly gasp at their results,” she says. The data showed that one in every 5 or 6 police stops of Black male drivers resulted in a vehicle search — a rate that was more than triple the national average, which was about one out of every 20 stops for drivers of any race or ethnicity, says Khadjavi.

Her decision to incorporate that policing data into her class was a pivotal moment in Khadjavi’s career — it led to a key publication and years of building expertise in using maths to study racial profiling and police practice. She sits on California’s Racial Identity and Profiling Advisory Board , which makes policy recommendations to state and local agencies on how to eliminate racial profiling in law enforcement.

In 2023, she was awarded the Association for Women in Mathematics’ inaugural Mary & Alfie Gray Award for Social Justice, named after a mathematician couple who championed human rights and equity in maths and government.

Sometimes, gaining access to data is a matter of networking. One of Khadjavi’s colleagues shared Khadjavi’s pivotal article with specialists at the American Civil Liberties Union. In turn, these specialists shared key data obtained through public-records requests with Khadjavi and her colleague. “Getting access to that data really changed what we could analyse,” Khadjavi says. “[It] allowed us to shine a light on the experiences of civilians and police in hundreds of thousands of stops made every year in Los Angeles.”

The data-intensive nature of this research can be an adjustment for some mathematicians, requiring them to develop new skills and approach problems differently. Such was the case for Tian An Wong, a mathematician at the University of Michigan-Dearborn who trained in number theory and representation theory.

In 2020, Wong wanted to know more about the controversial issue of mathematicians collaborating with the police, which involves, in many cases, using mathematical modelling and data analysis to support policing activities. Some mathematicians were protesting about the practice as part of a larger wave of protests around systemic racism , following the killing of George Floyd by police in Minneapolis, Minnesota. Wong’s research led them to a technique called predictive policing, which Wong describes as “the use of historical crime and other data to predict where future crime will occur, and [to] allocate policing resources based on those predictions”.

Wong wanted to know whether the tactics that mathematicians use to support police work could instead be used to critique it. But first, they needed to gain some additional statistics and data analysis skills. To do so, Wong took an online introductory statistics course, re-familiarized themself with the Python programming language, and connected with colleagues trained in statistical methods. They also got used to reading research papers across several disciplines.

Currently, Wong applies those skills to investigating the policing effectiveness of a technology that automatically locates gunshots by sound. That technology has been deployed in parts of Detroit, Michigan, where community members and organizations have raised concerns about its multimillion-dollar cost and about whether such police surveillance makes a difference to public safety.

Getting the lay of the land

For some mathematicians, social-justice work is a natural extension of their career trajectories. “My choice of mathematical epidemiology was also partially born out of out of my love for social justice,” Ortega says. Mathematical epidemiologists apply maths to study disease occurrence in specific populations and how to mitigate disease spread. When Ortega’s PhD adviser mentioned that she could study the uptake of a then-new rotovirus vaccine in the mid-2000s, she was hooked.

Mathematicians, who decide to jump into studying social-justice issues anew, must do their homework and dedicate time to consider how best to collaborate with colleagues of diverse backgrounds.

Jonathan Dawes, an applied mathematician at the University of Bath, UK, investigates links between the United Nations’ Sustainable Development Goals (SDGs) and their associated target actions. Adopted in 2015, the SDGs are “a universal call to action to end poverty, protect the planet, and ensure that by 2030 all people enjoy peace and prosperity,” according to the United Nations , and each one has a number of targets.

“As a global agenda, it’s an invitation to everybody to get involved,” says Dawes. From a mathematical perspective, analysing connections in the complex system of SDGs “is a nice level of problem,” Dawes says. “You’ve got 17 Sustainable Development Goals. Between them, they have 169 targets. [That’s] an amount of data that isn’t very large in big-data terms, but just big enough that it’s quite hard to hold all of it in your head.”

Dawes’ interest in the SDGs was piqued when he read a 2015 review that focused on how making progress on individual goals could affect progress on the entire set. For instance, if progress is made on the goal to end poverty how does that affect progress on the goal to achieve quality education for all, as well as the other 15 SDGs?

“If there’s a network and you can put some numbers on the strengths and signs of the edges, then you’ve got a mathematized version of the problem,” Dawes says. Some of his results describe how the properties of the network change if one or more of the links is perturbed, much like an ecological food web. His work aims to identify hierarchies in the SDG networks, pinpointing which SDGs should be prioritized for the health of the entire system.

As Dawes dug into the SDGs, he realized that he needed to expand what he was reading to include different journals, including publications that were “written in very different ways”. That involved “trying to learn a new language”, he explains. He also kept up to date with the output of researchers and organizations doing important SDG-related work, such as the International Institute for Applied Systems Analysis in Laxenburg, Austria, and the Stockholm Environment Institute.

Dawes’ research showed that interactions between the SDGs mean that “there are lots of positive reinforcing effects between poverty, hunger, health care, education, gender equity and so on.” So, “it’s possible to lift all of those up” when progress is made on even one of the goals. With one exception: managing and protecting the oceans. Making progress on some of the other SDGs could, in some cases, stall progress for, or even harm, life below water.

Collaboration care

Because social-justice projects are often inherently cross-disciplinary, mathematicians studying social justice say it’s key in those cases to work with community leaders, activists or community members affected by the issues.

Getting acquainted with these stakeholders might not always feel comfortable or natural. For instance, when Dawes started his SDG research, he realized that he was entering a field in which researchers already knew each other, followed each other’s work and had decades of experience. “There’s a sense of being like an uninvited guest at a party,” Dawes says. He became more comfortable after talking with other researchers, who showed a genuine interest in what he brought to the discussion, and when his work was accepted by the field’s journals. Over time, he realized “the interdisciplinary space was big enough for all of us to contribute to”.

Even when mathematicians have been invited to join a team of social-justice researchers, they still must take care, because first impressions can set the tone.

Michael Small is an applied mathematician and director of the Data Institute at the University of Western Australia in Perth. For much of his career, Small focused on the behaviour of complex systems, or those with many simple interacting parts, and dynamical systems theory, which addresses physical and mechanical problems.

But when a former vice-chancellor at the university asked him whether he would meet with a group of psychiatrists and psychologists to discuss their research on mental health and suicide in young people, it transformed his research. After considering the potential social impact of better understanding the causes and risks of suicide in teenagers and younger children, and thinking about how the problem meshed well with his research in complex systems and ‘non-linear dynamics’, Small agreed to collaborate with the group.

The project has required Small to see beyond the numbers. For the children’s families, the young people are much more than a single data point. “If I go into the room [of mental-health professionals] just talking about mathematics, mathematics, mathematics, and how this is good because we can prove this really cool theorem, then I’m sure I will get push back,” he says. Instead, he notes, it’s important to be open to insights and potential solutions from other fields. Listening before talking can go a long way.

Small’s collaborative mindset has led him to other mental-health projects, such as the Transforming Indigenous Mental Health and Wellbeing project to establish culturally sensitive mental-health support for Indigenous Australians.

Career considerations

Mathematicians who engage in social-justice projects say that helping to create real-world change can be tremendously gratifying. Small wants “to work on problems that I think can do good” in the world. Spending time pursuing them “makes sense both as a technical challenge [and] as a social choice”, he says.

However, pursuing this line of maths research is not without career hurdles. “It can be very difficult to get [these kinds of] results published,” Small says. Although his university supports, and encourages, his mental-health research, most of his publications are related to his standard mathematics research. As such, he sees “a need for balance” between the two lines of research, because a paucity of publications can be a career deal breaker.

Diaz Eaton says that mathematicians pursuing social-justice research could experience varying degrees of support from their universities. “I’ve seen places where the work is supported, but it doesn’t count for tenure [or] it won’t help you on the job market,” they say.

Finding out whether social-justice research will be supported “is about having some really open and transparent conversations. Are the people who are going to write your recommendation letters going to see that work as scholarship?” Diaz Eaton notes.

All things considered, mathematicians should not feel daunted by wading into solving the world’s messy problems, Khadjavi says: “I would like people to follow their passions. It’s okay to start small.”

This article is reproduced with permission and was first published on May 22, 2024 .

Top 10 Challenges to Teaching Math and Science Using Real Problems

• Share article

Nine in ten educators believe that using a problem-solving approach to teaching math and science can be motivating for students, according to an EdWeek Research Center survey.

But that doesn’t mean it’s easy.

Teachers perceive lack of time as a big hurdle. In fact, a third of educators—35 percent—worry that teaching math or science through real-world problems—rather than focusing on procedures—eats up too many precious instructional minutes.

Other challenges: About another third of educators said they weren’t given sufficient professional development in how to teach using a real-world problem-solving approach. Nearly a third say reading and writing take priority over STEM, leaving little bandwidth for this kind of instruction. About a quarter say that it’s tough to find instructional materials that embrace a problem-solving perspective.

Nearly one in five cited teachers’ lack of confidence in their own problem solving, the belief that this approach isn’t compatible with standardized tests, low parent support, and the belief that student behavior is so poor that this approach would not be feasible.

The nationally representative survey included 1,183 district leaders, school leaders, and teachers, and was conducted from March 27 to April 14. (Note: The chart below lists 11 challenges because the last two on the list—dealing with teacher preparation and student behavior—received the exact percentage of responses.)

Trying to incorporate a problem-solving approach to tackling math can require rethinking long-held beliefs about how students learn, said Elham Kazemi, a professor in the teacher education program at the University of Washington.

Most teachers were taught math using a procedural perspective when they were in school. While Kazemi believes that approach has merit, she advocates for exposing students to both types of instruction.

Many educators have “grown up around a particular model of thinking of teaching and learning as the teacher in the front of the room, imparting knowledge, showing kids how to do things,” Kazemi said.

To be sure, some teachers have figured out how to incorporate some real-world problem solving alongside more traditional methods. But it can be tough for their colleagues to learn from them because “teachers don’t have a lot of time to collaborate with one another and see each other teach,” Kazemi said.

What’s more, there are limited instructional materials emphasizing problem solving, Kazemi said.

Though that’s changing, many of the resources available have “reinforced the idea that the teacher demonstrates solutions for kids,” Kazemi said.

Molly Daley, a regional math coordinator for Education Service District 112, which serves about 30 districts near Vancouver, Wash., has heard teachers raise concerns that teaching math from a problem-solving perspective takes too long—particularly given the pressure to get through all the material students will need to perform well on state tests.

Daley believes, however, that being taught to think about math in a deeper way will help students tackle math questions on state assessments that may look different from what they’ve seen before.

“It’s myth that it’s possible to cover everything that will be on the test,” as it will appear, she said. “There’s actually no way to make sure that kids have seen every single possible thing the way it will show up. That’s kind of a losing proposition.”

But rushing through the material in a purely procedural way may actually be counterproductive, she said.

Teachers don’t want kids to “sit down at the test and say, ‘I haven’t seen this and therefore I can’t do it,’” Daley said. “I think a lot of times teachers can unintentionally foster that because they’re so urgently trying to cover everything. That’s where the kind of mindless [teaching] approaches come in.”

Teachers may think to themselves: “’OK, I’m gonna make this as simple as possible, make sure everyone knows how to follow the steps and then when they see it, they can follow it,” Daley said.

But that strategy might “take away their students’ confidence that they can figure out what to do when they don’t know what to do, which is really what you want them to be thinking when they go to approach a test,” Daley said.

Data analysis for this article was provided by the EdWeek Research Center. Learn more about the center’s work.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

Start your studies in Spanish and finish in English

• Academic Catalog
• Faculty Achievements
• Library & Tutoring
• Official Transcript
• Student Login
• Student Account
• Request Info
• Why St. Augustine?
• Academic Calendar
• Accreditations
• College Directory

• Our Approach
• Adult Education
• All Programs
• Student Achievement
• HLC Accreditation

School of STEAM

• Business Administration
• Business Management
• Computer Information Systems
• Culinary Arts
• Hospitality Management

School of Education

• Criminal Justice
• Child Development
• Early Childhood Education
• Liberal Arts and Humanities

School of Healthcare and Social Science

• Respiratory Therapy
• Social Work
• Office of Academic Effectiveness
• Request More Info
• Transfer Students
• International Students
• Undocumented & DACA Students
• Student Success Center
• Affordable for All
• Tuition + Fees
• Financial Aid

• Success Stories
• 2022 Clery Report

The Cognitive Benefits of Being Bilingual

May 30, 2024

In our globalized world, the benefits of being bilingual extend far beyond mere communication. While speaking more than one language opens doors to different cultures and communities, it also has profound effects on cognitive abilities. Let’s explore the cognitive benefits of being bilingual backed by scientific research.

Enhanced Problem-Solving Abilities

One of the cognitive benefits of being bilingual is improved problem-solving skills. Multiple studies have shown that bilingual individuals excel in tasks that require problem-solving, creativity, and pattern recognition. The constant practice of switching between languages enhances cognitive flexibility, making it easier to approach problems from different angles and develop innovative solutions. Studies have shown that bilingual people better understand math concepts and word problems when compared to their non-bilingual peers. 

Improved Memory and Multitasking

Improved memory and the ability to multitask are key advantages of being bilingual . Research indicates bilingual individuals often have better working memory than their monolingual peers. This is because managing two languages requires the brain to store and retrieve information more efficiently, strengthening overall memory capacity. 

Enhanced memory also contributes to better academic performance and daily task management. Ellen Bialystok highlights how bilinguals show improved focus, memory, and decision-making abilities​​ in her book ​​ Bilingualism in Development: Language, Literacy, and Cognition . This translates to the ability to multitask effectively as bilingual people frequently switch between languages, which trains the brain to handle multiple tasks simultaneously. 

Greater Attention and Focus

Another advantage of being bilingual is a tendency to exhibit more attention and focus. The brain’s ability to manage two languages enhances selective attention, enabling bilinguals to concentrate better and filter out distractions. Research shows that bilinguals are better at blocking out irrelevant information, even as early as seven months. This improved focus is particularly beneficial in environments that demand sustained attention and quick decision-making. 

Delayed Cognitive Decline and Increased Cognitive Reserve

One of the most significant cognitive benefits of bilingualism is its protective effect against cognitive decline. Research has demonstrated that bilingualism can delay the onset of dementia and Alzheimer’s disease by several years. The mental workout involved in using two languages keeps the brain active and engaged, which helps maintain cognitive functions longer. Bilingualism also contributes to increased cognitive reserve, which is the brain’s ability to improvise and find alternative ways of functioning when faced with challenges. This resilience is crucial for maintaining cognitive health and adapting to new situations or unexpected changes.

Enhanced Executive Function and Mental Agility

Executive function refers to the mental processes that allow us to plan, focus attention, remember instructions, and manage multiple tasks. Bilingual people often show enhanced executive function, as the brain’s need to manage two language systems requires greater planning and organizational skills. This translates into better decision-making and problem-solving abilities in everyday life. 

Additionally, being bilingual enhances mental agility, allowing individuals to switch between tasks and ideas more fluidly. This agility is beneficial in adapting to new environments and learning new skills​​ which is highly valued in the workforce, where the ability to adapt and multitask can lead to greater career opportunities. Check out our blog to learn more about the career benefits of being bilingual .

Unlock Your Potential

The benefits of being bilingual are profound and make a compelling case for learning and maintaining proficiency in multiple languages. It is never too late to learn, if you’re interested in improving your ability to speak English, check out our free ESL classes at St. Augustine College . Those who complete the ESL program at St.Augustine can enroll in a free college-level course offered in an ESL format to start their path toward numerous different career fields. Contact us to learn how you can start your journey today.

Take The Next Step

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson